Molecular dynamics simulations of nonpolarizable inorganic salt solution interfaces: NaCl, NaBr, and NaI in transferable intermolecular potential 4-point with charge dependent polarizability (TIP4P-QDP) water

Abstract

We present molecular dynamics simulations of the liquid-vapor interface of 1M salt solutions of nonpolarizable NaCl, NaBr, and NaI in polarizable transferable intermolecular potential 4-point with charge dependent polarizability water [B. A. Bauer , J. Chem. Theory Comput. 5, 359 (2009)]; this water model accommodates increased solvent polarizability (relative to the condensed phase) in the interfacial and vapor regions. We employ fixed-charge ion models developed in conjunction with the TIP4P-QDP water model to reproduce ab initio ion-water binding energies and ion-water distances for isolated ion-water pairs. The transferability of these ion models to the condensed phase was validated with hydration free energies computed using thermodynamic integration (TI) and appropriate energy corrections. Density profiles of Cl⁻, Br⁻, and I⁻ exhibit charge layering in the interfacial region; anions and cation interfacial probabilities show marked localization, with the anions penetrating further toward the vapor than the cations. Importantly, in none of the cases studied do anions favor the outermost regions of the interface; there is always an aqueous region between the anions and vapor phase. Observed interfacial charge layering is independent of the strength of anion-cation interactions as manifest in anion-cation contact ion pair peaks and solvent separated ion pair peaks; by artificially modulating the strength of anion-cation interactions (independent of their interactions with solvent), we find little dependence on charge layering particularly for the larger iodide anion. The present results reiterate the widely held view of the importance of solvent and ion polarizability in mediating specific anion surface segregation effects. Moreover, due to the higher parametrized polarizability of the TIP4P-QDP condensed phase {1.31 ų for TIP4P-QDP versus 1.1 ų (TIP4P-FQ) and 0.87 ų (POL3) [Ponder and Case, Adv. Protein Chem. 66, 27 (2003)]} based on ab initio calculations of the condensed-phase polarizability reduction in liquid water, the present simulations highlight the role of water polarizability in inducing water molecular dipole moments parallel to the interface normal (and within the interfacial region) so as to favorably oppose the macrodipole generated by the separation of anion and cation charge. Since the TIP4P-QDP water polarizability approaches that of the experimental vapor phase value for water, the present results suggest a fundamental role of solvent polarizability in accommodating the large spatial dipole generated by the separation of ion charges. The present results draw further attention to the question of what exact value of condensed phase water polarizability to incorporate in classical polarizable water force fields.

INTRODUCTION

Aqueous salt solution interfaces are central to various physicochemical processes, their properties having implications ranging from biology to the environment.^{1, 2, 3, 4, 5, 6, 7, 8, 9} Regarding the latter, concerns of the release of reactive ozone-attacking halogens into the atmosphere from sea-salt aerosols also necessitate a deeper understanding of aqueous salt solution interfaces.^{5, 6, 7, 8, 9}

Despite over a century’s worth of research, there are still conflicting views as to the presence of ions at the aqueous liquid-vapor interface. The classical view of aqueous salt solution interfaces utilizes Gibbs’ isotherm equation¹⁰ and the higher surface tension of aqueous salt solutions relative to pure water to describe an interface devoid of ions.^{11, 12, 13} In the 1990s, however, experimentalists suggested ion presence in the interface for NaI and NaBr solutions to account for measured uptake coefficients of diatomic iodine and bromine gases.⁶ Molecular dynamics (MD) simulations in which ion polarizability was explicitly considered provided theoretical support for the presence of Cl⁻, Br⁻, and I⁻ on the surface of water clusters;^{14, 15} these observations were later extended to the interface of bulk solutions.¹⁶

Studies of aqueous salt solution interfaces have continued throughout the past decade using molecular simulation^{8, 11, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29} and experimental methods.^{8, 22, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42} Nonlinear optical techniques such as second harmonic generation^{32, 33, 34, 35} and sum frequency generation^{36, 37, 38, 39, 40, 41, 42} directly probe molecules and ions at interfaces (approximately 1 nm depths) and provide a picture of distorted hydrogen bonding networks (relative to neat water) in interfacial systems containing highly polarizable ions such as Br⁻ and I⁻.⁴² Novel x-ray photoelectron spectroscopy (XPS) measurements support the presence of these polarizable inorganic ions in the interface. Ghosal et al.⁴³ applied XPS techniques to examine the relative anion∕cation concentration ratios at different inelastic mean free paths of the ejected core electron for droplets of KI and KBr solutions. The study showed higher ratios of I⁻∕cation than Br⁻∕cation for both probing depths examined, IMFP=5 Å and IMFP=10 Å. MD simulations using polarizable ions in a polarizable aqueous solvent also suggest the enhancement in the Cl⁻, Br⁻, and I⁻ ions in the interface.^{11, 16, 17, 28} Simulations employing nonpolarizable halide ions in polarizable TIP4P-FQ water, however, tend to show a depletion of ions in the interface, although nonpolarizable I⁻ shows moderate surface enhancement, attributable to the size of the anion as well as the hydration properties of the ion in TIP4P-FQ water model.¹⁷ Warren et al.¹⁷ observed the enhancement in anions at the aqueous liquid-vapor interface upon inclusion of explicit ion polarizability (Drude oscillator ion force fields).¹⁷ Furthermore, for nonpolarizable ions in polarizable TIP4P-FQ water, the authors observe charge layering of cations and anions (to varying degrees depending on the salt studied), though in all cases including nonpolarizable iodide (Fig. 8, left panels, in Ref. 17), no significant anion density is observed above the Gibbs dividing surface (GDS); this contrasts with the behavior observed for Drude polarizable ions that exhibit enhanced density well beyond the GDS in all cases studied (Fig. 8, right panels, in Ref. 17). This behavior was first reported for the various combinations of polarizable∕nonpolarizable water∕ion models by Vrbka and co-workers.¹⁶

From experiment and theory, major factors known to affect ion surface presence are anion size, anion polarizability, and solvent polarizability.^{11, 15, 16, 20, 21, 23, 26, 44, 45, 46, 47, 48} Although polarizable water and ion force fields have proven indispensable for the study of aqueous salt solution interfaces, an outstanding question remains regarding the appropriate value of condensed phase water polarizability to be used in developing classical polarizable water models; this is relevant in terms of assessing the relative importance of water and cation∕anion polarizability in defining interfacial behaviors∕properties since the fundamental electrostatic determinants governing specific ion effects arise from the interplay between water and ion polarizability (excluding for the moment issues related to ion size). One can easily imagine that assigning an extreme value of the polarizability to either component (water and∕or ion) can reweight the relative influence of that specie’s polarizability to specific ion effects at the interface unless a systematically balanced fitting protocol is applied. This of course requires a definition of the amount of reduction of water and ion polarizability in condensed-phase environments.

There is growing consensus that the condensed phase molecular polarizability of water (and other polar hydrogen bonding fluids) is lower than that of the isolated vapor-phase molecule; the exact extent of reduction, however, remains unclear.^{49, 50, 51} Generally accepted reductions fall either in the range of 7%–10% or 30%. Using the Hirshfeld partitioning scheme and density functional theory calculations, Krishtal et al.⁵⁰ explored the dependence of polarizability on water cluster size. They reported that the intrinsic molecular polarizability decreases with increasing cluster size, converging to a bulklike value in the limit of a significantly large cluster (n_H2O=20). Furthermore, their analysis of the hydrogen bond interactions within the cluster demonstrates that water molecules with more hydrogen bonds also feature a decreased intrinsic polarizability. This effect is most pronounced for water molecules acting as electron donors in which one or both lone pairs are engaged in hydrogen bonding.

A recent study by Schropp and Tavan⁵¹ has provided further support for a lower effective dipole polarizability for liquid water. The authors demonstrated that the reduction arises from inhomogeneity of the average electric field within the molecular volume of the water molecule. This study concludes that an effective scaling of 0.68 for the condensed phase polarizability is warranted, in surprising agreement with the empirical values employed by Lamoureux and Roux¹⁹ in their water models. Schropp and Tavan further argued that these inhomogeneous fields completely describe the reduction in polarizability.

Presently, we study interfacial structure and electrostatics of sodium salts of Cl⁻, Br⁻, and I⁻ using nonpolarizable ion models and a recently developed water model, transferable intermolecular potential 4-point with charge dependent polarizability (TIP4P-QDP).⁵² This water model possesses a condensed phase molecular polarizability reduced by 7% from its gas-phase value, and self-consistently modulates this property in response to local environment. This dynamically varies single-molecule polarizability from the bulk liquid through the interface into the vapor region. Furthermore, this water model possesses perhaps the highest condensed phase polarizability of all existing polarizable water models, while falling within theoretical bounds for the expected condensed-phase reduction.

Although the TIP4P-QDP water model possesses the ability to modulate the molecular polarizability of water from gas- to condensed-phase values, we do not consider isolating the effects of this behavior in the current study. This is largely due to the requirement of developing an equivalent static polarizability water model to which one can compare the results of the current phase-dependent polarizable model. Thus, we consider the implications of enhanced water polarizability on interfacial properties of aqueous inorganic salt solutions. By employing non-polarizable ion force fields in conjunction with a polarizable solvent model, we isolate the effects of solvent polarizability on interfacial behavior of ionic species. By employing a solvent model with a gas-phase polarizability (or near that value in the interfacial region), we characterize the effects of solvent polarizability in a limiting case, i.e., that in which the solvent model possesses the vacuum polarizability.

Section 2 discusses the charge equilibration (CHEQ) formalism for incorporating polarization in MD simulations (Sec. 2A) and the introduction of phase dependence to polarizability (Sec. 2B). The parameterization of the ions and the details of the MD simulations are presented in Secs. 2C, 2D, respectively. Results from condensed-phase and interfacial simulations are discussed in Sec. 3. We conclude in Sec. 4 with a summary of findings and implications for future studies.

COMPUTATIONAL METHODS AND FORCE FIELDS

CHEQ force fields

The CHEQ formalism offers one convenient route for incorporating local chemical environmental dependence of the molecular polarizability. This formalism is based on Sanderson’s idea of electronegativity equilibration,⁵³ which states that the polarization of the electronic density (modeled as a distribution of partial charges in a classical representation) is effected by the redistribution of charge density within the molecule in order to equalize the instantaneous electrostatic chemical potential in the presence of external electric fields arising from the surrounding molecules. The directionality and ease of charge redistribution are determined by parametrized physical properties of individual atoms. Interested readers are referred to the literature for additional information on CHEQ methods.^{53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64}

The CHEQ electrostatic energy of an N-atom molecule in the absence of an external electric field, each atom carrying partial charge Q_i, is

$$E\left(Q\right)=\sum _{i=1}^N\left({\chi }_i{Q}_i+\frac{1}{2}{\eta }_i{Q}_i^2\right)+\sum _{i<j}^N{Q}_i{Q}_j{J}_{ij}+\lambda \left(\sum _{i=1}^N{Q}_i-Q_{\text{total}}\right),$$ (1)

where the χ_i’s are atom electronegativities and the η_i’s are atomic hardnessess. The J_ij terms represent the interatomic hardness terms for each pair of atoms i and j within a molecule. Intermolecular atom-pair electrostatic interactions are treated with a standard Coulomb form. The last term in Eq. 1 describes a molecular charge constraint applied to the entire molecule and enforced via the Lagrange multiplier λ.

Phase-dependent polarizable model

While polarizable water force fields allow charge redistribution and thus inducible molecular dipole moments in classical simulations, they neglect the variation in molecular polarizability with phase. Numerous studies have demonstrated the difference in molecular polarizability between molecules in the gas and condensed phases.^{49, 50, 51} The TIP4P-QDP model of Bauer et al.⁵² introduces phase-dependent polarizability into a classical simulation. The electrostatic component of the Hamiltonian is modified such that the η and χ parameters are functions of the M-site (lone-pair site) charge,⁵⁴

$$E\left(Q\right)=\sum _{i=1}^N{\chi }_i\left(Q_M\right)Q_i+\frac{1}{2}\sum _{i=1}^N{\eta }_i\left(Q_M\right)Q_i^2+\sum _{i<j}^N{J}_{ij}\left(Q_M\right)Q_i{Q}_j+\lambda \left(\sum _{i=1}^N{Q}_i-Q_{\text{total}}\right).$$ (2)

The Q_M-dependence of each term is implemented via a scaling function g(Q_M) that monotonically modulates the hardnesses (vis-à-vis molecular polarizability) and electronegativities (vis-à-vis molecular dipole moment) from the gas-phase value to a lower condensed phase value. The result is a polarizability distribution in the condensed phase (centered about α=1.31 ų), which is a 6.5% reduction from the gas-phase value, in good agreement with ab initio estimates.⁴⁹ We direct interested readers to Ref. 52 for a more detailed discussion of the TIP4P-QDP model.

Since the TIP4P-QDP model was initially parameterized by adjusting water-water interactions to reproduce a range of vapor and pure water properties, the combination of the water model with charged ions resulted in undesirable overpolarization. To reduce such effects, the water oxygen atom Lennard-Jones radius was slightly increased (i.e., the R_min parameter was increased from 3.550 to 3.552 Å). This leads to minor changes in the pure water properties. The density and enthalpy of vaporization of the adjusted water model are 0.992(±0.001) g∕cm³ and 10.48(±0.01) kcal∕mol, slightly lower than the original predictions of 0.995 g∕cm³ and 10.51 kcal∕mol, respectively. We characterize additional bulk and vapor properties calculated using the current modified model in the supporting information (SI).⁶⁵ For most properties there are trivial differences between the two parameterizations; furthermore, pure TIP4P-QDP interfacial properties and radial distribution functions (RDFs) presented in this study show little deviation from those of the original model.

Parameterization

The ions Na⁺, Cl⁻, Br⁻, and I⁻ were each parameterized to reproduce the dimerization energy with a single water molecule and the gas-phase ion-oxygen distance. The details of the TIP4P-QDP parameterization were previously discussed,⁵² with a slight adjustment of water-water nonbond parameters as discussed above. Target values for parameterization of the ions were taken from ab initio results at the Møller-Plesset second-order perturbation (MP2) level of theory.^{66, 67} The parameterized Lennard-Jones (LJ) terms are presented in Table 1 along with the gas-phase ion-water energy and ion-oxygen distance.

Table 1.

Nonbond parameters for describing the interactions of ions in TIP4P-QDP water. R_min is radius at minimum potential in units of angstrom. ϵ is the well depth in units of kcal∕mol. U is the ion-water binding energy is units of kcal∕mol, and R is the ion-oxygen distance in angstrom. Target values are based on previously reported ab initio values at the MP2∕6-311++G^** level (for anions) (Ref. ⁶⁷) and MP2∕TZ2P level with BSSE correction (for sodium) (Ref. ⁶⁶).

Ion	LJ parameters		Parametrized		Target
	Rmin∕2	ϵ	−U	R	−U	R
Na+	1.347	0.0311	23.4	2.225	23.7	2.228
Cl−	2.821	0.0114	17.3	3.061	14.4±1.2	3.108
Br−	2.842	0.0574	13.0	3.380	12.7±0.9	3.316
I−	2.917	0.1569	10.7	3.647	10.6±0.6	3.632

The parameterized dimerization energies are generally in good agreement with the ab initio targets (1.5 kcal∕mol rms error), with all ions except Cl⁻ falling within the uncertainty of the target values. The ion-oxygen distances exhibit good agreement with the target distances (0.04 Å rms error relative to the ab initio data^{66, 67}).

Finally, the difficulty in simultaneously reproducingab initio dimerization energies and ion-oxygen distances, particularly for Cl⁻, is largely due to the anisotropic polarizability of the TIP4P-QDP water model (and fundamentally that of the TIP4P-FQ water model). In order to reproduce the isotropic molecular polarizability, the TIP4P-QDP and TIP4P-FQ water models compensate for the null out-of-plane polarizability with enhanced in-plane components (i.e., along the O–H bond vector). This leads to strong polarization of the water at short ion-water distances. For smaller anions the interaction energies at geometries close to the target ab initio values are quite favorable; however, this is not problematic since the ion hydration free energetics can be well reproduced to match experimentally-derived single ion solvation free energy values as discussed in the SI.⁶⁵

Simulation details

MD simulations were performed using CHARMM (Refs. ^{68, 69}) with custom modifications for the TIP4P-QDP model. Constant NVT (T=298 K) simulations of aqueous salt solution liquid-vapor interfaces consisted of 988 TIP4P-QDP water molecules and 18 sodium-halide anion pairs (≈1 M solutions). The simulation cell was 24 Å in the x and y directions and 100 Å in the z direction. Electrostatic interactions were treated using particle mesh Ewald (PME) (Ref. ⁷⁰) with 30 grid points in the x and y dimensions, 128 grid points in the z dimension, and κ=0.33. A 0.5 fs timestep is used for propagating the classical equations of motion using a Verlet leap-frog integrator. Fictitious charge degrees of freedom were assigned masses of 0.000 069 kcal∕mol∕ps². A Nosé–Hoover⁷¹ thermostat with mass of 0.005 kcal∕mol∕ps² maintains electronic temperature at 1 K. To further prevent spurious overpolarization of water charges arising from local density fluctuations in the condensed phase, charges on water molecules experience an additional harmonic restoring potential upon reaching a limiting value. The upper and lower limiting charge values are −0.6e and −1.6e for oxygen and 1.2e and 0.3e for hydrogen. These charge limits represent extremes for the atoms, ensuring that the harmonic restoring force is only applied to prevent undesired overpolarization. The harmonic restraint was assigned a force constant of 200.0 kcal∕mol∕esu² for each atom. From distributions of charges generated from simulation trajectories, we confirmed that this potential is seldom activated. The interfacial data presented are based on 100 ns of data accumulated for all salt solutions. Results of condensed-phase simulations are based on 10 ns of constant-NPT simulations of 988 TIP4P-QDP water molecules and 18 sodium-halide anion pairs in a cubic simulation cell with periodic boundary conditions in each direction using PME with 48 grid points in each dimension; all other simulation details are the same as those for interface simulations.

RESULTS

Condensed-phase simulations

Condensed-phase densities

The densities of each salt solution (Table 2) were computed from the average volume from NPT simulations and the mass of ions and water present in the system. In qualitative agreement with experiment, computed densities exhibit an increasing trend with ρ_NaCl<ρ_NaBr<ρ_NaI. Densities are underestimated by 1.1%, 1.7%, and 1.8% for NaCl, NaBr, and NaI, respectively. The slightly lower densities of the salt solutions can be attributed, in part, to the slightly reduced density (about 0.5%) of the pure TIP4P-QDP solvent. All salt solution densities are under 2% error, which is the typical error for reproducing condensed phase densities for small molecules encountered with modern empirical additive and nonadditive force fields. Since we did not explicitly parameterize the salts in an effort to reproduce the solution densities, the accuracy in predicted densities is satisfying.

Table 2.

Bulk densities, surface excesses, and surface tensions calculated for each 1.0M salt solution.

Salt model	ρbulk (g∕cm3)	ρbulk (g∕cm3), experiment	Γion (nm−2)	γ (dyn∕cm)
TIP4P-QDP	0.992(1)	0.997a	0.006(7)	71(2)
NaCl	1.026(1)	1.037b	−0.090(8)	71(2)
NaBr	1.055(1)	1.073c	−0.046(51)	70(2)
NaI	1.087(1)	1.107d	−0.036(13)	70(3)

^aReference ¹¹².

^bValue calculated using fitted model in Ref. 113 using a mass fraction of 0.0558.

^cValue calculated using fitted model in Ref. 113 using a mass fraction of 0.0942.

^dValue calculated using fitted model in Ref. 113 using a mass fraction of 0.1316.

Bulk solution RDFs

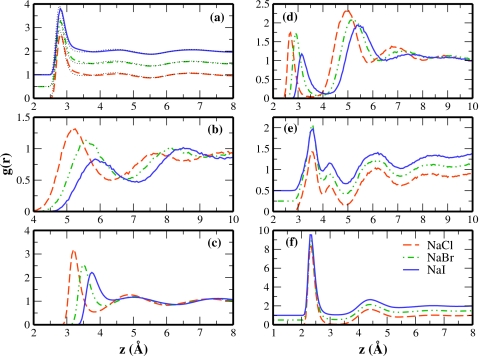
RDFs for the bulk salt solutions are shown in Fig. 1. Panel (a) displays the oxygen-oxygen (O–O) RDFs of each salt solution with a 0.5 vertical offset; the O–O RDF of pure TIP4P-QDP is included as the thin dotted line. The first O–O peak is consistently reduced for all salt solutions as a result of the disruption of local hydrogen bond networks in the presence of ions, as demonstrated explicitly in Fig. 1 in SI.⁶⁵ Furthermore, an enhanced density is observed between the first and second peaks. The reduced structure results from the increased variation of water’s local environment with ions present. The anion-anion RDF is shown in panel (b), and the anion-oxygen RDF in panel (c). We briefly comment on the effective size of chloride anion in bulk (as suggested by the anion-oxygen RDF) since this parameterization showed the greatest deviation from the ab initio target properties. The position of the maximum in chloride ion’s first solvation shell occurs at approximately 3.2 Å; this is consistent with the ranges of experimental (3.1–3.34 Å) and simulated (3.2±0.1 Å) Cl⁻–O distances (see Refs. ^{72, 73} and references therein). We note that the peak position of the first solvation shell increases as expected with the trend of increasing ionic radius. Such verification of the relative sizes of these anions is important for establishing the quality of these salt models since anionic size is commonly believed to influence their interfacial properties.

Figure 1.

RDFs specific for 1M solutions of NaCl (dashed line), NaBr (dashes and dots), and NaI (solid line) in TIP4P-QDP. (a) Oxygen-oxygen RDF (0.5 vertical offset). (b) Anion-anion RDF. (c) Anion-oxygen RDF. (d) Cation-anion RDF. (e) Cation-cation RDF (0.25 vertical offset). (f) Cation-oxygen RDF (0.5 vertical offset).

The cation-anion RDF is shown in panel (d). The magnitude of the first peak representing the contact ion pair (CIP) for each salt solution is smaller than that of the second peak or solvent separated ion pair (SSIP) peak. Previous studies^{17, 74} reported CIP peaks four to five times greater than observed here, suggesting a relative decrease in the anion-cation contact predicted by the present models. We attribute this in part to the slightly higher bulk dielectric constant of TIP4P-QDP, which can more effectively screen anion-cation interactions compared to TIP4P-FQ water. The SSIP peaks are of similar magnitude to those observed in Ref. 17. In the final analysis, the magnitude of the CIP peak relative to the SSIP peak is force-field sensitive. Ishiyama and Morita²⁷ also observed a CIP peak smaller than the SSIP peak. Since the strength of the cation-anion interaction could influence charge layering at the interface, we examine the effects of varying this interaction in Sec. 3B1. The cation-cation RDFs [panel (e)] are qualitatively similar for all salt solutions. Finally, the cation-oxygen RDFs are shown in panel (f). As expected, since we are considering the same cation (Na⁺) in all cases, the distributions are essentially indistinguishable between the different salt solutions.

Single ion hydration free energies

We further examine the quality of the water-ion interaction models used in this study by computing hydration free energies of each ion in TIP4P-QDP. We discuss the thermodynamic integration approach implemented and relevant corrections in the SI.⁶⁵ There are several available sets of experimental hydration free energies available for comparison.^{75, 76, 77, 78, 79, 80, 81} Hydration free energies and corrections calculated in this study are presented in Table 3 along with the experimental results of Tissandier et al.,⁷⁷ Marcus et al.,⁷⁶ and Schmid et al.⁷⁵ Our corrected results $\left(\Delta G_{\mathrm{hyd}}^{\text{real}}\right)$ compare well with the data of Tissandier et al. The larger anions (Br⁻ and I⁻) exhibit the greatest deviation from experiment, 7.5% and 3.0%, respectively. This is approximately the same accuracy obtained by Warren et al.⁸² for analogous anions in TIP4P-FQ. We obtain hydration free energies less favorable relative to experiment, whereas the results in TIP4P-FQ are more favorable than experiment by 3.7–8.4 kcal∕mol (5%–8%). The free energies of chloride and sodium agree well with experiment. These overall results are satisfying since the ion force fields have not been parameterized to reproduce this property. The current analysis of the hydration free energy arising from the ion-water interaction models employed for the current simulations provides a reference for the nature of hydration behavior of the ions. This is necessary in order to understand the role of the solvent’s ability to hydrate ions as it relates to interfacial charge layering.⁸³ Since the free energies of solvation for all anions compare equally well with experiment, conclusions relating to differences in interfacial behavior between various anions are not plagued by ambiguities due to systematic errors in ion-water interactions.

Table 3.

Hydration free energies and correction terms for each parameterized ion in TIP4P-QDP. $\Delta G_{\mathrm{hyd}}^{\mathrm{TI}}$ is the hydration free energy calculated via thermodynamic integration; ΔG_ϕW is the correction for the condensed phase ion self-energy term (the vacuum term is automatically included in $\Delta G_{\mathrm{hyd}}^{\mathrm{TI}}$); ΔG_ϵ corrects for periodic ion-solvent interactions; ΔG_κ is a correction term arising from the decoupling method; ΔG_LRC is a long-range correction; and ΔG_ϕM+ϕQ corrects for the interfacial potential. The sum of the thermodynamically integrated free energy and all the correction factors is presented as $\Delta G_{\mathrm{hyd}}^{\text{real}}$, which can be directly compared to experimentally derived values $\Delta G_{\exp }^{\text{real}}$. Error bars do not reflect uncertainty in the applied correction factors. All values are expressed in units of kcal∕mol.

Ion	$\Delta G_{\mathrm{hyd}}^{\mathrm{TI}}$	ΔGϕW	ΔGϵ	ΔGκ	ΔGLRC	ΔGϕM+ϕQ	$\Delta G_{\mathrm{hyd}}^{\text{real}}$	$\Delta G_{\exp }^{\text{real}}$a	$\Delta G_{\exp }^{\text{real}}$b	$\Delta G_{\exp }^{\text{real}}$c
Na+	−90.81	−0.22	0.18	−0.33	−0.01	−12.01	−103.21(9)	−103.2	−103.1	−102.2
Cl−	−86.15	−0.22	0.35	−0.33	−0.08	12.01	−74.43(23)	−74.4	−74.7	−73.9
Br−	−74.73	−0.22	0.42	−0.33	−0.20	12.01	−63.05(71)	−68.2	−68.2	−67.9
I−	−69.08	−0.22	0.46	−0.33	−0.36	12.01	−57.52(9)	−59.3	−59.9	−58.4

^aReference ⁷⁷.

^bReference ⁷⁵.

^cReference ⁷⁶.

Simulations of the liquid-vapor interface

Density profiles

Beginning in this section, we discuss interfacial properties for the solutions studied. Density profiles for the cation, anion, and water in each solution as a function of depth were computed from the number density of each species in regularly spaced slabs of thickness of 0.25 Å perpendicular to the interface normal; the values are normalized with the bulk density of the species as determined from bulk solution NPT simulations.

The z-position of the slab is relative to the GDS defined as the point where water density is approximately one-half its bulk value. The GDS is typically estimated by fitting the water density profile to a hyperbolic tangent function (tan h) (Refs. ^{84, 85, 86, 87, 88}) described by

$$\rho \left(z\right)=\frac{1}{2}\left({\rho }_L+{\rho }_V\right)-\frac{1}{2}\left({\rho }_L-{\rho }_V\right)\text{tan\hspace{0.17em}h}\left(\frac{z-z_0}{{\delta }_t}\right),$$ (3)

in which the fitting parameters ρ_L and ρ_V correspond to the liquid and vapor densities of the water, z₀ is the z-position of the GDS, and δ_t relates to the interfacial thickness. It has been suggested, however, that an error function (erf) better captures the curvature of the density profile,^{89, 90, 91}

$$\rho \left(z\right)=\frac{1}{2}\left({\rho }_L+{\rho }_V\right)-\frac{1}{2}\left({\rho }_L-{\rho }_V\right)\text{erf}\left(\frac{z-z_0}{{\delta }_e}\right).$$ (4)

The interfacial thickness are calculated from the tan h (δ_t) and erf (δ_e) fits as the 10–90 interfacial thickness⁹² (the region over which density transitions from 90% to 10% of its bulk value). Using this definition, the interfacial widths are calculated as ${\delta }_{10–90}^t=2.1972{\delta }_t$ and ${\delta }_{10–90}^e=1.8124{\delta }_e$ for the hyperbolic tangent and error function fits, respectively. The position GDS (relative to the system center of mass) and interfacial widths obtained from the two fits are summarized in Table 4. Density profiles are shown in Fig. 2. Among the salt solutions, the GDS position increases with increasing anion size as GDS_NaCl<GDS_{TIP4P-QDP,pure}<GDS_NaBr<GDS_NaI. Furthermore, the tan h and erf fits yield essentially identical GDS locations (±0.01 Å) as observed by Warren et al.¹⁷ Similarly, the interfacial widths of salt solutions increase with increasing effective ionic radius of the halides. The interfacial widths determined from the erf fit are consistently 0.06–0.08 Å smaller than those obtained from the tan h fit.

Table 4.

Parameters defining least-squares fits of a tan h and error function to the water density profiles each salt solution.

Salt	Hyperbolic tangent fit			Error function fit
	z0 (Å)	δt (Å)	${\delta }_{10–90}^t$ (Å)	z0 (Å)	δe (Å)	${\delta }_{10–90}^e$ (Å)
TIP4P-QDP	26.78(1)	1.52(2)	3.34(4)	26.78(0.01)	1.81(0.02)	3.28(4)
NaCl	26.44(1)	1.57(2)	3.45(5)	26.43(2)	1.86(3)	3.37(5)
NaBr	26.91(2)	1.63(3)	3.58(6)	26.91(2)	1.93(3)	3.50(6)
NaI	27.21(2)	1.68(3)	3.69(7)	27.21(2)	1.99(4)	3.61(7)

Figure 2.

Density profiles for (a) NaCl, (b) NaBr, and (c) NaI solutions (approximately 1M). Water (solid line), anion (dashed line), and cation (dotted line) density profiles are included for each solution. Densities are normalized by the bulk density from computed from NPT simulations. The z-position is relative to the GDS, which is featured as the dotted vertical line.

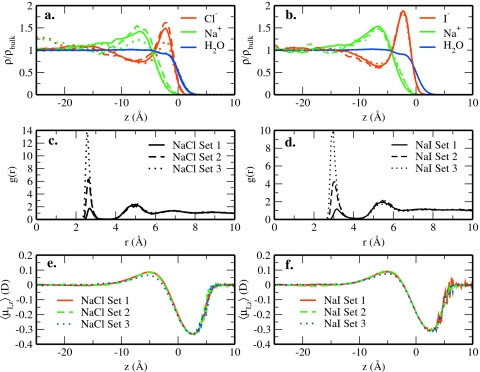
Figure 2 clearly shows interfacial charge layering for all salt solutions. This contrasts with the absence of charge layering (except for the large iodide ion) in TIP4P-FQ water as demonstrated in Ref. 17. In the present study, the extent of charge layering seems to have a dependence on the size of the ion since the amount of charge layering (as determined by the magnitude of the non-overlapping anion and cation peaks) increases along the sequence Cl⁻, Br⁻, and I⁻.

Anion density profiles do not extend significantly above the GDS regardless of the extent of charge layering. All systems show significant water density in the outermost regions of the interface, with all anions extending above the GDS to roughly equal extent. The degree to which anions are able to populate the interfacial region near the surface can be estimated from their density in the bulk. Anion densities greater than one in the bulk suggest little to no surface presence, while densities less than one in the bulk are indicative of surface excess. In general, the ion density profiles take on values greater than one in the bulk, suggesting negligible surface excess. Bulk ion densities approach one in the series of NaI to NaCl, indicating that larger anions favor the interface. These observations are quantified via the surface excess, Γ, which is discussed in Sec. 3B2. Based on the previous discussion and the density profiles, we do not expect significant ionic concentration at the surface for any parameterizations of the nonpolarizable salts in TIP4P-QDP. Furthermore, the tails of the anion density profiles do not coincide with those of water as observed in numerous previous studies explicitly treating ion polarizability.^{16, 17} The current combination of water and nonpolarizable ion force fields are qualitatively in agreement with numerous earlier studies emphasizing the importance of ion polarizability in accommodating surface states of ions.^{15, 16, 21, 93, 94}

Returning to the observation of weak contact ion pairing between anions and cations predicted by the current force fields [Fig. 1d], we consider whether interfacial charge layering arises, in part, due to this weaker interaction. One can conjecture that a stronger cation-anion attraction (observed for other force fields) might reduce or eliminate charge layering. We therefore examine the effect of artificially enhancing cation-anion interactions on charge layering. For this analysis, water-water and ion self-interaction parameters were not modified from the models used in this study, while the cation-anion Lennard-Jones interaction was adjusted to produce weakly interacting (the original model denoted as set 1), moderately interacting (set 2), and strongly interacting (set 3) models; bulk NPT MD simulations were performed using these modified potentials. The differences in cation-anion interaction strengths between sets 1, 2, and 3 are evident in the increasing CIP peaks in the anion-cation RDFs [Fig. 3b]. While the magnitude of this interaction (first peak heights in the cation-anion RDF) is inconsequential for the present analysis, we observe that the moderate interactions (set 2) yield RDF contact peaks that are similar to those reported in previous studies.^{17, 74} The CIP peaks associated with set 3 interaction model are significantly higher than those predicted by other models. Figure 3 shows interfacial density profiles for the different interaction sets. We selected chloride and iodide as the anions for this analysis since they demonstrate the weakest and strongest interfacial enhancement. The density profiles indicate that the formation of the ionic double layer is not influenced by cation-anion interaction strength since two distinct ion layers form in all cases; iodide, being the largest anion, experiences no effect. This suggests that the size of this anion is the dominant factor facilitating charge layering. Modulation of anion-cation interaction influences the magnitude of charge layering for NaCl. The strongest anion-cation interaction (set 3) leads to a slight reduction in the ion density near the interface. We note, however, that the NaCl set 3 contact peak [Fig. 3b] is substantially (and most likely unrealistically) higher than predictions from other models.^{18, 74}

Figure 3.

Effects of anion-cation interactions on charge layering at the interface. The NaCl density profiles (a) and RDFs (c) for varying sets of Na–Cl interaction energies. Panels (b) and (d) are the analogous figures for NaI. In all panels, the solid lines indicate data in which the interaction between anion and cation is determined via combining rules (set 1 data, which is the data presented previously in this work); the dashed and dotted lines represent data in which the interaction has been made increasingly favorable.

Surface tension and surface excess

Surface tension is calculated as the difference between normal and tangential elements of the internal pressure tensor⁹⁵

$$\gamma \left(z\right)=\frac{L_z}{2}\left(P_{zz}-\frac{P_{xx}+P_{yy}}{2}\right),$$ (5)

where P_xx, P_yy, are P_zz are the diagonal elements of the internal pressure tensor and L_z is the length of the simulation cell in the z-direction (normal to the surface). Simulation results are shown in Table 2. Within the uncertainty of our calculations, the surface tension of pure TIP4P-QDP, 71±2 dyn∕cm, agrees with experiment, 71.9 dyn∕cm.⁹⁶ Predicted surface tensions of all salt solutions are similar to that of pure water, varying by only 1%–2%. For NaCl, the present surface tension reduction is similar to that observed for 1.2M NaCl by D’Auria and co-workers.⁹⁷ Experimentally, salt solution surface tensions are higher than the pure water surface tension, with NaCl showing the greatest increase.¹² Due to the uncertainty associated with each surface tension reported, we cannot definitively comment on the surface tensions of salt solutions relative to pure water or any trends among the salt solutions. We also point out that our computed surface tension values do not include long-range correction for dispersion interactions, and these could possibly asymmetrically lead to an increase in surface tension with the addition of monovalent salts to TIP4P-QDP water.

Surface excess is related to the changes in surface tensions relative to those in ion concentration as dictated by Gibbs’ adsorption isotherm equation,¹⁰

$$\Gamma =-\frac{1}{RT}{\left(\frac{\partial \gamma }{\partial \text{\hspace{0.17em}ln\hspace{0.17em}}a}\right)}_{P,T}.$$ (6)

Surface excess is a quantitative measure of ion population at the interface; negative surface excess suggests repulsion of ions from the interface, while positive values suggest presence of ions at the surface. Surface excess is directly calculated by integrating the density profile as¹¹

$${\Gamma }_{\text{ion}}={\int }_0^{z_0}dz\left[{\rho }_{\text{ion}}\left(z\right)-{\rho }_{\text{ion},\text{bulk}}\right]+{\int }_{z_0}^{\infty }dz\left[{\rho }_{\text{ion}}\left(z\right)-{\rho }_{\text{ion},\text{gas}}\right],$$ (7)

where z₀ denotes the position of the GDS. We take ρ_ion,gas=0, and ρ_ion,bulk is taken from fitting the ion density in the plateau-region near the center of the slab to a constant representing the average bulk ion density; for the present work, we restrict the fit to the region closest (±5 Å) to the system center of mass. We use density profiles computed with a reduced bin size of 0.05 Å to minimize error introduced from the bounds of integration. Calculated surface excesses are reported in Table 2. We observe the anticipated trend of increasing surface excess in the series NaCl, NaBr, and NaI. Furthermore, the surface excess of each solution is negative, indicating net surface depletion. This is consistent with the value of relative bulk ion densities being greater than unity. However, we observe less negative Γ_NaCl and Γ_NaI than reported for nonpolarizable NaCl and NaI in TIP4P-FQ, consistent with the density enhancement of the respective anions in TIP4P-QDP.¹⁷ Finally, we remark that the surface excess of pure TIP4P-QDP should be zero based on the relationship to the GDS. We calculate Γ_TIP4P-QDP to be 0.006 nm⁻², which agrees with the anticipated value within uncertainty, validating our results and further supporting the quality of the GDS values obtained from functional fits.

Dielectric constant profiles

Debate continues regarding the fundamental driving forces for anion segregation at interfaces. One particular thought concerns an electrodynamic driving force originating from a gradient in solvent dielectric permittivity through the interface as this value changes from a bulk value to that of the gas (vacuum) phase.⁸³ To explore this idea, we compute the longitudinal (z-dependent) profile of the in-plane dielectric permittivity of water using the approach of Stern and Feller.^{98, 99, 100}

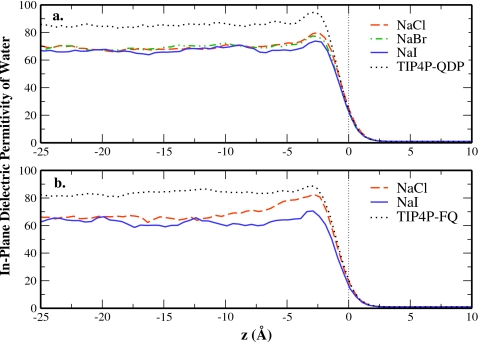
The water contribution to the in-plane dielectric constant is shown in Fig. 4 for each salt solution and the pure solvent. The top panel shows results using TIP4P-QDP as solvent and the bottom panel using TIP4P-FQ. Approaching the interface from the bulk, all systems show an increase of 2.5 Å before the GDS, followed by a rapid decrease through the interface.

Figure 4.

Water contribution to the in-plane dielectric constant as a function of depth relative to the GDS for salt solutions (a) in TIP4P-QDP solvent and (b) in TIP4P-FQ solvent.

The profile for pure TIP4P-QDP water shows a bulk in-plane average dielectric constant of 85.12, similar to the value reported for pure TIP4P-QDP;⁵² the corresponding profile for pure TIP4P-FQ converges to the expected value of 80.⁵⁴ Near the GDS, the in-plane dielectric constant of pure TIP4P-QDP shows an 11% enhancement over the average condensed-phase value; the analogous increase for pure TIP4P-FQ is less. This results from the permanent dipole vector of TIP4P-QDP water orienting more in the xy-plane than TIP4P-FQ just beneath the GDS. The interfacial orientational difference between the two water models is illustrated in Fig. 6a in Ref. 52. The larger contribution to the in-plane polarization density arising from the orientation of the TIP4P-QDP permanent dipole leads to a higher in-plane permittivity; this is evident from Eqs. 26, 69, and 71 for tinfoil, or conducting, boundary conditions in Ref. 98.

The salt solution profiles are qualitatively similar to the pure water profiles. They also exhibit enhancement over the bulk value below the GDS. The average in-plane dielectric constants of bulk salt solutions are lower than that of pure water, ranging from approximately 67–69 in qualitative agreement with experiment.^{101, 102} This decrease is caused by a reduction of the bulk solution dipole moment in the presence of ions relative to the pure water system (data not shown). Equations 26, 69, and 71 of Stern et al.⁹⁸ illustrate the relation between a lower in-plane dipole moment and lower in-plane dielectric permittivity.

The decrease in solvent dielectric in salt solutions has been previously discussed in the literature.^{83, 101, 103} The study of Hasted et al.¹⁰¹ discusses this reduction as arising from lowered dielectric permittivity of first hydration shell water molecules; in particular, the orientational dynamics of water molecules coordinating cations is reduced. This effectively lowers the dielectric response. The reduction in solvent dynamics in the first solvation shell of anions is less severe, though non-negligible for larger anions such as iodide. Interestingly, recent work by Grossfield¹⁰⁴ suggests that cations induce competition between water-water and water-cation interactions in the first hydration shell more so than anions; cations induce greater water ordering in the first hydration shell, thus frustrating water to a greater extent. This leads to relatively more efficient solvation of anions. Hasted et al. pointed out, however, that larger anions would exhibit analogous effects.

Finally, the enhancement in in-plane dielectric near the GDS decreases with increasing anionic size and extent of charge layering (Cl⁻<Br⁻<I⁻). This trend in the in-plane permittivity for solutions in TIP4P-QDP and TIP4P-FQ suggests a role of the dielectric constant as a probe of the surface residence of ions. For the case of NaCl in TIP4P-FQ, the work in Ref. 18 has shown the depletion of chloride ions from the interface. The dielectric constant profile in Fig. 4b shows how the in-plane permittivity of the NaCl solution is lower in the bulk than in pure TIP4P-FQ water but nearly matches the pure water case in the interfacial region. This indicates that the interfacial region of the aqueous solution in TIP4P-FQ water model is almost equivalent to the pure solvent; therefore, there is no surface excess. This is consistent with the relative bulk ion density greater than 1 as well as the computed negative surface excess in that study. Likewise for the present case, the increase in the interfacial dielectric for non-polarizable ions in TIP4P-QDP is consistent with the small, but negative computed surface excesses shown in Table 2.

Orientation profiles

We consider two angular orientations, θ and ϕ, of water in the presence of the nonpolarizable ions. The former is defined as the angle formed between the surface normal (z-axis) and the vector bisecting the H–O–H angle of the water molecule; the latter is the angle formed between the surface normal and the molecular plane of the water molecule. For convenience in comparing to previous studies, we show the cosine of each angle as a function of depth in Fig. 5; the absolute value of cos ϕ is shown since positive and negative values are indistinguishable. The cos θ(z) profile takes on an average value of zero for all solutions in the bulk region, which is anticipated for a randomly oriented system. In the region above the GDS (z=0 to z=5 Å), there is a strong preference for the water molecules to orient with the permanent dipole vector pointing into the vapor as indicated by the positive values of ⟨cos θ⟩ in this region.

Figure 5.

Orientational profiles of the water in each solution as a function of depth relative to the GDS. The upper panel (a) features the ⟨cos θ⟩ as a function of z, where θ is the angle made between the permanent dipole vector of the water molecule and the surface normal. The lower panel (b) features the ⟨|cos ϕ|⟩ as a function of z, where ϕ is the angle made between the molecular plane and the surface normal.

We observe that the region approximately 5–10 Å below the GDS also exhibits a strong orientational preference of the permanent water dipole toward the surface. This peak, absent for neat water, is a consequence of ion charge layering. Additionally, the depth of the maximum (z≈−5 Å) corresponds to the depth where the anion density surpasses cation density. The region just below the GDS (z=−5 to z=0 Å) shows a decrease in reorientation; however, there is still a net preference for the hydrogens to orient toward the surface. This is opposite to the behavior seen for pure TIP4P-QDP, which shows a preference for the hydrogens to point into the bulk. Finally, the extent of water reorientation is proportional to degree of charge separation (Fig. 2).

z-Induced dipole moment

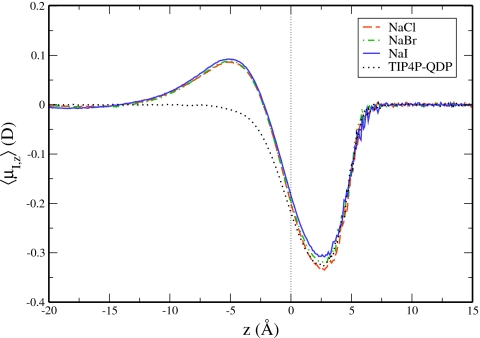
The depth-dependent profile of the average z-component of water’s induced dipole moment (henceforth referred to as z-induced dipole moment) is plotted for each salt solution in Fig. 6. As anticipated for an isotropic environment, the average z-induced dipole moment is zero in the bulklike regions at depths ≥20 Å below the GDS. At depths approximately 13 Å below the GDS, the average z-induced water dipole moment for the salt solutions begins to take positive values, indicating a net orientation of the induced dipoles toward the vapor phase. This depth coincides with the depth of the onset of the enhanced cation density. Transitioning through the ionic double layer from the bulk toward the GDS, z-induced dipole moments increase to a maximum at approximately 4–5 Å below the GDS. This depth corresponds to the location where the anion and cation densities are equal (see Fig. 2); this also corresponds to the position of maximum orientation for water (as discussed in Sec. 3B4). The magnitude of the peaks for each salt solution increases in a manner consistent with the extent of charge layering as seen in the density profiles. The largest z-induced dipole moment (≈0.1 D) is seen for the NaI solution. This peak is approximately twice the magnitude as that of nonpolarizable NaI in TIP4P-FQ,¹⁸ consistent with increased charge layering. However, there is an approximate 50% reduction compared to Drude-polarizable NaI in TIP4P-FQ,¹⁸ which showed approximately two times the extent of charge layering of the model presented here.

Figure 6.

Average magnitude of the z-induced dipole moment of water in each salt solution relative to the GDS.

Comparing the water z-induced dipole moments for the NaCl system in the present work to that of Warren et al.,¹⁸ we see that the higher polarizability of the TIP4P-QDP water model accommodates the large “macro”-dipole arising from charge layering of anions and cations. For the case of nonpolarizable NaCl in TIP4P-FQ studied by Warren et al., the authors observe roughly half the z-induced dipole moment of water, consistent with the nonexistent surface presence of anions and lower associated interfacial charge layering. We assert that the role of solvent polarizability, in the absence of ion polarizability, is to oppose the dipole generated by the spatial localization of anions and cations at the interface. We direct the reader’s attention to Fig. 3, which features the z-induced water dipole moment in salt solutions with varying interionic interaction strengths. Specifically, the set 3 NaCl data, which feature reduced ion densities in the interface, also demonstrate a reduced z-induced dipole moment in the region below the GDS. Consistent with our assertion above, the reduced macrodipole influenced by a lesser degree of ion layering is counteracted by a smaller z-induced dipole moment.

Additionally, by assigning a limiting value of molecular polarizability to our water model (i.e., the gas-phase value), we can isolate the effects of water polarizability in an extreme case. In the present work, we see that regardless of the strength of the solvent polarizability, nonpolarizable ions will not populate the extreme outer regions of the interface. These results are consistent with existing observations that ion polarizability specifically allows a purely surface state to emerge (vis-à-vis population of the outermost interfacial layer).

In the region −4<z<3, the z-induced dipole moments rapidly reorient as indicated by the transition from positive to negative values. The negative values suggest a net orientation of the z-induced dipole moment pointing into the bulk, which is opposite the orientational preference of the permanent dipole to point slightly toward the vapor phase as suggested by the ⟨cos θ⟩ profile (Fig. 5). The qualitative agreement of profiles of the salt solutions and pure TIP4P-QDP in this region suggests that the presence of anions in the outer interface does not have a significant effect on the structure of water. The slightly less negative minima of NaBr and NaI may suggest some water molecules reorient their induced dipole toward anions rather than directly into the bulk. Similar observations were more pronounced when polarizable NaI in TIP4P-FQ was considered due to a greater extent of surface activity of the anions.¹⁸

Interfacial potential profiles

Interfacial potential is a combined measure of electrostatic properties and orientation at the solution surface. The liquid-vapor interfacial potential for water in each solution was calculated by doubly integrating the charge density^{1, 93, 105, 106, 107} defined by

$$\Delta \Phi \left(z\right)=\Phi \left(z\right)-\Phi \left(z_0\right)=-{\int }_{z_0}^{z}d{z}^{\prime }{\int }_{z_0}^{z^{\prime }}d{z}^{″}\rho \left(z\right).$$ (8)

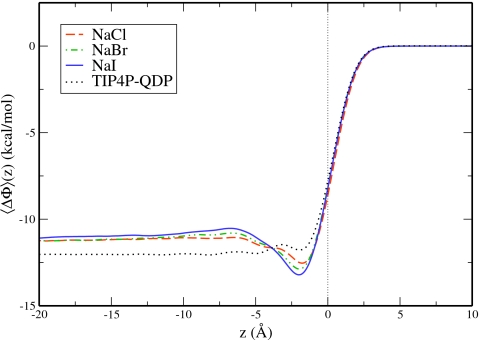
The z-direction is perpendicular to the surface, and z₀ specifies the center of mass of the slab. Figure 7 plots the interfacial potential profile as a function of depth relative to the GDS. In the region 1–4 Å below the GDS a noticeable well forms for the NaCl, NaBr, and NaI solutions, consistent with the increased anion concentrations in this region. Approximately 4 Å below the GDS, the salt solutions become less favorable than the neat water. This transition takes place at the depth where cation and anion densities are equal. The integrated values in Table 5 show that the interfacial potential becomes less favorable for the salt solutions with greater charge layering: ΔΦ_NaI>ΔΦ_NaBr>ΔΦ_NaCl>ΔΦ_{TIP4P-QDP,neat}. The observation of systematically more positive interfacial potentials for the salt solutions relative to pure water is in agreement with recent findings.^{11, 18, 27, 28, 108, 109}

Figure 7.

Interfacial potential for the water of each salt solution as a function of depth relative to the GDS.

Table 5.

Decomposition of the total interfacial potential into components arising from the total dipole moment of water (ΔΦ_M(H₂O)), water quadrupole moment (ΔΦ_Q(H₂O)), and ion monopoles (ΔΦ_q(H₂O)). The total interfacial potentials calculated from the sum of the contributions (ΔΦ_total) and from Eq. 8 are both presented. All values are in units of kcal∕mol.

Salt model	ΔΦM(H2O)	ΔΦQ(H2O)	ΔΦq(M+A−)	ΔΦtotal	ΔΦ (Eq. 8)
TIP4P-QDP	13.51	−25.58		−12.07	−12.01(4)
NaCl	−42.76	−24.95	56.48	−11.23	−11.17(12)
NaBr	−42.71	−24.56	56.09	−11.18	−11.14(8)
NaI	−46.16	−24.25	59.36	−11.05	−11.02(13)

Direct integration of charge density allows decomposition of the interfacial potential into dipole and quadrupolar contributions.¹¹⁰ Our analysis focuses on the partitioning of the total interfacial potential into three components:¹⁸ the monopole contributions due to the physical distribution of ionic point charges (ΔΔΦ_q(M⁺A⁻)), the total water dipole contribution (ΔΔΦ_M(H₂O)), and the water quadrupole contributions (ΔΔΦ_Q(H₂O)). Results are shown in Table 5. The quadrupole moment contribution is calculated from the difference of the local molecular quadrupole density Q_zz(z) and a reference value $Q_{zz}^{°}$,

$$\Delta {\Phi }_Q\left(z\right)=-\frac{1}{{ϵ}_0}\left[Q_{zz}\left(z\right)-Q_{zz}^{°}\right].$$ (9)

We take the reference $Q_{zz}^{°}=0$ and define the quadrupole moment density^{110, 111} as

$$Q_{zz}\left(z\right)=⟨\sum _m\delta \left(z-z_m\right)\left(\frac{1}{2}\sum _i{q}_{im}{z}_{im}^2\right)⟩,$$ (10)

in which m and i are the molecular and atomic sites within the molecule, respectively. The oxygen atom is taken to be the molecular center, z_m, for multipolar expansion. As in previous studies,¹⁸ the water quadrupole moment dominates the potential increments of the salt solutions over water, contributing over 65% of this quantity. The remaining two contributions (water dipole moment and ion monopole) are summed to give an effective dipole moment contribution since the magnitude of this sum is roughly equivalent to the magnitude of the dipole moment contribution for pure water.

The ion monopole contribution results from integrating Eq. 8 over charge density of ions only. The total dipole moment contribution is computed via the integration of the water dipole moment density, P_z(z) over z according to^{110, 111}

$$\Delta {\Phi }_M=-\frac{1}{{ϵ}_0}{\int }_{z_0}^{\infty }dz{P}_z\left(z\right),$$ (11)

where the dipole moment density is defined as

$$P_z\left(z\right)=⟨\sum _m\delta \left(z-z_m\right)\left(\sum _i{q}_{im}{z}_{im}\right)⟩.$$ (12)

The “effective” dipole moment complements the quadrupole moment contributions to completely describe the potential increment over pure water and the total interfacial potential. The interfacial potential as calculated from the sum of the contributions shows excellent agreement with the values calculated by double integration of the charge density [Eq. 8], differing by less than 1%.

CONCLUSIONS

We investigate the role of solvent polarizability in defining interfacial properties of solutions of nonpolarizable alkali-halide salts using the TIP4P-QDP water model, which features an average condensed-phase molecular polarizability higher than that of most current polarizable water models. This combination of water and nonpolarizable ion force fields leads to differences in interfacial charge layering compared to that observed in similar studies of non-polarizable ions in TIP4P-FQ.^{17, 18} Previous studies^{16, 17, 18} reported charge layering only in cases when the system is completely polarizable or when a large nonpolarizable anion (i.e., I⁻) is considered in a polarizable solvent. Here, despite treating all ions as nonpolarizable, we observe interfacial charge layering. Water polarizability induces a molecular dipole moment along the interface normal that stabilizes the dipole formed by spatially separated layers of ions. Since the TIP4P-QDP molecular polarizability approaches the gas-phase value through the interface, it induces a larger dipole moment along the interface normal and thus supports greater charge layering relative to the TIP4P-FQ water model.

One factor potentially contributing to charge layering at the liquid-vapor interface is the strength of anion-cation interactions. Since experimental data for contact ion pairing are not available, we contend with some ambiguity regarding the appropriate magnitude of the CIP peak relative to the SSIP peak in the cation-anion RDFs. In contrast to the studies of Warren et al.,¹⁷ we observe reduced contact ion pairing. Such a weak contact interaction could conceivably contribute to the charge separation observed here for all salt solutions. However, by artificially enhancing cation-anion interactions for sodium-chloride and sodium-iodide, we observe that the extent of charge separation is essentially unaltered.

Reiterating previous studies,^{11, 16, 26} our results show the inability of nonpolarizable ions to populate the outer regions of the liquid-vapor interface. The absence of such surface presence in the current study recapitulates the idea that ion polarizability is responsible for stabilizing ions at the surface, in agreement with recent nonperturbative theory,⁴⁸ as well as early work by Vrbka et al.¹⁶ The latter study of NaI solutions using combinations of polarizable∕nonpolarizable ions∕water explicitly showed that ions only penetrated into the outer regions of the surface when they were treated as polarizable entities. Our results agree with and reiterate numerous earlier studies that emphasize the importance of treating ion polarizability.^{15, 16, 21, 93, 94} As demonstrated by Vrbka et al. (Fig. 4 in Ref. 16), variation in ion polarizability profoundly effects interfacial charge layering. Though currently accepted values for Cl⁻, for instance, fall in the range of 3.2–4.0 ų (Ref. ²⁶), in general, the exact value must be determined in conjunction with the value of water polarizability. Further studies to narrow such polarizability ranges are warranted. Finally, based on computed in-plane dielectric permittivity profiles for nonpolarizable ions in TIP4P-QDP and TIP4P-FQ water, the value of the dielectric permittivity in the interfacial region relative to pure water and the bulk salt solution value potentially affords a metric to gauge the presence of ions at the interface.