Abstract
In the wheelchair propulsion literature it is common to report upper extremity joint kinetics as a means to express the load being experienced by the shoulder, elbow and wrist. The task of choosing the appropriate kinetic resolution coordinate system for upper extremity joint forces and moments has shown itself to be a lab-specific process. The differences which arise during interpretation may hinder a clear and broad understanding of upper extremity joint kinetics during wheelchair propulsion. The goal of this communication was to address the inconsistency of kinetic reporting in the wheelchair literature that addresses the pain and injury experienced by manual wheelchair users. To highlight the variety of reporting methods in wheelchair propulsion this note surveyed peer-reviewed, published manuscripts reporting wrist, elbow, or shoulder joint intersegmental forces and moments calculated from inverse dynamics during wheelchair propulsion. To correct this inconsistency, there may be a need for standardization to achieve the goal of a cohesive comprehension of wheelchair biomechanics. This communication is provided to open discussion on the anatomical and clinical relevance of currently employed coordinate systems and other available options, with the additional goal of providing an initial recommendation for kinetic representation during wheelchair propulsion.
Keywords: biomechanics, coordinate system, forces, joint kinetics, moments, rehabilitation, upper extremity, manual wheelchair propulsion, shoulder, elbow, wrist
INTRODUCTION
The quantification of mechanical loads has provided insight to the connection between wheelchair propulsion and the high incidence of upper extremity (UE) pathology in the manual wheelchair user population [1–6]. Mercer et al. [7] reported manual wheelchair users who demonstrated larger shoulder joint forces and moments during level wheelchair propulsion were more likely to exhibit signs of shoulder pathology on MRI examination than those experiencing smaller kinetics. This study highlighted the value of joint kinetics as a metric in investigating mechanisms underlying the development of UE pain among manual wheelchair users. Prior to and subsequently, many investigators have reported UE joint kinetics to approximate the mechanical load experienced by the shoulder, elbow, and wrist during wheelchair activities [7–17].
A variety of methods have been adopted for reporting UE joint kinetics. Boninger et al. [8] were the first in wheelchair propulsion literature to express the necessity to report joint kinetics in a local segment coordinate system when the goal is to relate biomechanical data to injury. The group explained that the local coordinate system should be anatomically relevant and hence, can be linked to physiological based motions and pathologies. While it has been the trend to express joint kinetics in a local coordinate system as opposed to a global reference, there have been varied definitions and combinations of proximal and distal coordinate systems used for the upper extremities. One frequently utilized approach has been to express both the intersegmental joint forces and moments in the proximal coordinate system [7, 11, 14, 16, 17]. A recent multisite study by Collinger et al. [12] reported shoulder forces in the coordinate system of the segment proximal to the joint and shoulder moments in the coordinate system of the segment distal to the joint. A third option for kinetic representation, not regularly employed in the wheelchair literature, is the non-orthogonal joint coordinate system (JCS) which uses a combination of axes from both segments about a joint[18]. The International Society of Biomechanics (ISB) recommends use of a non-orthogonal JCS for UE kinematics [18], but a similar recommendation for UE kinetics does not exist. Without a clear standard for use in upper extremity kinetics, the variety of available options for data representation can confound clinical interpretation.
The task of choosing the appropriate kinetic resolution coordinate system has shown itself to be a lab-specific process and may hinder a clear and broad understanding of UE joint kinetics during wheelchair propulsion. To correct this inconsistency, there may be a need for standardization to achieve the goal of a cohesive comprehension of wheelchair biomechanics. This communication is provided to open discussion on the anatomical and clinical relevance of currently employed coordinate systems and other available options, with the additional goal of providing an initial recommendation for kinetic representation during wheelchair propulsion.
METHODS
Local segment coordinate systems are commonly placed at either the proximal or distal end of a segment, and are generally located at a joint center. After performing an inverse dynamics procedure to calculate intersegmental joint forces and moments, the investigator can choose to represent the kinetics in any coordinate system their marker set allows them to define. Joint forces are most often represented in either an orthogonal proximal segment or orthogonal distal segment embedded coordinate system (Table 1, Figure 1). Joint moments can be reported in an orthogonal proximal or distal segment based coordinate system like forces, but joint moments can also be reported in a non-orthogonal JCS (Table 1, Figure 1). The non-orthogonal JCS is comprised of one fixed axis in the proximal segment, one fixed axis in the distal segment, and a third floating axis. To highlight the variety of reporting methods in wheelchair propulsion this note surveyed peer-reviewed, published manuscripts reporting wrist, elbow, or shoulder joint intersegmental forces and moments calculated from inverse dynamics during wheelchair propulsion. The literature search was performed in Pubmed, Medline, and Scopus using combinations of the following search terms: kinetics, wheelchair propulsion, upper extremity, shoulder, elbow and wrist. From the full collection of manuscripts addressing upper extremity kinetics during wheelchair propulsion, a subset was chosen for presentation in this note. The subset was chosen to characterize the full variety of data representation in the field without overlap of methods from the same investigator.
Table 1.
Resolution Coordinate System Definitions
| Joint | Distal Segment | Proximal Segment | JCS Definition |
|---|---|---|---|
| Shoulder | Upper arm | Trunk | Z-X-Z order e1: Z axis fixed in the trunk coordinate system e3: axial rotation around the Z axis of the upper arm e2: axis fixed in the upper arm coordinate system coincident with the X axis of the upper arm |
| Elbow | Forearm | Upper arm | Y-X-Z order e1: axis fixed in the proximal coordinate system coincident with the upper arm Y axis e3: axis fixed in the distal coordinate system coincident with the Z axis of the forearm e2: mutually perpendicular varus/valgus rotation axis |
| Wrist | Hand | Forearm | Y-X-Z order e1: axis fixed in the proximal coordinate system coincident with the forearm Y axis e3: axis fixed in the distal coordinate system coincident with the Z axis of the hand e2: mutually perpendicular ulnar/radial deviation axis |
Figure 1.
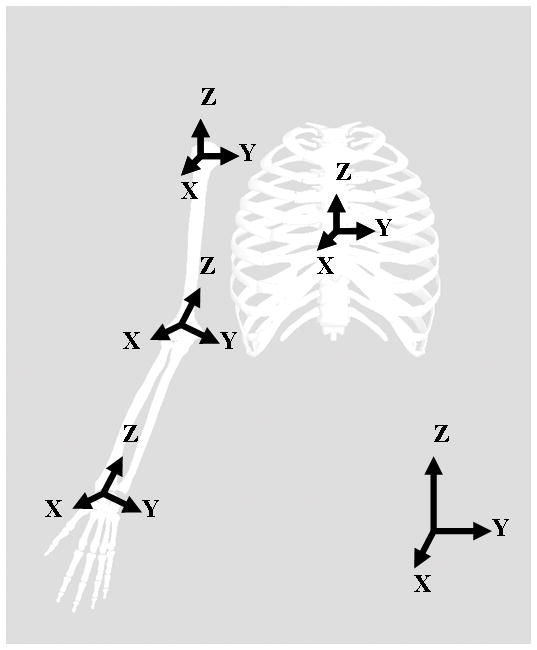
Segment coordinate systems for the trunk, upperarm, forearm, and hand.
RESULTS
Joint kinetics during wheelchair propulsion have been reported for the UE joints with varying reporting techniques (Table 2). The majority of wrist, elbow and shoulder forces were reported in the proximal coordinate systems (forearm, humerus, and trunk, respectively). One exception occurred at the wrist; Boninger et al. [8] expressed wrist forces in the distal, hand coordinate system with the origin at the wrist center. The elbow joint forces were generally expressed in the humerus coordinate system centered at the shoulder joint center [15]. The proximal coordinate system origin for the shoulder joint was either placed at the acromion, shoulder joint center, or midline of the trunk [7, 12, 14, 15, 19]. An older study performed by Kulig et al. [10], expressed the shoulder forces in a global, lab coordinate system, but this practice has not been repeated in the literature.
Table 2.
Wheelchair Propulsion Coordinate System Representations
| SHOULDER | |||||
|---|---|---|---|---|---|
| Lead Author | Year | Force Representation | Coordinate System Origin | Moment Representation | Coordinate System Origin |
| Collinger | 2008 | Trunk | Acromion and trunk midline (2 marker sets) | Humerus | Glenohumeral joint |
| Desroches | 2008 | NA | NA | Trunk | Trunk midline |
| Mercer | 2006 | Trunk | Acromion | Trunk | Acromion |
| van Drongelen | 2005 | NA | NA | Trunk | Trunk midline |
| Sabick | 2004 | Trunk | Midline trunk | Humerus (transverse) & Trunk (sagittal, frontal) | Shoulder joint center/Trunk center |
| Veeger | 2002 | NA | NA | Trunk | Trunk midline |
| Koontz | 2002 | Trunk | Shoulder joint center | Trunk | Shoulder joint center |
| Cooper | 1999 | 3 different trunk models | Shoulder joint center | 3 different trunk models | Shoulder joint center |
| Kulig | 1998 | Lab | Lab | Humerus | Shoulder joint center |
| ELBOW | |||||
| Lead Author | Year | Force Representation | Coordinate System Origin | Moment Representation | Coordinate System Origin |
| van Drongelen | 2005 | NA | NA | Forearm | Elbow center |
| Sabick | 2004 | Humerus | Shoulder Joint Center | Forearm (transverse) & Humerus (sagittal, frontal) | Elbow center/Shoulder center |
| WRIST | |||||
| Lead Author | Year | Force Representation | Coordinate System Origin | Moment Representation | Coordinate System Origin |
| Sabick | 2004 | Forearm | Elbow center | Hand (transverse) & forearm (sagittal, frontal) | Wrist center/Elbow center |
| Boninger | 1997 | Hand | Wrist center | Hand | Wrist center |
NA represents data not present in the referenced manuscript
A wide spectrum of coordinate systems were used in reporting joint moments (Table 2). Sabick et al. [15] reported moments at all joints using a combination of axes from the distal and proximal segments where the transverse rotation moment of a joint was reported in the distal segment and the frontal and sagittal plane moments were in the proximal coordinate system. Many of the authors represented the moment in the coordinate system proximal to the joint [7, 14, 16, 17, 19, 20], although the location of the coordinate system origins varied between studies. The remaining authors reported the moments in the coordinate system distal to the joint [8, 10, 12].
DISCUSSION
The central concern over which coordinate system to choose is in the value of the clinical interpretation. If the clinical interpretation is focused on injury prevention, then the joint anatomy and joint pathologies should guide the coordinate system selection. Common to all the joint pathologies is their etymological proximity to the joint itself; therefore, any joint kinetics used to describe the load on a particular joint need to be reported in a coordinate system centered in the joint itself, whether it is the coordinate system proximal or distal to the joint. While the previous statement may seem like common sense, it was shown in this communication that many published joint forces and moments have been expressed in local coordinate systems with their origin away from the joint of focus. For example, shoulder joint forces and moments have been reported in a trunk coordinate system that originates in the middle of the trunk and not near the shoulder joint by any respects [12, 15, 16]. It is an essential component to a clinically relevant reporting system to place the coordinate system origin in the proximity of the joint center for both joint forces and moments.
To address injury exploration and prevention in regards to wheelchair propulsion, it behooves us to consider the particular pathologies that commonly afflict this population and relate them to kinetic representation. The most common reported pathologies occurring at the shoulder are impingement syndrome and joint instability. Posterior-lateral instability of the proximal ulna occurs at the elbow [21], and the wrist is commonly affected by carpel tunnel syndrome [8]. At the shoulder, the superior migration of the humeral head potentially causes the impingement of the rotator cuff tendon, and the anterior and posterior displacement of the humeral head are associated with joint instability. In considering these pathologies and forces, the ideal system for reporting the intersegmental joint force would be a proximal coordinate system centered on the glenoid fossa. At the elbow, to address the posterior-lateral instability of the proximal ulna, the intersegmental joint force with reference to a distal coordinate system originating on the ulna would make sense. Without considering the pathology in the representation, the investigator may not be able to fully explore the clinical question. Moment representation is more complex than that of joint force because the chosen planes of motion should ideally represent those the musculature functions within, realizing that physiologically most muscles do not act entirely in one plane of motion. Schache and Baker [22] performed a study investigating lower extremity joint moments and their clinical interpretation when using differing reporting methods. In choosing the most appropriate reference frame, the authors explained that the choice should be based on which coordinate system is “most useful in understanding the biomechanics of gait with or without pathology.” This statement is of global importance in biomechanics and can be applied equally to the upper extremity. The group’s final recommendation was that a non-orthogonal JCS provides an implicit link with muscle activity and offers a clinical useful representation of what a joint moment actually represents [22]. For the same reasons, the non-orthogonal JCS can be argued as appropriate for the upper extremity joints as well. To elucidate this point, consider the elbow joint. With the elbow flexed to 90 degrees, the abduction-adduction moment based on the proximal coordinate system would be the same as the supination-pronation moment based on the distal coordinate system. This problem only grows when considering the shoulder. Changes in what is considered an abduction-adduction moment versus a flexion-extension moment change dramatically as soon as the humerus segment undergoes any axial rotation. This is the same problem experienced when trying to clearly represent shoulder kinematics with a classic Cardan sequence; hence, the ISB recommends using the JCS with an Eulerian sequence [18]. The JCS provides the functional and anatomical relevance for moment representations that is incompatible with orthogonal axes [23].
CONCLUSION
The goal of this communication was to address the inconsistency of kinetic reporting in the wheelchair literature that is attempting to address the clinical problems experienced by manual wheelchair users. This discussion is not relevant in purely academic practices, but is put forth for clinically directed motivations. In the future, authors should appropriately select coordinate systems that have the capability to address the clinically driven questions for which they seek answers. Whether attached to the coordinate system proximal or distal to a joint, coordinate systems for force and moment representation should be centered within the joint of interest. The JCS offers a less ambiguous and more anatomically relevant representation of joint moments and a clear demonstration of muscle activity. The future implementation of clinically significant standard practices will advance the field toward a full understanding of the link between wheelchair propulsion and pathology.
Acknowledgments
The authors acknowledge Kathie Bernhardt and Diana Hansen for their assistance with subject testing and data processing. All aspects of this study were funded by a grant from the National Institutes of Health (R01HD4878).
All aspects of this study were funded by a grant from the National Institutes of Health (R01HD48781)
Abbreviations
- ISB
International Society of Biomechanics
- JCS
joint coordinate system
- UE
upper extremity
References
- 1.Gellman H, Sie I, Waters RL. Late complications of the weight-bearing upper extremity in the paraplegic patient. Clin Orthop Relat Res. 1988 Aug;(233):132–5. [PubMed] [Google Scholar]
- 2.Wylie EJ, Chakera TM. Degenerative joint abnormalities in patients with paraplegia of duration greater than 20 years. Paraplegia. 1988 Apr;26(2):101–6. doi: 10.1038/sc.1988.20. [DOI] [PubMed] [Google Scholar]
- 3.Pentland WE, Twomey LT. Upper limb function in persons with long term paraplegia and implications for independence: Part II. Paraplegia. 1994 Apr;32(4):219–24. doi: 10.1038/sc.1994.41. [DOI] [PubMed] [Google Scholar]
- 4.Bayley JC, Cochran TP, Sledge CB. The weight-bearing shoulder. The impingement syndrome in paraplegics. J Bone Joint Surg Am. 1987 Jun;69(5):676–8. [PubMed] [Google Scholar]
- 5.Curtis KA, Drysdale GA, Lanza RD, Kolber M, Vitolo RS, West R. Shoulder pain in wheelchair users with tetraplegia and paraplegia. Archives of Physical Medicine & Rehabilitation. 1999 Apr;80(4):453–7. doi: 10.1016/s0003-9993(99)90285-x. [DOI] [PubMed] [Google Scholar]
- 6.Sie IH, Waters RL, Adkins RH, Gellman H. Upper extremity pain in the postrehabilitation spinal cord injured patient. Archives of Physical Medicine & Rehabilitation. 1992;73(1):44–8. [PubMed] [Google Scholar]
- 7.Mercer JL, Boninger M, Koontz A, Ren D, Dyson-Hudson T, Cooper R. Shoulder joint kinetics and pathology in manual wheelchair users. Clin Biomech (Bristol, Avon) 2006 Oct;21(8):781–9. doi: 10.1016/j.clinbiomech.2006.04.010. [DOI] [PubMed] [Google Scholar]
- 8.Boninger ML, Cooper RA, Robertson RN, Rudy TE. Wrist biomechanics during two speeds of wheelchair propulsion: an analysis using a local coordinate system. Archives of Physical Medicine & Rehabilitation. 1997;78(4):364–72. doi: 10.1016/s0003-9993(97)90227-6. [DOI] [PubMed] [Google Scholar]
- 9.Boninger ML, Cooper RA, Baldwin MA, Shimada SD, Koontz A. Wheelchair pushrim kinetics: body weight and median nerve function. Archives of Physical Medicine & Rehabilitation. 1999;80(8):910–5. doi: 10.1016/s0003-9993(99)90082-5. [DOI] [PubMed] [Google Scholar]
- 10.Kulig K, Rao SS, Mulroy SJ, Newsam CJ, Gronley JK, Bontrager EL, et al. Shoulder joint kinetics during the push phase of wheelchair propulsion. Clinical Orthopaedics & Related Research. 1998;354:132–43. doi: 10.1097/00003086-199809000-00016. [DOI] [PubMed] [Google Scholar]
- 11.Robertson RN, Boninger ML, Cooper RA, Shimada SD. Pushrim forces and joint kinetics during wheelchair propulsion. Archives of Physical Medicine & Rehabilitation. 1996;77(9):856–64. doi: 10.1016/s0003-9993(96)90270-1. [DOI] [PubMed] [Google Scholar]
- 12.Collinger JL, Boninger ML, Koontz AM, Price R, Sisto SA, Tolerico ML, et al. Shoulder biomechanics during the push phase of wheelchair propulsion: a multisite study of persons with paraplegia. Arch Phys Med Rehabil. 2008 Apr;89(4):667–76. doi: 10.1016/j.apmr.2007.09.052. [DOI] [PubMed] [Google Scholar]
- 13.Koontz AM, Yang Y, Price R, Tolerico ML, Digiovine CP, Sisto SA, et al. Multisite comparison of wheelchair propulsion kinetics in persons with paraplegia. J Rehabil Res Dev. 2007;44(3):449–58. doi: 10.1682/jrrd.2006.05.0048. [DOI] [PubMed] [Google Scholar]
- 14.Koontz AM, Cooper RA, Boninger ML, Souza AL, Fay BT. Shoulder kinematics and kinetics during two speeds of wheelchair propulsion. J Rehabil Res Dev. 2002 Nov–Dec;39(6):635–49. [PubMed] [Google Scholar]
- 15.Sabick MB, Kotajarvi BR, An KN. A new method to quantify demand on the upper extremity during manual wheelchair propulsion. Archives of Physical Medicine & Rehabilitation. 2004 Jul;85(7):1151–9. doi: 10.1016/j.apmr.2003.10.024. [DOI] [PubMed] [Google Scholar]
- 16.Van Drongelen S, Van der Woude LH, Janssen TW, Angenot EL, Chadwick EK, Veeger DH. Mechanical load on the upper extremity during wheelchair activities. Archives of Physical Medicine & Rehabilitation. 2005 Jun;86(6):1214–20. doi: 10.1016/j.apmr.2004.09.023. [DOI] [PubMed] [Google Scholar]
- 17.Veeger HE, Rozendaal LA, van der Helm FC. Load on the shoulder in low intensity wheelchair propulsion. Clinical Biomechanics. 2002;17(3):211–8. doi: 10.1016/s0268-0033(02)00008-6. [DOI] [PubMed] [Google Scholar]
- 18.Wu G, van der Helm FC, Veeger HE, Makhsous M, Van Roy P, Anglin C, et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion--Part II: shoulder, elbow, wrist and hand. J Biomech. 2005 May;38(5):981–92. doi: 10.1016/j.jbiomech.2004.05.042. [DOI] [PubMed] [Google Scholar]
- 19.Cooper RA, Boninger ML, Shimada SD, Lawrence BM. Glenohumeral joint kinematics and kinetics for three coordinate system representations during wheelchair propulsion. Am J Phys Med Rehabil. 1999 Sep–Oct;78(5):435–46. doi: 10.1097/00002060-199909000-00006. [DOI] [PubMed] [Google Scholar]
- 20.Desroches G, Aissaoui R, Bourbonnais D. Relationship between resultant force at the pushrim and the net shoulder joint moments during manual wheelchair propulsion in elderly persons. Arch Phys Med Rehabil. 2008 Jun;89(6):1155–61. doi: 10.1016/j.apmr.2007.10.040. [DOI] [PubMed] [Google Scholar]
- 21.Lin VW, editor. Spinal Cord Medicine. New York: Demos Medical Publishing, Inc; 2003. [Google Scholar]
- 22.Schache AG, Baker R. On the expression of joint moments during gait. Gait Posture. 2007 Mar;25(3):440–52. doi: 10.1016/j.gaitpost.2006.05.018. [DOI] [PubMed] [Google Scholar]
- 23.Dumas R, Cheze L. 3D inverse dynamics in non-orthonormal segment coordinate system. Med Biol Eng Comput. 2007 Mar;45(3):315–22. doi: 10.1007/s11517-006-0156-8. [DOI] [PubMed] [Google Scholar]


