Vortex interactions with flapping wings and fins can be unpredictable

Abstract

As they fly or swim, many animals generate a wake of vortices with their flapping fins and wings that reveals the dynamics of their locomotion. Previous studies have shown that the dynamic interaction of vortices in the wake with fins and wings can increase propulsive force. Here, we explore whether the dynamics of the vortex interactions could affect the predictability of propulsive forces. We studied the dynamics of the interactions between a symmetrically and periodically pitching and heaving foil and the vortices in its wake, in a soap-film tunnel. The phase-locked movie sequences reveal that abundant chaotic vortex-wake interactions occur at high Strouhal numbers. These high numbers are representative for the fins and wings of near-hovering animals. The chaotic wake limits the forecast horizon of the corresponding force and moment integrals. By contrast, we find periodic vortex wakes with an unlimited forecast horizon for the lower Strouhal numbers (0.2–0.4) at which many animals cruise. These findings suggest that swimming and flying animals could control the predictability of vortex-wake interactions, and the corresponding propulsive forces with their fins and wings.

1. Introduction

Many swimming and flying animals create large vortices with their fins and wings. These vortices are shed, and together they form the ‘footprint’ of the animal in the fluid: the wake. In the wake, vortices arrange in shapes and patterns that not only reflect the motion of animals, but also the dynamics of vortex–vortex and vortex–animal interactions. Two well-known examples of intense vortex–vortex interactions are vortex merging (Cerretelli & Williamson 2003) and stripping (Legras & Dritschel 1993). In some cases, vortex–animal interactions are beneficial to an animal's locomotory performance. Insects, for example, can recapture their vortex wake and thus generate extra lift (Dickinson et al. 1999) while some fishes tune their body wave to exploit vortices in the wake of obstacles in running water (Liao et al. 2003). The dynamics of wake vortices might, however, not always be as easy to tune into.

Vortex wakes of animals are typically envisioned as a periodic row of alternating vortices. This is contradicted by several computational fluid dynamic studies of two-dimensional pitching and heaving (flapping) foils that model swimming and flight (Lentink & Gerritsma 2003; Lewin & Haj-Hariri 2003; Alben & Shelley 2005; Blondeaux et al. 2005; Iima 2007), which report the existence of some aperiodic and chaotic vortex wakes. These chaotic vortex wakes mediate chaotic fluid forces on foils, with a corresponding strange attractor in the phase plot of fluid lift and thrust, and are accompanied by a broad frequency spectrum and sensitivity to initial conditions (Lentink & Gerritsma 2003). Further studies in which the foil propels itself through the fluid show that these chaotic forces result in chaotic body motion of which the extent is determined by the relative inertia of the foil (Alben & Shelley 2005; Iima 2007). If animals actually need to cope with chaotic vortex interactions and forces, it might well constrain their neural control of body motion. There exists, however, no experimental confirmation of chaotic vortex-wake interactions generated by pitching and heaving foils. Further, it is unknown to what extent vortex interactions are chaotic in the parametric domain of pitching and heaving foils representative for animal fins and wings. Here, we study these vortex interactions with a two-dimensional flapping foil in a soap tunnel for a wide range of kinematics representative for slender animal wings and fins (e.g. Lentink & Dickinson 2009).

2. Material and methods

We refer to Muijres & Lentink (2007) for a detailed description of the set-up and method, and to Lentink et al. (2008) for theory.

(a). Flapping foil in a soap tunnel

Our foil pitches and heaves periodically and symmetrically, with 90° out of phase sinusoidal kinematics, in a nearly horizontal, gravity driven, soap-film tunnel that flows at approximately 0.25 m s⁻¹. We chose symmetric and periodic foil kinematics to ensure that measured asymmetric and aperiodic vortex-wake interactions can be linked explicitly to vortex dynamics. The foil is 5 per cent thick and flaps at 4–25 Hz.

(b). Flapping parameters

The flapping foil generates thrust when the effective angle of attack is larger than zero: α_eff = α_ind − α₀ > 0° (figure 1), which occurs when the angle of attack amplitude induced by the foil's flapping motion α_ind = arctan (2π × A*/λ*) is larger than the pitch amplitude α₀ (A* = A/c, dimensionless heave amplitude; λ* = U_∞/fc, dimensionless heave length; A, heave amplitude; c, chord length; U_∞, free stream velocity; f, flap frequency). The combinations of (A*, λ*, α₀) studied here are all combinations of (A* = 0, 1, … , 4; λ* = 3, 5, … , 13; α₀ = 0°, 15°, … , 90°) for which α_eff ≥ 0°. The average Reynolds number Re of the foil is , in which Re_∞ = U_∞ × c/ν ≈ 1000 is the free stream Reynolds number (Re is of order 1000; soap-film kinematic viscosity ν ≈ 1 × 10⁻⁶ m² s⁻¹ (Martin & Wu 1995)).

Figure 1.

Phase-locked averages wake images reveal abundant chaotic vortex-wake interactions as a function of flapping foil kinematics; dimensionless heave amplitude A* and wavelength λ*, and pitch amplitude α₀, which are illustrated in (a). (a) A* = 1; (b) A* = 2. Empty spaces represent α_eff < 0° (no thrust) for which we made no measurements. White lines (dashed) indicate the borderline between chaotic and periodic flow according to λ* = 2π × A*/tan(50° + α₀/4) (see text for definition). The blue bar under the figure indicates the range of λ* at which swimming and flying animals are known to cruise for the corresponding A* (which together build up the corresponding Strouhal number range).

(c). Flow visualization and image analysis

We filmed the vortex wake of the foil time (500 Hz) and space resolved (1024 × 1280 pixels) as a function of (A*, λ*, α₀), and phase-locked over 99 periods; at stroke reversal and midstroke. We obtained interference fringes by illuminating the soap film with a monochromatic SOX lamp (Rutgers et al. 2001), which correlate strongly with the vorticity field (Rivera et al. 1998). For every single image, we calculated the absolute gradient field and median filtered it (Matlab 2007; medfilt2, 5 × 5 pixels) to eliminate background fringes. Next, small pollutants were automatically removed (Matlab; bwareaopen). After normalizing the intensity of these images, we averaged them over all 99 images for stroke reversal and midstroke. For periodic flows, this average image is identical to the individual images of the vortex wake, and therefore crisp (frame-by-frame inspection revealed no higher order harmonics, which is quantitatively supported by the electronic supplementary material, figure S2). For chaotic flow, the vortex wake varies erratically over the 99 frames and the average image is therefore blurred. We enhanced the dynamic range of all average images and coloured them using identical and automated Photoshop image adjustments (auto levels, shadow/highlight, tri-tone colouring).

(d). Force and moment integrals

We quantify chaos (Lorenz 1963) by calculating the standard deviation of the moment of area integrals of the 99 phase-locked image intensity fields I for stroke reversal and midstroke. This standard deviation should be close to zero for purely periodic flow. First, we create black and white images using a cut-off value of 0.17, which results in I = 1 where we visualized vortices and I = 0 elsewhere. Next, we determined the first three polar moments of area of I: 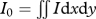; ; for the near wake (integration area starts c/4 behind the foil and has width 8c and height 16c). Wu (1980) shows that, if we calculate these moments using the vorticity field instead of I, I₀ would represent circulation, whereas I_1,r and I_2,r would be part of the integrals for calculating net force and moment, respectively. Because I = 1 represents the integration area where the vorticity is non-zero, we can assume that chaotic variation of I₀, I_1,r and I_2,r indicates that the corresponding circulation, force and moment integrals will vary chaotically too. The required fidelity for neural control depends on the short-term fluctuation. Therefore, we eliminated slow fluctuations by subtracting the period-16 Butterworth filtered time sequence (Matlab, fourth-order Butterworth). We use the (phase-averaged) standard deviation of the short-term variation as a quantitative proxy for chaos.

3. Results

The phase-locked average images of the vortex wakes reveal a boundary between a region of periodic (crisp images) and chaotic (blurred images) wakes as a function of flapping kinematics; figure 1 (A* = 1, 2) and figure 2a (A* = 3) (see the electronic supplementary material, figure S1 for A* = 0, 4). Several crisp images of common periodic wake types can be found at relatively low wavelengths for A* = 1, such as ‘two vortex pairs’ (λ* = 5, α₀ = 15°, 30°) and ‘two single vortices’ (λ* = 5, α₀ = 0°) per flap period (figure 1). Such periodic vortex configurations are both found in the wakes of fishes as a function of swimming kinematics (e.g. Müller et al. 2001; Borazjani & Sotiropoulos 2008). At shorter wavelengths and higher amplitudes, the wakes are chaotic resulting in blurred images of the wake, the border between periodic and chaotic vortex wakes shifts to higher wavelengths for higher amplitudes.

Figure 2.

(a) Phase-locked averages wake images for A* = 3 (figure 1). (b) Pooled normalized standard deviation of I₀, I_1,r and I_2,r (with respect to maximum value) as a function of α_ind at constant α₀ shows approximately exponential growth. Exponential fits from left to right for pooled I yield (α₀ = 0°; r² = 0.95); (α₀ = 15°; r² = 0.94); (α₀ = 30°; r² = 0.92); (α₀ = 45°; r² = 0.97); (α₀ = 60°; r² = 0.91). (c) Standard deviation of I₀ (outer circle), I_1,r (middle circle), and I_2,r, (inner circle) plotted as a function of α_eff and α_ind, which are colour-coded from minimum to maximum/2; (0.4c)² ≤ s(I₀) ≤ (2.6c)²; (1.2c)³ ≤ s(I_1,r) ≤ (4.1c)³; (2.1c)⁴ ≤ s(I_2,r) ≤ (5.6c)⁴. We find a periodic vortex-wake domain at low values of α_ind (which corresponds with Strouhal number) and a chaotic domain at high values (yellow area). The border between both domains can be described by α_eff = 247° − 3.15α_ind and represents the left border of the yellow area (crosses indicated the calculated intersections in (b) to which the borderline is fitted). Animals preferably cruise at low Strouhal numbers St, in the range 0.2–0.4 (Taylor et al. 2003), for which we find solely periodic vortex-wake interactions.

We find that the normalized standard deviation in I₀, I_1,r and I_2,r is similar valued (see the electronic supplementary material, figure S2 for evidence) and grow roughly exponentially as a function of α_ind at constant α₀, figure 2b. This illustrates the dramatic growth in variance in the moment of area integrals owing to chaos. We define the chaos boundary at 15 per cent of the maximum standard deviation in I₀, I_1,r and I_2,r in figure 2b and capture it through fitting the combined normalized standard deviations of I₀, I_1,r and I_2,r with an exponential function as a function of α_ind at constant α₀ (0°, 15°, 30°, 45°, 60°; we excluded 75°, because data lacked for a proper fit) and calculating the intersection.

To determine how relevant chaos could be for our understanding of animal propulsion through fluids, we plot our proxy for chaos, the standard deviations of I₀, I_1,r and I_2,r (§2), as a function of effective and induced angle of attack, figure 2c. This condensed plot for A* = 1–4 features our linear approximated borderline between chaotic and periodic wakes, which we calculated as follows. We linearly fitted the intersection values of α_ind at 15 per cent of the maximum standard deviation in figure 2b and the corresponding values of α_eff (plotted in figure 2c). The linear fit α_eff = 247° − 3.15α_ind describes the 15 per cent maximum standard deviation boundary between chaotic and periodic flows well (r² = 0.99). This boundary yields similar chaos boundaries in figures 1a,b and 2a: λ* = 2π × A*/tan(50° + α₀/4) (rounded coefficients) that match well with the transition between sharp (periodic) and blurry (chaotic) wake images.

4. Discussion

Our study of vortex wakes generated by a two-dimensional flapping foil reveals that vortex wakes of flapping foils are chaotic for λ* < 2π × A*/tan(50° + α₀/4) and (A* = 1−4; λ* = 3−13; α₀ = 0–90°; ). This borderline also predicts the wavelengths for which chaos (Lentink & Gerritsma 2003) and aperiodicity (Lentink et al. 2008) have been reported within the range of kinematics studied here (Lewin & Haj-Hariri (2003) and Alben & Shelley (2005) studied A* < 1, while Blondeaux et al. (2005) and Iima (2007) studied λ* < 3).

How relevant are chaotic vortex-wake interactions for swimming and flying animals? Our study is representative for cruising flight and swimming only, because we consider λ* ≥ 3 and because two-dimensional foils approximate the flow around foils of three-dimensional wings best during forward flight (Lentink & Dickinson 2009). During cruising, animals predominantly operate at Strouhal numbers St = tan(α_ind)/π in the range 0.2–0.4 (Taylor et al. 2003), which has been found to yield high propulsive efficiency (Triantafyllou et al. 1993). For this cruising St-range, we find only periodic vortex wakes; see blue region in figure 2c and the corresponding λ* range indicated with a blue horizontal bar in figure 1. Our model experiments suggest that swimming and flying animals might encounter chaotic vortex-wake interactions when swimming or flying slower than λ* < 2π × A*/tan(50° + α₀/4).

Even though our two-dimensional flapping foil model is a highly simplified representation of an animal wing or fin, which ignores three-dimensional flow and high Reynolds number effects, it seems unlikely that including these three-dimensional effects in a vortex-dynamic study of animal locomotion will suppress chaos altogether. We therefore predict that animals could tune their kinematics to evade the chaos of vortex-wake interactions. Butterflies might be interesting candidates for studying if some animals do exploit chaos—the so-called ‘butterfly effect’ of chaos might help make their flight paths more erratic to confound predators (Dudley 2000).