Periodic versus scale-free patterns in dryland vegetation

Abstract

Two major forms of vegetation patterns have been observed in drylands: nearly periodic patterns with characteristic length scales, and amorphous, scale-free patterns with wide patch-size distributions. The emergence of scale-free patterns has been attributed to global competition over a limiting resource, but the physical and ecological origin of this phenomenon is not understood. Using a spatially explicit mathematical model for vegetation dynamics in water-limited systems, we unravel a general mechanism for global competition: fast spatial distribution of the water resource relative to processes that exploit or absorb it. We study two possible realizations of this mechanism and identify physical and ecological conditions for scale-free patterns. We conclude by discussing the implications of this study for interpreting signals of imminent desertification.

1. Introduction

Vegetation patchiness in water-limited systems plays important roles in driving ecological processes at different temporal and spatial scales. Vegetation patchiness affects the distribution of limiting resources and seeds, modifies species distribution and diversity, and may contain information about imminent catastrophic shifts such as desertification (Kéfi et al. 2007a; Shachak et al. 2008). Field observations have revealed two contrasting types of vegetation landscapes: nearly periodic vegetation patterns with characteristic length scales, such as bands on hill slopes or spotted patterns (Valentin et al. 1999; Barbier et al. 2006), and scale-free patterns that lack characteristic length scales and follow broad, power-law-like patch-size distributions (Kéfi et al. 2007a; Scanlon et al. 2007).

The emergence of scale-free patterns can be attributed either to exogenous, random environmental factors (such as soil heterogeneity, micro-topography, grazing or fires; Lovett et al. 2005), or to self-organization owing to endogenous and deterministic local processes, involving negative and positive feedbacks between biomass and water and between below- and above-ground biomass (Rietkerk et al. 2004; Gilad et al. 2007a; Meron et al. 2007a,b; Barbier et al. 2008). Recent studies, based on simple cellular-automaton models (Kéfi et al. 2007a,b; Scanlon et al. 2007; Manor & Shnerb 2008a), have suggested that scale-free vegetation patterns are a result of self-organization under conditions of local facilitation and global resource competition. In another recent model study (Manor & Shnerb 2008b), global competition and scale-free patterns have been obtained in the limit of large ‘water diffusion’. However, the origin of global competition in terms of physical and ecological processes (such as overland water flow, soil-water diffusion, infiltration properties, water-uptake rates, etc.), and its attainability in practice, has remained poorly understood. Understanding the factors that lead to scale-free patterns and control the transitions to periodic patterns is most significant in light of recent suggestions that transitions to narrow patch-size distributions can be used as early signals for imminent desertification (Kéfi et al. 2007a,b; Manor & Shnerb 2008a).

Studying these questions calls for more elaborate models that upscale detailed eco-physical information at the single-patch scale to information about patterns at the landscape scale. Models of this kind have been proposed and used to explain the emergence of periodic vegetation patterns and their changes along environmental gradients (Borgogno et al. 2009). As many of these models capture the essential ingredients of overland water flow, soil-water dynamics and water-limited biomass growth, they should account for scale-free patterns too, provided these patterns are results of endogenous self-organization. Surprisingly, despite the vast literature on vegetation patchiness and the longstanding dichotomy of periodic versus scale-free patterns, studies along this direction have hardly been pursued (Manor & Shnerb 2008b). In this paper, we use the model that has been introduced by Gilad et al. (2004, 2007a) to unravel eco-physical conditions that give rise to scale-free vegetation patterns and to study transitions from scale-free patterns to periodic patterns when these conditions are not satisfied.

2. The Model

The Gilad et al. model contains the basic ingredients of earlier models, such as positive biomass–water feedbacks owing to shading and differential infiltration, but includes in addition the non-local water uptake by plant roots and the associated feedback between above-ground and below-ground biomass (root augmentation during vegetation growth). Varying the relative strength of these feedbacks allows studying their roles in controlling the sizes of patches and in forming patterns at the landscape scale, under different environmental conditions. The model does not take into account deposition–erosion processes (Saco et al. 2007), nutrient dynamics (Ravi et al. 2007) and vegetation–atmosphere feedbacks (Dekker et al. 2007), which are assumed here to be negligible.

The model equations for a uniform flat topography are

2.1

where represents biomass per unit area, describes the soil-water content per unit area and is the height of a thin above-ground water layer. Here, are the spatial coordinates, T is time and ∇² = ∂_X² + ∂_Y² is the Laplacian operator. We refer the reader to Gilad et al. (2004, 2007a) for a detailed presentation of the model. Here, we focus on the quantities and terms that are most relevant to the present study. We first note that the biomass growth rate, , the water-uptake (transpiration) rate, , the infiltration rate, , and the evaporation rate, , are all functions or functionals of the dynamical variables that model various feedbacks. Two feedbacks, which we refer to as the infiltration and the root-augmentation feedbacks, are particularly relevant here. They are both positive in the sense that they accelerate local biomass growth, and they both involve water-transport processes that induce long-range competition. The most relevant parameters to this study are: the precipitation rate, P, which serves here as a control parameter; the soil-water diffusion coefficient, D_W; and the surface–water transport coefficient, , which is inversely related to the ground-surface friction coefficient. Other parameters include the coefficient of local seed dispersal, ; the maximum standing biomass, K; and the biomass decay rate, M.

The infiltration feedback is associated with higher infiltration rates of surface water into vegetated soil relative to bare soil. Physical or biogenic crusts in arid areas may significantly reduce the infiltration rate in bare soil, increasing the surface-water flow towards vegetation patches (Campbell et al. 1989; Eldridge et al. 2000). This process favours the growth of newly formed vegetation patches (short-range facilitation), but also reduces the availability of the water resource at larger distances, introducing competition among different patches (long-range competition). The feedback is captured by a monotonously increasing dependence of the infiltration rate on the above-ground biomass, (Gilad et al. 2007a). This dependence is controlled by a parameter 0 ≤ f ≤ 1 that quantifies the infiltration contrast between vegetated and bare soil: when f = 1, the infiltration rate becomes biomass-independent, , and there is no infiltration contrast. When , the infiltration rate is very low in bare soil () but increases to in vegetation patches.

The root-augmentation feedback is a positive feedback between the above-ground biomass and the below-ground root system. As plants grow, their root systems extend in size and probe new soil regions. This increases the amount of water available to the plants and accelerates their growth. As in the case of the infiltration feedback, the accelerated growth of a vegetation patch comes at the expense of vegetation growth in its neighbourhood, thereby introducing long-range competition. The feedback is modelled by the following non-local forms of the biomass growth rate and of the water-uptake rate:

2.2

and

2.3

where the kernel represents the spatial extent of the root system. The root augmentation is captured by assuming a monotonously increasing dependence of the Gaussian width S on the above-ground biomass. Specifically, , where S₀ represents the root size of a seedling, and the parameter E provides a measure for the root-to-shoot allocation; the larger E, the farther the roots extend per given above-ground biomass. The long-range competition that the feedback induces is accounted for by the form of ; plants at deplete the soil-water content at X if their roots extend to that point.

Less important in this study is the positive feedback between biomass and water owing to shading and reduced evaporation, which we model as (Gilad et al. 2007b). This feedback does not involve water transport and therefore does not induce long-range competition as the infiltration and root-augmentation feedbacks do.

The model described above has been successfully applied to a wide range of self-organization problems in the context of water-limited vegetation. These include vegetation patterns and pattern transitions along environmental-stress gradients (rainfall, grazing; Gilad et al. 2004, 2007a), productivity–resilience trade-offs in banded vegetation on hill slopes (Yizhaq et al. 2005), mechanisms of vegetation-ring formation (Sheffer et al. 2007), plants as ecosystem engineers (Gilad et al. 2004, 2007a; Meron et al. 2007a,b), transition from competition to facilitation in woody-herbaceous systems along rainfall gradients (Gilad et al. 2007b), mechanisms of species coexistence associated with spatial patterning (Gilad et al. 2007b), and effects of stochastic rainfall on vegetation production and land coverage (Kletter et al. 2009).

3. Finite Competition Range Limits Patch Growth

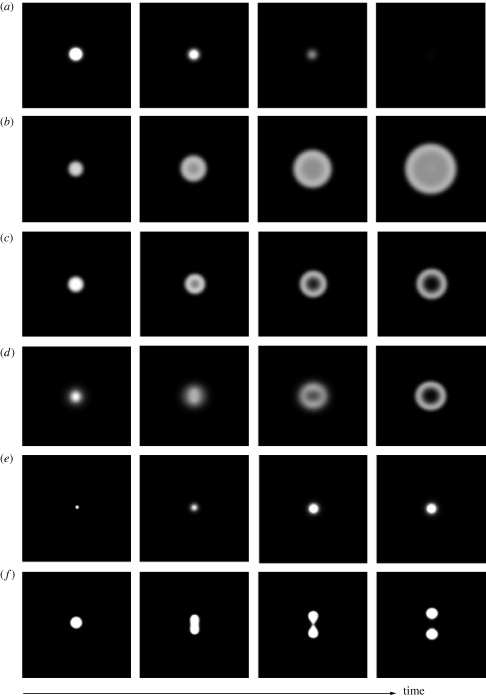
The two feedbacks described in the previous section act together to constrain the growth of vegetation patches under conditions of water deficiency. To understand the role of each feedback in limiting patch growth, we performed a series of highly idealized numerical experiments in which we turned on and off the two feedbacks independently. Each simulation was started with an initial isolated spot-like patch. Snapshots indicating various stages in the patch dynamics are shown in figure 1.

Figure 1.

Single-patch dynamics as affected by the infiltration and root-augmentation feedbacks. (a,b) No infiltration and root-augmentation feedbacks (f = 1, E = 0): an initial spot-like patch either (a) shrinks to zero, when the precipitation rate is low enough (P = 75 mm y⁻¹), or (b) expands indefinitely when the precipitation rate is high (P = 225 mm y⁻¹). (c) No root-augmentation feedback (f = 0.1, E = 0): when the precipitation rate is high enough (P = 105 mm y⁻¹), patches grow but their areas are limited by central dieback processes that lead to ring-shape patches. (d,e) No infiltration feedback and moderate root-augmentation feedback (f = 1, E = 1 m² kg⁻¹): (d) when the precipitation rate is sufficiently high (P = 165 mm y⁻¹), patches grow but form ring shapes owing to central dieback processes; (e) at lower precipitation rates (P = 140 mm y⁻¹) growing patches approach a fixed size. (f) No infiltration feedback and strong root-augmentation feedback (f = 1, E = 4 m² kg⁻¹): when the precipitation rate is sufficiently high (P = 195 mm y⁻¹), patches initially grow but then split owing to peripheral dieback processes. Other parameters are S₀ = 0.125 m, K = 1 kg m⁻², Q = 0.05 kg m⁻², M = 1.2 y⁻¹, A = 400 y⁻¹, N = 4 y⁻¹, Λ = 0.032 m² (kg y)⁻¹, Γ = 20 m² (kg y)⁻¹, D_B = 0.000625 m² y⁻¹, D_W = 0.0625 m² y⁻¹, D_H = 0.2 m⁴ (kg y)⁻¹, R = 10.

Turning off both the infiltration feedback and the root-augmentation feedback (f = 1, E = 0), we found that initial patches become smaller and smaller until they completely disappear, if the precipitation rate is low enough (figure 1a), or grow evenly in all directions to form arbitrarily large patches if the precipitation rate exceeds a threshold value (figure 1b). When the infiltration feedback is switched on (f = 0.1, E = 0) and the precipitation rate is lower than some critical value, initial patches shrink in size and disappear as found above for no infiltration feedback. Beyond that critical value, however, patches do not grow indefinitely; as the patch area increases, less runoff reaches the patch centre and a ring shape develops owing to increased competition and central dieback (figure 1c). Turning off the infiltration feedback and switching on a root-augmentation feedback of moderate strength (f = 1, E = 1 m² kg⁻¹) also leads to ring-shaped patches at sufficiently high precipitation rates (figure 1d), except that now the central dieback is due to increased water uptake at the patch centre by the roots of newly recruited individuals at the patch periphery. At relatively low precipitation rates, however, convergence to spot-like patches of fixed size can occur (figure 1e), for the water uptake ahead of the growing patches can deplete the soil-water content down to a level at which no further growth is possible. When the root-augmentation feedback is strong enough (E = 4 m² kg⁻¹), yet another behaviour can take place: strong competition over the water resource at the patch periphery can lead to a peripheral dieback and patch splitting (figure 1f).

The results described above manifest the long-range competition effects, associated with the infiltration and root-augmentation feedbacks, that act to limit patch sizes. These effects are generally balanced by short-range collective processes of facilitation (Rietkerk & van de Koppel 2008); a growing patch benefits from increased infiltration and reduced evaporation. These facilitative processes help small patches survive conditions of high water stress. We note, however, that vegetation patch formation can occur without facilitation; elimination of differential infiltration and shading (by setting f = 1 and R = 0) does not rule out vegetation pattern formation (including isolated patches) as long as the root-augmentation feedback is significant.

4. Global Competition and Scale-Free Patterns

Scale-free patterns characterized by broad patch-size distributions must contain very large patches approaching the size of the domain considered (in order of magnitude). How can the presence of such large patches be reconciled with the existence of the infiltration and root-augmentation feedbacks, which act to limit patch sizes? This fundamental question has been overlooked in most studies to date. However, important clues are contained in the numerical observations that scale-free patterns develop once a condition of global competition is imposed (Scanlon et al. 2007) or when water diffusion approaches infinity (Manor & Shnerb 2008b). Our main finding is that global competition can develop when the spatial distribution of the water resource becomes very fast compared with processes that exploit or absorb it. Under this ideal condition, any local depletion of the water resource is immediately compensated by fast water transport. The three processes that limit patch growth (central dieback, peripheral dieback and growth halt) become ineffective and large patches can develop as much as the global water content allows.

We found two different physical realizations of this condition. The first realization is associated with fast surface-water flow relative to the infiltration into vegetated soil. Under this condition, surface water can flow over long distances before infiltrating significantly into the soil. In the absence of other processes that limit patch growth, such as strong root-augmentation feedback, very large patches can develop because surface water can reach the patch centres rather than infiltrating mostly at the periphery and causing central dieback. If, in addition, the precipitation rate is sufficiently low, small patches will cease growing once the globally shared water resource is already exploited by all other patches. Under these conditions, wide patch-size distributions can develop.

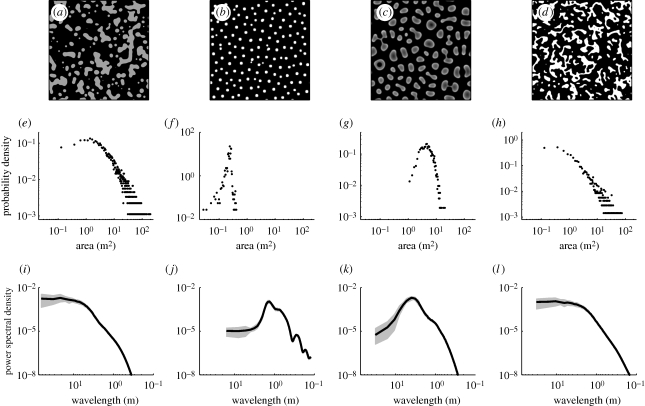
We confirmed these ideas by solving the model equations in the limit , switching off the root-augmentation feedback (E = 0) and choosing the precipitation rate to be below the existence threshold of uniform vegetation. Figure 2a shows a typical realization of vegetation patchiness under these conditions, starting with random initial conditions of the biomass variable. The pattern appears amorphous, with patches spanning a wide range of sizes and lacking a characteristic length scale, as shown by the patch-size distribution and power spectrum in figure 2e and figure 2i, respectively. However, switching on the root-augmentation feedback or slowing down the surface-water flow limits patch sizes and introduces characteristic correlation lengths, as the patch-size distributions and the peaked power spectra show in figure 2b,c,f,j,k.

Figure 2.

(a) A typical scale-free pattern, obtained for global competition induced by fast surface-water flow relative to infiltration and (b,c) the appearance of characteristic patch sizes upon decreasing the competition range, either by increasing the root-to-shoot allocation parameter E, or (c) by increasing the time scale of surface-water flow. Global competition induced by fast soil-water diffusion relative to water uptake also gives rise to scale-free patterns. (e–h) show patch-size distributions, determined by censuses of connected areas above 0.05 kg m⁻² in density. (i–l) show average power spectra. Grey bands indicate the range in which 94 per cent of 32 independent realizations fall. The domain size shown is 64 × 64 m² for (a), 16 × 16 m² for (b) and 32 × 32 m² for (c,d). In all simulations, the integration time is 166 y. Parameter values: (a,l,i): E = 0, D_H = ∞, f = 0.1; (b,f,j): E = 4 m² kg⁻¹, D_H = ∞, f = 0.1; (c,g,k) E = 0, D_H = 1 m⁴ (kg y)⁻¹, f = 0.1; (d,h,l) E = 2 m² kg⁻¹, D_W = ∞, Γ = 7.2 m² (kg y)⁻¹, f = 1. All panels: P = 120 mm y⁻¹, A = 40 y⁻¹. Other parameters are as in figure 1.

The conditions for this form of global competition can be quantified using dimensional analysis to estimate how the size S_P of the largest patch scales with the parameters that control the flow and infiltration of surface water. The estimate of the largest biomass patch relies on the estimate of the largest wet patch, assuming that the growth is not seed-limited. Denoting by C_F and τ_I the flow velocity and the infiltration time, respectively, the size of the largest wet patch is . These quantities should be expressible in terms of the precipitation rate, P, the infiltration rate, A, and the transport coefficient, D_H. The dimensions of these parameters are and , where M, L and T stand for mass, length and time, respectively. Writing the flow velocity as , we obtain α = β= 1/2 and γ = 0. This gives . Similarly, we find . We thus deduce the following scaling relation for the maximal patch size: . This relation is in good agreement with numerical studies of the model equations.

Another possible realization of global competition can be achieved when the soil-water diffusion is fast relative to the water-uptake rate. The infiltration contrast can be low in this case, but the root-augmentation feedback should be strong enough to allow for the formation of patterns. Large patches can develop in this case because central and peripheral dieback are prevented by the fast soil-water diffusion, while small patches can remain small owing to the limited globally shared water resource. Figure 2d shows a typical vegetation pattern obtained under these conditions in the limit and with no infiltration contrast (f = 1). The pattern appears amorphous, with patches spanning a wide range of sizes and lacking a characteristic length scale, as figure 2h,l indicates. The maximal patch size in this case can be estimated as , where is the hydraulic conductivity and is the uptake time. A dimensional analysis similar to that described above leads in this case to the scaling relation , where is the diffusion coefficient for soil water and Γ is the water uptake (transpiration) rate per unit biomass. Using empirical data for soil-water conductivity and uptake time in the Kalahari desert (de Vries et al. 2000; Porporato et al. 2003), we obtain the order of magnitude estimate S_P ∼ 10² m. This value is comparable with the largest patch sizes observed in the Kalahari desert, suggesting fast soil-water diffusion relative to uptake as a possible mechanism for the wide patch-size distributions observed by Scanlon et al. (2007).

As the precipitation rate is decreased towards the threshold value below which vegetation patches no longer survive, narrow patch-size distributions generally develop. The reason is that the global sharing of a small overall amount of water among many growing patches severely limits their growth. The narrowing down of patch-size distributions as aridity stress increases is in line with the observation by Kéfi et al. (2007a) of a similar distribution change with increased grazing stress, because the two types of stress are correlated (Gilad et al. 2007a). We note that although global competition can induce scale-free patterns, it does not necessarily lead to such patterns; the asymptotic patterns strongly depend on the initial biomass distributions, and with appropriate choices regular patterns with narrow patch-size distributions can be induced.

5. Discussion

Of the two mechanisms suggested for global competition, fast surface flow relative to infiltration will be favoured on slopes, on terrains with low surface roughness, for soils with low infiltration rates, for species forming relatively small patches (for which the flow time scale τ_F = S₀/C_F is very short) and for species with low root augmentation (e.g. species that grow roots mostly in the vertical direction). Clonal perennial grasses, such as Poa Bulbosa (Sheffer et al. 2007), are possible examples of such species. Global competition owing to fast soil-water diffusion relative to water uptake will be favoured in soils with high hydraulic conductivities (e.g. sandy soils) and for species with high root augmentation and low water-uptake rates.

Taking into account environmental and plant species information of this kind in monitoring environmental changes can provide deeper understanding of the ecological and physical processes at work, and their significance. An important example is related to the suggestion that transitions from scale-free patterns to patterns with characteristic length scales may serve as warning signals for imminent desertification (Kéfi et al. 2007a), and that such transitions can be identified by monitoring changes in patch statistics (Manor & Shnerb 2008a). As the time scale of such changes can be quite long (tens of years in the case of woody vegetation; Barbier et al. 2006), faster indicators are needed. Estimates of the likelihood of a given region to support scale-free patterns, based on soil properties and species traits, can be made in a relatively short time, and may provide such indicators. High likelihood for scale-free patterns, for example, may indicate potential vulnerability to desertification if narrow patch-size distributions are observed.

Another consideration that calls for a deeper understanding of the ecological and physical processes that take place during pattern transitions is change in community structure. Simulations of the model equations show, for example, that species with higher root-to-shoot allocations (larger E) out-compete species with lower allocations. As figure 2b suggests, such a competition may result in narrower patch-size distributions, which do not necessarily imply imminent desertification.