Competition between native topology and nonnative interactions in simple and complex folding kinetics of natural and designed proteins

Abstract

We compared folding properties of designed protein Top7 and natural protein S6 by using coarse-grained chain models with a mainly native-centric construct that accounted also for nonnative hydrophobic interactions and desolvation barriers. Top7 and S6 have similar secondary structure elements and are approximately equal in length and hydrophobic composition. Yet their experimental folding kinetics were drastically different. Consistent with experiment, our simulated folding chevron arm for Top7 exhibited a severe rollover, whereas that for S6 was essentially linear, and Top7 model kinetic relaxation was multiphasic under strongly folding conditions. The peculiar behavior of Top7 was associated with several classes of kinetic traps in our model. Significantly, the amino acid residues participating in nonnative interactions in trapped conformations in our Top7 model overlapped with those deduced experimentally. These affirmations suggest that the simple ingredients of native topology plus sequence-dependent nonnative interactions are sufficient to account for some key features of protein folding kinetics. Notably, when nonnative interactions were absent in the model, Top7 chevron rollover was not correctly predicted. In contrast, nonnative interactions had little effect on the quasi linearity of the model folding chevron arm for S6. This intriguing distinction indicates that folding cooperativity is governed by a subtle interplay between the sequence-dependent driving forces for native topology and the locations of favorable nonnative interactions entailed by the same sequence. Constructed with a capability to mimic this interplay, our simple modeling approach should be useful in general for assessing a designed sequence’s potential to fold cooperatively.

The study of protein folding is important not only for deciphering the folding process and how misfolding can occur. The principles developed in theoretical investigations of folding (1–3) have provided insights into a broad range of molecular-recognition phenomena and dynamic behaviors in biology. Recent examples include protein–protein interactions (4), function of biomolecular machines (5), effects of desolvation in self-assembly (6, 7), and switch-like properties in binding (8). Among naturally evolved proteins, many fold cooperatively in a two-state-like manner (9), which is a remarkable feat from the vantage point of polymer physics (10). Although not all natural proteins share this property (11), its commonality argues that folding cooperativity may serve crucial biological functions such as guarding against harmful aggregation (12).

If cooperative folding can be a desirable trait under certain circumstances, a fundamental question arises: Can all folded globular structures attain a high degree of folding cooperativity? A revealing case is the designed protein Top7 (13), which folds to a de novo target structure that did not exist previously in the Protein Data Bank (PDB) but does so noncooperatively (14, 15). One possible reason for Top7’s failure to fold cooperatively is that current sequence design techniques are inferior to natural selection in this regard (14, 15). A recent analysis suggested, however, that a deeper cause might be that the Top7 topology itself is not conducive to cooperative folding (16). This view is consistent with several model studies indicating that native topology can constrain folding cooperativity (17–20). Thus, motivated by the same perspective that led to the considerations of a target structure’s encodability (21) or designability (22), it is of interest to go a step further to assess a structure’s designability for folding cooperativity.

The thermodynamic and kinetic manifestations of folding cooperativity are closely related because folding rates reflect the free energy barriers to folding. For instance, the negative correlation between native contact order and folding rate among small proteins (23) is consistent with predictions (18–20, 24) that proteins with higher native topological complexity tend to have higher folding barriers and thus fold more cooperatively. Here we focus mainly on folding kinetics, which affords more accurate characterizations of folding cooperativity than thermodynamics alone. A telling example is that even some Gō model proteins with an overall folding barrier are found to be short on kinetic folding cooperativity because the model chevron plots have significant rollovers (25, 26).

The experimental observation of a severe chevron rollover for Top7 indicates that nonnative interactions are at play in its complex, multiphasic folding kinetics (15). This finding prompted us to further pursue a recent native-centric model augmented by sequence-dependent nonnative hydrophobic interactions (27) and to use an improved version of this model to investigate the interplaying roles of native topology and placement of hydrophobic residues in Top7’s noncooperative folding kinetics. As a control, we applied the same model to ribosomal protein S6 (28, 29), which folds much more cooperatively. Among several cooperatively folding proteins that have secondary structure elements similar to those in Top7 (e.g., acylphosphatase), we chose to study S6 because of the computational tractability engendered by its relatively fast folding rate.

Results

As detailed in Methods and SI Text, we used coarse-grained C^α chains to model the 92-residue Top7 (1qys) (13) and 97-residue S6 (1ris) (30) (Fig. 1). Two forms of native contact energy were considered: a 12-10 Lennard–Jones potential as in the common Gō-like model (31, 32) and a desolvation-barrier (db) potential that incorporates an energetic penalty against water expulsion (33–35). An improved excluded-volume term was implemented (Figs. S1 and S2). Favorable nonnative hydrophobic (hϕ) interactions specific to a protein’s amino acid sequence were included as well (16). The hϕ compositions of Top7 (38/92 = 0.41) and S6 (43/97 = 0.44) are similar. Their different hϕ packing patterns are highlighted in Fig. 1. Compared to S6, Top7 has more regularly alternating hϕ and polar residues along its β-strands. However, Top7 has a 10-residue stretch (FAAILIKVFA from F63 to A72) within its C-terminal helix that contains 9 hϕ residues. No such high local hϕ density exists along the S6 sequence.

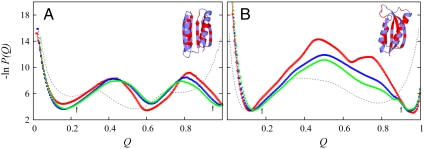
Fig. 1.

Simulated midpoint free energy profiles and PDB structures of Top7 (A) and S6 (B). P(Q) is normalized conformational population as a function of Q. In the ribbon diagrams, hydrophobic residues are in red; others are in blue. The profiles in red, blue, and green are for db + hϕ models with, respectively, κ²/ε = 0, 1, and 1.1. Profiles for the Gō models are in gray. The arrows indicate threshold Q_U and Q_F values used in our simulations of folding and unfolding kinetics. For Top7 and S6, respectively, Q_U = 0.23 and 0.18, and Q_F = 0.95 and 0.90. The profiles here are very similar to those obtained previously (16) with a slightly weaker excluded-volume repulsion (see Methods).

Native Topology Rationalizes Differences in Thermodynamic Folding Cooperativity of Top7 and S6.

Fig. 1 provides the free energy profiles for several models of Top7 and S6 simulated near their respective transition midpoints. For Top7 (Fig. 1A), the Gō model free energy profile (no favorable nonnative interactions) shows a global minimum at Q ≈ 0.55 with no barrier. With better accounting of desolvation effects, the Top7 profiles for the db + hϕ models exhibit two barriers; i.e., folding is thermodynamically three-state. For the S6 models, every profile in Fig. 1B shows an overall barrier, indicating that folding is thermodynamically two-state. Because db enhances folding cooperativity (7, 33, 35), the overall barriers in the db + hϕ S6 models are significantly higher than that in the Gō model. Consistent with experiment (14, 15, 28, 29), these model results demonstrate a lack of two-state folding cooperativity for Top7 and two-state-like folding for S6. Native topology is apparently a dominant factor that leads to the drastically different folding thermodynamics of Top7 and S6: Among the db + hϕ models examined in Fig. 1, nonnative hϕ interactions have only a minor impact on the free energy profiles of Top7. For S6, despite a rugged barrier (36) for the db (κ² = 0) model and a lowering of the folding barrier by nonnative hϕ interactions, all free energy profiles are two-state-like.

We consider only the db + hϕ models below because models that account for dbs are more realistic (6, 7, 33, 35, 37). In our analysis, the folded state and fully unfolded state were defined, respectively, by Q≥Q_F and Q ≤ Q_U. These demarcations (arrows in Fig. 1) were chosen to be near either the unfolded (small Q) or folded (Q ≈ 1) minimum but have a free energy (under midpoint conditions) ≈1.5k_BT higher to allow for conformational fluctuations. (k_B is the Boltzmann constant, and T is absolute temperature.) To compare experimental data measured at variable denaturant concentration with results simulated at variable interaction strength ε/T, we fit theoretical equilibrium folding transition curves against their experimental counterparts to arrive at a linear relationship between [GuHCl] and ε/T (Fig. 2). This method is equivalent to matching theoretical and experimental free energies of unfolding ΔG_U (20) (see Fig. S3). The rationale is that, similar to ε/T, denaturants have a rather uniform effect on the entire protein (38). Discussion of related procedures is provided in SI Text. Fig. 2 shows the fits for κ² = 1.1ε as well as the sigmoidal curves for fitting other κ² values. Fig. S3 shows that our fits entail extrapolating to zero denaturant from the transition region, because experimental data are not available for very low denaturant. In this regard, the premise of our linear fitting of ΔG_U against ε/T is no different from that on which the ΔG_U ∼ 13 kcal/mol estimate for Top7 (13) was based (Fig. S3a). It is instructive to note, however, that when partially folded conformations were included in the denatured population 1 - P_folded (including all Q < Q_F), both the simulated and experimental ΔG_Us in Fig. S3 exhibit nonlinear behaviors reminiscent of native-state hydrogen exchange isotherms (39).

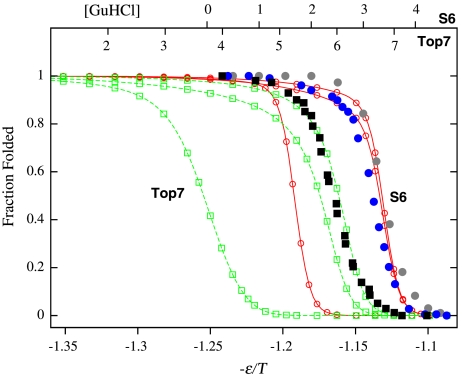
Fig. 2.

Matching simulated and experimental folded fractions (P_folded). Filled symbols are experimental folded fractions of Top7 (black squares, from ref. 14) and S6 (blue and gray circles, from refs. 28 and 29, respectively) as functions of denaturant concentration [GuHCl] (top scales, in M). Curves through open symbols are simulated folded fractions of Top7 (green) and S6 (red) as functions of interaction strength -ε/T (bottom scale) for db + hϕ models with κ²/ε = 0, 1, and 1.1 (from left to right for each set of curves). This figure shows the experimental [GuHCl] scales being fitted to the κ² = 1.1ε models. Fits for other models were attained by moving the -ε/T scale relative to the [GuHCl] scales. Midpoint ε/T value decreases with increasing κ² because nonnative hϕ interactions destabilize the folded structure.

Nonnative Hydrophobic Interactions Have Markedly Different Impacts on Top7 and S6 Folding Kinetics.

Fig. 3 compares simulated and experimental folding/unfolding kinetics. Among the simulated folding chevron arms (filled symbols), those for the Top7 models display much more prominent rollovers (downward concavity) compared to those for the S6 models. (Simulation results for ε/Ts corresponding to [GuHCl] < 0 are considered to be experimentally inaccessible.) In the db models without nonnative hϕ interactions (red squares), the folding arm of Top7 shows a rollover for [GuHCl] < 4 M, whereas that for S6 is essentially linear. When nonnative hϕ interaction strength κ² is increased to 1.0ε (blue circles) and 1.1ε (green triangles), folding-arm rollover for Top7 becomes increasingly severe. Unlike the simple relationship between folding thermodynamics and kinetics for highly cooperative folders (35), the sensitivity of Top7 model kinetics to κ² was not apparent from the free energy profiles in Fig. 1A that show only minor variations with κ². For κ² = 1.1ε in Fig. 3A, the Top7 model folding arm begins rolling downward at [GuHCl] ≈ 3 M. In contrast, for the S6 models, although rollover increases somewhat with κ², the rollover is mild even for κ² = 1.1ε. Echoing effects of nonspecific nonnative interactions (40), the specific nonnative hϕ interactions in our models speed up S6 folding, but they slow down Top7 folding under strongly folding conditions. In quantitative agreement with experiment (crosses in Fig. 3), transition-midpoint folding rates of Top7 models are ∼50 times faster than those of S6 models.

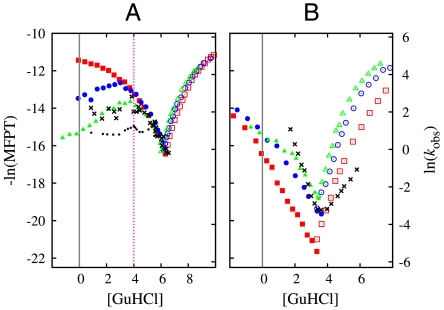
Fig. 3.

Chevron plots for Top7 (A) and S6 (B). Data points in red, blue, and green provide negative logarithm of simulated mean first passage time (MFPT) of folding (filled symbols) and unfolding (open symbols), for db + hϕ models with κ²/ε = 0, 1, and 1.1, respectively. Dependence of model MFPT on ε/T is translated to that on [GuHCl] (in M; see Fig. 2). Black crosses are experimental data for S6 (28) and Top7 (single-exponential rate for [GuHCl]≥4 M and fast-phase rate of the biexponential fit for [GuHCl] < 4 M in ref. 14; these data exhibit a trend similar to that of the middle phase in ref. 15). Vertical dashed lines mark [GuHCl] = 0 as well as the onset of severe experimental chevron rollover for Top7 at [GuHCl] = 4 M (14, 15). Black dots in (A) show - ln(A_middle/k_middle + A_slow/k_slow) calculated from the experimental middle- and slow-phase data in ref. 15; this quantity corresponds to the negative logarithm of the MFPT contributed by these two phases. We did not include fast-phase data in this calculation because of uncertainties entailed by the negative A_fast values in ref. 15.

Fig. 3 argues strongly that nonnative hϕ interactions are a critical part of real Top7 folding kinetics. In their absence, our simulation (red squares) failed utterly to mimic the experimental folding arm (black crosses). The onset of severe experimental rollover around [GuHCl] = 4 M (14) was reproduced only with a strong κ² = 1.1ε (green triangles). This trend suggests that the native-centric driving forces in Top7 are malleable; they can be overridden readily by nonnative forces. In contrast, the folding arms of the S6 models for different κ² values have only mildly different shapes (Fig. 3B). Thus, the native-centric driving forces in S6 are apparently robust against perturbations from the nonnative hϕ interactions entailed by its own amino acid sequence. For Top7, as [GuHCl] decreases below 4 M, the chevron folding arm of the κ² = 1.1ε model rolls downward, whereas the experimental middle and slow phases reported in ref. 15 show a nearly flat dependence. This apparent mismatch between theory and experiment might be partly caused by our model’s uniform treatment of [GuHCl] dependence for all interaction types. Assessing the true extent of the mismatch is difficult, however, because of uncertainties regarding the fast phase in ref. 15. After all, the effective - ln(MFPT) calculated for the experimental middle and slow phases (black dots in Fig. 3A) does show a downward trend when [GuHCl] is decreased from 4 to ∼3 M because of increase in slow-phase amplitude. For S6, our models’ chevron folding arms are similar to their experimental counterpart, but their slopes are not as steep. Thus, without many-body effects (10, 19, 20), the db + hϕ models for S6 are still a bit short on reproducing the full folding cooperativity of real S6.

Complex Top7 Folding Arises from Transiently Trapped Misfolded Conformations.

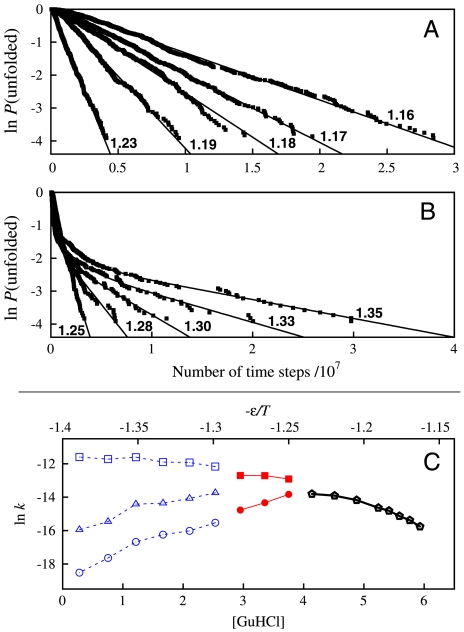
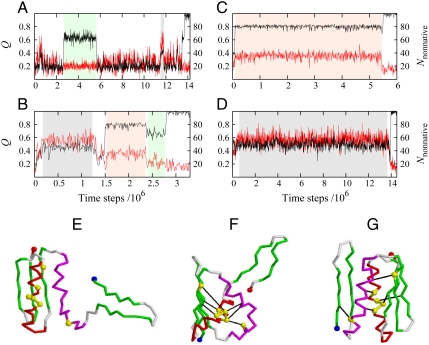
We now focus on the db + hϕ, κ² = 1.1ε Top7 model by which the overall experimental chevron trend was reasonably reproduced (Fig. 3A). Folding relaxation of this model is essentially single-exponential near the transition midpoint (1.16 ≤ ε/T ≤ 1.23, Fig. 4A) but clearly not single-exponential for stronger folding conditions (ε/T > 1.25, Fig. 4B). Following a common practice in analyzing experimental data (15), we fitted the unfolded population P(unfolded) to Σ_iA_i exp(-k_it) with one, two, or three exponentials, where k_is are relaxation rates and t is time (Fig. 4C): Near the midpoint (1.16 ≤ ε/T < 1.25), the only reasonable fit is a single exponential. Then, if three exponentials were used to fit the rest of our data (ε/T≥1.25), two of the fitted k_is turned out to be approximately equal for the ε/T values plotted in red in Fig. 4C. Thus, only two exponentials were used for those data. Fig. 4C summarizes our fits. As folding conditions become stronger (ε/T increases), k₁ for the fast phase (top curve) increases monotonically, but those of the middle and slow phases (k₂ and k₃, other curves) show a downward trend for ε/T≥1.3 and ε/T≥1.25, respectively. Consistent with experiment (15), the middle and slow phases in Fig. 4C display more prominent rollovers than the fast phase. Nonetheless, two issues that will require more effort should be noted. First, the middle- and slow-phase k_is in Fig. 4C decrease with increasing ε/T, but the corresponding experimental rates were essentially independent of [GuHCl] under strongly folding conditions (see above). Second, all fitted amplitudes in our model were positive (with middle-phase A₂ < 0.3, slow-phase A₃ < 0.2), whereas the experimental fast-phase amplitude was negative.

Fig. 4.

Simulated folding relaxation for Top7 for the db + hϕ model with κ² = 1.1ε. Data points in (A) and (B) show relaxation behaviors for selected ε/T values (as marked); curves are single or multiple exponential fits. Data points in (C) show the rates (k_is) from single- (black), two- (red), and three-exponential (blue) fits as functions of -ε/T and [GuHCl] (using the match in Fig. 2).

Although purely native-centric interactions can be consistent with mild chevron rollovers (25, 32) (see red squares for κ² = 0 in Fig. 3A), a severe rollover such as that exhibited by the green triangles (κ² = 1.1ε) in Fig. 3A are indicative of deep kinetic traps with nonnative contacts (3). We delineated the structural species underlying the complex Top7 model folding kinetics by monitoring both native and nonnative contacts along folding trajectories (Fig. 5A–D) and characterizing the transient intermediate structures (Fig. 5E–G). Near the midpoint (Fig. 5A, ε/T equivalent to [GuHCl] = 6 M), a partially folded ensemble with Q ∼ 0.6 and N_nonnative ∼ 20 nonnative contacts (green-shaded region) was populated occasionally. These conformations tend to have a folded C-terminal fragment and a disordered N-terminal fragment (Fig. 5E), similar to the equilibrium intermediate state under midpoint conditions (the “I state” in ref. 16). We now call this state I₀. When folding conditions were strengthened to an ε/T equivalent to [GuHCl] = 4 M (Fig. 5B), two intermediates with more nonnative contacts appeared more frequently (gray- and orange-shaded regions). Their prominence increases when folding conditions were further strengthened (Fig. 5C and D). Conformations in the gray-shaded regions have large N_nonnative ∼ 60 but only Q ∼ 0.5. Structurally, they are typified by Fig. 5F, which shows the C-terminal helix threading through an opening between the N-terminal helix and three β-strands. We call this ensemble I₁. These misfolded conformations clearly have to first unwrap before they can reach the Top7 native structure. In contrast, conformations in the orange-shaded regions have a high native content (Q ∼ 0.8) and are less nonnative (N_nonnative ∼ 35). Typified by Fig. 5G, these conformations, which we refer to collectively as I₂, may be viewed as mispacked, because both their N-terminal β-hairpin and C-terminal fragment are native-like but the N-terminal β-hairpin is far away from the C-terminal β-strands, and thus fail to form the native 5-strand β-sheet. More examples of folding trajectories are provided in Figs. S4–S6.

Fig. 5.

Simulated trajectories, folding intermediates, and kinetic traps of Top7 for the db + hϕ model with κ² = 1.1ε. (A–D) Fractional number of native contact Q (black traces, left scales) and number of nonnative contact N_nonnative (red traces, right scales) as functions of time. Data points at the end of every 5,000 simulation time steps were tracked. Example trajectories were simulated near the transition midpoint at ε/T = 1.16 (A), around the top of the chevron rollover at ε/T = 1.25 (B), and under strongly folding conditions at ε/T = 1.32 (C and D). (E) A typical I₀ conformation sampled during time periods shaded in green in (A) and (B). (F) A trapped structure representative of the I₁ conformations sampled during time periods shaded in gray in (B) and (D). (G) Another trapped structure, representative of the I₂ conformations sampled during time periods shaded in orange in (B) and (C). The N and C termini of the structures are depicted as blue and red spheres, respectively. Six of the seven residues suggested by experiment to stabilize nonnative states (see text) are marked as yellow spheres. Black lines in (F) and (G) indicate examples of significant nonnative contacts involving these residues (chosen from the maps in Fig. 6).

Nonnative Interactions Play Significant Roles in Top7 Folding.

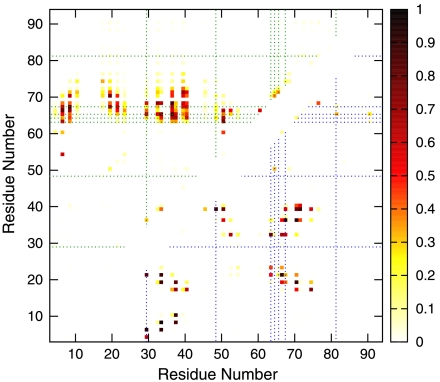
Fig. 6 gives the distribution of nonnative contacts in I₁ (upper left) and I₂ (lower right). Experiment has implicated L29, V48, F63, A64, A65, L67, and V81 in the formation and/or stabilization of nonnative states (15). Consistent with this finding, Fig. 6 shows that 6 of these 7 residues (except V81) participated in significant nonnative hϕ interactions in the kinetic intermediates of our model: (i) L29 made contact with A65 (itself suggested by experiment to be involved in nonnative interactions), I66, and V68 in I₁; L29 took part in nonnative contact with I4, V6, and Y21 in I₂ with even higher probabilities. (ii) V48 had one strong nonnative contact with Y39 in I₂. (iii) F63, A64, A65, and L67 are part of the extended stretch of hϕ residues in the C-terminal helix (see above). These four residues participated in numerous nonnative interactions in both intermediates, particularly in an extended region in I₁ between the C-terminal helix on one hand and the N-terminal helix and β-strands on the other (Fig. 5F). In Fig. 6, these contacts cluster along a horizontal band with a vertical span covering positions 63 to ∼71. We have also characterized two transition states along Top7’s free energy profile (Fig. 1A). Unlike small natural proteins that fold through transition states with native-like topologies (41), our model predicts that nonnative interactions are prevalent in Top7 folding transition states (see SI Text and Fig. S7).

Fig. 6.

Nonnative contact maps of simulated Top7 kinetic traps. Probabilities of nonnative contacts for I₁ and I₂: The upper left map is for I₁, determined from the gray-shaded regime in Fig. 5D; the sampled conformations are typified by Fig. 5F. The lower right map is for I₂, determined from the orange-shaded period in Fig. 5C; the sampled conformations are typified by Fig. 5G. Residues suggested by experiment to be involved in nonnative interactions (see text) are identified by dotted lines. Residue numbering in our contact maps is identical to that in the PDB.

Discussion

By modeling specific nonnative hϕ interactions, we have added substantially to the advances made in previous atomic simulation of the C-terminal fragment of Top7 (42) and Gō-like modeling of S6 (43, 44). Our results suggest that the drastically different folding kinetics of Top7 and S6 is an outcome of an omnipresent interplay between native-centric driving forces and sequence-specific nonnative hϕ interactions. This interplay is fundamentally a competition between native and alternative topologies, with many possible contributing factors. The scope of our study is limited. For example, the near-ideal geometry of the designed β-sheet in Top7 may make it easier to form nonnative strand arrangements, but tackling this question would require structural details beyond those considered in our model.

Despite our model’s simplicity, it succeeded in rationalizing key differences in the folding kinetics of Top7 and S6. Many nonnative interactions in our Top7 model involve a long stretch of hϕ residues, which is uncommon in natural globular proteins (45). We expect that much of Top7’s experimental folding complexity is related to this peculiarity. By comparison, S6 does not have such a long hϕ stretch, and effects of nonnative hϕ interactions (27, 39, 46) on experimental S6 folding are mild (47), possibly owing in part to the effects of “gatekeeper” residues (44). As a test, we have considered a db + hϕ model for a hypothetical S6 mutant with four hϕ substitutions to create a long hϕ stretch similar to that in Top7. This model (Fig. S8) predicts a severe chevron rollover, suggesting in general that a long hϕ stretch would likely lead to complex folding kinetics. However, it is not known experimentally whether such a sequence that increases the hϕ composition by ∼10% yet still folds to the same S6 native structure actually exists. It remains to be elucidated as well whether the long hϕ stretch or some similar hϕ sequence patterns are necessary for encoding the Top7 native topology. Thus, it will be enlightening to explore the experimental viability of designing the Top7 fold with no long hϕ stretch and designing the S6 fold with a long hϕ stretch. Results from such experiments may go a long way toward deciphering the origin of folding cooperativity.

The present results are broadly in line with the perspective that intermediates in protein folding are common (46). The central challenge in the interpretation of multiphasic folding kinetics is to infer the intermediate state(s) along the folding pathway(s). For Top7, Watters et al. proposed a four-state model on the basis of a three-exponential fit of the experimental relaxation data (15). Because our model relaxation data can also be fitted by three exponentials (Fig. 4), we used our results to explore the relationship between multiphasic kinetics and folding intermediates by inspecting a total of ∼1,400 folding trajectories under three classes of conditions: near midpoint (ε/T = 1.16,1.19), at the onset of severe chevron rollover (ε/T = 1.25,1.27), and strongly favorable to folding (ε/T = 1.32,1.37). Each trajectory was started from an open conformation in the unfolded state (U) and ended in the native state (N); examples are provided in Fig. 5A–D and Figs. S4–S6. Using Q and N_nonnative of transient populations to identify them with either I₀, I₁, or I₂, we observed that a significant fraction (∼16%) of all trajectories may be described as direct U → N pathways (e.g., the middle panel in the third row of Fig. S4). These trajectories apparently passed through the I₀ minimum along the thermodynamic free energy profile (Fig. 1A) rather quickly. Among pathways that involved transiently populated intermediates, U → I₀ → N was most probable near the midpoint (> 25%), but it became less likely under stronger folding conditions. In comparison, although U → I₁ → N and U → I₂ → N were rare near the midpoint, together they accounted for ∼12% of the folding trajectories under strongly folding conditions. Interestingly, in these pathways, the trapped I₁ or I₂ did not always have to go through an appreciable period of time in the U state before reaching N. Other less common pathways that we have observed include U → I₁ → I₂ → N, U → I₁ → I₀ → N, U → I₂ → I₀ → N, U → I₀ → I₂ → I₀ → N, U → I₂ → I₀ → I₂ → N, U → I₁ → I₂ → I₀ → N, and U → I₁ → I₀ → I₂ → N, but no pathway in which I₂ appeared before I₁ was observed. We also came across many trajectories that could not be identified with a pathway through a series of well-defined intermediate states. All in all, the diversity of these pathways indicates that although individual folding trajectories can be represented by various sequential pathways, there is no guarantee that complex folding kinetics such as that exhibited by Top7 is controlled by a simple network of transitions among a few discrete states.

In summary, we reemphasize that our model formulation should be useful as a tool in protein design to assess a target structure’s potential for cooperative folding (16). Recent progress in NMR techniques has made it possible to obtain detailed structural information on “invisible,” low-populated protein states (48, 49). In view of the agreement with experiment achieved here and our approach’s previous success in predicting specific nonnative interactions in the folding transition state of Fyn SH3 mutants (27), the predicted misfolded and mispacked Top7 structures (Figs. 5 and 6) as well as the nonnative contacts predicted for its transition states (Fig. S7) are worthy candidates to be tested by structural experiments. The present study has opened a window into an intriguing interplay between native topology and nonnative hydrophobic interactions. Deeper insights await further efforts in both theory and experiment.

Methods

Our coarse-grained C^α models were modified from (i) the common Gō-like model (31, 32) and (ii) a native-centric model that accounted for dbs (33–35). The db model is now augmented by sequence-dependent nonnative hϕ interactions (16, 27). Native contacts were determined from PDB structures by using a 4.5-Å separation cutoff between non-hydrogen atoms. Model potentials were parametrized by an energy ε > 0, a db height ε_db = 0.1ε, and a solvent-separated-minimum depth ε_ssm = 0.2ε as before (16, 35). The only modification we have made to the formulation in ref. 16 is on the excluded-volume part of the nonnative interactions. In previous studies, our group followed refs. 31 and 33 in using a repulsive term ε(r_rep/r_ij)¹² between residues not in contact in the native structure, where r_ij is the separation between C^α positions i and j, with r_rep = 4.0 Å (16, 32, 34, 35). This construct is adequate for many applications. But for predicting misfolded structures, r_rep = 4.0 Å is not always sufficient to avoid steric clashes in real proteins (Fig. S1). To alleviate this limitation, we adjusted r_rep on the basis of the following heuristic considerations.

(i) We retained 4.0 Å as the lower bound on r_rep because 4.0 Å is approximately the contact distance between two methanes (10), and thus it should correspond roughly to the closest possible approach between two C^α positions. (ii) The average volume of an amino acid residue ≈140 Å³ (50). If this volume were spherical, its radius would be ≈3.2 Å, and the separation between the centers of two such spheres would be ≈6.4 Å. Because real amino acid residues are not spheres, we stipulated a slightly smaller upper bound of 6 Å on r_rep. (iii) The maximum r_rep = 6 Å does not apply to all nonnative contact pairs because heterogeneity in residue sizes and protein core packing can result in a separation r₀ < 6 Å in the native structure between C^α positions that are not in native contact. For such cases, alternate packing between different rotamer pairs that allow for a closer approach between the C^α positions than that in the native structure might be possible; thus we chose 0.75r₀ as the repulsion radius. Taking these considerations together, we arrived at a modified repulsive energy between nonnative pairs E_rep = ε(σ₀/r_ij)¹², wherein

[1]

and Δ^(1/12) = 0.75 (Δ = 0.03). E_rep is the only term in the U_nonnative potential for nonnative interactions not involving hydrophobic residues (Fig. S2a).

As in our previous work, the attractive part of the nonnative hϕ interactions is the sum E_HP = -Σ_iΣ_jκ_iκ_j exp[-(r_ij - σ_hϕ)²/2] over hϕ residues, which include alanine, valine, leucine, isoleucine, methionine, tryptophan, phenylalanine, and tyrosine (27) in the Top7 or S6 sequence. We do not distinguish between hydrophobic residue types, so we set κ_i = κ. In view of the above modification on r_rep, we set σ_hϕ = σ₀ + 1 Å (instead of σ_hϕ = 5 Å in ref. 27). Further setting K_HP = 1 in the original formulation (27) to simplify notation, the total nonnative interaction between a pair of hϕ residues is now given by

[2]

Examples of this hϕ term are provided in Fig. S2b. Most of our results are for the db model augmented with nonnative hϕ interactions, in which case the total potential is E₀ - κ²Σ_iΣ_j exp[-(r_ij - σ₀ - 1 Å)²/2], where E₀ is the db potential with E_rep = ε(σ₀/r_ij)¹². We refer to this class of constructs as the db + hϕ model. The purely native-centric db model is equivalent to a db + hϕ model with κ² = 0. Further details of the simulation procedures are provided in SI Text.