Effects of CBV, CBF and Blood-Brain Barrier Permeability on Accuracy of PASL and VASO Measurements

Abstract

Cerebral blood flow (CBF), cerebral blood volume (CBV) and water permeability through blood-brain barrier (BBB) are important hemodynamic parameters in brain physiology. Pulsed arterial spin labeling (PASL) and vascular-space occupancy (VASO) techniques have been used to measure regional CBF and CBV, respectively. However, these techniques generally ignore the effects of one hemodynamic parameter on the measurement of others. For instances, the influences of CBV changes on ASL or the permeability effects on VASO typically was not accounted for in the quantification of blood flow or volume. In the current work, the biophysical effects of CBV on PASL and permeability on VASO signals are evaluated using a general two-compartment model. The dependence of these effects on the longitudinal relaxation time (T₁) at various field strengths is also assessed by simulations. Results indicate that CBV has negligible to small influences on PASL signal (< 6.6% at 3T) and permeability effects are negligible on VASO signal (< 0.1% at 3T) under normal physiological conditions. In addition, CBV effect on PASL is further diminished at high field strengths, but residual blood contamination in VASO signal may be enhanced at high fields due to the reduced difference between extra- and intra-vascular T₁ values.

INTRODUCTION

Cerebral blood flow (CBF), cerebral blood volume (CBV) and water permeability through blood-brain barrier (BBB) are important physiological parameters reflecting brain functions and dysfunctions (1, 2). Local CBF and CBV changes accompanying neuronal activity and metabolism have been used as neurophysiological indices for mapping functional neuroanatomy (1, 3) and the degradation of BBB permeability has been found in brain diseases including Alzheimer’s disease and multiple sclerosis (4, 5). Accurate measurements of these hemodynamic parameters, therefore, are essential for investigating brain functions and assessing brain pathologies (3, 6).

A number of MRI techniques have been developed to measure CBF, CBV and BBB permeability. Contrast agents such as monocrystalline iron oxide nanocolloid (MION) can be utilized to measure relative CBV changes (7) and ultra small paramagnetic iron oxide (USPIO) can assess BBB permeability (8, 9). Without exogenous contrast agents, arterial spin labeling (ASL) imaging uses magnetically labeled water in arteries as an endogenous tracer to obtain blood flow information (10), while vascular-space occupancy (VASO) imaging measures MR signals reflecting CBV changes associated with brain activation (11). Most of these techniques rely on biophysical models to quantify the physiological parameters from measured MR signals. Several fundamental assumptions have been used in these models to simplify the quantification/estimation procedures which in turn may reduce the accuracy in quantifying the physiological parameters. For instance in ASL, single-compartment models have been employed assuming an instant water exchange between blood and brain tissue (infinite BBB permeability) and constant CBV in both steady and dynamic states (10, 12). Other studies have attempted to improve quantification of CBF by using a two-compartment model and assuming limited permeability (13, 14). However, CBV has always been kept as a constant in ASL models which might not be appropriate during dynamic states such as neuronal activation. Similarly, the influences of permeability on CBV quantification in VASO are not well known.

As such, a systematic investigation of the hemodynamic effects on inversion recovery (IR) based fMRI sequences is necessary especially on pulsed ASL (PASL) and VASO. To achieve this goal, we evaluated the physiological effects on PASL and VASO signals using a modified two-compartment model at magnetic fields strengths with various longitudinal relaxation times (1.5 to 9.4 Tesla). The efficacies of VASO measurements were assessed under normal physiological conditions by simulating its signal sensitivity and blood contribution.

METHODS

In order to describe PASL and VASO signals in an IR-based biophysical model, a brief description of the single- and two-compartmental models are highlighted below. General solutions for these models are attached in the Appendix.

Single-compartment model

The most adopted model for ASL signal is the single-compartment model, as described in Eq. [1],

$$\frac{{dM}_T(t)}{dt}=\frac{M_T^0-M_T(t)}{T_1^T}+f·[M_a(t)-M_v(t)]$$ [1]

where M_T(t) is the total magnetization inside the imaging voxel, $M_T^0$ is the fully relaxed longitudinal magnetization of M_T(t), M_a(t), is the magnetization of arterial blood, M_v(t) is the magnetization of venous blood, and f is CBF. $T_1^T$ in the equation is the effective longitudinal relaxation time of the water in the voxel, which is equal to the inverse of the volume-fraction weighted sum of the intrinsic longitudinal relaxation rates of blood and extra-vascular tissue.

$$\frac{1}{T_1^T}=\frac{\mathit{CBV}}{T_1^b}+\frac{1-\mathit{CBV}}{T_1^e}$$ [2]

Eq. [2] is based on the assumption that water molecules inside the capillary exchange instantly with the water molecules in the extra-vascular space (15). Therefore, the magnetization in the venous component, M_v(t), would be linearly related to the average magnetization of the image voxel, M_v(t) = M_T(t)/λ, where λ is the blood-tissue partition coefficient. Due to this assumption of instant water exchange through BBB, permeability is considered to be infinitely high in the single-compartment model.

General two-compartment model

A two-compartment model with finite BBB permeability was developed by Parkes and Tofts to describe the ASL signal (14). In the present study the model was modified to a general form for IR sequences, which can be used to describe both PASL and VASO techniques. The concept of the two-compartment model is that the voxel is composed of intra-vascular blood and extra-vascular tissue, as shown in Fig. 1. Each component has its own temporal characteristic as described in Eq. [3–5]

Figure 1.

An illustration of two-compartment model with blood flow and permeability effects. Each compartment has its own magnetization (M) and longitudinal relaxation time (T₁).

$$\{\begin{array}{l}\frac{{dM}_b(t)}{dt}=\frac{M_b^0-M_b(t)}{T_1^b}+\frac{f}{v_{bw}}·[M_a(t)-M_v(t)]+\frac{PS}{v_{bw}}·[M_e(t)-M_b(t)]\hfill \\ \frac{{dM}_e(t)}{dt}=\frac{M_e^0-M_e(t)}{T_1^e}+\frac{PS}{v_{ew}}·[M_b(t)-M_e(t)]\hfill \\ \frac{{dM}_a(t)}{dt}=\frac{M_a^0-M_a(t)}{T_1^b}\hfill \end{array}$$ [3] [4] [5]

where M_b(t) is the magnetization from the capillary blood, M_e(t) is the magnetization from the extra-vascular tissue, M_a(t)is the magnetization from the arterial blood, $M_b^0,M_e^0$ and $M_a^0$ are equilibrium magnetizations of capillary blood, tissue, and arterial blood, respectively; $T_1^b$ and $T_1^e$ are intrinsic longitudinal relaxation times of blood and tissue, respectively; v_bw and v_ew are the water volume per blood/tissue unit volume, which is equal to the product of CBV and blood water content (ρ_b) and the product of (1-CBV) and extra-vascular water content (ρ_e), respectively; and PS is the permeability-surface area product. Among the three equations, Eq. [5] indicates that the arterial magnetization only relaxes with $T_1^b$ before entering the capillary, while Eq. [3] describes the magnetizations of the blood compartment including arterioles, capillaries, and venules. Provided that the longitudinal relaxation time of blood remains unchanged in the vascular components, Eq. [3] and Eq. [5] have the same $T_1^b$ as the relaxation time of blood (16). The middle term of Eq. [3] delineates the CBF effect including the inflow from the arterial (M_a) and outflow to the venous (M_v). The last term of Eq. [3] expresses the permeability effect, the exchange rate of water molecules between blood and tissue compartments. As shown in the Appendix, the blood magnetization is no longer a simple term but a function of CBF and permeability. Eq. [4] represents the extra-vascular compartment in the imaging voxel, with the relaxation term and water exchange term. The total magnetization in the imaging voxel is equal to the sum of the magnetization from each compartment multiplied by its relative volumes, i.e.

$$\begin{array}{ll}{M}_T(t)& =S_b(t)+S_e(t)\\ & =v_{bw}·M_b(t)+v_{ew}·M_e(t)\end{array}$$ [6]

where $M_b^0=M_e^0$ and $M_a^0={\rho }_b·M_b^0$ because the water molecules are assumed to be equally distributed at equilibrium. For PASL with alternative labeling and control scans, S(t) and M(t) in Eq. [6] can be expressed as ΔS(t) and ΔM(t), the difference signal/magnetization between labeling (selective IR) and control (non-selective IR) signals. In contrast, M(t) from the non-selective image is used to represent the VASO signal.

Scenarios of venous outflow for PASL

Similar to that of a single-compartment model, the two-compartment model described in Eq. [3–5] needs an assumption for M_v(t) to estimate the total magnetization in the voxel. The assumption typically used in the single-compartment model, M_v(t) = M_T(t)/λ, is no longer valid for the two-compartment model because water exchange between the two-compartments is not usually instantaneous (except for PS being infinitely high). Following the study of Parkes and Tofts (14), we consider two scenarios of venous outflow (M_v) for the PASL signal: slow perfusion and fast perfusion. Under the condition of slow perfusion, the labeled water from artery is assumed to exchange completely with the extra-vascular compartment so that the labeled water never leaves the voxel before image acquisition (ΔM_v = 0). This scenario is valid when the mean transit time is longer than the inversion time (TI), which is favorable for human brain studies. A low baseline CBF of 60 ml/100g/min was used in the simulation of slow perfusion. In contrast, because the labeled water flows rapidly under the condition of fast perfusion, it can be assumed that the outflow venous magnetization is the same as the capillary blood in the voxel at the measurement time (ΔM_v = ρ_b*ΔM_b). This scenario is expected for studies of small animals such as rats due to their faster perfusion rates (17–19). A high baseline CBF of 180 ml/100g/min was adopted in simulations of fast perfusion (17). It should be noted that both the slow and fast models are approximations and a more accurate model would consider distributed signal along the blood compartment such as that developed by St. Lawrence et al. (20). As for VASO signal, it is not necessary to consider slow/fast perfusion scenarios since the blood signal in all vascular regimes, including artery, capillary and venous, would be inverted uniformly over the coil coverage. Therefore, it is assumed that the outflow venous magnetization is equal to a weighted capillary blood magnetization inside the voxel (M_v = ρ_b*M_b).

Simulation parameters

The general solutions of the single-compartment and two-compartment model can be derived from Eq. [1,2] and Eq. [3–5], respectively (see Appendix). It can be seen that PASL and VASO signals are dependent on physiological, physical, and imaging parameters. Typical values of the physiological parameters at resting state and the physical and imaging acquisition parameters at 3T are listed in Table 1. Among these parameters, the adopted TR-TI pairs were different for PASL and VASO in order to reach their maximum individual contrasts. In the simulation, we assumed that these biophysical and physiological parameters do not change during neural activations except for CBF (70% increase, f ^actv = 60×1.7 = 112 ml/100g/min (21) and CBV (25% increase, CBV ^actv= 5×1.25 = 6.25 ml/100g-tissue (22). Since the goal of this work was to evaluate CBF, CBV and BBB permeability effects on PASL and VASO signals, wide ranges of CBF (0~150 ml blood/100g/min), CBV (5~7 ml/100g-tissue), and PS (0~700 ml water/100g/min) were utilized to evaluate these effects representing different physiological conditions for both slow and fast perfusion scenarios. These evaluations were also performed at various magnetic fields using the field-dependent parameters listed in Table 2.

Table 1.

Typical values of the physiological, physical and imaging parameters used in the simulations.

Name	Value	Reference
f (CBF)	60 ml blood/100g/min (slow perfusion & VASO)	(23)
	180 ml blood/100g/min (fast perfusion)	(17, 23)
CBV	5 ml/100g	(24, 25)
PS	150 ml water/100g/min	(29)
λ	0.9 ml blood/ml tissue	(23)
ρb	0.89 ml water/ml blood	(35)
ρe	0.87 ml water/ml EV space	(35)
T1b	1.63 s (3T)	(16)
T1e	1.21 s (3T)	(36)
α	0.9
TR	4 s (PASL)
	2 s (VASO)
TI	1.4 s (PASL)
	$T_1^b·log\left(\frac{2}{1+e^{-TR/T_1^b}}\right)\text{s}(\text{VASO})$	(11)

Table 2.

Biophysical parameters under different magnetic fields (TI was calculated using TR = 2 sec).

	1.5T	3T	4.7T	7T	9.4T
T1b	1.35 s§	1.63 s	1.92 s*	2.20 s*	2.44 s*
T1e	0.9 s§	1.21 s	1.55 s§	1.95 s§	2.35 s§
TI of VASO	0.66 s	0.71 s	0.75 s	0.78 s	0.80 s

^*Blood T₁s at multiple magnetic fields were measured by Dobre et al. (37)

^§Literature reviews for gray matter T₁s at multiple magnetic fields were collected by Wu et al. (38, 39)

RESULTS

To evaluate the CBV effect on PASL signal, simulations were performed on four presumed modes: 1) resting state with CBV of 5 ml/100g and CBF of 60 ml/100g/min (Base mode); 2) a 25% CBV increase without any CBF change (ΔV mode); 3) a 70% CBF increase without any CBV change (ΔF mode); and 4) activated state with a 25% CBV increase and a 70% CBF increase (Active mode). CBF changes relative to the Base mode in PASL were calculated for the single-compartment and two-compartment models at 3T (Table 3). In the single-compartment model, a CBV increase of 25% only caused a 0.2% change of CBF as shown in the ΔV mode. Comparing the CBF changes in the ΔF and Active modes (Active -ΔF), the CBV effect had a very small increase (0.3%). In the two-compartment model with slow perfusion, the CBV weighting on PASL signal is slightly higher than in the single-compartment model resulting in a 0.5% CBF change in the ΔV mode and a 0.9% increase in (Active -ΔF) mode. However, the CBV effect in the two-compartment model with fast perfusion was relatively large in contrast to the other two models with a 2.3% CBF change in the ΔV mode and a 5.4% CBF change in (Active -ΔF) mode. These simulation results indicate that the CBV effect on PASL signal is larger in the fast perfusion scenario than that in the slow perfusion.

Table 3.

Comparisons between single-compartment model (1-comp), two-compartment model with slow perfusion (2-comp^slow), and two-compartment model with fast perfusion (2-comp^fast) at 3T when TI = 1.4 sec and PS = 150 ml/100g/min.

Percent signal change relative to baseline	1-comp	2-compslow	2-compfast
25% CBV Change (ΔV)	0.2%	0.5%	2.3%
70% CBF Change (ΔF)	69.2%	70.0%	58.1%
Active (ΔV + ΔF)	69.5%	70.9%	63.5%

To reveal CBV effects on PASL signal in more realistic situations, we examined a CBV range of 5–7 ml/100g and assumed that the “real” CBF follows the Grubb’s equation (22):

$$\frac{\mathit{CBF}}{{\mathit{CBF}}_0}={\left(\frac{\mathit{CBV}}{{\mathit{CBV}}_0}\right)}^{2.63}$$ [7]

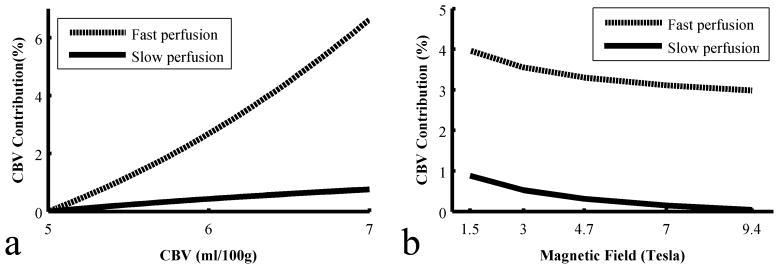
The CBF changes relative to the resting state were simulated in the PASL models. A CBV contribution ratio was defined as the difference of CBF changes in the Active and ΔF modes divided by CBF changes in the ΔF mode: CBV contribution = (CBF_Active – CBF_ΔF)/CBF_ΔF. Fig. 2a shows the CBV contribution ratio as a function of CBV at 3T. In the case of a two-compartment model with slow perfusion, when CBV increases from 5 to 7 ml/100g, the contribution ratio is less than 0.8% but reaches 6.6% in the fast perfusion scenario. Fig. 2b shows the CBV contribution ratios at multiple magnetic fields when CBV change is fixed to 25% (corresponding to 70% CBF change). The CBV effect on PASL signal is reduced at higher magnetic fields in both perfusion scenarios. At 9.4T, the CBV contribution ratio is 3.0% for fast perfusion and only 0.04% for slow perfusion.

Figure 2.

Estimations of percent CBV contribution (a) at different absolute CBV values at 3T, and (b) at different magnetic fields with absolute CBV = 5 ml/100g, under two types of perfusion scenarios.

Fig. 3a shows the VASO signal changes at multiple magnetic fields with a TR=2sec and PS=150 ml/100g/min. When field strength increases from 1.5T to 9.4T, the VASO signal change drops from −1.4% to −0.4%. This phenomenon is likely due to the reduced T₁ differences between blood (T₁^b) and tissue (T₁^e) at high magnetic fields. Disparity of VASO signal change between ΔV and Active modes, indicating CBF contribution in VASO, is small and diminishes along with field strength. Based on the two-compartment model and perfect flip angles and inversion times, the contrast-to-noise ratio (CNR) of VASO was estimated by multiplying the residual tissue signal acquired per unit time with the MRI sensitivity level. Fig. 3b shows the dependence of VASO CNR on TR and field strength. The optimal CNR is found between 3T to 7T with TR of 4 – 8 s.

Figure 3.

(a) Decomposition of CBF and CBV effects from VASO signal changes at different magnetic fields (b) Optimal CNR of VASO over multiple repetition times and field strengths.

As described before, the blood magnetization in the two-compartment model would be a function of CBF and PS, thus the strict requirement of blood elimination in VASO may not be fully met using the TI described in the equation: $T_1^b·log\left(\frac{2}{1+e^{-TR/T_1^b}}\right)$. Thus, the influence of permeability was further estimated by examining the percent blood contribution (i.e. residual blood signal over total VASO signal) under different physiological conditions. Fig. 4a plots the blood contribution for VASO as a function of PS at 3T (other parameters are listed in Table 1) at different CBF levels. At the CBF level of 60 ml/100g/min, the ideal blood-null point is achieved at PS=131 ml/100g/min. Beyond this null point, the blood contribution increases due to the fixed TI and the rise of residual blood signal caused by altered water exchange rate between intra- and extra-vascular compartments. Assuming CBF increases from 60 to 180 ml/100g/min, the residual blood signal is enhanced from 0.15% to 0.6% at PS=150 ml/100g/min. In Fig. 4b, the blood contribution is evaluated at the CBF level of 60 ml/100g/min at different field strengths. When PS=150 ml/100g/min, the blood contribution is 0.15% for 1.5 and 3T, 0.5% for 4.7T, 1.7% for 7T and 3.7% for 9.4T. Since the largest residual blood contribution is only 3.7% at 9.4T, the optimal TI for VASO was evaluated but remains similar for the field strengths (1.5–9.4T). Although the blood contribution is generally small, it should be noted that the null point no longer exists at high fields, implying that the blood elimination may not be perfectly achieved at high fields using a single TI.

Figure 4.

Percent blood contribution in VASO signal to evaluate the permeability effects. (a) under 3 baseline CBF conditions at 3T, (c) under multiple field strengths with CBF = 60 ml/100g/min.

DISCUSSION

In this study, a general two-compartmental biophysical model, which has previously been used to analyze the accuracy of perfusion quantification in ASL techniques (13, 14), was adopted to assess the hemodynamic signals in both PASL and VASO. Our simulations showed that the CBV effect on PASL and permeability effect on VASO are generally negligible or small. However, it should be noted that the CBV effect on PASL depends on baseline perfusion levels and the CBF and permeability effects on VASO may increase at high field strengths.

The simulation of PASL signal was based on two scenarios of venous outflow: slow perfusion and fast perfusion as used in a previous study (14). In our simulation, the CBV contributions to PASL are insensitive to the baseline CBF values but sensitive to the assumed slow or fast perfusion scenarios. The slow perfusion was based on the assumption that the labeled spins would stay in the capillary regime during the measurement so that no labeled spin exists in the venous compartment at the acquisition time, which is valid when the mean transit time (= CBV/CBF) is longer than the measurement time. Otherwise the fast perfusion should be assumed. In general, the slow perfusion can be assumed in human studies because the mean transit time in human brain is approximately five seconds (CBV/CBF = 0.05/0.01) which is much longer than the measurement time (~1–2 seconds in PASL) (23–25). Fast perfusion might be favorable in small animals because the CBF in small animals (e.g. rats) is several times higher than that in human subjects (17–19, 26, 27). Although the actual perfusion in a specific study might not fully comply with the assumptions, simulation results at the slow and fast perfusion scenarios still provide insights into the quantification of the PASL techniques.

Permeability is a crucial physiological indicator for vascular pathologies in the brain. The reported PS value in healthy human brains is around 150 ml/100g/min (28–30), although a recent study using a diffusion-weighted perfusion sequence at 3T reported measured permeability of 335 ml/100g/min in normal gray matter and up to 695 ml/100g/min in tumor lesions (31). Based on our simulated results, using an IR-based sequence only (PASL or VASO) to quantify the water permeability may not be feasible since the signal alteration caused by permeability is within the noise level using the current experimental settings. This argument is supported by recent studies (20, 32) and incorporating diffusion weighting into T₂/T₂^* based imaging techniques may be necessary in the quantification of water permeability. The permeability effect on VASO has been discussed at slow and fast water exchange cases using different biophysical models (11, 33). In this study, the two-compartment model was used to investigate the permeability effect at various water exchange rates. Our results showed the influence of permeability on VASO is generally small, which is in agreement with previous results (11, 33).

The blood contribution analyses examined the signal contribution of blood in VASO using the two-compartment model which should be 0 in an ideal case. However, the blood signal based on the two-compartment model depends not only on the intrinsic blood T₁ but also on CBF and permeability. In other words, these two physiological parameters’ effect on the residual blood signal may not be fully eliminated by a single TI. In addition, the “exchangeable” blood volume in the simulation might primarily reflect the capillary volume rather than the total CBV. Even though previous studies suggested that the arterial fraction of CBV may be as high as 37% and the capillary compartment may contribute significantly in ASL experiments (20, 34), the exact increase of “exchangeable” blood volume during brain activation is much less known. Therefore, it should be cautious in the interpretation of the data based on specific assumptions of the blood volume fraction. In the current model, the apparent blood T₁ decreases as CBF and PS values increase. In Fig. 4a, the intercepts at PS=0 ml/100g/min indicate the residual blood contribution with the presence of CBF effect leading to a longer apparent blood T₁ and approaching the ideal blood-nulling point with PS=131 ml/100g/min. With higher permeability values, the residual blood signal bounces back and enhances the blood contribution. Although the blood contribution is within 3%, this physiological phenomenon is worth noting, especially at high field strengths.

The longitudinal relaxation times in blood (T₁^b) and brain tissue (T₁^e) were obtained from literature (Table 2). The relative difference between T₁^b and T₁^e, defined as (T₁^b − T₁^e)/T₁^b, decreases at high fields. It is 33.3%, 25.8%, 19.3%, 11.4% and 3.7% at 1.5, 3, 4.7, 7 and 9.4T, respectively. VASO contrast is low at high fields because the nulling points for blood and tissue are close to each other due to the small difference in their T₁s (shown in Fig. 4b). In addition, the reduced T₁ difference between blood and tissue also increases the CBF weighting (higher intercepts) and decreases permeability weighting (flatter dependence on PS) on residual VASO blood signal. At 9.4T, the residual blood contribution would be enhanced up to 3.7%. Even though the optimal TI for blood nulling would not be altered drastically, caution should be exercised when estimating CBV by conducting VASO at high fields.

In summary, the effects of physiological and biophysical factors (CBF, CBV, permeability and T₁) on the accuracy of quantification in PASL and VASO techniques were evaluated using the two-compartmental biophysical model. The influence of CBV has negligible (<1%) to small (< 6.6%) influences on PASL signal obtained from the slow or fast flow scenarios at 3T, respectively, and the influences are reduced at higher fields. The effects of permeability and CBF on VASO signal are small at all observed magnetic fields. In addition, the residual blood contribution analyses in VASO indicate that CBV estimations using VASO may not be accurate at high magnetic fields using the blood-nulling TI. Overall, our results suggest that these physiological parameters do not influence the CBF and CBV estimations using PASL and VASO although caution should be exercised when conducting PASL in high perfusion cases and conducting VASO at high magnetic fields.

APPENDIX

Solution of single-compartment model

Eqs.[1–2] depict the dynamic change of magnetization in an imaging voxel based on the assumption of fast water exchange between blood and tissue. By introducing $M_a(t)=M_a^0\left(1-2e^{-\frac{TI}{T_1^b}}+e^{-\frac{TR}{T_1^b}}\right)$ and M_v(t) = M_T(t)/λ, the magnetization in the voxel, M_T(t), can be solved as Eq.[A1]:

$$M_T(t)=M_T^0·\lfloor 1-2·e^{-\frac{t}{T_1^{\ast }}}-2\frac{f}{\lambda }·\frac{e^{-\frac{t}{T_1^{\ast }}}-e^{-\frac{t}{T_1^b}}}{\frac{1}{T_1^b}-\frac{1}{T_1^{\ast }}}\rfloor$$ [A1]

where the apparent relaxation rate, $1/T_1^{\ast }$, is the sum of $1/T_1^T$ and the flow component f/λ. Other parameters in Eq.[A1] are the same as defined in the Method section.

Solution of two-compartment model

From Eqs.[3–5], the general solution of the extra-vascular compartment, M_e(t), can be expressed as the following equations:

$$\begin{array}{l}{M}_e(t)=E_1+E_2{e}^{-D·t}+E_3{e}^{Y·t}-E_4{e}^{Z·t}+E_5{e}^{-G·t}\\ E_1=\frac{\mathit{BAC}+\mathit{BGQ}}{G^{2}J-\mathit{GAB}}+\frac{C}{G}\\ E_2=\frac{(I_a-1)BK}{(D+Y)(D+Z)}\\ E_3=\frac{I_{b}B}{H}+\frac{(I_a-1)BK}{(Y+D)H}+\frac{(Q+I_{e}A)BY+\mathit{BAC}+\mathit{BGQ}}{(G+Y)YH}\\ E_4=\frac{I_{b}B}{H}+\frac{(I_a-1)BK}{(Z+D)H}+\frac{(Q+I_{e}A)BZ+\mathit{BAC}+\mathit{BGQ}}{(G+Z)ZH}\\ E_5=I_e-\frac{C}{G}+\frac{(Q+I_{e}A)BG-\mathit{BAC}-\mathit{BGQ}}{(G+Y)(G+Z)G}\end{array}$$ [A2]

where A = PS/v_bw, B = PS/v_ew, C = 1/T₁^e, D = 1/T₁^b, G = B+C, K=ρ_b* f/v_bw, Q = D+K, $\text{H}=\sqrt{4AB+{(J-G)}^2},\text{Y}=\frac{H-G-J}{2},\text{Z}=\frac{-H-G-J}{2}$. J is equal to (A+D) for the slow perfusion scenario, and (A+D+K) for the fast perfusion scenario. I_a, I_b and I_e are initial magnetization of arterial blood, capillary blood and extra-vascular tissue, respectively, relative to their equilibrium values after the inversion pulse. For example, I_a is equal to $M_a^0$ for the selective IR pulse representing the fresh inflow blood spins, and ${\text{I}}_{\text{a}}=-M_a^0$ for the non-selective IR pulse due to the ideal inversion with an infinite TR. With the same definition, the general solution of the capillary blood compartment, M_b(t), can be described as the following equation as well:

$$\begin{array}{l}{M}_b(t)=F_1+F_2{e}^{-D·t}+F_3{e}^{Y·t}-F_4{e}^{Z·t}\\ F_1=\frac{AC+GQ}{GJ-AB}\\ F_2=\frac{(I_a-1)(G-D)K}{(D+Y)(D+Z)}\\ F_3=\frac{(I_a-1)(Y+G)K}{(Y+D)H}+\frac{Y(Q+I_{e}A+I_{b}Y+I_{b}G)+AC+GQ}{YH}\\ F_4=\frac{(I_a-1)(Z+G)K}{(Z+D)H}+\frac{Z(Q+I_{e}A+I_{b}Y+I_{b}G)+AC+GQ}{ZH}\end{array}$$ [A3]

With Eqs.[A2] and [A3], we can simply define the PASL signal, ΔS(TI), as:

$$\mathrm{\Delta }S(TI){|}^{\mathit{PASL}}=S{(TI)}^{\mathit{selective}}-S{(TI)}^{\mathit{non}-\mathit{selective}}={[v_{ew}{M}_e(TI)+v_{bw}{M}_b(TI)]|}_{I_a=M_a^0}-{[v_{ew}{M}_e(TI)+v_{bw}{M}_b(TI)]|}_{I_a=M_a^0·\left(e^{-\frac{(TR-TI)}{T_1^b}}-1\right)}$$ [A4]

and the VASO signal can be obtained from Eq.[A5].

$$\begin{array}{l}S(TI){|}^{\mathit{VASO}}=S{(TI)}^{\mathit{non}-\mathit{selective}}\\ ={[v_{ew}{M}_e(TI)+v_{bw}{M}_b(TI)]|}_{I_a=M_a^0·\left(e^{-\frac{(TR-TI)}{T_1^b}}-1\right)}\end{array}$$ [A5]

where the initial signal of arterial blood from the non-selective IR sequence was represented as $M_a^0·\left(e^{-\frac{(TR-TI)}{T_1^b}}-1\right)$ for accounting the steady state signal after the inversion pulse.