Computational delineation of the catalytic step of a high-fidelity DNA polymerase

Abstract

The Bacillus fragment, belonging to a class of high-fidelity polymerases, demonstrates high processivity (adding ∼115 bases per DNA binding event) and exceptional accuracy (1 error in 10⁶ nucleotide incorporations) during DNA replication. We present analysis of structural rearrangements and energetics just before and during the chemical step (phosphodiester bond formation) using a combination of classical molecular dynamics, mixed quantum mechanics molecular mechanics simulations, and free energy computations. We find that the reaction is associative, proceeding via the two-metal-ion mechanism, and requiring the proton on the terminal primer O3′ to transfer to the pyrophosphate tail of the incoming nucleotide before the formation of the pentacovalent transition state. Different protonation states for key active site residues direct the system to alternative pathways of catalysis and we estimate a free energy barrier of ∼12 kcal/mol for the chemical step. We propose that the protonation of a highly conserved catalytic aspartic acid residue is essential for the high processivity demonstrated by the enzyme and suggest that global motions could be part of the reaction free energy landscape.

Introduction

The accurate replication and repair of DNA are vital to all organisms. DNA polymerases are critical enzymatic effectors of these processes, yet a detailed description of the molecular mechanisms of their fidelity with native and damaged DNA templates remains incomplete. The fidelity mechanisms in polymerases have a direct bearing on formation of mutational hot spots in the genome and have immense biomedical implications for cancers, neurological aberrations, and premature aging.¹

DNA polymerases serve a dual role: efficiency/versatility in handling different nucleotides and fidelity in incorporating the correct nucleotide, which necessitates the use of subtle and complex molecular paradigms in their machinery. Closed and open conformations of polymerases have been recorded in structural studies based on which an induced-fit mechanism^2,3 between the DNA-bound polymerase and the correct incoming nucleotide substrate is thought to lead to a “closed” tightly bound complex which is catalytically competent for a phosphodiester bond formation⁴; on the other hand, an incorrect incoming nucleotide is thought to lead to a DNA/polymerase complex with misaligned components.

DNA polymerase I large fragment from a thermostable strain of Bacillus stearothermophilus (Bacillus fragment or BF, shown in Fig. 1) is a highly processive replicative polymerase (112 nucleotides incorporated per DNA binding event) showing extensive structural homology with the Klenow fragment from E. coli.⁵ It lacks the 5′→3′ exonuclease and 3′→5′ proofreading exonuclease activities. BF polymerase–DNA structures have been solved for up to 6 base pair extensions for correct⁶ and incorrect mismatch⁷ extensions, which serve as reliable starting points for modeling studies. In addition to its extensive structural characterization, BF has the ability to misincorporate nucleotides with comparable efficiency to correct incorporation when encountering an oxidative lesion. This makes BF a well-characterized yet important system for study, as an in-depth analysis of the lesion-bypass mechanisms in BF can prove to be important for our understanding of lesion bypass in error-prone eukaryotic polymerases.

Figure 1.

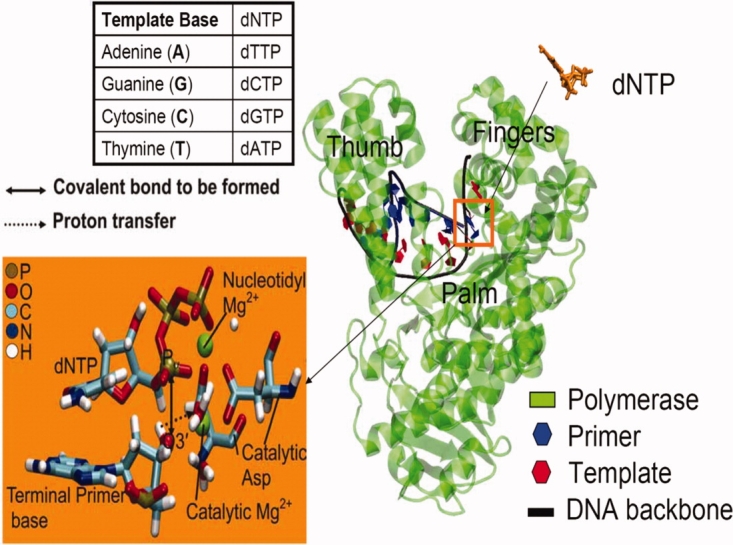
The bacillus fragment (BF) complexed with its DNA substrate and incoming deoxynucleotide triphosphate (dNTP); we study the incorporation of dCTP opposite a guanine (G) template base. The inset shows a magnified view of the catalytic site. The phosphoryl transfer reaction involves the formation of a covalent bond (solid line) between the α-phosphorous (P_α) of the incoming dNTP and O3′ oxygen of the terminal primer base, before which a proton present on O3′ has to transfer (dashed line) possibly to a highly conserved aspartic acid residue. [Color figure can be viewed in the online issue, which is available at http://www.interscience.wiley.com.]

Here, we propose to computationally delineate how the molecular machinery of the BF polymerase system operates during the chemical step, that is, along the reaction pathway of phosphoryl transfer during nucleotide incorporation. Nucleotide incorporation via the “two-metal-ion” catalyzed phosphoryl transfer mechanism is common to several DNA and RNA polymerases⁸; at the catalytic site of BF (see inset of Fig. 1), one divalent metal (Mg²⁺) ion coordinates the three phosphates (nucleotide binding) of the incoming dNTP. A second metal (Mg²⁺) ion positioned between the α-phosphate (P_α) of the incoming nucleotide and the hydroxyl terminus (O3′H3T) of the DNA primer facilitates the inline nucleophilic attack on P_α. Computational study by Fostergill suggests that the two Mg²⁺ ions collectively serve a crucial role of electrostatic stabilization of the active site⁹ and together with three acidic residues, which are highly conserved in polymerases (D830, D653, and D865 in BF), stabilize the catalytic site geometry in the reaction-competent closed or active state. There is clear experimental and theoretical evidence that the resulting attack of the nucleophilic oxygen anion (O3′) on the target phosphorous (P_α) proceeds via a trigonal-bipyramidal transition state.^8,10,11 Indeed the conformation close to the trigonal-bipyramidal geometry (referred to as the “ideal two-metal-ion geometry”) has been recently captured in structural studies,^10,11 which is saliently characterized by a distance between the nucleophilic oxygen and the target phosphorous of ∼2 Å.

Computational delineations of transition state structures and reaction intermediates for DNA pol I,⁹ T7 DNA pol,¹² correct incorporations in the X-family polymerase β,^13–17 incorrect incorporations in polymerase β,^13,18,19 the Y-family, low fidelity polymerase Dpo4,²⁰ hammerhead ribozyme,²¹ and the F1-ATPase^22,23 have provided detailed mechanistic insights on the associative mechanism for the phosphoryl transfer pathway. The method we have used in this work (see Section “Materials and Methods”) also uses quantum mechanics molecular mechanics (QMMM) simulations like the majority of the works described earlier. However, our approach is closest to that described in Ref. 21 in that we have relied on a delineation of the free energy landscape of the chemical step using QMMM umbrella sampling simulations and considered the effect of delocalized modes in shaping the free energy landscape using classical umbrella sampling simulations.

The significance of our approach can be appreciated by noting that in addition to catalytic-site dynamics, long range (delocalized) motions of the enzyme and substrates could couple to define the free energy landscape.^24–27 There is evidence that such a coupling of fast and slow dynamical modes may play a significant role in DNA polymerase mechanisms. Pioneering single molecule studies of polymerases replicating DNA stretched under differing tensions^28,29 showed that the replication rate is sensitive to forces exerted on the template strand. That the applied force on the DNA affects the rate limiting step highlights the importance of coupling between polymerase and DNA degrees of freedom. Indeed, in recent studies, we identified such coupled motions of the enzyme–substrate complex with significant correlations between fluctuations of the catalytic reactive distances and delocalized collective modes involving the DNA motions and hypothesized that the coupling could exert a significant influence on the reaction free energy landscape.^30,31 Hence, the focus of this article is on delineating the pathways and the energetics associated with the chemical step of correct nucleotide incorporation catalyzed by BF, the effect of protonation states on the reaction pathways, and the involvement of collective modes in defining the reaction free energy landscape.

Results

Effect of protonation states on the active-site geometry

Based on our recent report on the free energy landscape for preorganization of the catalytic site for DNA replication in BF,³⁰ we derived conformations corresponding to the active state of a ternary complex of BF/DNA/dCTP (where the incoming nucleotide dCTP pairs with a guanine base of the DNA template strand) and subjected them to quantum mechanics molecular mechanics (QMMM) simulations (see Section “Materials and Methods”). Table S1 in Supporting Information compares the ground state QMMM geometries with the MM results and the crystal structure. The catalytic site geometry in the ground state resulting from the QMMM simulations is better organized in comparison to that resulting from classical molecular mechanics (MM), with reductions in the O3′-P_α and O3′-catalytic Mg²⁺ distances, (see inset in Fig. 1). An alignment of the terminal primer hydroxyl hydrogen (H3T) to within 2.83 Å from D830:O1_δ and 3.16 Å of dCTP:O1_α suggests two possible routes for deprotonation of O3′ oxyanion before inline nucleophilic attack. Constrained QMMM optimizations which further reduce the O3′-P_α and O3′-catalytic Mg²⁺ distances to ∼2.0 Å indicated a shift in orientation of H3T toward the O1_δ oxygen of D830, suggesting a pathway of proton abstraction by the conserved catalytic aspartic acid residue. Such possibilities along with deprotonation to aqueous solution were examined in three recent simulation studies of polymerases^12–14: in T7 DNA pol,¹² energetic analysis showed the most likely pathway for the proton transfer was from O3′ to one of the catalytic aspartic acid residues with an activation barrier of 11 kcal/mol. For pol β, a similar proton transfer pathway was illustrated to occur from O3′ either directly or mediated by two water molecules to one of the catalytic aspartic acid residues.^13,14,16,17 Based on the exploration of the protonation states of titratable side chains in the catalytic site, namely D653, D830, and D865 (see Supporting Information Section S1.2), we focused on two models to compute the reaction paths: Model I (O3′ protonated, D830 unprotonated), and Model III (O3′ protonated, D830 protonated) of the BF/DNA/dCTP ternary complex.

Protonation state-dependent multiple pathways for phosphoryl transfer

To describe the sequence of events including the associated free energy landscape during the phosphoryl transfer reaction for models I and III of the BF/DNA/dCTP, we carried out umbrella sampling simulations using QMMM MD trajectories and using multiple reaction coordinates (see Section “Materials and Methods”). The choice of multiple reaction coordinates including some that describe proton transfer was motivated by recent studies.^21,32 We obtained complete reaction pathways for both models along with the identification of transient intermediates and the transition states; the schematics of the reaction pathways as obtained from our umbrella sampling studies for both models are depicted in Figure 2. For both pathways, the H3T proton attached to the A: O3′ transfers to the nearest aspartic acid residue D830 spontaneously (i.e., without explicit constraints on the H3T proton). Based on this, we rule out the alternative possibility of H3T proton transferring to dCTP:O1_α. In both models, the final step of A:O3′-dCTP: P_α bond formation and cleavage of the dCTP:P_α-dCTP:O3_α bond to liberate the pyrophosphate product takes place only after the H3T proton is transferred to the dNTP tail. In model III, the transfer is indirect as it is the extra proton on D830 which transfers to the dNTP tail while the H3T proton is transferred to D830. In model I, the H3T proton itself transfers to the dNTP tail after hopping to D830 as an intermediate step. We next describe the free energy surfaces for both models. The reaction pathway in model III (the most stable model for the ground state of BF) was seen to be more energetically favorable relative to model I and will be described first.

Figure 2.

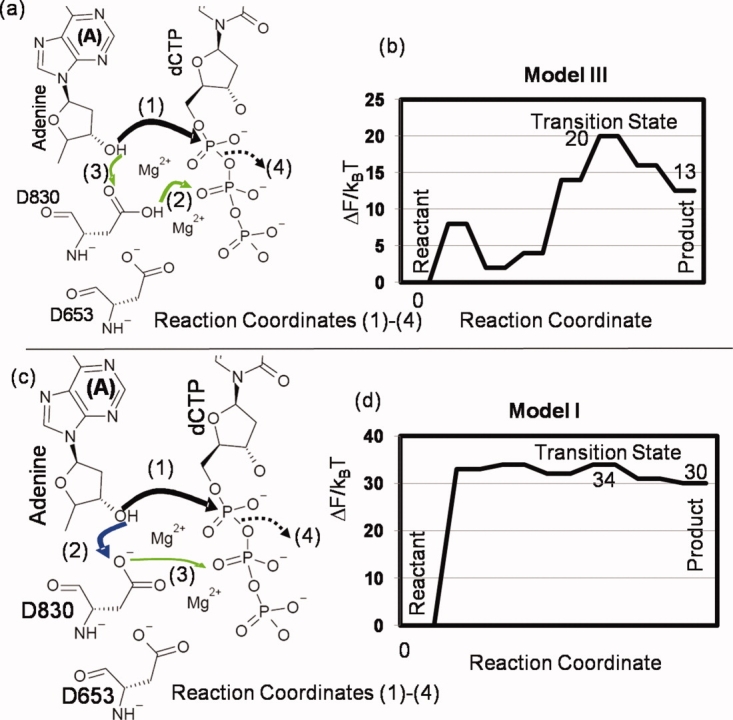
Schematics of the reaction pathway for catalysis (a) and (c). An effective 1-d free energy landscape along a generalized coordinate defined along the minimum free energy path (b) and (d) for two different models: model III (top row) and model I (bottom row). In (a) and (c), the newly forming O3′-P_α bond and cleaving P_α-O_3α bond are illustrated by solid and dashed black lines, respectively. The other arrows indicate different proton transfer steps. [Color figure can be viewed in the online issue, which is available at http://www.interscience.wiley.com.]

The free energy surfaces for phosphoryl transfer in model III are depicted in Figure 3. For the reactant state: the A:O3′-dCTP:P_α distance is 2.75 Å, both the D830:O2_δ and A:O3′ oxyanions are protonated and the dCTP:P_α-dCTP: O2_β distance is 1.7 Å. As the O3′-P_α distance reduces to 2.3 Å, there is a transfer of the proton from the D830:O2_δ position to the O2_β oxygen in the dCTP phosphate tail. Both steps proceed concurrently and the 2-d free energy landscape is shown in Figure 3(a). A further lowering of the O3′-P_α distance [Fig. 3(b)] triggers the shift of the H3T proton on the terminal primer hydroxyl to the D830:O1_δ oxygen [Fig. 3(c)] and an increase in the nucleophilic attack angle O3_δ-P_α-O3′ from 172 to 180° leading to the formation of the transition state (TS), that is, the trigonal-bipyramidal geometry and the perfect in-line attack geometry corresponding to an associative mechanism of phosphoryl transfer (see Supporting Information Fig. S1 and caption); we classify this mechanism as associative based on geometry alone, that is, the O3′-P_α and P_α-O3_α distances at the transition state are in the range 1.9–2.1 . The product is formed when the pyrophosphate group (PP_i) dissociates [Fig. 3(d)]. The reaction free energies depicted in shaded boxes in Figure 3 indicate the free energy changes relative to the reactant state, as one travels along the reaction coordinate. The overall free energy barrier of the chemical step is 20 k_BT and the free energy of the product relative to the reactant is +12.5 k_BT. We note that the transfer of the H2_δ proton to PP_i creates an additional positive charge on the dNTP pyrophosphate moiety, weakening the O3_α-P_α bond and coupled to the close proximity of the attacking primer O3′ nucleophile, leads to the cleavage and subsequent formation of the PP_i. The barrier of 20 k_BT is lower than the barrier for the overall nucleotide incorporation step inferred from enzyme kinetics (25 k_BT) which is consistent with the notion that for the correct incorporation, the chemical step is not rate limiting. The free energy of the product relative to the reactant is positive because our calculations do not include the closed to open conformational change and the PP_i dissociation: these steps are expected to reduce the free energy to make the overall reaction cycle favorable.

Figure 3.

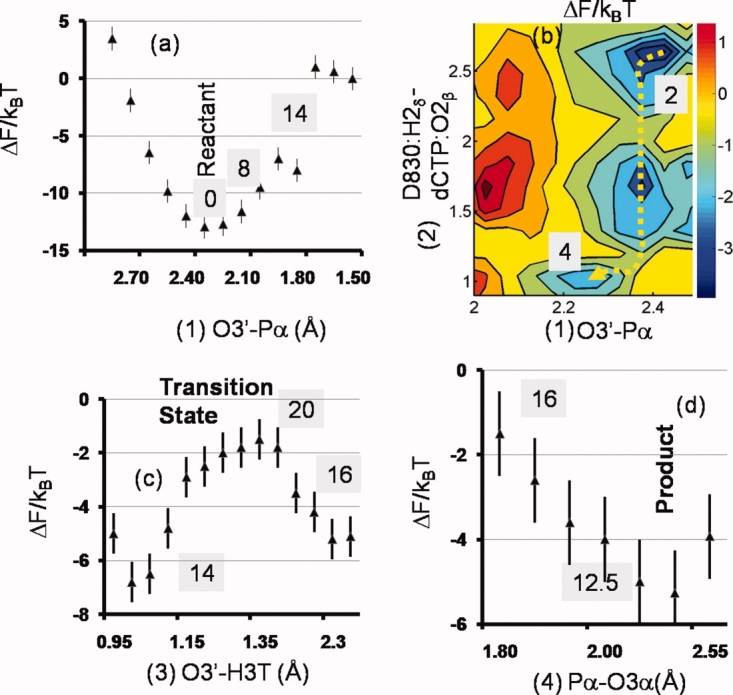
1-d and 2-d free energy surfaces for model III obtained from umbrella sampling simulations. The surfaces are labeled in chronological order (a)–(d) as the reaction proceeds from reactant to product. [Color figure can be viewed in the online issue, which is available at http://www.interscience.wiley.com.]

The free energy surfaces for model I are shown in Figure 4. For the reactant state: the A:O3′-dCTP:P_α distance is 2.75 Å, the A:O3′ oxyanions are protonated and the dCTP:P_α-dCTP: O2_β distance is 1.7 Å. As the nucleophilic attack (O3′-P_α) distance is decreased below 2.0 Å [Fig. 4(a)], the terminal primer hydroxyl group deprotonates and the H3T proton transfers to the proximal aspartic acid residue D830:O1_δ [Fig. 4(b)]. At this stage, the release of constraints results in the return of the system to the reactant state, (i.e., the proton transfers back to the terminal primer A) suggesting that the system has not surpassed the TS. With further slight reductions in O3′-P_α distance, the H3T proton migrates first to D830:O1_δ and then to dCTP:O1_β. This signifies the formation of the TS (see Supporting Information Fig. S1 and caption) corresponding to an associative mechanism of phosphoryl transfer as in model III. The H3T proton subsequently transfers to the O2_β oxygen of the dissociating pyrophosphate (PP_i). In the landscape for model I, the overall free energy barrier of the chemical step is 35 k_BT, and the free energy of the product relative to the reactant is +30 k_BT. The barrier of 35 k_BT is significantly higher than the barrier for the overall nucleotide incorporation step inferred from enzyme kinetics (25 k_BT), strongly suggesting that the pathway in model I and the associated protonation state of BF are not the preferred pathway/state of BF catalysis of correct nucleotide incorporation.

Figure 4.

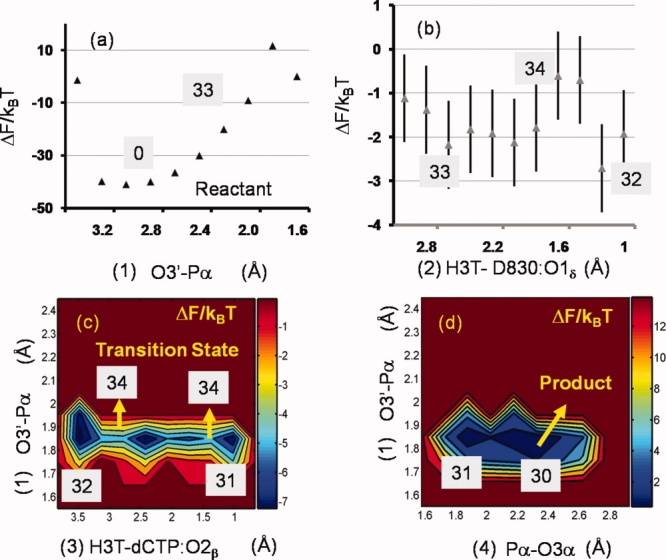
1-d and 2-d free energy surfaces for model I obtained from umbrella sampling simulations. The surfaces are labeled in chronological order (a)–(d) as the reaction proceeds from reactant to product. Error bars, when not visible, are smaller than the size of the symbols. [Color figure can be viewed in the online issue, which is available at http://www.interscience.wiley.com.]

Influence of collective modes on the reaction free energy landscape

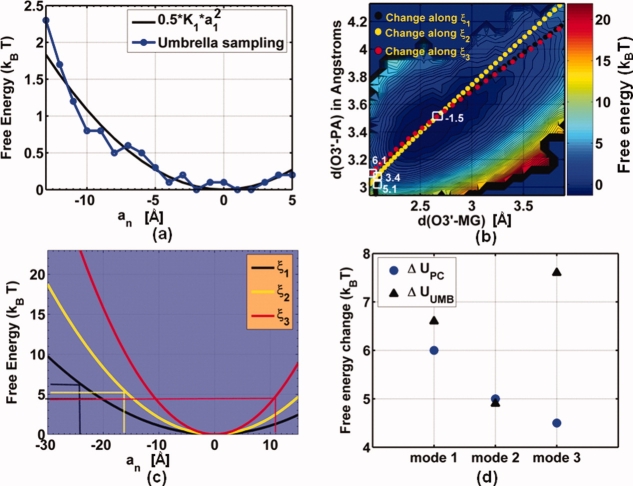
We note that the coordinates we have chosen are, at best, approximate surrogates to the exact reaction coordinate, which is very complex and multi (high) dimensional, and hence, our choices can lead to over or underestimation of the barrier height.³² Indeed, in previous work,^30,31 we showed that for correct nucleotide incorporation several delocalized modes of the protein–DNA complex characterized in particular by the top three principal component (PC) eigenvectors ξ_m, m = 1, 2, 3, are strongly correlated with catalytic site reactive distances d_a (O3′-P_α distance) and d_b (O3′- catalytic Mg²⁺ distance). To illustrate that such coupling can influence the free energy landscape of the chemical step, we compare the free energy cost of reducing the reactive distances d_a and d_b by traveling along the principal modes ξ₁, ξ₂, and ξ₃ to that obtained by directly reducing d_a and d_b in the context of MM simulations. The latter results (shown in Fig. 5 bottom left) were already available from our previous work.³⁰

Figure 5.

(a) A comparison of free energy change with displacement a₁ along principal component mode ξ₁ as obtained from umbrella sampling simulations (blue) and using the spring constant K₁ resulting from quasiharmonic analysis (black). (b) Free energy surface (ΔU_UMB in units of k_BT) obtained from classical umbrella sampling runs using the O3′-P_α and O3′-catalytic Mg²⁺ distances as reaction coordinates. The lines of filled green, yellow, and red squares represent the change in the two reaction coordinates for a displacement along the top three PC modes ξ₁,ξ₂, and ξ₃, respectively. The reference geometry is the minimum free energy state (white square marked 1.5 k_BT) and each mode is displaced by amplitudes yielding the maximum simultaneous reduction of both reaction coordinates (white squares marked 5.1 k_BT, 3.4 k_BT and 6.1 k_BT). (c) Free energy change ΔU_PC with displacement a_n (n = 1, 2, 3) along the top three PC modes ξ₁,ξ_2, and ξ₃ as obtained using their respective spring constants K₁, K_2^, and K₃ (resulting from quasiharmonic analysis). (d) comparison of free energy change ΔU_UMB to ΔU_PC for achieving the same reduction in distances d_a and d_b.

Each eigenvector ξ_m is a unit-normal vector representing a collective mode of motion in the active site region of the ternary complex, with a quasiharmonic spring constant K_m = k_BT/λ_m,³³ where λ_m is the eigenvalue for mode m. Displacing ξ_m with an amplitude a_m will lead to a change in the geometry R(0) of the active site region³¹ given by R(a_m) − R(0) = a_mξ_m, and with an associated free energy cost of 0.5*K_m*(a_m).² We validate this estimate by performing umbrella sampling along the slowest mode ξ₁, wherein the amplitude of the mode a₁ is varied so as to decrease d_a from 3.62 Å to 3.17 Å. Figure 5(a) shows a plot of free energy change ΔU_PC as a function of the amplitude along ξ₁. The energy change for a harmonic oscillator with spring constant K₁ = 2.17*10⁻² kcal/mol/Ų is given by the solid black curve, which is in excellent agreement with the trend obtained through umbrella sampling. Therefore, we calculate the free energy cost of traversing the reaction coordinates d_a and d_b for modes ξ_m (m = 1, 2, 3) directly using their respective quasiharmonic spring constants, see Figure 5(b). The lines of filled green, yellow, and red squares in Figure 5(b), superimposed on the classical free energy landscape of reaction coordinates d_a and d_b, show the change in d_a and d_b for a displacement along the top three principal modes, whereas the white square boxes show the initial values of d_a and d_b at a_m = 0 (m = 1, 2, 3) and final values corresponding to amplitudes a₁ = −24 Å, a₂ = −16 Å, a₃ = +11 Å, marked by vertical dashed lines in Figure 5(c); also shown are the corresponding free energies U_UMB at these coordinates. Figure 5(b) compares ΔU_UMB, the free energy change expected for a direct reduction of d_a and d_b, (i.e., from the free energy landscape in Figure 5(b) without the inclusion of the principal modes) with ΔU_PC, the free energy change to achieve the same degree of catalytic site reorganization specified in terms of the distances d_a and d_b by moving along a PC mode. The free energy change obtained by traversing modes 1 and 2 is comparable to the corresponding change by reducing d_a and d_b, directly; however, mode 3 reduces the barrier for preorganization significantly, by 3.1 k_BT or 1.86 kcal/mol. In general, a linear combination of PCs will provide an optimal lowering of the free energy barrier, and hence, the analysis we have presented in this section is simplistic. Nevertheless, our results imply that collective modes can exert a significant influence in defining the reaction free energy landscape.

Discussion

Using free energy studies based on a combination of classical molecular dynamics (MD) and mixed quantum mechanics molecular mechanics simulations, we have presented analysis of the energetics and structural rearrangements involved in the correct nucleotide incorporation by BF, just before and during, the chemical step. Based on the protonation states of conserved aspartic acid residues at the catalytic site, we considered reaction pathways in two models (models I and III). The pathways in both models were found to proceed through an associative two-metal-ion mechanism (based on the geometry of the transition state) involving a direct in-line attack, requiring the proton on the terminal primer O3′ to transfer to the pyrophosphate tail of the incoming nucleotide before the formation of the pentacovalent transition state with a perfect trigonal-bipyramidal geometry (see Supporting Information snapshots in Fig. S1). We compute the overall free energy barrier of the chemical step to be 20 k_BT (as reflected in calculations involving model III), which is lower than the barrier for the overall nucleotide incorporation step inferred from enzyme kinetics (25 k_BT). This is consistent with the notion that for the correct incorporation, the chemical step is not rate limiting; indeed, as described by pioneering enzymology studies of Benkovic et al., the rate-limiting step involves the precatalytic conformational change that brings the polymerase system from an inactive (open) to an active (closed) state.^3,34 Nevertheless, the energetics of the chemical step in model III is comparable to that for T7 DNA pol computed by Warshel and coworkers¹² and reflects the ability of BF to catalyze nucleotide incorporation even in a crystal. In contrast, the overall free energy barrier of the chemical step for model I is 35 k_BT, (significantly higher than the 25 k_BT barrier for the overall nucleotide incorporation), strongly suggesting that the pathway in model I is not preferred for correct nucleotide incorporation. The overall mechanism we have delineated in BF is consistent with the large body of mechanisms proposed in other related polymerase systems established through both theoretical and experimental studies.^{3,12–21,35,36}

From a design perspective, we reason that the mechanism in model III is optimal: for a processive enzyme such as BF, which can incorporate up to 115 nucleotides per DNA binding event, it would appear that protonation/deprotonation of the conserved D830 and subsequent transfer of the proton to the departing pyrophosphate will hamper the efficiency of the repeated cycles of nucleotide incorporation as the proton diffusion and cycling can become rate limiting. The pathway in model III provides an elegant respite by replenishing the proton on D830 (through the proton transfer from the O3′ of the terminal primer to D830) as the protonated D830 loses its proton to the departing PP_i.

Using classical free energy simulations, we have explored the influence of collective DNA-polymerase modes on the free energy landscape for traversing along the in-line attack distance in the active site and suggest that a complete depiction of the free energy landscape likely involves collective modes. Based on PCA on the active site, we further infer that the atomic motions in the DNA primer and template strands which constitute the top PC modes are strongly coupled to motions of atoms in the two O-helices belonging to the polymerase finger domain (see Supporting Information Fig. S2 and Table S3). Three of the polymerase residues, R615, Q797, and H829, which show significant correlation with DNA primer and template strands (see Supporting Information Table S3), have been shown in previous studies to participate in the catalytic activity of the polymerase,³⁷ with a mutation of any one of these residues greatly reducing polymerase–DNA binding. Experiments have proposed a role for a fourth residue, Y714, in stabilizing the template strand base paired opposite the incoming nucleotide in the closed (active) state of the polymerase,³⁸ which intriguingly enough, also shows significant correlations with the DNA template strand (Supporting Information Table S3). The presence of significant correlation between the polymerase residues and the DNA (as identified in Supporting Information Table S3) coupled with stacking interactions between the adjacent base pairs, provide a molecular basis for the possible coupling between the polymerase fingers and the catalytic site. Hence, it is reasonable to speculate that the polymerase uses a linear combination of such collective modes to preorganize the catalytic site and optimizes the free energy landscape during the catalytic step resulting in a lower free energy cost of reaching the transition state in comparison to the computed value of 20 k_BT we have reported. A quantitative estimate of the reduction in the free energy cost can only be obtained by including the slow modes in QMMM calculations using efficient long-time sampling approaches,^39–43 which we have not attempted.

The suggested coupling machinery can be validated using force-spectroscopy experiments.³¹ The predicted effects of protonation states on the reaction pathway can be validated using pH titration and NMR experiments. The paradigms highlighting the significance of the chemical environment (i.e., protonation states) and the role of the delocalized modes can help provide additional molecular insight into the residues critical for DNA replication in cognate settings. Role of such factors in noncognate environments such as incorrect incorporation or incorporation past damaged DNA bases is very important because the chemical step indeed becomes rate limiting in such scenarios.^3,31 Thus, this study sets the stage for interesting avenues for future theoretical and experimental work in noncognate systems with important biomedical consequences.

Materials and Methods

MD and quantum mechanics molecular mechanics simulations

A ternary complex of BF/DNA/dNTP (explicitly solvated) with correct dCTP opposite guanine G (or G:dCTP) was constructed as reported in our prior studies,^30,31 see Supporting Information Sections S1.1–1.4 and Table S1 in Supporting Information methods for a more detailed description. Protonation states of distal titratable residues were chosen simply based on individual pKa values in aqueous solution at a pH 7.0 (see Supporting Information Section S1.1), while those for the conserved catalytic site aspartic acid residues and the nucleophilic group in the active site (D653, D865, D830, and O3′ of the terminal base of the DNA primer strand) were determined using a Poisson–Boltzmann approach (see Supporting Information Section S1.2). We constructed different model systems for different protonation states of the aspartic acid residues (in these models, the terminal base of the primer strand was always capped as O3′H) — Model I: all three aspartic acid residues unprotonated; Model II: D653 protonated; Model III: D830 protonated; and Model IV: D865 protonated. Our calculations revealed that Models I and III were most stable (see Supporting Information Section S1.2).

Classical MD production trajectories (10 ns) were obtained for these two systems after equilibration protocols and the last 5 ns was used for further analysis. Starting structures for the quantum mechanics molecular mechanics (QMMM) calculations were obtained from the last 5 ns of classical MD production runs of solvated BF/DNA/dNTP ternary complexes. The system size was reduced to ∼15,000 atoms by excluding all solvent (water) molecules greater than 3.0 Å away from the protein, dNTP, and MG²⁺ ions. The quantum (QM) region includes the pyrophosphate moiety of the dNTP, the sugar of the terminal primer A, parts of the catalytic aspartic acid residues (D830 and D653), MG²⁺ ions, and two bound water molecules at the catalytic site, a total of 64 atoms (including 6 link atoms, see below). This region was treated using DFT (B3LYP functional). We used the Gaussian basis set 6–31G for all equilibration runs and 6–31G* for the umbrella sampling runs, see Section “Influence of collective modes on the reaction free energy landscape.” The MM region was treated using the CHARMM27 force field.⁴⁴ As the boundary between the QM and MM regions cuts through covalent bonds, we used the single link atom procedure to satisfy valences of broken bonds. Electrostatic terms involving the MM host atoms that connect to the QM region were excluded from the Hamiltonian. We have extensively explored this choice of the QMMM region (including sensitivity to the size of the QM region, and the functional/basis set combination in our prior studies of closely related systems^13,21,45; others have validated the choice of the link atom.⁴⁶ The system was first subjected to 1200 steps of the adopted basis Newton-Raphson (ABNR) minimization and subsequently 10 ps constant temperature production run using 1 fs timestep of integration.

Umbrella sampling

As model III (O3′ protonated, D830 protonated) shows the most stable ground state followed by model I (O3′ protonated, D830 unprotonated), see Supporting Information Section 1.2 and Table S2, we focused on these two models to compute the reaction paths. The free energy profile for the phosphodiester bond formation in models I and III was explored using multidimensional umbrella sampling. Through several restrained dynamics simulations harvested with a QMMM Hamiltonian (a higher 6–31G* basis set was used for the QM region here to describe the phosphorous chemistry), we performed umbrella sampling and explored a set of five distances as reaction coordinates for each model. For model I: terminal primer adenine O3′-dCTP P_α (d_a); terminal primer adenine O3′-Catalytic Mg²⁺ (d_b); proton H3T-dCTP:O1_α (d_c); proton H3T-dCTP:O2_β (d_d); and dCTP:O3_α-dCTP P_α (d_e). For Model 3, terminal primer adenine O3′-dCTP P_α (d_a); O3′-catalytic Mg²⁺ (d_b); proton D830:H2_δ-dCTP:O2_β (d_c); O3′-proton H3T (d_d); and dCTP:O3_α-dCTP P_α (d_e). We apply a harmonic restraint to each reaction coordinate d_i which adds a new potential bias 0.5*K_i*(d_i − d_i⁰)² to the QMMM Hamiltonian. Here K_i is the force constant of the coordinate d_i and d_i⁰ are the reference value around which the coordinate d_i is restrained. By varying the offset of the restrained potential in steps of 0.1–0.5 Å and the force constant K_i, (see Supporting Information Section S1.3 for a detailed description as we introduced variability in our choice of K_i in certain windows), such as to obtain overlapping windows, we effected the transition of the system from reactant to the product. At each window, we performed 100 steps of energy minimization using the steepest-descent (SD) method followed by 1.3 ps of Langevin dynamics at 300 K of which 0.5–1 ps of data obtained using K_i = 20 kcal/mol/Ų was used in the actual processing of the free energy depending on convergence of the sample in the window. Data from the different simulation windows were then combined to construct unbiased probability distributions and free energy surfaces by using the WHAM algorithm.⁴⁷ The error bars were estimated by running four independent runs for a few representative windows.

For each model, the total number of windows ranged from 40–50, and hence, the aggregate length of the QMMM trajectories amounted to ∼50–80 ps per model. As we harvested these trajectories in a parallel environment of 32–64 processors running Linux (each node with a clock speed of 3.2 GHz), we logged a throughput of 1 ps/day for our system. Hence, the total CPU hours for the production runs of the umbrella sampling amounted to 75,000–1,00,000 per model and the wall clock time amounted to ∼50–70 days per model. Data from the different windows of the umbrella sampling runs were combined using the weighted histogram analysis method (WHAM)⁴⁷ to project the potential of mean force (free energy density) along the a priori chosen set of reaction coordinates from which free energy changes were calculated by numerical integration.

Umbrella sampling along the PCs

Principal component analysis (PCA)⁴⁸ of the MD simulations was performed on a subsystem of the protein–DNA complex to obtain a set ξ= (ξ₁, ξ₂,…,ξ_3N−6) of orthogonal eigenvectors (or PCs) with eigenvalues λ= (λ₁, λ₂,…,λ_3N−6) sorted in descending order, that is, λ₁>λ₂,…,λ_3N−7>λ_3N−6. The subsystem included the region around the catalytic geometry (denoted as the active site region) which included all heavy atoms of the incoming dNTP, six residues of the DNA template strand (including the template G of the nascent base pair), four residues of the DNA primer strand (including the terminal A), the two Mg²⁺ ions, two aspartic acid residues D830 and D653 which coordinate the Mg²⁺ ions and bound waters at the catalytic site.

Displacement along a PC eigenvector ξ_m with amplitude a_m transforms the structure according to the relationship R(a_m) = R(0) + a_m*ξ_m. To obtain free energy profiles for displacement of the system along a eigenvector, for each PC the amplitude was scanned in N steps of unit displacements a_m = 0,1,2,...,N and corresponding structures of the active site region R(0), R(1), R(2),…,R(N) were obtained. The chosen eigenvectors show significant correlations with the catalytic site reaction coordinates d_a and d_b, (see Section “Umbrella Sampling”). When a_m = 0, d_a and d_b have values which correspond to average values from the 5 ns classical MD runs and the number of steps N is chosen for appropriate reductions in d_a and d_b for comparisons with free energy calculations with direct reductions of these coordinates. For each unit displacement window along the PC corresponding to amplitude a_m, the WHAM algorithm mentioned earlier was applied to the snapshots from the constrained simulations to obtain the unbiased probability distribution and the free energy as a function of root mean square deviation (RMSD) with respect to geometry R(a_m), see details in Supporting Information Section S1.4. We emphasize that the WHAM was applied to each window independently as the reference geometry R(a_m) around which the system is constrained changes from window to window. Subsequently, we constructed a 1-d free energy landscape as a function of amplitude a_m along the mth PC.

Glossary

Abbreviations and Symbols:

BF

bacillus fragment

dNTP

deoxy-nucleoside-triphosphate

MD

molecular dynamics

PC

principal components

PCA

principal component analysis

QMMM

quantum mechanics molecular mechanics

WHAM

weighted histogram analysis method.