A REVIEW OF NON-INVASIVE IMAGING METHODS AND APPLICATIONS IN CONTAMINANT HYDROGEOLOGY RESEARCH

1. INTRODUCTION

Investigation of contaminant hydrogeological processes often relies on indirect measurement of system parameters, or direct measurement at only a few locations, in some cases as a function of time. The primary reason is that porous media, and the processes occurring within them, are typically not amenable to direct observation. For example, tracer transport studies are often used to investigate heterogeneous permeability fields. Typically, the tracer concentration at a fixed point in space is monitored over time and then analyzed to infer tracer flow paths and the permeability field. In many cases, indirect observations can be interpreted in different ways and different results or conclusions can be reached (e.g., Barth et al., 2001), and multiple permeability distributions can give rise to indistinguishable tracer breakthrough profiles that obscure the underlying processes. This considerably complicates contaminant hydrogeology research. Hence, methods are needed that allow direct observation or imaging of porous media properties and the processes occurring within them.

In this paper we review four of the most common imaging methods applied to contaminant hydrogeology research. These are optical imaging using UV or visible light, imaging using dual-energy gamma-radiation, X-ray microtomography, and magnetic resonance imaging (MRI). Some of the most straightforward imaging methods are based on direct optical imaging. This approach requires that the pore space, or selected phases within the pore space, be amenable to direct illumination or excitation by visible or UV light. To achieve this, a variety of approaches have been taken, which all involve the creation of transparent model pore structures. Examples are two-dimensional (2D) pore structures etched into different substrates and covered with a transparent material (e.g., Wan and Wilson, 1994; Chomsurin and Werth, 2003), 2D flow cells created from transparent porous media held between clear plates (e.g., Kennedy and Lennox, 1997), and columns from similarly transparent materials (e.g., Montemagno and Gray, 1995). Processes imaged include fluid entrapment and flow, colloid transport, biological growth, and mixing-limited reactions. Transmitted visible light has been used to directly observe fluid color contrasts, and fluorescence solutes and particles have been used to enhance illumination.

More complex methods of imaging in porous media rely on indirect measurement through spectroscopic analysis. One of the more straightforward of these involves using dual-energy gamma-rays; these have typically been directed at a small section (e.g., 1×1 cm²) of a 2D flow cell containing porous media and fluid, and collected on the opposite side of the sample. The intensity of gamma rays exiting the sample is related to the properties of the fluid, and this can be calibrated to quantify the liquid distribution in the section analyzed. In contaminant hydrology, gamma-radiation has primarily been used to quantify the water and nonaqueous phase liquid (NAPL) saturations in porous media (e.g., Oostrom et al., 1990, 1999a; Illangasekare et al., 1995a; Brusseau et al., 2000; Jalbert et al., 2003; Ferré et al., 2005). In some cases, the gamma radiation source and detector were fixed to a moving table that traversed the height and length of the 2D flow cell.

Another complex method involves creating high-resolution three-dimensional (3D) images by mapping the absorption of X-rays directed through a sample. The amount of absorption depends on sample composition and energy of the X-ray. Materials with a higher atomic mass absorb more X-rays so contrast is provided when materials with different atomic masses are present (e.g., water and rock). Synchrotrons provide the highest energy X-rays, in addition to a high degree of collimation and the ability to tune the photon energy to image specific elements. Applications of synchrotron X-ray microtomography include characterization of porous media structure, characterization of the distribution of fluids at the pore scale, measurement of fluid-fluid interfacial area, and the pore-scale distribution of colloids (e.g., Betson et al., 2004; Nakashima et al., 2004; Schnaar and Brusseau, 2005; Al-Raoush and Wilson, 2005a).

Magnetic resonance imaging represents the last imaging method that will be reviewed in this paper. Magnetically susceptible nuclei such as ¹H, ¹³C, ¹⁹F, are selectively excited in space and time. Because different phases are characterized by either the same magnetically susceptible nuclei in different chemical environments, or different magnetically susceptible nuclei, they can be distinguished by a judicious choice of imaging parameters. Applications of MRI include 3D quantification of fluid saturations in saturated and unsaturated porous media or fractured rock packed into columns or flow cells, measurement of 3D water flow paths in packed columns and flow cells, and measurement of colloid transport and deposition in packed columns (e.g, Baumann and Werth, 2004; Caprihan and Fukushima, 1990; Dijk et al., 1999; Johns and Gladden, 1999; Chu et al., 2004; Zhang et al., 2007).

The overall goal of this review article is to communicate what applications in contaminant hydrogeology are possible with four existing imaging methods in order to stimulate future work and promote advances in the field. The specific objectives of this review are 1) to familiarize the reader with the basic operation and theory of each imaging method, 2) to demonstrate for each imaging method the range of applications in contaminant hydrogeology, the type of data collected, and the critical imaging parameters (e.g., image time, image resolution, and material constraints), and 3) to identify the advantages and disadvantages of each imaging method and provide recommendations for future work. For more specific details on each imaging method and application results, references are provided. This paper is organized into sections that correspond to the numbered set of objectives, and concludes by identifying what imaging methods are best for different application constraints.

2. IMAGING THEORY

2.1. Optical Imaging

A variety of optical methods are used to image flow and reactive transport in porous media, and the most common use visible and fluorescent light. Visible light is used to image processes that are visible to the unaided or aided eye. Fluorescent tracers emit light with a unique spectrum when excited by UV or visible light at a shorter wavelength. The spectral information can be used to visualize different tracers in parallel (e.g., Chomsurin and Werth, 2003). Many of the (fluorescent) dye tracers are sensitive to the chemical environment, e.g. to the pH-value (Jose and Cirpka, 2004), to the redox potential (Huang et al., 2003), to metal ions (Willingham et al., 2008), or to the vital state of cells (Wick et al., 2004), and can be used to map chemical and biological processes in porous media. Most optical imaging applications use charge-coupled device (CCD) cameras to digitally record incident light. When pore-scale processes are of interest, microscopes have to be used in combination with CCD cameras to enhance image resolution.

Visible light microscope techniques have been extensively reviewed in the literature (Pluta, 1993; Bradbury, 1998; Murphy, 2001), and include bright field microscopy, phase contrast microscopy, and reflected differential interference contrast microscopy (i.e., Nomarski microscopy). The first of these requires samples that transmit light, and fluids and pore structures that absorb different wavelengths or amounts of light are resolved through a microscope objective. The second of these is also used with samples that transmit light, and contrast is achieved when sample components cause a phase shift in the light passing through a sample. The third of these can be used with transparent or opaque samples; it involves projecting two beams of polarized light through slightly different path lengths onto a sample. Transmitted or reflected light from the two beams is combined, and the interference between them resolves features with different optical density.

Fluorescent light microscope techniques include standard fluorescence microscopy, and also confocal laser-scanning microscopy (e.g., Murphy, 2001). The former requires a mercury or xenon light source, and either transparent or opaque samples can be used. Incident light strikes a fluorescent molecule, and excites it to a higher energy state causing emission at a longer wavelength. The basic principle of confocal microscopy is the same, except that a laser is used to selectively excite a narrow plane of light. Images from multiple planes can be combined to create a three dimensional image.

Some attempts have been made to calibrate fluorescence intensity in order to quantify pore scale processes. For nonreactive tracers, this is theoretically a relatively straight-forward exercise that involves measuring the relationship between fluorophore concentration and fluorescence intensity. However, few light sources are perfectly uniform in space or time, and image correction and/or continuous reference measurements (Willingham et al., 2008) are often necessary for proper calibration. For reactive tracers, this may prove to be impossible because they often have a low level of background fluorescence in their non-reacted state. For example, the calcium sensitive fluorophore Oregon green bapta 488 exhibits low fluorescence in the absence of calcium, and high fluorescence in the presence of calcium (Willingham et al., 2008). The overlapping of these spectra confounds quantification through a calibration profile.

2.2. Gamma-Radiation

Gamma rays are electromagnetic photons that travel at the speed of light and are uncharged and unaffected by electrical or magnetic fields. Most gamma radiation systems currently in use are dual-energy systems with 241-americium and 137-cesium sources. The ²⁴¹Am source emits gamma radiation primarily at 60 KeV following α decay, while ¹³⁷Cs gamma rays, emitted after β decay, have an energy of 662 KeV. The gamma radiation technique is based on the attenuation of gamma rays by materials through photoelectric absorpton (Van Bavel et al., 1957). The equation of attenuation of gamma rays through a system with n components (i=1,n) can be written by Beers’ law as

$$I_j=I_j^o\text{exp}(\sum _{i=1}^n-{\mu }_{ij}{\rho }_i{\theta }_i{x}_i)$$ (1)

where I^o and I are the incident and emergent count rates, respectively, μ is the mass attenuation coefficient (L² M⁻¹), ρ the density (M L⁻³), θ the volumetric content, and x the path length (L). The subscript j denotes the source (e.g., j = a for ²⁴¹Am; j = c for ¹³⁷Cs) and i the component. The components may be solids, water, NAPL, and salt. The contribution of the gas phase to the attenuation of the gamma rays is typically ignored. Replacing the product μ_ij ρ_i by the volumetric attenuation coefficient typically obtained in a calibration procedure, U_ij (L⁻¹), gives

$$I_j=I_j^o\text{exp}(\sum _{i=1}^n-U_{ij}{\theta }_i{x}_i)$$ (2)

For a rigid porous medium, the incident count rate in Equation 2 can be replaced by the count rate through the column or cell when the porous medium is dry. Indirect methods for determining $I_j^o$ are necessary for columns and cells packed under saturated conditions and are provided by Oostrom et al. (1998). A drawback of dry packing is the possibility of cracking, settling, or consolidation of the porous medium, which affects the bulk density values. Packing under saturated conditions usually results in relatively large bulk density values, which remain stable in the course of an experiment.

The most widely used dual-energy gamma system configuration is the collinear beam configuration where the two sources are mounted rigidly in a lead or tungsten shield, with the ¹³⁷Cs source several centimeters behind the ²⁴¹Am source along a common collimator. The gamma beams simultaneously travel through the same sample section and a common detector collimator before reaching the detector (Figure 1). The detector is typically a thallium-activated sodium iodide scintillation crystal with a photomultiplier tube. The electronic components of a gamma system are a high-voltage power supply, amplifiers, spectrum stabilizers, single-or multi-channel analyzers, and counter/timers. Recently, internal computer boards with advanced spectroscopy capabilities have become available that combine all of the function of the mentioned electronic components. General laboratory software can be used for automated data acquisition and movement of the source holder and detector in horizontal and vertical directions.

Figure 1.

Dual-energy gamma system at Pacific Northwest National Laboratory with source holder, detector, and vertical movement configuration. In the picture, the gamma rays are traveling through a compartmental cell used for the determination of fluid attenuation coefficient.

Calibration of a gamma radiation system includes the determination of attenuation coefficients, path lengths, and incident count rates (Eq. 1). The attenuation coefficients of fluids and porous media are usually obtained by using a compartmental cell, and provide accurate results for the attenuation coefficients of liquids (e.g., Stillwater and Klute, 1988; Oostrom and Dane, 1990). However, it is more complicated to obtain accurate values of the attenuation coefficients of porous media because of the requirement of consistent packing, and because the average dry bulk density of the porous material in each compartment has to be determined. The path length at each location can be measured directly or computed indirectly using the count rates through the empty and water-filled column or cell (Oostrom et al., 1995). The next step is to obtain $I_j^o$ (incident count rates) values, which will subsequently result in dry bulk density and porosity values at locations where measurements will be taken during an actual experiment. The traditional dual-source calibration method is described by Oostrom et al. (1995) and Stillwater and Klute (1988). A new single-source is described by Oostrom et al. (1998); it has distinct advantages over the dual-source method. It is simpler and more accurate than the traditional dual-source method, and is recommended as a standard procedure in experiments.

2.3. X-ray Microtomography

X-ray computed tomography has been used for many years to obtain 3D images of biological, geological, and manufactured samples, and this method has become a mainstay for many imaging applications. For example, medical X-ray systems are now routinely used to obtain “CAT scans” of the human body. In addition, industrial X-ray systems are widely used to image geologic and manufactured samples. The basic concept behind synchrotron X-ray microtomography (SMT) is the same as for X-ray computed tomography. It is the availability of high-energy (synchrotron) sources and improvements in data collection and processing that has supported the development of SMT (e.g., Thompson et al., 1984; Bonse et al., 1986; Flannery et al., 1987a, b; Spanne and Rivers, 1987; Tjahjadi and Bowen, 1987; Kinney et al., 1988). The method is based on mapping the spatially-distributed differential absorption of an X-ray beam as it passes through the sample. The amount of absorption depends on sample composition and energy of the X-ray. Materials with a higher atomic mass absorb more X-rays, and thus materials of different atomic masses (e.g., water vs. rock) will attenuate the X-rays to different degrees. This allows one material to be distinguished from another material. The energy of the beam can be tuned to image specific elements, thus enhancing resolution. The X-ray beam is highly collimated, which further enhances resolution. This section and the associated sections below are focused on absorption-based microtomography, which is the most widely used method for subsurface science. Other synchrotron X-ray tomography methods have been employed, such as fluorescence microtomography (e.g, Betson et al., 2004), but will not be discussed.

In a typical implementation, the monochromatic X-ray beam is directed through the sample, perpendicular to the longitudinal axis as illustrated in Figure 2. The transmitted X-rays are converted to visible light with a single-crystal scintillator, and projected onto a surface. A photograph of the image on the surface is then taken with a high-resolution CCD camera. This image represents a 2D depth-integrated grayscale map of the linear attenuation of the X-ray beam as it passed through the sample. A large number of these 2D projections are needed to obtain a 3D spatially-distributed map of attenuation. Thus, after an image is collected, the sample is rotated about the longitudinal axis (typically 0.5° to 1°) and the image-acquisition process is repeated. In this manner, a total of 720 or 360 2D images of the sample are collected. Additionally, several backfield projections, or images of the beam without any sample present, are collected during each set of scans. The vertical image window (vertical beam thickness) is typically a few mm. Thus, the entire imaging process will need to be repeated after vertical translation of the sample if the sample is longer than a few mm’s.

Figure 2.

An illustration of X-ray microtomography system components (adapted from www.ctlab.geo.utexas.edu/overview/index.php).

To enhance discrimination amongst materials and phases, a target phase can be doped with a highly-absorbing compound. For example, iodide can be added to water to help distinguish between air and water, and an organic iodine compound can be added to an organic liquid to help distinguish it from water. To further enhance resolution, absorption-edge difference microtomography can be employed. With this approach, the synchrotron beam is tuned to specific incident energies to take advantage of the X-ray absorption K-edge of the doping compound. The K-edge refers to the X-ray energy at which the absorption of the beam by that element increases dramatically.

The set of 2D images collected for a given sample scan are processed and reconstructed with specially developed software. Reconstruction is used to build a single 3D image file from the 2D images. After reconstruction, the data can be visualized as “thin sections”, 2D slices in either the x-y (perpendicular to the longitudinal (rotational) axis of the column) or x-z (parallel to the rotational axis of the column) direction. The reconstructed thin sections show the attenuation (grayscale) of the X-ray beam in a discrete location (voxel), and thus the internal distribution of the attenuation is obtained. For the absorption-edge difference technique, reconstructed 3D images acquired with incident energy below the dopant K-edge are subtracted from the corresponding images obtained from above the dopant K-edge to produce images wherein only voxels comprising the target (doped) phase display grayscale values different from the background.

2.4. Magnetic Resonance Imaging

Magnetic resonance imaging (MRI) is based on nuclear spin or rotation, which is a fundamental property of elementary particles. Although all elementary particles have spin, only those atoms with uneven spin quantum numbers (1/2, 3/2, …) are magnetically susceptible and suitable for MRI. Among these the following are commonly used in imaging experiments (given with their spin quantum numbers) ¹H = 1/2, ¹³C = 1/2, ¹⁹F = 1/2, ⁵³Cr = −3/2, and ¹⁵⁵Gd = 7/2. Excellent introductory books on MRI are referred to for additional background information (Morgan and Hendee, 1984; Liang and Lauterbur, 1999).

Nuclear spin results in a magnetic moment, and the perturbation of this moment and associated spins during MRI are illustrated in Figure 3. To obtain an MR image the samples of interest are exposed to an external magnetic field (B₀). This causes the spins to align with the external magnetic field resulting in a precession movement at the Larmor frequency, either clockwise or counter-clockwise to B₀. The Larmor frequency, ω, or resonance frequency, is a function of the gyromagnetic ratio, γ (42.58 MHz/T for ¹H) of the nuclei and B₀: ω = γ B₀, where γ represents a proportionality constant between the magnetic moment and the angular momentum. Since slightly more spins precess clockwise, the net magnetic moment is parallel to B₀.

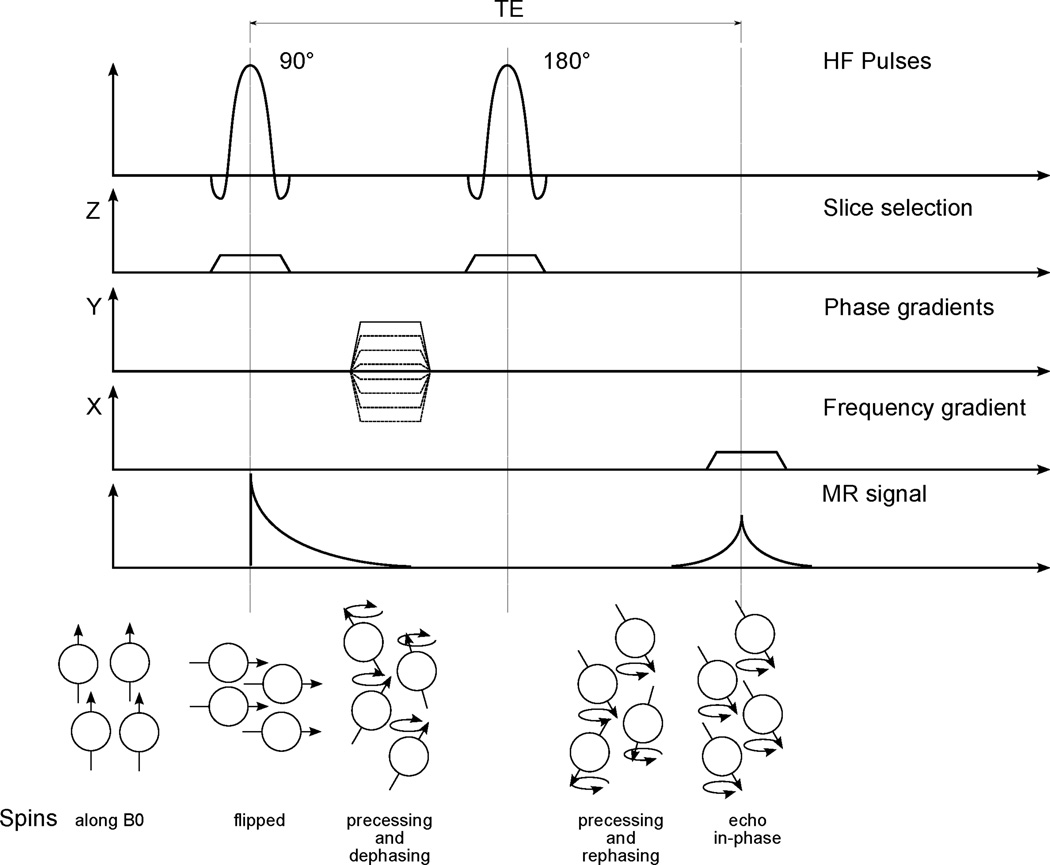
Figure 3.

Illustration of an MRI pulse sequence, associated perturbations of the net magnetic moment and nuclear spins, and the corresponding MRI signal.

Once the net magnetic moment is aligned with B₀, an external radio frequency pulse induced with an electromagnetic coil at the Larmor frequency flips the spins out of B₀. Once the radio frequency pulse is terminated, the spins relax back to their original state so the net magnetic moment is aligned with B₀. During relaxation, the magnetic moment from the in-phase spins induces an alternating current at the resonance frequency in the coil which is recorded as the MR signal. This signal decays exponentially during relaxation as the spins dephase and the net magnetic moment flip angle from B₀ becomes smaller. The time constant of the flip angle decay is called the longitudinal relaxation time, T₁, and is on the order of hundreds of milliseconds to several seconds; it is dependant on B₀. The time constant of decay due to spin dephasing is called the transverse relaxation time, T₂, and is on the order of tens of milliseconds. Local inhomogeneities of B₀ induce further decay described by T₂^* (Vlaardingerbroek and den Boer, 1999).

To obtain an MR image, magnetic field gradients are applied in X, Y, and Z directions. For example, a magnetic field gradient is applied along the Z-axis to select a slice in a sample. The position of a volume-element (voxel) in a slice is encoded with a phase (Y-axis) and a frequency gradient (X-axis). The resolution of an image depends mainly on the strength of the gradients: the higher the gradients, the better the resolution.

A basic Spin-Echo MRI sequence is shown in Figure 3. A 90° pulse is first applied to flip the spins from the Z-direction into the X,Y-plane; a 180° pulse is applied after a set time (i.e., T_E/2), causing the precession to be reversed and to be in phase after another time T_E/2, yielding a so called echo. The amplitude of the MR signal (A_E) can be expressed as (Liang and Lauterbur, 1999):

$$A_E=M_z^0(1-2e^{-(T_R-T_E/2)/T_1}+e^{-T_R/T_E}{e}^{-T_R/T_2})$$ (3)

Here, $M_z^0$ represents the spin density, T_E represents the echo time, and T_R is called the repetition time, representing the time beteen two 90° pulses. The MR imaging contrast depends on the spin density, T₁ and T₂/T₂^*. Also, differences in T₁ or T₂ among phases can be used to selectively excite one phase over another. A T₁-weighted image can be obtained using an appriopriate repetition time, T_R, and a short T_E, whereas a T₂-weighted image can be obtained using a long T_R and appropriate T_E.

The acquisition time during MRI is a function of T_R, T_E and the number of distinct phase gradients. Most fast imaging sequences (TSE, fast low angle shot, FLASH, echo-planar imaging, EPI) are single shot or echo train sequences. Partial readout sequences (single shot fast spin echo, SSFSE, half fourier acquisition single shot fast spin echo, HASTE) decrease the aqcuisition down to less than 1 sec but are limited to larger pores, because they depend on long T_E (Vlaardingerbroek and den Boer, 1999) (i.e., smaller pores increase the solid surface area to fluid volume ratio and this decreases T₁ and T₂).

The distribution of a fluid in porous media or fractures can be imaged through sequences sensitive to the spin density. The distribution of two or more imiscible fluids can be measured by either selective excitation of different magnetically susceptible nuclei in each fluid, or by selective excitation of each fluid based on differences in T₁ or T₂. Apparent diffusion coefficients, dispersion and advective velocities of selected nuclei can be imaged by applying pusle sequences that are sensitive to motion of the target nuclei (Pope and Yao, 1993; Fukushima, 1999), or by using a phase contrast agent as a tracer (Guillot et al., 1991; Greiner et al., 1997).

3. IMAGING APPLICATIONS

3.1. Optical Imaging

Optical imaging has been used in contaminant hydrogeology to characterize NAPL location, interfacial area, and saturation, to measure water and solute flow paths and velocities, to evaluate colloid transport mechanisms, and to study reactive transport processes, primarily in model pore structures and media, but also in 2D flow cells filled with natural sands. Below we describe relevant applications of optical imaging to study each of the aforementioned processes, in addition to the spatial and temporal scales of resolution. Important system parameters including imaging spatial resolution and time are summarized in Table 1, and example images representing different applications are shown in Figure 4.

Table 4-1.

Imaging method applications, associated parameters values, and method limitations. ¹

Imaging Method	Application	Description	Field of View (FOV) / Imaging Resolution (IR) [mm]	Time to Acquire a Single Image / Entire FOV [sec]	Comments	References
Optical Imaging	Multiphase Fluid Distribution	pore-scale NAPL/water/air distribution Darcy-scale NAPL/water/air distribution	1a)10×10 mm2 / 0.7×0.7 µm2 1b)150×300 mm2 / 0.15×0.15 mm2 2a)98×200 mm2 / 0.478×0.478mm2 2b)600×260 mm2/ 0.5×0.5 mm2	1a)1.2s / 400s 1b)0.3s / 0.3s 2a)30 – 300s 2b)20s / 20s	1a)fluorescent dyes and fluorescence microscopy 1b)transmitted light and CCD camera 2a)fluorescent dyes and CCD camera 2b)transmitted light and CCD camera	1a)Chomsurin and Werth, 2003; 1b)Zhong et al., 2001; 2a)Bridge et al., 2006, 2007; 2b)Glass et al., 2000, 2001.
	Solute Transport and Fluid Flow	pore-scale tracer imaging Darcy-scale tracer imaging	10 µm2 0.18×0.20 mm2	10s 1/50s	laser-induced fluorescence excitation transmitted UV light coupled with a CCD camera	Rashidi et al., 1996; Jones and Smith, 2005.
	Particle / Colloid Dynamics	pore-scale colloid imaging	1a)10×10 mm2 / 0.7×0.7µm2 1b)180×100 mm2/20×20 µm2	1a)0.5s / NA 1b)2 to 30 s	1a)fluorescent dyed colloids, epi-fluorescent microscope 1b)fluorescence and CCD camera	1a)Baumann and Werth, 2004; 1b)Zhang and Wang, 2006
	Reactive Transport	pore-scale Darcy-scale	1a)20×10mm2 / 1.5×1.5 µm2 1b)1×1 µm2 2)200×400 mm2 / 0.3×0.3 mm2	1a)NA 1b)1/30 s 2)0.7 s	1a&b)fluorescent dyes and fluorescence microscopy 2)transmitted light coupled with CCD camera	1a)Willingham et al., 2008; 1b)Baumann and Niessner, 2006. 2)Oates and Harvey, 2006.
Gamma	Porous Media Characterization	Darcy-scale	~30 mm2	45 seconds to several minutes per location	Porosity and dry bulk density	Oostrom et al. (2003)
	Multiphase Fluid Distribution	Darcy-scale	~30 mm2	45 seconds to several minutes per location	Simultaneous determination of water and NAPL saturation	Oostrom et al., (2005; 2006)
	Solute Transport	Darcy-scale	~30 mm2	45 seconds to several minutes per location	Application limited to NaI salts at concentration > 1 g/L	Oostrom et al., 1992a,b,c
X-ray	Porous Media Characterization	Pore network topology Statistical properties	10 × 10 mm2/0.001 – 0.01 mm	1–1.7 sec/900–1200 sec		Lindquist et al., 1996
	Multiphase Fluid Distribution	pore-scale NAPL/water/air distribution Darcy-scale NAPL/water/air distribution fluid body morphology fluid-fluid interfaces	same	same		Schnaar and Brusseau, 2005; Brusseau et al., 2008
	Particle / Colloid Dynamics	colloid distribution	same	same
MRI	Porous Media Characterization	pore structures sandstone and limestone fractures	39×39 mm2 / 0.15×0.15 mm2	N.A	T1 weighting / 2 T	Chen et al., 1996;
	Multiphase Fluid Distribution	pore-scale NAPL/water/air distribution Darcy-scale NAPL/water/air distribution	1a)50×50×128 / 0.390×0.390×1 1b)15×15×15 / 0.059×0.059×0.059 2)120×120×240 / 1.875×1.875×2.25	1a)N.A. 1b)68 min 2)2.2 min	1a)T1-weighting / 4.77T 1b)ρ-weighting / 4.7 T 2)ρ-weighting / 4.7 T	1a)Johns & Gladden, 1999; 1b)Zhang et al., 2002; 2)Zhang et al., 2007.
	Fluid Flow	pore-scale water flow without paramagnetic tracer Darcy scale water flow with paramagnetic tracer flow in rock fractures	1a)0.17×0.17×0.2 mm3 1b)0.156 mm3 2a)2.34×2.34×10 mm3 2b)1.875×1.875×2.25 mm3 3)2D: 0.12×0.06 mm3 3D: 0.23×0.13×0.18 mm3	1a)N.A. 1b)N.A. 2a)3.2 min 2b)2.2 min 3)2D: 1.5 min 3D: 1.2 hr	1a)5.0 T 1b)199.7 MHz 2a)63 MHz / Cu2+ 2b)4.7 T / Mn2+ 3)4.7 T	1a)Kutsovsky et al., 1996; 1b)Mantle et al., 2001; 2a)Greiner et al., 1997; 2b)Yoon et al., 2008; 3)Dijk et al., 1999.
	Particle / Colloid Dynamics	Darcy-scale abiotic particle imaging Darcy-scale biotic particle imaging biofilm imaging	0.2×0.2×1 mm3 0.33 mm 0.62×0.62×20 mm3	3 min N.A. 8.6 min	4.7 T 1.75 85 MHz	Baumann & Werth, 2005; Olson et al., 2004; Hoskins et al., 1999.
	Reactive Transport	CO2 adsorption on zeolite metal ions sorption on quartz sand	3.3 cm / 1 mm 1.05×1.05×2 mm3	11 min 1 min	2.35 T 63 MHz	Cheng et al., 2005; Nestle et al., 2003.

NA = Not Available

¹Please note the citations provided are for illustration purposes only, and do not represent an exhaustive list of all relevant work.

Figure 4.

Images of a) DNAPL (white) and water (light gray) in a silicon-etched regular pore structure, b) DNAPL (red) and water in the pores of a column filled with glass, c) colloids accumulating at the interface of an air bubble in a water filled glass-etched pore structure, d) DNAPL (white) migration pathway in a heterogeneous sand-packed flow cell, e) colloid travel paths (exposure time was long relative to travel distances) in water flowing around a cylinder in a silicon-etched pore structure, f) the product (higher intensity region along horizontal centerline) of a reaction between calcium and a calcium sensitive fluorophore in the same pore structure, and g) the product of a reaction between Trion and molybdate in a flow cell packed with circular inclusions of small glass beads in a bed of larger glass beads. Cylinders in 3.1-1a, c, e, and f are several hundred microns in diameter, images were taking using fluorescent microscopy, and water flow is from left to right. The images were adapted from a) Chomsurin and Werth (2003), b) Montemagno and Gray (1995), c) Wan and Wilson (1994), d) Glass et al. (2000), e) Baumann and Werth (2004), f) Willingham et al. (2008), and g) Oates and Harvey (2006) (PERMISSION BEING OBTAINED).

3.1.1. Fluid Distribution

Water and NAPL distribution have been determined through optical imaging in a number of model 2D pore structures, often as a function of mass remaining during dissolution. In some cases, images of NAPL and/or water were taken directly with a camera, and NAPL distribution and/or saturation was obtained (Soll et al., 1993; Jia et al., 1999; Zhong et al., 2001). In others, high resolution images (i.e., pixels are less than or equal to tens of microns) were captured with the aid of a microscope and NAPL morphology and/or interfacial area were also determined, often with the aid of fluorescent dyes to distinguish phases (Keller et al., 1997; Kennedy and Lennox, 1997; Sahloul et al., 2002; Chomsurin and Werth, 2003). In a few cases, surfactants were used to enhance NAPL mobilization or solubilization (Jeong et al., 2000; Jeong and Corapcioglu, 2003). Two-dimensional model pore structures were constructed from a monolayer of glass beads sandwiched between glass plates, and by etching pore structures into glass or silicon wafers. An example image of NAPL and water in a pore network is shown in Figure 4a (Chomsurin and Werth, 2003). The NAPL ganglia was stained with a hydrophobic fluorescent dye (i.e., Nile red), and water was stained with a hydrophilic fluorescent dye (i.e., Alexa Fluor). The dyes and the silicon posts were characterized by different intensities so interfacial areas could be determined using intensity thresholding and an edge-detection algorithm.

In a limited number of studies, optical methods were used to distinguish NAPL distribution and morphology at the pore-scale in three dimensions. High-resolution images (i.e., 1 µm resolution) were obtained using photoluminescent volumetric imaging, a technique where optical-quality quartz sand and refractive-indexed matched immiscible fluid containing fluorescent dyes are imaged with the aid of laser-induced fluorescence (LIF) (Montemagno and Gray, 1995) (Figure 4b). Fontenot and Vigil (2002) used this technique (refractive-index matched LIF) to characterize the size and shape of NAPL ganglia during surfactant-enhanced dissolution. Stohr et al. (2003) reported using LIF to obtain 3D images of water displacement of silicone oil in refractive-index matched solid and liquid phases at a resolution of 0.07×0.07× 0.5 mm³. Ovdat and Berkowitz (2006) applied the LIF technique to study immiscible displacement of dibutyl phthalate (as the wetting phase) by glycerol (nonwetting phase).

NAPL and/or water distribution has also been imaged at the Darcy scale in 2D flow cells. In one set of studies (Glass et al., 2000, 2001), flow cells were filled with sand from an automated hopper that allowed controlled delivery of different sand fractions and the creation of “facies-like” geometric structures. The NAPL was dyed with Oil-Red-O, and the intensity of light transmitted through the flow cell was used to determined NAPL location (Figure 4d). In another study, water was dyed with fluorescein and the fluorescence intensity captured by a CCD camera was directly related to water saturation (Bridge et al., 2007). In the aforementioned 2D flow cells with facies-like geometric structures, the effects of surfactant flushing and permanganate oxidation on NAPL removal were also evaluated (Conrad et al., 2002). Some imaging artifacts were encountered when the NAPL dissolved in preference to the Oil-Red-O dye (e.g., residual color remained after NAPL removed).

3.1.2. Solute and Fluid Transport

A large number of tracer breakthrough experiments have been imaged in etched pore structures, 2D flow cells, and columns. A common approach is to image the spatial distribution of an aqueous phase colored- or fluorescent-dye as it flows through a model pore structure. This approach has been used to capture images of conservative tracers flowing through 2D pore networks etched into glass (Corapcioglu et al., 1997) or silicon (Nambi et al., 2003; Willingham et al., 2008), or fabricated from quartz sand or glass beads held between two glass or acrylic plates (Corapcioglu and Fedirchuk, 1999; Zinn et al., 2004; Jones and Smith, 2005; Bridge et al., 2006), or through a polymethylmethacrylate (PMMA) column packed with beads from the same material and refractive index matched fluid (Rashidi et al., 1996). When calibrated against standards of known dye concentration, image intensity can be correlated to dye concentration and breakthrough can be quantified. To enhance pore-scale resolution, fluorescence and transmitted-light microscopy have been used to enhance magnification and reduce the field of view (Nambi et al., 2003; Willingham et al., 2008), and laser-induced fluorescence excitation has been used to image selected 2D planes in three dimensional pore networks (Rashidi et al., 1996). Alternatively, a uniform UV light source coupled with a CCD camera has been used for fluorophore excitation and subsequent image capture at the Darcy scale (Jones and Smith, 2005).

Variations of solute breakthrough experiments using fluorescent dyes have been performed to measure mixing of one or more solutes. Typically, fluorescent or color tracers were injected into flow fields to create transverse or longitudinal mixing zones with adjacent tracer-free water. At the pore scale, epi-fluorescence microscopy was used to image transverse mixing in pore structures etched into silicon wafers (Willingham et al., 2008). At the Darcy scale, both visible (Rahman et al., 2005) and UV light sources (Huang et al., 2002) have been used to image transverse mixing of a food dye (Cochineal Red A) and fluorescein, respectively, both in flow cells created by packing sand between two transparent plates.

In only one set of studies was imaging used to determine fluid saturations for three phases simultaneously during flow (Darnault et al., 1998; Darnault et al., 2001; Darnault et al., 2002). Water was dyed blue with CuSO₄ (or FD&C blue #1), and the hue and intensity of visible light transmitted through a 2D flow cell packed with sand was used to quantify the spatial saturations of water, air, and NAPL.

3.1.3. Particle Dynamics

Optical methods have been used to image both abiotic and biotic (e.g., bacteria) particles in model porous media (e.g., review by Keller and Auset, 2007). Abiotic particles have been imaged in 2D pore structures etched into glass (Wan and Wilson, 1994) (Figure 4c) or silicon (Baumann and Werth, 2004; Sirivithayapakorn and Keller, 2003a, b), imprinted on polydimethylsiloxane (PDMS) (Auset and Keller, 2004, 2006), or created by sandwiching a thin layer of sand or glass beads between glass or acrylic plates (Crist et al., 2004; Bradford et al., 2005; Bridge et al., 2006, 2007; Zhang and Wang, 2006). Fluorescent particles were also imaged flowing through a PMMA column packed with beads from the same material and refractive index matched fluid (Northrup et al., 1993; Peurrung et al., 1995; Rashidi et al., 1996). In most cases, functionalized latex microspheres were used with either bright field or fluorescent microscopy, depending on whether colloids were stained with a fluorescent dye. However, clay particles were imaged in one case (Wan and Wilson, 1994), and air bubbles were imaged in other studies (Moroni and Cushman, 2001a, b). Colloid transport and retention mechanisms were studied including pore size exclusion, straining, filtration, and retention at air-water interfaces, and colloid flow paths were compared to simulated flow paths. An example image of fluorescent-dyed latex particle flow paths in a silicon-etched pore structure is shown in Figure 4e (Baumann and Werth, 2004). The CCD camera exposure time was set to 500 ms, and this allowed the colloid flow paths to be captured in one image. Individual colloid particles were resolved in most imaging experiments performed with 2D model porous media. However, in two studies (Bridge et al., 2006; Zhang and Wang, 2006), a coarser resolution was used and total fluorescence intensity was related to particle concentration.

Individual, dispersions, and aggregates of biologically active particles (e.g., biofilms) have also been imaged. At the pore scale, individual viruses were observed in pore structures etched into silicon using fluorescent microscopy to evaluate retention mechanisms at air-water interfaces (Sirivithayapakorn and Keller, 2003b). At the Darcy scale, a step input of bacteria suspended in water was imaged during breakthrough using light scattering in an etched-glass pore structure (Lanning and Ford, 2002); dispersion coefficients were obtained via modeling of breakthrough data. A large number of studies have imaged biomass growth and/or detachment in etched pore structures or 2D flow cells. These include applications where biomass growth was restricted to one or more transverse mixing zones between electron donor and acceptor (e.g., Thullner et al., 2002; Nambi et al., 2003), and where substrates were well mixed and biomass growth occurred throughout the pore structure (e.g., Paulsen et al., 1997; Dupin and McCarty, 1999, 2000; Kim and Fogler, 2000; Stewart and Fogler, 2001; Dunsmore et al., 2004). Different nutrient conditions (e.g., nutrient rich versus nutrient poor), flow rates, pore geometries, and inoculums were evaluated, and the effects on biomass morphology and location, biomass stability, permeability, and/or substrate degradation were evaluated.

3.1.4. Reactive Transport

A variety of reactive transport applications have been evaluated using optical imaging methods over a range of length scales. One of the most common involves imaging aqueous reactants or the product of an instantaneous reaction in porous media, in most cases to evaluate the effects of mixing on reaction. Example reactants are tracers that fluoresce when complexed to an aqueous solute (e.g., fluorescein and protons, Oregon Green 488 Bapta-5N and calcium) (Jose and Cirpka, 2004; Willingham et al., 2008), tracers who’s fluorescence is quenched in the presence of an aqueous solute (e..g, ruthenium (II)-dichlorotris(1,10-phenanthroline) and oxygen) (Huang et al., 2003), and tracers that change colors upon reaction or produce a colored product (e.g., thymol blue or methyl red and protons, Tiron and molybdate, CuSO₄ and EDTA⁴⁻) (Gramling et al., 2002; Rahman et al., 2005; Cirpka et al., 2006; Oates and Harvey, 2006). Two example images of reactive transport are shown in Figure 4. One is at the pore scale (Willingham et al., 2008), and shows the product formed between Oregon Green 488 Bapta-5N and calcium, that mix transverse to the flow in a pore structure etched into a silicon wafer (Figure 4f). The other is at the Darcy scale (Oates and Harvey, 2006), and shows the product formed between Tiron and molybdate in a flow cell packed with circular inclusions of small glass beads in a bed of larger glass beads (Figure 4g). The first was imaged using epi-fluorescence microscopy, and the latter with a uniform visible light source transmitted through the flow cell.

Several elegant approaches have been employed to image biological activity in flow cells packed with sand or glass beads at the Darcy scale. One approach used the aforementioned dye; its fluorescence is quenched in the presence of oxygen and allowed delineation of the zone where an acetate plume was undergoing biodegradation (Huang et al., 2003). Another more complicated approach used a bacterium that was genetically engineered to carry a plasmid with bioluminescence inducible by salicylate and dependent on oxygen (Oates et al., 2005). Salicylate was kept constant and oxygen utilization was related to bioluminescence.

The effects of sorption/partitioning on transport have also been evaluated via imaging. The spatial distribution of a partitioning fluorescent tracer over time was compared to that for a non-partitioning fluorescent tracer to estimate residual NAPL saturation (Jones and Smith, 2005). Also, the repartitioning of colloid bound hydrophobic contaminants at the interface to NAPL has been visualized and quantified at the pore scale (Baumann and Niessner, 2006). In only one study has the effect of reaction on the formation of a solid phase precipitate been visualized (Tartakovsky et al., 2008). Here, calcite precipitation along the mixing zone between aqueous phase calcium and carbonate in a two-dimensional flow cell was imaged using visible light.

3.2. Gamma-Radiation

Noninvasive dual-energy gamma radiation has been primarily used in contaminant hydrogeology to image the saturation of one or more fluids in porous media, including water and nonaqueous phase liquids. However, indirect measurement of porous media heterogeneity is possible through differences in water saturation, solute transport has been evaluated using salt tracers, and fluid flow has been imaged by taking sequential images of fluid saturation in transient experiments. Dual-energy gamma radiation has been used to study processes relevant to contaminant hydrogeology in columns, and in 2D flow cells of varying size (cm’s to m’s). Below we describe relevant applications of dual-energy gamma radiation. Important system parameters including imaging spatial resolution and time are summarized in Table 1, and example images of water and nonaqueous phase fluid saturation are shown in Figure 5.

Figure 5.

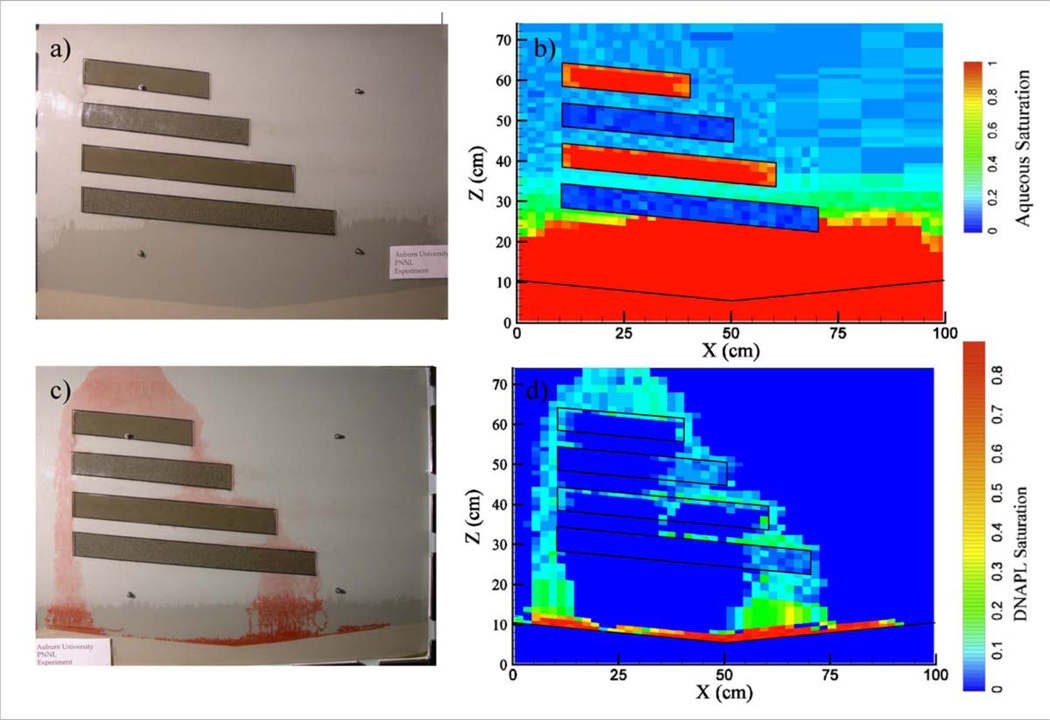
(a) Picture (b) and aqueous phase saturation gamma scan of unsaturated flow cell before carbon tetrachloride injection, and (c) picture (d) and carbon tetrachloride saturation gamma scan of the same flow cell at the end of the fluid redistribution period. The images were adapted from Oostrom et al. (2005) (PERMISSION BEING OBTAINED).

3.2.1. Porous Media Characterization

The gamma radiation technique was traditionally used to determine porosity and dry bulk density values (e.g., Van Bavel et al., 1957; Soane, 1967; Gardner et al., 1972). For more recent applications to NAPL infiltration and redistribution and salt concentration measurements, porosity and dry bulk density values are still obtained as part of the system calibration procedure. Several flow cells imaged using dual-energy gamma radiation have been packed with lenses of low or high permeability materials, surrounded by one or more contrasting permeability zones (e.g., Illangasekare et al. 1995b; Oostrom and Lenhard, 2003). As a result, permeability fields were well known and dual-energy gamma radiation has not been explicitly used to characterize permeability variations. Nevertheless, permeability variations in flow cells have been delineated through imaging of water saturation in unsaturated flow cells. An example is shown in Figure 5b, where several low permeability lenses have higher water saturation than the surrounding high permeability sand.

3.2.2. Fluid Distribution

Dual-energy gamma radiation has been used to image the distribution of one or more fluids for a variety of applications, primarily to obtain parameters for relative permeability (k), fluid saturation (S) and pressure (P) constitutive models, to study multi-fluid flow behavior, to test NAPL removal techniques by aqueous dissolution and enhanced remediation techniques, and to quantify NAPL saturations using partitioning tracers. In some cases, the flow behavior studies were conducted to test k-S-P models. Since the minimum counting time for gamma systems is on the order of a minute, fast imaging is often not possible for column and flow cell experiments. Only a few experiments, to be discussed in the next section, have been conducted where fluid saturations have been determined at selected locations during transient phases of an experiment. The other applications are discussed below in this section.

An important first use of gamma radiation imaging for contaminant hydrogeology research was to generate fluid saturations (Ferguson and Gardner, 1962; Fritton, 1969), in some cases to compute parameter values for saturation-pressure relations (Ferrand et al., 1986; Dane et al., 1992; Hofstee et al., 1997; White et al., 2004). Measurements with gamma radiation assure the determination of such curves locally within a porous medium, rather than providing data averaged over the total volume of a relatively large sample, as determined with typical pressure cells. For example, Dane et al. (1992) showed that a gamma radiation system could be used to determine both water and DNAPL trichloroethene (TCE) saturations every 1 cm along a 1-m-long column; this coupled with fluid pressure distributions at hydraulic equilibrium were used to develop saturation-pressure relationships. Hofstee et al. (1997) used a similar approach to measure water and DNAPL perchloroethene (PCE) saturations at eight different locations along a 1-m-long column. These measurements were used to investigate the nonspreading behavior of the PCE in unsaturated conditions. White et al. (2004) and Lenhard et al. (1988) also measured water and NAPL saturations at multiple locations along a column, but LNAPLs were used (i.e., Soltrol^® 220 and/or dodecane). Measurements were compared to predictions from three-phase constitutive theory.

The first quantitative 2-D flow cell experiment with NAPL saturations obtained with a gamma system was described by Host-Madsen and Jensen (1992). They reported two simple experiments where LNAPL was injected into partly saturated medium- and fine-grained sands. Since fairly weak sources were used, counting times of 2–3 minutes were needed for each measurement. However, the total measurement period was kept relatively short because a fairly coarse 10-cm × 10-cm grid was used and measurements were taken only at locations where NAPL was visually present. A more detailed LNAPL infiltration and redistribution experiment in an unsaturated system was reported by Oostrom et al. (1997) and tested against various k-S-P models. For this experiment, dual-energy gamma radiation data were obtained at >1000 locations. The experiments described by Host-Madsen and Jensen (1992) and by Oostrom et al. (1997) were relatively simple since they only involved infiltration and redistribution of a LNAPL spill in a homogeneous system.

More complex experiments in heterogeneous systems with DNAPLs were reported by Hofstee et al. (1998a,b), Oostrom and Lenhard (2003), and Oostrom et al. (2003). In each of these four studies, DNAPL was released from a point source and allowed to infiltrate into a two-dimensional flow cell packed with a layer of fine-grained material surrounded by coarser grained material. The DNAPL and water saturation were then determined from γ-radiation imaging after no further migration of the injected DNAPL was apparent. In one case (Hofstee et al., 1998b), the system was water-saturated, in all others the fine-grained material and most of the coarse-grained material were unsaturated. Also in one case (Oostrom and Lenhard, 2003), the fine-grained material was caliche; in all others it was fine sand. In two cases (Hofstee et al., 1998a,b), PCE was the DNAPL, while in the other two it was carbon tetrachloride (CT). A significant advancement in imaging for flow cells was the development of an automated track system that quickly moved the γ-radiation scanner to a desired location. This allowed the same locations to be imaged at different imaging times, or many locations to be imaged at one imaging time. For example, more than 1,300 locations (1×1 cm²) were imaged in a flow cell at one imaging time by Hofstee et al. (1998b).

An even more heterogeneous flow cell experiment was evaluated with dual energy γ-radiation imaging by Oostrom et al. (2005). Two unsaturated fine layers and two unsaturated course layers were embedded at the same sloping angle in an unsaturated medium sand matrix (Figure 5a), and DNAPL PCE was released from a point source and allowed to infiltrate until no further migration was apparent. Dual energy γ-radiation imaging was used to determine the water and DNAPL saturation, and then soil vapor extraction was initiated. Periodic images were then taken during soil vapor extraction to investigate DNAPL removal mechanisms. A gamma scan showing the water saturation at ~1200 locations is shown in Figure 5b.

More complex NAPL migration histories have been evaluated using dual energy γ-radiation imaging. Oostrom et al. (2006) released two sequential volumes of a LNAPL mixture (i.e., lard oil and 1-iodoheptane) into a two-dimensional flow cell packed with an unsaturated sand; after LNAPL migration was no longer apparent, the water table in the flow cell was raised and part of the LNAPL was mobilized upward. Dual energy γ-radiation imaging was first used before LNAPL was present to image water saturation and determine if the water content in the sand was at equilibrium. It was then just before and at periodic intervals during the raising of the water table. Over 1800 locations were evaluated during each imaging time.

In addition to NAPL migration studies, dual-energy γ-radiation imaging has been used to measure NAPL saturation during NAPL dissolution, and during NAPL remediation using surfactant flushing. DNAPL saturation was measured during dissolution from emplaced source zones in two dimensional flow cells (Brusseau et al., 2000, 2002, 2008a). The number and geometry of source zones varied among studies, as well the type (e.g., TCE, CT, 1,2-dichloroethane) and initial saturation of DNAPL. In the most recent study (Brusseau et al., 2008), the mass flux of DNAPL from source zones with different geometry and initial saturations was determined as a function of DNAPL mass remaining. DNAPL TCE saturation measurements during surfactant flushing have been used to evaluate removal efficiency as a function of local DNAPL saturation, and to evaluate downward DNAPL migration into fine permeability layers due to a reduction in interfacial tension (Oostrom et al., 1999a, b). They have also been used to help develop a mass transfer correlation for DNAPL dissolution during surfactant flooding (Schaerlaekens and Feyen, 2004).

NAPL saturations determined using dual energy γ-radiation have been compared to NAPL saturations determined with partitioning tracers (Nelson et al., 1999; Jalbert et al., 2003; Barth et al., 2003; Moreno-Barbero et al., 2007) to evaluate limitations of the latter. The saturations were determined just after the NAPL became trapped in the flow cell, and after a period when NAPL dissolution occurred. The effect of porous media heterogeneity, NAPL saturation and distribution, nonequilibrium partitioning, and flow bypassing were evaluated.

3.2.3. Solute and Fluid Transport

Solute transport has been evaluated using gamma radiation in only a few applications. Studies of solute transport are limited to applications involving breakthrough of a saline solution in a column experiment (Oostrom et al., 1992a), and to an experiment where density effects were imaged in a 2D flow cell (Oostrom et al., 1992b,c). Gamma measurements of salt concentrations require heavy ions such as I⁻ in NaI or Pb²⁺ in Pb(NO₃)₂ (Grismer et al., 1986), and salt concentrations as high as 1 g/L are needed to accurately quantify salt concentrations (Oostrom et al., 1998). In the column experiment, breakthrough fronts of saline water containing I⁻ were imaged in order to determine porous media dispersivities (Oostrom et al. 1992a). In the 2D flow cell, a saline plume was injected into a salt-free water saturated porous media, and plume stability was determined by imaging salt breakthrough at selected locations. (Oostrom et al., 1992b,c).

Fluid transport has been more widely studied using gamma radiation, but transient fluid flow has only been measured in just a few studies. In these experiments (Illangasekare et al., 1995a,b; Hofstee et al., 1998a,b; Oostrom et al., 1999a), changes in NAPL saturation were recorded as a function of time at either a transect or at one or more locations of interest. The experiments described by Illangasekare et al. (1995a) involved LNAPL infiltration into homogenous and layered systems with moving groundwater due to an imposed hydraulic gradient. The authors showed the obtained saturations at selected vertical profiles, instead of images of 2D areas, during the redistribution period. Saturations in subsequent experiments involving infiltration of various DNAPLs into layered unsaturated and saturated systems (Illangasekare et al., 1995b) were also obtained at vertical transects.

The flow cell experiments by Hofstee et al. (1998a,b) were used to investigate the behavior of the DNAPL PCE in saturated and unsaturated flow cells containing a rather large fine-grained sand layer surrounded by coarse-grained sand. In the saturated experiments (Hofstee et al., 1998b), the initial infiltration of PCE was in the form of fingers. Measured saturations obtained during infiltration at locations within the zone through which the PCE migrated were low because of the preferential flow paths. Since gamma systems determine average saturations over the width of the column or flow cell, saturation measurements in these unstable systems are not very valuable.

3.3. X-ray Microtomography

Standard (non-synchrotron) X-ray computed tomography (CT) has been used for more than two decades in subsurface science fields. In particular, it has seen significant use in characterizing porous-media structure and fluid-displacement processes for the purpose of improving our understanding of oil recovery (e.g., Wang et al., 1984; Hove et al., 1987; Vinegar and Wellington, 1987; Wellington and Vinegar, 1987; Withjack, 1988; Hicks et al., 1992). Standard X-ray CT has also been used in the environmental field, for example, to measure fluid saturations during bench-scale experiments investigating the migration of organic liquid (e.g., Fagerlund et al., 2007; Goldstein et al., 2007). This method is conducted with medical or industrial X-ray sources, and associated resolutions range from 100’s to 1000’s of µm. With this range of resolutions, the CT method is limited generally to producing measurements of fluid saturation and characterizing porous-media structure and fluid distributions at the “macroscopic” scale. The advent of synchrotron X-ray microtomography, with resolutions ranging from 1 to 10 µm, has provided a means with which it is possible to characterize individual fluid bodies and to measure fluid-fluid interfacial areas in natural porous media. An overview of synchrotron X-ray microtomography applications in subsurface science is provided below, examples of results and images are shown in Figure 6, and example values of important imaging parameters are listed in Table 1. In some cases, non-synchrotron microtomography applications will be included when resolutions are close to those achievable with synchrotron systems.

Figure 6.

a) Pore network structure extracted from SMT data, b) distribution of wetting fluid at residual saturation in a bead pack, c) distribution of colloids (red) in a glass-bead pack (blue), d) residual organic-liquid saturation for a three-phase system: organic liquid is white, the aqueous phase is dark gray, air is black, and porous-medium grains are light gray, and e) 3D renderings of the organic-liquid blobs entrapped in the packed column as a function of water flushing (time sequence is left to right). The images were adapted from a) Al-Raoush and Willson (2005a), b) Turner et al. (2004), c) Gaillard et al. (2007), d) Schnaar and Brusseau (2006a), e) and Schnaar and Brusseau (2006b) (PERMISSION BEING OBTAINED).

3.3.1. Porous Media Characterization

Some of the first applications of SMT for investigating subsurface-science related issues were conducted at the National Synchrotron Light Source located at Brookhaven National Laboratory, and were focused on characterization of porous-media physical properties (Dunsmuir et al., 1992; D’Amico et al., 1992). Specifically, the image data collected with the SMT method has sufficient resolution to allow production of 3D maps of the pore network for a range of porous media types. This information has been used to enhance understanding of the relationship between pore-scale properties and continuum-scale measurements such as porosity, pore-size distribution, specific solid surface area, tortuosity, and permeability. Such analyses have been applied to unconsolidated (glass beads, soil) and consolidated (sandstone, carbonate rock, chalk, basalt) media (e.g., Schwartz et al., 1994; Spanne et al., 1994; Coker et al., 1996, Lindquist et al., 1996; Auzerais et al., 1996; Song et al., 2001; Nakashima et al., 2004, Arns et al., 2005; Lehmann et al., 2006; Nunan et al., 2006; Øren et al., 2007). High-resolution non-synchrotron MT has been used to examine physical properties of soil, such as pore structure (e.g., Macedo et al., 1999; Perret et al., 2000; Cislerova and Votrubova, 2002), and of fractured media (e.g., Karpyn et al., 2007, Noiriel et al., 2007; Peth et al., 2008).

The pore-network data produced with SMT has been used to support the development and application of pore-scale mathematical modeling efforts. For example, the 3D pore-network maps obtained from SMT have been used as input for Lattice Boltzmann modeling (e.g., Ferreol and Rothman, 1995; Auzerais et al., 1996; Coles et al., 1998a,b; Hazlett et al., 1998; Arns et al., 2003; Turner et al., 2004; Lehmann et al., 2006; Prodanovic et al., 2007). Additionally, SMT has been used to quantitatively characterize the pore-network topology of porous media, wherein algorithms are used to extract information about the 3D spatial distribution of pore-bodies and pore-throats, pore-body size distribution, pore-throat size distribution, and pore connectivity (Figure 6a). This has been done for both unconsolidated media such as glass beads and sands and consolidated media including sandstone (e.g., Lindquist et al., 2000, Seidler et al., 2000; Al-Raoush and Willson, 2005a; Al-Kharusi and Blunt, 2007). This data has been used as input for pore network models (e.g., Hazlett, 1995; Coles et al., 1998a,b; Øren et al., 1998; Valvatne and Blunt, 2004; Karpyn and Piri, 2007; Piri and Karpyn, 2007).

3.3.2. Fluid Distribution and Immiscible Displacement

While the initial applications of SMT were focused on characterizing pore networks, the method can also be used to characterize fluids within the pore network. For example, SMT can be used to measure fluid saturations during immiscible-displacement processes (e.g, Di Carlo et al., 1997). An early use of SMT for characterizing pore-scale fluid distributions as well as saturations associated with immiscible-displacement processes was reported by Coles et al. (1998a,b), who characterized the distribution of water and oil in a sandstone core after an immiscible displacement. Seright et al. (2002, 2003) and Prodanovic et al. (2007) investigated the impact of gels on permeability reduction for water-wet and oil-wet systems. Turner et al. (2004) imaged drainage experiments performed for a sintered monodisperse plastic bead pack and observed residual (trapped) wetting fluid present as pendular rings, bridges between adjacent grains, and lenses within pore throats (Figure 6b). They also examined fluid distributions for a sandstone core. The pore-scale distribution of residual non-wetting fluid was examined for a pack of octadecyltrichlorosilane-coated glass beads by Al-Raoush and Willson (2005b). The distribution of residual non-wetting fluid was compared for two natural sands and a soil by Schnaar and Brusseau (2005). Wildenschild et al. (2005) examined the distribution of air and water during water drainage conditions for a sand. Culligan et al. (2006) compared the distribution of wetting and non-wetting fluids for oil-water and air-water systems for glass-bead packs. Schnaar and Brusseau (2006a) compared pore-scale fluid distributions for two-phase (immiscible organic liquid, water) and three-phase (air, immiscible organic liquid, water) systems for two natural sands and a soil. A significant portion of the organic liquid in the three-phase systems was observed to exist as lenses and films in contact with air (see Figure 6d).

In addition to characterizing pore-scale fluid distribution, SMT has been used recently to quantitatively characterize the morphology of individual fluid bodies and determine statistics of the population (e.g., blob-size distribution). This has been done for several porous media, specifically octadecyltrichlorosilane-coated glass beads (Al-Raoush and Willson, 2005b), natural sands and soil (Schnaar and Brusseau, 2005), oil–wet polyethylene cores (Prodanovic et al., 2006), and sandstone cores (Prodanovic et al., 2007). The influence of porous-medium texture was examined in the work presented by Schnaar and Brusseau (2005). They observed that the sizes and shapes of the organic-liquid (nonwetting phase) blobs varied greatly, ranging from small spherical singlets (~0.03 mm in diameter) to large, amorphous ganglia with mean lengths of 4–5 mm.

The availability of synchrotron X-ray microtomography, with its higher resolution, has provided a means by which to measure fluid-fluid interfaces in natural porous media. This method has recently been used to measure interfacial areas for air/water (Culligan et al., 2004; Brusseau et al., 2006, 2007; Costanza-Robinson et al., 2008), organic-liquid/water (Al-Raoush and Willson, 2005b; Schnaar and Brusseau, 2005, 2006a; Culligan et al., 2006; Prodanovic et al., 2006; Brusseau et al., 2008b), and air/organic-liquid/water (Schnaar and Brusseau, 2006b) systems. Specific air-water interfacial areas as a function of water saturation were presented by Brusseau et al. (2007) for a sandy soil. The total (film+capillary) specific interfacial area increases linearly with decreasing water saturation over the measured range. Conversely, capillary-associated interfacial area first increases and then decreases with decreasing saturation.

The resolution of the SMT method provides a means by which to characterize the pore-scale dissolution of organic immiscible-liquid blobs residing within natural porous media. Schnaar and Brusseau (2006b) used SMT to characterize the morphology of the organic-liquid (trichloroethene) blobs as a function of dissolution in columns packed with one of two sandy porous media, and to quantify changes in total organic-liquid volume, surface area, and organic-liquid/water interfacial area. In addition to dissolution-induced shrinkage, some blobs were observed to separate into multiple distinct sub-units (Figure 6e). Changes in the measured aqueous-phase trichloroethene effluent concentrations were adequately described by a first-order mass transfer expression employing a constant value of the dissolution rate coefficient, with values for the organic-liquid/water interfacial area obtained independently by use of the microtomography data.

3.3.3. Fluid Displacement and Solute Transport

Non-synchrotron X-ray tomography has been used in several studies to examine flow and solute transport under miscible-displacement (e.g., Anderson et al., 1992; Johns et al., 1993; Perret et al., 2000; Olivier et al., 2005). Miscible displacement work primarily focused on imaging the breakthrough of x-ray sensitive contrast agents (e.g., iodine, barium) in water at selected locations in columns. There appears to have been minimal application of SMT to miscible-displacment problems. Fluorescence-based SMT was used to characterize solute diffusion in chalk samples (Betson et al., 2005).

3.3.4. Particle Dynamics

SMT has been used to examine particle distribution and transport in porous media. Gaillard et al. (2007) examined the distribution of ZrO₂ particles in a glass bead pack after a suspension of the particles was injected via miscible displacement (Figure 6c). Li et al. (2006) used non-synchrotron MT to examine the distribution of gold-coated microspheres in glass-bead and sand packs.

3.3.5. Reactive Transport

Studies of reactive transport using SMT are relatively limited. Altman et al (2005) used SMT to map the iron content within a column packed with subsurface sediment, to qualitatively image the adsorption of cesium, and to delineate the relationship of cesium adsorption with iron-bearing materials. Noiriel et al. (2005) used SMT to examine the impact of acidic-water-induced dissolution on porosity and permeability of limestone.

3.4. Magnetic Resonance Imaging

Magnetic resonance imaging has been used in contaminant hydrogeology research to characterize porous media properties such as grain size and porosity, to determine NAPL location, interfacial area, and saturation, to measure water and solute flow paths and velocities, to evaluate colloid transport mechanisms, and to study reactive transport processes. Imaging resolution and scan time varies with sample size, sample characteristics, and scanner. Maximum resolution of cm-scale samples is on the order of a few tens of microns, whereas resolution of m-scale samples is on the order of mm’s. Below we describe relevant applications of MRI to study each of the aforementioned processes, and we note the spatial and temporal scales of resolution. Important system parameters including imaging spatial resolution and time are summarized in Table 1, and example images representing different applications are in Figures 7 and 8.

Figure 7.

Magnetic resonance images of (a) octanol (white) trapped in glass beads (dark) initially saturated with water (grey); (b) dodecane invasion (red) of a rock fracture at selected time points; (c) nonaqueous phase trifluorobenzene ganglia at the pore scale trapped in a column packed with water saturated silica gel; d) nonaqueous phase trifluorobenzene trapped as ganglia and pools in a spatially correlated random permeability field. The images were adapted from (a)Johns and Gladden (1999); (b) Becker et al.(2003); (c) Zhang et al. (2002); (d) Zhang et al. (2007) (PERMISSION BEING OBTAINED).

Figure 8.

Magnetic resonance images of (a) flow paths of a paramagnetic tracer injected into a spatially correlated random permeability field; (b) colloids advecting through a homogeneously packed column after 15 minutes of flow; (c) adsorptive retention of Cr³⁺ ions (in green) from a 3 mg/L solution flowing through 0.1 – 0.4 mm quartz sand at selected time points. The images were adapted from (a) Yoon et al. (2008); (b) Baumann and Werth (2005); (c) Nestle et al. (2003) (PERMISSION BEING OBTAINED).

3.4.1. Porous Media Characterization

Pore size distribution, grain size distribution, porosity, and permeability have all been studied using NMR or MRI (e.g., Gladden et al., 1995; Song, 2000; Song et al., 2000). Pore and grain size distribution require imaging at the pore scale. Porosity and permeability are macroscopic properties of porous media that can affect relaxation behavior of water protons (¹H), making it possible to study pore size distribution via indirect measurement of NMR parameters or direct visualization via spin-density or T₁ or T₂-mapping. Howard et al. (1993) found ¹H longitudinal relaxation time, T₁, in water saturated reservoir sandstones is closely related to pore size distribution. Issa and Mansfield (1994) used a T₁-mapping approach to correlate the permeability of sandstones to T₁ distributions. Gleeson et al. (1993) obtained 2D and 3D images of pore structures of limestone at 0.1×0.1×0.3 mm³ resolution. Chen et al. (1996) obtained images of sandstone and limestone fractures at a spatial resolution of 0.15×0.15×5 mm³. Baldwin et al. (1996) obtained spin-density weighted 3D images of a column filled with 6 mm glass beads at a resolution of 0.2×0.4×0.4 mm³, and volume images were used to evaluate a void space identification algorithm. Gingras et al. (2002a, b) applied a T₁-weighting MRI technique to characterize the porosity distribution in biogenic sandstones. Zhang et al. (2007) visualized the permeability distribution of a heterogeneously packed quartz sand via T₂-weighting ¹H MRI at a resolution of 1.875×1.875×2.25 mm³. In other studies, unsaturated porous media have also been characterized and water relative permeability can be determined by measuring NMR relaxation time (T₁, T₂) distributions under drainage conditions (Attard et al., 1994; Chen et al., 1996; Choi et al., 1997; Bird et al., 2005; Ioannidis, 2006).

3.4.2. Fluid Distribution

Water and NAPL distributions have been studied in a number of different porous media at a variety of scales using MRI. At the pore scale, the exact location and morphology of individual NAPL ganglia were resolved, typically in three dimensions, and in a variety of low-iron bearing porous media including glass beads (Johns and Gladden, 1999) (Figure 7a), rock fractures (Becker et al., 2003) (Figure 7b), silica gel (Zhang et al., 2002) (Figure 7c), organic-rich soil cores (Simpson et al., 2007) and estuarine sediments (Reeves and Chudek, 2001). In several cases, measured NAPL surface area and/or NAPL-water interfacial area were determined at selected time points during column flushing with water, and the corresponding effects on NAPL dissolution were evaluated (Johns and Gladden, 1999; Zhang et al., 2002). A common approach to distinguish NAPL from water and/or air involves imaging hydrocarbons using T₁ or T₂-weighting. Fluorinated NAPLs (e.g., 1,3,5-trifluorobenzene) can also be used and imaged at a different resonance frequency than protons in water.

At the Darcy scale, a number of studies have used MRI to evaluate water and NAPL saturations in heterogeneous media packed in 3D flow cells (Zhang, 2006; Zhang et al., 2007, 2008a, b) using fluorinated organics (Figure 7d). The NAPL saturation information was used to evaluate NAPL dissolution under water flushing (Zhang et al., 2007, 2008a), as well as surfactant-enhanced remediation (Zhang et al., 2008b). Spatially dependent NAPL dissolution rates were directly compared to spatially dependent water velocities, also determined with MRI (see section 3.4.3.). The NAPL saturation distribution has also been determined in unsaturated systems (Chu et al., 2004). The saturation distribution of decane trapped in unsaturated silica gel sand was studied during vapor purging; the time period between successive images was sufficiently short to observe NAPL flow from low to high permeability zones induced by capillary pressure gradients created during soil vapor extraction.

3.4.3. Solute and Fluid Transport

MRI has been used to directly image water flow at both the pore (e.g., Kutsovsky et al., 1996; Manz et al., 1999a; Deurer et al., 2004) and Darcy scale, and indirectly at the Darcy scale using paramagnetic tracers (e.g. Guillot et al., 1991; Greiner et al., 1997; Irwin et al., 1999, 2000; Yoon et al., 2008). At the pore scale, Kutsovsky et al. (1996) applied a flow encoding pulse sequence to measure the axial velocity profile in the pore space of 6 mm glass beads packed in a column (4cm ID). Pore water velocity was found to increase toward the center of the pores and the profiles are roughly parabolic. Manz et al. (1999a) obtained 3D images of velocity profile at a resolution of 0.086 × 0.086 × 0.5 mm³ in a 1 cm ID column containing 1 mm glass beads. MRI velocity profiles were compared to Lattice-Boltzmann (LB) velocity maps determined directly from a lattice derived from the MRI experimental 3D images of the pore structure. Good agreement between MRI and LB was found. In a separate study, Mantle et al. (2001) measured 3D MRI velocity in columns packed with alumina pellets 1.3 – 3.0 mm in diameter and 3.0 – 6 mm in length. Three orthogonal components of velocity were acquired at a resolution of 156 µm, and the flow field through the pore space was shown to be highly heterogeneous, i.e., 40% of the fluid flows through 10% of the pores. Okamoto et al. (2001) measured longitudinal water flow velocities in 39mm ID column packed with 3mm glass beads and also containing trapped silicone oil. A chemical shift imaging method was used to acquire 2D multi-slice images of silicone oil, and a phase encoding method was used to obtain velocities at 11 cross sections along the column, both at a resolution of 0.2×0.2×0.5 mm³. The authors observed that the decrease in flow rate for large, oil-blocked pores was compensated for by the increase from the greater number of small pores. Deurer et al. (2004) imaged water flow through a column (ID = 1.4cm) filled with 2 mm glass beads and mean velocities were determined for various slice thickness ranging from 2mm to 40 mm perpendicular to the flow (in plane resolution: 156×156 µm2). The representative elementary volume (REV) to reach the mean velocity was found to be greater than 2 grain diameters.

At the Darcy scale, Greiner et al. (1997) used a whole body MR scanner operating at 63 MHz for ¹H and a 2D spin echo pulse sequence to image the paramagnetic tracer, CuSO₄, as it flowed through columns filled with homogeneous (0.5 mm) or heterogeneous (0.25 – 0.6 mm) glass beads. Density contrast between water with and without tracer was 0.1%. A field of view of 300×300 mm was used, and 24 contiguous 10 mm slices with in-plane resolution of 2.34×2.34mm was used (128×128). Duration of each 3D scan was 3.2 min. Tracer mass determined by MRI matched the input mass. First and second moment calculations were used to calculate pore water velocities and dispersivities form the MRI data. Pore water velocities were consistent with input values. Reasonable dispersivities (on the order of the grain diameter) were obtained. Baumann et al. (2000) used MRI to directly image water flow through a column (10 cm ID, 20 cm length) filled with heterogeneous natural sediments at a spatial resolution of 1.32×1.32×5mm³. The mean flow velocity from MRI measurements was in good agreement with the velocity determined from a numerical flow model. Herrmann et al. (2002) used a pulsed gradient spin echo sequence to image dispersion in static and flowing water in columns (6 cm ID, 18 cm length) filled with either 2mm glass beads or the glass beads mixed with 0.15 mm quartz sand. Resolution was from 1.25×1.25 mm² to 2.25×2.25mm² with a slice thickness of 4mm. Local dispersion coefficients determined for the 2mm glass beads in static water were close to the molecular diffusion coefficient of free water, and they increased linearly with the flow velocity from 0 – 0.14 mm/s. Column averaged dispersion coefficients are on the order of those determined from classical breakthrough studies. Zhang et al. (2007) imaged the 3D transport of the paramagnetic tracer through a 14×9×9 cm flow cell packed with a heterogeneous distribution of 1cm blocks containing one of five different sand types. Breakthrough profiles were obtained at every one of the ~100,000 voxels.

In other applications, MRI has also been used to measure ion diffusion through water saturated porous media (Pearl et al., 1991; Baumann et al., 2000), dispersion (Guillot et al., 1991; Seymour and Callaghan, 1997; Amin et al., 1997; Stapf et al., 1998; Manz et al., 1999a, b; Deurer et al., 2004), density dependent flow in porous media (Pearl et al., 1993; Hoffman et al., 1996; Oswald et al., 2002; Oswald and Kinzelbach, 2004), and water flow in rock fractures (Mansfield and Issa, 1994; Dijk et al., 1999; Dijk and Berkowitz, 1999). Oswald et al. (2002) imaged density driven flow in a 20cm³ Plexiglas tank filled with 1.2mm glass beads and freshwater flow above saltwater using Cu²⁺ as contrast agent, at a spatial resolution of 2.5×2.5×4 mm³ (1.5T magnet). They observed that the saltwater remained relatively stagnant with a narrow transition zone (<1cm) between fresh and salt water, and saltwater did not experience upconing near the freshwater outlet. Dijk et al. (1999) applied 2D and 3D flow-encoded spin-echo pulse sequence to obtain water flow velocity maps in rough-walled rock fractures. Water flow was found to be heterogeneous and represented by asymmetrical parabolic velocity profiles.

3.4.4. Particle and Biofilm Dynamics

Both abiotic and biotic (e.g., bacteria) particles have been imaged in porous media using MRI, in all cases at the Darcy scale. With respect to abiotic particles, super paramagnetic colloids were imaged during transport in columns packed with either uniform silica gel or a fine-grained core surrounded by a coarse-grained shell (Baumann and Werth, 2005); an example image is shown in Figure 8b. Colloid exchange between coarse and fine-grained materials was observed, as well as attachment to the porous media. MRI has also been used to study the effects of fine particle deposition in porous media on porosity and water flow (Sederman et al., 2001; Amitay-Rosen et al., 2005). Amitay-Rosen et al. (2005) applied MRI to study 1 or 12 µm poly(tetrafluoroethylene) (PTFE) particle deposition and mobilization in water saturated polystyrene beads 160 – 300 µm in diameter. Spin-density weighted multi-slice images were obtained at spatial resolution of 0.12×0.12×2 mm³. Dynamic changes in porosity and velocity as a result of particle deposition and subsequent mobilization were measured.

With respect to biotic particles, MRI has been used to image bacterial chemotaxis in columns packed with glass coated polystyrene beads (Olson et al., 2004). Imaging was possible because magnetite particles were attached to Pseudomonas putida F1 via a monoclonal antibody specific to the organism. Sherwood et al. (2003) studied bacterial random motility in 0.25 – 0.33 mm polystyrene beads coated with glass using MRI and E. Coli cells labeled with magnetite particles. A 1D T₂-weighted spin-echo pulse sequence was used to achieve a spatial resolution of 0.33×2.9 mm², and Brownian diffusion was found to be solely responsible for the transport of nonmotile cells.

In several studies, NMR/MRI was used to measure biofilm growth in porous media (Potter et al., 1996; Hoskins et al., 1999; Seymour et al., 2004a) and their impacts on flow and transport (Lewandowski et al., 1992; Seymour et al., 2004a, b). Diffusion of intracellular water is restricted by the cell walls, and hence leads to signal attenuation under a magnetic field gradient. Based on this principle, Potter et al. (1996) applied a pulsed-field-gradient spin-echo (PGSE) technique to characterize biofilms in tubes packed with quartz sand. Hoskins et al. (1999) imaged stationary biomass in open flow and glass bead (1 – 1.5 mm in diameter) filled parallel plate reactors, and biofilms were found to reduce both T₁ and T₂ of water. In porous media systems, T₁-weighting was shown to be more effective in resolving biofilm. Seymour et al. (2004b) applied T₂-mapping to image biofilms in columns (5 mm ID) packed with 0.24 mm polystyrene beads and the PGSE technique to characterize the impacts of biofilm on hydrodynamic dispersion.

3.4.5. Reactive Transport

MRI has been used to study reaction kinetics and spatial distribution of reactants in catalytic reactors (e.g., Gladden et al., 2002, 2006; Yuen et al., 2002). Gladden et al. (2002) demonstrated that by monitoring the ¹H chemical shift, spatial variation in liquid phase esterification of methanol and acetic acid in fixed bed reactors under flow conditions could be visualized. A limited number of studies have applied MRI to investigate reactive transport in porous media, including CO₂ adsoption/desorption on zeolites (Cheng et al., 2005), and metal ion sorption on glass beads (Moradi, 2008) and quartz sands (Nestle et al., 2003). Cheng et al. (2005) applied ¹³C MRI (2.35T magnet, 100 Gauss/cm) to investigate the adsorption / desorption kinetics of pure gas and condensed phase CO₂ on 8 – 12 mesh zeolite 5A beads, and a centric scan spin-echo single point imaging technique was employed to obtain transient 1D CO₂ density profiles with a 1 mm resolution.

Nestle et al. (2003) used MRI (63 MHz) to study transport of Mn²⁺, Cu²⁺, Cr³⁺, and Gd³⁺ ions in columns filled with 0.1 – 0.5 mm quartz sand (Figure 8c). A multislice spin-echo pulse sequence was used to obtain images (via T₁- or T₂-weighting) of spatial distribution of metal ions at 1.05×1.05×2 mm³, and image acquisition time was on the order of minutes. Absorption and mobilization of metal ions were visualized via image contrast associated with adsorbed metal ion concentration. Moradi et al. (2008) used T₁-mapping to study nickel ion (Ni²⁺) sorption on 0.4 – 1 mm glass beads at a spatial resolution of 0.58×0.58×15 mm³ and temporal resolution of less than 1 min.

4. ADVANTAGES AND DISADVANTAGES OF IMAGING METHODS

4.1. Optical Imaging

The advantages of direct optical imaging methods are their relative low cost, high resolution, and fast acquisition time. Starting from direct imaging with a CCD camera and moving to microscopic techniques, image resolution and the cost of equipment increases. Also, with increasing imaging resolution the field of view decreases, which can be overcome by scanning the sample, but at the cost of reducing the temporal resolution. Acquisition of spectral information from the sample further limits the temporal resolution. Costs are incurred to fabricate flow cells amenable to optical imaging. Those constructed from two glass plates that sandwich glass beads or sand are conceptually simple to create and, for small samples, can be relatively inexpensive. However, the more exotic microfluidic-based flow cells that allow precise etching of pore structures in silicon or polymer substrates require considerable expertise and infrastructure. An overview of microfluidic fabrication methods is available at Gad-el-Hak (2001).

The resolution of optical imaging is limited by the wavelength of light, the desired field of view, and the pixel density of the digital camera. Microscopic resolution is approximately 0.5 µm, while the resolution using a digital camera and a macro objective is on the order of 10 µm. The field of view is usually 100 to 1000 times larger than the image resolution. An exception is fluorescent particles that can project an image much larger than their actual size due to light diffraction (i.e., outshining). The projected particle diameter is a function of the numerical aperture, image magnification, the wavelength of recording light, and particle diameter. Per Meinhart et al. (1999), fluorescent particles as small as 200 nm can project an effective diameter of 30 microns with a 60× objective. The time to acquire images depends on the intensity of the light source and on the photon quantum yield of the sample. The fastest shutter speeds are on the order of milliseconds or up to 100 frames/s for digital video cameras. However, when the photon density of the imaged sample is low, exposure times on the order of seconds per image may be necessary to resolve features.

The primary disadvantage of optical imaging is that model porous media or very simple representations of heterogeneity are typically used. Many imaging experiments, apart from confocal laser scanning imaging, are limited to a two dimensional acquisition, either because the microfluidic channel is 2D or because of averaging in the third dimension. For example, uniform clean sands or glass beads are typically packed into larger flow cells and dyed water is visualized, and patterned pore structures are etched into various substrates. Upscaling procedures have to take the simplified topology and the reduced spatial complexity of 2D interfaces compared to a 3D natural system into account. Optical methods are also limited to translucent media, which are clearly an exception in natural environments. Quantification of processes requires a calibration of the fluorescence signal, which is another challenge. Variations in light intensity can be caused by a variety of factors including a nonuniform light source, variable packing density in a flow cell, imperfections or dirt on flow cell substrates, background light, and photo-bleaching. Great care must be taken to eliminate or correct these issues. As a result, many applications in contaminant hydrogeology have been evaluated qualitatively or semi-quantitatively

4.2. Gamma Radiation

An advantage of the gamma imaging method is the ability to work with a relatively large range in column and flow cell sizes, ranging from just a few cm to several meters. Another major advantage is that this method has the potential to obtain accurate and precise data sets. Well-designed and calibrated gamma systems have been used to create porosity and saturation data sets that have been successfully compared with data obtained with other methods. Although the design and construction of a gamma system is not trivial, actual maintenance once the system has been completed is minimal.

The gamma imaging method also has several disadvantages. The relatively large counting times (45 seconds or larger) needed for an accurate determination at a single (~1 cm²) location limit this method to applications where imaging is used at conditions close to or at steady state. For intermediate-scale flow cell applications, total counting times of several hours up to one day have been reported to produce an image. For total counting times in that range, the images are only meaningful when the saturation changes over the duration of a scan are small. Another disadvantage is that the obtained saturation information is always averaged over the width of the column and flow cell. A consequence of this averaging is that for gamma imaging applications, observed flow and transport phenomena should be nominally 1D in columns and 2D in flow cells. In addition, the porous medium width cannot be too small to too large. For most applications, the width should be between 5 and 7.5 cm, provided the wall material is glass or plastic. Finally, the calibration procedure needed before quality data can be obtained with this method is time-consuming. A typical calibration procedure for a flow cell experiment easily takes several days to complete and requires highly-trained operators and careful experimental planning.

4.3. X-ray Microtomography

A major advantage of synchrotron X-ray microtomography is the high resolution, typically in the range of 1–10 µm, which is generally the greatest resolution among the imaging methods that are applied to 3D systems. This resolution allows the method to be used for quantitative characterization of the pore network and fluid distributions for many natural materials. Data obtained with SMT have helped advance our understanding of the pore-scale dependency of continuum-scale porous medium properties. It has also helped advance pore-scale modeling efforts by providing more realistic input information. The high resolution of SMT also allows quantitative measurement of fluid-fluid interfacial areas for natural media. Despite the relatively high resolutions, application of the method would likely be constrained for media with high fractions of very fine particles (<1 um), wherein it would be difficult to resolve the smaller pore and fluid bodies. Smaller image domains can be used in an attempt to increase the resolution, but at some point the reduced volumes may not satisfy REV issues.

A major disadvantage is the need to use a synchrotron facility. Another disadvantage is the time required for a complete 3D scan, which ranges from approximately 10 to 30 minutes. This limits the ability of the method for characterizing systems wherein fluid is flowing. The number of rotations used to collect individual scans could be reduced to decrease overall imaging time, at the expense of quantitative 3-D resolution. Another limitation is the relatively small sample size (several cm at most). Discrimination amongst the various fluid and solid phases is generally satisfactory for glass bead and sand type porous media, and thus use of a dopant is not required. However, a dopant is typically required for more complex media. The potential impact of the dopant, which is typically in the few-percent range, on fluid properties and behavior is of concern. Initial examination of this issue indicated no measurable impact of the dopant on measured properties (saturation, blob volumes and surface areas) for the systems investigated (Schnaar and Brusseau, 2005). This issue should be examined for each application of interest.

4.4. Magnetic Resonance Imaging

The main advantage of MRI is that it can directly visualize 1D, 2D and 3D processes occurring in porous media from pore to continuum scale. Unlike other imaging techniques, the MRI signal is generated directly from fluid or solid phases, the external magnetic field and gradient can be manipulated in a variety of ways to distinguish different chemical species of interest, and to resolve the flow field with or without a tracer. MRI also has the advantage of flexibility in terms of spatial and temporal resolution. When higher spatial resolution is desired, 3D volumetric imaging can be used to achieve resolution up to tens of micron, and fast imaging pulse sequences (e.g., 2D slice-by-slice imaging) are available to capture transient effects on the time scale of seconds.

Despite the advantages of MRI, there are of course a number of disadvantages. First and foremost, the MRI signal is attenuated by ferromagnetic materials, and by paramagnetic species when present in sufficient quantities. This means researchers must use model porous materials with low levels of ferromagnetic materials, such as polystyrene beads, glass beads, silica gel, quartz sand, or limestone. Second, the spatial and temporal resolutions of MRI are limited by the magnetic field and gradient strength; a stronger gradient is desired for faster imaging or higher spatial resolution. Third, the largest samples sizes are approximately one by two meters in size; gamma radiation can be used to scan samples of any size. Fourth, image resolution generally scales with sample size; the finest resolution is obtained with the smallest samples and vice-versa. Fifth, MRI requires a magnetic resonance scanner; these are very costly and complex to maintain and operate.

5. CONCLUSIONS AND RECOMMENDATIONS FOR FUTURE WORK

Non-invasive imaging techniques have a unique niche in contaminant hydrogeology research, and have provided valuable insights into a variety of complex systems and processes. These include porous media characterization, multiphase fluid distribution, fluid flow, solute transport and mixing, colloidal transport and deposition, and reactions. Four key methods used for non-invasive imaging in contaminant hydrogeology were reviewed in this work: optical imaging, gamma radiation imaging, synchrotron-based X-ray imaging, and magnetic resonance imaging. There is no perfect method or tool for non-invasive imaging; they each have their advantages and disadvantages, and the method used is often based on what is available. In general, optical methods present the least expensive and easiest options for imaging fluid distribution, solute and fluid flow, colloid transport, and reactions in artificial 2D porous media. Gamma radiation methods present the best opportunity for characterization of fluid distributions in 2D at the Darcy scale. X-ray methods present the highest resolution and flexibility for 3D natural porous media characterization, and 3D characterization of fluid distributions in natural porous media. And MRI presents the best option for 3D characterization of fluid distribution, fluid flow, colloid transport, and reaction in artificial porous media.

Obvious deficiencies or gaps in non-invasive imaging include the ability to image transient processes such as fluid flow and colloid transport in natural porous media in three-dimensions, the ability to image many reactions of environmental interest in artificial and natural porous media, and the ability to image selected processes over a range of scales in artificial and natural porous media. Desirable advances to address one or more of these shortcomings include faster acquisition of 3D images using X-ray, application of MRI to increasingly ferromagnetic materials, faster acquisition of images using gamma radiation, and extension of gamma radiation imaging to three dimensions.