Inter-limb interference during bimanual adaptation to dynamic environments

Abstract

Skillful manipulation of objects often requires the spatio-temporal coordination of both hands and, at the same time, the compensation of environmental forces. In bimanual coordination, movements of the two hands may be coupled because each hand needs to compensate the forces generated by the other hand or by an object operated by both hands (dynamic coupling), or because the two hands share the same workspace (spatial coupling). We examined how spatial coupling influences bimanual coordination, by looking at the adaptation of velocity-dependent force fields during a task in which the two hands simultaneously perform center-out reaching movements with the same initial position and the same targets, equally spaced on a circle.

Subjects were randomly allocated to two groups, which differed in terms of the force fields they were exposed to: in one group (CW-CW), force fields had equal clockwise orientations in both hands; in the other group (CCW-CW), they had opposite orientations. In both groups, in randomly selected trials (catch trials) of the adaptation phase, the force fields were unexpectedly removed. Adaptation was quantified in terms of the changes of directional error for both hand trajectories. Bimanual coordination was quantified in terms of inter-limb longitudinal and sideways displacements, in force field and in catch trials.

Experimental results indicate that both arms could simultaneously adapt to the two force fields. However, in the CCW-CW group, adaptation was incomplete for the movements from the central position to the more distant targets with respect to the body. In addition, in this group the left hand systematically leads in the movements toward targets on the left of the starting position, whereas the right hand leads in the movements to targets on the right.

We show that these effects are due to a gradual sideways shift of the hands, so that during movements the left hand tends to consistently remain at the left of the right hand. These findings can be interpreted in terms of a neural mechanism of bimanual coordination/interaction, triggered by the force field adaptation process but largely independent from it, which opposes movements that may lead to the crossing of the hands.

In conclusion, our results reveal a concurrent interplay of two task-dependent modules of motor-cognitive processing: an adaptive control module and a ‘protective’ module that opposes potentially ‘dangerous’ (or cognitively costly) bimanual interactions.

1 Introduction

Skillful manipulation of objects often requires the spatio-temporal coordination of both hands and, at the same time, the compensation of environmental forces (Swinnen and Wenderoth 2004). For example, both hands may need to simultaneously reach for an object, while compensating dynamic interaction forces and/or external disturbances.

Since the seminal work of Shadmehr and Mussa Ivaldi (1994), adaptation to robot-generated force fields has been established as a standard paradigm for the experimental investigation of sensorimotor adaptation to dynamic disturbances. These studies have clarified that subjects gradually recover their original performance by learning to predict the robot-generated forces. Adaptation still occurs in absence of visual feedback (Franklin et al. 2007), thus suggesting a crucial role for proprioception in developing an internal model of the disturbance. More recently, the paradigm has been extended to probe into the mechanisms underlying bimanual coordination and its adaptive properties. Two basic scenarios have been investigated: coupled control, in which the two hands act cooperatively to manipulate the same object, and uncoupled situations in which the two hands act separately in manipulating different objects.

As regards uncoupled scenarios, Tcheang et al. (2007) studied force field adaptation in a non-symmetric bimanual task, in which subjects made reaching movements with both hands, moving in separate, non-overlapping workspaces and toward different targets, under the effect of force fields with either equal or opposite orientations. They found no differences in the ability of the two hands to adapt to both types of force fields, and no evidence of interference between the two learning processes. Still in an uncoupled scenario, Nozaki et al. (2006; 2009) focused on the transfer between unimanual and bimanual adaptation (in a symmetric bimanual task). They only found a limited transfer, thus suggesting an incomplete overlap between the learning processes underlying uni- and bi-manual adaptation.

Bays and Wolpert (2006) and Jackson and Miall (2008) investigated coupled control scenarios, using a pair of robots to study how predictive forces develop to anticipate and to compensate disturbance forces generated by motion of the other limb. Coupled scenarios are often characterized by task redundancy (the same goal can be achieved through different contributions of the two arms). Diedrichsen (2007) investigated bimanual coordination from the point of view of optimal control, and found that adaptation is task-dependent and, in particular, it affects either one or both arms, depending on whether the scenario is, respectively, uncoupled or coupled (Diedrichsen and Dowling 2009). In the same optimization framework, (Reed et al. 2006) and (O’Sullivan et al. 2009) investigated the performance advantages of bimanual (i.e. redundant) over unimanual control.

Howard et al. (2008) studied the transfer between coupled and uncoupled scenarios. Their results suggested that the motor system may use partially separate representations for coupled and uncoupled contexts, and partially independent representations of the dynamics of the two arms. Again, in this study the hands moved in two physically separate workspaces.

In all the above experiments, bimanual coupling was obtained by applying to each hand perturbing forces which depended on the movement of either or both arms (Bays and Wolpert 2006; Howard et al. 2008; Jackson and Miall 2008), and/or by displaying ‘virtual’ targets, whose movement was determined by that of both arms (Diedrichsen 2007). In all cases, the hands moved in physically separate workspaces. However, bimanual coupling may take place not only when the task requires that both arms interact directly (dynamic coupling), but also when both hands share a common workspace (spatial or geometric coupling). This different type of bimanual coupling can be unveiled by experiments designed to create conflicts between the movements of the two hands occurring within the same workspace.

Spatial bimanual coupling has been associated to inter-hemispheric transmission throughout the corpus callosum, and several spatial interaction effects have been reported. In unimanual movements, when one hand has to reach visual targets located in the opposite hemi-space with respect to a body-centered reference frame, reaction times are greater than in the ipsilateral situation, an effect that has been related to the need for extra inter-hemispheric processing. However, in choice reaction tasks the effect is reversed if the hands are crossed. The same reversal is observed when the targets are reached by means of crossed sticks (Riggio et al. 1986). These findings suggest a general tendency to respond to stimuli in one hemi-space with the congruent hand, i.e. according to a principle of spatial stimulus-response compatibility (Fitts and Seeger 1953) which cannot be explained as a simple pre-wired ‘internal reflex’. Hand crossing also affects temporal order judgements in tactile stimulation tasks (Yamamoto and Kitazawa 2001; Shore et al. 2002) and causes an overall increase in the reaction time with respect to the uncrossed situation in reaction time tasks (Anzola et al. 1977; Riggio et al. 1986). The neural circuitry underlying crossed-hand interference and that related to spatial compatibility effects have been recently dissociated in a fMRI study (Matsumoto et al. 2004).

The above findings do not directly relate with bimanual coordination, but in children the development of the ability to reach a target by crossing the midline has been found to correlate with that of bimanual coordination (van Hof et al. 2002). On the other hand, training reduces spatial compatibility effects (Wenderoth et al. 2003) as well as hand crossing interference in making temporal order judgements (Craig and Belser 2006), further supporting the idea that hand-crossing avoidance is a plastic mechanism, possibly available as a default internal constraint for synergy formation.

In this study, we use force field adaptation as a probe to induce spatial coupling, and possibly interference effects, in an otherwise symmetric and uncoupled bimanual motor task. The two hands share the same workspace, and subjects are required to perform the same movement to the same target, while two identical manipulanda apply velocity-dependent forces, directed orthogonally with respect to movement directions, with either the same or opposite orientations.

In terms of the task, this experiment corresponds to an uncoupled scenario. Therefore, we expect that the subjects will be able to adapt simultaneously to both fields with little or no interference. However, the two hands are spatially coupled and, depending on the movement directions, the two force fields may tend to either favour or oppose hand crossing. We shall specifically look at how hand crossing and adaptation affect each other.

Materials and Methods

1.1 Subjects

The experiment involved fourteen right-handed subjects, naïve to the task and with no known neuromuscular disorders. All subjects completed the Edinburgh Handedness questionnaire (Oldfield 1971), and were ranked accordingly. Their laterality index was greater than 30 on a [−100, 100] scale (−100: completely left handed; 100: completely right handed). Subjects were randomly allocated to two age-matched and gender-balanced groups (see below): (i) Group 1: 3 males and 4 females (age: 25.7±1.8); (ii) Group 2: 4 males and 3 females (age: 25.3±2.6).

The research conforms to the ethical standards laid down in the 1964 Declaration of Helsinki that protects research subjects. Each subject signed a consent form that conforms to these guidelines.

1.2 Experimental apparatus and task

We used a bimanual robot system, consisting of two identical planar manipulanda, each with two degrees of freedom, mounted in a mirrored configuration on the same frame. The set-up allowed for independent regulation of vertical and horizontal position; see Figure 1 (top). The system (BdF2, Celin srl, La Spezia, Italy) is a direct evolution of the uni-manual robot manipulandum Braccio di Ferro (BdF) (Casadio et al. 2006).

Figure 1.

Two views of the experimental set-up (top panel) and layout of the eight targets (2 cm in diameter), equally spaced on a circle (20 cm in diameter). In the data analysis subset of targets are considered: ‘right’ subset (T1, T2, T8), ‘left’ subset (T4, T5, T6), ‘proximal’ subset (T6, T7, T8), ‘distal’ subset (T2, T3, T4).

The two robots were positioned horizontally as close as possible (distance between the axes of the motors: 38.5 cm), in order to maximize the overlap between the corresponding workspaces. The vertical position of the robot linked to the right hand was adjusted for each subject in order to keep the right arm approximately horizontal. The other robot was slightly shifted downward in order to avoid interference between the two arms. For the same reason, the handle of the former robot was directed upward, whereas the handle of the latter robot was directed downward. The vertical distance between the two hands (second metacarpal joint) was 18 cm; see Figure 1, right. The positions of the two end effectors were calibrated with respect to a common reference frame, which was also used to specify the movement targets.

Subjects were seated on a chair, with their torso and wrist restrained by means of suitable holders while grasping the handles of the two manipulanda, in such a way to limit the arm movements to shoulder and elbow rotations. A 24″ computer screen, positioned right in front of the subjects, about 1 m away, was used to display the current position of both hands and that of the movement targets. The scale factor of the display was 1:1, i.e. 1 cm on the screen corresponded to 1 cm in the robot workspace.

Subjects performed reaching movements with both hands, with common initial and target positions. Targets were displayed as round circles (diameter 2 cm). The positions of the left and right hand were continuously displayed as smaller circles (diameter 0.4 cm) of different colours.

Subjects were instructed to reach the target with both hands at the same time, and were encouraged to keep the reaching time approximately constant (600±100 ms) by means of acoustic and visual feedback. More specifically, if the estimated movement duration was within this range, a positive feedback/reward to the subject (a pleasant sound) was provided. If the measure was outside that range, no sound was generated and the color of the target was changed.

The experiment involved eight targets, equally spaced on a circle with a 10 cm diameter, plus one ‘home’ target in the center (Figure 1, bottom). The position of the home target was adjusted in such a way to have, in both arms, flexion angles of about 90° for the elbow and about 45° for the shoulder. The sequence of target presentations alternated the central target and one of the peripheral targets. The experiment was organized into target sets. The order of presentation of the peripheral targets within a target set was randomised. Each target set included 6 reaching movements for each peripheral target, for a total of 6×8=48 center-out movements, plus 48 ‘homing’ movements.

For both arms we used the force field adaptation paradigm originally proposed by (Shadmehr and Mussa-Ivaldi 1994). The experimental protocol was organized into the following phases:

1. Familiarization (4 target sets: 48×4=192 trials), in which the robot generated no forces, with the purpose of evaluating the background performance level;

2. Adaptation (6 target sets: 48×6=288 trials), in which the force fields were turned on.

3. Wash-out (2 target sets: 48×6=96 trials), in which the force fields were turned off to evaluate the persistence of the induced adaptation (if any).

Each target set lasted approximately 5 min, and subjects were allowed to rest between sets. During the adaptation phase, in 1/6 of the movements (i.e., one movement per direction per target set), the force field was unexpectedly turned off (catch trials).

During the adaptation phase, the two manipulanda generated independent rotational (curl) force fields, in which the instantaneous values of the applied forces were computed as proportional to hand speed but perpendicular to the hand velocity vector. This was achieved by using the following control equations:

$$\{\begin{array}{l}{\overrightarrow{F}}_R=\left[\begin{array}{cc}0& b_R\\ -b_R& 0\end{array}\right]·{\overrightarrow{v}}_R\hfill \\ {\overrightarrow{F}}_L=\left[\begin{array}{cc}0& b_L\\ -b_L& 0\end{array}\right]·{\overrightarrow{v}}_L\hfill \end{array}$$ (1)

where F⃗_R and F⃗_L are the force vectors applied to the two hands; v⃗_R and v⃗_L are the corresponding instantaneous velocity vectors; b_R and b_L are the viscosity coefficients of the two fields, whose magnitude was set to 20 Ns/m. The sign of the viscosity coefficient determines the direction of rotation of the corresponding force field: clockwise (CW) if b is positive and counter-clockwise (CCW) if b is negative. In the two groups of subjects, the force fields applied to the two hands had either equal or opposite rotation orientations. More specifically, in Group 1 the force field was clockwise in both hands (CW-CW group). In Group 2 the field was counter-clockwise on the left hand and clockwise on the right hand (CCW-CW group). The frequency of the control loop was 1 kHz, but hand trajectories were sampled at 100 Hz and stored for the subsequent data analysis.

1.3 Data Analysis

Hand trajectories

p⃗_L(t) and p⃗_R(t) - were collected according to a body-centered reference frame. The X component corresponds to sideways movements of the hand, and the Y component to forward/backward movements. The trajectories were smoothed by means of a 6th order Savitzky-Golay filter with a 170 ms window (cut-off frequency: ~11 Hz). The subsequent analysis mostly focused on the center-out portion of movements.

We specifically focused on movement curvature and inter-limb coordination. In particular, we investigated how these indicators changed during adaptation. To this purpose, we looked at their time course in both the force field trials and the catch trials. We specifically focused on the right hand, because it was exposed to the same force field in both experimental groups.

Furthermore, we looked at signs of interference between the left and right hand adaptation processes.

Directional error

If subjects learn to compensate the perturbation by developing an internal model that modifies the original motor commands (Shadmehr and Mussa-Ivaldi 1994), the large errors in the direction of the field, exhibited in earlier force field trials, would gradually decrease with practice. In contrast, the errors in the catch trials should have an orientation opposite to that of force and should increase with practice. Different measures of directional error have been proposed to quantify the adaptation to curl fields or visuomotor rotations. We chose the method proposed by Bock et al. (2005), i.e. we took as error measure the directional error (DE) at peak speed, calculated as the difference between the direction of the target and that of the point of the actual trajectory which corresponds to peak speed. This measure is highly sensitive to the force field and is relatively unaffected by the initiation and termination portions of the trajectory. We conventionally took errors as positive if they corresponded to leftward displacements of the trajectory; negative if the trajectory was displaced toward the right.

Moreover, we used a ‘learning index’, based on a comparison of the directional errors in force and catch trials during the adaptation phase (Smith and Shadmehr 2005), which is defined as follows:

$$\text{LI}=\frac{{DE}_c}{|{DE}_c-{DE}_f|}$$ (2)

where DE_f and DE_c are the directional errors in the field trials and in the catch trials, respectively. LI is zero (no learning) if the error in catch trials is zero; it is one if the error in field trials is zero.

Longitudinal inter-limb displacement

In order to assess how the movements of the two hands are coordinated while performing the task we computed the instantaneous displacement vector:

$$\mathrm{\Delta }{\overrightarrow{p}}_{RL}(t)={\overrightarrow{p}}_R(t)-{\overrightarrow{p}}_L(t)$$ (3)

where p⃗_R (t) and are, respectively, the position of the right and the left hands at time t. Therefore Δp⃗_RL (t) indicates the inter-limb position vector difference at time t. This quantity can be decomposed into a longitudinal and a transverse component, respectively, with respect to the nominal movement direction, from the home to the peripheral target, denoted by the unit vector u⃗_d.

In particular, we defined a ‘longitudinal inter-limb displacement’ indicator as the average of the longitudinal component, computed over a suitable time interval, [t_a, t_b]. We focused on the central part of the movements, which typically display less variability. We defined [t_a, t_b] as the time interval during which the distance of the hands from the target remained between 30% and 70% of the inter-target distance, i.e. 3 cm and 7 cm:

$$\mathrm{\Delta }{p}_{RL}^{\mathit{long}}=\frac{1}{N}\sum _{n=1}^N{{\overrightarrow{u}}_d}^T·\mathrm{\Delta }{\overrightarrow{p}}_{RL}(t_n)$$ (4)

where n is the sample number and N is the number of data samples between t_a and t_b (assuming t₁=t_a and t_N=t_b).

This is a signed quantity: a positive value denotes that the right hand leads the movement, while a negative value indicates that the left hand leads and the right hand lags behind.

Longitudinal displacement is affected by the inertia of the robots and the subject’s arms, whose dependence on direction is different in the left and right hands. Subjects were explicitly required to reach the target at the same time with both hands. As the effect of the force fields is to increase directional errors, we would expect little or no effect on longitudinal displacement. On the contrary, an effect of the force field on longitudinal displacement would point at an interaction between adaptation and bimanual coordination.

Sideways inter-limb displacement

To explicitly test the tendency to maintain the two hands uncrossed, we also looked at the average sideways displacement of the right and left hands, with respect to a body-centered coordinate reference:

$$\mathrm{\Delta }{p}_{RL}^{\mathit{sideways}}=\frac{1}{N}\sum _{n=1}^N\mathrm{\Delta }{x}_{RL}(t_n)$$ (5)

where Δx_RL is the x-component of the instantaneous displacement vector, Δp⃗_RL and the time interval is defined as before.

2.4 Statistical Analysis

We assessed adaptation in two ways, respectively by looking at (i) the two hands separately – in terms of the directional error – and at (ii) bimanual coordination – in terms of longitudinal and sideways right-left hand displacement. To do this, in the force field trials we ran a repeated-measures ANOVA with three factors: group (CW-CW or CCW-CW), epoch (early vs. late, i.e. the first and last target set in the adaptation phase, or in other phases depending on the specific hypothesis under test), and target direction (T1–T8).

Movement performance depends on target direction. In reaching movements with no perturbing forces, the directional error has been shown to correlate with the anisotropy of arm inertia(Gordon et al. 1994). To eliminate this dependence, as in (Smith and Shadmehr 2005), the directional error was adjusted for any bias that may have been present during the last familiarization target set for each direction. To do so, for each direction and for each hand we calculated the average directional error during the last target set in the Familiarization phase. We then subtracted this value, direction by direction from all the directional errors measured throughout the experiment. Therefore, directional errors in the field sets and in the catch trials are referred to change from errors in the last familiarization target set.

The bimanual task introduces a second possible source of direction dependence, related to spatial compatibility effects. Coordination and/or adaptation may differ in the left and right hemi-spaces, as well as in movements performed toward targets located either more proximally or more distally with respect to the subject. To test for these effects, we ran a contrast analysis by taking the following groups of directions: (i) ‘left’ (T4, T5, T6), (ii) ‘right’ (T1, T2, T8); (iii) ‘proximal’ (T6, T7, T8) and (iv) ‘distal’ (T2, T3, T4). More specifically, we compared the two groups (CW-CW and CCW-CW) and tested whether or not the performance of the right hand (same force field for the two groups) is affected by the direction of the force field applied to the left hand, which is same in the CW-CW group and opposite in the CCW-CW one.

2 Results

Figure 2 shows the trajectories of both hands at the end of the adaptation phase for two representative subjects, one for each group. Adaptation to the force field is suggested by the opposite patterns of curvature in both subjects and in both hands. A detailed analysis of the adaptation process is provided in the following sections.

Figure 2.

Movement trajectories at the beginning (left) and end (right) of the force field adaptation phase, for two subjects, one in the CW-CW group (S6) and one in the CCW-CW group (S11). Lines in grey and black denote, respectively, the left and right hand. Scale bar: 2 cm.

2.1 Directional error

Figure 3A,B illustrates the temporal evolution of the directional error, in both the catch trials and the force field trials. As expected, the catch trial trajectories are curved in opposite directions with respect to those performed under the influence of the force field.

Figure 3.

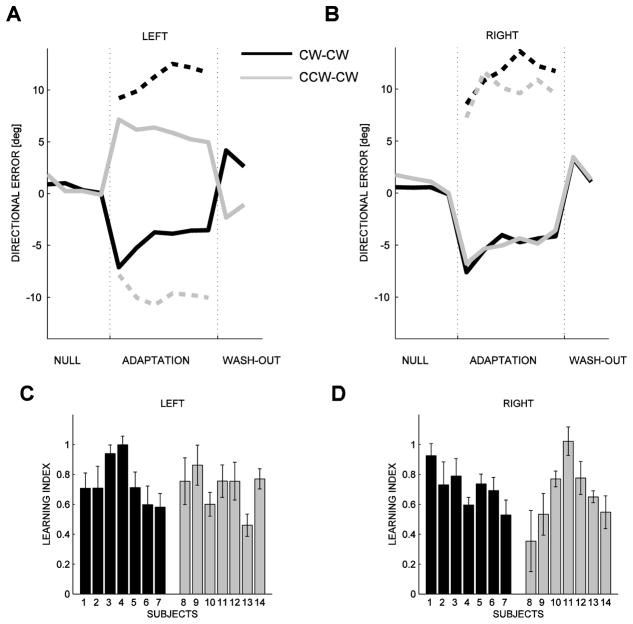
A, B: Evolution of the directional error for the left (A) and right (B) hand for two subjects, one in the CW-CW group (S6, black line) and one in the CCW-CW group (S11, grey line). Positive directions denote counter-clockwise deviations. Dashed lines indicate catch trials, solid lines indicate force field trials. C, D: Learning indexes for each subjects in the two groups (CW-CW: black; CCW-CW: grey), for the left (C) and right hand (D). Error bars indicate ± SE.

Adaptation occurs in both subject groups and in both hands. Statistical analysis - summarized in Table 1 - confirms this observation.

Table 1.

Statistical Analysis of the Directional Error, for the left and right hand movements.

Effect	Left hand					Right hand
	SS	df	MS	F	p	SS	df	MS	F	p
Group	7516.	1	7516.	114.3	<.00001**	19.	1	19.	.41	.533
Epoch	26.	1	26.	1.3	.277	615.	1	615.	22.90	.00044**
Epoch×Group	454.	1	454.	23.0	.00044**	0.7	1	0.7	.03	.876
Direction	1216.	7	174.	3.8	.0014**	785.	7	112.	2.92	<.009**
Direction×Group	252.	7	36.	.8	.607	531.	7	75.9	1.97	.068
Epoch×Direction	119.	7	17.	1.6	.136	213.	7	30.4	2.31	.033*
Epoch×Direction×Group	332.	7	47.	4.6	.00024**	138.	7	19.7.	1.50	.179

The table reports Sum of Squares (SS), degrees of freedom (df), Mean Squares (MS), F-statistic (F) and p-value (p). Significant effects are highlighted in bold.

^*p<0.05 (significant),

^**p<0.01 (highly significant)

In the early phase of adaptation, (i.e. during the first target set), when the forces are directed clockwise (right hand in both groups and left hand in the CW-CCW group) the directional errors are expected to be negative, whereas when the forces are directed counter-clockwise (left hand in the CCW-CW group only) the directional errors are expected to be positive. The actual results are consistent with these predictions in both hands and in both groups, and this effect is clearly visible in all movement directions. In particular, in the right hand, which experiences the same force field in both groups, we found no significant between-group differences. In contrast, in the left hand we found a highly significant group effect; see Table 1.

In movements of the right hand, the curvature of the trajectories decreases during adaptation (highly significant epoch effect) in a similar way in both groups (non-significant epoch×group interaction); see Table 1. As regards the left hand, we found both a non-significant epoch effect and a highly significant epoch×group interaction. This result is due to the different force field directions (see Figure 3). In fact, in the left hand, adaptation occurs (significant epoch effect) in both groups if they are considered separately (CW-CW group: F(1,12)=17.60, p=0.0012; CCW-CW group: F(1,12)=6.67, p=0.024).

These findings are confirmed by the analysis of the catch trials. In both hands and both groups, errors in the catch trials have an opposite direction with respect to those observed during force trials. This supports the hypothesis that the observed adaptation is determined by an improved prediction of the force field, not by an increased hand stiffness. Moreover, again in catch trials we found a significant epoch effect in the right hand (F(1,12)=7.86, p=0.016). In contrast, as in force field trials, in the left hand we found a non-significant epoch effect. Different from force field trials, the epoch×group interaction was also non-significant (p=0.069). This may seem inconsistent with Figure 3A, but it should be noted that catch trials are only 1/6 of the total and their variability is greater than that of field trials.

The overall effectiveness of the learning process in this bimanual paradigm is also verified by the analysis of the learning index (Figure 3C, D), which shows that the degree of adaptation is the same in both hands and in both groups (no statistically significant group effect).

In order to detect a possible interference between the two hands while they adapt to the dynamic environment, it is crucial to look at the responses as a function of target direction as this effect is likely to be direction-dependent. The results of this analysis are summarized in the polar plots of Figure 4, which displays the distribution of the directional error for both hands (left and right), in both experimental conditions, (CW-CW: black lines; CCW-CW: grey lines), and in different phases of the experimental protocol (late part of the familiarization phase; early and late part of the field adaptation phase).

Figure 4.

Polar plots of the directional error (average over subjects), as a function of the movement direction, for both hands (left, right) and both groups (CW-CW: black lines; CCW-CW: gray lines). The circle corresponds to null directional error. Positive errors are plotted outside the circle and correspond to counter-clockwise deviations. The radius of the circle is equivalent to a deviation of 20 deg. In the familiarization phase, the errors shown are absolute. In the other phases, the errors at the end of the familiarization phase have been subtracted from the total errors (see text).

Systematic directional errors in the absence of force fields can be attributed to the anisotropy of the arm+robot inertial tensor and, as a consequence, they can be expected to be approximately symmetric in magnitude (but with inverted signs) in the left and right hands. The top panel of Figure 4 shows that this is indeed the case. In the left hand the directional error is greatest (negative) for T4 and T8; in the right hand the error is greatest (this time, positive) in T2 and T6. As explained in the Methods section, these directional errors were subtracted from the errors evaluated in the force field trials in order to isolate the effect of the force field from the bias introduced by anisotropy of arm inertia.

During adaptation we found highly significant direction effects in both hands. In addition, in the right hand we also found a significant epoch×direction effect, but no epoch×direction×group effect; see Table 1.

When looking at the patterns of adaptation in the different directions, we could observe clear differences between groups in both hands. We specifically compared movements to targets in the ‘left’ vs. ‘right’ hemi-spaces of the workspace (T4, T5, T6 vs. T1, T2, T8) and movements to targets in the ‘distal’ vs. ‘proximal’ hemi-spaces (T2, T3, T4 vs. T6, T7, T8): see Figure 5.

Figure 5.

Comparison among movements to ‘proximal’ targets (black) and ‘distal’ targets (grey) during the adaptation phase (average over all subjects). A: forward (center-out) movements; B: backward (return) movements. Error bars indicate ± SE. C, D: temporal evolution of the directional errors (CCW-CW group) in the left (C) and right hand (D). Dashed lines indicate catch trials, solid lines indicate force field trials.

In the right hand, we found no significant epoch×group effects in the ‘left’, ‘right’ and ‘proximal’ hemi-spaces. In contrast, we found a significant epoch×group effect (F(1,12)=6.68, p=0.024) in the ‘distal’ hemi-space. More specifically, in these directions, the two groups differ significantly in the directional error exhibited during the late adaptation phase (group effect for late adaptation in distal directions: F(1,12)=5.96, p=0.043). If the two groups are considered separately, in the distal hemi-space the CW-CW group adapts to the force field (significant epoch effect, F(1,12)=10.59, p=0.0069) whereas the CCW-CW group does not (non-significant epoch effect, p=0.69): see Figure 5A.

We found similar results in the left hand (Figure 5A). In ‘distal’ directions, the CW-CW group adapts to the force field (statistically significant epoch effect: F(1,12)=7.36, p=0.019), whereas in the CCW-CW group the epoch effect is not statistically significant (p=0.64). In contrast, in the ‘proximal’ directions, adaptation occurs in both groups (CW-CW: F(1,12)=10.09, p=0.0080; CCW-CW: F(1,12)=12.80, p=0.0038). Likewise, in both groups adaptation is present in both the left and right hemi-spaces.

A similar effect is also found in the ‘return’ portion of the movements, with reverse behaviors in the ‘distal’ and ‘proximal’ subsets of directions, i.e. no adaptation in the ‘proximal’ directions (see Figure 5B).

2.2 Sideways inter-limb displacement

The effect of adaptation in the different directions and in the two groups is further revealed by looking at sideways displacement. Figure 6A,B illustrates the time courses of sideways displacement during the different epochs, averaged over subjects in both the CW-CW and the CCW-CW groups.

Figure 6.

A, B: Evolution of the inter-limb sideways displacement over epochs, for the CW-CW group (A) and CCW-CW group (B), averaged over all target directions. C, D: the different behavior of movements to ‘proximal’ targets (black lines) or ‘distal’ targets (grey lines). Catch trials are indicated by dashed lines.

During the familiarization phase, in both groups no systematic hand crossing effect was observed, i.e. the average horizontal displacement was close to zero. During the adaptation phase, the displacement remained virtually zero in the CW-CW group (Figure 6A), whereas it gradually increased in the CCW-CW group (Figure 6B), i.e. the two hands tended to increasingly stay far apart. These observations were confirmed by statistical analysis: significant epoch×group interaction (F(1, 12)=5.73 p=0.034).

Similar to the longitudinal displacement, this indicator displayed a significant direction effect (F(7, 84)=13.44, p<0.000001) and a significant group×direction interaction (F(7, 84)=32.22, p<0.00001). Moreover, in the CCW-CW case, uncrossing was retained during the wash-out phase and was still visible at the end of the experiment.

Contrast analysis showed that in the adaptation phase, in the CCW-CW group (but not in CW-CW) there is a significant epoch effect (F(1,12) = 20.16, p<0.00074) in the ‘proximal’, but not in the ‘distal’ directions: see Figure 6C,D. A smaller effect was also found in the ‘left’ and the ‘right’ directions (F(1,12)=12.43, p=0.0041 and F(1,12) = 6.06; p=0.030, respectively). The trend toward hand uncrossing in the CCW-CW group was also observed in the catch trials (dashed lines in Figure 6).

In summary, at the end of adaptation phase, in the CCW-CW group - but not in the CW-CW group - the two hands tend to firmly uncross, i.e. the left hand stays consistently at the left of the right hand.

2.3 Longitudinal inter-limb displacement

Bimanual coordination was also explored by looking at the displacement of the two hands along the target direction. In the familiarization phase, longitudinal displacement has a complex pattern of variation (Figure 7A). The two groups display no statistically significant differences in this phase, but an highly significant (F(7,84)=5.197; p<0.0001) direction effect. Likewise, the group × direction interaction is not significant.

Figure 7.

Analysis of longitudinal inter-limb coordination. A, B, C (top): Polar plots of the longitudinal distance between hands, as a function of the movement direction, for familiarization (A), adaptation (B) and wash-out phases (C). Black and grey lines indicate, respectively, the CW-CW and the CCW-CW groups. The circle (radius: 2 cm) indicates zero longitudinal displacement. The points outside the circle denote positive displacement (i.e. the right hand leads the left hand). D, E (middle): Evolution over epochs of the longitudinal distance between hands, for the CW-CW (D) and the CCW-CW group (E), for targets in the left hemi-space (grey lines) and the right hemi-space (black lines). F, G (bottom): time course of the hand speed and the longitudinal component of the inter-hand hand distance at the end of the adaptation phase, for a movement to target T5 (LEFT) or to target T1 (RIGHT), for a representative subject of the CW-CW group (F) and a representative subject of the CCW-CW group (G). Left hand: grey lines; right hand: black lines; dashed lines: catch trials.

The analysis of the adaptation phase shows that there are no epoch and group effects. However, there is a highly significant (F(7,84)=6.237, p<0.0001) direction effect and a significant (F(7,84)=2.519, p=0.021) group×direction interaction (Figure 7B). These effects tend to increase as adaptation proceeds (Figure 7D,E) and are still visible at the end of the wash-out phase (direction effect: F(7,84)=3.97, p<0.0001, group×direction interaction effect: F(7,84)=2.501, p=0.022). Contrast analysis showed that in the adaptation phase there is a significant group effect for the ‘right’ subset of targets (F(1,12)=6.20, p=0.028) and for the ‘proximal’ subset (F(1,12)=5.46, p=0.037), but not for the ‘left’ and the ‘distal’ subsets of targets.

Figure 7B clearly shows that the effect is predominantly left-right and for this reason we further explored this aspect. Consider, for example, the time course of the longitudinal hand displacement for the CW-CW and CCW-CW groups (Figure 7D,E). During the familiarization phase, for both groups the longitudinal displacement tends, on average, to be negative in both the ‘left’ and ‘right’ directions (no significant left-right and group differences). In other words, in most directions the left hand tends to lead the right hand in both leftward and rightward movements.

During the adaptation phase, the behaviors of the two groups diverge substantially. In the CW-CW group, longitudinal displacement does not change significantly in both left and right directions. In contrast, in the CCW-CW group the displacement changes little (non-significant epoch effect) in the ‘left’ directions, whereas it increases substantially in movements directed to the ‘right’ (significant epoch effect: F(1,12)=6.84 p=0.022). In the latter case, the longitudinal displacement between hands even becomes positive, i.e. the right hand is now the one which leads. In summary, in the CCW-CW group at the end of adaptation, the left hand leads in movements to the left, whereas the right hand leads in movements to the right. The overall effect is that the two hands tend to stay uncrossed, even when they move far from the midline of the workspace.

A look at the speed profiles of the two hands (see Figure 7F, G) suggests that the effect is caused by an anticipation of the speed peak in the right hand (in movements to the right) and in the left hand (in movements to the left). When the force field is unexpectedly removed during adaptation (catch trials), the effect is similar: modest left-right differences in the CW-CW group; right hand leading in movements to the right and left hand leading in movements to the left, in the CCW-CW group.

3 Discussion

We addressed bimanual coordination by analysing the modifications of the hand trajectories in a bimanual reaching task under the effect of two force fields, which elicited adaptation processes in both left and right arm movements. The task is similar to those used in uncoupled scenarios, but in the present experiment the two hands are spatially coupled, in the sense that they share the same initial position, the same target and the same recommended movement duration. We compared movements and adaptation in two conditions (force fields with equal or opposite orientations) in order to emphasize effects related to bimanual coordination.

During familiarization, when the robots generate no forces, the curvature of the trajectory was found to be direction-dependent and symmetric in the left and right hands; see Figure 4, top. Direction dependence can be interpreted in terms of hand inertia anisotropy (Gordon et al. 1994), and largely reflects that observed in movements with one arm alone; see for instance (Casadio et al. 2008). This suggests that the movements of the left and right hands are controlled independently, with little or no bimanual interaction. These results are also consistent with (Franz et al. 2001), who found no interference in bimanual ‘single’ tasks.

3.1 Simultaneous adaptation to CCW and CW force fields

When subjects are exposed to a curl force field, hand trajectories initially exhibit large curvatures, but these errors decrease with practice. In late catch trials, the hand deviates in the opposite direction with respect to the errors observed during early exposure, suggesting that the brain is developing an ability to predict the robot-generated forces (Shadmehr and Mussa-Ivaldi 1994).

Our results suggest that subjects simultaneously adapt to the two force fields, irrespective of whether they have equal or opposite orientations. The two arms exhibit similar rates of adaptation under both conditions, as illustrated by Figure 3. These findings are consistent with other studies that investigated bimanual adaptation in uncoupled scenarios. For instance, Tcheang et al. (2007) found that the two hands can independently adapt to bilateral force fields (either different or the same) while moving in different hemi-spaces and in different directions. Similar rates of adaptation for the two hands while adapting to both equal and opposite fields were also found by Diedrichsen (2007).

Remarkably, bimanual adaptation to visual rotations exhibits response patterns that are similar to those observed in force field adaptation. Bock et al. (2005) found concurrent and non-interfering adaptation to 60° visual rotations that were opposite in the two arms (CW in left arm, CCW in right arm). This result was later confirmed by Galea and Miall (2006); the difference is that, in the former study, the two arms moved in alternation in separate, short blocks of trials, whereas, in the latter, the protocol was performed with strict trial-based alternation of movements of the two arms. Both studies reported similar rates of adaptation for the two hands, suggesting that the two adaptation processes were carried out concurrently. However, in the bimanual condition the adaptation rate was found to be slower than in the unimanual case, thus suggesting that some form of negative interference occurs in the bimanual case.

Overall, the observation of similar rates of adaptation in different experimental protocols supports the idea that the adaptation mechanism is robust and can operate equally well under different task constraints and sensorimotor conditions.

3.2 Inter-limb interference during adaptation to opposite force fields

Although the amount and modalities of adaptation appeared to be the same in both hands and both groups, substantial differences became apparent when the directional errors were examined separately in the different movement directions.

When the left and right force fields have the same orientation (CW-CW condition), adaptation is observed in both hands and in all movement directions. In contrast, when the force fields have opposite orientations (CCW-CW condition), recovery of straight line trajectories is almost complete in the ‘proximal’ set of directions, whereas it is incomplete or absent in the ‘distal’ set. This effect is found in both hands (Figures 4–5).

A direct look at the interaction among the two hands suggests that in the same (CCW-CW) group, during the adaptation phase the hands tend to move farther apart (the left hand on the left, the right hand on the right; see Figure 6). Again in the CCW-CW group, a similar effect is observed in the longitudinal displacement of the hands (Figure 7): in leftward movements, the left hand tends to lead; in rightward movements the right hand is the one that leads.

No such effects are observed when the force fields have the same orientation (CW-CW group). How can we explain these small but robust interference effects? A possible interpretation may involve biomechanical/geometric factors (Gordon et al. 1994), somewhat extending the arguments proposed to explain spatial compatibility effects (Carey et al. 1996; Carey and Otto-de Haart 2001): the anisotropy of inertial, viscous, and elastic properties of the two arms and of the two manipulanda might determine a different effect of the force fields in different movement directions. However, such explanation cannot explain why, in the right hand, the same force field (CW) has different effects in the two experimental conditions, i.e. in relation with the direction of the force field applied to the other hand. For the same reason, the reported results cannot be accounted for by the fact that the two hands move in planes that are slightly shifted (see Figure 1).

Another possibility is that interference originates from a visual mismatch. Moving the two hands together may induce a misinterpretation of the mapping between arm and cursor position. For instance, subjects may incorrectly associate the leftmost cursor to the left arm, and the rightmost cursor to the right arm. As a consequence, adaptation of the left arm would be driven by the leftmost cursor, whereas adaptation of the right arm would be driven by the rightmost cursor. This may have strong effects if the force fields are different (CCW-CW condition). However, such a visual mismatch is unlikely to occur, as the left and right cursors are displayed in different colors. Moreover, if the mismatch was in fact the cause of the observed interference patterns, adaptation would be altered in proximal, but not in distal movements (i.e. the directions where the two hands tend to cross under the action of the two fields). This consideration is also confirmed by the analysis of the ‘return’ movements (from the peripheral target to the home target): the directional differences in the amount of adaptation are still present, but reversed; see Figure 5B. The same reversal of the effect occurs in longitudinal displacement when considering the ‘return’ subset of movements. More specifically, in ‘return’ movements originating from left targets, the right hand is the one which leads, whereas, in ‘return’ movements originating from right targets, the left hand is the one that stays ahead. In conclusion, the observed reversed effect in ‘return’ movements is inconsistent with explanations based on sensory mismatch.

Still another possibility is that the interference patterns among the two arms have a purely motor origin; that is, motor commands may change as the result of the exposition to opposite force fields (CCW-CW condition). For instance, opposite force fields may elicit an increase of hand stiffness in some directions, similar to what is done by unstable force fields; see, for instance, Burdet et al. (2001). However, the force fields used in our experiments are not unstable and the catch trials exhibit opposite directional errors with respect to the force trials, which are inconsistent with a stiffness strategy. This suggests that adaptation actually occurs in all directions, and that the observed inter-limb interference is due to a separate mechanism, which does not prevent force field adaptation but, rather, only affects movement execution. A plausible origin of this mechanism is analyzed in the next section.

3.3 Inter-limb interference as a tendency to oppose hand crossing

One possible unifying interpretation posits a cognitive mechanism that opposes hand crossing. In multi-robot control, one major problem is to avoid destructive interactions (collisions). This requires some supervision of the robot movements and, if necessary, their modulation to stay away from dangerous configurations. We suggest that adaptation to opposite force fields may elicit a ‘protective’ mechanism, specifically aimed at opposing hand crossing, even if in the experimental setup mechanical interference is prevented by the slight vertical shift of the two planes of action. This mechanism would counteract situations that bring the left and right hands to cross each other, whereas it would have no effect on experimental conditions in which the two hands do not cross. Our experiment provides instances of both situations. In the CCW-CW group, opposition to hand crossing would favor adaptation in the movements performed to ‘proximal’ targets, in which the force fields tend to pull the left hand rightwards and the right hand leftwards (thus inducing hand crossing). The same mechanism would oppose adaptation in distal directions, where the force fields tend to increase the left-right ‘confinement’, thus making hand crossing less likely. Similar effects of opposition to situations that tend to bring the hands to cross each other have been reported in human bimanual tasks (Viviani et al. 1997). This same mechanism might account for the changes observed in the relative displacement of left and right hand during the movements: in order to counteract hand crossing, in leftward movements the left hand should lead, vice versa in rightward movements.

Opposition to hand crossing would also predict the observed reversal of the effect in ‘return’ movements. Opposition to hand crossing is consistent with the cognitive disadvantage effect, described by Mooshagian et al. (2008) in relation with an increased inter-hemispheric processing in ongoing visual (feedback) hand control. Hand crossing has been reported to interfere with spatial attention and with making temporal order judgements in tactile stimulation tasks (Yamamoto and Kitazawa 2001; Shore et al. 2002). If the hands are uncrossed, their visual control would be faster, with less need for inter-hemispheric communication. Such a mechanism would be expected to be largely independent from force field adaptation, which likely involves different anatomic structures (Smith and Shadmehr 2005; Shadmehr and Krakauer 2008).

The observed effect may be interpreted in terms of optimal feedback control (Todorov and Jordan 2002; Shadmehr and Krakauer 2008) by assuming that for a spatially coupled bimanual task the ‘cost function’ that qualifies performance includes a specific term reflecting the cognitive ‘cost’ for hand crossing (higher cost if hands are crossed, lower cost if hands are uncrossed), in addition to endpoint error and muscle effort terms (in both cases, one per hand). In this sense, our results would be another instance where, as suggested by Diedrichsen (2007), the modalities of bimanual coordination appear to be task-dependent.

The hand uncrossing effect is task-dependent in another aspect. Our results suggest that the effect is triggered by adaptation (no such effect is observed during the familiarization phase, see Figure 6), develops gradually and has a slow wash-out – at least, slower than that of force field adaptation, as it is not completely cancelled at the end of the wash-out phase.

This finding (interaction increases while adaptation develops) is in apparent contrast with other reports that hand crossing interference is reduced by training (Craig and Belser 2006); see also (Mooshagian et al. 2008). However, in those experimental protocols hand interference has a minor behavioural relevance, thus it makes sense that the effect fades away with training. In our case, on the contrary, the presence of an external disturbance (i.e. force field) may be perceived as a potentially dangerous situation, which may motivate the nervous system to prevent hand interference. The slow wash-out of the effect is also consistent with the optimisation framework, in which opposition to hand crossing develops as an optimal strategy for this task. As a consequence, there is no need for it to reduce over repetitions. In other words, the behavior at the end of adaptation (prediction of the force field and left-right confinement) would be in fact the cost-optimal behavior.

In conclusion, this spatially coupled, bimanual adaptation task has unveiled a concurrent interplay of two task-dependent modules of motor-cognitive processing: an adaptive control module and a ‘protective’ module that opposes potentially ‘dangerous’ (or cognitively costly) bimanual interactions.