Encoding and decoding amplitude-modulated cochlear implant stimuli—a point process analysis

Abstract

Cochlear implant speech processors stimulate the auditory nerve by delivering amplitude-modulated electrical pulse trains to intracochlear electrodes. Studying how auditory nerve cells encode modulation information is of fundamental importance, therefore, to understanding cochlear implant function and improving speech perception in cochlear implant users. In this paper, we analyze simulated responses of the auditory nerve to amplitude-modulated cochlear implant stimuli using a point process model. First, we quantify the information encoded in the spike trains by testing an ideal observer’s ability to detect amplitude modulation in a two-alternative forced-choice task. We vary the amount of information available to the observer to probe how spike timing and averaged firing rate encode modulation. Second, we construct a neural decoding method that predicts several qualitative trends observed in psychophysical tests of amplitude modulation detection in cochlear implant listeners. We find that modulation information is primarily available in the sequence of spike times. The performance of an ideal observer, however, is inconsistent with observed trends in psychophysical data. Using a neural decoding method that jitters spike times to degrade its temporal resolution and then computes a common measure of phase locking from spike trains of a heterogeneous population of model nerve cells, we predict the correct qualitative dependence of modulation detection thresholds on modulation frequency and stimulus level. The decoder does not predict the observed loss of modulation sensitivity at high carrier pulse rates, but this framework can be applied to future models that better represent auditory nerve responses to high carrier pulse rate stimuli. The supplemental material of this article contains the article’s data in an active, re-usable format.

1 Introduction

Cochlear implants (CIs) are neural prostheses that restore a sense of hearing by electrically stimulating the auditory nerve (AN) with intracochlear electrodes. Most contemporary CIs use interleaved pulsatile stimulation strategies (Wilson 2004). These devices deliver current to the electrodes in the form of amplitude-modulated (AM) biphasic rectangular pulses as shown in Fig. 1. The temporal pattern of current delivered to each electrode follows the slow variations in the amplitude spectrum of the sound (the temporal envelope). This is the only source of temporal information that pulsatile CI stimulation strategies provide to CI users. Psychophysical tests of modulation detection have found evidence that speech perception is correlated with performance on modulation detection tasks. For instance, Fu (2002) has shown that modulation detection thresholds (MDTs), when averaged across a subject’s dynamic range, are correlated with phoneme recognition. Cazals et al. (1994) also found correlations between modulation detection and recognition of consonants and vowels. It is of both theoretical and practical importance, therefore, to understand the neural coding of AM pulse trains since improving modulation detection may lead to improvements in clinical outcomes for CI users.

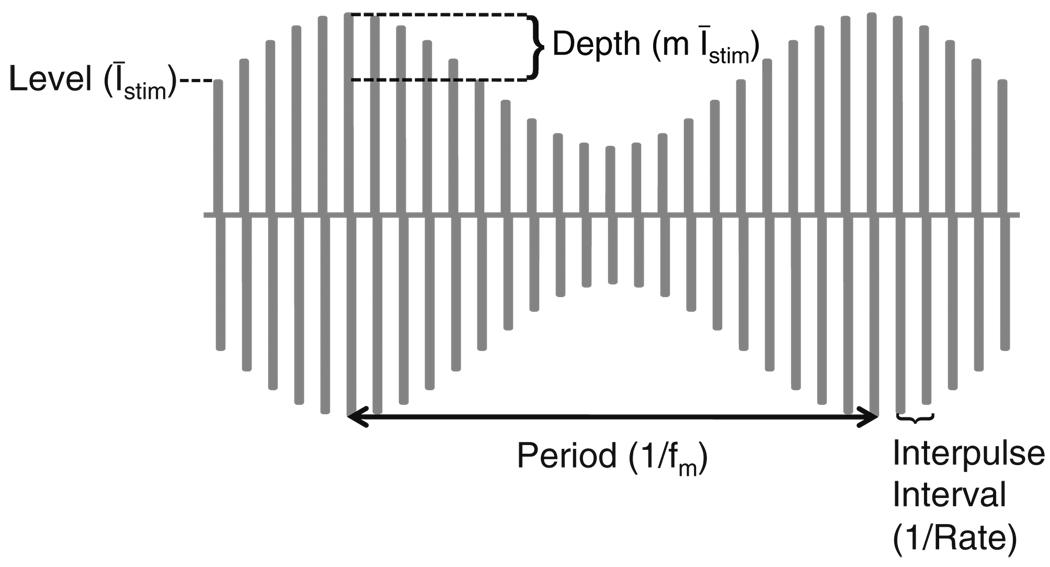
Fig. 1.

Current delivered to CI electrode is AM train of biphasic rectangular pulses. AM pulse trains are parameterized by the average pulse level (Ī_stim), carrier pulse rate, modulation depth (m), and modulation frequency (f_m). The intensity of each pulse is given in Eq. (1)

The sensitivity of CI listeners to AM can be tested with a two-alternative forced-choice listening task. In this task, an unmodulated and modulated signal are presented to a listener and the smallest modulation depth for which the two stimuli can reliably be discriminated defines the MDT. Figure 1 illustrates the current waveform for a sinusoidally AM pulse train. The mean current level of the pulses (and the level of every pulse in an unmodulated pulse train) is denoted Ī_stim. The current level of the nth pulse of the modulated pulse train is

$$I_{\text{stim}}(n)={\overline{I}}_{\text{stim}}(1+m\text{sin}(2\pi f_m{t}_n))$$ (1)

where m is the modulation depth, f_m is the frequency of modulation, and t_n is the time of the nth pulse, which depends on the carrier pulse rate. AM detection experiments have evaluated the dependence of MDTs on frequency of modulation (Busby et al. 1993; Shannon 1992), stimulation level (Fu 2002; Galvin and Fu 2005; Pfingst et al. 2007; Shannon 1992), and carrier pulse rate (Busby et al. 1993; Galvin and Fu 2005; Pfingst et al. 2007).

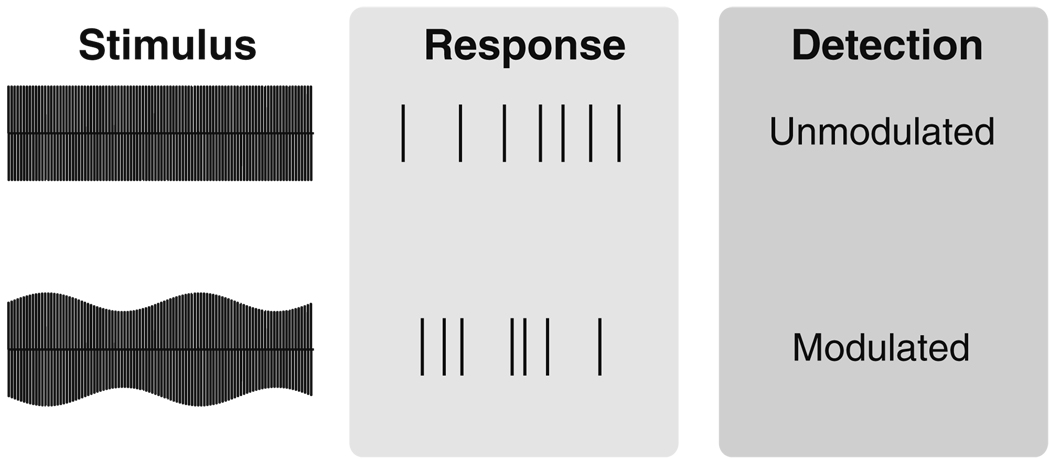
In this paper, we present a computational study of AM detection in a two-alternative forced-choice task. An illustration of the simulation procedure is shown in Fig. 2. Unmodulated and modulated stimuli are used as inputs to a stochastic AN model. The spike trains generated by the computational model are then analyzed by testing the ability of an ideal observer to correctly discriminate between the two stimuli on the basis of the simulated neural responses.

Fig. 2.

Method for simulating AM detection in a two-alternative forced-choice task with a computational model of the AN. Un-modulated and modulated stimuli are used as inputs to the AN model. An ideal observer then attempts to perform the detection task based on information in the simulated AN spike trains

We use this procedure to perform two analyses. First, we test how modulation information is encoded by the AN. To accomplish this, we determine an ideal observer’s ability to detect amplitude modulation based on various features of simulated neural responses such as spike timing, spike rate, and the strength of phase locking. We further investigate how this encoding depends on stimulus parameters (modulation frequency, stimulus level, and carrier pulse rate) as well as parameters that describe the model AN neuron. Our second goal is to infer what aspects of the AN response are consistent with known psychophysical results—that is, to define a decoding of AN spikes that is consistent with behavior. Our approach is motivated by the studies of Heinz et al. (2001a, b), in which signal detection theory was used to test how spike timing and spike count information could explain performance limits in normal hearing listeners. In the context of cochlear implant research, there is also a pragmatic motivation for constructing a neural decoder that is consistent with behavior. In particular, a computational method for relating simulated neural responses to psychophysical data would be a useful tool for evaluating novel speech processing strategies that seek to improve clinical outcomes for CI users.

We simulate AN spike trains using the computational model developed by Bruce et al. (1999a, b). We choose this model because it can be analyzed using the mathematical theory of point processes (Snyder and Miller 1991; Daley and Vere-Jones 2003, e.g.) and because it has been used in previous studies to model CI psychophysical experiments (Bruce et al. 1999b; Xu and Collins 2007). The Bruce model represents a relatively simplified description of the response of the AN to CI stimulation, but it does contain probabilistic spiking and refractory effects. These are two basic phenomena that are thought to affect how stimulus information is represented in temporal patterns of spikes. More sophisticated models of neural dynamics exist in the CI literature including Hodgkin–Huxley type models (Briaire and Frijns 2000; Rattay and Felix 2001; Rattay et al. 2001), and Markov chain models of ion channel kinetics (Imennov and Rubinstein 2009; Woo et al. 2009), but these models cannot be directly analyzed with point process theory. A particular advantage of working with a point process model is that it is possible to define a likelihood function for simulated spike trains. This likelihood function can then be used to perform maximum-likelihood discrimination of the simulated spike trains in order to quantify, as in Heinz et al. (2001a), all of the information about the stimulus that is carried by the spike trains.

The AN model used in this paper has been employed previously to simulate psychophysical tests of intensity discrimination (Bruce et al. 1999b; Xu and Collins 2007) and modulation frequency discrimination (Xu and Collins 2007). The study of Xu and Collins is most similar to the present study because it simulated frequency discrimination of sinusoidally AM stimuli and tested the effects of varying population size and carrier pulse rate. The modulation depth used in those simulations was 100%, far larger than the depths used in the psychophysics tasks studied here. A crucial distinction is that the decoding method used by Xu and Collins neglects all temporal information in the AN spike trains. Modulation frequency discrimination was simulated by comparing the total number of AN spikes summed over the entire 200 ms period of stimulation. In studies recording neural responses to acoustic AM stimuli, firing rate in AN fibers does not appear to depend on modulation depth (Joris and Yin 1992). Spike count based decoding, therefore, is not expected to predict CI users’ performance on the AM detection task.

In this study we consider several measures that quantify the contribution of temporal information in simulated AN spike trains to AM detection. Signal detection based on the precise timing of AN spikes has been used in a past computational study of the peripheral response to acoustic stimulation to predict just-noticeable-differences in tone frequency and stimulus level (Heinz et al. 2001a) and to model a random-level frequency discrimination task (Heinz et al. 2001b). Those studies, however, focused on acoustic hearing, and the measure of discriminability used in that model relied on the fact that AN spikes were generated via an inhomogeneous Poisson process. The AN model that we use for electric hearing incorporates refractory effects, and is therefore not Poissonian.

Past studies that have used the model developed by Bruce et al. (1999a, c) have formulated methods for computing the probability of observing a given spike train response. Bruce et al. (2000) observed that, for a stimulus pulse train of identical pulses, the spike times can be described by a renewal process and the renewal time distribution can be computed. For an AM stimulus, the assumption of identical pulses does not hold. An alternative approach uses a recursive algorithm that is valid for more general pulsatile stimuli including AM pulse trains (Xu and Collins 2007). This method, however, cannot be used for analog stimuli and it has limited temporal resolution since the AN spikes are associated with pulse numbers, not precise spike times. In Section 2.3.1, we introduce a method that uses the theory of point processes to define a likelihood function for observing spike trains that could eventually be used to analyze more general stimulus waveforms and more detailed point process models.

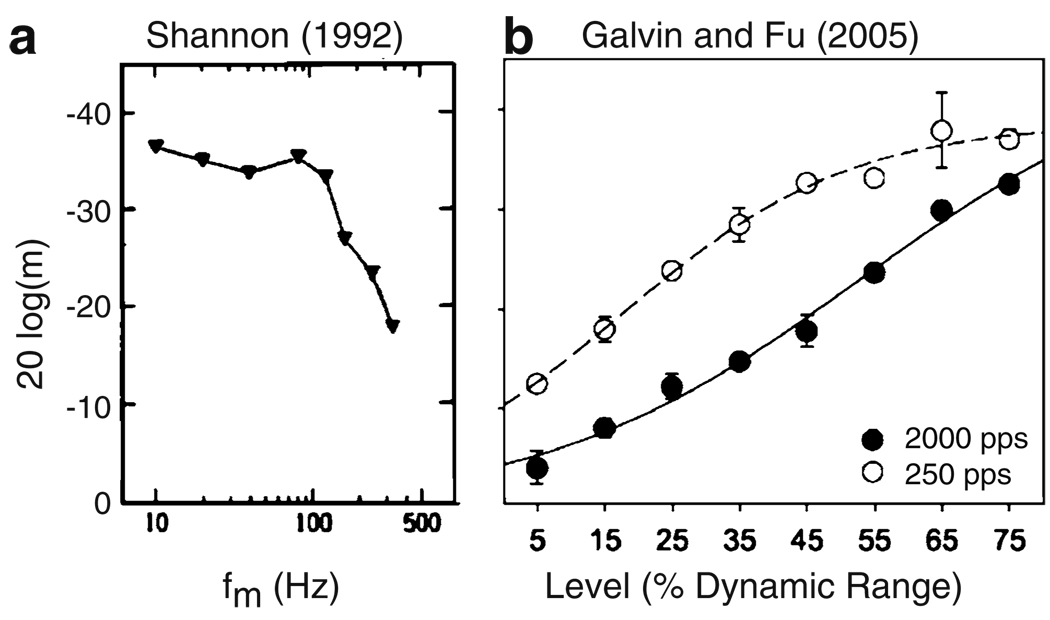
The goal of predicting psychophysical results is challenging because MDTs can vary widely from subject to subject and can depend on which electrode within the CI array is activated (Pfingst et al. 2008). We restrict our analysis to qualitative trends that are typical in the sense that they are commonly observed when measuring MDTs in CI users. These qualitative trends are evident in the data from two CI listeners shown in Fig. 3 (figures reproduced from Shannon (1992) and Galvin and Fu (2005)) and are summarized below.

• Modulation frequency: CI users can detect smaller modulation depths at low modulation frequencies than at high modulation frequencies. MDTs increase rapidly for modulation frequencies greater than approximately 140 Hz (Shannon 1992). See Fig. 3(a).

• Stimulation level: CI users can detect smaller modulation depths as mean stimulus level increases (Galvin and Fu 2005; Pfingst et al. 2007). See Fig. 3(b).

• Carrier pulse rate: CI users can detect smaller modulation depths when stimuli are presented at a low carrier pulse rate than at high carrier pulse rates. Galvin and Fu (2005) found that CI listeners have lower MDTs (better detection) for a 250 pps carrier pulse rate compared to a 2,000 pps. Pfingst et al. (2007) found a similar result comparing detection using 250 pps and 4,000 pps carrier pulse rates. See Fig. 3(b).

Fig. 3.

Example of data from two CI listeners that illustrate the key qualitative trends in MDTs that will be modeled. Ordinate is MDT presented with a logarithmic scale. More negative values of 20 log(m) (i.e. higher on the y-axis) correspond to smaller MDTs (i.e. better performance on the detection task). a Subject N2 in Shannon (1992). The abscissa is modulation frequency. The key qualitative trend in these data are that MDTs increase at high modulation frequencies (above 100 Hz for this subject). Reprinted with permission from Shannon (1992). Copyright 1992, Acoustical Society of America. b Subject S1 in Galvin and Fu (2005). The abscissa is stimulus level and two curves are shown to represent results for a low carrier pulse rate (dashed line) and a high carrier pulse rate (black line). The key qualitative trends in these data are that MDTs decrease with level and are higher (i.e. worse performance on the detection task) when the stimuli are presented with a high carrier pulse rate. Reprinted with permission from Galvin and Fu (2005). Copyright 2005, Association for Research in Otolaryngology

The balance of the paper proceeds as follows. Section 2 introduces the AN model and ideal observer methodology used in this study. An analysis of how AM stimuli are encoded in the AN is then presented in Section 3.1. In Section 3.2, we construct a decoding method that predicts two of the three qualitative trends in the psychophysical data (dependence on modulation frequency and stimulus level). The main findings and limitations of our study, including model driven insights for what mechanisms may account for the third trend, are then discussed in Section 4.

2 Method

2.1 Auditory nerve model

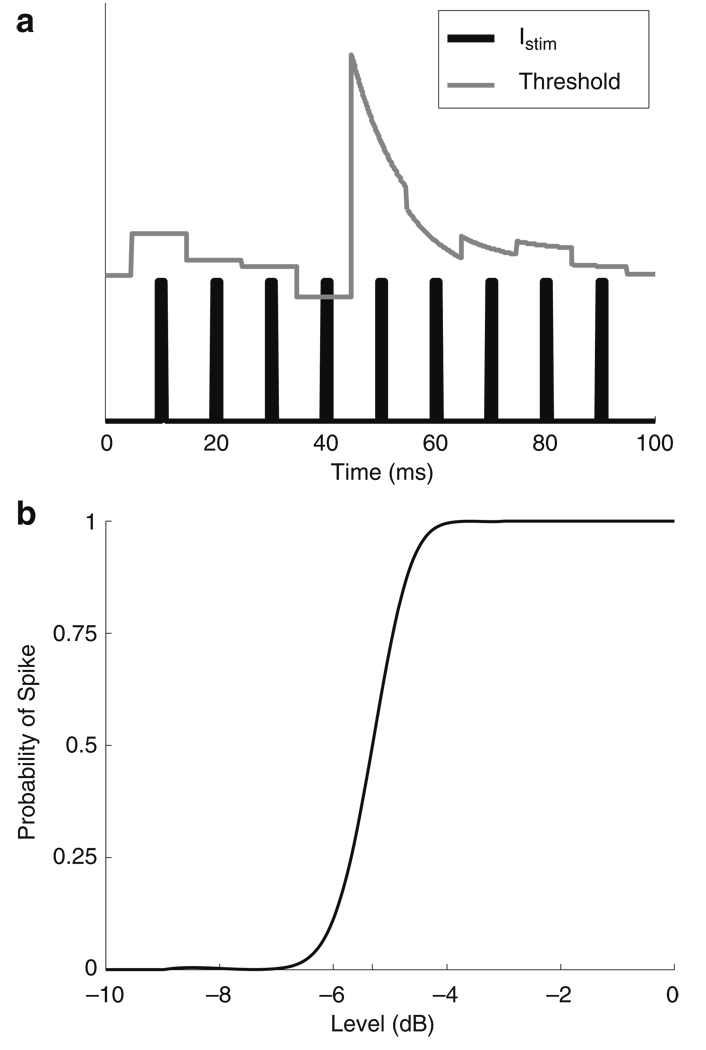
Responses of the AN to CI stimulation are simulated with the stochastic threshold model introduced by Bruce et al. (1999a, c). Figure 4(a) provides an illustration of the threshold crossing process. For each pulse of the CI stimulus, the level of stimulation (I_stim, black line) is compared to the threshold of the neuron (gray line). If the stimulus level exceeds the threshold, then the model neuron produces a spike. This occurs in response to the fourth pulse in Fig. 4(a). Figure 4(a) also shows how a refractory effect is included in the model. The threshold increases immediately after a spike and then relaxes back to the resting threshold. The spiking process is stochastic because, for each pulse, the neural threshold is drawn from a normal distribution with a mean and standard deviation chosen to fit physiological data. As a result, the probability of any single pulse eliciting a spike is determined by an integrated Gaussian function. This input-output function, also known as the firing efficiency curve, is shown in Fig. 4(b). The probability that the nth pulse in a stimulating pulse train elicits a spike depends on stimulus level (I_stim(n)) and the time since the last spike (t_LS) (Bruce et al. 1999a):

$$p_n=\mathbf{\{}\begin{array}{cc}0\hfill & \text{if}{t}_n-t_{\mathit{\text{LS}}}<t_{\mathit{\text{ab}}s}\hfill \\ \frac{1}{2}\left[1+\text{erf}\mathbf{\left(}\frac{I_{\text{stim}}(n)-I_{\mathit{\text{thr}}}{I}_{\mathit{\text{ref}}}(t_n-t_{\mathit{\text{LS}}})}{\sqrt{2}RS{I}_{\mathit{\text{thr}}}}\mathbf{\right)}\right]\hfill & \text{otherwise}\hfill \end{array}.$$ (2)

This function includes refractory effects since there are no spikes if the time since the last spike (t_LS) is less than the absolute refractory period (t_abs) and the relative refractory function (I_ref) increases the effective threshold immediately after a spike. For the simulations in this study, the absolute refractory period is 0.332 ms, which is the mean value recorded in AN fibers of cat by Miller et al. (2001). The other parameters that control the response properties of the model are the neural threshold (I_thr), the relative spread (RS), and the relative refractory effect. Unless otherwise stated, we set RS = 6.28% and I_thr = −5.31 dB relative to 1 mA.¹ These are the mean values reported by Miller et al. (1999) for AN action potentials evoked by cathodic, 39 µs pulse duration, monopolar CI stimulation in cat. The stimulus intensity of the nth pulse, I_stim(n), is the amount of current delivered to the stimulating electrode. For AM pulse trains, Eq. (1) defines I_stim(n).

Fig. 4.

a The AN model introduced by Bruce et al. (1999a, b) is a stochastic threshold crossing model. The stimulus level of each pulse (I_stim, black line) is compared to the threshold level (gray line). The model generates a spike if the stimulus level exceeds the threshold. The threshold is stochastic due to an additive Gaussian noise term applied at each pulse. In this example, the threshold is crossed at the fourth pulse. The threshold is temporarily elevated immediately after a spike and relaxes back to baseline level due to the refractory effect. b The probability that an isolated pulse will elicit a neural spike depends on the stimulus level and is defined in Eq. (2). This function is referred to as the firing efficiency curve and has a sigmoidal shape due to the additive Gaussian noise term

The neural threshold I_thr is defined to be the stimulus level for which, in the absence of refractory effects (I_ref(t_n − t_LS) = 0), the probability of spiking is 0.5. A relative refractory period is implemented via the term I_ref(t_n − t_LS). This term reduces the probability of spiking depending on elapsed time since the last spike (t_LS) and time at the onset of a given pulse (t_n). Miller et al. (2001) found that the relative refractory effect in cat AN fibers stimulated electrically could be modeled as

$$I_{\mathit{\text{ref}}}(t_n-t_{\mathit{\text{LS}}})={\left[1-\text{exp}\left(-\frac{t_n-t_{\mathit{\text{LS}}}-t_{\mathit{\text{ab}}s}}{{\tau }_{\mathit{\text{ref}}}}\right)\right]}^{-1}$$ (3)

where the time constant is τ_ref = 0.411 ms.

To analyze the temporal encoding properties of the AN model it is useful to reformulate it as a point process. In order to do this, we derive the conditional intensity function (CIF) which completely describes the point process (Daley and Vere-Jones 2003). The CIF is a useful tool for modeling and analyzing neural spike trains with spike history and dynamic inputs (Truccolo et al. 2005, e.g.). It defines the probability of observing a spike in an infinitesimally small time bin given the past history of the stimulus and spike times, denoted H_t:

$$\lambda (t|H_t)=\underset{\mathrm{\text{Δ}}\to 0}{\text{lim}}\frac{P\{N\{t+\mathrm{\text{Δ}})-N(t)=1|H_t\}}{\mathrm{\text{Δ}}},$$ (4)

where N(t) is the number of spikes that have occurred by time t. λ(t|H_t) is a stochastic process since the spike times, and therefore the spike history effect, will be different for each realization of a spike train.

A basic result from the theory of point processes gives the probability of not having a spike in a given interval of time as the negative exponential of the integral of the intensity during that interval (Snyder and Miller 1991). The probability of not having a spike during the nth pulse can also be written as 1 − p_n so we have:

$$p_n=1-\mathit{\text{exp}}\left[-{\displaystyle {\int }_{t_n}^{t_n+D}\lambda (t|H_t)\mathrm{d}t}\right],$$ (5)

where t_n is the time at the beginning of the nth pulse, D is the pulse duration, and p_n is defined in Eq. (2).

To determine λ(t|H_t), first note that the model assumes that spikes can only occur during a pulse. Second, since the absolute refractory period (332 µs) is longer than the pulse duration (100 µs), there can be at most one spike within a pulse. Third, we make the additional assumption that the CIF is constant within a pulse. Under these assumptions, Eq. (5) can be solved for the CIF:

$$\lambda (t|H_t)=\mathbf{\{}\begin{array}{cc}0\hfill & \text{if}{t}_n\text{is}\text{not}\text{within}\mathrm{a}\text{pulse}\hfill \\ -\frac{1}{D}\mathit{\text{log}}(1-p_n)\hfill & \text{otherwise}\hfill \end{array}.$$ (6)

The original model of Bruce et al. (1999a, b) could only determine whether a spike had occurred on a given pulse whereas simulating the model as a point process with a known CIF makes it possible to generate spike trains with exact spike times.

2.2 Maximum likelihood discrimination

To simulate the modulation detection task, neural responses (r₀ and r_m) are generated in response to unmodulated and modulated stimuli (s₀ and s_m, respectively). We then test the ability of an ideal observer to identify which stimulus is modulated based on the observed responses. The optimal decision is found by computing the likelihood of all possible response-stimulus pairings. We first compute the likelihood ratios $\frac{P(r_0|s_0)}{P(r_0|s_m)}$ and $\frac{P(r_m|s_0)}{P(r_m|s_m)}$ and then define the decision variable

$$R(0,m)=\frac{P(r_0|s_0)P(r_m|s_m)}{P(r_0|s_m)P(r_m|s_0)}.$$ (7)

If R(0, m) is greater than 1, then the ideal observer correctly performs the detection task. This is the optimal decision rule for the two-alternative forced-choice paradigm (Green and Swets 1966; Rieke et al. 1999). This approach has been used previously by Pillow et al. (2005) to analyze temporal encoding in models of retinal ganglion cells.

By applying the maximum likelihood decision rule to numerous simulated spike trains, we can measure how the percentage of correct detections varies changes with modulation depth and other stimulus parameters. To compare results to psychophysical data, we report our results in terms of the modulation detection threshold (MDT). MDT is defined throughout this study as the modulation depth at which the modulated and unmodulated stimuli can be successfully distinguished on 79.4% of trials. This value is chosen to match the experimental procedure of Shannon (1992). To estimate MDTs, we use an adaptive version of the Robbins–Monro stochastic approximation method (Robbins and Monro 1951; Kesten 1958). Conceptually, this method is similar to an adaptive up-down staircase method commonly used in two-alternative forced-choice experiments, but it converges more accurately to the defined detection threshold level (Faes et al. 2007). The details of this algorithm are included in the Appendix.

2.3 Characterizing spike train responses

To perform the AM detection task using the maximum likelihood decision rule, the ideal observer must compute the likelihood ratio in Eq. (7). This, in turn, depends on how the conditional probabilities P(r|s) and the response variable r are defined. For instance, the extent to which average firing rate encodes amplitude modulation can be tested by defining r as the total number of spikes fired during the duration of the stimulus. If modulation information is encoded in the timing with which the spikes occur over the course of the trial, however, one would need to include spike times in the definition of r. By simulating the ability of an ideal observer to detect modulation detection using several definitions of P(r|s) and the response variable r, we can probe the neural code to determine what features of the neural response encode amplitude modulation. Furthermore, by comparing the performance of the ideal observer to the performance of CI listeners, we can attempt to infer what information is preserved by downstream processing and what information is lost.

We will use four different response variables for r. First, we will take r to be the simulated spike train itself (i.e. a precise sequence of spike times). This provides an upper bound for the amount of information encoded in the AN response. Following Heinz et al. (2001a), we will refer to this response variable, together with maximum-likelihood decoding of the AN, as the all-information measure. Second, we will define P(r|s) as if the neuron were modeled as an inhomogeneous Poisson process. This Poisson measure captures the temporal information in time-dependent firing rates, but neglects interactions among the times of different spikes. Comparing the Poisson and all-information results, therefore, allows us to test the importance of temporal correlations in the spike train. Third, we will consider whether temporal information in the spike train can be captured by reducing the neural response variable to a common measure of phase locking to the period of modulation. This Vector Strength (VS) measure is similar to the approach used by Middlebrooks (2008b). Lastly we test whether average firing rate alone, with no temporal information, is sufficient to detect amplitude modulation. This spike count measure defines the response variable r to be the total number of spikes produced during the duration of the stimulus and was the method used by Xu and Collins (2007) to simulate modulation frequency discrimination. We now discuss how these measures are computed.

2.3.1 All-information

For a given spike train with spike times given by ${\{t_i\}}_{i=1}^N$, the likelihood function for the all-information measure can be written as (Daley and Vere-Jones 2003):

$$P(r|s)=\mathbf{\left(}{\displaystyle \prod _{i=1}^N\lambda (t_i|H_{t_i})}\mathbf{\right)}\text{exp}\left[-{\displaystyle {\int }_0^T\lambda (t|H_t)\mathrm{d}t}\right]$$ (8)

where and λ(t|H_t) is the conditional intensity function defined in Eq. (6) and T is the duration of the stimulus. This probability distribution requires complete knowledge of the precise spike times as well as the refractory effects and stimulus levels that define the conditional intensity function. Using this equation to compute the likelihood ratio (Eq. 7), it is possible to perform maximum likelihood discrimination using the all-information measure. The advantage of this approach is that it makes no assumptions about stimulus representation or neural read-out mechanisms. It assesses all stimulus information in the AN spike trains. A similar approach was been used by Heinz et al. (2001a,b) to investigate how auditory nerve responses limit frequency and intensity discrimination in acoustic hearing.

2.3.2 Poisson

For the Poisson measure, likelihood functions are computed as if the spike train were defined by an inhomogeneous Poisson process. The Poisson measure assumes that the ideal observer does not have a priori knowledge of the refractory period or the true CIF. This measure neglects serial and higher order temporal correlations.

An inhomogeneous Poisson process is described by its instantaneous firing rate. We estimate this for the model by discretizing time in Δt = 0.5 ms bins and computing the probability of observing a spike in each bin. This value for Δt was chosen so that individual pulses could be resolved even at the highest carrier pulse rate simulated (2,000 pulses per second) and the instantaneous firing rate was estimated as the mean of 2 × 10⁴ repeated simulations of the model. This large number of samples guaranteed that the standard error of the estimate of the instantaneous firing rate was less than 1%.

Denote the estimated instantaneous firing rate as λ̃(t), then the likelihood function for this measure is given by the likelihood function of the conditionally independent Bernoulli process, which is the discrete version of Eq. (8) (Truccolo et al. 2005):

$$P(r|s)\approx {\displaystyle \prod _{i=1}^N(\tilde{\lambda }(t_i)\mathrm{\text{Δ}}t){\displaystyle \prod _j(1-\tilde{\lambda }(t_j)\mathrm{\text{Δ}}t)}}$$ (9)

where i indexes the time bins in which there was a spike and j indexes all other time bins.

2.3.3 Vector strength

The third measure that includes spike time information is Vector Strength. VS is a measure of how strongly a spike train is phase locked to a periodic stimulus. Let θ_i ∈ [0, 2π] (i = 1, … , N) be the phase of the ith spike relative to the period of modulation. Then the VS is defined to be (Goldberg and Brown 1969):

$$r=\frac{\sqrt{{({\displaystyle {\sum }_i\text{sin}{\theta }_i})}^2+{({\displaystyle {\sum }_i\text{sin}{\theta }_i})}^2}}{N}$$ (10)

By this definition, r = 0 if spikes are randomly distributed in time and r increases to 1 (i.e. perfect phase locking) if all spikes occur at the same time relative to the period of modulation. The VS measure does not provide useful information when there is only a small number of spikes. For instance, by this definition, r = 1 (perfect phase locking) if there is only one spike in the spike train. This could lead to unintended discrimination of modulated and unmodulated stimuli. To avoid this, we set r = 0 when the spike train includes fewer than three spikes.

VS is commonly used to analyze spike train responses to AM stimuli (Joris et al. 2004, e.g.) and has recently been used to compute MDTs based on the response to CI stimulation of neurons in auditory cortex of guinea pigs (Middlebrooks 2008b). The conditional probability P(r|s) cannot be computed explicitly in this case, but since VS is expected to increase with modulation depth, the maximum likelihood decision rule simplifies to assuming that the spike train with the greater VS value was produced by the modulated stimulus. To compute VS, the ideal observer must have prior knowledge of the modulation frequency. Unlike the all-information and Poisson measures, however, the observer does not require information about the modulation depth, stimulus level, or the conditional intensity function (in the case of the all-information measure).

2.3.4 Spike count

The final measure that we consider is the spike count measure. This neglects all temporal information in the spike train and quantifies how well modulation can be encoded by the number of spikes produced by the model AN cell over the entire duration of the stimulus. Due to refractory effects, there is no simple expression for P(r|s), but it can be approximated by repeated simulations of the model. Histograms for the number of spikes produced in response to a stimulus of a given modulation depth are computed from 2 × 10⁴ repeated simulations of the model. To approximate the distribution of spike counts, the value in each histogram bin is divided by the number of repetitions. As in the estimate of the Poisson measure, this number of samples reduces the standard error in the estimate of values of the probability mass function to less than 1%.

2.4 Simulation of amplitude modulation detection experiments

We simulate modulation detection and investigate the effects of varying three stimulus parameters that have been studied in past psychophysical experiments: modulation frequency, stimulus level, and carrier pulse rate. Stimulus parameters are chosen, when possible, to match the values reported in the AM detection experiments of Shannon (1992). In particular, the duration of the stimuli is 400 ms and the pulse duration is 100 µs. Unless otherwise noted, the pulse train is presented at a rate of 1,000 pps as in Shannon (1992) and the modulation frequency is 20 Hz as in (Galvin and Fu 2005). Due to technical limitations in the CI devices, pulse duration is often modulated in psychophysical experiments instead of pulse amplitude (Shannon 1992, e.g.). Simulation results are nearly identical regardless of whether pulse duration or level was modulated. All results reported in this paper are from simulations in which the modulation was applied to stimulus level and pulse duration is fixed at 100 µs.

It is not known how to relate stimulus levels used in the model directly to the levels used in psychophysical experiments. For instance, Shannon reported that the stimulus levels were set to comfortable loud levels. This is a subjective measure that cannot be replicated in the model so, unless otherwise stated, we set the stimulus level to be Ī_stim = −5.31 dB re 1 mA. This is the mean threshold level reported by Miller et al. (1999).

The set of simulations that test the effect of changing the carrier pulse rate follows the experiment of Galvin and Fu, so modulation frequency is held at f_m = 20 Hz. It is commonly observed that high carrier pulse rate stimuli sound louder to CI users. This requires experimenters to vary stimulus level with carrier pulse rate so that the perceived loudness of the stimuli is held constant as pulse rate is varied. The neural code for loudness is unknown so it is impossible to perform loudness balancing in the context of the model. As in a past study using the Bruce AN model, we approximate loudness as the total the number of spikes elicited in a trial (Bruce et al. 1999b).

2.5 Computer code

All simulations were written in Fortran95 and are available at:http://www.amath.washington.edu/~jgoldwyn/CIcode.html. The AN model was adapted from Matlab code that is freely available at Dr. Ian Bruce’s website: http://www.ece.mcmaster.ca/~ibruce/CImodels/.

3 Results

3.1 Encoding properties of the AN

3.1.1 Effect of model parameters

The nonlinear firing efficiency curve given in Eq. (2) and the refractory effect defined in Eq. (3) completely determine the spiking dynamics of the model. The two parameters that define the firing efficiency curve in Eq. (2) are the neural threshold level (I_thr) and the relative spread (RS). I_thr is defined as the stimulus level expected to evoke a spike on 50% of presentations in the absence of any refractory effect. RS is the standard deviation in the spiking probability normalized by the threshold value. A range of values for these parameters have been reported in past neurophysiological studies measuring the response of cat AN fibers to CI stimulation. For instance, Miller et al. (1999) measured RS values as low as 1% and greater than 30% in cat AN fibers. It is therefore of interest to understand how changes in these parameter values affect encoding of amplitude modulation in the periphery.

The effects of varying these two parameters independently is shown in Fig. 5. We vary stimulus level and hold modulation frequency and carrier pulse rate constant at 20 Hz and 1,000 pps, respectively. MDTs are computed using the all-information measure which gives a theoretical upper bound to the amount of information encoded by the simulated AN cell. As in all subsequent plots of MDTs, the stimulus duration is 400 ms, each data point is defined as the mean threshold value from ten repetitions of the stochastic approximation algorithm, and the error bars show the standard error of the mean (see Appendix for details).

Fig. 5.

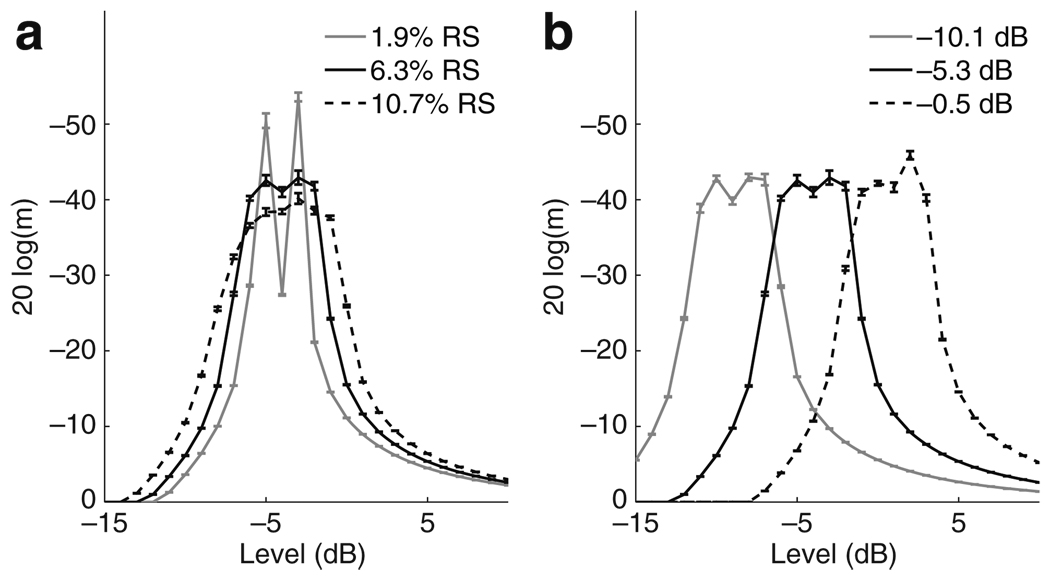
Effect of neural parameters on AM encoding. MDTs are computed from the mean of 10 runs of the stochastic approximation algorithm and error bars represent the standard error of the mean. MDTs are plotted against mean stimulus level. a Varying RS: mean (black line), low (gray line), and high (dotted line) RS values are chosen according to data reported by Miller et al. (1999). MDTs improve near threshold as RS decreases, but the range of levels over which the model neuron can effectively encode AM also decreases with decreasing RS. b Varying neural threshold: mean (black line), low (gray line), and high (dotted line) neural threshold values are chosen according to data reported by Miller et al. (1999). The primary effect of changing the threshold value is to shift the range of stimulus levels over which the model neuron can effectively encode modulation

Panel A of Fig. 5 shows the effects of varying RS away from its mean value. The black line corresponds to the mean value RS = 6.28% reported in Miller et al. (1999). The standard deviation in the RS values measured by Miller et al. (1999) was 4.4%. The gray and dashed lines are computed for RS plus or minus one standard deviation, respectively. As the value of RS decreases, the firing efficiency curve (Eq. 2) approaches a step function. This has two competing effects on coding. First, it narrows the dynamic range of the model neuron so the mean stimulus levels over which modulation information can be encoded is smaller. Second, the variability in spike initiation is reduced. This causes the model neuron to be sensitive to modulation over a more narrow rage of current levels, although there are some current levels within this narrow range where coding is improved when RS is small.

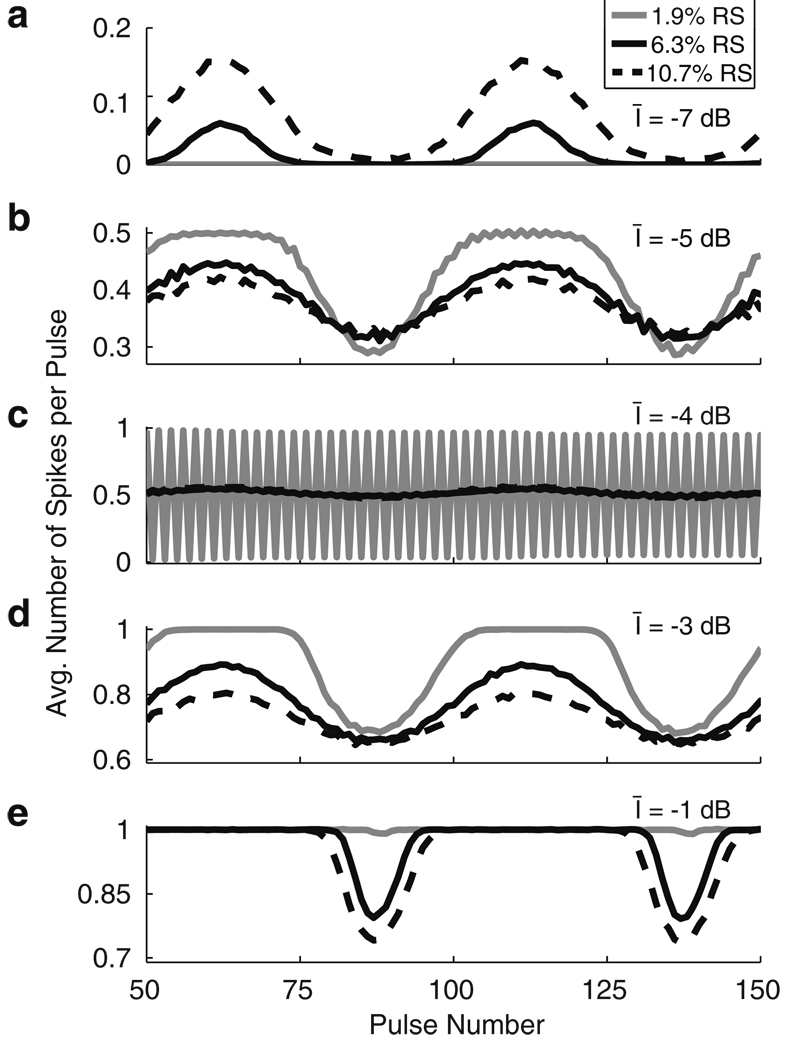
To further illustrate the effect of varying RS, we explore simulated responses at a number of current levels. Figure 6 shows the number of spikes per pulse, averaged over 1,000 repeated simulations of the AN model at five different levels (top to bottom) for the three different RS values shown in Fig. 5. The top panel shows that at low stimulus levels (Ī_stim = −7 dB in Panel A), there is a noise-induced coding advantage whereby, in this subthreshold regime, the neuron is only likely to spike at the peaks of modulation and the probability of spiking at the peaks is enhanced when RS is high. Panels B and D show that for some stimulus levels (Ī_stim = −5 dB and Ī_stim = −3 dB) MDTs improve with smaller RS values. The slope of the firing efficiency curve near threshold is steeper for smaller RS values and it therefore becomes more likely that spikes will occur near the maxima of the modulated waveform. Panel C shows a peculiar firing pattern. Due to the refractory effects and the very steep firing efficiency curve for the low RS value, the spike train in the case of low RS is nearly deterministic. Small amounts of modulation are not enough to alter the response pattern and the model neuron fires in response to every other pulse. This is a case where greater variability (higher RS) leads to improved encoding since the added noise avoids this deterministic firing pattern. Panel E shows results for Ī_stim = −1 dB. At this high stimulus level there is again a coding advantage for more variable neural responses (high RS values). Higher RS values lead to better encoding in this regime because the probability of firing in the trough of the modulated waveform is lower.

Fig. 6.

Illustration of the effect of changing RS values on coding. The abscissa is the pulse number and the ordinate is the probability of observing a spike in response to that pulse, obtained by averaging over 1,000 repeated simulations of the model in response to modulated stimuli. Modulation depth is −30 dB modulation depth (m ≈ 3%) for all simulations except Panel E. Modulation depth in Panel E is 20% so that differences between RS values are visible. RS values are the same as Fig. 5. a Ī_stim = −7 dB. Higher RS improves encoding at low stimulus levels by increasing the number of spikes at the peak of the modulated stimulus. b Ī_stim = −5 dB. Lower RS values improve encoding by increasing the number of spikes at the peaks of the modulated stimulus. c Ī_stim = −4 dB. The neuron fires to every other pulse in a nearly deterministic fashion for low RS values. High RS values break this pattern and allows for greater discriminability between modulated and unmodulated stimuli. d Ī_stim = −3 dB. Lower RS values improve encoding by increasing the number of spikes at the peaks of the modulated stimulus. e Ī_stim = −1 dB. Higher RS improves encoding at high stimulus levels by decreasing the number of spikes during the troughs of the modulated stimulus

Panel B of Fig. 5 shows MDTs calculated for three values of I_thr. The primary effect of changing this parameter value is to shift the levels over which the model neuron can effectively encode modulation information. Since the standard deviation in the firing probability (the denominator in Eq. (2)) depends on the product of RS and I_thr, one might expect that increasing I_thr would have a similar effect as increasing RS. There is no appreciable difference in the widths of the curves in Fig. 5(b), however, which shows that this effect is negligible for the range of parameter values reported by Miller et al. (1999).

3.1.2 Comparison of spike train measures

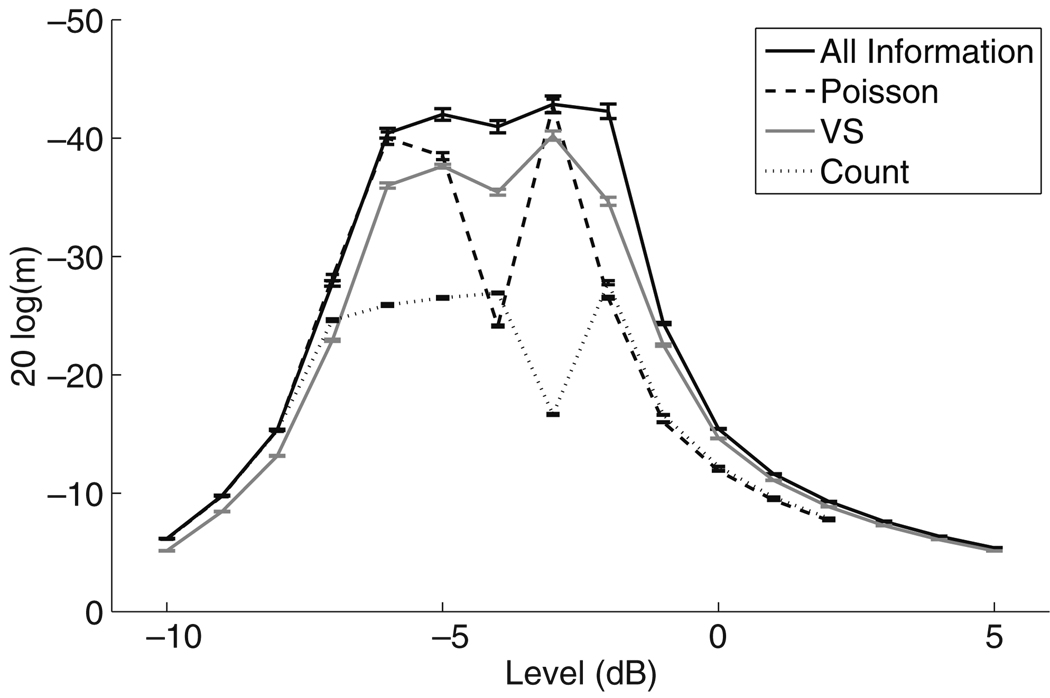
Figure 7 shows MDTs as a function of stimulus level computed using the four spike train measures discussed in Section 2.3. The neural parameters are set to their mean values and, as in Fig. 5, modulation frequency is f_m = 20 Hz, and carrier pulse rate is 1,000 pps. The all-information measure (black line), represents the theoretical upper bound to the amount of information encoded by the model AN cell because the ideal observer in this case has complete knowledge of precise spike times and the underlying conditional intensity function. AM encoding is maximal when the stimulus is near the neural threshold and degrades when the stimulus level increases or decreases beyond the dynamic range of the model neuron.

Fig. 7.

MDTs as a function of level computed for a single model neuron using the four spike train response variables. Modulation frequency is f_m = 20 Hz and carrier pulse rate is 1,000 pps. MDTs are computed from the mean of 10 runs of the stochastic approximation algorithm and error bars represent the standard error of the mean

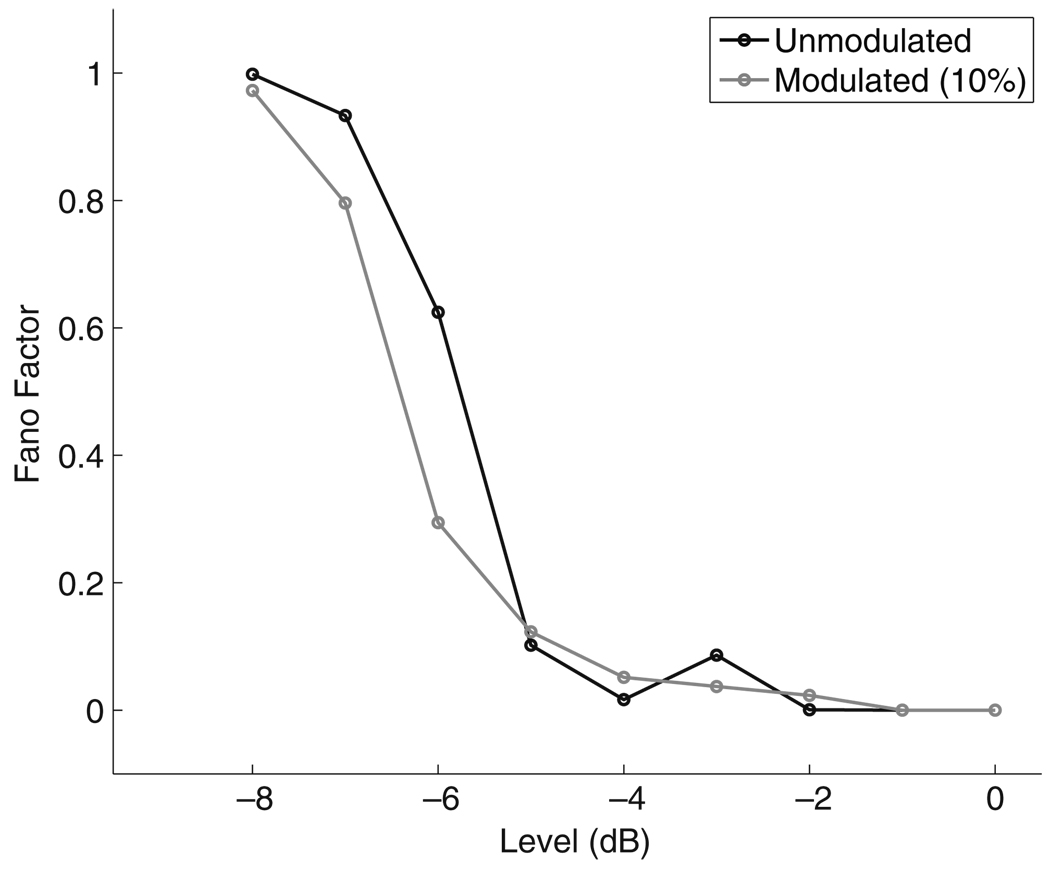
The Poisson measure (dashed line) matches the all-information measure for stimulus levels less than approximately −7 dB. At these low levels, the firing rate of the neuron is low and the interspike intervals are long relative to the refractory period so the Poisson approximation is valid. Figure 8 shows the Fano factor for spike trains in response to an unmodulated stimulus (black line) and a modulated stimulus with modulation depth m = 10% (gray line). As expected, the Fano factor is near one for low stimulus levels indicating the spike train behaves like an inhomogeneous Poisson process. At high stimulus levels, it is common for spikes to occur within the relative refractory period so temporal correlations matter in determining spike timing. This is reflected in the rapid decrease in the Fano factor for levels above −7 dB. At these higher stimulus levels the Poisson measure does not reach the upper limit set by the all-information measure. For some levels (Ī_stim = −4 dB), the refractory effect shapes the estimated Poisson intensity in a way that degrades the performance of the Poisson measure. At others (Ī_stim = −3 dB), the Poisson measure approaches the value of the all-information measure even though the Fano factor is near zero indicating the response is highly non-Poisson.

Fig. 8.

Fano factor as a function of stimulus level for unmodulated (black) and AM (gray) pulse trains. Modulation depth is 10% and modulation frequency is 20 Hz for the AM stimulus. The Fano factor approaches zero as the stimulus level increases beyond −4 dB indicating that the Poisson approximation is not valid at high stimulus levels

The VS measure (gray line) reveals how much of the timing information in the spike train can be extracted by computing a simple measure of phase locking to the period of the modulated stimulus. Figure 7 shows that MDTs computed with VS are, at most, ∼7 dB higher than those computed with all-information. Thus there is some information that is lost in reducing the spike train to this single statistic. The loss of information is most apparent at low levels when the Poisson measure provides a better approximation to the all-information measure. In general, the loss of information is relatively small, and the behavior of the VS measure appears qualitatively similar to the all-information measure. The VS measure also preserves within-trial spike time correlations so, at high stimulus levels, it can encode more information than the Poisson measure.

Thresholds computed with the spike count measure (dotted line) are higher than the MDTs computed using the all-information and vector strength measures for moderate stimulus levels. This indicates that the temporal patterns of spike times are more informative than the long-term spike rate. Nonetheless, MDTs for the spike count measure are equal to those for the all-information measure at low levels and reach as low as −27 dB (≈ 5%). At one level (−4 dB), spike count encodes slightly more information than the Poisson measure. This finding is nonintuitive, but is related to the fact that the response of the neuron is highly non-Poisson at this level. Overall, the finding that spike count measure can carry relevant information to performing the modulation detection task is unexpected because it has been observed in neurophysiological studies of the response of the AN to amplitude-modulated acoustic stimuli that firing rate in the AN does not depend on modulation frequency or depth (Joris and Yin 1992).

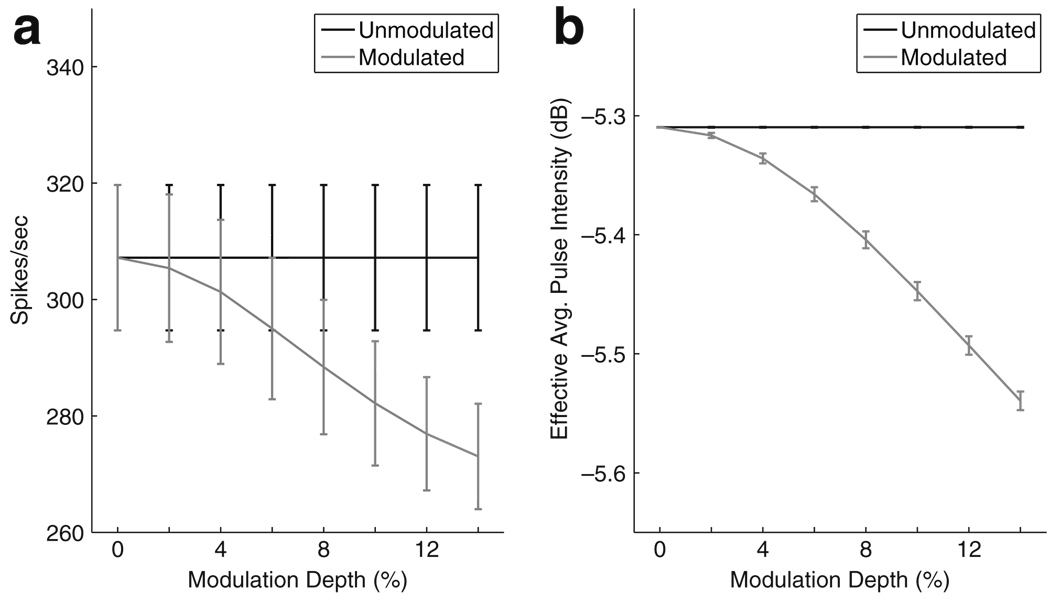
There are two mechanisms in the model that cause spike count to change with modulation depth. The nonlinear shape of the firing efficiency curve distorts the effect of the amplitude modulation so that the mean firing probability averaged over all pulses in a stimulus is not symmetric about a fixed mean value but biased upward at low stimulus levels and downward at high stimulus levels. The second mechanism is the refractory period. As shown in Fig. 9(a), for f_m = 20Hz and I_stim = −5.31 dB the firing rate of the model neuron is suppressed as modulation depth increases. This is due to the fact that, at this relatively low modulation frequency, the model neuron is more likely to be in a refractory state when the stimulus is at an above average level (i.e. near the peak of the modulated waveform). To illustrate this point, we define an effective average pulse intensity by removing all pulses in the stimulus pulse train that immediately follow a spike. The justification for removing the pulse immediately following a spike is that, at moderate stimulus levels and 1,000 pps carrier pulse rate, the relative refractory effect will prevent spike initiation in the pulse immediately following a spike so, in a sense, this pulse has no effect on the simulated spike train. Figure 9(b) shows that, by this measure, as modulation depth increases the effective average pulse intensity decreases. This confirms that the refractory period can act to suppress the firing rate as modulation depth increases. More generally, depending on the stimulus level, the interplay of the nonlinear firing efficiency curve and the refractory period can give rise to modulation detectability based on the spike count measure.

Fig. 9.

a Spike count as a function of modulation depth. Error bars are standard deviation of 1,000 repeated simulations of the model. Spike count decreases as modulation depth increases (gray line). b Effective average pulse intensity is defined as the average stimulus level of all pulses in the train excluding those that fall immediately after a spike. Effective average pulse intensity decreases with modulation depth indicating that the dependence of spike count on modulation depth shown in (a) is due to the refractory period

3.1.3 Effect of stimulus parameters

In addition to stimulus level (discussed above), psychophysical experiments commonly investigate modulation detection performance as a function of modulation frequency and carrier pulse rates. We now analyze the effects of varying these two stimulus parameters.

Modulation frequency

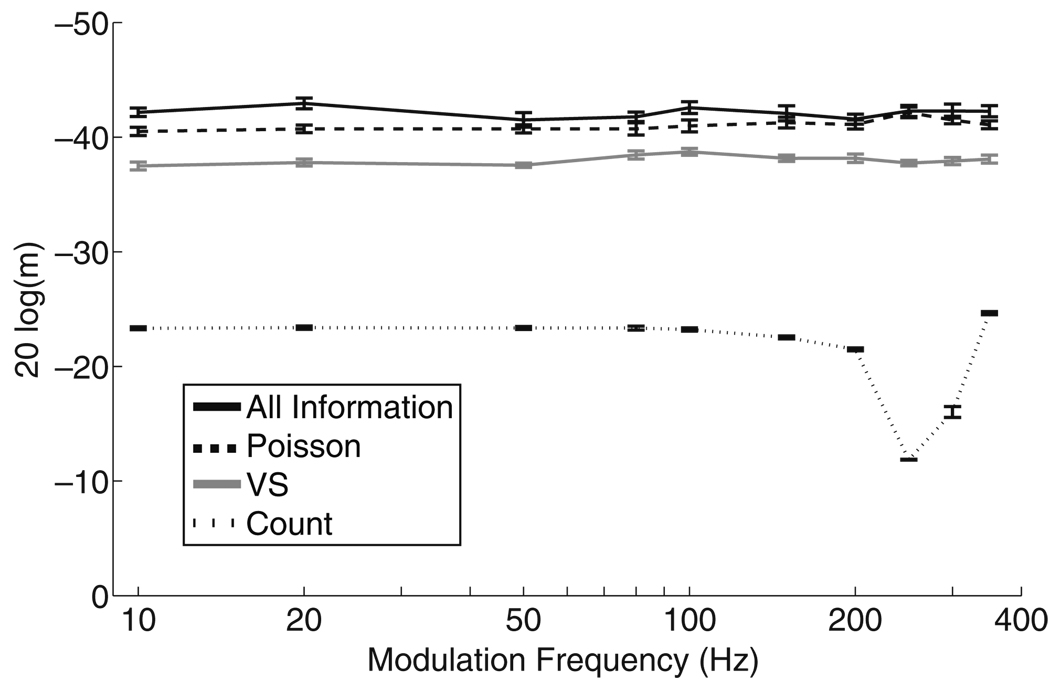
Figure 10 shows how MDT depends on f_m where MDTs are computed using the four maximum likelihood measures described in Section 2.3. MDTs computed using some aspect of spike timing information (i.e. all-information, Poisson, and VS) approach or are lower than the MDTs commonly observed in CI listeners. Moreover, MDTs computed using these measures remain nearly constant for all values of f_m. This analysis shows that modulation encoding by a single model AN does not degrade at high f_m.

Fig. 10.

MDTs as a function of modulation frequency computed for a single model neuron using the four spike train response variables. Mean stimulus level is Ī_stim = −5.31 dB and carrier pulse rate is 1,000 pps. MDTs are computed from the mean of 10 runs of the stochastic approximation algorithm and error bars represent the standard error of the mean

Carrier pulse rate

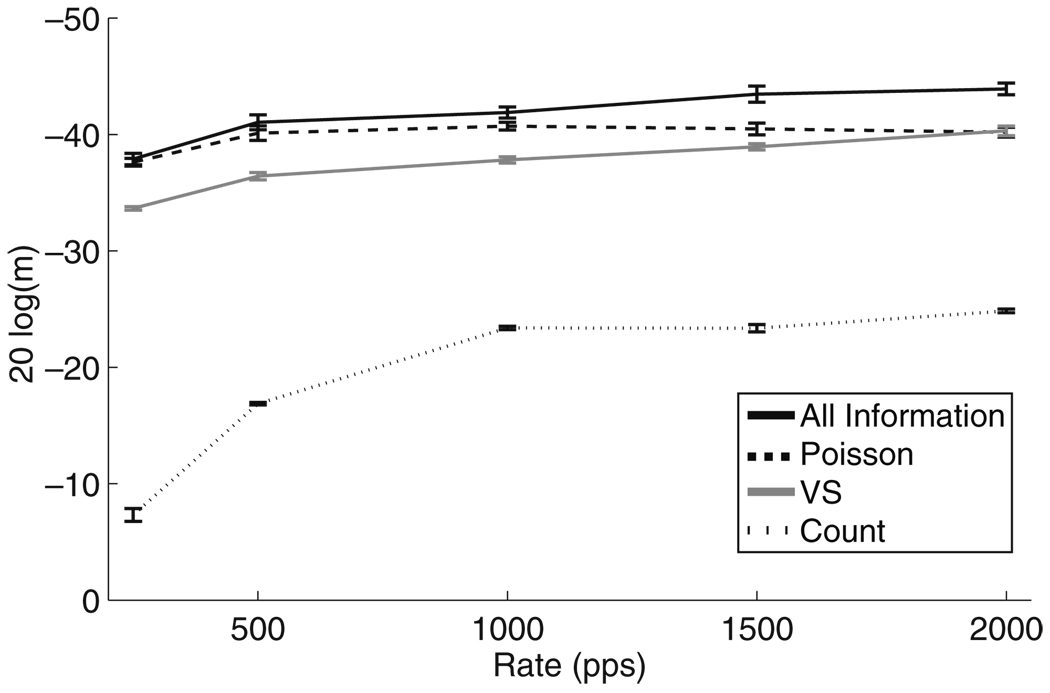
Figure 11 shows how MDTs depend on carrier pulse rate. The all-information and VS measures show slight improvements as carrier pulse rate increases. The Poisson measure predicts that MDTs at low carrier pulse rates are close to the optimal values defined by the all-information measure. As carrier pulse rate increases, the model neurons are stimulated within the relative refractory period and the Poisson approximation becomes less valid. The MDTs increase and approach the level of the VS measure. MDTs computed using the spike count measure improve from −7.3 dB (m ≈ 43%) at a pulse rate of 250 pps to −24.8 dB (m ≈ 6%) at higher pulse rates. As expected, spike timing provides much more modulation information than the long-term spike rate. Figure 11 shows that there is no loss of temporal information in the model AN responses to high rate stimuli. In fact, the opposite trend is found when using the all-information, VS, and spike count measures. The analysis does not predict, therefore, that that temporal encoding properties of the AN model pose a limitation on AM detection at high carrier pulse rates.

Fig. 11.

MDTs as a function of carrier pulse rate computed for a single model AN using the four spike train response variables. Modulation frequency is f_m = 20 Hz and mean stimulus level is Ī_stim = −5.31 dB

3.2 AN decoder and psychophysics simulations

The second aim of this study is to replicate certain qualitative trends that are commonly observed in the psychophysics literature. Our method is to construct a decoder that takes simulated AN spike trains as its input and predicts performance on the AM detection task. The physiological basis for AM processing remains uncertain, so the decoder will not be constructed in a way that explicitly accounts for the properties of cochlear nucleus cells or other cells in the auditory pathway. The form of the decoder will instead be informed by our preceding analysis of the encoding properties of the model AN, the measured performance limits of CI listeners, and the goal of formulating a computationally tractable method for relating simulated AN spike trains to psychophysical data.

The analysis of encoding shows that an ideal observer can perform the modulation detection task more effectively with access to spike timing information. It is possible for an ideal observer to perform the AM detection task using spike count information alone, but performance is much improved if the observer has access to temporal information. We will construct a neural decoding method using the VS measure. Reducing all spike timing information to a VS value may neglect certain aspects of spike-time information that are preserved in other reduced measures such as the Poisson measure, but there are several reasons why VS provides a useful method for simulating AM detection based on spike timing information. First, the encoding results indicate that an ideal observer performing AM detection based on VS has MDTs that are near the theoretical upper bound set by the all-information measure and show qualitatively the same dependence on stimulus parameters. Second, it is a measure of phase-locking which others have identified as a potential code for amplitude modulation (see the review paper of Joris et al. (2004)). Third, it is computationally and conceptually simple so it allows us to decode the output of a heterogeneous population of model AN cells with temporal jitter added to each spike time, as we explain below.

3.2.1 Modulation frequency

AM experiments typically reveal that CI subjects have difficulty performing the AM detection task for f_m above approximately 140 Hz (Shannon 1992, e.g.). The simulation results in Fig. 10 show that an ideal observer analysis of the responses of a single model AN cell does not predict this result.

We hypothesize, therefore that modulation information is adequately encoded in AN responses but that there is a limit to the temporal resolution of the central decoder. To simulate this decoding limitation, a random amount of jitter is added to each spike time generated by the AN model. There is no explicit physiological basis for incorporating jitter in this manner, but we view this as a parsimonious method for controlling the temporal resolution of the decoder. The amount of jitter is drawn from independent samples from a normal distribution with mean 0 and standard deviation σ. The standard deviation determines the temporal resolution of the decoder.

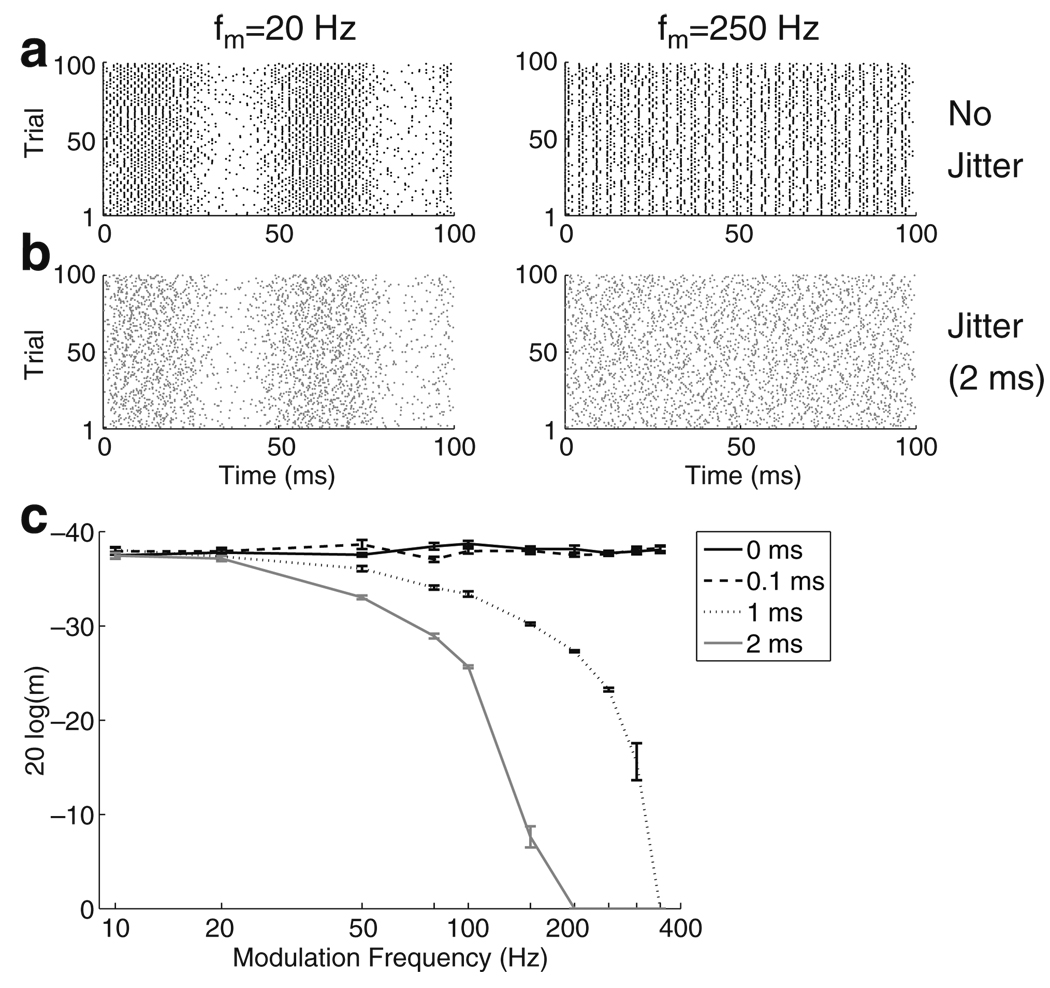
Figure 12(a) shows raster plots for repeated simulations of the AN model. Responses are shown for f_m = 20 Hz (left) and f_m = 250 Hz (right). In Fig. 12(b), the raster plots are modified by adding temporal jitter to each spike time by drawing increments from a normal distribution with standard deviation σ = 2 ms. At the low modulation frequency (left), the periodic pattern of spike times is preserved after the addition of jitter. At the high modulation frequency (right), the jittered spike times appear to be completely random and there is no obvious cue to indicate that these spike trains were evoked by an AM stimulus. We expect, therefore, that AM sensitivity will degrade at high modulation frequencies if the decoder only has access to the jittered spike trains.

Fig. 12.

a Raster plot for 100 repeated simulated responses of a single model neuron to AM stimuli (m = 10%). Left f_m = 20 Hz. Right f_m = 250 Hz. b Spike times in (a) are jittered by adding random increments drawn from a Gaussian distribution with zero mean and standard deviation σ = 2 ms. c MDTs as a function of f_m for varying amounts of jitter (σ) using the VS spike train measure. Increasing σ degrades the temporal resolution of the decoder and results in MDTs that are qualitatively consistent with psychophysical data

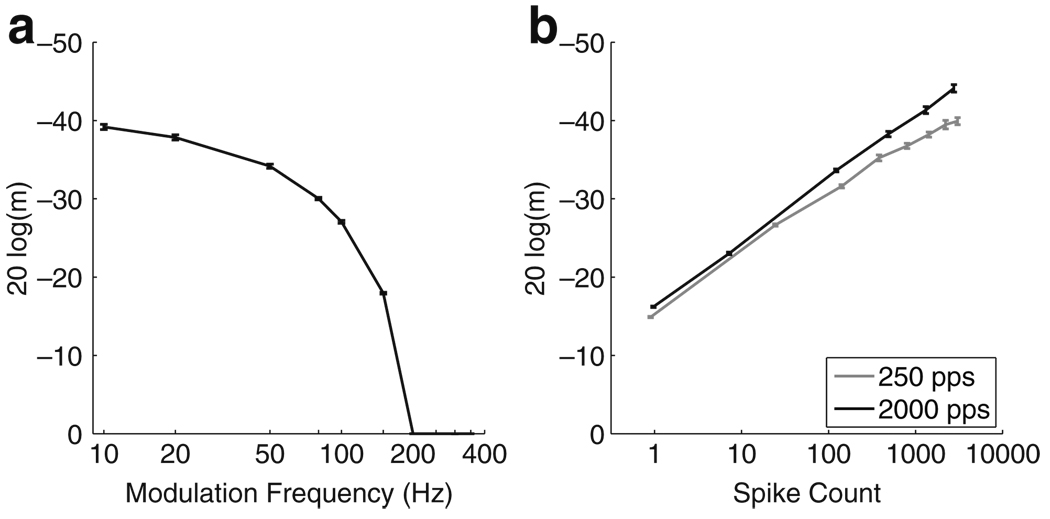
Figure 12(c) confirms this. In the absence of jitter (black line), or for small amounts of jitter (dashed line, σ = 0.1 ms), MDTs remain constant for all values of f_m. As σ increases, the decoder’s performance worsens at high f_m. It is important to note that the AN model produces spike time jitter on the order of 0.01 ms which does not represent the amount of jitter that has been measured in animal models of CI stimulation. For instance, in the auditory nerve of cat, Miller et al. (1999) measured spike time jitter of approximately 0.1 ms. The results for σ = 0.1 ms (dashed line) show that when accounting for a physiologically realistic amount of jitter at the level of the AN, the decoder does not predict performance limitations on the AM detection task. It is necessary, therefore, to further degrade the temporal resolution of the decoder. In particular, the results for σ = 2 ms (gray line) qualitatively match the experimental data of Shannon (1992) since AM sensitivity degrades rapidly at high modulation frequencies.

3.2.2 Stimulus level

AM detection in CI listeners typically improves as stimulus level increases. For the subjects in the study of Galvin and Fu (2005), this improvement with stimulus level extends over a range of approximately 5 dB (for the 250 pps pulse train) to 10 dB (for the 2, 000 pps pulsetrain). As shown in Fig. 5, the range of current levels over which a single model AN cell can encode AM information is limited to a few dB near the neural threshold level.

To construct a decoder that can match psychophysical trends over a wider range of stimulus levels, we let a heterogeneous population of AN cells provide the input to the decoder. Each individual spike train is jittered (using σ = 2 ms, based on the previous simulation results), and VS is computed after combining together all incoming AN spike trains. The population is heterogenous because RS and I_thr are varied for each cell in the population according to the distributions of these values reported by Miller et al. (1999). For a population of 50 model AN cells, for instance, a normal distribution with mean −5.31 dB and standard deviation 4.4 dB is partitioned into 50 regions with equal area and threshold values are defined by the midpoints of each region. RS values are then assigned to each model AN cell based on the relationship

$$\mathit{\text{RS}}=0.1*{0.2}^{\frac{I_{\mathit{\text{thr}}}+13}{23}}$$ (11)

which is estimated from the best fit line plotted in Fig. 6 of Miller et al. (1999). The neural threshold, I_thr, in Eq. (11) is expressed in units of dB relative to 1 mA.

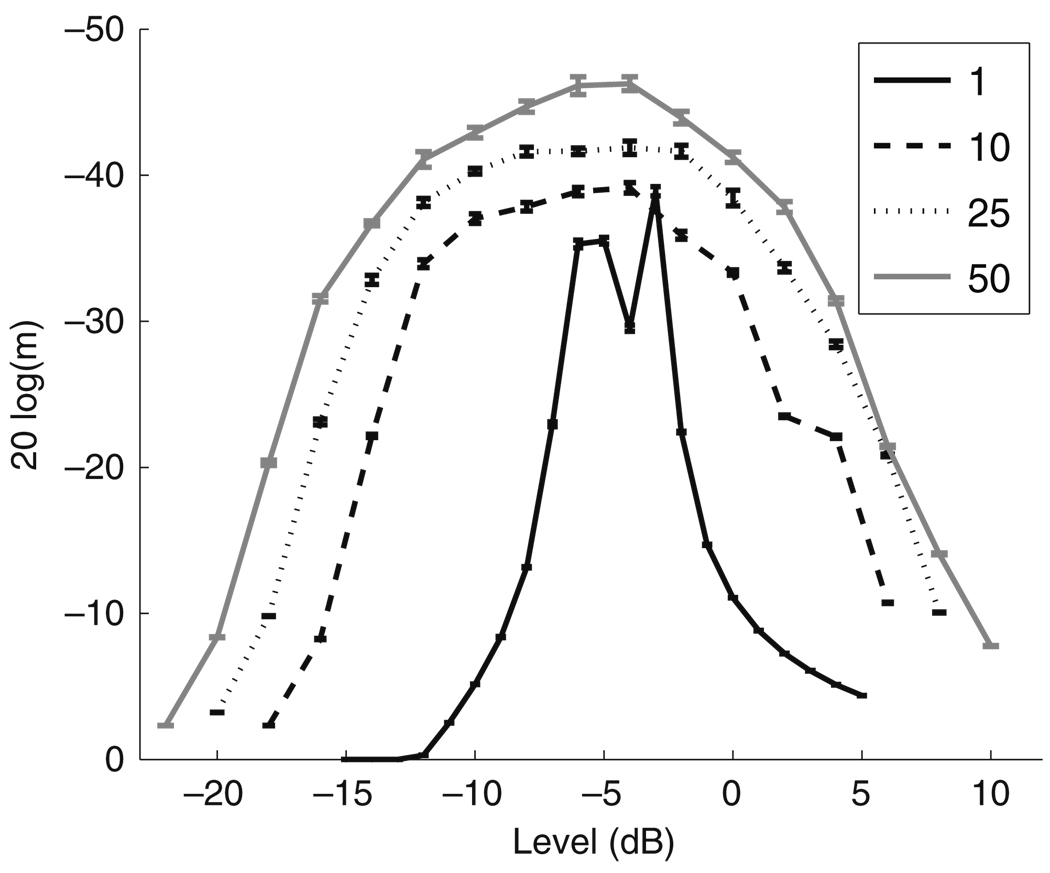
Simulation results are shown in Fig. 13. The decoder with a single AN input (black line) shows an improvement for a narrow range of Ī_stim near I_thr whereas the results for the populations of 10 (dashed line), 25 (dotted line), and 50 (gray line) AN cells show that, as population size increases, the decoder improves over a larger range of stimulus levels. We conclude that a decoder that computes VS based on the combined input of 50 jittered AN spike trains is sufficient to predict an improvement of MDTs over a range of stimulus levels that is broad enough to match typical values in CI users. Figure 13 also indicates that, in order for the computed MDTs to improve monotonically as in the psychophysical data, Ī_stim must be restricted to levels less than the mean neural threshold of the population.

Fig. 13.

MDTs as a function of stimulus level and varying the number of model AN cells that are used as inputs to the VS decoder. RS and I_thr are varied according to the distribution of data reported in Miller et al. (1999). A population of 50 model AN cells (gray line) is needed to produce MDTs that monotonically improve over a range of current levels of approximately 10 dB, consistent with typical dynamic ranges in CI users. MDTs are computed from the mean of 10 runs of the stochastic approximation algorithm and error bars represent the standard error of the mean

3.2.3 Pulse rate

The final AM detection experiment that we simulate tests the effects of varying carrier pulse rate. We test the performance of the VS decoder applied to the jittered (σ = 2 ms) spike trains of a heterogeneous population of 50 model AN cells at low (250 pps) and high (2,000 pps) carrier pulse rates. Figure 14(a) shows MDTs computed as a function of stimulus level. The VS decoder applied to the high pulse rate stimuli (black line) outperforms the decoder applied to the low carrier pulse rate stimuli (gray line) at all stimulus levels. This result is the opposite of what has been observed in psychophysical experiments (Galvin and Fu 2005, e.g.).

Fig. 14.

MDTs as a function of stimulus level for 250 pps pulse train (gray line) and 2,000 pps pulse train (black line) for the VS decoder applied to the jittered spike trains of 50 heterogeneous model AN cells. a Abscissa is current level (Ī_stim) measured in dB relative to 1 mA. b Abscissa is the average number of spikes evoked by the unmodulated stimulus. This provides a proxy for loudness that is used to balance stimulus levels at the two carrier pulse rates. In both cases, MDTs are smaller (better detection) for the high carrier pulse rate. MDTs are computed from the mean of 10 runs of the stochastic approximation algorithm and error bars represent the standard error of the mean

An important caveat in interpreting these results is that, for a fixed stimulus level, CI listeners can perceive stimuli to be louder when carrier pulse rate is increased. In order to compare MDTs measured at different carrier pulse rates, experimenters employ loudness balancing schemes whereby stimulus levels are decreased at high carrier pulse rates so that the perceived loudness of the unmodulated stimulus is held constant as carrier pulse rate is changed. AM detection degrades as stimulus level is decreased, so poor performance at high carrier pulse rates may be due, in part, to this stimulus level effect. Controlling for loudness in the model is difficult because loudness is a subjective measure and its relation to AN activity is not fully understood. The simplest model for loudness that has been used in past computational studies of electric hearing is to use the total number of spikes evoked by a stimulus as a measure of loudness (Bruce et al. 1999b). Figure 14(b) replots the results from Fig. 14(a), where the abscissa is now the total number of spikes evoked by the unmodulated stimulus. Stimulus levels for which the unmodulated stimulus evokes, on average, fewer than one spike are excluded. Using this spike count balancing scheme as a proxy for loudness balancing, we still find that the decoder has better AM sensitivity at the higher carrier pulse rate for all stimulus levels. Thus the stochastic AN model coupled with the VS decoding algorithm does not predict the experimental finding that AM detection is degraded at high carrier pulse rates.

4 Discussion

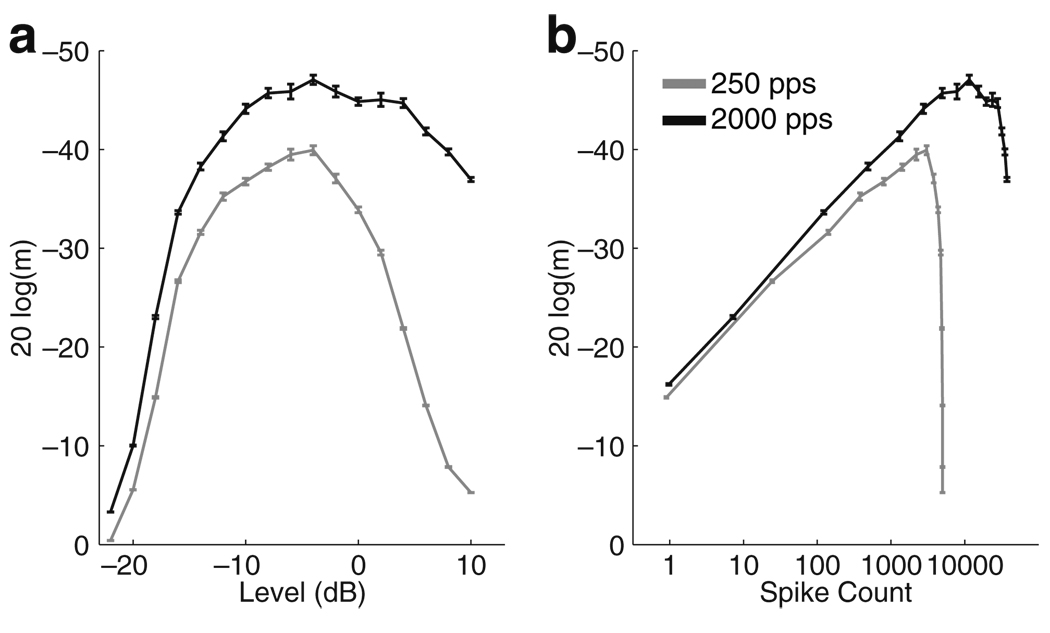
Figure 15 summarizes the results of the psychophysics simulations. Comparing these results to psychophysical data such as those shown in Fig. 3 shows that the AN model and decoding method qualitatively predict the dependence of MDTs on modulation frequency and stimulus level. In Fig. 15(a), the stimulus level is chosen so that the unmodulated stimulus elicits approximately 500 total spikes. Figure 15(b) is the same as Fig. 14(b) with one modification. The range of current levels is restricted so that a monotonic improvement in MDTs is seen, consistent with the psychophysical data. Under this assumption, the ranges of current levels are approximately 10 and 7 dB for the low and high carrier pulse rate stimuli, respectively.

Fig. 15.

Summary of predictions of the VS decoder (compare to Fig. 3). Average number of spikes elicited by unmodulated stimuli are used as a proxy for loudness. a MDTs as a function of f_m with stimulus level set so that 500 spikes are elicited by the unmodulated stimulus. This falls in the middle of the range of levels shown in b and therefore serves as a comfortable loud level. The decoder’s performance falls off at high modulation frequency, consistent with the performance of CI users. b MDTs as a function of spike count for 250 pps (gray line) and 2,000 pps (black line) carrier pulse rates. This figure replots Fig. 14(b) in order to emphasize the relation to psychophysical experiments. Stimulus levels for which the unmodulated pulse train does not elicit, on average, one spike are excluded because it is assumed that such levels would be below perceptual threshold. Maximum stimulus levels are set so that the curves are monotonically increasing, consistent with CI psychophysics data

In sum, the main findings of this study are:

1. Temporal properties of spike train responses carry a major component of the information that the AN encodes about amplitude-modulated CI stimulation, and vector strength provides a simple and close approximation to this information.

2. None of the four ideal observer methods predict modulation detection thresholds that decrease with modulation frequency and carrier pulse rate. The ideal observer results are not consistent, therefore, with observed trends in psychophysical data.

3. A decoder with imperfect temporal resolution produces results that are qualitatively similar to psychophysical data. In particular, a VS decoder applied to the jittered (2 ms standard deviation) spike train output of a heterogeneous population of 50 model AN cells predicts that AM sensitivity degrades for modulation frequency above 100 Hz and modulation detection improves with stimulus level, but the decoder does not predict the experimental finding that AM sensitivity is degraded at high carrier pulse rates.

These results, along with limitations of the AN model and directions for future work, are discussed in more detail below.

4.1 Analysis of encoding of amplitude-modulated stimuli

The first aim of this study was to analyze peripheral encoding of AM stimuli. We tested different sources of information in spike trains using an ideal observer analysis and found that the temporal pattern of spikes is more informative than the overall spike rate. We further probed the temporal features of AN spike trains by comparing the Poisson and VS measures to the all-information measure. The Poisson measure makes the assumption that the spike trains can be described by an inhomogeneous Poisson process. When MDTs computed using Poisson measure differed from the theoretical upper bound set by the all-information measure, we concluded that the temporal correlations in the spike train contribute to the encoding of amplitude modulation. Temporal correlations had a substantial impact at high stimulus levels, and therefore high firing rates, because refractory effects strongly affected spike timing in this region.

VS measures the strength of phase-locking of the simulated spike times to the period of modulation. MDTs computed with the all-information measure typically exceeded MDTs computed with the VS measure, but the differences were relatively small and there were similar qualitative trends between the two. These results indicate that the spike timing information that is present in the AN response to AM stimuli may be primarily represented by the strength of phase locking. Physiological evidence for the importance of phase locking in response to CI stimuli also comes from the study of Litvak et al. (2001) in which it was shown that there can be appreciable phase locking to CI stimuli with modulation depths as small as 1% and that phase locking increased with stimulus level.

At more central stages of auditory processing, temporal information could be either propagated directly or transformed into an alternate representation. For instance, Krishna and Semple (2000) have shown that many cells in the inferior colliculus appear to have firing rates tuned to a preferred frequency of modulation. Snyder et al. (2000) have shown similar response properties of inferior colliculus cells in response to cochlear implant stimulation. Dau et al. (1997) have theorized the presence of a modulation filterbank and other researchers have proposed a variety of neural circuits that could convert synchronized neural activity into a rate code (Hewitt and Meddis 1994; Langner 1997; Nelson and Carney 2004; Dicke et al. 2007), but the biological details of such circuitry remains to be fully identified. There is also evidence that temporal information can be preserved in the timing of spikes in auditory cortex. Middlebrooks (2008a) observed significant phase locking in the spike timing of cortical cells of guinea pigs in response to AM CI stimulation. The contribution of the present approach is that, by quantifying the information in the AN and comparing the performance of ideal observers with CI listeners, we have shown that phase locking captures much of the information in the neural response. This motivates future work that can seek to identify how phase locked neural activity is processed and propagated by the auditory system.

One unexpected finding from this model was that firing rate can depend on modulation depth. We identified two mechanisms in this model that produce a dependence of firing rate on modulation depth: the nonlinear firing efficiency curve and the effect of the refractory period to selectively suppress the contribution of high intensity pulses. Although AN firing rates do not appear to depend on modulation depth for acoustic stimuli (Joris and Yin 1992), to our knowledge there are no neurophysiological data that address this question for electric stimulation. Intriguingly, CI listeners typically report that modulated stimuli sound louder than unmodulated stimuli (Pfingst et al. 2007; Shannon 1992, e.g.). This may indicate that modulated electric stimuli can increase firing rates in the AN and therefore may indicate a fundamental difference between peripheral processing of modulated stimuli in normal and electric hearing.

4.2 Encoding properties of the auditory nerve model

The AN model used in this study was formulated by Bruce et al. (1999a, b). It is useful for modeling temporal encoding properties of the AN because it can be directly analyzed with point process methods. Two findings from this study are that, based on this model of the AN, the loss of AM sensitivity that is commonly seen at high modulation frequencies and at high carrier pulse rates is not attributable to specific properties of the AN. The validity of these findings is limited by the fidelity of the computational model. A major limitation of the current AN model is that it does not include pulse-to-pulse interactions that are most relevant at high carrier pulse rates. These include subthreshold integration of multiple pulses, active membrane kinetics and the increased variability in spike initiations (Miller et al. 2001) and spike rate adaptation (Litvak et al. 2001; Zhang et al. 2007) that have been observed in the responses of AN fibers in cats to high carrier pulse rate stimulation. It is possible to modify the Bruce model to include spike history dependent variability and spike rate adaption and a preliminary investigation found that including these effects would not substantially alter the conclusions of this study. In particular, neither effect appeared to alter the simulated AN responses in a way that would suggest that the loss of modulation sensitivity at high modulation frequencies and high carrier pulse rates is due to response properties of the AN model. More generally, the model could be extended by defining a conditional intensity function that is valid for a larger class of possible input stimuli and includes additional temporal dynamics using the generalized linear model framework (Paninski 2004; Truccolo et al. 2005). These models have desirable theoretical properties for fitting model parameters to a class of inputs, evaluating decoding properties of the model, and estimating information theoretic quantities (Paninski 2004). More sophisticated, biophysically-detailed computer models that use stochastic ion channel kinetics and Hodgkin-Huxley-like dynamics have been developed to model the AN response to CI stimulation (Imennov and Rubinstein 2009; Woo et al. 2009, e.g.). Future work can use these models to test the validity of the point process framework and to test which, if any, of the neural response properties are relevant to coding amplitude-modulated CI stimulation.

Another limitation in our modeling approach is that we have not included any description of the intracochlear electric field or spatial spread of excitation. Numerous computer models have been developed to analyze this problem (Briaire and Frijns 2000; Finley et al. 1990; Frijns et al. 1995; Rattay and Felix 2001; Rattay et al. 2001; Whiten 2006) and such models could be incorporated in future studies of AM stimulation. Spread of excitation may also be related to loudness levels. In order to compare MDTs computed for different carrier pulse rates we used the total number of spikes as a proxy for loudness. More elaborate models of loudness have been developed (McKay et al. 2001, e.g.) and could be included in future computational studies of AM detection.

4.3 Predictions of the decoding model

In Section 3.2, a decoder was constructed in an attempt to predict qualitative trends in psychophysical data. The decoder was constrained by the type of information encoded in the AN response and by the performance limitations of CI listeners. In order to predict the loss of modulation sensitivity at high f_m, we provided the decoder with jittered spike trains. This can be thought of as a simple method to quantify how temporal information is lost as AN spike trains are propagated forward along the auditory pathway. The method of jittering spike trains and applying a VS decoder is not the only way to degrade the temporal resolution. For instance, a Poisson decoder applied to jittered spike trains may predict a similar loss of modulation sensitivity at high modulation frequencies. We emphasize, however, that including jitter and decoding with VS was motivated by our goal of developing a computational method that relates simulated AN spike trains to performance on the AM detection task. The random jitter is not meant to represent explicitly any central stages of neural processing.

Nonetheless, there are physiological data to support the interpretation that temporal information is lost at more central stages of the auditory system. For instance, the upper limit of modulation frequencies to which neurons can phase lock progressively decreases at each stage of the auditory pathway (Joris et al. 2004). The model makes a quantitative prediction in terms of the amount of jitter needed to replicate the loss of AM sensitivity at high modulation frequencies. We found that the temporal resolution of a putative central decoder is on the order of a few milliseconds. This time scale for the temporal resolution of the decoder is consistent with the time constant assumed in the multiple looks theory of temporal integration (approximately 3 ms) (Donaldson et al. 1997; Viemeister and Wakefield 1991).

Based on the results of the encoding properties of the model AN and the relative simplicity of computing the VS measure, a VS decoder proved a natural framework to simulate AM detection. The VS decoder is also attractive because, as mentioned above, Middlebrooks (2008a, b) has shown that VS may be present and useful for modulation detection at the level of the auditory cortex. There are some drawbacks to using the VS decoder. It is unknown if the auditory system can compute VS since an ideal observer using VS to perform the detection task must have prior knowledge of the modulation frequency. A more realistic decoding model would assume the observer is performing the detection task based on some prior assumption about the distribution of possible stimuli. The VS decoder is relatively simple to implement, however, because it only requires prior knowledge of modulation frequency. The Poisson and spike count measures depend on estimations of the instantaneous firing rate and spike count distributions, respectively, both of which can change with modulation depth as well as modulation frequency. It is important to note that the limitations in the AN model, as discussed in Section 4.2, influence the performance of the decoder so future work should investigate the sensitivity of the read-out method to the properties of the AN input.

The one trend that our decoding method did not reproduce is that modulation detection is degraded at high carrier pulse rates. One possible reason for this shortcoming is that Bruce and colleagues developed their model based on responses to single pulses (Bruce et al. 1999c) and pulse trains with carrier rates less than 800 pps (Bruce et al. 1999a). The model does not characterize response properties at high carrier pulse rates. To test this, we conducted a preliminary investigation that included two dynamical effects that have been observed in the responses of cat AN fibers to high rate stimulation. Simple modifications to account for spike history dependent relative spread (Miller et al. 2001) and spike rate adaptation (Zhang et al. 2007) do not appear to substantially change the conclusions of our analysis. Further work is needed, however, to comprehensively study the neural response to high carrier rate pulse trains. Another potential cause of the discrepancy between the decoder predictions and psychophysical data is the presence of loudness cues in modulation detection tasks. McKay and Henshall (2010) have shown that for carrier pulse rates below 8 kpps loudness increases with modulation depth, especially at high current levels. They argue that these loudness cues, as opposed to temporal cues due to the pattern of modulation, may account for differences in modulation detection at low and high carrier pulse rate. Future work could seek to test this prediction by devising decoding methods that could include loudness cues.

Finally, we note that our approach in this study has been limited to investigating qualitative trends in psychophysical data. Ideally, one would like to construct computational models that accurately predict psychophysical data for individual CI listeners. This is a difficult task because there is great variability in MDTs recorded for different CI subjects. Moreover, MDTs can vary within a single subject depending on the place of stimulation (Pfingst et al. 2008). Cohen (2009a, b, c, d, e) has recently presented a technique for fitting parameters in the Bruce model to individual patients using a combination of psychophysical, electrophysiological, radiological, and modeling methods. Future work could seek to combine the analysis presented in this paper with patient-specific models to investigate how inter- and intra-subject factors (such as etiology, electrode position, degeneration of the AN cells) affects AM encoding and detection. This model-based approach can be a useful tool for formulating and evaluating hypotheses regarding how to improve the transmission of temporal information in CI speech processing strategies.

Appendix: Stochastic approximation algorithm

For a given trial at a given modulation depth (m), the correct discrimination is made if R(0, m) > 1, where R(0, m) is the likelihood ratio defined in Eq. (7). In order to compute MDTs from the model, define the binary random variable

$$X(m)=\mathbf{\{}\begin{array}{c}1\text{if}R(0,m)>1\hfill \\ 0\text{else}\hfill \end{array}.$$ (12)

Then the MDT is defined as the smallest value of m for which E[X(m)] = 0.794. Since X(m) is a random variable, the problem can be solved with a stochastic approximation method (Robbins and Monro 1951). We use an adaptive stochastic approximation algorithm that accelerates the convergence of the algorithm (Kesten 1958; Faes et al. 2007).

In most cases we initialize the algorithm with a value that is relatively far from the MDT (m₀ = 0.5) and use a large step size (Δm = 0.5). Occasionally other initial values and step sizes are needed if there are multiple modulation depths that produce E[X(m)] = 0.794. After each trial, the algorithm updates m_k according to the equation:

$$m_{k+1}=m_k-\frac{\mathrm{\text{Δ}}m}{n_{\mathit{\text{reverse}}}+1}[X(m_k)-0.794].$$ (13)

where n_reverse is the number of times the algorithm has reversed (i.e. the number of times that X(m_k−1) = 0 and X(m_k) = 1, or vice versa). m_k is restricted to the interval [0, 1] for all k.

The stochastic approximation algorithm has the useful theoretical property that the sequence {m_k} is guaranteed to converge in probability to the MDT (Robbins and Monro 1951; Kesten 1958). Faes et al. (2007) have suggested that it may be a suitable alternative to traditional up-down staircase methods used for threshold estimation because of its more accurate convergence properties. In this study, we did not investigate the small sample size convergence properties of the algorithm, rather we used a large number of iterations (2,000) so that we could be confident that the algorithm had nearly converged. To further test for error in this approximation, we repeated this procedure to obtain ten estimates of the MDT. We defined the MDT to be the mean of these ten estimates. The error bars in all plots of MDTs represent the standard error of the mean.