Quantifying Fluid Shear Stress in a Rocking Culture Dish

Abstract

Fluid shear stress (FSS) is an important stimulus for cell functions. Compared with the well established parallel-plate and cone-and-plate systems, a rocking “see-saw” system offers some advantages such as easy operation, low cost and high throughput. However, the FSS spatiotemporal pattern in the system has not been quantified. In the present study, we developed a lubrication-based model to analyze the FSS distributions in a rocking rectangular culture dish. We identified an important parameter (the critical flip angle) that controls the FSS behaviors in the dish and suggested the right conditions to achieving temporally oscillating and spatially relatively uniform FSS. If the maximal rocking angle is kept smaller than the critical flip angle, which is defined as the angle when the fluid free surface intersects the outer edge of the dish, the dish bottom remains covered with a thin layer culture medium and the spatial variations of the peak FSS within the central 84% and 50% dish bottom is limited to 41% and 17%, respectively. The magnitude of FSS was found to be proportional to fluid viscosity and maximal rocking angle, and inversely proportional to the square of fluid depth-to-length ratio and rocking period. For a commercial rectangular dish (length of 37.6mm) filled with ~2 mL culture medium, the FSS at the center of the dish bottom is expected to be on the order of 0.9 dyn/cm² when the dish is rocked ±5° at 1 cycle per sec. Our analysis suggests that a rocking “see-saw” system, if controlled well, can be used as an alternative method to provide low-magnitude, dynamic FSS to cultured cells.

Introduction

Fluid shear stress (FSS) plays an important role in modulating functions of many types of cells (Weinbaum et al. 1994; Davies 1995; Kreke et al. 2005; Yamamoto et al. 2005) and several laboratory systems have been developed to apply FSS to cells (Brown 2000). FSS induces both short-term and long-term biochemical responses on cells including (but not limited to) endothelial cells (Davies 1995), bone cells (Weinbaum et al. 1994), and stem cells (Kreke et al. 2005; Yamamoto et al. 2005). To study cellular responses to FSS, several shearing systems have been developed to apply well-defined FSS to cultured cells (see an excellent review, Brown 2000). Besides the two commonly used fluid shear systems, the parallel plate flow chamber system (Levesque et al. 1985; Reich et al. 1990; Hung et al. 1995; Ajubi et al. 1996; Mohtai et al. 1996; Jacobs et al. 1998) and the cone-and-plate system (Dewey 1984; Frangos et al. 1988), more specialized systems were also developed to introduce high temporal gradients of FSS (LaPlaca et al. 1997), spatial gradients of FSS (Tardy et al. 1997), combination of stretch and FSS (Owan et al. 1997), combination of FSS and normal stress (Ohata et al. 1997), and an oscillating orbital shaker system (Hubbe 1981; Pearce et al. 1996). As pointed out in Brown (2000), FSS in these specialized systems remains less well quantified.

In the present study, we aim to quantify the FSS in a rocking “see-saw” system, where multiple culture dishes can be placed on a platform that rocks up and down in the vertical plane. Unlike the most common systems, this simple rocking scheme uses regular culture dishes, does not need special chambers or involves moving parts close to the cells. The system is easier and cheaper to operate, and has higher outputs with multiple experiments running simultaneously. Since a smaller amount of culture medium (~2–3 mL for a regular culture dish) is used, it can save expensive reagents added to the medium to treat the cells and it also avoids dilution of biofactors released by the cells during FSS for better analysis and detection. When the rocking system is sterilized and used inside an incubator, the duration of uninterrupted FSS experiments can last as long as the culture medium sustains the cellular needs, which is usually 2 to 3 days. However, the FSS pattern in a rocking dish is apparently complex and spatially heterogeneous. The goal of this study was, therefore, to develop a mathematical model to quantify the spatiotemporal pattern of the FSS in the system. We first identified an important operating parameter, the critical flip angle, which dictates the overall FSS patterns. We then suggested some guidance of fining-tuning the system to meet specific needs. Our analysis suggested that a rocking “see-saw” system, if with well controlled parameters, can be used as an alternative method to provide low-magnitude, dynamic FSS to cultured cells.

Methods

Model Descriptions

In this model, a rectangular culture dish with seeded cells on the bottom is placed on a platform that flips up and down in the vertical plane at small angles around a horizontal rotation axis. A side view of the rocking dish of length L and width b with a depth of h₀ of culture medium was shown in Fig. 1, where the entire dish rotates in the vertical plane (x-z) along a pivotal point (O). The rocking angle θ is assumed to be a sinusoidal function of time with a maximal flip angle θ_max and a time period of T for a cycle.

Fig. 1.

Mathematical model of a rocking system. (A) The side view of a culture dish of length L and width b that contains culture medium of depth of h₀ rocks up and down sinusoidally in the vertical plane (xz) along the pivotal point O. The critical flip angle (θ₀) is defined when the fluid free surface contacts the outer edge P of the dish bottom. Depending the maximal flip angle θ_max, there are two cases considered. (B) If θ_max ≤ θ₀, the entire dish bottom is covered by the medium and a finite fluid depth z_e occurs at the outer edge of the dish; (C) If θ_max > θ₀, some peripheral region of the dish bottom including points O and P may be exposed to air during the rocking. The fluid free surface makes a contact with the dish bottom at the location of x_e. For both cases and at an arbitrary location x, the fluid height h_f at the vertical cross-section (dashed line) and the fluid volume V_f located on the right side of the cross-section can be estimated from purely geometric considerations, assuming a horizontal free fluid surface.

$$\theta ={\theta }_{max}sin\frac{2\pi t}{T}$$ (1)

The following assumptions are also made to simplify the problem. Firstly, the fluid flow in the culture dish is mainly driven by gravity, and the fluid free surface is assumed to remain horizontal during rocking. This assumption is reasonable when the gravity effect is much stronger than the viscous effect. This assumption requires relatively low rocking speed and small fluid viscosity (detailed analysis is included in the Discussion). Secondly, the centrifugal force acting on the fluid during rotation is neglected, due to the slow angular speed and low acceleration. Thirdly, because the fluid depth h₀ is usually much smaller than the dish length L and width b, lubrication approximation is applicable, where the velocity component normal to the dish bottom as well as the pressure gradient along the fluid depth are neglected (Lister 1992). The effect of the vertical walls on the flow is also neglected due to the thin fluid layer (L > 10h₀).

Velocity Profile and FSS

A Cartesian coordinate system is created with x axis along the dish bottom, z axis along the dish side wall, and the origin (O) located at the rotation center (Fig. 1). Due to the cyclic nature of rocking dish, only the first ¼ cycle is presented here. As the dish bottom flips counter-clockwise from the horizontal position (θ = 0) towards θ_max, fluid moves from the right side of the dish to the left side. Recall that the ratio of the fluid depth to the dish length (δ = h₀/L) is small. A critical flip angle (θ₀ = arctan(2δ) ≈ 2δ) is defined as the angle when the fluid free surface makes contact with the dish bottom exactly at the right-bottom corner (P) (Fig. 1A).

Depending on the relative values of θ_max and θ₀, two possible scenarios may occur: (1) if θ_max ≤ θ₀, the entire dish bottom is always covered by the medium and a finite fluid depth z_e occurs at the outer edge of the dish (Fig. 1B); (2) if θ_max > θ₀, some peripheral region of the dish bottom including points O and P may be exposed to air when the flipping angle θ is larger than θ_0; and the fluid free surface makes a contact with the dish bottom at the location of x_e (Fig. 1C). In both cases, for an arbitrary location x, the fluid height h_f at the vertical cross-section (dashed lines in Fig. 1) and the fluid volume V_f located on the right side of the cross-section are estimated from dish geometry, based on the assumption of the fluid free surface always remaining horizontal, as follows:

$$h_f=\{\begin{array}{ll}{h}_0+(L/2-x)tan\theta ,\hfill & \theta \le {\theta }_0\hfill \\ \sqrt{2h_{0}Ltan\theta }-xtan\theta ,\hfill & \theta >{\theta }_0\hfill \end{array}$$ (2)

$$V_f=\{\begin{array}{ll}b\left(h_0-\frac{x}{2}tan\theta \right)(L-x),\hfill & \theta \le {\theta }_0\hfill \\ {bh}_{0}L{\left(1-\frac{x}{\sqrt{2h_{0}Lcot\theta }}\right)}^2,\hfill & \theta >{\theta }_0\hfill \end{array}$$ (3)

where b is the width of the rocking dish, h₀ is the initial fluid depth, L is the length of the dish, x is the location considered (0<x<L), θ is the rocking angle, and θ₀ is the critical flip angle.

Recall that the rocking angle is a time varying function (Eq. 1). The fluid flux q across the vertical plane at x is thus obtained by taking the time derivative of V_f (Eq. 3) and found to be as follows:

$$q=-\frac{\partial V_f}{\partial t}=\{\begin{array}{ll}\frac{\pi {\theta }_{max}bx(L-x)}{T{cos}^2\theta }cos\frac{2\pi t}{T},\hfill & \theta \le {\theta }_0\hfill \\ \frac{\pi {\theta }_{max}bx\left(\sqrt{2h_{0}Lcot\theta }-x\right)}{T{cos}^2\theta }cos\frac{2\pi t}{T},\hfill & \theta >{\theta }_0\hfill \end{array}$$ (4)

Based on lubrication approximation (Lister 1992) as well as the non-slip boundary condition at the bottom of the dish and zero velocity gradient at the fluid free surface, the velocity profile on this vertical cross-section at location x is obtained as follows:

$$u=\frac{3q}{2{bh}_f^3}z\left(2h_f-z\right)$$ (5)

Therefore, the wall shear stress at the bottom of the rocking dish can be determined as the following:

$$\mid {\tau }_w\mid ={\mu \frac{\partial u}{\partial z}|}_{z=0}=\{\begin{array}{ll}\frac{3\pi \mu {\theta }_{max}x(L-x)}{T{[h_{0}cot\theta +L/2-x]}^2{sin}^2\theta }cos\frac{2\pi t}{T},\hfill & \theta \le {\theta }_0\hfill \\ \frac{3\pi \mu {\theta }_{max}x}{T\left(\sqrt{2h_{0}Lcot\theta }-x\right){sin}^2\theta }cos\frac{2\pi t}{T},\hfill & \theta >{\theta }_0\hfill \end{array}$$ (6)

Normalized FSS field

Dimensionless variables are introduced as follows:

$$x^{\ast }=\frac{x}{L},{\theta }^{\ast }=\frac{\theta }{{\theta }_0}$$ (7)

The characteristic shear stress is defined as the shear stress at the center of dish bottom when the dish is horizontal (θ = 0, x = 0.5L)

$$\mid {\stackrel{\sim }{\tau }}_w\mid =\frac{3\pi \mu {\theta }_{max}}{4{\delta }^{2}T}$$ (8)

Because the rocking angle is usually small, (cot(θ) ≈ θ⁻¹ and sin(θ) ≈ θ), we obtain the normalized shear stress, relative to the characteristic shear stress, as a function of x^*, θ^* and θ_max^* (i.e., θ_max/θ₀).

$$\mid {\tau }_w^{\ast }\mid =\frac{\mid {\tau }_w\mid }{\mid {\stackrel{\sim }{\tau }}_w\mid }=\{\begin{array}{ll}\frac{x^{\ast }\left(1-x^{\ast }\right)\sqrt{1-{\theta }^{\ast 2}/{\theta }_{max}^{\ast 2}}}{{\left[0.5+{\theta }^{\ast }\left(0.5-x^{\ast }\right)\right]}^2},\hfill & {\theta }^{\ast }\le 1\hfill \\ \frac{x^{\ast }\sqrt{1-{\theta }^{\ast 2}/{\theta }_{max}^{\ast 2}}}{{\theta }^{\ast 2}\left({\theta }^{\ast -0.5}-x^{\ast }\right)},\hfill & {\theta }^{\ast }>1\hfill \end{array}$$ (9)

FSS in two typical rocking configurations

Two typical rocking schemes are analyzed, according to the two scenarios illustrated in Fig. 1B (θ_max ≤ θ₀) and Fig. 1C (θ_max > θ₀). A single well in a commercial available 8-well rectangular dish (Thermal Fisher Scientific, Nunc, 8-Well rectangular dish, Cat#267062) with dimensions of 37.6×27.9 mm (L×b) is modeled here containing 1.86 mL culture medium. The initial fluid depth h₀ is 1.77 mm and the critical flip angle θ₀ is 5.4°. The rocking period T is set to be 1 sec. The maximum rocking θ_max is chosen to be either 5° or 10°, i.e, the dimensionless maximum angle θ_max^* is either 0.92, or 1.85. The viscosity of fluid μ is set to be 10⁻³ Pa.s.

Results

The characteristic shear stress, for the center of the dish bottom at the horizontal position, is found to be proportional to fluid viscosity and maximum rocking angle, and is inversely proportional to square of fluid depth-to-length ratio and rocking period (Eq. 8). For the two specific experimental setups described above (i.e., 37.6×27.9 mm dish, 1.86 mL culture medium, ±5° or ±10° flip angles, and 1 cycle per sec), the characteristic shear stress is 0.9, and 1.8 dyn/cm², respectively.

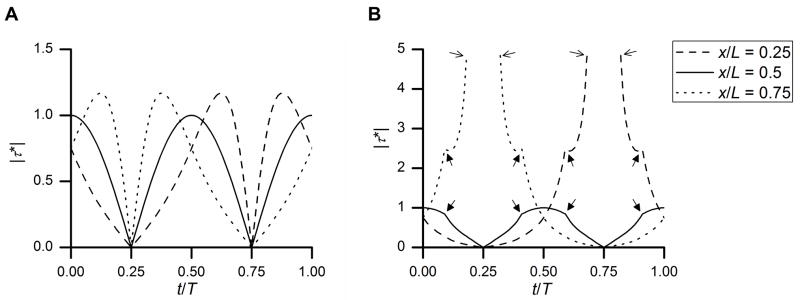
The temporal profiles of the normalized shear stress (relative to the characteristic shear stress) demonstrate an oscillating but spatially non-uniform pattern (Fig. 2). The time course of the FSS for three equally spaced locations (x^* = 0.25, 0.5, 0.75) is shown during one period of rocking (t = 0 to T) (Fig. 2). In the first case (θ_max^*≤1, Fig. 2A), the entire dish bottom remains covered by fluid during rocking and the FSS varies smoothly in time and space without any singularity. The normalized FSS varies from 0 to 1 at the center of the dish bottom (x^* = 0.5), while that at the other two locations (x^* = 0.25, 0.75) varies from 0 to 1.17 (Fig. 2A). The peak FSS and the temporal gradient of the FSS differ among the three locations examined. The locations of x^* = 0.25, 0.75, due to their symmetry to the center of dish and the “see-saw” effect, show almost identical FSS patterns except for a 180 degree (i.e., half cycle, T/2) of phase difference (Fig. 2A). In the second case (θ_max^*>1, Fig. 2B), the dish bottom is partially exposed to air after the rocking angle exceeds the critical flip angle and discontinuity of FSS occurs at the air-liquid contact regions. Although the center of the dish, which is always covered with liquid, still has oscillating FSS from 0 to 1, the other two locations exhibit FSS singularity (approaching to infinite) as they are exposed to air (Fig. 2B). The temporal gradients of the FSS exhibit large variations among the three locations and also during the rocking cycle, due to the presence of discontinuity at the critical flip angle (solid arrows) as well as the singularity at the fluid-air contact points (thin arrows) (Fig. 2B).

Fig. 2.

Oscillating but spatially non-uniform FSS, which is normalized with the characteristic FSS at the center of the dish bottom and at the horizontal rocking angle, is plotted for three equally spaced locations (x* = 0.25, 0.50, 0.75) during one rocking cycle. (A) In the case of θ_max^* = 0.92, the entire bottom of the dish remains covered with fluid. FSS varies temporally and spatially. No singularity occurs. (B) In the case of maximum angle θ_max^* = 1.85, the fluid free surface becomes in contact with the dish bottom during the rocking, introducing discontinuity of FSS at the critical angle (θ^* =1, indicated with solid arrows) and singularity of FSS when the locations of x* = 0.25, and 0.75 are exposed with air (indicated with thin arrows) during rocking. The temporal gradients of the FSS exhibit large variations in the second case.

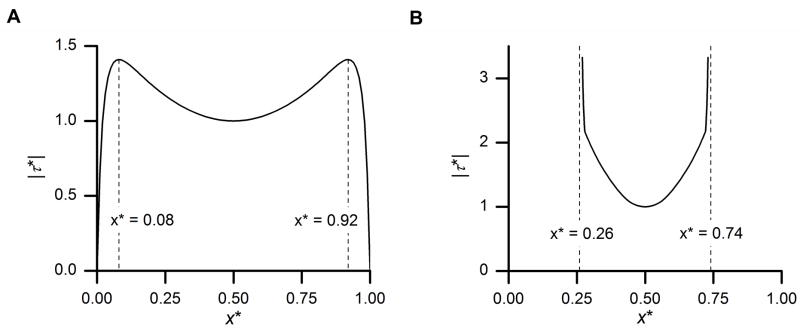
The magnitude of peak FSS is symmetric along the center of the dish (x^* =0.50) and the spatial variation of the peak FSS is highly sensitive to the maximal rocking angle (Fig. 3). For the first case (θ_max^* ≤ 1), we found that, based on Eq. 9, the normalized FSS peaks with a value of 1 at x^* = 0.5 if θ_max < 0.707, and peaks with a value of ${\left(2{\theta }_{max}^{\ast }\sqrt{1-{\theta }_{max}^{\ast 2}}\right)}^{-1}$ at two locations $x^{\ast }=0.5\pm 0.5\sqrt{2{\theta }_{max}^{\ast 2}-1}$ if 0.707 < θ_max^* < 1. Therefore, for the case of 0.707 < θ_max^* < 1, the region between the two peaks has a width of $\sqrt{2{\theta }_{max}^{\ast 2}-1}$ with the corresponding FSS variation of ${\left(2{\theta }_{max}^2\sqrt{1-{\theta }_{max}^{\ast 2}}\right)}^{-1}-1$. For the case of θ_max^* = 0.92, the normalized FSS peaks with a value of 1 at two locations (x^* = 0.08 and 0.92) and remains zero at the edges of the dish (x^* = 0 and 1). The peak FSS at the central region (x^* =0.25 to 0.75) shows relatively small variations (<17%) (Fig. 3A). In contrast, for the second case (θ_max^* = 1.85), large variations (> 200%) of FSS are shown for the central region of the dish (x^* =0.25 to 0.75) and singularity occurs at x^*=0.74 and 0.26 (Fig. 3B).

Fig. 3.

Normalized peak FSS shows spatial symmetry relative to the dish center and its variation is highly sensitive to the maximal rocking angle θ_max^*. (A) In the case of θ_max^* = 0.92, the variation of FSS is 17% for the central 50% region (x^* = 0.25 to 0.75) and 41% for the majority (84%) of the dish bottom (x^* = 0.08 to 0.92); (B) In the case of θ_max^* = 1.85, singularity occurs and large variations (> 200%) of FSS for the central region (x^* = 0.25 to 0.75). Note: different scales are used in the two panels.

Discussion

Using a simple lubrication-based model, we demonstrate that dynamic oscillating FSS can be applied to cultured cells by simply rocking the culture dish up and down in the vertical plane. Although the peak FSS is non-uniform within the dish, relatively small variations (~20%) of the FSS can be achieved if the rocking conditions are well controlled (Fig. 3). In addition, the magnitude of FSS can be easily modulated by adjusting the flip angle, the rocking period (T) or frequency, viscosity and volume of the culture medium, as well as the dimensions of the dish (Eq. 8 and 9). Compared with other commonly used FSS systems, the rocking dish system provides advantages such as i) using smaller amount of culture medium and saving treatment cost, ii) simplifying operation and allowing up to several days shearing experiments in an incubator setting, and iii) high throughput.

One critical requirement for using the rocking system is that the maximal rocking angle should be smaller than the critical flip angle, so that the dish bottom remains covered by a thin layer of culture medium all the time (Figs. 2A and 3A). The situation of the dish bottom being exposed to air (Figs. 2B and 3B) should be avoided based on biological considerations as well as controlling the FSS. At the air-dish bottom contact point, FSS singularity happens in our model due to the finite velocity and zero depth of fluid (Huh et al. 1971). Because fluid surface is expected to be curved and slip effect would be significant near the contact point, the actual FSS should be finite, but is difficult to estimate using the current model. Thus we recommend avoiding the FSS singularity during rocking.

There are several parameters that can be fine-tuned to increase the FSS level. One can choose the maximal rocking angle close to the critical flip angle (θ₀ = arctan(2δ) ≈ 2δ, δ = h₀/L). In this case, the characteristic FSS at the dish center can be rewritten from Eq. 8 as

$$\mid {\stackrel{\sim }{\tau }}_w\mid =\frac{3\pi \mu L}{2h_{0}T},$$ (Eq. 10)

One can adjust the FSS level by customizing the culture dish dimensions (L), adjusting the filled fluid volume and thus thickness (h₀), rocking period (T), or viscosity of the medium. For example, compared with the case of the 8-well dish (L = 37.6 mm) analyzed above, the characteristic FSS is expected to increase by 2.1- and 3.2-fold for the 4- or 1-well rectangular dishes (Thermal Fisher Scientific, Nunc, Cat#267061, #267060) with longer length (L = 78 and 121.4 mm, respectively), assuming that all the dishes are covered with fluid of the same thickness and rocked with the same frequency (1 cycle/sec) at their corresponding critical flip angles. We recognize that the room for these adjustments may be limited in practice and the range of FSS achieved may be limited to relatively low levels.

Dynamic FSS stimulation can be achieved using the rocking system. As we demonstrated for one commercial product (Nunc, 8-well rectangular dish, Cat#267062, 37.6×27.9 mm dish), with a culture medium of 1.86 mL, rocking up and down ±5° every 1 sec per cycle, a small FSS at the level of 0.9 dyn/cm² can be achieved. FSS varies from 0.9 to 1.1 dyn/cm² within the central 50% region (x^* = 0.25, 0.75) and varies from 0.9 to 1.3 dyn/cm² for the majority (84%) of the dish (x^* = 0.08, 0.92) (Fig. 3A). Unlike the flow chamber and the plate-and-cone systems that introduce spatially uniform FSS to cells, the rocking system produces spatially non-uniform FSS along the dish bottom (Fig. 3), and the temporal gradients of FSS also varies as shown in Fig. 2. The influences of the FSS magnitude and spatiotemporal variations on cellular responses are not clear in the literature. Although the normal physiological ranges of FSS for endothelial cells and bone cells are relatively clear (on the order of 20 dyn/cm², Davies 1995, Weinbaum et al. 1994), the FSS experienced by cells in other tissues such as cartilage, ligaments, or bone marrow is largely unknown. However, reduced FSS magnitudes are expected in these tissues due to the absence of significant flows. We believe that the rocking system would be suitable to investigate whether and how cells respond to FSS with low magnitude (on the order of 1 dyn/cm²) and spatiotemporal variations. We are currently studying the interaction between hypoxia challenge and FSS stimulation in vitro, for which the rocking system appears to be the only practical option (Liu 2009). We did observe a consistent recovery of the hypoxia-induced damage in cementoblasts cultured in the rocking system, suggesting that the cells responded to the low magnitude FSS (Liu 2009).

One main assumption in the model is that the fluid free surface remains horizontal all the time, which is valid only if gravity can produce enough fluid flux (i.e. the flux in Eq.4) with a small change in the slope of the fluid surface. The flux produced by gravity was derived from the Navier-Stoke equation in Lister (1992) as follows:

$$q^{(g)}=\frac{\rho gb{h}_f^3}{3\mu }\mathrm{\Delta }\theta ,$$ (Eq. 11)

where Δθ is the slope of fluid surface. In order to satisfy the requirement that the gravity-driven flux equal the flux in the rocking system (q^(g) = q), the local change of fluid surface slope can be estimated:

$$\frac{\mathrm{\Delta }\theta }{{\theta }_0}=\mathrm{\Phi }\frac{x^{\ast }\left(1-x^{\ast }\right)\sqrt{1-{\theta }^{\ast 2}/{\theta }_{max}^{\ast 2}}}{2{\left[0.5+\left(0.5-x^{\ast }\right){\theta }^{\ast }\right]}^3},{\theta }^{\ast }\le 1$$ (Eq. 12)

where $\mathrm{\Phi }=\frac{3\pi \mu L^3{\theta }_{max}}{8\rho g{h}_0^{4}T}$ is a dimensionless number which can be determined with experimental parameters. In our recommended experimental setup (θ^*_max ≃1), Δθ/θ₀ is at the same order as Φ. If Φ is reasonably small (<1), we can conclude that the gravity effect is strong enough so that the horizontal fluid surface approximation is valid. For the first experiment setup whereθ^*_max = 0.92, Φ = 0.17, so the horizontal surface approximation is reasonable. In addition, turbulence and waves near the fluid surface should also be minimized in order to use our model. Adopting a sinusoidal rocking pattern may significantly reduce the impact force, and thus is strongly recommended.

The wall FSS at the bottom of a circular culture dish placed in a rocking platform was also analyzed using the same approach described above. Because the cross-sectional area for the fluid flux is varying spatially along the dish bottom, the characteristic FSS in the circular dish is typical smaller than that in a rectangular dish, assuming the same critical flip angle and flipping parameters (i.e., maximal rocking angle and rocking period). However, the spatial distribution of the FSS for the circular dish is very similar to that of the rectangular dish. The detailed analysis for the circular rocking dish and the comparison between the circular and rectangular dishes are presented in the Supplemental Material, which is published online in the journal website. As a practical guidance, the commonly used circular dish with a diameter of 35 mm, if filled with 1.5, 2, or 3 mL culture medium, and rocked up and down at 1 cycle/sec to the critical flip angle, a dynamic FSS at the level of 0.70, 0.53, or 0.35 dyn/cm² can be achieved at the center of the dish bottom.

In summary, the present study quantitatively analyzes the spatiotemporal patterns of wall FSS in a rocking “see-saw” system. By adjusting the system setups such as fluid depth, flip angle, rocking speed, and dish dimensions, the rocking system can be used as an alternative method to provide low-magnitude (~ 1 dyn/cm²) and oscillating FSS stimuli to cultured cells. It is particular useful for high throughput shearing experiments (shearing multiple dishes).