Estimation of Cell Proliferation Dynamics Using CFSE Data

Abstract

Advances in fluorescent labeling of cells as measured by flow cytometry have allowed for quantitative studies of proliferating populations of cells. The investigations (Luzyanina et al. in J. Math. Biol. 54:57–89, 2007; J. Math. Biol., 2009; Theor. Biol. Med. Model. 4:1–26, 2007) contain a mathematical model with fluorescence intensity as a structure variable to describe the evolution in time of proliferating cells labeled by carboxyfluorescein succinimidyl ester (CFSE). Here, this model and several extensions/modifications are discussed. Suggestions for improvements are presented and analyzed with respect to statistical significance for better agreement between model solutions and experimental data. These investigations suggest that the new decay/label loss and time dependent effective proliferation and death rates do indeed provide improved fits of the model to data. Statistical models for the observed variability/noise in the data are discussed with implications for uncertainty quantification. The resulting new cell dynamics model should prove useful in proliferation assay tracking and modeling, with numerous applications in the biomedical sciences.

1. Introduction

Much progress in the quantification of cell population dynamics has been made in the last several years. Such improvements have allowed for the application of these methods to the investigation of questions in the life sciences in which proliferation plays a key role. For example, accurate quantification of changes in the rates at which various lymphocytes divide, differentiate and die can be used as a marker for changes in an immune response. Thus, better understanding of cell proliferation can lead to improvements in treatment for disease (such as cancer, HIV, and other viruses, etc.) progression. In the past several decades, proliferative assays have been carried out through incorporation of 5-Bromo-2′-deoxyuridine (BrdU) or tritiated thymine deoxyriboside (3HTdr) (Lyons and Doherty, 2004), both of which take the place of thymidine in the DNA of dividing cells, the latter of which is radioactive. In comparison to these two, carboxyfluorescein succinimidyl ester (CFSE) is more stably and evenly incorporated into cells, is detected easily by flow cytometry, and is nonradioactive (Bonhoeffer et al., 2000; Lyons and Doherty, 2004; Quah et al., 2007). It is not surprising then that CFSE has become the de facto staining method for many cell labeling studies (Hawkins et al., 2007; Lyons, 1999; Quah et al., 2007). The development of CFSE-based cytometry assays (Lyons and Parish, 1994) in conjunction with a Fluorescence-Activated Cell Sorter (FACS) provides biologists with the ability to measure some of these fundamental properties of a population of cells quickly and efficiently. However, there may be distinct benefits to be gained from alternative modeling approaches. To that end, the development of models of the type discussed in this work can contribute to the quantitative understanding of cellular behavior as represented by FACS data.

CFSE is introduced into a population of cells as (membrane permeable) carboxyfluorescein diacetate succinimidyl ester (CFDA-SE). After CFDA-SE diffuses across the cell membrane, enzyme reactions with cellular esterases cleave the acetate groups, resulting in highly fluorescent and membrane impermeable CFSE. At reasonable concentrations and near neutral pH, the incorporation of CFSE does not in any way adversely affect the function of the cell. As cells divide, the CFSE fluorescence intensity (FI) is split roughly evenly between the two daughter cells. Thus, measurement of FI provides an indirect measure of the number of divisions a cell has undergone. After staining, the cell population is analyzed at regular time intervals via FACS, which returns a histogram of the number of cells as a function of CFSE FI. Typically, CFSE can be used to track up to 8 rounds of division before the CFSE FI is reduced to the autofluorescence level of unstained cells. More information regarding the biological processes and experimental protocol can be found in Hawkins et al. (2007), Lyons (1999), Lyons and Doherty (2004), Lyons and Parish (1994), Matera et al. (2004), Quah et al. (2007).

While the ability to track a population of cells through multiple rounds of divisions has been greatly improved by the use of CFSE labeling and quantitative methods, there are possible improvements. In addition to the work of Luzyanina et al. (2007) upon which this work is based, many cell proliferation models have focused on describing growth and division dynamics of cells as a function of the number of divisions undergone, which is strongly correlated with CFSE intensity. The Smith–Martin cell cycle model (Smith and Martin, 1973), in which the cell cycle is divided into a stochastic resting G₁ phase and a deterministic dividing SG₂M phase, provides the basis for many of these papers (Bernard et al., 2003; Chao et al., 2003; de Boer et al., 2006; Ganusov et al., 2005; Hawkins et al., 2007; Le, 2004; Luzyanina et al., 2007). These models vary in structure, drawing on a range of techniques including compartmental modeling, agent-based modeling and probability-based modeling. While this is by no means an exhaustive list, there are a number of areas of study in which these approaches have contributed: immunoglobulin class switching in B cells (Hodgkin et al., 1996), cytokine regulation of T cells (Gett and Hodgkin, 2000), and surface molecule expression or internal expression of cytokines (Bird et al., 1998; Gett and Hodgkin, 1998). One notable recent effort is the paper by Lee et al. (2009), in which a generalized Smith–Martin model with division-dependent death rate is compared to a cyton model (developed in Hawkins et al., 2007). The validated cyton model is then used to study the effects of IL-4, thought to protect against apoptosis, on B cell population dynamics.

While these models are typically strongly biologically motivated, there are some drawbacks when considering their use with flow cytometry data. Some deconvolution is required of the CFSE data to obtain the number of cells as a function of the number of divisions undergone since initiation of the assay. In this process, a distribution for the CFSE across cells of the same division number is assumed, which may be reasonable in most cases. However, it is possible that there may be certain cell populations, either normal or abnormal that do not fit these distributions. Even if the assumed distribution is reasonable, it is possible that errors are made in counting some cells near the tails of the distributions corresponding to a given number of divisions. The alternative modeling approach we discuss in this manuscript is somewhat less restrictive in that it does not assume any distribution of label uptake of the cells. An additional benefit to this approach is that model solutions are directly compared to histograms obtained by flow cytometry, eliminating any possible misinterpretation of such data.

Building upon the work in Luzyanina et al. (2007, 2009), we seek to update these models (in which age is a discrete variable corresponding to division number) with a hyperbolic partial differential equation (PDE) model for the label-structured population density in which CFSE FI is a continuous state variable. Because FI intensity is determined by cellular events included in the model, it is useful to study cells as a function of FI in time. Divisions of cells are seen in model solutions, just as in histograms obtained by flow cytometry, but specifying division number is unnecessary. Meanwhile, because FI can range continuously, the nonuniform uptake of CFSE (and hence the resulting nonuniform distribution of CFSE in each generation) is preserved.

Previous work (Luzyanina et al., 2007) has already demonstrated the advantages of this type of PDE model as compared to some compartmental modeling efforts. While this model provided a reasonable way to mathematically reproduce experimentally observed proliferation dynamics, there was still room for improvement as peaks/generations of cells were incorrectly predicted by the best fit model solution. In this report, careful consideration is given to the biological and mathematical assumptions of the original model and refinements in both interpretation and parameter/mechanism formulations are proposed. First, the proliferation and death rate functions from Luzyanina et al. (2007) are redefined on a domain which strongly correlates with division number, and the proliferation rate function is changed so that it is time varying. It is shown via a model comparison test that the resulting model provides a statistically significant improved fit to an experimental data set over the previous model. Evidence is then offered to suggest that the death rate for cells should remain division dependent when compared to fitting the data set with a constant rate. Next, improvements to the treatment of the label loss rate are considered. It is found that the best fit to the data is not improved significantly when this function is either affine in form or taken to be a probability distribution of constant label loss rates within the population. For each version of the model, the parameters are estimated in an ordinary least squares inverse problem and the resulting cost functions are tested statistically to quantitatively assess the improvement in fitting to the data. Statistical models for the noise structure in the data are also discussed. It is shown that the noise in the data does not appear to have either constant variance (ordinary least squares formulation for absolute error) or variance proportional to the magnitude of the observation (generalized least squares formulation for relative error). Implications for the corresponding quantification of parameter uncertainty via confidence intervals are discussed.

The investigations in this paper demonstrate that the proposed PDE models can be used successfully in an interpretive framework for cell division dynamics and lay the groundwork for the continued refinement and extension of these models and their application to additional data sets. Specifically, two new features in the current models offer a dramatic improvement in fits to data in the context of biologically supportable model mechanisms. First, we introduce a decay dependent translation of intensity coordinate resulting in a dependent variable more strongly correlated to division number with which we define new effective proliferation and death rates. A further extension of the effective proliferation rates (which depend implicitly on time) to depend explicitly on time accounts for differences in proliferation rates beyond division dependence also results in statistically significant improved performance of the models. The ability to estimate from data these effective rates (relative to the new coordinates) allows for their comparison in healthy cell populations versus cell populations with abnormal growth and/or proliferation dynamics. The characterization of these differences can potentially improve our detection, identification and understanding of the disease or conditions responsible for the change in dynamics.

2. Preliminaries

2.1. Data

An original data set (shown in Fig. 1) containing time-series snapshots of the CFSE FI distribution of a population of dividing cells was used (Luzyanina et al., 2007). Briefly, this data set is the result of an in vitro proliferation assay with human peripheral blood mononuclear cells (PBMCs) from healthy blood donors. After isolation of the PBMCs from “buffy coats” by density centrifugation, 5 × 10⁶ to 5 × 10⁷ were stained with 5 μM CFDA-SE (Invitrogen, Germany) in phosphate-buffered saline containing 5% fetal calf serum (FCS). The cells were stimulated with 2.5 μg/mL phytohemagglutinine (Sigma, Germany) at time t = 0 hrs and plated in 24 well plates at 1 × 10⁶ cells/mL RPMI-1640/10% FCS medium. Beginning at day 3, every 24 hrs one third of the medium was exchanged with fresh medium to ensure sustained cell nutrition. To not disturb the proliferating cell populations, cells from a single well were harvested for each time point. Cells were then stained with CD4 antibodies. This staining makes it possible to distinguish the CD4+ cells from other cells in the PBMC culture while simultaneously measuring CFSE expression in individual cells through FACS. This measurement process is high-speed (thousands of cells in seconds), and provides data for individual cells (Hawkins et al., 2007; Quah et al., 2007).

Fig. 1.

Original CFSE histogram data.

The CFSE FI data is reported on a logarithmic scale, z = log₁₀x where x is the CFSE FI of a given cell. The output of the measurement procedure is the counts c_ij of cells at time t_i with log-intensity z_j. The data set obtained for this report tracks cells from 0 to 120 hours in 24 hour intervals; the discretization of the z-axis into bins changes with each measurement in time (j = 1, …, J(i) for each time t_i). Data for the entire population density can then be obtained by the transformation

$$n_{ij}^d=\frac{c_{ij}{T}_i}{C_i},$$

where T_i is the total number of cells in the population at time t_i and C_i is the total number of cells counted at time t_i. This processing of the data was performed by Luzyanina et al. (2007) so that the data set obtained already consisted of the population density data $n_{ij}^d$.

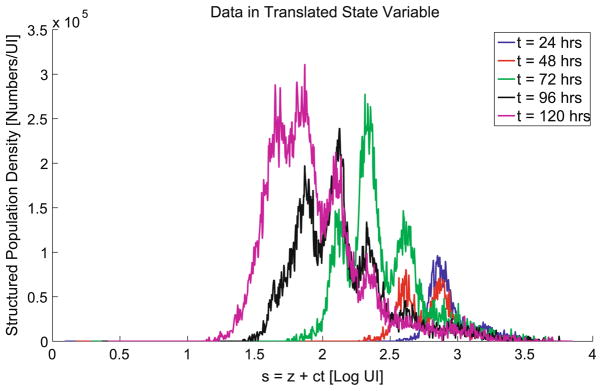
Note in Fig. 1 that an initially unimodal peak becomes multimodal as cohorts of cells begin to divide at different times. Each of these division peaks also slowly drifts to the left as FI is lost over time due to catabolic activity within the cell (Lyons, 1999). The noise in the data is typical for such experiments and is the result of any number of processes, from counting errors to variations in cell shape and size to the functioning of the machine itself (Luzyanina et al., 2007; Wikipedia, 2010).

As alluded to in the introduction and discussed at greater length in Luzyanina et al. (2007), Quah et al. (2007), many approaches to cell division tracking have involved the determination of the number of cells having undergone a certain number of divisions, but this information is not available from the experimental data without some sort of deconvolution technique to separate out the division peaks. These techniques invariably involve the definition of FI borders between subsequent division peaks. However, such techniques do not account for the inherent heterogeneity of the cell population due to variation in initial CFSE uptake, variability across cells in catabolism, proliferation, etc. that may result in cells at a given FI having undergone a different number of divisions. Moreover, this heterogeneity can make subsequent division peaks very difficult to resolve, introducing additional error into these traditional approaches. Hence, an advantage of the current approach is that it eliminates the need for these deconvolution techniques by explicitly accounting for the heterogeneity of the population through the use of CFSE FI as a continuous state variable.

2.2. Mathematical model

The model for the dynamics of life and death processes of a population of cells labeled with CFSE is proposed in Luzyanina et al. (2007) as a variation of a Bell–Anderson (Bell and Anderson, 1967) or Sinko–Streifer (Sinko and Streifer, 1967) population model. The solutions of these models may be directly compared to time snapshots of flow cytometry histograms, which usually depict cells of multiple generations. That is, the models aim to predict the number of cells at a given fluorescence intensity and time under specified dynamics. Let x denote the CFSE FI (in units of intensity, UI) of a cell and let n(t, x) be the label-structured population density (cells/UI) of cells with FI x at time t. Then the opulation density is governed by a hyperbolic partial differential equation (PDE)

$$\frac{\partial n}{\partial t}(t,x)+\frac{\partial [v(x)n(t,x)]}{\partial x}=-(\alpha (x)+\beta (x))n(t,x)+{\chi }_{[x_{min},x_{max}/\gamma ]}2\gamma \alpha (\gamma x)n(t,\gamma x),$$ (1)

where ν(x) is the label loss rate, α(x) is the cell proliferation rate, β(x) is the cell death rate, x ∈ [x_min, x_max] and t > 0. Because cells naturally lose FI over time even in the absence of division (due to catabolic activity (Lyons, 1999)), the term ν(x) represents the natural label loss rate (UI/hr). The parameter γ is the label dilution factor, representing the ratio of FI of a mother cell to FI of a daughter cell. Division is coupled with immediate rapid growth of the new daughter cells. The observed or estimated value of γ reflects underlying dynamics (involving mechanisms regulating the growth and division) which occur on a faster time scale and have effectively been integrated over in time. A derivation of this model following the mass conservation principles of Sinko–Streifer (Sinko and Streifer, 1967) or Bell–Anderson (Bell and Anderson, 1967) models is presented in the Appendix.

Because FACS returns data on a logarithmic scale, it is convenient to make the change of variables z = log₁₀ x. Assuming the natural label loss is proportional to the amount of label, we take ν(x) = −cx, a form which has been seen (Luzyanina et al., 2007) to better fit this data set than constant label loss assumptions. The resulting model, along with the change of variable ñ(t, z)= n(t, 10^z) gives

$$\frac{\partial \stackrel{\sim }{n}}{\partial t}(t,z)+\frac{\partial [\stackrel{\sim }{v}(z)\stackrel{\sim }{n}(t,z)]}{\partial z}=-(\stackrel{\sim }{\alpha }(z)+\stackrel{\sim }{\beta }(z))\stackrel{\sim }{n}(t,z)+{\chi }_{[z_{min},z_{max}-{log}_{10}\gamma ]}2\gamma \stackrel{\sim }{\alpha }(z+{log}_{10}\gamma )\stackrel{\sim }{n}(t,z+{log}_{10}\gamma ),$$ (2)

where ν̃(z) = −c̃ = −c/ln 10, and α̃, β̃ are appropriately defined cell proliferation and death rates, respectively. The initial and boundary conditions for the model are

$$\begin{array}{l}\stackrel{\sim }{n}(0,z)={\stackrel{\sim }{n}}_0(z)\\ \stackrel{\sim }{n}(t,z_{max})=0.\end{array}$$

In our subsequent discussions, we will drop the tildes on the parameters α, β, c, ν, and the states n in (2) and take this equation as our fundamental model to be investigated and modified. From the structure of the above model, we deduce that some key tacit assumptions are:

1. Division numbers are strongly correlated with FI.

2. FI is proportional to total CFSE content (amount).

3. Total CFSE is divided equally among daughter cells with each division.

4. The rate of label loss v(z), the proliferation rate α(z), and the death rate β(z) do not depend on time.

Assumption (ii) appears to be tacitly made in the discussions of CFSE content or amount, CFSE FI and the definition of the parameter γ on p. 4 of Luzyanina et al. (2007) which we will understand here as being defined by the mother/daughter ratio of CFSE FI. Assumptions (i)–(iii) would imply that the state variable z is strongly correlated with, although not exactly equal to, division number. Hence, assumption (iv) would then be equivalent to stating that birth, death, and label loss rates, largely depending on division number, can be determined as functions of label intensity z. (It will later be shown, however, that we can modify some of these assumptions in their interpretation and implementation to obtain model extensions to produce significantly improved model agreement with the data.) Given the formulation (2), the goal is to use the CFSE data described in Section 2.1 in order to estimate the functions α(z), β(z), and ν(z) as well as the parameter γ. Following by now standard inverse problem procedures (Banks and Kunsich, 1989; Banks et al., 1996), these functions are parameterized by finite-dimensional approximations so that the estimation is computationally tractable (and theoretically sound—see the convergence arguments of Banks and Kunsich (1989), Banks and Pedersen (2009), Banks et al. (1996) in such inverse problem approximations). Both α(z) and β(z) are approximated by linear splines

$$\alpha (z)=\sum _{i=1}^{M_{\alpha }}{a}_i{\phi }_i(z),\beta (z)=\sum _{i=1}^{M_{\beta }}{b}_i{\phi }_i(z),$$

where φ_i(z) are piecewise linear spline functions satisfying

$${\phi }_i(z_j)=\{\begin{array}{ll}1,\hfill & i=j\hfill \\ 0,\hfill & i\ne j.\hfill \end{array}$$

Note that a_i = 0 or b_i = 0 indicates zero birth or death, respectively, while a_i = 1 or b_i = 1 indicates that all cells at the given FI are dividing or dying on average once per hour, which is clearly a greater rate than these events actually occur. Thus, the parameters a_i and b_i are constrained to be between 0 and 1. As already noted above, it is assumed that the rate of label loss is proportional to label intensity (ν(x) = −c̄x, where c̄ ∈ ℝ⁺). Thus, after the change of variables, we have ν(z) = −c = −c̄/ln 10. Simulations of the model (2) demonstrate that 0.0025 ≤ c ≤ 0.0055 provides a reasonable range of possible values for the label loss rate. Similarly, γ is reasonably constrained to γ ∈ [1, 2]. For biological interpretation of this range, see Section 3.2.

The set of parameters to be estimated in the inverse problem is given in Table 1. Given a set of these parameters, the forward problem is solved numerically over a specified time interval using a publicly available vectorized version of the Lax–Wendroff method with a nonlinear filter developed by Shampine (2005) for solving hyperbolic PDEs in MATLAB. In order to obtain solution points on the nonuniform z-grid of the data points, different with each time t_j, the solution was calculated (for all time points) on a grid of 500 evenly spaced points for each time point and then interpolated onto the data grid using linear interpolation with MATLAB’s interp1 routine. Throughout this report, it is assumed that [z_min, z_max] = [0, 3.5].

Table 1.

Summary of parameters to be estimated, with minimum values, maximum values, and units.

Parameter	Minimum	Maximum	Units
ai	0	1	hr−1
bi	0	1	hr−1
c	0.0025	0.0055	UI/hr
γ	1	2	[none]

The a_i and b_i are coefficients of the effective proliferation and death functions, respectively. The parameter c scales the label loss as a function of fluorescence intensity, and γ is the observed ratio of mother to daughter cell CFSE concentration

After a brief discussion of the theory and implementation of the inverse problem in Section 2.3, computational results which attempt to fit the above model to the data are presented in Section 3. Then in an attempt to improve the fit of the model to the data, a transformed intensity variable depending on time and label loss is introduced into the model so that new effective proliferation and death rate functions are defined on a domain which is strongly correlated with division number. Next, the effective proliferation rate function (depending implicitly on time) will also be allowed to vary explicitly in time. Finally, further considerations regarding the use of a constant death rate and alternative parameterizations of the label loss rate are discussed. In each case, biological and physical justifications for the changes are given.

2.3. Mathematical and statistical aspects of the inverse problem

2.3.1. Ordinary least squares (OLS)

Given the mathematical model (2) for the label-structured population density n(t, z; θ⃗) at time t, log intensity z and parameters θ⃗ (see Table 1), the CFSE time-series histogram data constitutes a direct observation of the physical process. A statistical model for the observation process is given by

$$N_{ij}^d=n(t_i,z_j;{\overrightarrow{\theta }}_0)+{\mathcal{E}}_{ij},$$ (3)

where n(t_i, z_j ; θ⃗₀) is the solution to the model (2) at time t_i (t_i ∈ [t₁, …, t_I ]) and log FI z_j(z_j ∈ [z₁, … z_{J (i)}]) given the assumed true parameters θ⃗₀ ∈ ℝ^p that generate observations $N_{ij}^d$. The statistical model (3) relies on the assumption that the random errors in the data do not depend on the magnitude of the observations themselves. The noise ε_ij are independent identically distributed (i.i.d.) random variables with mean zero which represent the measurement error. Hence, $N_{ij}^d$ are random variables as well, and the given data represent one realization of this random variable, i.e.,

$$n_{ij}^d=n(t_i,z_j;{\overrightarrow{\theta }}_0)+{\epsilon }_{ij}.$$

In the absence of any information regarding the distribution of ε_ij, it is assumed only that the variance $var({\mathcal{E}}_{ij})={\sigma }_0^2$ does not depend on t or z (because ε_ij are i.i.d.). The ordinary least squares (OLS) estimator is defined as

$${\overrightarrow{\theta }}_{\text{OLS}}=arg\underset{\overrightarrow{\theta }\in \mathrm{\Theta }}{min}\sum _{i=1}^I\sum _{j=1}^{J(i)}{(N_{ij}^d-n(t_i,z_j;\overrightarrow{\theta }))}^2,$$ (4)

where Θ is a set of admissible parameters for the model. Given the data as a realization for this random variable, the OLS estimate is

$${\overrightarrow{\theta }}_{\text{OLS}}=arg\underset{\overrightarrow{\theta }\in \mathrm{\Theta }}{min}\sum _{i=1}^I\sum _{j=1}^{J(i)}{(n_{ij}^d-n(t_i,z_j;\overrightarrow{\theta }))}^2=arg\underset{\overrightarrow{\theta }\in \mathrm{\Theta }}{min}{F}_{\text{OLS}}(\overrightarrow{\theta }).$$ (5)

The MATLAB constrained global minimization package fmincon, a gradient-based method for problems where the objective and constraint functions are continuous and have continuous first derivatives, was used to solve for the OLS estimate θ̂_OLS.

The true covariance ${\sigma }_0^2$ of the random variables ε_ij is given by

$${\sigma }_0^2=\frac{1}{N}E\left[\sum _{i=1}^I\sum _{j=1}^{J(i)}{(N_{ij}^d-n(t_i,z_j;{\overrightarrow{\theta }}_0))}^2\right]$$

where $N={\sum }_{i=1}^{I}J(i)$. The bias-corrected estimate of the variance with observations { $n_{ij}^d$} is

$${\widehat{\sigma }}_{\text{OLS}}^2=\frac{1}{N-p}{F}_{\text{OLS}}({\widehat{\theta }}_{\text{OLS}}).$$

One can also use an asymptotic theory involving sensitivity matrices for the corresponding covariance matrix Σ(θ̂_OLS) associated with the estimated parameters. This can be used to compute standard errors and confidence intervals (see the detailed discussions in Banks et al., 2009; Banks and Tran, 2009; Seber and Wild, 2003).

Rewriting Eq. (3), we have ${\mathcal{E}}_{ij}=N_{ij}^d-n(t_i,z_j;{\overrightarrow{\theta }}_0)$. Thus, the residuals

$$r_{ij}=n_{ij}^d-n(t_i,z_j,{\widehat{\theta }}_{\text{OLS}})$$ (6)

are a realization of the error in the data and, given a mathematical model for a set of data with constant variance (CV), these residuals should be randomly distributed (Fig. 2, left) when plotted against the model values, n(t_i, z_j ; θ̂_OLS). In many situations, the variance in the observations is not constant but is proportional to the magnitude of the observations. If OLS is used with such data, the same plot will not be random but rather will exhibit a characteristic fanning pattern (Fig. 2, right), indicating dependence of the residuals on model quantities. In that case, a generalized least squares (GLS) procedure, described in the next section, is appropriate. Thus, the shape of the residuals after data fitting by a least squares minimization provides a means of investigating the reliability of the assumptions of the statistical model.

Fig. 2.

Left: OLS Residuals vs. Model for observations with constant variance. Right: OLS Residuals vs. Model for observations with nonconstant variance.

2.3.2. Generalized least squares (GLS)

When observational error is proportional to the magnitude of the observation, the statistical model is given by

$$N_{ij}^d=n(t_i,z_j;{\overrightarrow{\theta }}_0)(1+{\mathcal{E}}_{ij}),$$ (7)

where ε_ij are defined as before. Then $var(N_{ij}^d)={\sigma }_0^2{n}^2(t_i,z_j;{\overrightarrow{\theta }}_0)$. Accordingly, the generalized least squares (GLS) cost functional weights the observations according to their variance and the GLS estimator is

$${\overrightarrow{\theta }}_{\text{GLS}}=arg\underset{\overrightarrow{\theta }\in \mathrm{\Theta }}{min}\sum _{i=1}^I\sum _{j=1}^{J(i)}{w}_{ij}{(N_{ij}^d-n(t_i,z_j;\overrightarrow{\theta }))}^2=arg\underset{\overrightarrow{\theta }\in \mathrm{\Theta }}{min}{F}_{\text{GLS}}(\overrightarrow{\theta }),$$ (8)

where the weights are

$$w_{ij}=\{\begin{array}{ll}{n}^{-2}(t_i,z_j;\overrightarrow{\theta }),\hfill & n(t_i,z_j;\overrightarrow{\theta })\ge N^{\ast }\hfill \\ 0,\hfill & n(t_i,z_j;\overrightarrow{\theta })<N^{\ast }.\hfill \end{array}$$ (9)

This definition of the weights prevents the GLS algorithm from giving unreasonably large weight to points where the model is near zero (Banks and Samuels, 2009). The value of N^* is chosen so that the maximum number of data points are chosen without the minimization algorithm stagnating or converging erroneously as a result of assigning little weight to larger-magnitude observations. The computation of the GLS estimate θ̂_GLS is an iterative procedure and is given as follows:

1. Compute the OLS estimate ${\widehat{\theta }}_{\text{OLS}}^k$ according to Eq. (5). Set k =0.

   Form the weights

   $$w_{ij}^k=\{\begin{array}{ll}{n}^{-2}(t_i,z_j;{\widehat{\theta }}_{\text{OLS}}^k),\hfill & n(t_i,z_j;{\widehat{\theta }}_{\text{OLS}}^k)\ge N^{\ast }\hfill \\ 0,\hfill & n(t_i,z_j;{\widehat{\theta }}_{\text{OLS}}^k)<N^{\ast }.\hfill \end{array}$$

2. Compute the approximation to the GLS estimate

   $${\stackrel{\sim }{\theta }}^{k+1}=arg\underset{\overrightarrow{\theta }\in \mathrm{\Theta }}{min}\sum _{i=1}^I\sum _{j=1}^{J(i)}{w}_{ij}^k{(n_{ij}^d-n(t_i,z_j;\overrightarrow{\theta }))}^2.$$

3. Repeat steps (ii) and (iii), incrementing k by one with each iteration, until the successive estimates satisfy

   $$\sum _{i=1}^p\mid {\stackrel{\sim }{\theta }}_i^{k+1}-{\stackrel{\sim }{\theta }}_i^k{\mid }^2<\epsilon ,$$

   where ε is small, representing the predetermined desired convergence.

A more complete discussion of the GLS motivation, algorithm, and convergence can be found in Banks et al. (2009), Banks and Tran (2009) and the references therein. The result of the algorithm is the GLS estimate θ̂_GLS. The variance coefficient may be estimated as

$${\widehat{\sigma }}_{\text{GLS}}^2=\frac{1}{N-p}{F}_{\text{GLS}}({\widehat{\theta }}_{\text{GLS}}).$$ (10)

Given these values, an asymptotic theory similar to that for the OLS estimator can be invoked to quantify uncertainty in the GLS estimate using standard errors and confidence intervals (again see Banks et al., 2009; Banks and Tran, 2009 for details).

Rewriting Eq. (7), we have ${\mathcal{E}}_{ij}=(N_{ij}^d-n(t_i,z_j;{\overrightarrow{\theta }}_0))/n(t_i,z_j;{\overrightarrow{\theta }}_0)$. Thus, the residuals

$${\stackrel{\sim }{r}}_{ij}=(n_{ij}^d-n(t_i,z_j;{\widehat{\theta }}_{\text{GLS}}))/n(t_i,z_j;{\widehat{\theta }}_{\text{GLS}})$$ (11)

are a realization of the error in the data and should have constant variance. When GLS estimation is used with data in which the noise is proportional to the magnitude of the observations, and hence data for which this statistical model is appropriate, these residuals should appear random when plotted as a function of the model values n(t_i, z_j ; θ̂_GLS). Figure 3 depicts a typical example of these residuals for data with variance proportional to the magnitude of the observation.

Fig. 3.

Modified residuals for observations with nonconstant variance.

2.3.3. Model comparison test

When forming a mathematical model in an effort to describe a physical, biological, or sociological process, there is often the possibility of adding an additional term and/or mechanism into the model in an effort to better fit the data. In the case of such a re-finement, the resulting cost function (OLS or GLS) will at least remain unchanged but will likely decrease because of the additional degrees of freedom (in essence, minimizing over a less constrained set). However, the question must be asked whether the resulting decrease in the cost function reflects a significant improvement in the model fit to data, beyond a simple increase in degrees of freedom, to warrant the addition of that mechanism into the model. Alternatively, it may be sufficient to employ the less sophisticated mathematical model with fewer parameters. In this section, mathematical and statistical tools are used to help answer these questions are summarized.

In the statistical models discussed above, it is assumed that the true parameter θ⃗₀ is contained in some set Θ of admissible parameters. Following the notation of Banks and Tran (2009), consider the constrained parameter space Θ_H, a subset of the parameter space of the more complex model Θ, defined by

$${\mathrm{\Theta }}_H=\{\overrightarrow{\theta }\in \mathrm{\Theta }\mid H\theta =d\}$$ (12)

where H is an r × p matrix with full rank and d is an r-dimensional vector. The goal is to develop a statistical test of the null hypothesis, H₀: θ⃗₀ ∈ Θ_H. Let F(θ⃗) be the cost function (OLS or GLS) associated with a given model and data set and define

$${\widehat{\theta }}_H=arg\underset{\overrightarrow{\theta }\in {\mathrm{\Theta }}_H}{min}F(\overrightarrow{\theta }),\widehat{\theta }=arg\underset{\overrightarrow{\theta }\in \mathrm{\Theta }}{min}F(\overrightarrow{\theta }).$$

Then it is possible to define the test statistic

$$U_N=\frac{N[F({\widehat{\theta }}_H)-F(\widehat{\theta })]}{F(\widehat{\theta })},$$ (13)

where N is the total number of data points. It follows from an asymptotic theory (see Banks and Fitzpatrick, 1989, 1990; Banks and Kunsich, 1989; Banks and Tran, 2009) and references therein), different from those mentioned above for standard errors and confidence intervals that if H₀ is true, U_N converges in distribution (as the number of data points go to infinity) to a χ ² distribution with r degrees of freedom. Moreover, if η = P(U > U_N) where U ~ χ²(r), then we may reject H₀ with confidence (1 − η)100%.

For example: suppose in the parameter set shown in Table 1 that four nodes are being used in the estimation of the death rate function β(z), b₁, …, b₄. For simplicity, it will also be assumed that these are the only four parameters being estimated; that is c, {a_i }, and γ are fixed. It may be of interest whether or not this death rate could be treated as a constant function. Then the restricted set of admissible parameters Θ_H is given by (12) where

$$H=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill -1\hfill \end{array}\right),d=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right).$$

Note in this example that r = 3 for the χ² test. Such examples along with others are discussed in Banks and Kunsich (1989), Banks and Tran (2009).

3. Model modifications

We first discuss the best fit we can obtain with the original model (given in Eq. (2)). The same data set was fit in Luzyanina et al. (2007), but exact values were not given for the proliferation and death rates (although they were depicted graphically). Also, we did not perform Tikhonov regularization and, therefore, our problem is not convexified to ensure only one minimum for a modified objective functional. Instead, we begin with the best fit parameters from Luzyanina et al. (2007), with the proliferation and death rates estimated to the best of our ability, and proceeded to obtain an OLS estimate of the parameters. In Section 3.2, we propose modifications to the model (2), and accept or reject these changes based on whether they result in a statistically significant improvement of the agreement between model solutions and experimental data.

3.1. Data fit with the original model

First the original model (2) is fit to data. The resulting discrepancies between the observed data and the best fit model solution are then used to provide motivation for improvements to the model. For the current discussion, focus will remain on the OLS estimation of the parameters. The alternative use of the GLS procedure is discussed in Section 4.

The death rate of cells is expected to vary little after the initial rounds of divisions. Thus, only four nodes are used in the estimation of the death rate function. In the region z ∈ [0, 2.5], the death rate is treated as a constant, β(z) = b₁. The proliferation rate function, on the other hand, should vary with division number and more nodes are needed (particularly in regions of rapid division). The placement of the nodes for the proliferation and death rate functions is given in Tables 2 and 3, respectively. These nodes were chosen after considerable trial and error running both forward simulations and inverse problem parameter estimations. Nodes chosen too close together cause instabilities due to over-discretization, while nodes chosen too far apart do not provide sufficient information regarding the behavior of the population. After OLS minimization, the best fit parameter estimate θ̂_OLS had a cost F_OLS(θ̂_OLS) = 3.2112 × 10¹². The best fit proliferation and death rate functions are depicted in Fig. 4. The best fit values for the label loss rate and label dilution factor were ĉ = 0.004421 and γ̂ = 1.5751. The model solution evaluated at the best fit parameters is shown in comparison to the data in Figs. 5 and 6.

Table 2.

Nodes and estimated values (OLS) for the proliferation rate function in the original formulation using Eq. (2)

zi	ai
1.2500	0.0020
1.5000	0.0112
1.6250	0.0169
1.7500	0.0161
1.8750	0.0091
2.0000	0.0222
2.1250	0.0015
2.2500	0.0505
2.3750	0.0117
2.5000	0.0027
2.6250	0.0231
2.7500	0.0016
2.8750	0.0076
3.0000	0.0076

Table 3.

Nodes and estimated values (OLS) for the death rate function in the original formulation using Eq. (2)

zi	bi
2.5000	0.0085
2.7500	0.0248
3.0000	0.0000
3.5000	0.0000

Fig. 4.

Graphical presentation of estimated (OLS) birth and death rate functions α(z) (left) and β(z) (right).

Fig. 5.

OLS best fit model solution to original PDE formulation with Eq. (2) in comparison to the data: t = 0, 24, 48 hrs.

Fig. 6.

OLS best fit model solution to original PDE formulation with Eq. (2) in comparison to the data: t = 72, 96, 120 hrs.

3.2. Modified model

It is clear from Figs. 5 and 6 that the fit of the model to the data can be improved. It appears that the model is not quite capturing the dynamics of the cells in the proliferation assay. Moreover, the label dilution factor γ must be less than 2 in order to accurately fit the data. If we were to interpret the measurement of fluorescence as a mass measurement, or a measurement of total quantity (assumption (ii)), then in the model (2), this definition would require γ = 2. Values of γ < 2 would then imply a creation of label during proliferation, or that the amount of CFSE in the mother cell is less than twice that of the daughter cell. Clearly, this is biologically infeasible and physically implausible so the interpretation is incorrect and FI is not a mass measurement. However, if we interpret the fluorescence intensity as a concentration measurement (as discussed in Lyons, 1999; Lyons and Parish, 1994; Wikipedia, 2010), and the same amount of CFSE in a larger volume fluoresces at a lower intensity, then a feasible range for γ is (Banks et al., 1988, 2003). The reason this parameter is not exactly γ = 1 is that while the concentration immediately after division of the daughter cells is identical to that of the original mother cell, a marked growth in cell volume immediately following division results in a dilution of the CFSE, and daughter cells are detected at a lower fluorescence intensity. However, the daughter cells do not fluoresce at half the original intensity (represented by γ = 2) until they reach the size of the mother cell, which occurs much later as the cell progresses through the nonmitotic phases of the cell cycle. While not actually a change in the mathematical model, this change in interpretation of the parameter γ provides for a more satisfactory discussion of the results of the model. The parameter γ effectively represents cellular mechanisms governing the timing of initial growth of daughter cells after division. These underlying dynamics likely occur on a much faster scale than the other observed processes in this model and have essentially been integrated over in time and are absorbed in the parameter γ. Thus, it is not likely that its value will be estimated in this type of experimental setting as the precise value γ = 1 which would reflect the strict biological interpretation as the ratio of mother to daughter label concentration.

Because of the natural loss of FI over time due to catabolic activity, assumption (i) is not to be taken in an exact sense—histograms of cells as a function of FI can be used to see division as it occurs, but no simple relationship between FI and division number exists. While the cells fluorescing at the intensity of the peaks seen in the data have all likely undergone the same number of divisions, cells of fluorescence intensity in the valleys in the data may have undergone different numbers of divisions since the start of the experiment. The natural label loss causes cells to slowly drift to the left on the FI scale. For that reason, no particular region of FI can be definitively linked to a particular division number in Fig. 1. However, we can define a new variable s = z + ct in terms of which we can more intuitively define the proliferation and death rates. As we shall see, this time dependent translation of the domain can be seen (in Fig. 7 below) to result in a data plot which does, in fact, correlate well with division number. (To see this, compare Fig. 7 below to Fig. 1.) To better capture this in our model, we replace the rates α(z), β(z) in our model by new translated effective proliferation and death rates α(s) = α(z + ct), β(s) = β(z + ct), respectively. It should be noted that the label loss rate function ν(z) does not undergo a similar translation/replacement because of the assumption that label loss rate depends on CFSE label intensity or FI, but not division number.

Fig. 7.

Original data sets shown in translated log intensity s = z + ct, with c = ĉ = .0032888, as estimated with the OLS procedure for the modified model (14). Note that subsequent division peaks are now strongly correlated with specific regions in the state variable, unlike the original log intensity variable z (see Fig. 1).

In an attempt to interpret these effective rates of proliferation and death introduced in the efforts here, we recall for readers that, while not common in the biological sciences, it is altogether common in the physical sciences and engineering to consider velocities (i.e., rates of change) relative to different coordinate or reference frames. For example, in mechanics and motion of continua (elasticity and fluids) and deformable bodies (Banks and Lybeck, 1996; Fung 1993, 1994; Marsden and Hughes, 1994; Ogden, 1984), it is frequent to encounter velocities relative to a fixed coordinate system (in a Lagrangian formulation) or relative to a moving coordinate system (in an Eulerian formulation). More precisely, when analyzing the deformation or motion of solids, or the flow of fluids, it is necessary to describe the sequence or evolution of configurations throughout time. One description for motion is made in terms of the material or fixed referential coordinates, and is called a material description or the Lagrangian description—also called an initial/referential, material, undeformed, or fixed frame formulation. In this formulation, an observer standing in the fixed referential frame observes the changes in the position and physical properties as the material body moves in space as time progresses. In other words, this formulation focuses on individual particles as they move through space and time. The other description for motion is made in terms of the spatial or current coordinates, called a spatial description or Eulerian description—also called a current/present, space, deformed, or moving frame formulation. In this approach, one focuses on the current configuration of the body, giving attention to what is occurring at a moving material point in space as time progresses. That is, the coordinate system is relative to a moving point in the body, and hence is a moving coordinate system. An intuitive comparison of these two descriptions would be that in the Eulerian description one places the coordinate or reference system for motion of an object on the object as it moves through a moving fluid (e.g., on a boat in a river) while in the Lagrangian description one observes and describes the motion of the object from a fixed vantage point (e.g., motion of the boat from a fixed point on a bridge over the river or on the side of the river.).

Finally, biological evidence suggests that the proliferation rate might also depend in some way on time (Hawkins et al., 2007) in addition to division number, as the time to first division is clearly seen to differ from that of subsequent divisions. The assumption that the death rate depends only on division number is supported in literature (Hawkins et al., 2007; Luzyanina et al., 2007; Quah et al., 2007), and is not investigated here. The consideration of time dependence in the proliferation rate as introduced here will later be tested (with positive affirmation) for statistical significance, which is one way of determining whether the effect might be present in the experimental data. This is also seen in the data set. At t = 24 hours, all cells are still in the original (undivided) generation, indicating a proliferation rate of zero in the first 24 hrs. However, these cells do divide, producing the additional peaks seen at later times. Thus, it must be that α (at least as represented in the data) changes in time. In a given longitudinal in vitro data set such as we are considering here, the apparent proliferation rate does depend on time in some specific way related both to division times and label loss. Indeed, in defining the effective proliferation and death rates, we introduce time implicitly into the rates. Thus, permitting explicit time dependence in the effective proliferation rate α is a rather natural modification to also consider.

Taking all of these considerations into account, we modify the model (2) to obtain

$$\frac{\partial n(t,z)}{\partial t}+\frac{\partial [v(z)n(t,z)]}{\partial z}=-(\alpha (t,z+ct)+\beta (z+ct))n(t,z)+{\chi }_{[z_{min},z_{max}-log\gamma ]}2\gamma \alpha (t,z+ct+log\gamma )n(t,z+log\gamma ).$$ (14)

Again, the ultimate goal is to estimate the functions α(t, s), β(s), and ν(z) and the parameter γ such that the model best fits a given set of data. Because the death rate β(s) is expected to be relatively constant after the initial rounds of division, it will be treated as a constant, β(s) = b₁ for all s ∈ [0, 2.5]. For s ∈ [2.5, 4], β(s) will be constructed as a piecewise linear function,

$$\beta (s)=\sum _{i=1}^{M_{\beta }}{b}_i{\phi }_i(s),$$ (15)

where φ_i(s) are piecewise linear splines defined as before. The proliferation rate function α(t, s) will be represented by linear combinations of products of one dimensional piecewise linear splines ξ_j,ψ_i, i.e.,

$$\alpha (t,s)=\sum _{i=1}^{M_{\alpha }^t}\sum _{j=1}^{M_{\alpha }^z}{a}_{ij}{\xi }_j(t){\psi }_i(s).$$ (16)

As before, a_ij = 0 or b_i = 0 indicates zero birth or death, respectively, while a_ij = 1 or b_i = 1 indicates that cells at the given location in time and/or translated log are dividing or dying once per hour. This is clearly much faster than the actual or true value, so the interval [0, 1] should cover the true value for each a_ij and b_i. To reduce the total number of parameters, α(t, s) will be set to zero for s ∈ [0, 1]. No cells enter this region, and hence the birth rate is arbitrary there. The s-nodes are not evenly spaced (see Table 4) but were chosen after considerable trials with both forward simulations and parameter estimations. As a general rule, the s-nodes need to be closely spaced in order to accurately model the data. Choosing too few nodes results in a poor estimation of the proliferation rate, often with the result of additional generations of cells appearing too early in the model solution. Choosing too many nodes leads to over-discretization and the additional need for some type of regularization. Here, we employ so-called regularization by discretization as described in Banks and Iles (1987), Banks and Kunsich (1989). The time nodes are evenly spaced every 12 hours in the region t ∈ [36, 120]. For t ∈ [0, 24], α(t, s) is set to zero as it is clear from the data that no proliferation occurs during this time.

Table 4.

Best fit (OLS) parameters shown along with the s (left column) and t (top row) nodes for the proliferation rate α(t, s). The function α(t, s) is shown graphically in Fig. 8. Note that α(0, s) = α(12, s) = α(24, s) = 0 and was not estimated

sj\ti	36	48	60	72	84	96	108	120
1.2500	0.0000a	0.0000a	0.0000a	0.0000a	0.2023	0.0158	0.0004	0.0002
1.5000	0.0000a	0.0000a	0.0000a	0.0000a	0.0187	0.0020	0.0014	0.0159
1.6250	0.0000a	0.0000a	0.7755	0.0045	0.0000	0.0022	0.0152	0.0226
1.7500	0.0000a	0.0000a	0.0468	0.1303	0.0130	0.0179	0.0342	0.0684
1.8750	0.0000a	0.0000a	0.0309	0.0231	0.0496	0.0143	0.0079	0.0796
2.0000	0.0000a	0.0000a	0.0000	0.0000	0.0435	0.0588	0.0415	0.1467
2.1250	0.1103	0.4173	0.0876	0.0000	0.1019	0.0001	0.0447	0.0715
2.2500	0.0082	0.0001	0.0014	0.0390	0.0001	0.1491	0.1954	0.2255
2.3750	0.1354	0.0002	0.1775	0.0055	0.0806	0.0000	0.0868	0.1318
2.5000	0.0111	0.0003	0.0020	0.2003	0.0000	0.2007	0.1694	0.3725
2.6250	0.0015	0.0148	0.2894	0.0000	0.1658	0.0006	0.0761	0.2036
2.7500	0.0008	0.1159	0.2415	0.3985	0.0011	0.1409	0.4961	0.2110
2.8750	0.0159	0.0013	0.0230	0.1588	0.0000	0.0514	0.0005	0.4284
3.0000	0.0000	0.0378	0.0005	0.2418	0.0064	0.0870	0.0035	0.9661

^aParameter was not estimated but was set to zero as there are no cells observed in our data set at these fluorescent levels at the given times

Also as before, it will be assumed that the rate of label loss is proportional to total label concentration, resulting in ν(z) = −c in the model (14). This form was found in Luzyanina et al. (2007) to provide a better fit to this data set as compared to constant label loss. Forward simulations indicate c ∈ [0.0025, 0.0055] to be a reasonable range. The ranges of values for the parameters to be estimated in the modified model (14) are then no different from those given in Table 1, for estimating parameters in the original model (2).

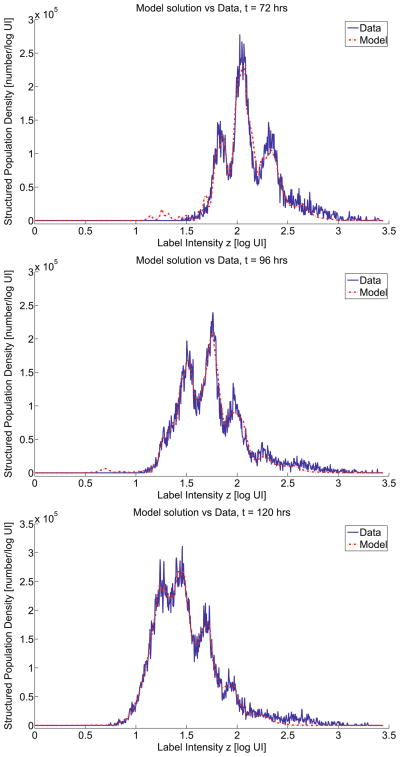
We used the modified model (14)–(16) in an OLS procedure with the data. The corresponding OLS estimation results in ĉ = 0.003288 and γ̂ = 1.5169 with a cost F_OLS(θ̂_OLS) = 5.3181 × 10¹¹. Using this value of c in the translated log intensity coordinate s = z + ct, we plotted the experimental data relative to this coordinate. As seen in Fig. 7, this results in a data plot that correlates remarkably well with division number. The corresponding estimated effective proliferation rate function α̂(t, s) is depicted graphically in Fig. 8 with node values given in Table 4. Similarly, the estimated effective death rate function β̂(s) is shown in Fig. 8 with nodal values given in Table 5. The model solution evaluated at the best-fit parameter vector is compared to the data in Figs. 9 and 10.

Fig. 8.

Graphical representation of the best fit (OLS) death rate β(s) (top) and proliferation rate α(t, s) (bottom). Numerical values are given in Tables 4 and 5.

Table 5.

Best fit (OLS) parameters shown along with the s nodes (left column) for the death rate β(s). In the region s ∈ [0, 2.5], β(s) = b₁ = 0.0665. The functions β(s) is shown graphically in Fig. 8

si	bi
0.0000	0.1003
2.5000	0.1003
2.7500	0.0237
3.0000	0.0000
4.0000	0.0000

Fig. 9.

Improved model solution evaluated at the best fit (OLS) parameters in comparison to the original data: t = 0, 24, 48 hrs.

Fig. 10.

Improved model solution evaluated at the best fit (OLS) parameters in comparison to the original data: t = 72, 96, 120 hrs.

The improvement of the fit to the data is substantial both visually and in terms of lowering the OLS cost function value. The assumption of time dependence for the birth rate function appears justified not only biologically but also by the model/data fits. To verify that this is not merely due to an increase in the number of degrees of freedom, we use the model comparison statistic to test if the reduction in residual sum of squares is statistically significant. When the original model (of Eq. (2) with α not time dependent and only 20 unknown parameters: c, γ, 4 nodes for β(z), 14 nodes for α(z)) is only modified by allowing for time dependence in the proliferation rate α(t, z) with now 102 unknown parameters, the statistic corresponding to the resulting additional r = 82 degrees of freedom is given by

$$U_N=\frac{N(3.2112\times {10}^{12}-9.8423\times {10}^{11})}{9.8423\times {10}^{11}}=12110$$

for N = 5352. This statistic suggests that it is unlikely at extremely high levels of confidence that this improvement in residual would have occurred by chance or by simply the act of increasing the number of degrees of freedom in the model, and supports the inclusion of explicit time dependence in the proliferation rates. We remark that in any such efforts with nonconstant parameters, one could (as is often done in general parametric estimation) substantially reduce the number of parameters to be estimated by employing a distributional form (a reduced order parameter shape or representation) instead of the general parameter representations as in (15)–(16). However, just as in using a maximum likelihood estimator (where assumption of a distributional representation for measurement error is required) or in general Bayesian approaches to estimation, one often loses information by an incorrect assumption regarding an a priori form for the distribution or shape function being estimated. In any case, this part of the model analysis strongly suggests that explicit time dependence in proliferation rates is important in accurately representing and understanding such data sets.

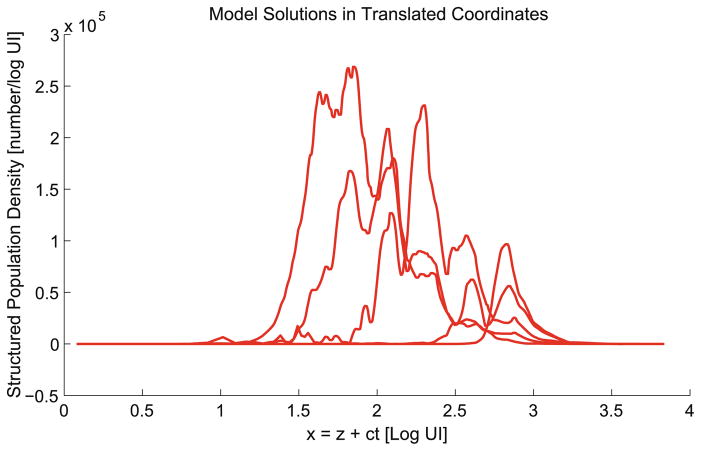
The translation of the intensity variable, in addition to its justification by the experimental setup, provides greater insight into how the proliferation rate varies both in time and with subsequent generations of cells. This modification does not change the number of parameters so we can directly look to the value of the cost functional, which is lower at F_OLS(θ̂_OLS) = 5.3181 × 10¹¹. As a means of reference, the model solution in the translated intensity coordinate is graphed in Fig. 11. Note that the subsequent generation peaks align very closely. Compare also the data in the translated coordinate (Fig. 7).

Fig. 11.

Best fit (OLS) model solution shown in terms of the translated coordinate s = z + ct.

There is some evidence (Luzyanina et al., 2007, 2009) that the death rate function might be treated as a constant, β(s) = β, thereby reducing the total number of parameters while still accurately fitting the data. Adding this restriction to the present formulation (14) and running the OLS estimation procedure again, we obtained a best fit cost of F_OLS(θ̂_OLS) = 8.2045 × 10¹¹. The corresponding test statistic is U_N = 2905, for which it may be concluded from the χ²(3) distribution with very high confidence (>99.999%) that β(z) cannot be treated as a constant for the current data set.

It has been assumed that label loss is strictly proportional to CFSE concentration (ν(x) = −cx; ν(z) = −c), but it may in fact vary in a more complex way based upon the nature of the catabolic activity within the cell. Thus, the possibility is considered that the label loss function might have the form ν(z) = ν₀z − c. Returning to the OLS minimization, we obtained the result ν̂₀ = 7.8921 × 10⁻⁵ with a corresponding cost F_OLS(θ̂_OLS) = 5.3152 × 10¹¹. The other parameters in the model remained largely unchanged. The resulting test statistic (for ν₀ = 0) is U_N = 2.92, and the additional term in the form of the label loss rate would only be supported with 91.25% confidence. The fit of this model to the data is not noticeably different from that depicted in Figs. 9 and 10.

Considering other possibilities, we note that there is also a large body of work on so-called Growth Rate Distribution (GRD) (or Class Rate Distribution (CRD)) models (Banks et al., 1988; Banks and Davis, 2007; Banks and Fitzpatrick, 1991). Adapted to the present application, these models assume that the population is divided into small groups of individuals which share a common label loss rate (the “class” rate) within the group. This is in place of assuming the affine term in the above paragraph. The dynamics of the total population are then defined by the probability distribution of label loss rates within the population. Such variability within the overall population may readily be biologically justified by the variety of catabolic mechanisms underlying the label loss. With a slight change of notation, let n(t, z; c_k) be the structured population density of a cohort of cells all of which have label loss rate c_k. We consider only the parameter c as being distributed as the affine term has already been shown to offer no statistically significant improvement. For simplicity, assume there are a finite number of c_k ’s and that there is a discrete probability measure P defining their distribution within the total population. Then the total population is given by

$$N(t,z;P)=\sum _{k}n(t,z;c_k)p_k.$$

The estimation of the probabilities p_k can be reduced to a quadratic programming problem (as described in Banks and Davis, 2007) which can be quickly and easily solved via MATLAB’s quadprog routine provided the other parameters of the model are fixed. For the current problem, 21 evenly spaced label loss rates in the region c ∈ [0.0015, 0.0055] were considered. In the interest of computational efficiency, fminconand quadprog were used in an alternating fashion in a hybrid algorithm. First, fmincon was used to estimate the other parameters leaving the p_k fixed, and then quadprog was used to estimate the p_k holding the other parameters fixed. Doing so results in a final cost of F_OLS(θ̂_OLS) = 5.3137 × 10¹¹, which gives a model comparison statistic of U_N = 4.43. This is not sufficient to warrant the inclusion of this additional complexity when U_N is compared to the critical values for a χ²(20) distribution. (For similar results in other modeling attempts, see Banks et al., 2003.) The estimated distribution of label loss rates within the population is depicted in Fig. 12. The modifications made from the model in Eq. (14) and the corresponding statistics are summarized in Table 6.

Fig. 12.

Estimated probability distribution of label loss rates c within the population.

Table 6.

Model comparison statistic for the modifications in the table: constant death rate β, affine label loss ν(z) = ν₀z − c, and distributed label loss ν(z) = c ~ P. These are all compared to the version of the model in Eq. (14) with α(t, s), β(s), ν(z) = −c, with a cost functional of F_OLS(θ̂_OLS) = 5.3181 × 10¹¹. Note the row labeled r contains the degrees of freedom for the χ² distribution that the model comparison statistic U_N is to be compared. The bottom row depicts whether or not the more complex model is supported by the statistic

	β	ν(z) = ν0z − c	ν(z) ~ P
FOLS(θ̂OLS)	8.2045 × 1011	5.3152 × 1011	5.3137 × 1011
UN	2905	2.92	4.43
r	3	1	20
Improvement	Yes	No	No

Together, these improvements result in a final model of the form

$$\frac{\partial n(t,z)}{\partial t}+\frac{\partial [-cn(t,z)]}{\partial z}=-(\alpha (t,z+ct)+\beta (z+ct))n(t,z)+{\chi }_{[z_{min},z_{max}-log\gamma ]}2\gamma \alpha (t,z+ct+log\gamma )n(t,z+log\gamma ).$$ (17)

It is worth noting that this particular model, at least at the present, has only been modified to fit the particular data set shown. It is certainly possible that there are biomechanisms which are not manifested in the available data set, and hence are not incorporated into this model. As this mathematical model is applied to different cell types and proliferation assays, it is expected that the model may take on slightly different forms. Still, the techniques used in obtaining this improved model as well as the overall form of the model lay a solid foundation for future work. Given the accuracy of the current model in replicating the experimental data, it is now reasonable to turn to a discussion of the validity of the statistical assumptions underlying the OLS minimization procedure.

4. Estimation improvements

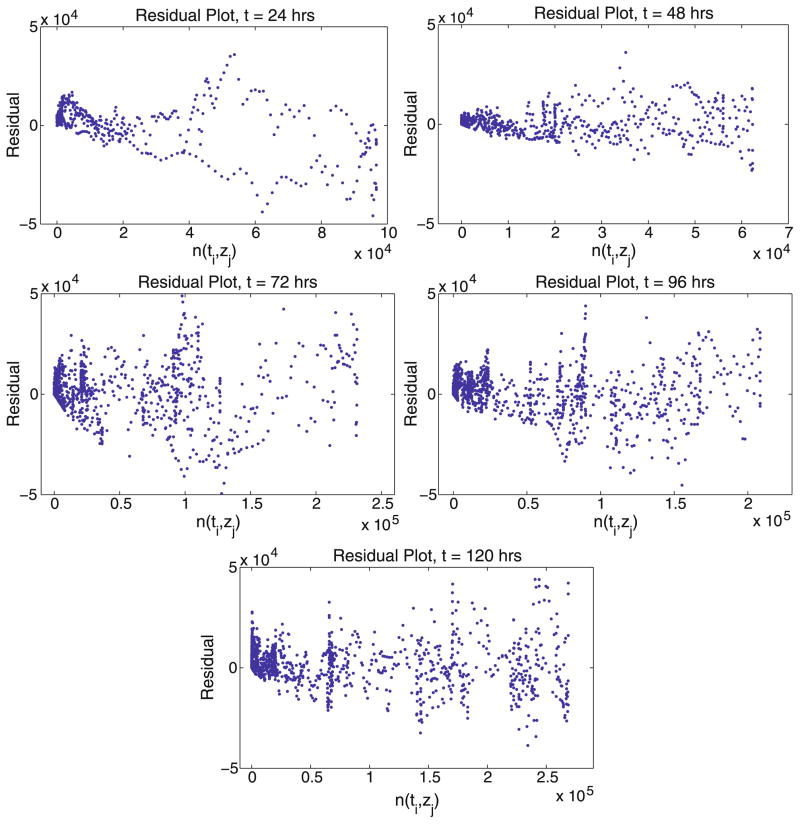
To this point, our focus has remained on the OLS formulation of the inverse problem. Given the best fit model (17) and the best fit OLS estimate θ̂_OLS, the resulting residuals r_ij versus the model values are plotted in Fig. 13.

Fig. 13.

OLS residuals as a function of model value for each time measurement.

On one hand, these residuals certainly do not exhibit the fan-like structure characteristic of data sets in which noise is proportional to the magnitude of the observation (see Fig. 2). However, they do not appear to be random either, slowly growing in variation as the model values increase. Thus, it appears that the assumption of constant variance may not be particularly accurate, and perhaps another assumed error structure should be investigated, resulting in a more general least squares estimation approach, distinct from the two somewhat standard formulations used here.

The results (e.g., model fits, estimated parameter values) of the GLS procedure under the assumption of relative error (i.e., statistical model (7)) that we obtained are sufficiently similar to the results presented in the previous section so that separate graphics and tables are not included here. What is of interest for the current discussion are the residuals r̃_ij, shown in Fig. 14. It is clear that the GLS residuals are not random but slowly decay in time. The conclusion then, is that the underlying statistical model for the variation in our data may have neither CV noise nor noise which is proportional to the magnitude of the observation. This is not surprising given the complexity of the error in the observation or measurement process (see Wikipedia, 2010 for a discussion of the general analysis of error in data collection procedures). We remark that we do not use log likelihood estimation or error quantification methodology here because such an approach explicitly (by the form of the likelihood function employed) implies that we know a priori the distribution for measurement error in the underlying statistical model (e.g., see the discussions in Banks et al., 2009).

Fig. 14.

GLS residuals as a function of model value for each time measurement.

In order to accurately and correctly compute standard errors and confidence intervals, the assumptions of the underlying statistical model must be reasonably correct (for the asymptotic formulae to be meaningful; see Banks et al., 2009). However, it appears that the error is not represented well by the statistical models in either the OLS (with constant variance error) or GLS (with proportional error) formulations. Therefore, estimations of the reliability of the parameter estimates (e.g., standard errors and confidence intervals) would be invalid and are not pursued further in this work. One could, of course, use bootstrapping to compute standard errors, but that is extremely computationally expensive for our problem and also involves some underlying assumptions (Banks et al., 2010), perhaps unsatisfied for our problem. Indeed, the error structure of the observed data may take several different forms. One possibility is that the noise may be proportional to some power λ of the observations

$$N_{ij}^d=n(t_i,z_j;{\overrightarrow{\theta }}_0)+n^{\lambda }(t_i,z_j;{\overrightarrow{\theta }}_0){\mathcal{E}}_{ij},$$

where λ is now an additional parameter to be estimated (see Carroll and Ruppert, 2000; Davidian and Giltinan, 1995 for discussions). More generally, the noise could depend on some general function g of n(t_i, z_j ; θ⃗₀):

$$N_{ij}^d=n(t_i,z_j;{\overrightarrow{\theta }}_0)+g(t_i,z_j;{\overrightarrow{\theta }}_0,n(t_i,z_j;{\overrightarrow{\theta }}_0)){\mathcal{E}}_{ij}.$$

The determination of the parameter λ or the function g represents a difficult computational challenge and is a topic for future work that will require more careful analysis of the data collection process in the context of multiple data sets. Once ascertained and verified by the appropriate residual plots, the statistical model could then be used to quantify uncertainty in the estimates of the parameters of the model.

It is worth one further remark to note that the inaccuracies in the underlying statistical models do not invalidate the entire parameter estimation procedures we have pursued. The various methods of parameter estimation (OLS, GLS, etc.) all give very similar results and the figures of the previous sections demonstrate the accuracy of those results. The determination and validation of the statistical model simply provides an improvement to the estimation procedure that would permit the accurate quantification of uncertainty in the resulting estimated parameters.

5. Concluding remarks

The use of CFSE-based proliferation assays has been and will continue to be a powerful technique for monitoring a dividing cell population. Coupled with the high-throughput capacity of FACS, there are near limitless possibilities for the use of this technology to track cell divisions and division dependent changes. In this report, a mathematical model governing the population density of a population of proliferating CD4+ lymphocytes is proposed and its remarkable agreement with a FACS data set is demonstrated. This approach provides an alternative to current modeling efforts and does not require prescribed distributions on CFSE or other birth and death events. It also allows for direct comparison of solutions to data without preprocessing.

The current model demonstrates that the effective rate of proliferation within a population of cells depends not only on the number of divisions undergone, but also on the elapsed time since stimulation, as supported by a model comparison statistic. In addition to quantifying this effect, the estimation of the proliferation and death rate functions defined on a translated domain (which correlates more closely with division number than CFSE intensity alone at the current time) permits a better quantitative understanding of how these rates change with division number.

The effective rates of proliferation α(t, z + ct) and death β(z + ct) introduced in our models here can be correctly viewed as rates relative to the moving coordinate system s = z + ct (which corresponds more closely with division number) as compared to rates relative to the more obvious fixed coordinate z of log intensity. As in other fields of science and engineering, it can also be valuable in biological rate estimation to use such quantities to compare, characterize, or delineate cell populations with respect to their normality or lack thereof (as in diseased, infected, etc., cell populations). Specifically, if one can effectively use inverse problem techniques to reliably estimate these effective or relative rates from CFSE data on cell populations, this could lead to a significant new disease identification procedure.

Analysis of the statistical models underlying the noise in the data reveals that the noise in the data may have neither constant variance nor variance proportional to the magnitude of the observation itself. While this does not invalidate the results presented, it does suggest a possible direction for future computational work which will aid in the accurate quantification of the uncertainty associated with the estimated parameters in such problems.

While the current report focuses only on cell proliferation and death rates in terms of the number of divisions undergone, other division dependent properties (cell surface marker exhibition, cytokine content, etc.) can also be measured simultaneously by FACS during a proliferation assay (Quah et al., 2007). This, along with the applicability of the technique to a wide variety of cell types, has potentially profound applications in oncology (cancer metastasis and differentiation from normal cells), virology (latent viruses, HIV), and immunology (allergens, tissue grafting), either in the context of an interpretive framework, as a diagnostic tool, or even as part of a control mechanism (see, e.g. Bellomo and Preziosi, 2000; Gyllenberg and Webb, 1990; Hawkins et al., 2007; Komarova, 2006; Komarova and Wodarz, 2007).

Appendix: Derivation of model

The original PDE model proposed in Luzyanina et al. (2007) is a case of the Bell–Anderson model (Bell and Anderson, 1967) for populations which divide by fission. It was published like the Sinko–Streifer model (Sinko and Streifer, 1967) in 1967, and arrives at the same general equation form. Let n(t, x) be the population density of a labeled population with structure variable x, where x represents the fluorescence intensity (FI) of a cell. Then

$$N(t)={\int }_{x_0}^{x_1}n(t,x)dx.$$ (A.1)

represents the total number of cells with fluorescence intensity in (x₀, x₁). Here, x₀ and x₁ are arbitrary with the exception that [x₀, x₁] ⊂ [x_min, x_max/γ] or [x₀, x₁] ⊂ (x_max/γ, x_max]. Let Δx(t, x, Δt) be the average increase of FI of cells with initial intensity x during the interval (t, t + Δt) and assume that Δt is chosen such that |Δx| ≪ x₁ − x₀, so that the number of cells which move into the region via division and subsequently divide, die, or drift out of the region is negligible. It should be noted that Δx will be nonpositive as cells cannot increase in FI. Thus, subtraction by Δx actually results in a larger value. While counterintuitive, this definition is maintained in order to harmonize with other structured population models.

Consider the change in N (t) during the time interval (t, t + Δt), i.e., the quantity N (t + Δt) − N (t). Five possible contributions will be considered:

1. Cells of intensity in the interval [x₁, x₁ − Δx(t, x₁, Δt)], losing FI according to Δx:

   $${\int }_{x_1}^{x_1-\mathrm{\Delta }x(t,x_1,\mathrm{\Delta }t)}n(t,x)dx.$$

2. Cells of intensity in the interval [x₀, x₀ − Δx(t, x₀, Δt)], losing FI according to Δx:

   $${\int }_{x_0}^{x_0-\mathrm{\Delta }x(t,x_0,\mathrm{\Delta }t)}n(t,x)dx.$$

3. Cells which would have contributed to N (t + Δt) had they not died:

   $${\int }_t^{t+\mathrm{\Delta }t}{\int }_{x_0-\mathrm{\Delta }x(t,x_0,\tau -t)}^{x_1-\mathrm{\Delta }x(t,x_1,\tau -t)}\beta (x)n(\tau ,x)dxd\tau .$$

4. The disappearance of cells from the region due to proliferation:

   $${\int }_t^{t+\mathrm{\Delta }t}{\int }_{x_0-\mathrm{\Delta }x(t,x_0,\tau -t)}^{x_1-\mathrm{\Delta }x(t,x_1,\tau -t)}\alpha (x)n(\tau ,x)dxd\tau .$$

5. The gain of daughter cells (two of them) in the region as a result of proliferation in the parent region:

   $${\chi }_{[x_{min},x_{max/\gamma }]}2{\int }_t^{t+\mathrm{\Delta }t}{\int }_{\gamma x_0}^{\gamma x_1}\alpha (x)n(\tau ,x)\mathit{dxd}\tau .$$

Then the difference ΔN(t) can be computed by summing the quantities in items (i) through (iv) in the following way: N (t + Δt) − N (t) = (i) – (ii) – (iii) – (iv) + (v). Following the standard procedure of dividing by Δt and letting Δt → 0, this gives $\frac{dN}{dt}$ on the left side. For the first term on the right side, if n(t, x) is continuous in t and x (a reasonable assumption), the Mean Value Theorem (MVT) implies that there exists a θ ∈ [x₁, x₁ − Δx(t, x₁, Δt)] such that

$${\int }_{x_1}^{x_1-\mathrm{\Delta }x(t,x_1,\mathrm{\Delta }t)}n(t,x)dx=-\mathrm{\Delta }x(t,x_1,\mathrm{\Delta }t)n(t,\theta ).$$ (A.2)

Assuming Δx is continuous in Δt (that is, there is no instantaneous label loss) and varies smoothly, we have

$$\underset{\mathrm{\Delta }t\to 0}{lim}\frac{-\mathrm{\Delta }x(t,x_1,\mathrm{\Delta }t)}{\mathrm{\Delta }t}n(t,\theta )d\theta =-v(x_1)n(t,x_1),$$ (A.3)

where $\frac{dx}{dt}=v(x)$, the rate of FI change of cells of intensity x. Applying the same argument for the second term, we find

$${\int }_{x_0}^{x_0-\mathrm{\Delta }x(t,x_0,\mathrm{\Delta }t)}n(t,x)dx=-v(x_0)n(t,x_0).$$ (A.4)

In the consideration of the third term, define

$$u_{\beta }(\tau )={\int }_{x_0-\mathrm{\Delta }x(t,x_0,\tau -t)}^{x_1-\mathrm{\Delta }x(t,x_1,\tau -t)}\beta (x)n(\tau ,x)dx.$$ (A.5)

Then if Δx(t, x, Δt) and β(x)n(t, x) are continuous functions of their variables, so is u_β (τ) and by the MVT, there exists a θ′ [t, t + Δt] such that

$$\frac{1}{\mathrm{\Delta }t}{\int }_t^{t+\mathrm{\Delta }t}{u}_{\beta }(\tau )d\tau =u_{\beta }({\theta }^{\prime }).$$ (A.6)

Thus, it follows that

$$\underset{\mathrm{\Delta }t\to 0}{lim}{u}_{\beta }({\theta }^{\prime })=u(t)={\int }_{x_0}^{x_1}\beta (x)n(t,x)dx,$$ (A.7)

assuming Δx(t, x, 0) = 0 for all t, x (which follows from the previous assertion regarding the smoothness of Δx in Δt). Using a similar argument for the fourth term, we have

$$\underset{\mathrm{\Delta }t\to 0}{lim}{u}_{\alpha }({\theta }^{\prime })=u_{\alpha }(t)={\int }_{x_0}^{x_1}\alpha (x)n(t,x)dx,$$ (A.8)

where u_α (τ) has the obvious definition.

For the final term, the same argument along with the change of variables ξ = x/γ results in

$${\chi }_{[x_{min},x_{max/\gamma }]}2\underset{\mathrm{\Delta }t\to 0}{lim}{u}_{\stackrel{\sim }{\alpha }}({\theta }^{\prime })={\chi }_{[x_{min},x_{max/\gamma }]}2\gamma {\int }_{x_0}^{x_1}\alpha (\gamma x)n(t,\gamma x)dx.$$ (A.9)

Altogether,

$$\frac{dN}{dt}=-v(x_1)n(t,x_1)+v(x_0)n(t,x_0)-{\int }_{x_0}^{x_1}\beta (x)n(t,x)dx-{\int }_{x_0}^{x_1}\alpha (x)n(t,x)dx+{\chi }_{[x_{min},x_{max/\gamma }]}2\gamma {\int }_{x_0}^{x_1}\alpha (\gamma x)n(t,\gamma x)dx.$$ (A.10)

On the left side, differentiating $N(t)={\int }_{x_0}^{x_1}n(t,x)dx$ with respect to t we find

$$\frac{dN}{dt}={\int }_{x_0}^{x_1}\frac{\partial n(t,x)}{\partial t}dx.$$ (A.11)

Finally, by applying the fundamental theorem of calculus to the first two terms of (A.10), simplifying and rearranging, we have

$${\int }_{x_0}^{x_1}\frac{\partial n(t,x)}{\partial t}+{\int }_{x_0}^{x_1}\frac{\partial (v(x)n(t,x)}{\partial x}=-{\int }_{x_0}^{x_1}(\alpha (x)+\beta (x))n(t,x)+{\chi }_{[x_{min},x_{max/\gamma }]}2\gamma {\int }_{x_0}^{x_1}\alpha (\gamma x)n(t,\gamma x).$$ (A.12)

Equivalently (because x₀ and x₁ were arbitrary),

$$\frac{\partial n(t,x)}{\partial t}+\frac{\partial [v(x)n(t,x)]}{\partial x}=-(\alpha (x)+\beta (x))n(t,x)+{\chi }_{[x_{min},x_{max/\gamma }]}2\gamma \alpha (\gamma x)n(t,\gamma x).$$ (A.13)