Optimal Spacing of Surface Electrode Arrays for Brain Machine Interface Applications

Abstract

Brain-machine interfaces (BMIs) use signals recorded directly from the brain to control an external device, such as a computer cursor or prosthetic limb. These control signals have been recorded from different levels of the brain, from field potentials at the scalp or cortical surface to single neuron action potentials. At present, the more invasive recordings have better signal quality, but also lower stability over time. Recently, subdural field potentials have been proposed as a stable, good quality source of control signals, with the potential for higher spatial and temporal bandwidth than EEG. Here we used finite element modeling in rats and humans and spatial spectral analysis in rats to compare the spatial resolution of signals recorded epidurally (outside the dura), with those recorded from subdural and scalp locations. Resolution of epidural and subdural signals was very similar in rats, and somewhat less so in human models. Both were substantially better than signals recorded at the scalp. Resolution of epidural and subdural signals in humans was much more similar when the cerebrospinal fluid layer thickness was reduced. This suggests that the less invasive epidural recordings may yield signals of similar quality to subdural recordings, and hence may be more attractive as a source of control signals for BMIs.

1. Introduction

Brain-machine interfaces (BMIs) have the potential to improve the quality of life of thousands of people who have been paralyzed by disorders including stroke, spinal cord injury, and amyotrophic lateral sclerosis (ALS). Potential applications of BMIs range from providing a computer interface for environmental control and communication [1-3] to restoring the use of a paralyzed limb [4, 5]. The field of brain-machine interfacing has undergone tremendous growth in the last decade, and many groups have developed unique approaches. Control signals for BMIs have been successfully derived from the scalp (electroencephalography; EEG) [1, 2, 6-8], the surface of the pia mater (subdural, electrocorticography; ECoG) [9-12], and from intracortical single- and multi-unit action potentials (spikes) [3, 13, 14]. Scalp EEG has the advantage of being noninvasive, but it contains less information than either intracortical or subdural signals due to both temporal and spatial filtering by intervening tissues and cerebrospinal fluid. However, current intracortical arrays can record action potentials for only a limited time [15], typically a few years [16]. One possible source of control signals that has been only minimally investigated is the surface of the dura. Two groups have used these epidural field potentials (EFPs) in humans to control a simple binary switch. One compared visual evoked potentials from occipital cortex to a template waveform [17] and the other detected threshold crossings of the signal recorded from a skull screw over motor cortex when the subject moved his foot [18]. A third group has shown some preliminary evidence that EFPs can be used for proportional cursor control [19]. We hope to show that these signals have the potential to provide even greater amounts of information. Placing electrodes outside the dura could allow us to record signals similar in quality to ECoG without incising the dura. This would significantly reduce the risk of stroke, hemorrhage, or infection associated with the electrodes—an infected subdural electrode could cause a serious infection of the brain parenchyma itself, while infection of epidural electrodes would be very unlikely to involve the brain.

Thus far, information rates from scalp- and spike-controlled BMIs have been compared only indirectly, retrospectively using widely different numbers of electrodes, species, and behavioral tasks [2]. Moreover, the optimal inter-electrode spacing of the arrays used to record these signals has not been investigated at any of these levels. This is an important step. We may, for example, be losing information by sampling ECoG with the standard 1 cm clinical electrode spacing.

This study systematically investigated the optimal spacing of subdural, epidural, and scalp electrodes. We used both a cortical dipole computer model and spatial spectral analysis [20] of data recorded from rats to determine the optimal inter-electrode spacing at each level. The results of both techniques in rats were in close agreement.

2. Methods

2.1. Finite element model

Finite element (FE) methods have been used frequently to solve the forward problem in EEG analysis, that is, to compute the potential at the surface of the scalp that would result from a layer of current sources [21-25]. Although these sources are time-varying, the quasi-static approximation [26] states that for frequencies under 1 kHz, brain impedances are predominantly resistive [27], and thus time-varying sources can be modeled electrostatically, i.e. as static dipoles. In this study, we used an FE model to determine the minimum electrode spacing at which the signals from cortical dipoles could be distinguished from one another based on how sharply the potential from a single, small dipole source attenuated with distance parallel to the brain's surface. We considered the minimum spacing necessary to avoid detection of the signal by multiple electrodes to be the distance at which the potential decreased to 10% of its peak. The FE method was used to generate models of both rat and human heads using both simple and more realistic geometries. The rodent models included five layers of tissues (gray matter, cerebrospinal fluid (CSF), dura matter, skull, and scalp) and the human models included an additional white matter layer. The dipole was placed in layers II-III of the cortex, thought to be the origin of the field potential signals recorded outside the brain [28, 29]. The dipole was modeled as two point sources with opposite current at two separate nodes of the model [23]. The potential generated by a current source is given by the Poisson equation [30]

$$\nabla \cdot (\sigma \nabla (V))=J,$$ (1)

where ∇ is the gradient operator, V is the potential and J is the current source density of the dipole. The solution to the Poisson equation in a single layer is given by

$$V=I/(4\pi r\sigma ),$$ (2)

where I is the magnitude of each source, σ is the conductivity, and r is the distance from the source. Because our model consists of multiple layers with different conductivities, boundary conditions need to be considered. Charge cannot accumulate on the boundary between two layers, so the interior boundary conditions can be given by the equations:

$$J_1\cdot e_{\text{n}}=J_2\cdot e_{\text{n}\text{'}},$$ (3)

$$({\sigma }_1\nabla (V_1))\cdot e_n=({\sigma }_2\nabla (V_2))\cdot e_{n\text{'}},$$ (4)

where e_n = e_n′ and is the normal component to the surface of the boundary and the subscripts denote layers 1 and 2. No current can be injected into the scalp layer from the surrounding air due to its very low conductivity (10^-10 S/m). Thus the boundary condition for the scalp layer is

$$J_1\cdot e_{\text{n}}=0.$$ (5)

These boundary conditions constitute the Neumann boundary conditions for the model [23, 30]. The Dirichlet boundary conditions state that there cannot be voltage discontinuities when crossing the interface from one layer to another:

$$V_1=V_2.$$ (6)

2.1.1. Rat Model

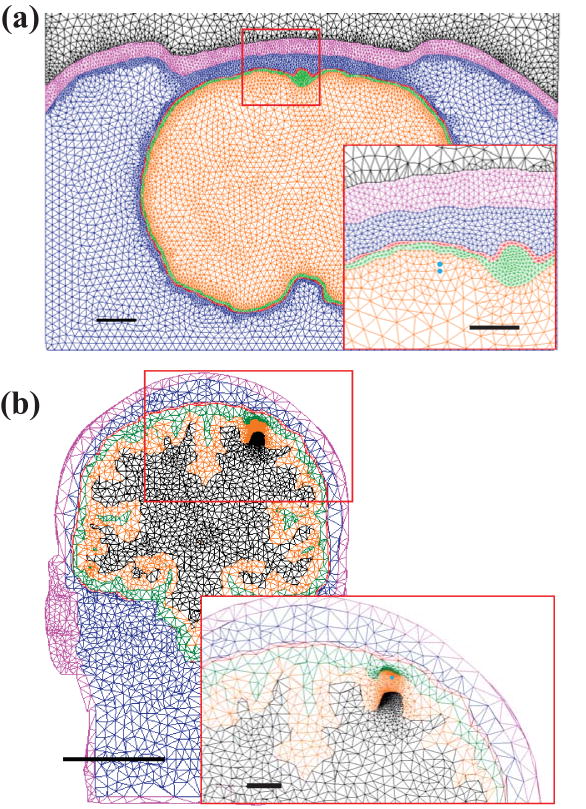
The realistic rat model was constructed from MR images. A sagittal slice through the sensorimotor cortex (see Figure 1(a)) was chosen, and regions of brain, CSF, dura, bone and scalp were segmented using Materialise Mimics (Leuven, Belgium) and MSC Patran (Santa Ana, CA). Conductivity values were 0.27, 1.79, 0.065, 0.02, and 0.465 S/m, respectively (see Table 1), in accordance with the literature [31-35]. These layers were rotated around the superior-inferior axis to create a 3D model that contained realistic geometry. A dipole was placed in layers II-III of the motor cortex with the poles 0.3 and 0.4 mm below the cortical surface (Figure 1(a), inset). The mesh density around the dipole was increased to ensure accurate results. The model consisted of approximately 1.26 million tetrahedral elements with a spacing of about 20 μm in the region of the dipole. This model was solved [36] using ANSYS (Canonsberg, PA). The simpler model consisted of five concentric spheres (representing the same layers as those of the realistic model), and was also built and simulated using COMSOL Multiphysics (Burlington, MA). We used the simpler model to investigate effects of variation of model parameters, due to the complexity and computational cost involved in altering and simulating the realistic model. For the realistic model, all tetrahedra were represented by ten node elements which allowed a quadratic solution to the equations.

Figure 1.

Schematic of segmented coronal images of (a) rat and (b) human heads. Layers from the inside out are gray matter, CSF, dura, skull, scalp, and air. Dipole location (not actual size) is shown by the blue dots (inset). Scale bars represent (a) 1 mm (0.5 mm inset) for rats and (b) 50 mm (10 mm inset) for humans.

Table 1.

Summary of conductivity and layer thicknesses used in the spherical finite element models. Conductivity ranges in brackets refer to those values that were varied to examine effects of inhomogeneity. In the rat model, all brain tissue was treated as gray matter.

Tissue	Conductivity (S/m)	Thickness (mm)
		Human	Rat
Scalp	0.465	5.0	0.5
Skull	0.02 [0.02-0.08]	5.0	0.5
Dura mater	0.065	0.36	0.1
CSF	1.79	3.1	0.1
Gray matter	0.27	3.7	5.0
White matter	0.126 [0.126-1.0]	60	--
Dipole depth		0.8-1.0	0.3-0.4

2.1.2. Human Head Model

Human MR images at a resolution of 1 mm were used to construct the realistic 3D human head model (shown in Figure 1(b)). The images were segmented into regions of white matter, gray matter, CSF, dura, bone, and scalp. White matter conductivity was set to 0.126 S/m and conductivities of the other layers matched those of the rat models (Table 1). A dipole was placed at a depth of 0.8 - 1.0 mm below the surface of the brain. This model consisted of approximately 1.08 million tetrahedral elements with a spacing of about 50 μm in the region of the dipole. The simple, concentric spherical human head model was built using outer radii of 60, 63.7, 66.8, 67.16, 72.16 and 77.16 mm.

Each tissue layer was treated as a homogeneous conductor. To check this assumption, we also varied bone conductivity and WM conductivity in the spherical model. For most simulations, all layers were assumed to be isotropic; however we did briefly assess the effect of this assumption by including anisotropy in the skull and white matter in the spherical model using conductivities satisfying Wang's constraint [37, 38] for the relation between isotropic and anisotropic conductivities. Characterization of white matter anisotropy in a realistic head model requires diffusion tensor imaging, which was not available to us for this study.

2.2. Experimental methods

2.2.1. Electrode array construction

Electrode arrays were built using sheets of medical-grade silicone (Silastic, BioPlexus Corp, Saticoy, CA). Teflon-insulated platinum or platinum-iridium wires (0.125 mm diameter, Cooner Wire Co., Chatsworth, CA) were embedded in the sheet using a stereotaxic micromanipulator. Wires were spaced 0.5 mm apart in a 16×1 array (or 32×1 for scalp recordings) and trimmed to lie flush with the Silastic sheet. A polyvinylsiloxane adhesive was used to secure the wires, which were attached to a skull-mounted connector.

2.2.2. Experimental design

All surgical and experimental procedures were approved by the Animal Care and Use Committee of Northwestern University. Adult male Long-Evans rats were anesthetized with ketamine and xylazine and placed in a stereotaxic frame. The skin and soft tissue were retracted, and a craniectomy was made over the right sensorimotor cortex leaving the dura intact. The electrode array was placed in an anterior-posterior orientation from approximately 3.5 mm posterior to bregma to 4.5 mm anterior to bregma, and from 2 to 3 mm lateral to the midline. Ground and reference wires were attached to skull screws. Both acute (non-survival) and chronic experiments were performed. For chronic implants, the array and craniectomy were covered with medical-grade silicone adhesive, and the entire exposed site was covered with dental acrylic (polymethyl methacrylate).

Recordings were made under one of three conditions: anesthetized, anesthetized with peripheral electrical stimulation, and freely moving. During acute experiments, sequential recordings were made with the same electrode array from scalp, epidural, and subdural locations. Peripheral cutaneous stimulation (1-3 mA, 140-180 μs pulses at 5 Hz) was performed at several sites to produce somatosensory evoked potentials (SSEPs). Epidural field potentials were also recorded while chronically-implanted rats moved freely inside an enclosure. Signals were conditioned using a high-impedance headstage (Tucker Davis Technologies, Alachua, FL), then band-pass filtered from 5-180 Hz, and sampled at 400 Hz.

2.3. Spatial spectral analysis

Spatial spectral analysis [20] was performed as follows. At each sample in time, the 16- or 32-channel data vector was padded with zeros to produce a 32- or 64-point vector, respectively. A Hamming window was applied, and then a 32- or 64-point FFT was used to calculate the power spectrum. Zero-padding and windowing smoothed out the power spectra slightly, but did not significantly alter the result [28]. The resulting power spectra were averaged over ten separate segments of data, each 10 s (4,000 samples) long. The ten mean spatial spectra were plotted on a log-log scale. Figure 2 shows an idealized spectrum consisting of a segment in mid-spatial frequencies that declined according to an inverse power law (i.e., as $\stackrel{1}{}/\underset{f^{\alpha }}{}$). At higher spatial frequencies, the power spectrum is flat, corresponding to white noise. The intersection of the $\stackrel{1}{}/\underset{f^{\alpha }}{}$ and flat regions at F_c marks the high end of the spatial passband of the signal, i.e., the maximum spatial frequency not dominated by white noise. In an earlier study of spatial spectral analysis in human ECoG, these two regions were fit using linear least-squares regression [28]. However, in our experience, there was substantial variability in the fits depending on the somewhat arbitrary decision of which points were used to fit the 1/f^α region. Therefore, we used a slightly different approach to determine F_c. Starting at the highest frequency and moving to the left on the plot, one-tailed t-tests were performed to determine the first spatial frequency at which the 10 data points (one from each spatial spectrum) had significantly more power than the points to the right (i.e., the noise floor). A p value of 0.15 gave the most consistent results compared to visual inspection by multiple investigators. The Nyquist criterion applied to F_c yielded the maximum inter-electrode spacing that would avoid spatial aliasing: $\frac{1}{2^{\ast }{F}_c}$.

Figure 2.

An idealized spatial spectrum. The dotted line represents the spectrum of one 4,000 point subset of the data. F_c marks the upper end of the spatial passband above which the signal becomes dominated by white noise.

Since referencing schemes can affect the properties of recorded signals, we also examined the effect on the spatial spectra of two commonly used methods: bipolar referencing, equivalent to the spatial difference of the signals, and common average referencing [39].

3. Results

3.1. Modeling results

3.1.1. Rat model

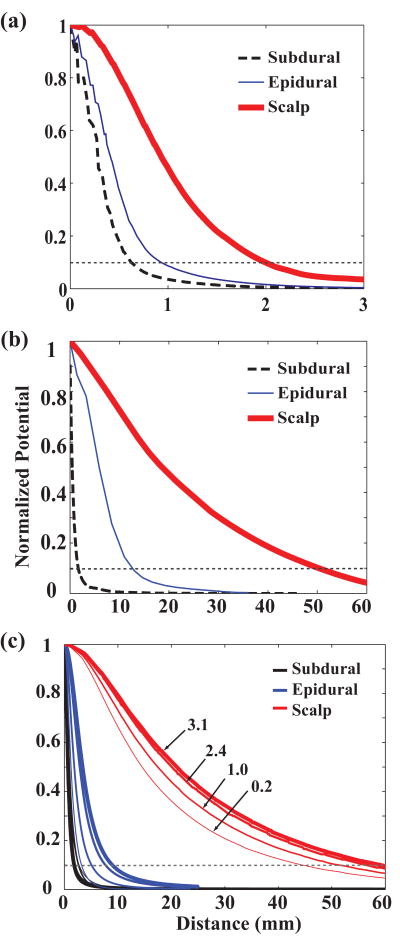
Since the potential distributions were circularly symmetric in all cases, we examined 1-D cross sections for simplicity. Figure 3(a) shows the normalized potential distributions at subdural (dashed black), epidural (thin blue), and scalp (thick red) locations. As expected, the potential at the scalp had a much broader distribution than either the subdural and epidural potentials, which were similar to each other. The subdural and epidural potentials crossed the 10% threshold at 0.6 mm and 0.9 mm, respectively, while the scalp potential crossed at 2.0 mm. Results from the spherical model of the rat head using the same layer thicknesses showed slightly broader potential distributions than the realistic model: subdural and epidural crossings at 10% were 0.8 and 1.1 mm, respectively, while the scalp crossed at 4.5 mm. Because of some uncertainty in the depth of the source of surface potentials, we varied dipole depth from 0.35 mm to 0.75 mm. Potential distributions (measured at the 10% threshold) for subdural, epidural, and scalp broadened by 83%, 60%, and 11%, respectively, as the dipole depth increased.

Figure 3.

Finite element model normalized potential distributions. (a) Rat realistic head model. Subdural (black dashed) and epidural (blue thin) potentials cross the 10% line (gray dotted) at 0.5 and 0.7 mm, while scalp (thick red) crosses at 2.2 mm. (b) Human realistic head model. Epidural potential is broader than subdural but still much sharper than scalp. (c) Human spherical model using CSF thicknesses from 0.2 to 3.1 mm. As CSF layer gets thinner (thinner lines), epidural (blue) and scalp (red) curves sharpen dramatically and epidural potential approaches subdural potential (black).

3.1.2. Human model

Figure 3(b) shows the normalized potential distributions in the realistic human model with the dipole centered at 0.9 mm below the cortical surface. The threshold crossings for the realistic model were 1.7, 13.0, and 51.0 mm, for subdural, epidural and scalp, respectively, while the spherical model produced results of 1.8, 9.0, and 59.1 mm. While threshold crossings were larger for epidural than subdural, that for scalp was vastly larger than either. Since placement of electrodes outside the dura is likely to compress the CSF layer, we examined the effect of different CSF layer thicknesses (ranging from 0.2 mm to 3.1 mm). As seen in Figure 3(c), as the CSF layer thinned (thinner lines), the epidural distribution (blue lines) approached the subdural distribution (black lines). At 0.2 mm thickness, the subdural and epidural threshold crossings differed by only 0.6 mm (2.6 and 3.2 mm, respectively). Thus, by compressing the CSF layer, it may be possible to increase epidural resolution to a level nearly as good as subdural resolution. As in rats, the distributions broadened with increasing dipole depth from 0.9 to 1.4 mm by 67%, 9%, and 5% at subdural, epidural and scalp, respectively. Thus any uncertainty in dipole location mainly affected subdural estimates.

We also investigated whether the broadening of the potentials from subdural to scalp was due more to distance than to conductivity. Since the layers with the extreme values of conductivity were CSF, skull, and scalp, we hypothesized that these conductivities would have the greatest effect on potential distributions. Therefore, we first set the conductivities of white matter, CSF and dura to be equal to that of the gray matter. This caused no change in the subdural potential, slight (8%) sharpening of the epidural potential, and a 12% sharpening of the scalp potential. These modest changes suggest that much of the difference between epidural and subdural potentials was due to the thickness of the CSF, rather than its high conductivity. When instead, we set the skull and scalp layer conductivities to the same value as the dura, the potentials broadened negligibly for subdural and 5% for epidural, but sharpened significantly (by 48%) for scalp. Finally, setting the conductivities of all layers equal to that of gray matter affected primarily the scalp potential (49% sharpening) with no change to subdural, and 4% broadening of epidural potentials. This suggests that the bone and scalp conductivities have a significant effect on the scalp, but not on subdural or epidural potentials.

To assess whether tissue anisotropy or inhomogeneity might affect our results, we first varied bone conductivity from 0.02 to 0.08 S/m (corresponding to the difference in cortical and cancellous bone conductivity, respectively [31]). This had no effect on subdural and epidural potentials but sharpened the scalp potential by 28%. We then included skull anisotropy in the model using a conductivity tangential to the surface of 0.040 S/m and radial conductivity of 0.004 S/m [38]. This affected only the scalp potential, broadening it by 7%. Varying white matter conductivity from 0.13 to 1.0 S/m produced a 5% broader subdural potential, a 10% broader epidural potential, and a 3% broader scalp potential. We then incorporated white matter anisotropy using radial conductivity (along white matter fibers) of 0.40 S/m and tangential conductivity of 0.04 S/m. The anisotropic model produced slightly broader potentials: 7% for subdural, 16% for epidural, and 12% for scalp. When we incorporated white matter anisotropy into the model with CSF thickness of 0.2 mm, there was only a 2% widening of subdural and epidural potentials and a 10% widening of scalp potentials. Since these effects were relatively small, we did not incorporate anisotropy into the rest of our models.

3.2. Spatial spectral analysis results

3.2.1. Acute experiments

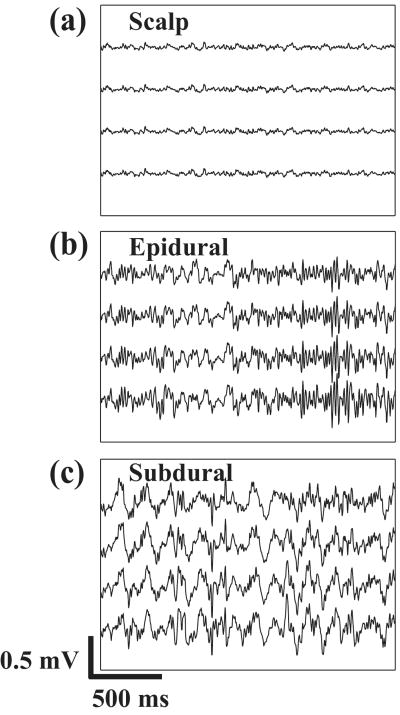
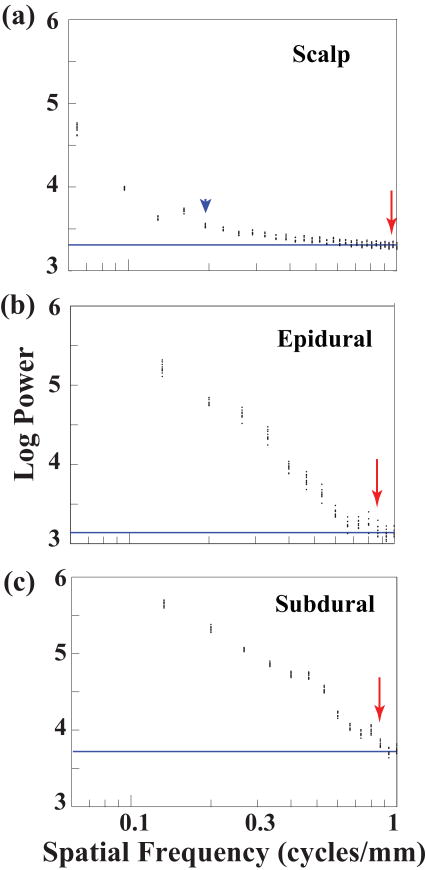
Figure 4 shows examples of signals recorded under anesthesia from scalp, epidural, and subdural locations. As expected, amplitude increased from scalp to subdural locations. Examples of spatial spectra from these acute experiments are shown in Figure 5. The estimated noise floor is shown by the horizontal blue line. The maximum spatial bandwidth (minimum electrode spacing, red arrow) was very similar for epidural (Figure 5(b)) and subdural (Figure 5(c)) recordings. Due to the small amplitude of the scalp recordings, the baseline fluctuated quite a bit, making the t-test method rather unreliable. This is seen in Figure 5(a), where the spatial bandwidth estimate given by the t-test was 0.96 c/mm (red arrow), while visual inspection suggests that the bandwidth should be closer to 0.19 c/mm (blue arrowhead). Therefore, the spatial bandwidth estimates for the scalp were made by inspection, and were probably less accurate than epidural and subdural estimates. In any case, the spatial bandwidth at the scalp was noticeably much smaller than at the epidural and subdural locations. Spatial spectra for recordings done with and without peripheral stimulation were similar (not shown). Hence, spectral data were combined for both conditions. The mean optimal spacing values over 11 data sets for each condition from 5 rats are summarized (together with results from chronic experiments described below) in Figure 8. Epidural and subdural mean optimal spacing estimates were both 0.6 mm, while scalp spacing was much larger at 2.2 mm.

Figure 4.

Sample recordings from four neighboring electrodes in one acute experiment at (a) scalp, (b) epidural, and (c) subdural locations. Signals were band-pass filtered from 5-180 Hz. Amplitudes were noticeably smaller at the scalp than at epidural or subdural locations.

Figure 5.

Spatial spectra for recordings from the same rat at (a) scalp, (b) epidural, and (c) subdural locations. Each 4,000-point segment of data yields one spatial spectral estimate. Since there are 10 data segments, this translates to 10 data points at each spatial frequency. Inspection of the scalp spectrum suggests that the spatial bandwidth should be closer to 0.19 c/mm (blue arrowhead) rather than the bandwidth found by the t-test method (red arrow). Epidural and subdural locations have much higher spatial bandwidths (red arrows) than scalp. Baseline in each panel is denoted by the solid blue line.

Figure 8.

Mean (±sd) optimal spacing estimates for acute (scalp, epidural, subdural, n=11) and chronic (anesthetized, awake, n=10) conditions. Epidural and subdural spacings were very similar in the acute experiments, and there was no difference between awake/moving and anesthetized states in chronic epidural experiments.

We also performed analysis of spatial spectra of the same data sets after two types of re-referencing (i.e., spatial filtering): common average referencing and a one-dimensional spatial difference (i.e., bipolar referencing). Common average referencing had minimal effect on the spectra; just a slight low-frequency attenuation. The spatial bandwidth (and hence, the optimum spacing) was not affected. Bipolar referencing had a much stronger high-pass filtering effect, especially notable in the scalp spectra where the noise was the highest. Again, spatial bandwidth was minimally affected: subdural and epidural mean optimal spacing estimates were 0.6 mm and 0.7 mm, respectively, while scalp spacing increased to 3.2 mm. This scalp estimate was more difficult to make since the spectra were flatter than with monopolar referencing.

3.2.2. Chronic experiments

Chronic epidural data were recorded from rats both under anesthesia (without stimulation) and on subsequent days while they were awake and moving freely in a large enclosure. Figure 6 shows an example of 2 seconds of data from 16 epidural electrodes in an awake rat. The corresponding spatial spectra are shown in Figure 7. The spatial bandwidth under these conditions was similar to that of the acute epidural experiment (Figure 5(b)). This observation held true over 10 sessions for each of 5 rats during both anesthetized and awake states, as seen in Figure 8. Mean optimal spacing was 0.7 mm for both anesthetized and awake rats, similar to the value for acute epidural experiments.

Figure 6.

Epidural signals recorded from a chronically implanted, moving rat. All 16 channels are shown.

Figure 7.

Spatial spectra from the epidural signals corresponding to Figure 6. The spatial bandwidth (red arrow) is approximately the same for this moving rat as for the anesthetized rat in Figure 5(b). Baseline is denoted by solid blue line.

4. Discussion

This study used finite element modeling and spatial spectral analysis (SSA) to investigate optimal inter-electrode spacing for surface electrode arrays. The FE model found the minimum spacing necessary to minimize overlap of signal between electrodes, while SSA established the maximum interelectrode spacing necessary to avoid spatial aliasing. Both methods found spacings of 0.6, 0.6-0.9, and 2.0-2.2 mm for subdural, epidural, and scalp locations, respectively. The fact that these two methods agree suggests that they are accurate. For the human, minimum spacings suggested by the spherical and realistic FE models were 1.7-1.8 mm for subdural, 9-13 mm for epidural, and 50-59 mm for the scalp. Thus, the optimal spacing for epidural and subdural arrays is approximately the same for rats, similar for humans, and both have much smaller spacing than scalp arrays.

The potential distributions generated by the human FE model varied significantly with the thickness of the highly-conductive CSF and the low conductivity of the skull. Scalp potential distributions were influenced mostly by the low skull conductivity and much less by its thickness. Epidural potentials were influenced mainly by the CSF, which is much thicker in humans than in rats. Variations in thickness appeared to have more than three times the influence of conductivity changes on the epidural potentials (65% vs. 8% change in spacing for 15-fold and 6-fold reductions in respective parameters). When the CSF layer was quite thin, the epidural spacing estimate was much closer to that of the subdural estimate. This is important since, in an epidural BMI application, the CSF layer could likely be compressed, both by the array itself (about 1 mm thickness) and extra spacers such as surgical sponges, if necessary, without extra risk to the brain. Finally, it is likely that the very high scalp spacing estimates from the human model are related to the wide disparity in reported skin conductivities. Thus our estimate of optimal scalp potentials in humans has a good deal of uncertainty, but optimal spacing at the scalp is clearly much greater than at the dural surface.

The conclusions drawn above were obtained with models assuming homogeneous, isotropic tissues. The assumption of homogeneity in the layers is common in EEG modeling and valid for our purposes given that the dipole was close to the surface of the cortex, and the CSF, dura, and scalp are homogeneous. Moreover, changes in skull conductivity within the ranges reported for cancellous and cortical bone [31] had little effect on subdural and epidural potentials, although they did affect scalp potentials. Thus, it is possible that including inhomogeneity in the model may sharpen the scalp potential distributions somewhat, but the results for subdural and epidural resolutions would not change. Given that gray matter, CSF, dura, and skin are essentially isotropic tissues, and that skull anisotropy has been found to have an effect on the forward problem of less than 10% [40], model layers were treated as isotropic media for most simulations. This assumption was validated by the fact that our simulation that included skull anisotropy had a very small effect on all three potentials. While white matter is anisotropic, it is deeper than the dipole in this model, and has been shown to have little effect (about 5%) on the forward model for cortical dipoles [38]. Further, including white matter anisotropy in our spherical model caused only about a 10% difference in potential distributions at the three layers, and even less effect when a thin CSF layer was used. Thus the inclusion of anisotropy would not significantly alter the findings of this study.

Spatial spectral analysis has been used to analyze epidural signals in rabbits [20], though not for the purpose of determining optimal spacing. It has also been used to analyze signals recorded at the scalp [41] and subdural levels in anesthetized [28] and awake [42] humans. However, this study is the first that compares spatial spectra from different levels of recording in the same animals. We have also shown that these estimates are independent of simple re-referencing techniques. This makes sense if one considers that the re-referencing methods do not actually increase spatial bandwidth, but rather act as high-pass spatial filters. This is also the first study to show that the spacing estimate was the same for epidural recordings in the awake and anesthetized states. Moreover, it suggests that we can extrapolate the results from multiple signal sources in anesthetized rats to rats that are awake and moving. This implies that epidural recordings would have the same spatial bandwidth as subdural recordings not just for anesthetized states but also for movement-related potentials. This is important, since movement-related potentials have the greatest relevance for BMI applications.

Why not just sample with electrodes spaced as closely as possible? Adding more electrodes at closer spacing would add to the cost and complexity of the array. Also, packing more electrodes into a fixed area requires smaller electrodes having higher impedance, which means a smaller, noisier signal recorded at each electrode. Moreover, adding too many electrodes could invoke the curse of dimensionality—given a fixed amount of input samples, increasing the dimension of the input space will eventually decrease the quality of classification [43]. Given these constraints, we consider our spacing estimate to be an optimal one, as it provides the maximum spatial bandwidth with minimal sampling.

Using spatial spectral analysis in humans, the optimal spacing for subdural electrodes has been estimated to be 1.25 mm [28], about twice what we found for rats. If our findings hold true for humans, this analysis would suggest that an optimal epidural spacing would be approximately 1.4 mm. Our human FE model results suggest that with only a thin layer of CSF, epidural spacing as low as 3.2 mm could be achieved. Moreover, the 10% cutoff that we used for distinguishing between two dipoles was somewhat arbitrary and conservative – a higher threshold may still allow for good discrimination, in which case, optimal spacings would shrink further. This is considerably denser spacing than any surface arrays that have been used for online BMIs thus far—the closest subdural grid spacing reported was 5 mm [11]. It is possible that increasing the density of subdural or epidural electrodes will enable BMIs to achieve more complex goals that require greater bandwidth and more degrees of freedom, such as restoring arm function with functional electrical stimulation [4, 5]. These results do not tell us whether the additional bandwidth we might gain from closer spacing would actually provide more information relevant to motor control, i.e., whether the additional bandwidth will provide better control of a BMI. For the simplest applications, such as discriminating among a small number of potential movement targets, some of the information from additional electrodes may be redundant. However, offline decoding of phonemes performed with subdural electrodes spaced at 3 mm [44] and an offline study examining information about wrist flexion/extension movements from subdural microelectrodes at 1 mm [45] both provide some evidence to support the notion that information is present at a smaller spatial scale. Together with those studies, the results of this study suggest that examination of the performance of arrays of greater density in a real-time BMI is warranted.

5. Conclusion

We have used experimental and modeling methods to investigate the optimal inter-electrode spacing of surface electrodes for use in a BMI. The spatial bandwidths of epidural and subdural signals were very similar, and both were much broader than that of scalp signals. This suggests that more information could be obtained from subdural and epidural recordings simply by applying more closely-spaced electrodes than have been used thus far. Moreover, it suggests that epidural electrodes, which would provide BMI control signals in a less-invasive fashion than ECoG, may do so with little or no loss in signal quality. We plan to investigate the performance of epidural field potentials as inputs to decoders of movement related signals.