Partition of compounds from water and from air into amides

Abstract

Literature data on partitioning of compounds from the gas phase to a number of amides and from water to the amides has been collected and analyzed through the Abraham solvation equations. The resulting equations are statistically good enough to be used for the prediction of further partition coefficients, and allow deductions to be made about the chemical properties of the amides, as solvents. For example, tertiary amides have no hydrogen bond property at all, secondary amides are rather weak hydrogen bond acids, and primary amides are stronger hydrogen bond acids than are alcohols as solvents. Equations for partitioning from the gas phase to amide solvents can also be used to test if the amides are possible models for a number of biological phases and biological processes. It is shown that no organic solvent is a suitable model for phases such as blood, brain, muscle, liver, heart or kidney, but that a number of rather non-polar solvents are models for fat. N-methylformamide is shown to be the best (and excellent) model for eye irritation and nasal pungency in humans, suggesting that the receptor site in these processes is protein-like.

Introduction

We have previously reported on the partition of compounds from water and from air into a number of solvents. The solvents can be saturated with water, that is ‘wet’ solvents, or they can be ‘dry’ solvents. In a number of cases, solvation of compounds in the dry and wet solvents is essentially the same, so that the same equations can be used to fit partition coefficients and to predict further partition coefficients into either wet or dry solvents. These solvents include hexadecane, ^{1, 2} olive oil, ¹ the lower alkanes, ² cyclohexane, ² chloroform, ³ dodecane, ⁴ undecane, ⁴ isopropyl myristate, ⁵ butane,⁶ 1,2-dichloroethane, ⁷ and the monohalobenzenes. ⁸ On the other hand, there are many solvents in which solvation of compounds into the wet or dry solvents is not the same, and different equations must be used for the correlation and prediction of partition coefficients in the wet and dry solvents. These solvents include aliphatic ethers, ^{9, 10} alcohols, ^{11, 12} acetates ¹³ and ketones. ¹⁴ In all these solvent series, solvation into the wet and dry solvents differed considerably for the lower homologs, in which water was very soluble, but less so for the higher homologs in which water was not very soluble.

We have previously constructed equations for solvation of solutes in a few amides, using an old version of our linear free energy relationships, LFERs.¹⁵ However, the range of solute type was small, and the number of solutes not very large. The first aim of the present work is to set out updated equations that will be useful in the prediction of further gas to amide partition coefficients. The second aim is to compare coefficients in the equations for gas to amide partitions, and also in the (hypothetical) water to amide partitions, with corresponding equations that we have already obtained for a variety of biological phases, including blood, ^{16, 17} brain, ^{18, 19} fat, ²⁰ muscle, ²¹ liver, ²² lung ²³ and skin. ²⁴ Since the constituents of these phases are mostly water, protein and fat, it is possible that amides, with the peptide =N-C(=O)- bond, could be possible models for the solution properties of some of these phases.

Methodology

The amides that we shall consider are all miscible with water, and so the prime experimental data will be partitioning from the gas phase into the dry solvents, in terms of the gas to solvent partition coefficient K_s, defined through eqn (1).

$$K_s=\text{concentration}\text{of}\text{solute}\text{in}\text{solution}/\text{concentration}\text{of}\text{solute}\text{in}\text{the}\text{gas}\text{phase}$$ (1)

If concentrations in the gas phase and in solution are in the same units, for example mol dm⁻³, then K_s has no units and is equivalent to the Ostwald absorption coefficient. Values of K_s can be converted into the hypothetical water to dry solvent partition coefficient, P_s, through eqn (2) where K_w is the air to water partition coefficient. ^{9–14, 25–29}

$$\text{Log}{P}_s=log{K}_s-log{K}_w$$ (2)

Various experimental data can be used to obtain K_s values for partitioning into the dry amides. For volatile solutes K_s can be determined directly. Air to solvent partition coefficients can also be obtained from the experimentally determined Henry’s Law constants and the experimentally known solute vapour pressure, and also from the solute activity coefficient at infinite dilution in the solvent, together with the solute vapour pressure. In addition, a very useful method is to use the amide solvent as the stationary phase in gas liquid chromatography. Then measurement of the volume of elution of a solute gives K_s directly.

The LFERs, eqn (3) and eqn (4), are used to analyze the partition coefficients, as log K_s and log Ps. ^{30, 31}

$$\text{Log}{K}_s=\text{c}+\text{e}E+\text{s}S+\text{a}A+\text{b}B+1L$$ (3)

$$\text{Log}Ps=\text{c}+\text{e}E+\text{s}S+\text{a}A+\text{b}B+\text{v}V$$ (4)

The independent variables in eqn (3) and eqn.(4) are solute descriptors as described before. ^{30, 31} E is the solute excess molar refraction in units of (cm³ mol⁻¹)/10, S is the solute dipolarity/polarizability, A and B are the overall or summation solute hydrogen bond acidity and basicity, V is the McGowan characteristic volume ¹⁵ in units of (cm³ mol⁻¹)/100, and L is the logarithm of the gas to hexadecane partition coefficient at 298 K.

Results

N,N-Dimethylformamide, DMF

All data refer to dry DMF at 298K. We were able to assemble values of log K_s for 171 solutes. Values were derived from Henry’s Law constants or activity coefficients ^16–55 or from solubilities ^56–68 as referenced in Table S1. Methyl 4-hydroxybenzoate was left out, because the solubility in DMF is very large (4.8 mol dm⁻³), and 3-nitrobenzoic acid was omitted because it forms a solvate with DMF.⁶⁷ This left 169 compounds for which the log K_s values together with the corresponding log P_s values and descriptors are given in Table S1. Application of eqn (3) yielded the LFER, eqn (5); the term in bB was not significant and was omitted to yield eqn (6).

$$\begin{array}{l}\text{Log}{K}_s(\text{DMF})=-0.391(0.045)-0.869(0.100)E+2.107(0.108)S+3.774(0.146)A\\ +1.011(0.011)L\\ N=169,R^2=0.991,SD=0.355,F=4591,Q^2=0.990,\text{PRESS}=22.275,\\ \text{PSD}=0.368\end{array}$$ (5)

$$\begin{array}{l}\text{Log}{P}_s(\text{DMF})=-0.305(0.054)-0.058(0.102)E+0.343(0.140)S+0.358(0.151)A\\ -4.865(0.162)\text{B}+4.486(0.040)V\\ N=169,R^2=0.989,SD=0.363,F=2924,Q^2=0.988,\text{PRESS}=23.713,\\ \text{PSD}=0.381\end{array}$$ (6)

In eqn (5) and eqn (6), N is the number of data points (the number of compounds), R is the correlation coefficient, SD is the regression standard deviation, and F is the F-statistic. The leave-one-out statistics are Q², PRESS, and PSD the ‘predictive’ standard deviation, as defined previously. ¹⁴

N,N-Dimethylacetamide, DMA

For dry DMA at 298K we could collect values of log K_s and log P_s for 102 solutes, from primary data on the solubility of gases and vapors, ^{15, 32, 33, 34, 44, 50, 52, 69, 70, 71,72} and on the solubility of solids. ^{56, 57, 59, 61, 73, 74, 75} Methyl 4-hydroxybenzoate was again an outlier, to leave 101 data points, as shown in Table S2. The equations for log K_s (DMA) and log P_s (DMA) are as follows. For the former equation, the term in bB was not significant.

$$\begin{array}{l}\text{Log}{K}_s(\text{DMA})=-0.308(0.059)-0.736(0.103)E+1.802(0.126)S+4.361(0.221)A\\ +1.028(0.010)L\\ N=101,R^2=0.992,SD=0.313,F=2932,Q^2=0.990,\text{PRESS}=10.907,\\ \text{PSD}=0.337\end{array}$$ (7)

$$\begin{array}{l}\text{Log}{P}_s(\text{DMA})=-0.271(0.065)+0.084(0.107)E+0.209(0.155)S+0.915(0.216)A\\ -5.003(0.189)B+4.557(0.036)V\\ N=101,R^2=0.996,SD=0.295,F=4323,Q^2=0.995,\text{PRESS}=9.904,\\ \text{PSD}=0.323\end{array}$$ (8)

N-Methylpyrrolidin-2-one, NMP

Data on the solubility of gases and vapors ^{15, 32, 33, 46, 50, 55, 61, 69, 70, 76–87} and solids ^{73,88, 89} in NMP were available. The compounds p-toluic acid, ⁸⁸ benzoic acid, ⁸⁸ and methyl 4-hydroxybenzoate ⁶¹ were outliers. In the latter two cases, the solubilities in NMP are rather high, but for p-toluic acid we have no explanation. This left 118 compounds for analysis, see Table S3. In the regression for log K_s (NMP), the term in bB was not significant and the resulting equation was:

$$\begin{array}{l}\text{Log}{K}_s(\text{NMP})=-0.128(0.032)-0.029(0.0065)E+2.217(0.064)S+4.429(0.102)A\\ +0.777(0.104)L\\ N=118,R^2=0.995,SD=0.161,F=5996,Q^2=0.994,\text{PRESS}=3.281,\\ \text{PSD}=0.170\end{array}$$ (9)

The corresponding equation for log P_s (NMP) was:

$$\begin{array}{l}\text{Log}{P}_s(\text{NMP})=0.147(0.050)+0.532(0.065)E+0.225(0.095)S+0.840(0.114)A\\ -4.794(0.122)B+3.674(0.059)V\\ N=118,R^2=0.988,SD=0.174,F=1913,Q^2=0.987,\text{PRESS}=3.937,\\ \text{PSD}=0.187\end{array}$$ (10)

N-Formylmorpholine, NFM

Krummen and Gmehling ⁸⁴ and Weidich et al. ⁸⁵ have published GLC data on solubilities of gases in NFM at temperatures between 303 and 343K and between 313 and 373K. We have extrapolated these to 298K through plots of log γ^∞ against 1/T(K) or plots of log Vg^o against 1/T(K) for each solute and obtained values of log K_s and log P_s for 50 solutes. In addition, there are data for a few more gases, ^{90, 91} making 55 solutes in all as given in Table S4. Application of eqn (3) yielded eqn (11). Although the term in b.B is statistically significant, it is chemically unreasonable; the tertiary amide has no hydrogen bond acidity and hence the b.B should be zero (as is the case for the other tertiary amides we have studied). If the term is omitted, eqn (12) results.

$$\begin{array}{l}\text{Log}{K}_s(\text{NFM})=-0.402(0.055)+0.477(0.162)E+1.817(0.240)S+3.542(0.277)A\\ +0.969(0.275)B+0.698(0.019)L\\ N=55,R^2=0.989,SD=0.119,F=893,Q^2=0.985,\text{PRESS}=0.923,\\ \text{PSD}=0.137\end{array}$$ (11)

$$\begin{array}{l}\text{Log}{K}_s(\text{NFM})=-0.437(0.024)+0.024(0.109)E+2.631(0.071)S+4.318(0.187)A\\ +0.712(0.021)L\\ N=55,R^2=0.986,SD=0.132,F=906,Q^2=0.984,\text{PRESS}=1.034,\\ \text{PSD}=0.144\end{array}$$ (12)

The corresponding equation for log P_s is eqn (13)

$$\begin{array}{l}\text{Log}{P}_s(\text{NFM})=-0.032(0.080)+0.696(0.172)E-0.062(0.272)S+0.014(0.311)A\\ -4.092(0.310)B+3.405(0.079)V\\ N=55,R^2=0.993,SD=0.134,F=1424,Q^2=0.991,\text{PRESS}=1.155,\\ \text{PSD}=0.153\end{array}$$ (13)

N,N-Diethylacetamide (DEA)

The only data on the solubilities of gases in DEA are those of Krummen et al ⁹² who used a GLC method to determine activity coefficients of 27 solutes at temperatures between 303K and 333K. We have extrapolated them to 298K and then obtained the corresponding log K_s (DEA) and log P_s (DEA) values in Table S5. No other data on solubilities in DEA appeared to be available, and the obtained equations are as follows.

$$\begin{array}{l}\text{Log}{K}_s(\text{DEA})=-0.075(0.142)-0.434(0.161)E+1.911(0.130)S+4.801(0.234)A\\ +0.899(0.049)L\\ N=27,R^2=0.970,SD=0.107,F=177,Q^2=0.957,\text{PRESS}=0.359,\\ \text{PSD}=0.128\end{array}$$ (14)

$$\begin{array}{l}\text{Log}{P}_s(\text{DEA})=0.213(0.135)+0.034(0.151)E+0.089(0.149)S+1.342(0.193)A\\ -5.084(0.110)B+4.088(0.131)V\\ N=27,R^2=0.998,SD=0.083,F=2113,Q^2=0.997,\text{PRESS}=0.237,\\ \text{PSD}=0.104\end{array}$$ (15)

N,N-Dibutylformamide (DBF)

Möllmann and Gmehling ⁷² used a GLC method to obtain activity coefficients of 43 solutes in DBF from 303K to 333K. We extrapolated the data to 298K and obtained the corresponding log K_s (DBF) and log P_s (DBF) values shown in Table S6. No other data appeared to be available and the equations based on the data of Möllmann and Gmehling are as eqn (16) and eqn (17). We left out chlorobenzene, which was a considerable outlier and also water, because of the possibility of adsorption.⁷²

$$\begin{array}{l}\text{Log}{K}_s(\text{DBF})=-0.002(0.082)-0.239(0.086)E+1.402(0.070)S+4.029(0.120)A\\ +0.900(0.027)L\\ N=41,R^2=0.981,SD=0.086,F=468,Q^2=0.976,\text{PRESS}=0.346,\\ \text{PSD}=0.098\end{array}$$ (16)

$$\begin{array}{l}\text{Log}{P}_s(\text{DBF})=0.332(0.104)+0.302(0.106)E-0.436(0.105)S+0.358(0.140)A\\ -4.902(0.097)B+3.952(0.103)V\\ N=41,R^2=0.997,SD=0.087,F=2256,Q^2=0.995,\text{PRESS}=0.379,\\ \text{PSD}=0.104\end{array}$$ (17)

N-Methyl-2-piperidone, NMPip

Gruber et al. ⁹³ obtained activity coefficients for 36 volatile solutes on N-methyl-2-piperidone by a GLC method at 303.4, 313.4 and 323.4K. We have extrapolated these to 298K and obtained the corresponding log K_s (NMPip) and log P_s (NMPip) values shown in Table S7. The regression equations are given as eqn (18) and eqn (19).

$$\begin{array}{l}\text{Log}{K}_s(\text{NMPip})=-0.264(0.099)-0.171(0.110)E+2.086(0.071)S+5.056(0.209)A\\ +0.883(0.036)L\\ N=36,R^2=0.982,SD=0.092,F=420,Q^2=0.980,\text{PRESS}=0.361,\\ \text{PSD}=0.108\end{array}$$ (18)

$$\begin{array}{l}\text{Log}{P}_s(\text{NMPip})=0.056(0.118)+0.332(0.130)E+0.257(0.111)S+1.556(0.210)A\\ -5.035(0.104)B+3.983(0.120)V\\ N=36,R^2=0.997,SD=0.088,F=1956,Q^2=0.995,\text{PRESS}=0.344,\\ \text{PSD}=0.107\end{array}$$ (19)

Krummen et al. ⁹⁴ have used the same method to obtain activity coefficients for 23 volatile solutes in the tertiary amides 1,5-dimethylpyrrolidinone and 1-ethylpyrrolidinone. Unfortunately, no hydrogen bond acids were examined, and so it is not possible to obtain the full regression equations.

N-Methylformamide, NMF

Activity coefficients at temperatures between 303 and 333K have been determined by Gruber et al., ⁹⁵ using a GLC method, and we have extrapolated these to 298K and then obtained the corresponding log K_s (NMF) and log P_s (NMF) values for 30 solutes, as given in Table S8; there is also an additional value for 1,4-dioxane. ⁷⁰ Bruckel and Kim ³³ have determined the solubility of three gases in NMF, and both Smiley ⁶⁹ and Castells et al. ³² have obtained activity coefficients for a number of hydrocarbons, some of which overlap with the solutes used by Gruber et al. ⁹⁵ There is also a value for the solubility of oxygen, ⁹⁶ in NMF.

Zielkiewicz ⁹⁷ has determined vapor-liquid equilibria for the binary systems water-NMF, methanol-NMF, and ethanol-NMF. The corresponding activity coefficients for methanol and ethanol agree well with those of Gruber; ⁹⁵ that for water in NMF is a new value. There are also solubility data for anthracene, ⁷⁴ pyrene, ⁷⁴ acenaphthene, ⁷⁴ benzoic acid, ⁵⁹ methyl 4-hydroxybenzoate ⁶¹ and 4-hydroxybenzoic acid, ⁶¹ and NMF itself can be included with an activity coefficient of unity. This leaves a total of 52 solutes, see Table S8. There were no outliers, and the regression equations are eqn 20 and eqn 21.

$$\begin{array}{l}\text{Log}{K}_s(\text{NMF})=-0.249(0.033)-0.142(0.064)E+1.661(0.090)S+4.147(0.083)A\\ +0.817(0.093)B+0.739(0.013)L\\ N=52,R^2=0.998,SD=0.092,F=5830,Q^2=0.997,\text{PRESS}=0.676,\\ \text{PSD}=0.121\end{array}$$ (20)

$$\begin{array}{l}\text{Log}{P}_s(\text{NMF})=0.114(0.055)+0.407(0.071)E-0.287(0.109)S+0.542(0.100)A\\ -4.085(0.112)B+3.471(0.061)V\\ N=52,R^2=0.995,SD=0.111,F=1976,Q^2=0.993,\text{PRESS}=0.815,\\ \text{PSD}=0.133\end{array}$$ (21)

As expected for a secondary amide, the b-coefficient in eqn 20 is statistically very significant (T = 8.74, p < 0.001).

N-Methylacetamide, NMA

The main set of data is the experimental activity coefficients of Möllmann and Gmehling ⁷² for 43 compounds, obtained at 303, 318 and 333K. We have extrapolated these to 298K and calculated the corresponding log K_s (NMA) and log P_s (NMA) values. Smiley ⁶⁹ has reported activity coefficients for eight hydrocarbons in NMA and again we have extrapolated these to 298K before calculating the log K_s (NMA) and log P_s (NMA) values. We also have a value for NMA itself taking the activity coefficient as unity. Log K_s (NMA) values are available for helium,⁹⁸ argon, ⁹⁹ nitrogen ⁷⁷ and ethane, ¹⁰⁰ making a total of 55 compounds (pentane was studied twice),^{69, 72} as listed in Table S9. There were no outliers and the equations for log K_s (NMA) and log P_s (NMA) are given as eqn 22 and eqn 23.

$$\begin{array}{l}\text{Log}{K}_s(\text{NMA})=-0.197(0.035)-0.175(0.114)E+1.608(0.084)S+4.867(0.111)A\\ +0.375(0.100)B+0.837(0.016)L\\ N=55,R^2=0.995,SD=0.103,F=1829,Q^2=0.993,\text{PRESS}=0.723,\\ \text{PSD}=0.121\end{array}$$ (22)

$$\begin{array}{l}\text{Log}{P}_s(\text{NMA})=0.090(0.061)+0.205(0.118)E-0.172(0.101)S+1.305(0.132)A\\ -4.589(0.117)B+3.833(0.079)V\\ N=55,R^2=0.993,SD=0.117,F=1337,Q^2=0.989,\text{PRESS}=0.976,\\ \text{PSD}=0.141\end{array}$$ (23)

N-Ethylformamide, NEF

The only data available are the activity coefficients for 26 solutes obtained by Topphoff et al. ¹⁰¹ Although the number of solutes is very small, it does include alcohols, and so it is possible to obtain regression equations for log K_s (NEF) and log P_s (NEF). The data used is in Table S10.

$$\begin{array}{l}\text{Log}{K}_s(\text{NEF})=-0.220(0.117)-0.302(0.155)E+1.743(0.131)S+4.498(0.192)A\\ +0.480(0.104)B+0.824(0.040)L\\ N=26,R^2=0.984,SD=0.079,F=247,Q^2=0.973,\text{PRESS}=0.210,\\ \text{PSD}=0.102\end{array}$$ (24)

$$\begin{array}{l}\text{Log}{P}_s(\text{NEF})=0.220(0.131)+0.034(0.138)E-0.166(0.134)S+0.935(0.184)A\\ -4.589(0.098)B+3.730(0.128)V\\ N=26,R^2=0.998,SD=0.075,F=2122,Q^2=0.997,\text{PRESS}=0.188,\\ \text{PSD}=0.097\end{array}$$ (25)

Both equations indicate that the secondary amide is a moderate hydrogen bond acid (B = 0.480 in eqn 24). Although they are based on only 26 solutes, eqn 24 and eqn 25 should be capable of predicting log K_s (NEF) and log P_s (NEF) for further solutes to within about 0.10 log units, as indicated by the PSD values, provided that the descriptors of the solutes are within the range of those used to set up eqn 24 and eqn 25.

N-Ethylacetamide, NEA

The main set of activity coefficients for 27 solutes is that of Krummen et al. ⁹² supplemented by the data of Smiley. ⁶⁹ A number of alcohols is included in the data set, ⁹² and equations for log K_s (NEA) and log P_s (NEA) are as follows. The data used are in Table S11.

$$\begin{array}{l}\text{Log}{K}_s(\text{NEA})=-0.018(0.074)-0.157(0.127)E+1.352(0.190)S+4.588(0.150)A\\ +0.357(0.094)B+0.824(0.027)L\\ N=33,R^2=0.986,SD=0.074,F=387,Q^2=0.979,\text{PRESS}=0.226,\\ \text{PSD}=0.091\end{array}$$ (26)

$$\begin{array}{l}\text{Log}{P}_s(\text{NEA})=0.284(0.091)+0.128(0.111)E-0.442(0.109)S+1.180(0.145)A\\ -4.728(0.087)B+3.856(0.093)V\\ N=33,R^2=0.998,SD=0.068,F=3324,Q^2=0.997,\text{PRESS}=0.184,\\ \text{PSD}=0.082\end{array}$$ (27)

As expected, the secondary amide is a moderate hydrogen bond acid. The PSD values suggest that predictions of log K_s (NEA) and log P_s (NEA) for new solutes can be made to about 0.09 log units, again provided that the descriptors for the new solutes are within the range of those used to set up eqn 26 and eqn 27.

Formamide, F

The only primary amide for which there are enough solubility data to construct equations is formamide. There have been a number of studies of the solubility of volatile solutes in this solvent. Castells ¹⁰² used a GLC method to obtain retention volumes, Vg, of 22 hydrocarbons at 298 K on a formamide stationary phase, corrected for adsorption. Bai and Li ¹⁰³ used the same method to obtain Vg values for nine solutes, again at 298 K. These Vg values are directly related to the K_s(F) values at 298 K that we require. In a much earlier publication, Novák and Janák ¹⁰⁴ used the GLC method to study eight homologous series of solutes, but expressed their results as activity coefficients at 323 K. If activity coefficients at 298 K are assumed to be the same as those at 323 K, we can calculate the corresponding K_s(F) partition coefficients at 298 K. A comparison of the log K_s(F) values from the three sets of data is in Table 1. Rather surprisingly, the log K_s(F) values calculated from the 323 K activity coefficients of Novák and Janák are very close to those obtained from the two sets of GLC experiments at 298K. We have therefore used the approximation that log K_s(F) values at 298 K can be calculated from the 323 K activity coefficients for the remaining solutes studied by Novák and Janák. For multiple values, we took those of Castells ¹⁰² where available, otherwise we took the average. Additional values of log K_s(F) values at 298 K have been determined by Cox et al.¹⁰⁵ for the solutes acetonitrile, nitromethane and water. Details are in Table S12.

Table 1.

Calculation of gas to formamide partition coefficients, log K_s(F), at 298K

	Log Ks(F) calculated from
	γ at 323 K	Vg at 298 K	Vg at 298 K
Solute	Ref 104	Ref 102	Ref 103
Hexane	0.52	0.39
Heptane	0.78	0.66	0.82
Octane	1.03	0.93
Nonane	1.32	1.22
Benzene	2.02	1.97	1.98
Toluene	2.26	2.20
Ethylbenzene	2.45	2.39
Propylbenzene	2.66	2.56
Cyclohexane	1.02	0.99	1.01
Methylcyclohexane	1.09	1.04
Ethylcyclohexane	1.24	1.33
Propanone	2.70		2.79

Solubilities of a number of solids in formamide have been reported and can be used to obtain values of log P_s(F) and then of log K_s(F). The solids are methyl 4-hydroxybenzoate, ⁶¹ diclofenac, ⁶⁰ 2-hydroxybenzoic acid, ⁶⁰ niflumic acid, ⁶⁵ ibuprofen, ⁶⁶ and piroxicam.⁶⁵ Richardson et al. ¹⁰⁶ report the solubility of temazepam in formamide, but this was considerably out of line and was omitted. Details of all the solutes used are in Table S12, which contains values for 73 solutes. The equations for log K_s(F) and log P_s(F) are shown as eqn 28 and eqn 29.

$$\begin{array}{l}\text{Log}{K}_s(\text{F})=-0.800(0.050)+0.310(0.123)E+2.292(0.132)S+4.130(0.102)A\\ +1.933(0.174)B+0.442(0.018)L\\ N=73,R^2=0.996,SD=0.169,F=3568,Q^2=0.995,\text{PRESS}=2.639,\\ \text{PSD}=0.198\end{array}$$ (28)

$$\begin{array}{l}\text{Log}{P}_s(\text{F})=-0.171(0.059)+0.070(0.103)E+0.308(0.129)S+0.589(0.099)A\\ -3.152(0.166)B+2.432(0.063)V\\ N=73,R^2=0.974,SD=0.159,F=494,Q^2=0.966,\text{PRESS}=2.175,\\ \text{PSD}=0.180\end{array}$$ (29)

Both eqn 28 and eqn 29 are statistically satisfactory. Judging from PSD, further values could be predicted to about 0.20 log units. The b-coefficient in eqn 28 is quite considerable, thus indicating that formamide as a solvent has appreciable hydrogen bond acidity.

Discussion

General discussion

The various equations for log K_s are all statistically reasonable, and can be used to predict further values for solutes for which the required descriptors are available. There is almost nothing with which to compare these equations. Li et al.¹⁰⁷ have calculated Gibbs energies of solvation (equivalent to log K_s) for solutes in a very large number of solvents and have compared calculated values with experimental ones. The solvents included DMF, DMA and NMA, but only five solutes were studied in each case.

It is important to note that predictions of further values should only be made for solutes with values of descriptors within (or possibly just outside) the descriptor space used to set up the equations. In the Supplementary material, we give the minimum and maximum values of the descriptors for each amide solvent. The minimum values are not so critical (the minimum values of A and B are always zero), and the maximum values are collected in Table 2. In order to ascertain the effect of predictions outside the correct descriptor space, we repeated the equation for log K_s(NMA), eqn 22 with 55 solutes, using only the 27 solutes that were used in the equation for DEA and then predicted values of log K_s(NMA) for the remaining 28 solutes. We found SD = 0.145 log units between observed and predicted values, as compared to PSD = 0.121 log units in eqn 22. Hence extrapolation some way outside the original data space (compare DEA and NMA in Table 2) still leads to reasonable predictions. However, when we repeated this, using the 27 solutes in the DEA equation to obtain an equation for log K_s(DMA), and then using the equation to predict values for log K_s(DMA) for the remaining 74 solutes; we obtained SD = 1.06 log units. Thus extrapolation well outside the original descriptor space (compare DEA and DMA in Table 2) will result in very poor predictions.

Table 2.

Maximum values of the descriptors used in equations 5 to 29, and the number of solutes in the equations..

Amide	N	E	S	A	B	V	L
DMF	169	2.81	2.71	1.04	1.43	4.0538	13.780
DMA	101	2.81	2.12	0.81	0.80	4.0538	13.780
NMP	118	2.29	1.86	1.03	0.79	1.5176	8.002
NFM	55	0.69	1.38	0.43	0.99	1.5176	4.686
DEA	27	0.61	0.70	0.43	0.57	1.2358	3.677
DBF	41	0.72	0.90	0.43	0.64	1.1536	3.778
NMPip	36	0.61	0.90	0.43	0.57	1.2358	3.677
NMF	52	2.81	1.71	0.81	0.64	1.5846	8.833
NMA	55	0.72	1.28	0.59	0.71	1.1536	3.778
NEF	26	0.61	0.70	0.43	0.57	1.2358	3.677
NEA	33	0.61	0.70	0.43	0.57	1.2358	3.677
F	73	2.56	2.71	0.82	1.21	2.2500	12.210

One important use of amide solvents is in the selective solution of aromatic compounds over aliphatic compounds in processes such as gas stripping. We can use the various equations in log K_s to predict values for typical aromatic and aliphatic solutes, and hence to predict selective solution of aromatic compounds. Results are in Table 3 for a tertiary amide (DMF), a secondary amide (NMF) and a primary amide (formamide), together with a number of other well-known solvents. We chose acetophenone and 4-methylcyclohexanone and phenol and cyclohexanol as two pairs of aromatic/aliphatic solutes. Results in Table 3 are not entirely as expected. Dimethylsulfoxide, DMSO, is more selective than the amides, and for the pair of solutes acetophenone/4-methylcyclohexanone only formamide is much more selective than the aliphatic solvent, butanone. For the other pair, DMSO is again the most selective solvent, but all the amides are more selective towards phenol than are the aliphatic solvents. A similar analysis can be carried out for almost any pair of solutes used in chemical engineering processes, for a large number of solvents.

Table 3.

Selectivity of solvents: calculated values of log K_s(aromatic solute) - log K_s (aliphatic solute)

Solvent	Acetophenone/4-methylcyclohexanone	Phenol/cyclohexanol
Formamide	0.566	1.547
NMF	0.443	1.478
DMF	0.353	1.503
Butanone	0.422	1.234
DMSO	0.840	2.568
Ethylene glycol	0.392	1.203
Octanol	0.300	0.945

It is of some interest to compare the coefficients of the various equations with those for other solvents. Some values are in Table 4. The amide solvents are all strong hydrogen bond bases, with a-coefficients from 3.77 to 4.15, bested only by ethylene glycol and DMSO. The secondary amide, NMF, is a rather weak hydrogen bond acid with a b-coefficient of 0.817, but formamide itself is a substantial hydrogen bond acid, stronger than methanol. The l-coefficient is interesting, in that it seems to be related to the lipophilicity of the solvent. Many organic solvents have l-coefficients in the range 0.90 – 1.00, as does DMF itself. A few solvents have lower l-coefficients, especially ethylene glycol (l = 0.558) and now formamide with the smallest l-coefficient yet observed for an organic solvent.

Table 4.

Coefficients in equations for log K_s.

solvent	c	e	s	a	b	L
DMF	−0.391	−0.869	2.107	3.774	0.000	1.011
NMF	−0.249	−0.142	1.661	4.147	0.817	0.739
Formamide	−0.800	0.310	2.292	4.130	1.933	0.442
Water	−1.271	0.822	2.743	3.904	4.814	−0.213
Methanol	−0.004	−0.215	1.173	3.701	1.432	0.769
Ethylene glycol	−0.876	0.278	1.431	4.584	2.525	0.558
DMSO	−0.619	0.131	2.811	5.474	0.000	0.734
Butanone	0.112	−0.474	1.671	2.878	0.000	0.916
Ethyl ether	0.206	−0.169	0.873	3.402	0.000	0.882
Chloroform	0.168	−0.595	1.256	0.280	1.370	0.981

Comparison with biological phases

Over the last few years, we have set out equations for the partition of solutes from the gas phase into a variety of biological phases, and it is of considerable interest to compare these equations with those for partition into organic solvents. In the early part of the 20^th century, olive oil ^{108, 109} and then oleyl alcohol ¹¹⁰ were used as model solvents for biological processes and biological phases. Much later, Hansch and Fujita ¹¹¹ suggested octanol (or rather wet octanol) as a more suitable model solvent, and this has remained the solvent of choice. However, it is unrealistic to expect that any given solvent would be a suitable model for biological phases as different as fat, muscle and blood. Compositions as wt% water, protein and lipid are in Table 5. ¹¹²

Table 5.

Composition of biological phases, as wt%

Phase	Water	Protein	Lipid
Blood	96	1	1
Muscle	79	17	2
Brain	79	8	11
Lung	78	18	1
Kidney	77	17	5
Heart	73	17	10
Liver	72	18	7
Fat	15	5	80

Over the last few years, we have set out equations based on eqn 3 for the gas to biological phase partition coefficients of solutes in a variety of biological phases, including blood,¹¹³ muscle, ¹¹⁴ brain, ¹¹⁵ lung, ¹¹⁶ kidney, ¹¹⁷ heart, ¹¹⁷ liver ¹¹⁸ and fat ¹¹⁹ at 310 K. Having the coefficients in eqn 3 available for the biological phases, we can now compare these coefficients with those for various solvents, including olive oil ¹²⁰ as well as the amide solvents studied in this work.

We have also examined the effect of volatile solutes on nasal pungency thresholds (NPT), eye irritation thresholds (EIT) and odor detection thresholds (ODT) in humans, and have obtained equations based on eqn 3 for log(1/NPT), ¹²¹ log(1/EIT) ¹²² and log (1/ODT). ¹²¹ Coefficients for the most up-to-date data ¹²³ are given in Table 6. In addition, we have obtained ¹²⁴ an equation for inhalation anesthesia on rats for log(1/MAC) where MAC is the minimum alveolar concentration of an inhaled anesthetic that prevents movement in 50% of rats; coefficients are in Table 6.

Table 6.

A comparison of coefficients for solubility of gases and vapors in biological phases, and coefficients for biological activity, with coefficients for solubility in organic solvents.

Solvent phase a	No	c	e	s	a	B	l
Blood	1	−1.069	0.456	1.083	3.738	2.580	0.376
Muscle	2	−1.140	0.544	0.216	3.471	2.924	0.578
Brain	3	−1.074	0.427	0.286	2.781	2.787	0.609
Lung	4	−1.300	0.667	0.680	3.539	3.350	0.458
Kidney	5	−1.084	0.417	0.226	3.624	2.926	0.534
Heart	6	−1.208	0.128	0.987	0.643	1.783	0.597
Liver	7	−1.031	0.059	0.774	0.593	1.049	0.654
Fat	8	−0.294	−0.172	0.729	1.747	0.219	0.895
Nasal pungency	9	−7.815	−0.014	1.760	3.581	0.750	0.806
Eye irritation	10	−7.910	−0.375	1.880	3.779	1.192	0.792
Odor detection	11	−5.771	−0.915	3.483	4.099	−0.092	0.914
Anesthesia	12	−0.752	−0.034	1.559	3.594	1.411	0.687
DMF	13	−0.391	−0.869	2.107	3.774	0.000	1.011
NMF	14	−0.249	−0.142	1.661	4.147	0.817	0.739
Formamide	15	−0.800	0.310	2.292	4.130	1.933	0.442
Water ( 310K)	16	−1.361	1.055	2.630	3.742	4.495	−0.245
Water (298K)	17	−1.271	0.822	2.743	3.904	4.814	−0.213
Methanol	18	−0.004	−0.215	1.173	3.701	1.432	0.769
Ethylene glycol	19	−0.876	0.278	1.431	4.584	2.525	0.558
Wet butanol	20	−0.095	0.262	1.396	3.405	2.565	0.523
Wet hexanol	21	−0.302	−0.046	0.880	3.609	1.785	0.824
Wet octanol	22	−0.222	0.088	0.701	3.478	1.477	0.851
Olive oil	23	−0.159	−0.277	0.904	1.695	−0.090	0.876
Decanol	24	−0.136	−0.068	0.325	3.674	0.767	0.947
Butanone	25	0.112	−0.474	1.671	2.878	0.000	0.916
Ethyl ether	26	0.206	−0.169	0.873	3.402	0.000	0.882
Chloroform	27	0.168	−0.595	1.256	0.280	1.370	0.981

^aThe results for the biological phases and biological activity are at 310K, and those for solubility in organic solvents are at 298K

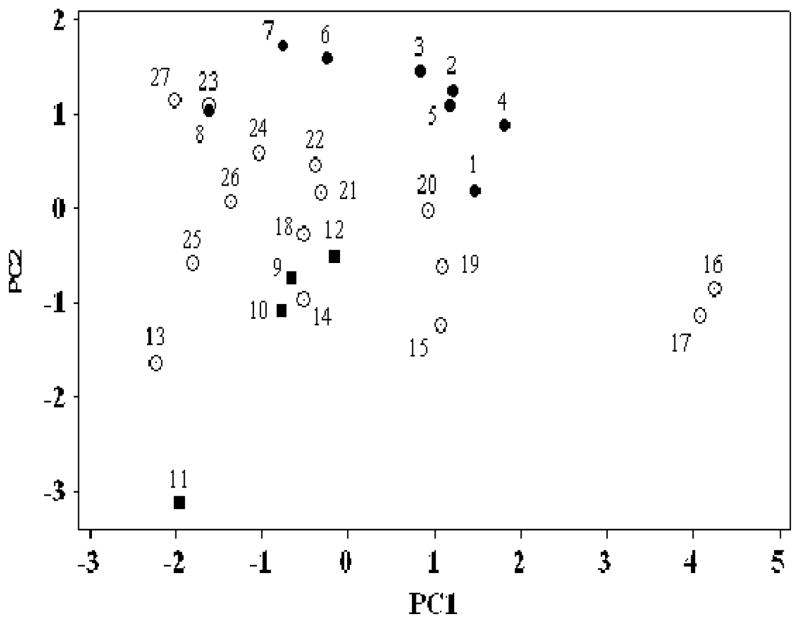
It is not very easy to judge which of the sets of coefficients in Table 6 are near to each other, but a simple visualization can be achieved using principal components analysis (PCA) of the five coefficients e, s, a, b, and l. The relevant five columns of data in Table 6 are transformed into five principal components that are mutually orthogonal. The scores for the first two PCs contain (in the present case) 84% of the total information, and so a simple two-dimensional plot of PC2 against PC1 will give a reasonable indication of which processes are chemically similar, in terms of the coefficients in the appropriate equations. Such a plot is shown in Figure 1.

Fig. 1.

A plot of the scores of PC2 against PC1 for the systems in Table 6: filled circles represent the biological phases Nos 1– 8, squares represent the biological processes Nos 9 – 12, circles represent the solvents Nos 13 – 27.

It is clear that except for fat, there is little correspondence between the biological phases and the various solvents; wet butanol (No 20) is quite close to blood (No 1) but that is all. No doubt the large amount of water in these biological phases precludes the dry organic solvents as suitable models. It is no coincidence that wet butanol contains more water than the other wet solvents. For fat, the rather non-polar solvents olive oil and chloroform are suitable models, and no doubt other non-polar solvents will also be suitable models. Since fat is 80% lipid, this is not surprising.

In contrast, there are a number of suitable model solvents for eye irritation, nasal pungency and inhalation anesthesia, especially N-methylformamide (No 14) and methanol (No 18). The closeness of methanol as a model solvent for inhalation anesthesia has already been noticed. ¹²⁴ However, NMF is a much more reasonable model for processes in which the main step is transfer from the gas phase to a receptor site/area that probably consists of proteins, as is likely the case for nasal pungency ¹²¹ and eye irritation ¹²². In fact, various studies have shown that many chemicals produce chemical sensory irritation (i.e., chemesthesis) via activation of proteins from various subfamilies of transient receptor potential (TRP) ion channels.^125–129

The PCA method provides a useful visual method of comparing coefficients, but there are two rigorous methods that yield exact comparisons for the assessment of the closeness of equations based on eqn 3. In the procedure of Ishihama and Asakawa ¹³⁰ the five coefficients, e to l, define a line in five dimensional space. Then for two equations, the angle between the two lines, θ, yields information as to how close the equations are in a correlation sense. As θ approaches zero, and cos θ approaches unity, the two lines coincide and the correlation between the two sets of properties approaches unity. In the method of Abraham and Martins ^{131, 132} the five coefficients, e to l, define a point in five dimensional space, and for two equations the distance between the points, D′, now yields information on how close the equations are in a chemical sense. The PCA analysis, above, is a two-dimensional visual approximation of this method. In both analyses, one particular equation, or set of coefficients, is taken as the standard. We shall take the set of coefficients for nasal pungency thresholds as the standard, with cos θ = 1, and D′ = 0.

Results of the analysis of Abraham and Martins and of Ishihama and Asakawa are in Table 7, with respect to nasal pungency thresholds. The D′ parameter shows how close systems are to NPT in chemical terms, and yields accurate values for what the PCA graph expresses approximately. Abraham and Martins ¹³² suggested that for a good chemical model, D′ should be less than about 0.5 to 0.8 units. On this basis, the ‘nearest’ systems are NMF (No 14, D′ = 0.597), eye irritation thresholds (No 10, D′ = 0.616) and inhalation anesthesia (No 12, D′ = 0.702). The nearest systems on a correlative basis are again NMF (No 14, cos θ = 0.996), eye irritation thresholds (No 10, cos θ = 0.993) and inhalation anesthesia (No 12, cos θ = 0.986). Although cos θ refers to the correlation between values for two systems, there is no exact connection between cos _ and the correlation coefficient or R². From previous work we estimate that if cos θ = 0.990 then a maximum expected value of R² is 0.95 and if cos θ = 0.975 then a maximum expected value of R² is 0.90. Note that only expected maximum values can be estimated, because the method does not take into account the errors in the data. Thus, in practical terms, the correlation observed will always be less than the expected maximum. However, there should still be a good correlation between values of log (1/NPT) and log K(NMF) since cos θ = 0.996 for NMF( No 14). Eye irritation and inhalation anesthesia are also good correlative models. Thus both in chemical terms and as regards correlation, we can deduce that NMF is an excellent model for nasal pungency thresholds. As noted, this agrees with the proteinaceous nature of chemesthetic TRP ion channels.

Table 7.

A comparison of phases in terms of the parameters D′ and cos θ, with respect to nasal pungency thresholds

Solvent phase a	No	D′	Cos θ
Blood	1	2.059	0.899
Muscle	2	2.736	0.810
Brain	3	2.683	0.784
Lung	4	2.918	0.811
Kidney	5	2.711	0.820
Heart	6	3.219	0.637
Liver	7	3.165	0.736
Fat	8	2.178	0.964
Nasal pungency	9	0.000	1.000
Eye irritation	10	0.616	0.993
Odor detection	11	2.184	0.938
Anesthesia	12	0.702	0.986
DMF	13	1.222	0.964
NMF	14	0.597	0.996
Formamide	15	1.490	0.971
Water ( 310)	16	4.129	0.787
Water (298)	17	4.395	0.786
Methanol	18	0.931	0.975
Ethylene glycol	19	2.100	0.941
Wet butanol	20	1.901	0.907
Wet hexanol	21	1.360	0.947
Wet octanol	22	1.294	0.950
Olive oil	23	2.252	0.941
Decanol	24	1.447	0.937
Butanone	25	1.136	0.970
Ethyl ether	26	1.189	0.962
Chloroform	27	3.450	0.553

Unlike the PCA analysis, where distances between any two points can visually be estimated, the two exact analyses have to be recalculated when another system is taken as the reference. If we use eye irritation thresholds as the reference, then NMF, nasal pungency thresholds and inhalation anesthesia again emerge as the ‘nearest’ systems, with D′ = 0.617 and cos θ = 0.991 for NMF, D′ = 0.616 and cos θ = 0.993 for NPT, and D′ = 0.559 and cos θ = 0.993 for inhalation anesthesia. Hence we conclude that N-methylformamide should be a good model solvent for eye irritation thresholds, although not as good a model as for nasal pungency thresholds (D′ = 0.597 and cos θ = 0.996).

There are very few solutes that are in each of the NPT and the NMF datasets, and so we have checked our prediction by using eqn 20 to calculate values of log Ks (NMF) and then regressing the experimental values of log (1/NPT) against the calculated values of log Ks (NMF). For comparison we give the full equation (data from ref 121) for log (1/NPT) as eqn 30.

$$\begin{array}{l}\text{Log}(1/\text{NPT})=-7.815(0.374)-0.014(0.346)E+1.760(0.385)S+3.581(0.280)A\\ +0.750(0.426)B+0.806(0.053)L\\ N=48,R^2=0.877,SD=0.359,F=60.0,Q^2=0.825,\text{PRESS}=7.701,\\ \text{PSD}=0.428\end{array}$$ (30)

$$\begin{array}{l}\text{Log}(1/\text{NPT})=-7.176(0.250)+0.952(0.060)log\mathit{Ks}(\text{NMF},\text{calc})\\ N=48,R^2=0.846,SD=0.384,F=252.3,Q^2=0.832,\text{PRESS}=7.385,\\ \text{PSD}=0.401\end{array}$$ (31)

The correlation of log (1/NPT) against the calculated values of log Ks (NMF), eqn 31, is statistically about as good as eqn 30, thus showing that, as we predicted, NMF is an excellent model for the nasal pungency biological process. NMF is not quite such a good model for inhalation anesthesia, with D′ = 0.827 and cos θ = 0.986; compare methanol with D′ = 0.448 and cos θ = 0.994

Our prediction that NMF will be a good model for eye irritation thresholds, although not as good a model as for nasal pungency thresholds is substantiated through eqn 32, obtained in the same manner as eqn 31.

$$\begin{array}{l}\text{Log}(1/\text{EIT})=-7.102(0.463)+0.955(0.107)log\mathit{Ks}(\text{NMF},\text{calc})\\ N=23,R^2=0.790,SD=0.512,F=79.0,Q^2=0.743,\text{PRESS}=6.74278,\\ \text{PSD}=0.567\end{array}$$ (32)

It is of some interest that wet octanol (No 22) appears to be a poor model for all the biological phases and processes that we have considered. This does not preclude log P(wet octanol) being used as a descriptor in a multiple descriptor analysis of biological phases and processes, but our analysis shows that it cannot be taken for granted that wet octanol is a good model (or even the best model) for any particular biological phase or process.

Conclusion

We have set out equations for the solubility of gases and vapors in a variety of tertiary, secondary and primary amides. These equations are statistically good enough to use to predict further values of the gas to amide partition coefficients at 298K. The equations contain valuable data on the chemical properties of the amides as solvents, and can be used to predict separation factors for mixtures of solutes. A detailed investigation of organic solvents as possible models for biological phases and biological processes reveals that no pure organic solvent can be used as a model for the solubility of gases and vapors in a variety of biological phases. However, N-methylformamide is revealed as an excellent model for nasal pungency thresholds and eye irritation thresholds in humans, and suggests that the receptor site must be protein-like in character.