Two-dimensional FSI simulation of closing dynamics of a tilting disc mechanical heart valve

Abstract

The fluid dynamics during valve closure resulting in high shear flows and large residence times of particles has been implicated in platelet activation and thrombus formation in mechanical heart valves. Our previous studies with bi-leaflet valves have shown that large shear stresses induced in the gap between the leaflet edge and the valve housing results in relatively high platelet activation levels whereas flow between the leaflets results in shed vortices not conducive to platelet damage. In this study we compare the result of closing dynamics of a tilting disc valve with that of a bi-leaflet valve. The two-dimensional fluid-structure interaction analysis of a tilting disc valve closure mechanics is performed with a fixed grid Cartesian mesh flow solver with local mesh refinement, and a Lagrangian particle dynamic analysis for computation of potential for platelet activation. Throughout the simulation the flow remains in the laminar regime and the flow through the gap width is marked by the development of a shear layer which separates from the leaflet downstream of the valve. Zones of re-circulation are observed in the gap between the leaflet edge and the valve housing on the major orifice region of the tilting disc valve and are seen to be migrating towards the minor orifice region. Jet flow is observed at the minor orifice region and a vortex is formed which sheds in the direction of fluid motion as observed in experiments using PIV measurements. The activation parameter computed for the tilting disc valve, at the time of closure was found to be 2.7 times greater than that of the bi-leaflet mechanical valve and was found to be in the vicinity of the minor orifice region mainly due to the migration of vortical structures from the major to the minor orifice region during the leaflet rebound of the closing phase.

Introduction

Mechanical valves are typically preferred as a substitute when native heart valves fail to perform normally due to valvular stenosis and/or incompetence, especially in younger patients. This preference is due to the fact that the mechanical valves are durable and can last a patient’s lifetime. Even after years of research which have led to the development of new designs, problems associated with the mechanical heart valves are not completely eliminated and an ideal mechanical valve is yet to be designed. Significant problems with implanted mechanical valves include thrombus formation and ensuing embolic complications, hemolytic complications, tissue overgrowth, and paravalvular leak [1–3]. To counter the thrombus formation, the patients are administered with anti-coagulant therapy which could cause anti-coagulant related hemorrhage. Studies [4] have shown that the risk of embolism is 4 per 100 patients with risk being double in the mitral position than the aortic as the mitral valve faces the harshest environment in the heart especially during the period of valve closure. This study also showed that incidences of thrombus formation were higher with caged ball valves compared to those for tilting disc and bi-leaflet valves.

Thrombus formation is initiated by the activation of platelets by flow-induced stresses and subsequent deposition and aggregation in arterial thrombosis [5]. Fluidinduced viscous and Reynolds shear stresses have been implicated in the activation of platelets and subsequent initiation of thrombus in flow past mechanical heart valves [6–8]. Nobili et al. [9] have presented a damage accumulation model for platelet activation due to hemodynamic shear stresses. Several experimental studies have been reported in the literature on the detailed measurement of the velocity profiles and shear stresses in the vicinity of the mechanical heart valves. Computational simulations have also been exploited to delineate the complex fluid dynamics past the mechanical heart valves particularly in the vicinity of the valve structures where experimental studies are impractical. A recent review of the computational simulations that have been employed to analyze the flow past mechanical heart valves can be found in Sotirospoulos and Borazjani[10] and recent articles relevant to this work are briefly reviewed below. Borazjani et al. report an immersed boundary method for the computational analysis of fluid structure interaction of complex rigid body structures such as mechanical heart valve flow dynamics [11]. Dasi et al.[12] presented the detailed simulation of the complex three-dimensional (3D) vorticity dynamics with flow past a bileaflet heart valve in an axisymmetric aortic geometry using a combination of DNS computations and experimental measurements employing particle image velocimetry. Complex interaction of the vortices generated during the first half of the forward flow phase from the valve housing and leaflets result in shedding of vortices and flow instabilities that persist during the second half of the forward flow phase as well as when the valve has closed. Ge et al. [13] performed a follow-up study to compute the viscous and Reynolds stresses in the axisymmetric aortic geometry resulting from the flow past the bileaflet valve and concluded that the viscous shear stresses can potentially activate the platelets but were not high enough to damage the red blood cells. Furthermore, they argued that Reynolds shear stresses do not directly contribute to the mechanical load on the blood cells. Similar conclusions were also presented by De Tullio et al. [14] who performed a DNS analysis of pulsatile flow past a bileaflet heart valve. Nobili et al. [15] also reported on a fluid structure interaction analysis for flow past bileaflet mechanical heart valve prosthesis. However, these simulations did not incorporate the details of the flow structures in the small gap widths between the leaflets and the valve housing or in the hinge region which are also potential sites where red blood cell damage and platelet activation can be anticipated.

As the blood elements pass through the mechanical heart valves which possess a rigid structure unlike a compliant native heart valve during the valve closing phase, large pressure transients and flows with relatively high velocity magnitudes are present during valve closure in the gap regions between the leaflet and the valve housing. Damage to blood cells and activation of platelets can also be anticipated in the clearance region between the edge of the leaflets and the valve housing as well as in the hinge region of bileaflet valves during the closing phase [16] of the mechanical valve dynamics. Lamson et al. [17] have demonstrated that the relative blood damage during the valve closing phase is comparable to that in the valve opening phase. The analysis of the complex flow dynamics in the vicinity of the valve structure during the valve closing phase may also provide valuable information on the potential for thrombus deposition with mechanical valves and contribute towards improved designs.

Both experimental and computational studies have reported flow separation and vortex shedding at the edge of the valve leaflets [16, 18–20]. The gap widths provided between the leaflet edge and the housing gives rise to leakage jet flow accompanied by relatively high shear stress [16]. Platelets passing through this flow region may be activated due to high shear stresses and subsequently get trapped in the recirculation region in the vicinity of the leaflets resulting in platelet aggregation and thrombus initiation. In this regard it is of interest to analyze valve designs to determine which designs offer potential for mitigation of platelet activation and subsequent thrombogenesis. The mechanisms by which the platelet damage can occur need to be elucidated so that valve designs can be directed towards discouraging fluid dynamic phenomena that encourage platelet activation. We had reported on the fluid dynamics in the clearance region as the leaflet moves from the fully open to the fully closed position with a bileaflet mechanical valve in the mitral position. The initial simulation was restricted to a 2D analysis [21] and was subsequently extended to a 3D analysis [22]. Both these studies demonstrated the presence of high shear stresses on the edge of the valve in the clearance region and vortical flow in the vicinity of the leaflet in the upstream region indicating large residence time for particles entrapped in the recirculating flow region. Comparison of the results also suggested that the 2D analysis results in the computed pressure and velocity fields are comparable to those with the 3D analysis and hence 2D analysis may be sufficient for the analysis of valve design so that different leaflet configurations can be analyzed and optimal design chosen before further prototype development and detailed 3D simulations and experimental studies are undertaken. In the analysis of the valve closure dynamics in the above two studies, the leaflet position during the closing phase was specified. Subsequently, we developed a fluid-structure interaction analysis for the analysis of mechanical valve closing dynamics and the computational algorithms developed in our laboratory also incorporated a local mesh refinement algorithm so that the mesh were refined without user intervention so that the flow within the clearance region gap width could be accurately resolved. We used this algorithm with a 2D analysis to delineate the flow within the clearance region of a bileaflet valve during the closing phase and more recently to analyze the impact of design parameters on the bileaflet valve closure flow dynamics [23].

Most of the simulations of flow past mechanical valve dynamics described above have been restricted to the bileaflet valve models. Compared to the nearly symmetrical flow through the two peripheral orifices and through the central orifice for the bi-leaflet valve, flow past a tilting disc valve is asymmetric with the flow unevenly divided between the major and minor orifices. Thrombus formation and tissue overgrowth have been observed in the minor orifice region in the tilting disc valve which could occlude the flow further [24]. This study measured a peak shear stress of 70 Pa and 15 Pa at the major and minor orifice region, respectively, during the forward flow phase Manning et al. [20] measured the flow characteristics within the housing of a tilting disc valve mounted in a single shot chamber using three component laser Doppler velocimetry. Instantaneous velocities were measured during mitral valve closure and maximum shear rates were calculated. It was observed that the magnitude of the wall shear rate was as high as 100,000 s⁻¹ closest to the valve housing and that the maximum closure jet velocity was approximately 20 m/s. It was concluded that these shear rates provide a potential for significant blood damage, especially since the measurements were acquired at a lower loading condition.

The present study focuses on the numerical simulation of the closing dynamics of a tilting disc valve in a two dimensional setting and compares its fluid dynamics with that of a bi-leaflet heart valve giving due importance to the dynamics of leakage flow jets between the leaflet and the housing . In particular, we compare and contrast the local fluid dynamics in the peripheral and central clearance regions of a bi-leaflet valve with those in the major and minor orifice regions of the tilting disc valve during the time when the occluder moves to the fully closed position.

Fluid-structure Interaction (FSI) analysis methods

An FSI analysis is employed for the fluid dynamics during the phase when the mechanical valve occluder moves from the fully open to the fully closed position with the valve in the mitral position. The details of the FSI analysis techniques are included in Krishnan et al. [16] and a brief description is included below.

The leaflet in the 2D model is assumed to rotate about a pivot due to the external momentum applied on the leaflet surfaces due to the pressure and shear forces from the surrounding fluid and the buoyancy forces. The governing equations for the fluid are solved employing an Eulerian level-set based sharp interface Cartesian grid flow solver. The Cartesian grid approach has been used successfully to capture the flow dynamics in the bi-leaflet heart valve. This method uses a fixed rectangular mesh with the valve geometry superimposed on it [16, 25–26]. One of the biggest challenges in modeling the heart valve dynamics is the disparity in the length scales. For example, differences in length scales between a typical valve orifice and its gap width can be of two orders of magnitude. These different length scales need to resolved to capture the flow dynamics in a heart valve problem. Flow in the gap widths is a significant part of flow dynamics as they could play a major role in platelet activation and thrombus formation. A local mesh refinement algorithm which adapts mesh automatically to the gradients of flow is incorporated for computation efficiency and accuracy.

Simulation condition

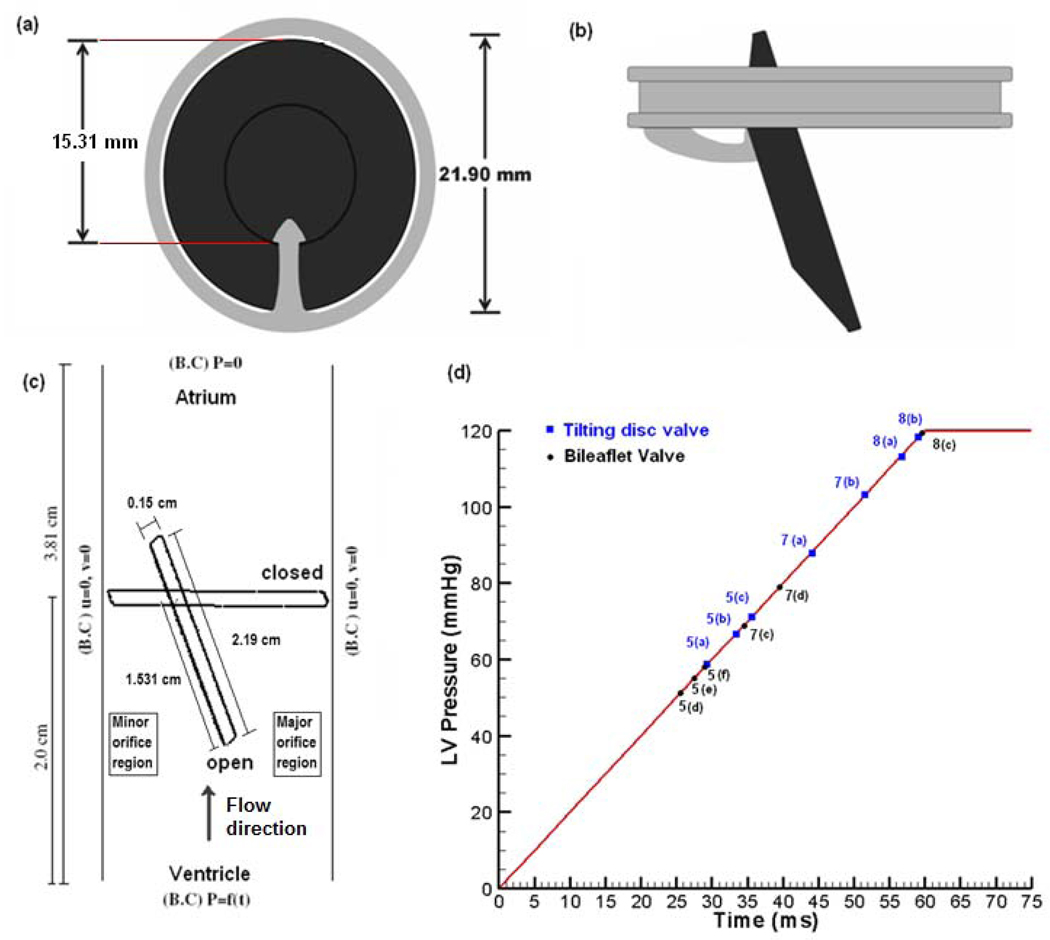
The nominal dimensions for a 27 mm Bjork-Shiley Monostrut (BSM) tilting disc valve are employed for this simulation. Figure 1(a) and (b) show a graphical representation of a 27 mm BSM valve at the fully closed and open position. Figure 1(c) represents the 2D model employed in this simulation with nominal dimensions for the leaflets and the gap width between the leaflet edges and the valve housing in the major and minor orifices, and the pivot point representing the point where the leaflet pivots about the strut. The simulation represents the valve closure phase in the mitral position and the ventricular pressure rise rate of 2000 mm Hg/s [27] inducing the motion of the valve towards closure, shown in Figure 1(d). The valve is fully open at 20° to the vertical axis and rotates a complete 70° angle to complete closure. The fluid is assumed to be incompressible and Newtonian with the density of 1056 kg/m³ and viscosity of 3.5 cp, typical magnitudes for whole human blood at 37°C. The remaining boundaries are walls where no- slip conditions prevail. The leaflet moves according to the fluid forces and platelets, assumed as point particles, are seeded throughout the domain with one-way coupling [28].

Figure 1.

(a): Schematic depiction of a 27 mm BSM valve in the closed position, (b): Leaflet in the fully open position with disc at 20° to the vertical rotates 70° to reach the fully closed position; (c): Schematic of the 2-D computational domain with the leaflet shown in the fully open and closed position with the disc pivoted at the position of the strut; and (d) Applied inlet ventricular pressure boundary condition. The data points in the plot refer to the time during the leaflet closure phase at which the computational results are presented in Figure 5, Figure 7, and Figure 8.

In order to compare in detail the fluid dynamics during valve closure between the tilting disc and the bi-leaflet valves, we repeated the simulation for a bi-leaflet valve as described in Krishnan et al. [16]. The nominal dimensions for a St. Jude Medical 27 mm bi-leaflet valve were employed in this simulation. Referring to Figure 1(c), the left side wall for the tilting disc valve close to the minor orifice region will represent the symmetric line between the two leaflets for the bi-leaflet valve and the flow on the left edge of the leaflet will represent the flow between the leaflets. In the fully open position the leaflet for this valve is at about 5° from the vertical and the leaflet rotates by about 55° to the fully closed position.

Simulation of platelet activation

When platelets are exposed to high shear followed by their entrapment in the regions of re-circulation with high residence time in the vicinity of valve structures such as the disc and the housing, potential exists for the activation and aggregation of platelets leading to thrombus deposition. A dynamic platelet activation model that includes the effects of shear stress and exposure time similar to that used by Bluestein’s group [5, 8–9] is used in this simulation as shown below.

$${\alpha }_T={\displaystyle \underset{0}{\overset{T}{\int }}\left|\tau \right|dt}$$ (1)

Here the limit T represents the residence time of every particle seeded in the flow domain and the shear stress is computed for each particle at its location. Thus, with the model proposed above, we are able to encompass both the shear stress and its exposure time upon which the activation potential depends.

Platelets are modeled as point particles by a Lagrangian particle tracking algorithm as explained by Chen et al. [28] assuming that platelet length scales are very small compared to the fluid length scales. One way coupling is assumed such that the particles are affected by the flow, but the flow is not affected by the particles, and also particle-particle interactions are neglected. All particles have the same diameter of 2µm and the carrier fluid is incompressible and Newtonian. A particle momentum equation as given below is solved to calculate the particle velocity

$$\frac{d\overrightarrow{v}}{dt}=\frac{\partial \overrightarrow{v}}{\partial t}+\overrightarrow{v}\cdot \nabla \overrightarrow{v}=\overrightarrow{f}$$ (2)

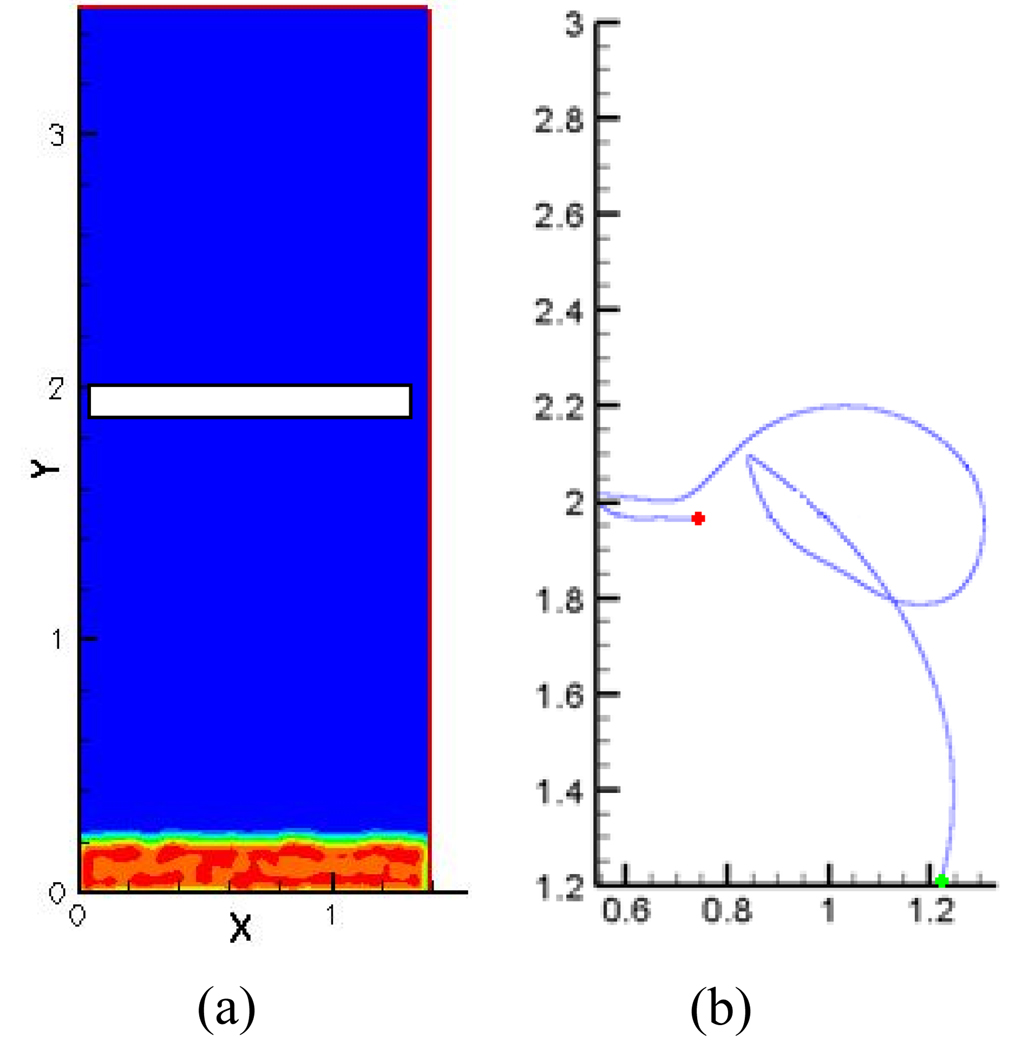
where v⃗ is the non-dimensional particle velocity vector and f⃗ is the non-dimensional total contact force on the particle including drag and lift. These drag and lift forces acting on the particle depend on the particle’s mass and size and influence the motion of the particles. Details regarding the particle transport algorithm and its implementation have been presented in previous work [16]. Dilute particulate flow is assumed so that approximately 12000 particles are present in the computational domain at a given time. Field variables such as particle concentration and activation parameter are calculated and stored at particle locations. As these variables are calculated cumulatively (during the course of a cardiac cycle) and depend on time, particles are present in the computational domain throughout the simulation. No wake effects are included and particles follow a one way coupling with the fluid. Initially the particles are distributed randomly at the inlet. This can be observed from Figure 2a where particle concentrations are high at the region close to the inlet (red) and no particles are present in the bulk of the domain (blue). But as pressure begins to rise in the ventricular region forcing the particles to move up with the flow, particles begin to passively follow the flow and get trapped in the zones of re-circulation. To ensure that particle concentration in the entire computational domain remains constant in time, a periodic boundary condition is applied at the inlet and outlet so that particles are automatically inserted as they are emitted out of the domain. Figure 2b is an example of a single particle path being traced over time. The green dot at the inlet shows the starting point of the particle that is initially in the ventricular region and the red dot shows the ending point of particle path at the end of the closure phase of the valve. We can see that this particular particle moves from the ventricular region as the valve begins to close owing to the ventricular pressure rise, migrates towards the atrial side through the major orifice region and finally settles in the minor orifice region where it was observed to have a high likelihood of platelet activation. This particle therefore experiences high residence times in the flow domain.

Figure 2.

a) Particle distribution in the flow regime at the beginning of the computational cycle with high particle concentration at the inlet (red) and no particles present in the rest of the flow regime; b) Example of a single particle being traced over time with the green dot indicating the starting point and the red dot the end point of the particle path during the closing phase. The activation parameter is calculated cumulatively for each particle within the flow domain.

Simulation of leaflet rebound

The valve leaflet, after rotating through its specified angular displacement rebounds after hitting the stopper; since the stopper is not modeled in this study, the disc is made to bounce back after it moves to the fully closed position. The equation for disc rebound dynamics is given below

$${\omega }_2=-\sigma {\omega }_1$$ (3)

where σ is the co-efficient of resilience and depends on the disc and the housing material, and ω₁ and ω₂ are the angular velocity before and after impact. Lacking experimental data, in our previous simulations a value of 0.5 was assumed as the resilience factor during the impact between the leaflet and the housing [16]. In this study, the resilience factor was determined based on experimental measurements of the leaflet rebound. Employing the in vitro experimental set up described by Kini et al. [29], the leaflet angular position was measured as a function of time during the valve closure phase and the measurements were continued to obtain data during the first rebound of the leaflet after closure. The data on the valve closure angle as a function of time were compared with the magnitudes obtained in our simulation with the initial value of 0.5 specified for the resilience factor. The resilience factor was adjusted in the course of several trial simulations until the rebound amplitudes predicted by the simulation agreed with the data from the experiments. Figure 3 shows the comparison of the experimental data and the computational results of the angular position. The magnitude of the resilience factor of 0.78 used in the final simulation resulted in good agreement of the leaflet rebound magnitude between the simulations and the experimental data as seen in the figure. The same resilience factor was employed for the simulations of both the tilting disc and the bi-leaflet valve models as described in the results below.

Figure 3.

Comparison of angular position of the leaflets during the closing phase and the first rebound from the experimental study with the simulation results.

Results

Leaflet closing dynamics

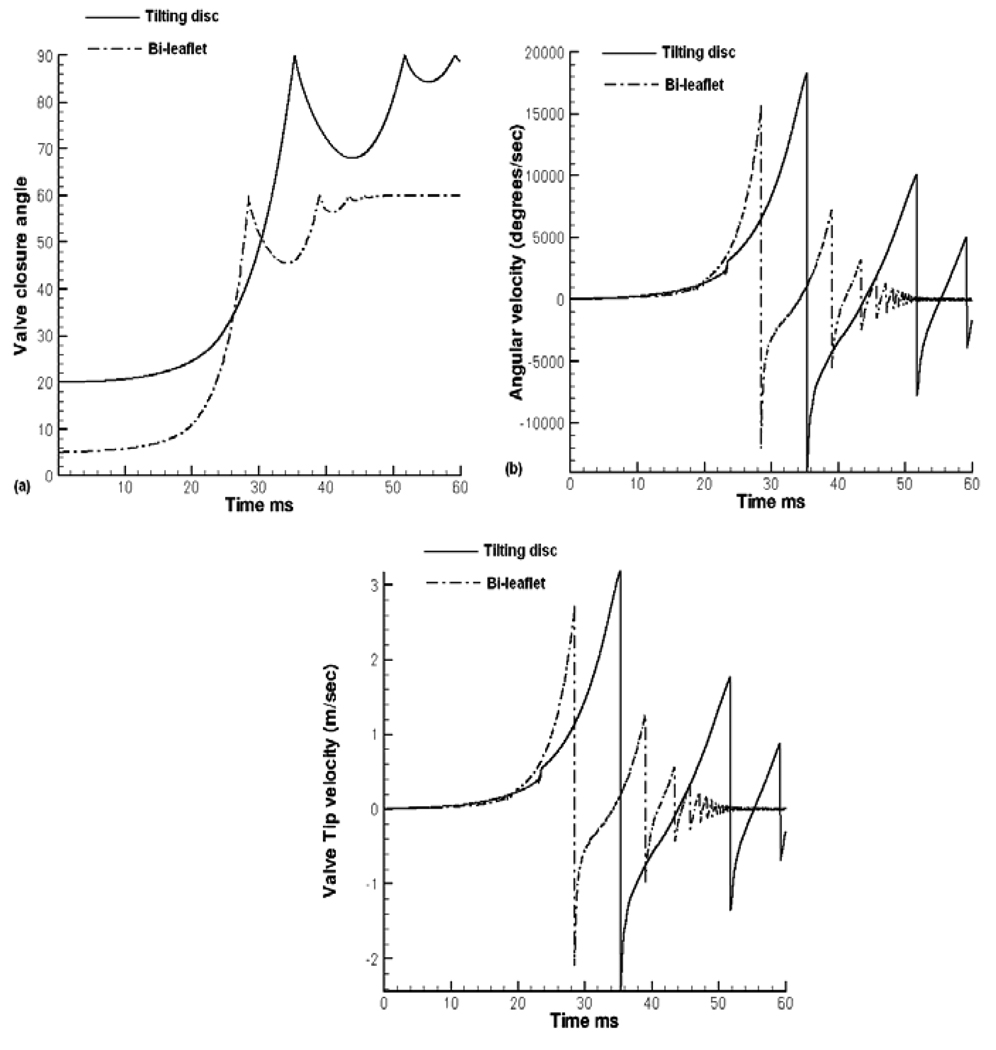
The leaflet closing angle, the angular velocity, as well as the linear tip velocity as a function of time for the tilting disc valve is compared to that for the bi-leaflet valve in Figure 4. In the beginning of the valve closure, the leaflet moves slowly towards closure and the angular velocity starts increasing for both the valves. For the tilting disc valve, the leaflet takes about 31ms to complete the initial 35° of rotation and only 4 ms to move to the fully closed position as seen in Figure 4(a). With the bi-leaflet heart valve, the first half of closure takes approximately 25 ms and then the leaflet takes approximately 3.4 ms to complete the latter half of closure resulting in an exponential rise in the leaflet rotation. The leaflet reaches complete closure and rebounds at impact, reversing the angular velocity. In order to compare the local fluid dynamics during the rebound phase as well, the simulation is continued for another 10 ms after the initial leaflet closure. Figure 4(b) shows the comparison of the angular velocity of the two valves. The tilting disc valve reaches a maximum angular velocity of 18300° /sec at the instant of closure and the bi-leaflet valve around 16700° /sec. As mentioned earlier the tilting disc valve takes about 6 ms longer than the bi-leaflet valve to complete the initial half of closure. As the disc moves towards closure for the tilting disc valve, the occluder in the minor orifice region moves in the direction opposing the flow, thereby offering resistance to forward motion. The length of the occluder in the minor orifice region is larger than the distance between the hinge of the bi-leaflet valve and its left edge. Hence the bi-leaflet valve provides less resistance towards the closing motion.

Figure 4.

Comparison of Leaflet closing dynamics for the tilting disc and the bi-leaflet valves: (a) Angular position of the leaflet closure with time during the closing and rebound phases; (b) Leaflet angular velocity; and (c) Leaflet tip velocity.

The tilting disc valve has to rotate another 35° to reach the fully closed position which is completed in approximately 4 ms. The bi-leaflet valve takes about 3.4 milliseconds to reach complete closure rotating about 27.5°. As the second half of closure starts later for the tilting disc valve, the tilting disc valve experiences a higher ventricular pressure than the bi-leaflet valve during the latter half of closure resulting in an exponential rise in angular velocity. Looking at Figure 1(d), the tilting disc valve starts its second half of closure at a ventricular pressure of about 62 mmHg and complete closure is attained at a ventricular pressure of about 73 mmHg. Comparing that with the bi-leaflet valve, the second half of closure starts at a pressure of 45 mmHg and ends at 52 mmHg. From these values, it is obvious that a higher force is exerted on the tilting disc valve during the second half of closure explaining the resultant higher angular velocity and valve tip velocity as shown in Figures 4(b) and 4(c), respectively. The tilting disc valve has a tip velocity of about 3.2 m/sec and the bi-leaflet velocity had a valve tip velocity of approximately 2.7 m/sec at the instant of leaflet closure prior to the rebound.

Flow dynamics during leaflet closure

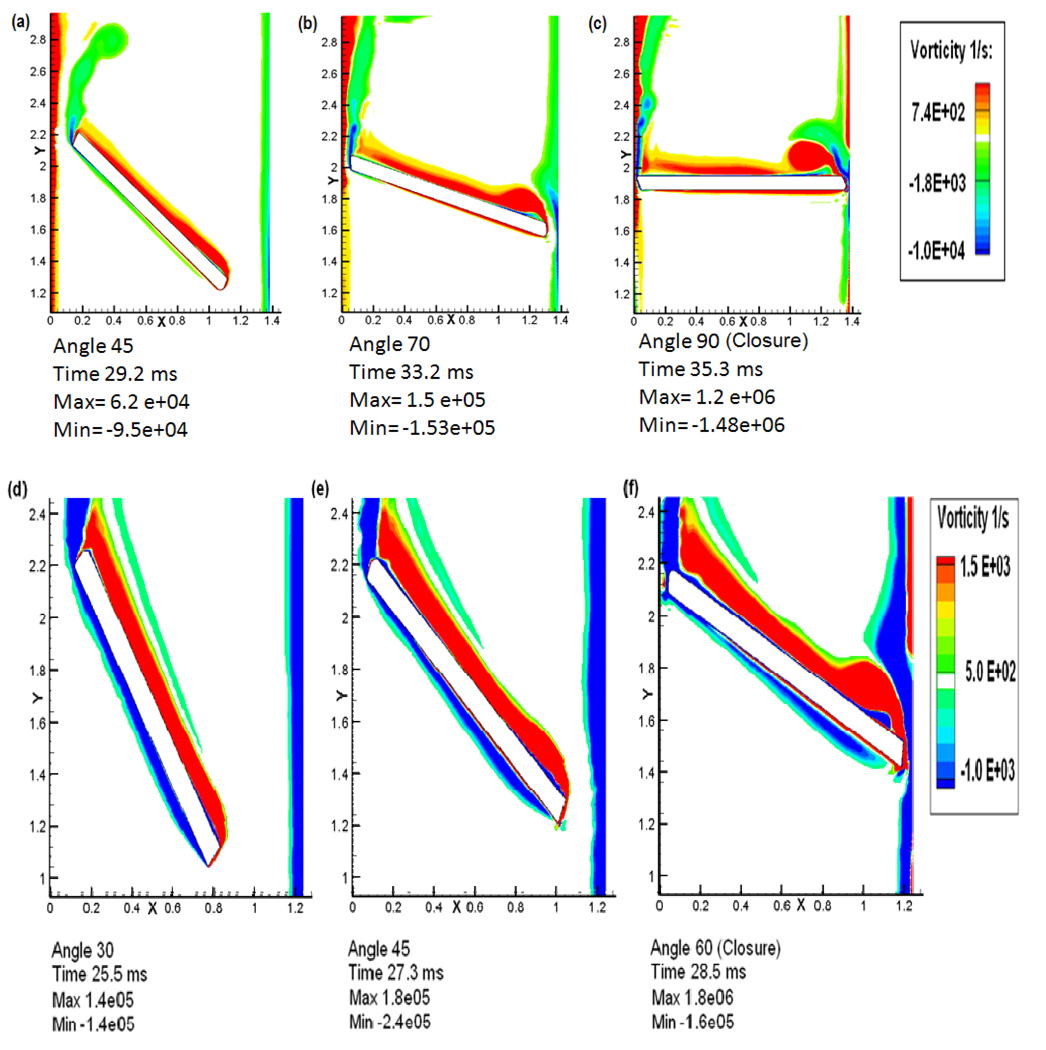
Plots of the vorticity contours during the valve closure phase for both the valves are shown in Figure 5 and the shear stress distribution, concentration of platelets and the calculated activation parameter in the vicinity of the leaflet are plotted in Figure 6. The top panel in both the figures includes the simulation results for the tilting disc valve and the corresponding plots for the bi-leaflet valve are included in the bottom panel. The time during the closure phase when the vorticity distribution is plotted is indicated in Figure 1d. When the closure phase starts with the tilting disc valve, the flow is mainly divided into two unequal portions in the minor and major orifice regions. The flow at the minor orifice region is marked with boundary layer separation followed by the rolling up of unstable wakes forming into vortices. The vorticity contours when the disc is at 45° to the vertical axis in Figure 5(a), show the wake rolling up to form shed vortices. This rapid shedding of vortices happens periodically at the minor orifice region until closure due to a higher leakage flow velocity resulting from the progressively reducing gap width in the minor orifice region augmented by the effect of the motion of the disc in a direction opposing the flow. An independent weak circulating flow downstream of the valve is observed with the leaflet in the fully closed position. The major orifice region of the tilting disc valve presents a totally different flow pattern compared to the minor orifice. Even at the initial stage, the boundary layer starts thickening and separates from the disc. This is followed by the development of a vortex with re-circulating flow in the vicinity of the disc as shown in the vorticity contours in Figure 5(a) when the valve is at 45° to closure. But this vortex does not shed from the disc, in contrast to that from the minor orifice region, and stays in the vicinity of the rotating disc. The reason could be that, at the minor orifice side, the disc is moving in an opposite direction to the flow whereas at the major orifice side, the disc is moving along with the direction of flow with a very high velocity. However, at the very end of the closure stage, the large vortex at the major orifice seems to be shedding after getting separated from the wake as shown in Figure 5(b) and (c). Another interesting phenomenon to be noted on the major orifice side from the vortex contours is the boundary layer that develops on the housing side. As the valve moves towards closure, the wake that develops on the housing is dragged towards the atrial region resulting in a small re-circulating flow in the opposite direction to recirculating flow formed at the edge of the disc at the major orifice side. Also, the bulk of the flow is carried across to the atrial side through the major orifice; platelets which pass through the major orifice area are subjected to high shear stresses and have the potential to be trapped in these two re-circulating flows. The flow behavior in the major orifice region during the initial closing phase is observed to be similar to that for the bi-leaflet valve as shown below.

Figure 5.

Comparison of vorticity plots between the tilting disc valve and the bi-leaflet valve during the closing phase. Top panel (a, b, and c): plots for the tilting disc valve; and Bottom panel (d, e, and f): Plots for the bi-leaflet valve.

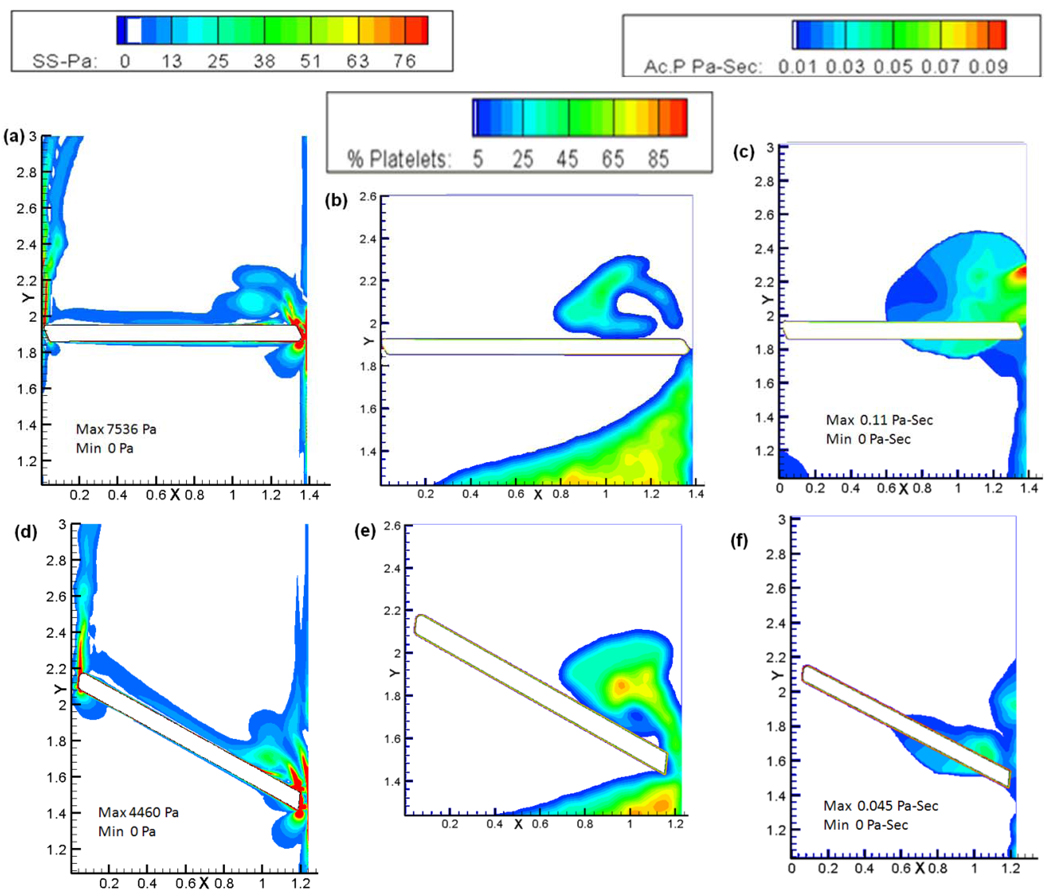
Figure 6.

Plots of the shear stress, platelet concentration, and platelet activation parameter for the tilting disc valve (top panel: a, b, and c) and the bi-leaflet valve (bottom panel: d, e, and f) at the instant of closure.

The bottom panel of Figure 5 shows the vorticity contours at various stages of bi-leaflet valve closure. The boundary layer from the peripheral edge starts separating and rolls up into vortical structures. However, the rolling up of vortices does not happen in the case of the bi-leaflet valve until it reaches the very end of closure as seen in Figure 5(f). A comparison of the plots indicates that the development of re-circulation zones starts early in the case of the tilting disc valve when compared to the bi-leaflet valve. It should also be noted that the tilting disc valve attains its closure much later when ventricular pressure is higher compared to that experienced at the instant of bi-leaflet valve closure. Thus, a prolonged recirculation experienced by the tilting disc valve means a higher residence time for platelets in the vicinity of the tilting disc valve suggesting that the flow dynamics experienced by the tilting disc valve is more favorable to platelet activation and aggregation compared to the bi-leaflet valve.

The maximum velocity in the minor orifice region gap was computed to be around 9 m/sec at complete closure and decreased downstream from the gap. At a distance of 3 mm away from the gap, the velocity magnitude was approximately 4.5 m/sec which is close to the experimentally measured leakage flow velocity at the minor orifice side obtained by Kini et al. [29]. It can be observed that the jet velocity at the minor orifice is much lower than that in the major orifice at complete closure. It was also observed that, during the initial stages of closure, the magnitudes of velocity were higher at the minor orifice region than the major orifice owing to the much smaller gap. Towards the later stage of closure, a strong leakage jet develops at the major orifice region and is intensified to its maximum at the instant of valve closure. The maximum speed in the major orifice region was computed to be about 41.8 m/s in the gap with a maximum Reynolds number of 415. This magnitude is close to the experimental data from Manning et al. [24] who measured a closure (regurgitant) jet velocity of about 20 m/s near the leaflet, though outside the gap, where the velocity will be lower.

Figure 6(a) and 6(d) compares the shear stress contours at the instant of closure for both the valves. For the tilting disc valve (top panel), as the disc on the minor orifice side is moving against the direction of flow, it could be expected that the shear stress during the beginning of the closing motion could be higher on the minor orifice side. This is observed to be the case in the simulation where the disc is at 45° to the vertical when the maximum shear stress is found at the minor orifice region. As the closure continues, the maximum shear stress gets shifted to the major orifice region. When the disc reaches an angular position of 70° to the vertical, shear stress magnitudes in both the minor and major orifice gaps are comparable with a magnitude of around 700 Pa. When the valve reaches the instant of closure, higher values of shear stress are observed predominantly in the major orifice region compared to the minor orifice region. At the instant of leaflet closure as shown in Figure 6(a), the maximum shear stress at the major orifice was about 7500 Pa whereas the shear stress at the minor orifice region was around 1200 Pa. These magnitudes can be compared with the maximum shear stresses computed at the peripheral gap for the bileaflet valve at closure of about 4600 Pa shown in Figure 6(d) (bottom panel). It is evident from the shear stress magnitudes that the platelets which pass through the gaps of the tilting disc valve experience a much higher shear stress than the bi-leaflet valve suggesting a higher potential for activation.

Figure 6(b) and (c) show the platelet concentration and the activation parameter, respectively, for the tilting disc valve at the instant of closure. It can be seen that the platelet concentration at the minor orifice region is relatively less than that of the major orifice region suggesting that the bulk of the flow is carried to the atrial region through the major orifice region during the later stages of closure and the activation parameter at this site was found to be 0.11 Pa-s as seen in Figure 6(c). Platelets passing through this high shear region can be potentially activated and get entrapped in the regions of recirculation above the leaflet as shown in the concentration plot. A much higher concentration of platelets passing through the major orifice regions gap width could also suggest that the dynamics in the minor orifice side does not contribute to the activation of platelets compared to the major orifice side during the initial closure stages of the valve. Platelet concentration in the bi-leaflet valve was also found to be relatively higher near the peripheral edge as seen in Figure 6(e). Comparing to the tilting disc valve, the activation parameter for the bi-leaflet valve was calculated to be 0.045 Pa-s at the instant of closure near the peripheral edge as seen in Figure 6(f). The lesser magnitude of activation parameter could be due to the re-circulation zones developing much later during closure as explained previously and a smaller shear stress value at the gap width.

Valve Rebound

In the case of both types of valves, the simulation was continued for another 10 ms to study the effect of flow during the leaflet rebound phase and its implication on the platelet activation. From Figure 4(a), it is seen that the bi-leaflet valve rebounds to about 14.5° in the first rebound with the rebound amplitude decreasing with subsequent rebounds. In the case of the tilting disc valve, the initial rebound amplitude was about 22°. It can also be noted that the duration of rebound is higher for the tilting disc valve compared to that for the bi-leaflet valve. This could mean that, during the rebound phase, more platelets are being passed into the downstream side of tilting disc valve dominated by higher shear stress magnitudes and re-circulation.

The top two panels of Figure 7 show the vorticity, shear stress and the calculated platelet activation contours during the first rebound and subsequent closure of the tilting disc valve and the bottom panels show the corresponding plots for the bi-leaflet valve. Figure 7(a) shows contours for the tilting disc at 68°, the maximum angle reached by the leaflet after the initial rebound. The most significant feature observed in the figure is the boundary layer separating from the housing and the disc edge, and the two vortex structures come closer and start interacting with each other. Due to this interaction of vortices with opposite signs, secondary vortices are formed which move away from the major orifice toward the minor orifice region. As the valve moves back towards closure, the independent recirculation region is seen migrating toward the minor orifice region as observed in Figure 7(b). The movement of the vortical structures towards the minor orifice region could be due to the final closing angle of the tilting disc valve, which helps the vortical structures move along with it. We saw earlier that the vortices do not shed from the disc but rather choose to stay in the vicinity of the leaflets at the instant of closure. As the valve rebounds and moves backwards, vortical structures start separating, and move towards the minor orifice region. Flow dynamics during the initial rebound of the bi-leaflet valve and its subsequent closure is shown in Figure 7(c) and (d). During rebound, similar dynamics followed in the right edge of the leaflet, but the separated vortical structures slowly start to move downstream from the vicinity of the leaflet right edge as observed from vorticity contours in Figure 7(c) and (d). This could be due to the closure angle of the two valves; the bi-leaflet valve reaches its closure at about 60° to the vertical whereas the angle of tilting disc is 90° in the fully closed position. Platelets passing through the narrow gap width of the major orifice region are trapped in these regions of recirculation and get carried along with the vortices that migrate towards the minor orifice region. The dynamics of the flow in the major orifice gap also increases the fluid shear stress as shown in the shear stress contour (second column) of Figure 7(b). The high shear stress coupled with the high residence time in the recirculation zones makes this a potential site for activation of platelets as shown in platelet activation contours (third column) of Figure 7. The platelet activation at the end of the first rebound was calculated to be approximately 1.1 Pa-s in the vicinity of the minor orifice region as shown in the Figure 7(b) as opposed to the bi-leaflet valve with a magnitude of 0.27 Pa-s near the peripheral edge of the leaflet as in Figure 7(d).

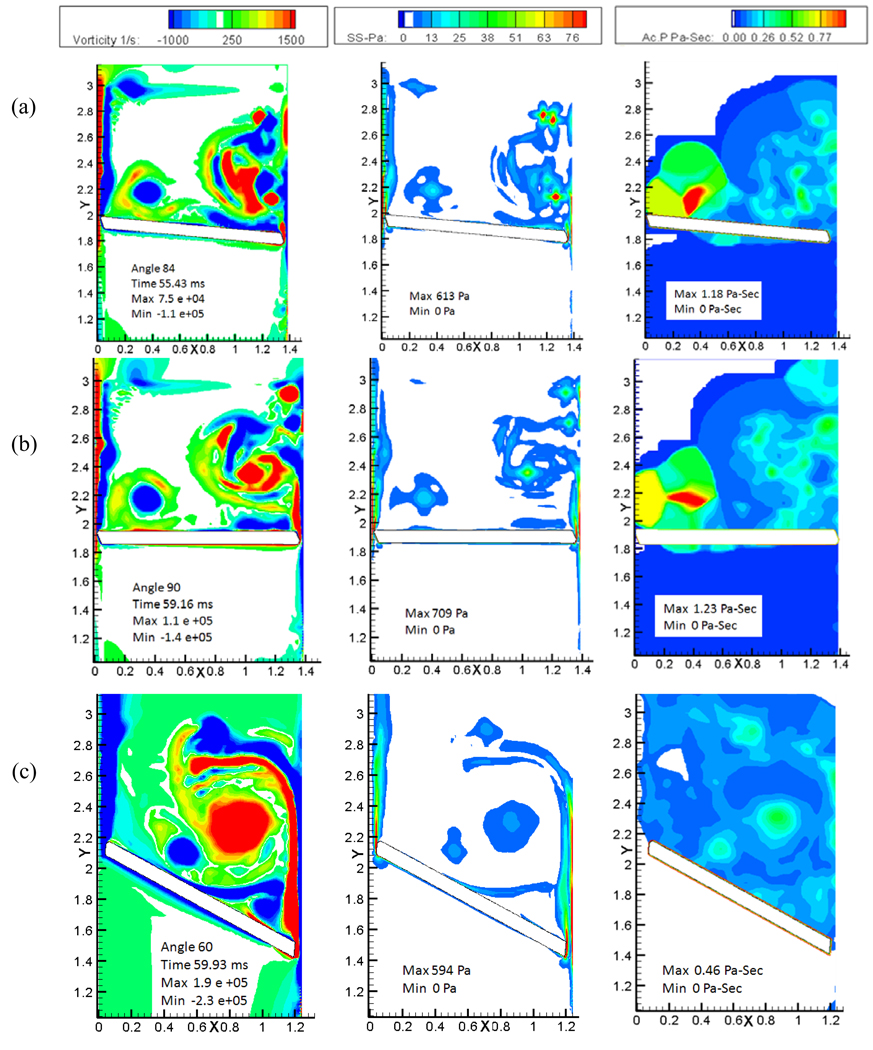
Figure 7.

Plots of the vorticity (left column) , shear stress (middle column), and the calculated platelet activation contours( right column): (a) First rebound phase; and (b) closure following the first rebound for the tilting disc valve. (c) First rebound phase; and (d) closure following the first rebound for the bi-leaflet valve.

Figure 8 (a) shows the second rebound phase of the tilting disc valve and figure 8(b) shows the closure following rebound. During this phase, where the leaflet rebounds to about 6°, the recirculation zone that had developed during the first rebound has not advected away but migrated further towards the minor orifice region and separated from the major orifice side. At the major orifice gap width, similar phenomenon as observed earlier is repeated where the interaction of opposite vortical structures take place which leads to the formation of separate vortical zones. The vortical structures developing during the closure remained in the vicinity of the disc during the entire simulation and seemed to be settling down at the minor orifice region. The vortex of opposite sign which resulted from the housing region was also carried to the minor orifice region which can be seen in the figures as well. The recirculation region persists in the valve vicinity for more than 25 ms with the tilting disc valve. Since the amplitude for the second rebound is significantly smaller for the bi-leaflet valve as observed in Figure 4, plots for only the second rebound phase are included in Figure 8 (c) for the same. It can be observed that the vortical structures have completely separated from the leaflet, with a weakened intensity and moving downstream towards the atrial region. This process starts as early as the first rebound as shown in Figure 7(c). Krishnan et al. [16] also observed that the vortices persist near the leaflet for about 5–10 ms after valve closure. The current bileaflet study, using a resilience factor for rebound based on experimental data, observed that the vortical structures were present in the vicinity of the leaflet for approximately 10 ms after closure. Our simulations show that the time spent by the platelets in the region of high shear in the vicinity of the valve after being squeezed out of the gap width is greater for the tilting disc valve than the bi-leaflet valve. The cumulative activation parameter at the end of simulation is shown in Figure 8(b) and (c) for the tilting disc and the bi-leaflet valve, respectively. The platelet activation factor at the end of the second rebound was calculated to be 1.23 Pa-sec for the tilting disc valve which is approximately 2.7 times more than what was calculated for the bi-leaflet. In our simulation as well as in our earlier study [16], it was observed that the maximum platelet activation was near the right edge of the leaflet for the bi-leaflet valve, whereas in the case of the tilting disc valve, we observed the maximum activation to be in the vicinity of the minor orifice region. Studies have reported that thrombus formation has been observed in the vicinity of the minor orifice region with the tilting disc valves [24] and our simulations indicate the possible mechanisms for the prevalence of damaged platelets in this region. However, it should be noted that our simulation indicates that the maximum activation in the vicinity of the minor orifice region is due to the dynamics presented by the major orifice region as well as the closing angle of the tilting disc valve.

Figure 8.

Plots of vorticity (left column) , shear stress (middle column), and the calculated platelet activation contours (right column) : (a) second rebound phase; and (b) closure following the second rebound for the tilting disc valve. (c) during the final closure of the bi-leaflet valve.

Discussion and conclusion

This study examined the flow structures through the gap width of a 27 mm tilting disc mechanical heart valve and its implication on the platelet activation under physiological conditions in the mitral position focusing on the closure phase of the valve. The flow structures were then critically compared with that of a bi-leaflet valve. A Cartesian mesh was employed for the study and a local mesh refinement algorithm was used to enhance the accuracy and efficiency of computation. Various previous studies [5, 9, 11, 20] have been conducted on understanding the flow through a tilting disc valve and all have reported the presence of re-circulation regions and high shear flows as observed in this study. Platelets entrapped in such vortical structures are likely to remain in the vicinity of the heart valve. This two-dimensional computational study enabled us to compute the details of the flow dynamics in the narrow gap width between the occluder and the housing at complete closure. Fluid-structure interaction analysis was performed to allow the passive valve to close under the influence of ventricular pressure rise. The flow in the major orifice was marked with high shear flow and recirculation whereas the minor orifice region noted a weaker jet flow and a quicker vortex shedding. It was observed that platelets are entrained into the boundary layer, subject to high shears and then transported into the vortical structures. It was interesting to note that vortical structures shed from the major orifice region migrated towards the minor orifice region where it stayed for a longer time thus, making the dynamics very different when compared to the bi-leaflet valve. This combination of high-shear environment experienced on the surface of the valve and the resulting re-circulating, long residence time fluid presents the potential for thrombus formation. It was observed that the activation parameter for the tilting disc valve was nearly 2.7 times greater than the bi-leaflet valve. The activation parameter was calculated on every particle seeded in the domain using a Lagrangian particle tracking algorithm with one way coupling. The results were mainly divided into two sections focusing on the minor and major orifice flows in the case of the tilting disc valve. It was observed that the flow in the major orifice region posed much potential for activation compared to the minor orifice region. The flow dynamics in the major orifice region was compared to the flow presented by the peripheral edge of the bi-leaflet valve.

This study focused mainly on the closure dynamics of the tilting disc valve and neglected the opening or the forward flow phase. Many studies have focused on the opening phase and have observed stagnation and flow reversal zones downstream of the valve. Yoganathan et al. [24] studied the fluid dynamics in the partially occluded and fully functional Bjork-Shiley valve and observed flow stagnation and vortex formation in both the cases. They calculated the peak shear stress of 70 Pa near the major orifice region. Lim et al. [30], using PIV measured the velocity and flow stress in the opening phase to evaluate the performance of four different aortic valves in which two were single tilting disc valves. This study also reported flow stagnation and recirculation and the peak Reynolds stress reached about 100 Pa. Though all phases of mechanical valve function have been known to contribute to blood damage, studies have reported that the closure phase is more deleterious to blood elements than the opening phase. This is because of the high pressure drop developed during the late closure stage, which would induce a high velocity through the small gap width resulting in high shear stress. The present study as well as the study on the bi-leaflet valve [16] report shear stress in the order of 10³ Pa indicating that the closure phase is more damaging than the opening phase.

This study enabled us to delineate some of the essential flow dynamics in a tilting disc valve, particularly the detailed fluid dynamic analysis in the gaps between the leaflet and the valve housing at the instant of valve closure and subsequent rebound. The FSI analysis coupled with the local mesh refinement enabled us to resolve the high shear flows in the minor and major orifice regions of the valve during the closing phase accurately. Many studies have been performed to understand the flow dynamics of tilting disc valves in a three dimensional setting [5, 9, 11] which focused on the opening phase. Furthermore, these studies failed to adequately resolve the flow dynamics in the critical narrow gaps that arise in the closure phase at the major as well as minor orifice side. The present simulations, although in 2-dimensions, succeeded in resolving these critical regions of the flow by means of the local adaptive mesh refinement technique.

There are several limitations to the simulation presented in this study that must be pointed out. With the valve closure, the leaflet rebound depends upon the points of contact of the leaflet with the valve housing or guiding struts based on the 3D design of the valves. In this two dimensional approximation, we have defined a single resilience factor and the magnitude of the same was derived by adjusting the value so that the predicted leaflet tip rebound amplitude from the simulation agreed with experimentally determined magnitude for a bileaflet disc valve model. We assumed the same magnitude for the resilience factor for both the valve designs in this simulation.

Our simulations represent the valve mounted in the mitral position and the leaflet moves from the fully open position to the closed position with the left ventricular pressure rise rate initiated by the ventricular contraction acting as the predominant load initiating the leaflet movement towards closure. The additional load induced by the left ventricular change shear forces that may be present on the leaflets can only be simulated with a 3D analysis including the LV chamber geometry, but we believe that the pressure rise rate specified as the load on the leaflet will dominate the leaflet behavior since the blood velocity within the left ventricular chamber near the mitral valve at end diastole will be relatively small.

Our primary focus in this comparative study was to delineate the effects of gap width presented by the valves at the edges between the leaflet and the housing and its implication on the activation of platelets during closure which have been known to be more lethal to the platelets. The presence of a strut in the minor orifice region could alter the flow and affect the flow dynamics in the minor orifice region which was not included in this study. In order to extend the analysis to the actual three-dimensional geometry for the mechanical valve with adequate resolution of the flow dynamics in the small gap width, parallelization of the code and conducting the simulations with a cluster of processors is required. Efforts are underway to perform such calculations which could give much more accurate computational results using a three-dimensional simulation. With regard to particle flow, particles had one way coupling with the fluid and two-way coupling including the size effects would have to be included for accurate results. A platelet model used in this study adopted from Bluestein et al. [5, 8–9] is solely based on shear stress time integral experienced by the platelets. Apart from shear stress, there are many other factors which could influence the process of platelet activation, such as the interaction between platelets and red blood cells in the large shear flows in the clearance gap region, presence of foreign surfaces such as the mechanical valve leaflet, agonist synthesis and release by activated platelets and concentration, platelet-phospholipid dependent thrombin generation, and thrombin inhibition by heparin etc. These complex biochemical effects were not included in the present model.