On the Investigation of Coarse-Grained Models for Water: Balancing Computational Efficiency and the Retention of Structural Properties

Abstract

Developing accurate models of water for use in computer simulations is important for the study of many chemical and biological systems, including lipid bilayer self-assembly. The large temporal and spatial scales needed to study such self-assembly have led to the development and application of coarse-grained models for the lipid-lipid, lipid-solvent and solvent-solvent interactions. Unfortunately, popular center-of-mass-based coarse-graining techniques are limited to modeling water with one-water per bead. In this work, we have utilized the K-means algorithm to determine the optimal clustering of waters to allow the mapping of multiple waters to single coarse-grained beads. Through the study of a simple mixture between water and an amphiphilic solute (1-pentanol), we find a 4-water bead model has the optimal balance between computational efficiency and accurate solvation and structural properties when compared to water models ranging from 1 to 9 waters per bead. The 4-water model was subsequently utilized in studies of the solvation of hexadecanoic acid and the structure, as measured via radial distribution functions, for the hydrophobic tails and the bulk water phase were found to agree well with experimental data and their atomistic targets.

1. Introduction

Water is unquestionably the most common solvent in experimental and computational studies,¹ particularly for biological systems. It serves as the reference fluid for many properties (e.g. specific gravity is measured relative to water density and heat capacity was originally defined in terms of the heat needed to raise the temperature of water) and is the most abundant chemical on earth. Water also has many unique properties, such as expansion upon freezing and a high surface tension, which complicates its dynamics and physics compared to other solvents.² Both its ubiquitous use and unusual properties make water an interesting and challenging system to study computationally and has led to the development of many different models to describe the properties and behavior of water (see for example the review of Guillot³ for water models proposed up to 2002 and the more recent work of Vega et al.⁴).

The models for water essentially vary in terms of their choice of interaction potential and purpose. For example, commonly used water models, such as TIP3P and SPC, are three site models with rigid bonds and angles, and point charges on the oxygen and hydrogens of the water to describe polarity. While these models reproduce many experimental properties such as enthalpy and liquid densities, other properties such as self-diffusion coefficients are not well reproduced.⁵ More recent models have included additional complexity to improve the ability of the model to reproduce other properties, such as the density maximum at 4°C and isothermal compressibilities, by incorporating flexible bonds and angles,⁶ polarizability,⁷ and delocalized charges;^8,9 however, more detail does not always lead to increased accuracy. For example, Hess and van der Vegt¹⁰ compared the SPC, SPC/E, TIP3P, TIP4P and TIP4P-Ew water models to study the solvation of amino acids and found accuracy in reproducing experimental thermodynamic properties did not necessarily correlate with the complexity of the water model.¹⁰ In particular, it was found that the more complex TIP4P-Ew model underestimated the hydration heat capacity compared to the SPC and TIP3P models, which were in good agreement with the experimental values; overall, however, the SPC/E model,¹¹ which, similar to SPC and TIP3P, is a 3-site, rigid, non-polarizable model, was found to be most accurate over the widest range of structural and thermodynamic properties.

An alternative approach to the development of increasingly realistic water models is to explore the ability of very simple models to predict certain features of the properties of water. For example, work done by Nezbeda and coworkers¹² has focused on the so-called primitive model, which describes water as a spherical segment with an attractive square-well potential to model hydrogen-bonding interactions and a hard sphere potential for all other interactions. Although the Nezbeda model is not suited to molecular dynamics simulations because of the discontinuous nature of the interaction potential, it is computationally efficient and able to quantitatively describe the PVT behavior of water.¹² In a similar vain, Dill and coworkers developed the Mercedes-Benz¹³ water model in which water is described as a planar Lennard-Jones disk with three orientation-dependent hydrogen-bonding arms. While the Mercedes-Benz model can capture, at least qualitatively, a number of the anomalous properties of water, the original version is only a 2-dimensionsal model. A 3-dimensional version has been developed by Bizjak et al.,¹⁴ however, implementation within common open source codes is difficult due to the orientation-based hydrogen-bonding potential.

Although these models, compared to TIP3P⁸ and SPC¹⁵ water models, for example, involve simple interactions, they are still very computationally expensive when used in studies of biological systems that involve large quantities of water to be simulated over long time-scales. As a result, an additional class of water model has been developed for use in coarse-grained, rather than atomistic, simulations,¹⁶ in which each bead or site in the model represents the collective interactions of a group of atoms. Coarse-grained models are typically developed using center-of-mass-based methods, in which the trajectory from an atomistic simulation is mapped to the CG level and the center of mass of the atoms within each bead determines the coordinates of that coarse-grained bead. By fitting the interactions of the coarse-grained model to reproduce specific target properties or aspects of the atomistic system, an accurate model on the coarse-grained level can be derived. While several different center-of-mass-based techniques, including force-matching¹⁷, reverse Monte Carlo¹⁸, and the iterative method developed by Reith, Pütz, and Müller-Plathe (RPM),^19,20 can be used to develop coarse-grained models, they all result in numerical potentials for the coarse-grained model interactions.

For typical solute molecules, mapping schemes develop simply and naturally from the covalently bonded structure of the molecule. Subsequently, one can readily produce a target coarse-grained trajectory from an atomistic trajectory based on the center of mass of the heavy atoms within each coarse-grained bead. While for computational efficiency and consistency, one would like to map several water molecules to a single bead, center-of-mass based methods are limited to one water molecule per bead due to the loose association of water molecules through hydrogen-bonding interactions. Therefore, while 3 or 4 water molecules may be associating in an atomistic simulation and could be assigned to a single bead centered on the center of mass of the clustered water molecules, the waters are only loosely associated and so will move somewhat independently of each other during the atomistic simulation, requiring reassignment of the waters to different coarse-grained beads. Without an efficient method to dynamically re-assign atomistic waters to the coarse-grained beads, to date, center-of-mass-based methods map water on a 1:1 basis, thus limiting the improvement in computational efficiency obtained through coarse graining. We note that, while coarse-grained models in which multiple waters are represented by a single coarse-grained bead have been developed, for example by Marrink²¹ and Klein,²² such models are not compatible with center-of-mass-based coarse graining methods (i.e., an atomistic trajectory cannot be mapped to the coarse-grained level and then used to derive target properties for parameterization of the cross interactions with solute molecules).

In this work, in order to develop an efficient coarse-grained model for water with multiple water molecules mapped to one bead, we utilize a clustering algorithm, called the K-means algorithm.²³ Several degrees of coarse-graining have been studied and tested to determine the optimum balance between computational efficiency and accuracy. In sections 2 through 4, we describe the new coarse-grained water model, provide details of the simulations performed to develop and test the model, and then discuss the general strategy and methodology adopted to develop and parameterize the model. In section 5, we present the results for the different multi-water models, consider the most appropriate level of coarse-graining, and then apply the chosen model to a simple system of biological interest.

2. Coarse-Grained Model and Force Field Development

All coarse-grained models are designed to retain key features from the atomistic simulations on which they are based, typically at the cost of accuracy in other properties. We are primarily interested in developing a coarse-grained water model to be used in biological simulations of self-assembly; therefore, the model will be optimized to retain structural features, rather than focus on properties such as phase behavior or transport properties. To aid in the model development, atomistic simulations have been performed for pure water, selected pure solutes, and solute/water mixtures, and the trajectories mapped to the coarse-grained level, using the center of mass of the atoms contained within a specified site or bead, as described above in the Introduction. To ensure the structural behavior of water and the solutes are retained on the coarse-grained level, radial distribution functions (RDF) from the atomistic trajectory mapped to the coarse-grained level serve as the target properties for the optimization. The coarse-graining method of Reith, Pütz, and Müller-Plathe (RPM)¹⁹ has been used to determine the coarse-grained force field which iteratively optimizes the interactions until the coarse-grained RDF matches its target.

In order to develop a coarse-grained model for water that maps multiple water molecules to one bead, and so is on an equal footing with typical coarse-grained beads that contain 3 - 5 heavy atoms per bead, we have explored the use of the K-means algorithm.^23,24 The K-means algorithm finds the optimal grouping of a large number of data points, which, in our application, corresponds to the coordinates of the atomistic water molecules. The K-means procedure locates which waters (the data points) are clustered together and determines the coordinates for the cluster (the location of the coarse-grained bead). As such the K-means algorithm allows for a dynamic mapping scheme, i.e., it allows for the allocation of specific waters to a coarse-grained bead to change from frame-to-frame of the atomistic trajectory. The algorithm is schematically illustrated in Figure 1; the first step requires allocation of the number of clusters, k, to be used. For our model development, k is equal to the number of beads used to model water on the coarse-grained level and so relates to the degree of coarse-graining of the water. As shown in the example in Figure 1, if we map four waters (the squares) to each bead (the circles), a system with twelve waters would contain three beads (i.e., k equals three). The next step is to determine an initial location for each of the k clusters, which is chosen from the coordinates of random water oxygen atoms found within the simulation. After initializing the positions of the beads, each data point (the location of water oxygens) is allocated to the cluster with the smallest distance between the cluster and data point. In the example provided, two waters would be allocated to the green cluster, six waters grouped within the red cluster, and four waters placed in the blue cluster. Once the allocation is determined, the center of mass of the waters within a cluster is calculated as the new coordinates for that cluster, as indicated by the arrows in Figure 1. These steps are repeated until the termination criteria,

Figure 1.

Schematic illustration of the K-means algorithm. Circles represent cluster locations, squares represent water locations, and shaded regions represent the allocation of waters to each cluster in a color-coded fashion.

$${\sum _{n=1}^k\left(r_n^{i+1}-r_n^i\right)}^2<\mathit{\text{tol}},$$ (1)

has been satisfied, where $r_n^i$ represents the location of bead n at iteration i and tol is the tolerance set by the user (0.01 Å was used in this work). In the example provided, convergence is achieved in two iterations. For each subsequent frame of the trajectory, the location of the clusters from the previous frame are used as the initial guess for the next frame in order to reproduce a more continuous target trajectory.

Using the K-means algorithm, a user-defined number of water molecules can be assigned to each bead. Thus, a goal of this work is to determine the degree of coarse-graining that provides an optimum balance between accuracy and computational efficiency. Water models containing 1, 3 - 6, 8, and 9 atomistic waters mapped to each bead (denoted H2OX, where X is the number of waters mapped to each bead) were parameterized and studied through simulations of pure water and simple mixtures of water and amphiphilic solutes; 1-pentanol was chosen as a representative amphiphilic solute because of its size and simplicity and hexadecanoic acid chosen as a model lipid. The coarse-grained mapping scheme for both molecules is shown in Figure 2. Pentanol is mapped to two equally sized beads, with PALC representing the hydrophilic region of the molecule containing the alcohol group, and ALK the hydrophobic alkane portion. For hexadecanoic acid, three bead types are used following earlier work:²⁵ HEAD to represent the acid head group, TAIL for the beads in the hydrocarbon tail, and TRM2 for the terminal bead that contains the last 2 carbons in the hydrocarbon tail. It is anticipated that if the water model can properly solvate these coarse-grained molecules as mapped in Figure 2, it should provide the correct solvation and necessary driving forces for self-assembly in more complex biological systems.

Figure 2.

Schematic illustrating the mapping of the atomistic 1-pentanol (left) and C16:0 (right) to the coarse-grained level.

3. Simulation Details

All simulations, atomistic and coarse grained, were performed within the open source molecular dynamics program, DL_POLY 2.14.²⁶ The CHARMM force field²⁷ was utilized for the solutes due to its accuracy with respect to biological molecules and TIP3P⁸ was used as the model for water since solvation within the CHARMM force field is based on this water model. The Nosé-Hoover²⁸ algorithm was used for temperature and pressure control as needed and the reaction field method²⁹ employed to calculate the electrostatic interactions.

The pure TIP3P water simulations initially contained 901 water molecules and the pure solute systems contained 100 molecules, each at a density comparable to their experimental values under the same state conditions. The mixture systems were equiatom; 1-pentanol and water contained 75 solute molecules and 452 solvent molecules and the acid mixture contained 50 solute molecules and 833 waters. All systems were equilibrated for 500 ps - 1 ns, first in an NVT, and then in the NPT ensemble, to verify that the correct density was obtained.³⁰ The production runs for pure water and pure pentanol were then further simulated in both ensembles, while the mixture systems were studied in only the NVT ensemble as the RPM pressure correction process was not required since the pure potentials were pressure-corrected. All simulations were then run using a 1.0 fs timestep for an additional 1.0 ns, which was found to produce enough sampling for this system size as defined by minimal changes in the target radial distribution functions.

4. Methodology

In previous work,²⁵ a coarse-grained model for fatty acids was developed using the RPM method to fit atomistic target RDF's based on the mapping shown in Figure 2. These potentials were used for the hexadecanoic acid studied in this work and as starting points in the optimization of the 1-pentanol model (i.e., the HEAD potential was used as an initial guess for the PALC potential and the TAIL bead served as the starting potential for the 1-pentanol ALK interaction). Studies have shown that the choice of initial potential has a negligible effect on the final optimized potential, but can reduce the number of iterations required for convergence.³¹ For the water models the HEAD-HEAD potential was used as the initial guess. Using these initial interaction potentials, RDFs were calculated from the production runs, and the initial potentials subsequently updated via a Boltzmann inversion,

$$V_{j+1}(r)=V_j(r)+\mathit{\text{kT}}ln\frac{g_j(r)}{g^{\ast }(r)}$$ (2)

where V_j (r) is the potential, g_j (r) is the CG RDF, and g* (r) the target RDF, at distance r and iteration number j. A negligible change in the potential determines when convergence occurs. Given that the potentials for pentanol are fitted, only the RDF between the ALK beads is shown in Figure 3 as a representative result to illustrate the agreement achieved between the target RDF and the RDF obtained from the coarse-grained model.

Figure 3.

Radial distribution function between two hydrophobic beads (ALK-ALK) from a coarse-grained simulation (diamonds) and the target atomistic simulation (solid line) of pure 1-pentanol.

Once the pure model potentials are optimized by fitting to the RDFs extracted from the target atomistic trajectory, the cross interactions in the mixed solute/solvent systems must be determined. In all of the mixtures, the potentials from the pure simulations (i.e., H2OX-H2OX for water and ALK-ALK, PALC-PALC, and ALK-PALC for pentanol) were used in a transferable fashion in the mixed systems, while the cross-interactions (H2OX-ALK and H2OX-PALC) were optimized to fit the target RDF's. In addition to the water models already mentioned, the cross-interactions between the coarse-grained alcohol and fully atomistic TIP3P water was also optimized to assess the difference between a high and low detail model with respect to solvating a coarse-grained solute.

Finally, the force field for the solute molecules requires intramolecular potential parameters, which are also derived from the atomistic target trajectory. For the bond lengths and bond angles the distribution of distances between two bonded sites, or angles between three angled sites, is determined and fitted to a single-peak Gaussian. Before normalization, following the original RPM method,²⁰ the angle distributions are weighted by a factor of sin(θ) as given by,

$$P(\theta )=f_{n}p(\theta )/sin(\theta )$$ (3)

where f_n is the normalization factor, p(θ) the distribution, P(θ) the normalized distribution, and θ the angle. A Boltzmann inversion is then applied to the fitted Gaussian distribution and the parameters of a harmonic oscillator emerge from the simplification of the inversion as seen in equations (4) through (6):²⁰

$$P(\theta )=\frac{A}{w\sqrt{\pi /2}}{exp}^{-2\frac{{(\theta -{\theta }_{eq})}^2}{w^2}}$$ (4)

$$V(\theta )=-\mathit{\text{kT}}ln\left(\frac{A}{w\sqrt{\pi /2}}{exp}^{-2\frac{{(\theta -{\theta }_{eq})}^2}{w^2}}\right)$$ (5)

$$V(\theta )=\frac{2kT}{w^2}{(\theta -{\theta }_{eq})}^2+\mathit{\text{const}},$$ (6)

where A is the Gaussian area, w the Gaussian width, θ_eq the equilibrium angle, k Boltzmann's constant, and T the temperature. For hexadecanoic acid,³² the bonded potential was developed as described above in previous work.^25,32 For 1-pentanol the distribution of bond lengths obtained from the atomistic simulation trajectory mapped to the coarse-grained level, along with its Gaussian fit, for the single coarse-grained bond is shown in Figure 4. The molecule is flexible on the atomistic level, and as a result, produces a very wide bond-length distribution, therefore, a fairly low force constant of 35.6 kJ/Ų/mol on the coarse-grained level is measured.

Figure 4.

Probability distribution of a PALC-ALK bond length from an atomistic trajectory (diamonds) mapped to the coarse-grained level and fitted by a Gaussian curve (solid line).

To determine how many water molecules should be mapped per bead on the coarsegrained level, several models, all with different numbers of atomistic water molecules within a coarse-grained bead, were optimized and their individual accuracy assessed through a comparison of the results for three key properties, namely computational efficiency, density, and solvation. Computational efficiency is obviously an important factor and was measured by the reduction in simulation time for the pure coarse-grained water models compared to the atomistic simulation. The computational speed-up is represented as the ratio of the coarsegrained simulation time to the simulation time for pure atomistic water, as shown in equation (7) and reported by DL_POLY,

$$\mathit{\text{speed}}\mathit{\text{scale}}=\frac{\mathit{\text{CG}}\mathit{\text{Time}}}{\mathit{\text{Atomistic}}\mathit{\text{Time}}}.$$ (7)

To judge the accuracy of the model with respect to reproducing the bulk phase density of water, the percentage difference between the atomistic TIP3P water density and that from the CG water models was determined from constant pressure simulations. Finally, the solvation properties of the water model was verified by comparing the difference between the RDF for two ALK beads (the key solute interaction) from the coarse-grained mixture simulation to the target RDF via a merit function,

$$f=\int w(r){(g(r)-g^{\ast }(r))}^{2}dr,$$ (8)

where w(r) is a weighting function described by,

$$w(r)=g^{\ast -2}(r_{max})exp\left(\frac{-|r-r_{max}|}{r_{max}}\right),$$ (9)

and r_max the distance where the highest peak is located. The quantity within the exponential term provides the greatest weight to values near the highest peak and is normalized by r_max. The g*⁻² (r_max) term was added to normalize equation (8) so the values of the merit function could be compared between different systems.

These three criteria for assessing the most appropriate level of coarse-graining water were equally weighted and combined into a scoring function described by,

$$S_{\mathit{\text{fxn}}}=\frac{\mathit{\text{Speed}}\mathit{\text{Scale}}}{\%\mathit{\text{diff}}({\rho }_{\mathit{\text{pure}}})\ast f}.$$ (10)

The model with the highest value of S_fxn was then utilized in a mixture of hexadecanoic acid and water, mimicking a simple biological lipid system.

5. Results and Discussion

We first discuss the results from the development of the non-bonded potential for the different pure water models studied followed by the coarse-grained model development for the solute molecules. We then consider the results for the solute-solvent mixtures studied.

5.1. Pure Water

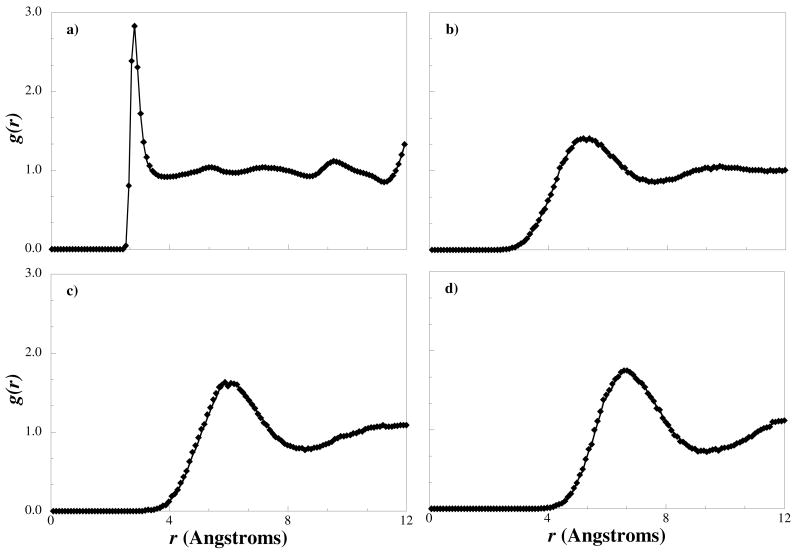
Using the RPM method, the target RDF for each water model was fitted to within line thickness. As an example the water - water RDF for the H2O1, H2O4, H2O6, and H2O8 models is presented in Figure 5. Similar RDFs for the remaining water models are not shown as they exhibit the same general shape and similar degrees of fit with respect to the target RDFs as seen in Figure 5. From Figure 5a, we note the H2O1 model produces an RDF with a first peak that is much narrower and higher than the other models, indicating a much smaller bead and higher degree of structure. The high degree of structure most likely comes from the retention of hydrogen bonds between the water sites. Although without explicit hydrogens, the coarse-grained beads do not hydrogen bond, the atomistic hydrogen bonds do directly affect the target RDFs, and so those interactions are implicitly found within the coarse-grained non-bonded potential. In the H2O1 model, this implicit interaction has a larger contribution to the non-bonded potential than that found between multiple water beads. In the multiple water models, the hydrogen bonding is within the boundaries of the water bead and so the hydrogen bonding between beads is of less significance compared to the sum of the non-bonded interaction between beads, i.e., on the atomistic level two water molecules mapped to the coarse-grained level and assigned to two different four-water beads may be hydrogen-bonded, but the potential between these two molecules is small compared to the potential shared between the beads that represent four water molecules.

Figure 5.

Radial distribution function between a) one-water beads (H2O1-H2O1), b) four-water beads (H2O4-H2O4), c) six-water beads (H2O6-H2O6), and d) eight-water beads (H2O8-H2O8), from a coarse-grained simulation (diamonds) and from the atomistic target simulation (solid line).

Wang et al.³³ observed similar behavior when they applied the RPM method to the TIP3P, SPC, and SCP/E water models to develop coarse-grained models with a single water molecule per coarse-grained bead. They found that a one-water bead with an isotropic potential was not as accurate as models where orientation is incorporated into the coarsegrained model representation, such as the PM¹² or Mercedes-Benz water models,^13,14 and concluded that this was due to the isotropic nature of the interactions in one water models that do not allow for the orientation-specific hydrogen bonding observed atomistically.³³

The difference in the models can also be seen in the fitted potentials as shown in Figure 6. With the multi-water models, the potentials are found to be very similar to a Lennard-Jones potential, with the depth of the well increasing with the degree of coarse-graining. The location of the energy minimum also shifts to larger r, indicating that the size of the bead is increasing as the degree of coarse-graining increases. From the figure, we note that the H2O1 potential is very different in shape to that seen for the multi-water potentials, but follows the same trend in terms of the depth and position of the potential well with respect to the degree of coarse-graining. The multiple wells and erratic shape are most likely a product of the high degree of structuring and hydrogen-bonding features found in the target RDF, as discussed above.

Figure 6.

Interaction potential between one-water beads (H2O1-H2O1) (diamonds), four-water beads (H2O4-H2O4) (triangles), six-water beads (H2O6-H2O6) (circles), and eight-water beads (H2O8-H2O8) (crosses) fitted from the pure water system.

The increase in speed for the coarse-grained water models compared to the atomistic model is reported in Table 1, from which we see, for example, that H2O9 provides a factor of 1234 speed-up. However, the speed-scale plateaus with increasing coarse-graining, indicating that the gain in calculation efficiency is greater between H2O4 and H2O3 (a ratio of 1.67) than between H2O9 and H2O8 (ratio of 1.26). Also reported in Table 1 is the accuracy of each model in reproducing the density of pure water. H2O4 is found to provide the most accurate water density with a difference of 0.1% compared to the atomistic value, which is reasonable if one takes into account the fact that the coordination number of water is 4.35.³⁴

TABLE 1.

Comparison of the results obtained from the different water models studied.

Waters/bead Speed scale		Density of pure water	% Difference in density	RDF merit function	Sfxn
atomistic	1.00	0.9983	0.0%	1.88E-03	n/a
1	16.7	0.9741	-2.4%	1.86E-02	3.76E+02
3	152	0.9343	-6.4%	3.38E-03	7.04E+03
4	254	0.9996	0.1%	7.75E-03	3.28E+05
5	401	0.9815	-1.7%	2.35E-02	1.01E+04
6	562	1.0942	9.6%	5.00E-02	1.17E+03
8	979	1.0190	2.1%	5.18E-02	9.00E+03
9	1234	0.9412	5.7%	5.35E-02	4.05E+03

5.2. Water/pentanol

We now consider the coarse-grained pentanol-solvent simulations to further test and evaluate the different coarse-grained water models. As described above, the ALK-ALK and PALC-PALC potentials used in the water-pentanol simulations were taken from the simulation of pure pentanol and used transferably, while the cross-interactions were fitted. In Figures 7a and 7b, the RDF between the ALK beads of pentanol is compared from simulations using each of the different water models to the atomistic target. From the figures, we see that the agreement between the RDF and its target generally deteriorates with an increase in the coarse-graining of the water, i.e., the highest detail model (atomistic TIP3P) provides the best solvation for the coarse-grained solute, but the H2O9 model does not properly solvate the 1-pentanol. The deterioration can also be seen numerically in Table 1 where we report the RDF merit functions. Although not shown, the same trend is seen in the corresponding RDFs for the PALC-PALC and ALK-PALC interactions. An exception is seen for the pentanol - H2O1 system, shown in Figure 7a, as more coarse-grained models provide better agreement. We believe this also reflects the differences in hydrogen bonding for the H2O1 and multi-water models, as discussed previously.

Figure 7.

Radial distribution function between two hydrophobic beads (ALK-ALK) from simulations of 1-pentanol with a) atomistic (crosses), H2O1 (squares), H2O3 (triangles), H2O4 (diamonds), and H2O5 (circles) water models, compared to the target atomistic simulation (solid line) and b) radial distribution function between two hydrophobic beads (ALK-ALK) from simulations of 1-pentanol with H2O4 (diamonds), H2O5 (circles), H2O6 (squares), H2O8 (crosses), and H2O9 (triangles) water models, compared to the target atomistic simulation (solid line).

In Figure 8, we compare the water-water RDF from simulations of the water-pentanol mixture with the single-water coarse-grained model (H2O1) and a representative multi-water coarse-grained model (H2O4) against the atomistic target data. From the figures, we can see that the level of interaction between H2O4 beads (Figure 8b) is in good agreement with the target data, as indicated by the agreement in the RDFs, while the pure H2O1 potential (Figure 8a) produces a first peak that is much lower than that for the target RDF. Although the RDF in the pure water simulations of H2O1 is much taller than the other water models because of its hydrogen bonding (Figure 5a), it is not structured enough to produce an appropriately strong interaction in the mixed system. The multi-water model on the other hand has the necessary water-water interaction strength, since it does not require the pure water potential to account for hydrogen bonding, i.e., the hydrogen bonding is predominately found within the coarse-grained bead rather than between beads. The relative strength of attraction between water beads can also be seen in Figure 6, where the well is found to be much deeper for the H2O4 model compared to H2O1. As a result, an isotropic interaction accurately accounts for the water-water structure in the multiple-water coarse-grained model.

Figure 8.

Radial distribution function between a) one-water beads (H2O1-H2O1) and b) four-water beads (H2O4-H2O4) from a coarse-grained simulation (diamonds) and an atomistic simulation (solid line) of the water-1-pentanol mixture.

We note that Wang et al., also observed a lack of structure in one-water coarse-grained models developed for the atomistic TIP3P, SPC, and SPC/E water models.³³ This was attributed to the fact that RDFs fitted via the RPM method did not reproduce water's tetrahedral packing; if the potential was modified to reproduce the tetrahedral packing, the resulting RDF exhibited a much higher degree of structure. Based on this work, better agreement for the water RDF in the pentanol-H2O1 mixture could likely be achieved by re-optimizing the H2O1 model to reproduce the tetrahedral packing in pure water; however, a discrepancy in the pure RDF would result. Wang et al.'s findings also support our conclusion that the sharpness of the H2O1 RDF peak in Figure 5a can be attributed to hydrogen bonding. By fitting the tetrahedral packing, the existence of the hydrogen bonds is reinforced, and, as a result, the coarse-grained peak becomes taller and thinner than the target.

From the results for the pure and mixed systems studied and reported in Table 1, we can now determine the scoring function, S_fxn, for each water model as defined by the computational efficiency (speed-scale), the percentage difference in the density for the coarse-grained models compared to the atomistic model, and the RDF merit function. From the table, we note that the H2O4 model has the highest scoring function, indicating it has the optimal trade-off between speed and accuracy, even though H2O3 is the most accurate with respect to the transferred RDF for the pure hydrophobic bead interaction.

5.3. Water/ hexadecanoic acid

With the highest scoring function, the four waters-per-bead model (H2O4) was chosen as the coarse-grained water model for use in the water-hexadecanoic acid system. In this preliminary study of a solvated lipid system, the cross-interactions between water and hexadecanoic acid (H2O4-HEAD, H2O4-TAIL, and H2O4-TER2), were optimized at 298 K and 1.0 bar. The RPM method was able to optimize the potentials such that the coarse-grained RDF and its target value agree within line thickness; the results are therefore not shown and we focus instead on the transferred RDFs.

In Figure 9a, we compare the transferred pure TAIL-TAIL interaction to its target. The coarse-grained and target RDF is in good agreement, with the location of the peak indicating the hydrocarbon tails are structuring themselves on the coarse-grained level in the same way as on the atomistic level; however, the height of the coarse-grained RDF is somewhat higher than its target, indicating a higher degree of clustering of the tail beads in the coarse-grained model compared to the target. In a bilayer system, this behavior could lead to a stronger tendency to phase separate from water and induce structure in the hydrophobic region of the bilayer. In Figure 9b, we see a similar trend for the H2O4-H2O4 RDF using the water interaction transferred from the pure simulation, indicating that the structure of water in the bulk phase is retained on the coarse-grained level. Finally, the RDF for the transferred HEAD-HEAD interaction is shown in Figure 9c, where the coarse-grained RDF is found to possess a distinctive peak not seen in the target.

Figure 9.

Radial distribution function between a) tail beads (TAIL-TAIL), b) four-water beads (H2O4-H2O4), and c) head beads (HEAD-HEAD), for the hexadecanoic acid-water mixture from a coarse-grained simulation (diamonds) and from the target atomistic simulation (solid line).

To investigate the possible reasons for the observed discrepancy, we consider the simpler (and computationally cheaper) alcohol system. As shown in Figure 10a, similar behavior is observed, in that the PALC-PALC interaction in the H2O4-pentanol mixture is also higher than the atomistic target. Similar behavior is seen for the other coarse-grained water models studied and in simulations with the TIP3P model (also shown in Figure 10a), indicating that the discrepancy is independent of the water model used and mostly likely dependent on the solute potential. To investigate the effect of the PALC potentials, all of the interactions (pure and mixed) for the coarse-grained H2O4-pentanol system were re-optimized against the target RDFs measured from the atomistic simulation. The RDF from the re-optimized PALC-PALC interaction is also presented in Figure 10a and, as expected, can be fitted within line thickness using the RPM method. If these re-optimized interactions (PALC-PALC, PALC-ALK and ALK-ALK) are then transferred and used in a simulation of pure pentanol, the coarse-grained PALC-PALC peak is found to be much lower than the target value, as shown in Figure 10b. As such, the interaction fitted from the mixture does not exhibit the same interaction strength, or, most likely, the same hydrogen-bonding network as the potential fitted in the pure system.

Figure 10.

Radial distribution function between a) alcohol beads (PALC-PALC) from a coarse-grained simulation of pentanol with atomistic water (crosses), H2O4 using the pure potential transferred to the water-pentanol mixture (triangles), H2O4 using the potential fitted to the pentanol mixture (plusses), and H2O4 using the ALK-H2O4 interaction replaced by the attractive PALC-ALK potential (diamonds), compared to the target atomistic simulation (solid line), and (b) radial distribution function between alcohol beads (PALC-PALC) in a simulation of pure pentanol using the potential fitted from a mixture simulation (diamonds) and the atomistic target (solid line) and (c) fitted radial distribution function between the hydrophobic bead of pentanol and a 4-water bead (ALK-H2O4) from a coarse-grained simulation of the water-pentanol mixture (diamonds) and the target atomistic simulation (solid line).

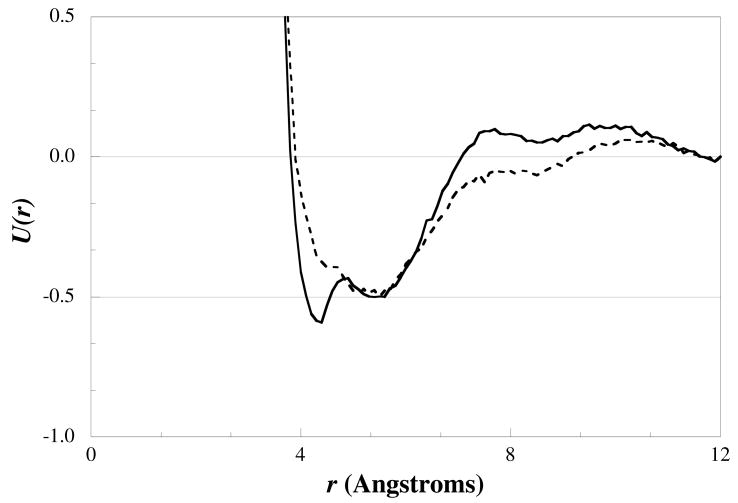
The depeleted level of hydrogen bonding is supported when considering the trends for the pure water potential, where more explicit hydrogen bonding resulted in taller RDFs. The differences in the PALC-PALC potentials fitted from the pure RDFs and the mixture RDFs (seen in Figure 11) also support the reduced structuring with the mixture fitted potential. While the potentials are very similar, the potential from the pure simulation possesses an additional well, similar to that found for the pure H2O1 potential shown in Figure 6, suggesting that this is the hydrogen-bonding component of the coarse-grained potential. In addition, this well is deeper than the large well at larger r and steeper on both sides of the minimum, indicating the beads most likely get caught in the first minimum to produce the peak seen in Figure 10a.

Figure 11.

Interaction potential between alcohol beads (PALC-PALC) fitted from a pure simulation (solid line) and fitted from the mixture simulation (dashed line).

Izvekov and Voth³⁵ observed similar results in their study of cholesterol within a dipalmitoylphosphatidylcholine (DPPC) bilayer using coarse-grained force fields derived through the force-matching procedure, in that they found that the cholesterol head group, whilst having the same forces on both the atomistic and coarse-grained level, produced a strong peak in the coarse-grained RDF while only a weak peak was found on the atomistic level. As a result the interaction between hydrophobic sites and water had a repulsive component at larger separation distances compared to the interaction between the cholesterol head beads and the interaction between the cholesterol head bead and water. The authors concluded that the discrepancy in the RDFs was due to the fact that the forces are being derived from a system where the hydrophobic beads maintain a larger average separation distance from the water beads than the hydrophilic beads and so have minimal direct contact with water. Based on their work, we hypothesize that the observed disagreement in the HEAD-HEAD RDF is independent of the coarse-graining methodology and also due to unavoidable sampling issues. This is further supported by the fact that the RDF between the ALK and H2O4 bead, as shown in Figure 10c, indicates that the fitted potential will possess a larger repulsive region in the potential. This can also be seen in Figure 12, where the fitted potential for ALK-H2O4 is compared to the more attractive PALC-ALK potential; although there is an attractive component in the ALK-H2O4 potential, the range of attractive separation distances is much smaller than for PALC-ALK interaction.

Figure 12.

Interaction potentials between hydrophobic (ALK) and water (H2O4) beads (solid line) and the hydrophilic (PALC) and hydrophobic (ALK) beads (dashed line).

In summary, if the PALC-PALC interaction is fitted to the atomistic mixture RDFs, the interaction strength is too low to produce the RDF peak seen in the pure pentanol system. In addition, if the ALK-H2O4 interaction is replaced by a potential with a larger attractive interaction region (i.e., PALC-ALK, as shown in Figure 12), the RDF of the PALC-PALC interaction transferred from the pure system to the mixture is in better agreement with the target RDF (Figure 10a). This indicates that the hydrophilic head group exhibits two priorities: to hydrogen bond with itself and to provide hydrophobic shielding between the water and the carbons in the hydrocarbon tail. The hydrophobic sites maintain minimal contact with water, because of the large repulsive interaction region in the ALK-H2O4 interaction. As a result, the PALC beads do not need to shield ALK beads from water and instead associate with each other at a separation distance corresponding to the first well of the potential from Figure 11, resulting in a high RDF peak. Atomistically, there is a level of attraction between the atoms of the hydrophilic bead and the water, so the atoms of the hydrophilic bead must sacrifice optimal hydrogen bonding to shield the water from the rest of the hydrophobic solute.

6. Conclusions

The K-means algorithm was successfully used to develop a coarse-grained model for water with multiple water molecules mapped to a single bead by enabling dynamic assignment of the water molecules to coarse-grained beads from analysis of atomistic trajectory data. Coarsegrained water models representing one to nine waters per bead were optimized and studied in both the pure state and in mixtures with 1-pentanol, a representative amphiphilic solute. Based on the increase in computational efficiency, the ability to reproduce the density of pure water, and to solvate the solute, 1-pentanol, as measured by the RDF for the key ALK-ALK solute potential relative to the target RDF, the 4-water model (H2O4) was chosen as the optimal water model.

The H2O4 model was then used in simulations of a water-hexadecanoic acid binary mixture. The solvation properties of the 4-water model provided for the correct structuring of the hydrophobic component of hexadecanoic acid as shown by the RDF between the TAIL beads derived from the mixture simulation; however, the RDF between HEAD beads appeared to be more attractive and structured than the atomistic target. A similar behavior was also observed for the hydrophilic interaction of the 1-pentanol/water mixture. By altering the potentials in the alcohol/water mixture, it was found that the discrepancy was independent of the water model, and the hydrophobic shielding and hydrogen bonding behavior of the atomistic alcohol are mutually exclusive properties on the coarse-grained level. In developing the coarse-grained model, the hydrophobic shielding is essentially sacrificed in order to retain the hydrogen bonding, which will force the hydrophilic RDF's to have higher structure than is seen atomistically, but will ensure the clustering of the HEAD beads. As a result, the hydrophilic groups will tend to associate and promote self-assembly; therefore, this property of the model must be retained.