Single-molecule sequence detection via microfluidic planar extensional flow at a stagnation point

Abstract

We demonstrate the use of a microfluidic stagnation point flow to trap and extend single molecules of double-stranded (ds) genomic DNA for detection of target sequences along the DNA backbone. Mutant EcoRI-based fluorescent markers are bound sequence-specifically to fluorescently labeled ds λ-DNA. The marker-DNA complexes are introduced into a microfluidic cross slot consisting of flow channels that intersect at ninety degrees. Buffered solution containing the marker-DNA complexes flows in one channel of the cross slot, pure buffer flows in the opposing channel at the same flow rate, and fluid exits the two channels at ninety degrees from the inlet channels. This creates a stagnation point at the center of a planar extensional flow, where marker-DNA complexes may be trapped and elongated along the outflow axis. The degree of elongation can be controlled using the flow strength (i.e., a non-dimensional flow rate) in the device. Both the DNA backbone and the markers bound along the stretched DNA are observed directly using fluorescence microscopy and the location of the markers along the DNA backbone is measured. We find that our method permits detection of each of the five expected target site positions to within 1.5 kb with standard deviations of <1.5 kb. We compare the method’s precision and accuracy at molecular extensions of 68% and 88% of the contour length to binding distributions from similar data obtained via molecular combing. We also provide evidence that increased mixing of the sample during binding of the marker to the DNA improves binding to internal target sequences of dsDNA, presumably by extending the DNA and making the internal binding sites more accessible.

Introduction

Single-molecule methods offer the potential of detecting the locations of widely spaced target sequences across genomic lengths of DNA while preserving information about order. Recent research has demonstrated the direct, single-molecule detection of particular target sequences, such as transcription factor binding sites¹ and single-nucleotide polymorphisms², which have been associated with human disease.^3,4

To determine the locations of target sites on single DNA molecules with adequate resolution, many single-molecule techniques require extension of the DNA from a random coil, as it exists in free solution, to a linear conformation. Molecular combing,⁵ which involves DNA adsorption to a functionalized surface as it is stretched by the action of a receding meniscus, is the method most commonly employed by sequence-detection schemes.^6–8 One drawback to this method, however, is that surface immobilization prevents the molecules from being available to downstream processes for integrated lab-on-a-chip applications. Surface immobilization also may make some sites sterically inaccessible, inhibit the binding of certain probes or markers, or result in overstretching of the DNA.^9,10

In contrast, flow-based extension methods offer the potential for continuous on-chip DNA processing. Single DNA molecules have been unraveled for potential sequence-detection applications using electrokinetically driven flows in both micro- and nanochannels.^11–14 DNA molecules have also been extended and observed in microfluidic contraction flows^15,16 and in flow past a post array.¹⁷ Unfortunately, DNA entrained in these complex flows experiences a range of flow types and strain histories, resulting in a wide variety of molecular conformations.¹⁸ Further, molecules either moving in flow or rapidly adsorbed onto surfaces may not have achieved steady-state conformations prior to analysis, and therefore extension along the molecule is not necessarily uniform, predictable, or easily controlled.

As an alternative, stagnation-point flows can be exploited to trap objects in flow fields that are spatially and temporally uniform by purely hydrodynamic means.¹⁹ These flows have been used to study objects such as DNA, cells, droplets, and vesicles and can be generated using microfluidic geometries such as T-junctions²⁰, microfluidic four-roll mills^21,22, and cross slots^23–28. The cross slot consists of two perpendicular, intersecting channels with two inlets and two outlets. When flow is directed into the opposing inlets, fluid exits at 90° through the outlets. This establishes a planar extensional flow with a stagnation point – a point of zero velocity at which a DNA molecule may be trapped – centered at the channel intersection. At the stagnation point, objects experience compression along the inflow axis and extension along the outflow axis (Fig. 1a).

Figure 1.

(a) Cross-slot trapping scheme. Tagged λ-DNA complexes are introduced through one channel, opposed by buffer containing no fluorescent particles. Flow exits through the two outlet channels to one fixed-height and one variable height reservoir, adjustment of which permits trapping at the stagnation point. Device depth is 130 µm. Image area for DNA studies is an 80-µm square centered at the stagnation point. (b) Streak image showing stagnation point and particle path lines arising from planar extensional flow. (c) Strain rate map for flow in an 800-µm-wide cross slot, calculated using 2D fluid dynamics simulations with v_max = 892 µm/s. Contours represent lines of constant ε̇, spaced 0.25 s⁻¹ apart. Strain rate remains constant to within 95% of the peak strain rate over a 100-µm radius about the stagnation point.

In their study of polymer uncoiling dynamics in a cross slot, Perkins et al. showed that DNA molecules trapped at the stagnation point of a planar extensional flow elongate along the outflow direction to a degree dependent on the flow strength.²³ While individual molecules exhibit tremendous heterogeneity in their unraveling dynamics (i.e. “molecular individualism”)²⁹, DNA molecules trapped via this method result in predictable, narrow distributions of steady-state extensions. In fact, at high flow strengths, fractional extensions vary by only a few percent (Fig. S-1). The degree of steady-state extension can be controlled through the flow strength, and near complete extension of the molecules has been achieved.^23,30 In addition, because they are not physically tethered, the trapped molecules remain available for downstream processing.

Here, we present the first use of hydrodynamic trapping in a microfluidic stagnation point flow for target-sequence detection and marker-position determination. We demonstrate proof of principle using planar extensional flow in a cross slot to trap and extend single, site-specifically-tagged dsDNA molecules. Using this method, we identify the positions of five known EcoRI target sites on λ-DNA that are tagged with a previously characterized mutant EcoRI-based fluorescent marker³¹. We determine our method’s accuracy and precision and compare the detection resolution to other single-molecule methods.

Methods

Marker-DNA complex preparation

The marker consists of two components coupled through a biotin-avidin interaction. A biotinylated restriction endonuclease (REase) serves as a site-specific, DNA-binding molecule, while a NeutrAvidin-coated fluorescent bead permits optical detection of the binding position. Typically, REases bind to and cleave dsDNA at particular sequences. In the absence of Mg²⁺ – a condition that prevents DNA cleavage – most Type II REases continue to bind to their target sequences with high affinity and specificity.^32,33

The type II REase EcoRI binds to dsDNA at its recognition sequence 5’ GAATTC 3’ up to 90,000 times better than it binds to sites having a single incorrect base pair.^34,35 This sequence appears five times in λ-DNA. For these studies, a mutant of the REase EcoRI (K249C) is biotinylated at the mutation site using maleimide chemistry.³¹ The K249C mutation is well removed from the enzyme’s recognition and catalytic interface, and biotinylation does not affect binding of the enzyme to the target sequence on DNA.³¹ In fact, this marker has been shown to discriminate against sites with only one incorrect base-pair.³¹

Marker-DNA complexes are prepared in bulk solution as described previously.³¹ First, 0.33 nM λ-DNA are incubated for 1 hr at 4°C with 8 nM biotinylated mutant EcoRI and 100 µg/ml BSA in a buffer containing 20 mM sodium phosphate pH 7.3, 100 mM NaCl, 1 mM EDTA, and 1 M triethylene glycol. Next, NeutrAvidin-coated, fluorescent (580/605) 40-nm spheres (FluoSpheres, Molecular Probes) are introduced at 3.3 nM, and the sample is incubated for another 1 hr at 4°C. Samples are mixed continuously during both incubation steps at 8 rpm using a rotary mixer (Barnstead Labquake Rotisserie) unless otherwise indicated.

To prepare the marker-DNA complexes for stretching and visualization in the cross-slot device, DNA complexes are stained as described previously³¹ using the intercalating dye YOYO-1 (Invitrogen) at a ratio of 4:1 (bp:dye molecules). After staining, the mixture is diluted to 0.6 pM DNA in viscosified visualization buffer (10 mM sodium phosphate pH 7.3, 10 mM NaCl, 1 mM EDTA, 17.9% PEG-8000, 1% w/v glucose). An oxygen scavenging system consisting of 1% v/v 2-mercaptoethanol, 50 µg/ml glucose oxidase, and 10 µg/ml catalase was added to the viscosified visualization buffer to reduce DNA photocleavage.³⁶ The viscosity of this solution has been measured to be 17 cP at 21°C using a Gemini rheometer (Malvern Instruments) with cone and plate geometry.

Cross slot preparation

Microfluidic cross slots with channel widths of 800 µm and inlet lengths of 3 mm are prepared using standard soft lithography techniques.³⁷ Device masters are fabricated to a 130-µm depth using SU-8 2100 resist (MicroChem). PDMS (Sylgard 184, Dow Corning) molds are cast from the master, and inlets and outlets are created using a 16-gauge blunt-tipped needle. Molds are sealed to glass coverslips after treatment with oxygen plasma. Microbore tubing (Tygon, 0.02” ID) is seated directly into the inlet and outlet holes, providing a water-tight seal.

Prior to each experiment, tubing and interior surfaces of the sealed microfluidic device are treated for 10 min at room temperature with isopropyl alcohol and subsequently rinsed with ultrapure (18 MΩ) water. This reduces the incidence of trapped air bubbles during channel loading. Next, the tubing and device are incubated for 10 min with 10 mg/ml BSA in PBS buffer (100 mM sodium phosphate, 1.37 mM NaCl, 27 mM KCl, pH 7.4), which helps to reduce surface adsorption of the fluorescent beads. BSA is rinsed out of the device using ultrapure water. Immediately before experiments, the tubing and microfluidic device are first primed by loading viscosified visualization buffer into the device. Following experiments, devices are flushed thoroughly with water.

Flow experiments in the cross slot

A schematic of the experimental setup is depicted in Fig. 1a. Solution containing stained, marker-tagged DNA complexes is introduced through one inlet of the cross slot, and a stream of viscosity-matched visualization buffer containing oxygen scavengers, but no fluorescent particles or DNA, is introduced into the opposing channel. A planar extensional flow is established and a stagnation point is generated at the center of the channel intersection. A single syringe pump (Harvard Apparatus PhD2000) was used to drive the two inlet flows. Fluid exits the device through the two outlet channels to one fixed-height reservoir and one variable-height reservoir, which is manually controlled to trap complexes at the stagnation point. A DNA molecule may be trapped at the stagnation point for minutes at a time by adjusting the outlet reservoir height.

A streak image (Fig. 1b) demonstrating this flow was obtained using an aqueous solution of 0.001% (v/w) 2-µm fluorescent polystyrene beads (Duke) introduced into both inlets of the cross slot at a flow rate that produced a maximum velocity v_max = 133.7 µm/s. Flow movies were captured at the mid-plane of the device depth at 30 fps using a cooled CCD camera (Photometrics 512b) and Simple PCI software. The streak image was constructed by overlaying sequential images from the planar extensional flow using Scion Image software.

In the vicinity of the stagnation point, the velocity field can be described by ν_x = ε̇x and ν_y = −ε̇y where ε̇ represents the strain rate and the axes are indicated in Fig 1c. Strain rates are calculated from two-dimensional (2D) fluid dynamics simulations (Comsol) for the particular cross-slot geometry and the flow conditions. The inlet fluid velocity in the simulations is specified as a parabolic profile with maximum velocity given by the centerline velocity for flow in a rectangular channel³⁸ having the dimensions of the inlet channels. A strain rate map (Fig. 1c) produced using 2D fluid dynamics simulations of the flow in an 800-µm-wide cross slot indicates that the entire length of the tagged λ-DNA complex (contour length L=22 µm³⁹), once trapped, will experience < 1% variation in strain rate. In fact, the strain rate varies less than 5% within a 100-µm radius from the stagnation point, which would permit the analysis of even longer molecules under a nearly uniform strain rate.

The steady-state extension of the complexes is tuned by adjusting the Deborah number (De), a dimensionless ratio of DNA relaxation and flow time scales that parameterizes the flow strength. Here, we define the flow time scale as ${\mathrm{\epsilon ̇}}_p^{-1}$ where ε̇_p is the peak strain rate, and the DNA relaxation time as τ, giving De = ε̇_pτ. The polymer coil-stretch transition is predicted to occur at De ≈ 0.5 for planar extensional flow⁴⁰ and has been demonstrated experimentally.^23,41 Near 100% extension can be achieved at De > ~ 40.³⁰ The relaxation time of λ-DNA has been measured by others^23,30 in solvents of different viscosities. We estimate τ ≈ 1.6 s for our solution by linearly scaling the relaxation time with the solvent viscosity using the relationship given by Texiera³⁴, which applies because these solutions are all dilute in DNA. Average extensions of stained, λ-DNA measured at four different De (Fig. S-1, using ensembles of molecules, N > 22) are in good agreement with those measured by others.²³

Data capture and image analysis

For sequence-detection experiments, an 80-µm square region centered about the stagnation point is visualized using a fluorescence microscope (Leica DMIRE II) equipped with a dual-band excitation/emission filter (Chroma 51004v2), permitting the excitation of, and the emission capture for, both the intercalated YOYO-1 and the beads. Flow through the devices is viewed in real-time and captured for review using a monochrome, image-intensified, cooled CCD camera (Photometrics Cascade 512b) and the software SimplePCI. Visualization is performed at the mid-plane of the device depth.

Recorded movies are reviewed using the software Image J. Measurements are made on bead-DNA complexes that have been trapped at the stagnation point for at least three dimensionless strain units, with a unit of strain ε = ε̇t_trap. Trapping time t_trap is determined based on the frame rate and the number of frames between the measured frame and that in which the bead-DNA complex first moved within one contour length (L=22 µm³⁹) of the stagnation point.²³ Bead position is measured on a single frame by taking a 1D-projection of the molecule’s length along the extensional axis and generating an intensity profile using Image J. Fractional bead location is determined by normalizing the position of the intensity maximum by the total measured length of the extended DNA molecule. Fractional location is converted to DNA position by multiplying by 48.502 kb, the total length of λ-DNA. With the ends of the DNA being optically indistinguishable in this protocol, fractional locations are assigned to yield the best match to the expected target locations of EcoRI on λ-DNA, as prior work has shown the EcoRI-based marker to bind with stringent specificity to its recognition sequence with no detected binding to miscognate (5/6 bp match) and nonspecific (≤ 4/6 bp match) sites under the conditions used in the present experiments.³¹

Results and Discussion

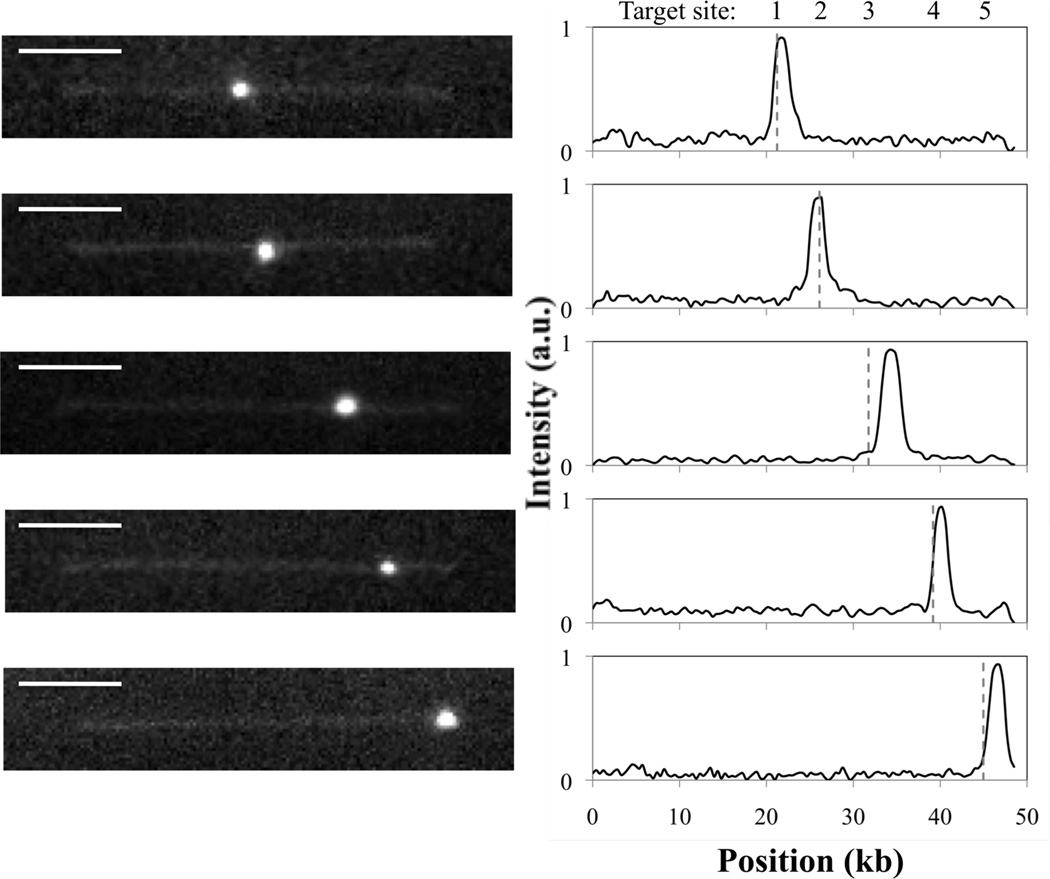
Direct observations of tagged DNA complexes at the stagnation point have been made at De = 1, 1.5, 2, and 3.9, yielding molecules stretched to average steady-state extensions of 68%, 71%, 79%, and 88% of the stained contour length, respectively. The marker does not have a measurable effect on the average extension experienced by the DNA at a given De (Fig. S-1); however, deviations from the mean extension are 200% higher when markers are bound. DNA with markers bound to each of the five EcoRI target sites on λ-DNA have been observed (Fig. 2) at the four De probed. Although most complexes have only a single marker bound, this can likely be attributed to low efficiency probe-DNA complexation conditions rather than the flow conditions, as the scarcity of molecules hosting multiple probes is consistent with previous work, where complexes were prepared in the same manner but stretched using slide immobilization.³¹

Figure 2.

Representative fluorescence images of marker-DNA complexes trapped at the stagnation point and stretched in planar extensional flow (De = 3.9), with corresponding fluorescence intensity profiles. Peaks in intensity indicate marker positions. Dashed vertical lines denote expected target locations for EcoRI on fully extended λ-DNA. Scale bar is 5 µm.

Histograms of bead binding positions compiled for complexes stretched at both De = 1 (Fig. 3a) and De = 3.9 (Fig. 3b) possess five distinct peaks and reveal the locations of all five expected EcoRI target sites on λ-DNA. Similar trends were obtained at the intermediate flow strengths of De = 1.5 and De = 2 (data not shown). Thus, stretching tagged DNA complexes in planar extensional flow is a viable method for target-sequence detection in genomic-length DNA, here enabling the identification of target sites up to 24 kb apart.

Figure 3.

Binding distributions for mutant-EcoRI markers bound to stained λ-DNA stretched in planar extensional flow. The number of markers measured is (a) N = 132 at De = 1 and (b) N = 263 markers at De = 3.9. Solid line is a best fit to the data using a linear combination of Gaussians. Dashed vertical gray lines indicate expected target locations of EcoRI on fully extended λ-DNA.

We assess the accuracy and precision of the stretching technique by fitting a linear combination of Gaussians to each histogram. The parameters are summarized in Table 1. At the two De examined, the method permits target-site prediction to within 1.5 kb for all five sites with an average accuracy < 1 kb. At the centermost sites, the error is as low as 0.1 kb at the highest De. Total errors of up to ~ 5 kb can be expected when the 48.502 kb λ-DNA molecule is only 90% extended, which is consistent with our findings. Accuracy improves by 0.1–0.3 kb for each site as De is increased from 1 to 3.9. While the full data sets for De = 1 and De = 3.9 contain different numbers of molecules, the error shows no clear trend with number of molecules at a fixed target site (Fig. S-2). The clearest trends, including data for De = 1.5 (N = 67), are with site position and with De (Fig. S-3). Therefore, we hypothesize that the accuracy improvement with increasing De is most likely due to the increase in average molecular extension from 68% to 88%, which increases the degree of linearity of the molecule and the distance between topologically remote base pairs. We anticipate that accuracy will approach the diffraction limit as De is increased enough to yield near full extension of the DNA. The use of smaller markers (for example, quantum dots) may also improve determination of the probe position. Measurement precision, gauged using standard deviation, ranges from 0.5–1.4 kb for this extensional flow technique and shows no clear trend with increasing extension for the De range explored.

Table 1.

Gaussian best-fit statistics for histograms produced using marker-DNA complexes trapped and stretched at the stagnation point of a planar extensional flow. N is the number of measured marker positions included in the ensemble-average fractional extension, <x>/L, where standard deviation is provided in parenthesis. Error is reported as Δ, the distance in kb from the expected EcoRI target site on λ-DNA; e.g. for an experimentally determined binding location of 21.1 kb, Δ = 21.1 kb – 21.226 kb = −0.1 kb. Precision is reported as σ, the standard deviation of each Gaussian peak.

De	N	<x>/L	Site 1: 21.226 kb		Site 2: 26.105 kb		Site 3: 31.747 kb		Site 4: 39.169 kb		Site 5: 44.973 kb
			Δ (kb)	σ (kb)	Δ (kb)	σ (kb)	Δ (kb)	σ (kb)	Δ (kb)	σ (kb)	Δ (kb)	σ (kb)
1	132	0.68 (0.06)	−0.4	0.8	−0.2	0.5	+1.0	1.4	+1.3	1.2	+1.4	0.8
3.9	263	0.88 (0.04)	−0.1	0.8	−0.1	0.7	+0.7	1.3	+1.2	0.8	+1.3	0.8

Probe position prediction is least accurate at the ends of the molecule. In fact, the error in predicted target position increases monotonically with distance from the center of the DNA. This suggests a systematic change in base-pair density along the molecule with distance from the stagnation point. Thus, at the De investigated, the molecules appear to be, on average, more extended at the center than the ends. Although fully extended λ-DNA molecules centered at the stagnation point theoretically experience less than 1% variation in strain rate from center to end, the tension in the DNA chain is highest at the chain center and decreases towards the free ends.

Fluctuations will thus predominantly affect the chain ends, and any Brownian fluctuation that results in the chain sampling a reduced strain rate will permit some relaxation in the molecule, which has been shown to proceed inward from the free ends⁴³ and is consistent with the higher observed errors at the ends of the molecule. Indeed, in uniform flows, others have shown that the extension of a DNA molecule tethered at one end is not homogeneous along its length.^39,44,45 Instead, spacing between base pairs actually decreases with distance from the tether point, creating higher monomer densities toward the free end of the molecule. Numerical simulations of DNA in planar extensional flow would allow the ability to correct for this slight bias in errors towards the ends of the chain.

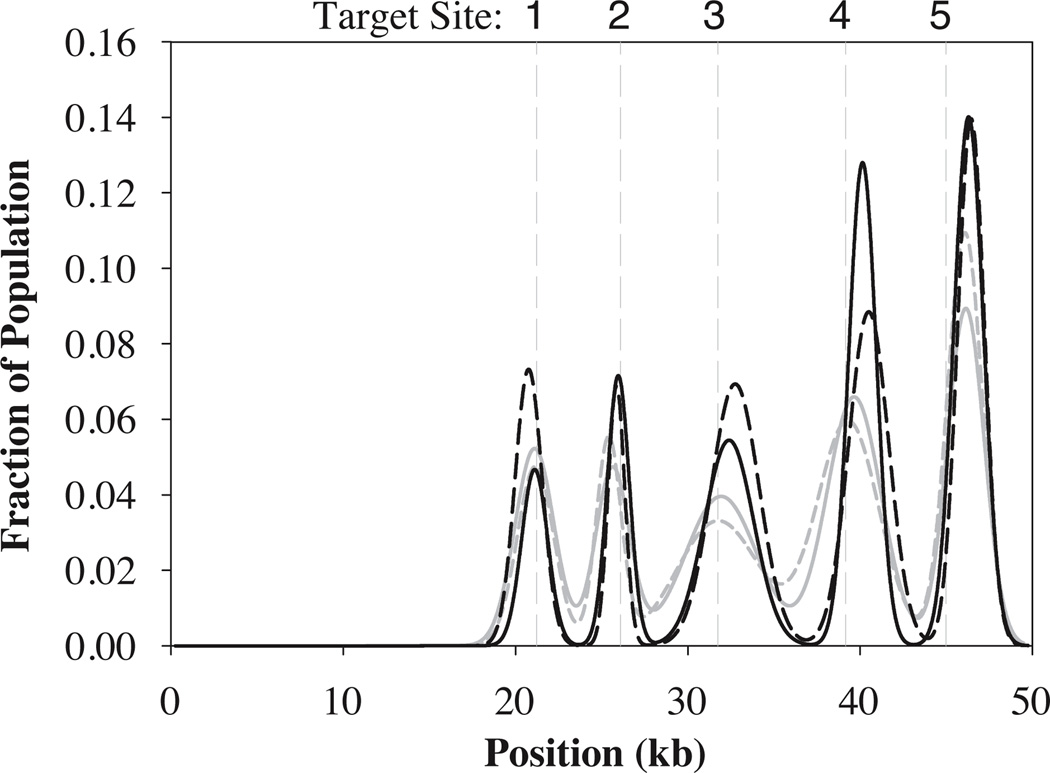
Best-fit binding distributions obtained for flow-stretched complexes at 68% and 88% extension may be directly compared with those obtained for mutant EcoRI-tagged complexes stretched and immobilized on slides (Fig. 4), with populations characterized by extensions of 79% and 92% of the DNA contour length. Statistics for the slide-stretched data are provided in Table 2. Although the slide-stretched data slightly more accurately predict the target site positions, especially toward the ends of the molecule, the difference in precision between the two methods – evident in the differences in the breadth of the peaks in Figure 4 – is striking. On average, the extensional-flow stretching technique results in a 50% reduction in the standard deviation compared to stretching on slides. This is not merely a function of the number of molecules analyzed, as the ensemble at De = 1 is significantly smaller than the others yet the standard deviations are comparable to those of De = 3.9.

Figure 4.

Comparison of best Gaussian fits from binding distributions obtained from slide-stretched DNA (solid gray: 79% extension, broken gray: 92% extension) and flow-stretched DNA (solid black: De = 1, broken black: De = 3.9). Dashed vertical gray lines indicate expected target locations of EcoRI on fully extended λ-DNA.

Table 2.

Gaussian best-fit statistics for histograms produced using complexes stretched and immobilized on slides by molecular combing. Individual molecules having a fractional extension x/L > 0.75, were included in a sub-population with a higher ensemble-average fractional extension <x>/L. Error Δ and precision σ are reported as described in Table 1.

x/L	N	<x>/L	Site 1: 21.226 kb		Site 2: 26.105 kb		Site 3: 31.747 kb		Site 4: 39.169 kb		Site 5: 44.973 kb
			Δ (kb)	σ (kb)	Δ (kb)	σ (kb)	Δ (kb)	σ (kb)	Δ (kb)	σ (kb)	Δ (kb)	σ (kb)
All	322	0.79 (0.2)	0	1.1	−0.7	0.7	+0.1	2.4	+0.1	1.8	+1.1	1.0
> 0.75	204	0.92 (0.1)	−0.1	1.1	−0.5	1.0	+0.2	2.1	+0.5	1.6	+1.1	1.1

Smaller standard deviations are important because detection resolution is limited by peak width.⁴⁶ Using the average FWHM to estimate resolution,⁴⁶ the extensional-flow stretching method may be able to discriminate between target sequences separated by as little as 2 kb, an improvement over the resolution reported for Direct Linear Analysis (DLA), where DNA are entrained and stretched in a contraction flow.^16,47 For comparison, peak resolutions of 1–5 kb (based on FWHM) have recently been demonstrated^48–50 for ensembles of 100–600 slide-immobilized samples. Ultimately, any method based on optical detection for a population of molecules will likely be diffraction limited with a minimum resolution of ~ 0.5 kb for fully extended stained DNA. Although measurement techniques^51,52 have permitted single-measurement resolution of two fluorophores or nanospheres to within tens of nanometers demonstration of comparable resolution for populations of molecules has not been demonstrated, no doubt in part due to the heterogeneity of molecular stretching during immobilization (see below).

Stretching DNA in planar extensional flow has some advantages that may contribute to the observed increase in precision. In contrast with slide immobilization techniques, where markers can adsorb to the surface near the DNA, in the cross slot, unbound or weakly bound markers are swept off the trapped molecules by flow. Therefore, only tightly bound markers are included in the analysis, thereby reducing the incidence of non-specific binding and eliminating coincidental co-location of markers and DNA. In addition, because steady-state extensions can be achieved at a given De, narrow distributions of known molecular extension (Fig. S-1) are obtained. In comparison, other extension methods usually result in much broader length distributions (see Fig. S-4 for a comparison of slide immobilization and flow-stretched distributions) for a given extension and often require applying a threshold to the data to include only the longest molecules.^6,16,47,48 Further, knowledge of the expected steady-state length of the molecule at a known De provides the ability to distinguish more clearly among intact DNA, DNA fragments, and tangled molecules or concatemers and provides a meaningful criterion for data exclusion. Occasionally in flow experiments, we observed two DNA tangled about a marker, which we were easily able to exclude from analysis based on length. We expect this same phenomenon occurred during the slide-immobilization experiments, but, as a wide variation of stretching was observed, we could not differentiate between one DNA molecule 100% extended and two DNA molecules 50% extended. Undoubtedly, this uncertainty reduces localization precision in experiments involving slide immobilization.

Gains in precision achieved by trapping and extending DNA in the cross slot permit us to better evaluate differences in binding between populations of molecules. For example, when the data at De = 3.9 are divided into populations based on whether or not the samples were mixed during incubation of the DNA with markers (Fig. 5), we observe a difference in the distribution of markers among the five target sites, where site 1 is located nearest the molecule’s center and site 5 is nearest the end. Without mixing, the target sites at the ends of the molecule are much more populated than the innermost sites. However, with mixing, the markers are more evenly distributed from center to end across the molecule. Similar changes in binding distribution across the different target sites have been observed for this system using the slide-stretching method³¹ and by stretching in flow at low De (data not shown).

Figure 5.

Comparison of binding distributions obtained from (a) N = 130 markers bound to DNA with no mixing during incubation, and (b) N = 133 markers bound to DNA with continuous mixing during incubation. Solid lines depict Gaussian best fits to the data, while dashed vertical gray lines indicate expected target locations of EcoRI on fully extended λ-DNA. Statistics from best fits are provided in Table S-1. (c) Unmixed population (open circles) is distributed differently among the five target sites compared to mixed population (filled circles).

Studies have shown evidence that shear and extensional flows improve binding to large DNA molecules.^53–55 Thus, we postulate that the observed improvement in binding to internal sequences results from the shear flow-driven extension of the DNA molecule, which provides greater exposure of the internal DNA target sequences to the probe during the incubation. Shear flow strengths can be characterized by the dimensionless Weissenberg number, Wi = γ̇τ, where γ̇ is the applied shear rate and τ is again the longest relaxation time of the DNA. Here, γ̇ was estimated by assuming that the 200-µl sample volume was transported in a ~100-µm-deep fluid film at 8 rpm along the 7-mm-diameter tube. Buffer viscosity was measured to be ~2 cP at 21°C using a Gemini rheometer with cone and plate geometry. Relaxation time was scaled based on the solution viscosity as described in the Methods section; however, this estimate is low, as the mixing was actually performed at 4°C (where we anticipate the solution viscosity is higher). Using these assumptions, we determined that the DNA periodically experiences a maximum Wi ~ 80, a condition where DNA molecules have been shown to extend, on average, to 40% of their contour length in shear flow.³⁰ Therefore, binding differences can likely be attributed to improved marker access to the internal sequences that may be buried when the molecule is coiled. By extending the DNA molecule during mixing, we presumably decrease three-dimensional diffusional resistances to such sites. We note that the stagnation point flow in the cross slot provides an excellent platform for potential single-molecule studies of the effect of DNA conformation on binding specificity and kinetics at different binding sites.

Conclusions

We have demonstrated that stretching of DNA molecules using planar extensional flow enables determination of the location of EcoRI target sites on λ-DNA with an average accuracy and precision of < 1 kb at both 68% and 88% extensions. Because molecules may be directly observed in the cross slot without tethering, they remain available for use in downstream processes in integrated lab-on-a-chip devices. Throughput could be improved over the proof-of-concept device by multiplexing the geometry and automating trapping control. In addition, introduction of a flow-focusing element ahead of the entrance channel would both direct molecules toward the stagnation point, as well as reduce the analyte volume required.

The utility of planar extensional flow for single-molecule DNA analysis extends far beyond sequence detection. For example, the ability to control the location of the stagnation point for trapping the molecule also permits sorting. Trapped molecules may be directed to one exit channel or another based on the presence or absence of tags. In addition, the ability to trap and observe the DNA for extended periods suggests the possibility of in situ observation of binding dynamics or other single-molecule reactions. Finally, the effect of extension on such reactions can be directly probed in the cross slot, because different mean DNA lengths can be reproducibly attained by adjusting De. This is especially relevant, as our data suggest that marker binding to genomic DNA may be improved with greater access to interior DNA sequences.