Skip to main content
NCBI home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2010 Apr 19;107(18):8183–8188. doi: 10.1073/pnas.0911107107

Net charge per residue modulates conformational ensembles of intrinsically disordered proteins

Albert H Mao a,b,c, Scott L Crick b,d, Andreas Vitalis a,b, Caitlin L Chicoine d, Rohit V Pappu a,b,d,1
PMCID: PMC2889596  PMID: 20404210

Abstract

Intrinsically disordered proteins (IDPs) adopt heterogeneous ensembles of conformations under physiological conditions. Understanding the relationship between amino acid sequence and conformational ensembles of IDPs can help clarify the role of disorder in physiological function. Recent studies revealed that polar IDPs favor collapsed ensembles in water despite the absence of hydrophobic groups—a result that holds for polypeptide backbones as well. By studying highly charged polypeptides, a different archetype of IDPs, we assess how charge content modulates the intrinsic preference of polypeptide backbones for collapsed structures. We characterized conformational ensembles for a set of protamines in aqueous milieus using molecular simulations and fluorescence measurements. Protamines are arginine-rich IDPs involved in the condensation of chromatin during spermatogenesis. Simulations based on the ABSINTH implicit solvation model predict the existence of a globule-to-coil transition, with net charge per residue serving as the discriminating order parameter. The transition is supported by quantitative agreement between simulation and experiment. Local conformational preferences partially explain the observed trends of polymeric properties. Our results lead to the proposal of a schematic protein phase diagram that should enable prediction of polymeric attributes for IDP conformational ensembles using easily calculated physicochemical properties of amino acid sequences. Although sequence composition allows the prediction of polymeric properties, interresidue contact preferences of protamines with similar polymeric attributes suggest that certain details of conformational ensembles depend on the sequence. This provides a plausible mechanism for specificity in the functions of IDPs.

Keywords: Monte Carlo, polyampholyte, polyelectrolyte

Intrinsically disordered proteins (IDPs) are a class of proteins that fail to fold autonomously in aqueous solutions to well-defined three-dimensional structures (1, 2). This “intrinsic disorder” has been implicated in a range of regulatory functions that require IDPs to interact with other macromolecular ligands (3–11). Many of these interactions promote disorder-to-order transitions within IDPs (3, 9), and different mechanistic models (3, 12, 13) have been proposed for coupled folding and binding. To develop a better understanding of how disorder is used in function (2), we have pursued quantitative, polymer-physics-based descriptions (14–16) for conformational ensembles of IDPs (17–20).

Low hydrophobicity is a defining characteristic of IDP sequences (21, 22). This suggests that IDPs cannot collapse to form compact, globular conformations in aqueous solutions (21). However, spectroscopic (23–27) and computational investigations (17, 28) have shown that polar tracts form heterogeneous ensembles of collapsed structures in aqueous solutions. These sequences are rich in uncharged, polar amino acids and are devoid of canonical hydrophobic residues. Collapse of polar tracts has been observed for polyglutamine (17, 20, 23, 26–28), the N domain of the yeast prion Sup35 (25), and glycine-serine block copolypeptides (19, 24). Studies of polyglycine (19) have shown that polypeptide backbones also form heterogeneous ensembles of collapsed structures in water, suggesting that water is a poor solvent for these constructs and other polar tracts.

For homopolymers, the thermodynamic preference for collapsed globules versus swollen coils can be inferred from expressions for the free energy of a polymer in solvent written in terms of chain length (N) and effective two- and three-body terms (ω2 and ω3, respectively) that quantify average, solvent-mediated interactions between chain monomers (29). Due to excluded volume considerations, ω3 is always positive (30–32). For a given set of solution conditions (set by the temperature T in theories and simulations), the lower entropy globule phase is favored when ω2 is negative (low T) and the higher entropy coil phase is favored when ω2 is positive.

We have reported results from atomistic simulations (20) based on the OPLS-AA/L (Optimal Potentials for Liquid Simulations–All Atom/LMP2) charge set (33) and the ABSINTH implicit solvation model (34) to study homopolymeric polyglutamine. The energy function used is of the form E = Utor + Ws + Wel + UEV + UDisp. Here, Utor denotes torsional potentials and Ws is the direct mean-field interaction term, that uses experimentally determined free energies of solvation for model compounds; Wel denotes the mean-field electrostatic term. Ws and Wel are modulated by the degree of solvation for each atom through a nonlinear function of the solvent accessible volume. UEV + UDisp models van der Waals interactions using the Lennard–Jones model, where UEV and UDisp refer to short-range repulsive and attractive terms, respectively. When all terms except UEV are turned off, the simulations sample conformations from self-avoiding random walk ensembles (17, 20) because ω2 > 0. Conversely, when the only nonzero terms in the Hamiltonian are UEV and UDisp, conformations are sampled from an ensemble of nonspecific globules (17, 20). For simulations of polyglutamine with the full Hamiltonian, the ensemble of preferred conformations is predominantly globular for a range of physiologically relevant temperatures (20). These results are congruent with experimental data and a speculative rationalization is provided below.

Based on model compound studies, polar amino acids such as glutamine are classified as being hydrophilic (35). This is based on transfer free energies of model compounds (36, 37) from oil into water and the favorable free energies of solvation (free energy of transfer from gas phase into solvent) of these compounds in water. Naive extrapolation suggests that sequences such as polar polyglutamine should be miscible in water and form structures that maximize the solute–solvent interface. In reality, these expectations do not hold; instead, polyglutamine forms compact globules in water (23, 26–28). In polyglutamine, each residue experiences a reduction in translational entropy when compared to free glutamines diffusing in solvent. Mean-field models show that the entropy of mixing between solute and solvent molecules is reduced by a factor of N if we compare the entropy of mixing for N freely diffusing solute molecules to N residues in a polymer (32). Additionally, polymers have access to different phases such as globules and coils. In globules, the concentration of chain units around each other is independent of N, whereas in coils this concentration decreases as N-0.77 (32). As a result, within globules, residues have access to cooperative intrachain interactions that can compete against additive interactions of individual residues with the solvent. If the effects of these cooperative self-interactions are stronger than the sum of individually favorable interactions of repeating units with solvent, then these favorable self-solvation interactions combined with the diminished translational entropy per residue yield the globule as the preferred phase. Studies of model compounds do not account for the diminution in translational entropy nor do they account for the competition between cooperative intrapolymer and additive polymer–solvent interactions. Such effects may be quantified either by measuring free energies of solvation of appropriate polymeric constructs or by measuring these quantities for model compounds near their solubility limits to account for the competition between self- and cross-interactions.

One might be tempted to conclude that all IDPs form heterogeneous ensembles of collapsed structures in aqueous solvents. Uversky et al. (21) showed that many IDP sequences have high net charge per residue. In a two-dimensional space defined by mean hydrophobicity 〈H〉 and mean net charge 〈q〉, a single line 〈q〉 = 2.785 〈H〉-1.151 separates IDPs from those with well-defined folds (21). Consequently, we focus here on the effect of net charge on the phase behavior of archetypal IDPs in aqueous solvents. Specifically, we present results from molecular simulations using the ABSINTH model and fluorescence experiments for protamines and protamine-like polypeptides. These are naturally occurring arginine-rich IDPs (38, 39) that are associated with condensation of chromatin during spermatogenesis (40, 41) and packaging of viral genomes (42).

Results and Discussion

Characteristics of Protamine Sequences Used in This Study.

Fig. 1 summarizes the properties of all protamine sequences used in our study. In our simulations, we assumed that the protonation states of ionizable residues are those of isolated amino acids at pH 7.4. For each sequence, Fig. 1 shows values of f+ and f-, which refer to the fraction of positively and negatively charged residues, respectively, and the values of the net charge per residue defined as (f+ - f-). Protamines with nonzero values of both f+ and f- are asymmetric polyampholytes, whereas sequences for which f+ > 0 and f- = 0 are polyelectrolytes. All of the protamines fall within the intrinsically disordered region of the net charge/hydropathy plane of Uversky et al. (21). This is confirmed by the disorder scores computed using the VSL2B predictor (43). For all protamines, the disorder score is close to unity.

Fig. 1.

Fig. 1.

Open in a new tab

Inventory of protamine sequences. For each protamine, the columns show numeric and graphic identifiers, amino acid sequence, number of residues, UniProtKB accession code, f+, f-, mean Kyte–Doolittle hydropathy score, and the minimum VSL2B disorder prediction score over all residues. Sequences are sorted by their net charge per residue, f+ - f-. The symbols shown here are used throughout the paper (Figs. 2–8) as protamine identifiers. Note that filled shapes (solid diamonds, circles, and squares) denote polyelectrolytes, whereas thin or hollow shapes denote polyampholytes.

Net Charge Per Residue Segregates Protamine Conformations Along a Globule-to-Coil Transition.

Fig. 2 shows the ensemble-average radii of gyration (〈Rg〉) plotted against net charge per residue. Each 〈Rg〉 value was divided by that of the same protamine simulated as a self-avoiding random walk, effectively normalizing it by a random coil reference state. Fig. 2 suggests the existence of a globule-to-coil transition as the net charge per residue increases. In the range 0.4 < (f+ - f-) < 0.65, polyelectrolytic protamines have slightly larger 〈Rg〉 values than their polyampholytic counterparts. This is true even for polyelectrolyte-polyampholyte pairs with similar/identical values of (f+ - f-). To probe the robustness of net charge per residue as an order parameter, we simulated polypeptides with identical composition to protamine 4. The results, discussed in the SI Appendix, demonstrate that variations of 〈Rg〉 with sequence rearrangements are small.

Fig. 2.

Fig. 2.

Open in a new tab

Normalized 〈Rg〉 plotted against net charge per residue. To enable comparisons between polypeptides of different length, the 〈Rg〉 values obtained using the full ABSINTH Hamiltonian were divided by that of the same protamine simulated as a self-avoiding random walk. Error bars denote the standard error of the mean (SEM).

Additional Tests of the Proposed Globule-to-Coil Transition.

Analysis of other properties confirms the globule-to-coil transition suggested in Fig. 2. Asphericity (δ∗) quantifies the extent of deviation from a perfect sphere (δ∗ = 0), attaining its maximum value of one for a perfect rod. For polymers in theta solvents, δ∗ = 0.39, whereas δ∗ = 0.43 (44) for self-avoiding random walks (45). Fig. 3 shows that protamine asphericities change from 0.15 to 0.53 as the net charge per residue increases from 0.24 to 0.4. This is consistent with a transition from nearly spherical globules to ellipsoidal coils. The globule-to-coil transition is also evident in Fig. 4, which shows the scaling of ensemble-average interresidue distances plotted against their linear sequence separations. Protamines 5-21, which are on the coil side of the transition, reveal their fractal character, in that, spatial distances between residues i and j increase with sequence separation |j-i| as expected for statistical coils. They also show increased swelling vis-à-vis the self-avoiding reference chain as net charge per residue increases. Conversely, protamines 1-3 exhibit the characteristic flattening of their internal scaling curves, which is expected for globules (17, 20, 46). Details regarding the calculation of asphericities and internal scaling profiles are provided in the SI Appendix.

Fig. 3.

Fig. 3.

Open in a new tab

Asphericity δ∗ plotted against net charge per residue. Error bars denote the SEM.

Fig. 4.

Fig. 4.

Open in a new tab

Scaling of the ensemble-average internal distances, 〈Rij〉, between residues i and j plotted against chain separation, |j-i|. Capping groups at the N and C termini were included in all calculations of internal distances. Gray squares and circles show data obtained from reference simulations for atomistic self-avoiding random walks and self-attracting versions of sequences 16 and 7, respectively. For the self-avoiding random walks, all interactions except the nonbonded steric repulsions are turned off; the self-attracting reference also includes the van der Waals dispersions. Gray diamonds denote the internal scaling profile for a reference rod-like chain. The latter data were obtained from a fully extended conformation for a 25-residue polyarginine chain with all backbone and side chain dihedral angles in trans.

Fluorescence Experiments.

To test the predictions made in Figs. 2–4, we studied a subset of the protamines (2, 4, 5, 6, 8, 11, 12, 16, 18, and 21) using fluorescence correlation spectroscopy (FCS) and fluorescence anisotropy. Both sets of measurements were performed using peptides labeled at their C termini with tetramethylrhodamine-5-maleimide (TMR). Quantitative comparison between simulation results and FCS was achieved using HYDROPRO (47), which allows us to calculate the ensemble-average translational diffusion coefficient from simulation results.

Fig. 5 shows quantitative agreement between measured and calculated translational diffusion coefficients—the latter obtained from analysis of simulation results. No adjustment to simulation or HYDROPRO parameters was performed to optimize fitting. The fluorescent dye was not included in the simulated systems. To test the contributions from the fluorophore, we also performed FCS measurements using peptides labeled with an AlexaFluor-488-C5-maleimide (Alexa), which differs from TMR in terms of its charge, molecular weight, and flexibility of the linker. Results shown in the SI Appendix demonstrate that the bulkier, charged, and flexible Alexa dye weakens the quantitative agreement between measured and calculated diffusion coefficients for sequences that form globules. However, both datasets show that simulations based on ABSINTH yield quantitatively accurate descriptions of features such as the scaling of overall sizes of IDPs as a function of the net charge per residue.

Fig. 5.

Fig. 5.

Open in a new tab

Comparison of translational diffusion coefficients obtained from analysis of simulation results (ordinate) and FCS experiments (abscissa). The black line is the result of linear regression. The regression parameters are such that calculated D = 11.2 μm2/s + 0.94 × measured D. The relevant quantities for comparing numbers from simulation and experimental data are the Pearson r value, which is 0.96 and the rmsd between calculated and measured values of D, which is 7.05 μm2/s. Error bars denote the SEM.

We also used steady-state fluorescence anisotropy measurements to assess how rotational diffusion varies with increasing net charge per residue. Fluorescence anisotropy (r) is influenced by the average shape and size of a labeled polymer (48). Data for r plotted against the net charge per residue are shown in Fig. 6 for protamines 2, 4, 5, 6, 8, 11, 12, 16, 18, and 21, respectively. Because both size and shape influence rotational diffusion, both 〈Rg〉 and δ∗ should be correlated to r, and these correlations are plotted in the SI Appendix. Taken together, the FCS and fluorescence anisotropy measurements provide two independent tests of predictions that result from molecular simulations.

Fig. 6.

Fig. 6.

Open in a new tab

Steady-state fluorescence anisotropy r plotted against the net charge per residue. The data convolve contributions from size and shape, and this explains the increased anisotropy of protamine 8, which is a 44-mer, vis-à-vis those with higher net charge per residue.

Assessment of Local Conformational Preferences.

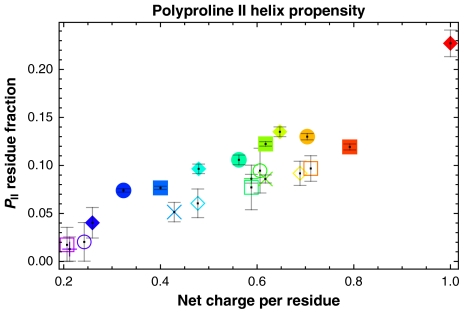
Krimm and Mark proposed that left-handed, three-residue-per-turn helices such as polyproline II (PII) are optimal regular conformations for minimizing electrostatic repulsions between charged side chains in polyelectrolytic sequences (49). We analyzed the preferences of each simulated protamine for these conformations. Fig. 7 plots the PII population for each protamine; these were calculated as the average fraction of conformations with at least three contiguous residues in PII bins. This population is smallest for globule-forming sequences and largest for the polyarginine sequence; in accord with the predictions of Krimm and Mark (49), the preference for PII increases with increasing net charge per residue. For sequences with similar net charge per residue, this preference is smaller for the asymmetric polyampholytes than for the polyelectrolytes.

Fig. 7.

Fig. 7.

Open in a new tab

Ensemble-average values for PII propensity plotted against net charge per residue. Error bars denote the SEM.

Sequence-Specificity in Conformational Properties of Protamines.

Analysis of conformational characteristics in terms of 〈H〉 and net charge per residue can mask sequence-specific conformational preferences that distinguish protamines with similar values for either parameter. Column 1 in Fig. 8 compares contact maps for protamines 8 and 9, which have similar hydrophobicity and identical net charge per residue. Protamine 8 has a higher fraction of charged residues and is an asymmetric polyampholyte, whereas protamine 9 is a polyelectrolyte. The contact map for protamine 8 indicates a finite probability of forming a compact microdomain at the C terminus. This is realized through electrostatic interactions involving the C-terminal arginine residues and two aspartate residues that are directly N-terminal to the arginine cluster. In contrast, protamine 9 exhibits quantifiable preference for nonlocal contacts within its C-terminal region, which is consistent with depletion of charged residues in this region. Column 2 in Fig. 8 compares the contact maps of protamines 11 and 12, respectively. They have identical lengths, net charge per residue, and values for f+ and f-. They differ only at positions 6, 17, and 23 and exhibit similar radii of gyration, asphericities, and PII populations. However, the contact maps reveal differences in the extent and location of segmental alpha helical preference. These results suggest that atomistic simulations and experimental characterization are needed to discern the preferred local and nonlocal contact patterns that are specified by the details of amino acid sequence.

Fig. 8.

Fig. 8.

Open in a new tab

Selected ensemble-average contact maps. Protamines 8 and 9 are shown in the first column, and protamines 11 and 12 are shown in the second column. Each contact map is annotated with a structure taken from the simulated ensemble and is intended to assist in visual interpretation of the contact maps.

Classification of Different Collapsed States.

The increase of 〈Rg〉 with increasing net charge per residue can be rationalized as a consequence of intramolecular electrostatic repulsions between arginine side chains and the favorable solvation of these moieties. The observed preference for collapsed states in three of the 21 protamines merits further discussion. Results from previous studies and data in Figs. 2–6 suggest the existence of at least three classes of globule-forming sequences for which 〈H〉 ≈ 0 or 〈H〉 is sufficiently small and (f+ - f-) ≤ 0.2. These are as follows: (i) Polar tracts, where f+ = f- = (f+ - f-) = 0, which collapse as discussed earlier. (ii) Weak polyelectrolytes/polyampholytes, where |f+ - f-| ≤ 0.2 and each of f+ and f- are small. In weak polyelectrolytes, favorable free energies of solvation of the charged moieties in the side chains and intramolecular electrostatic repulsions cannot overcome the driving force that leads to collapse of polar tracts. In polyampholytic variants, electrostatic interactions between oppositely charged side chains provide an additional source of stabilization for globules. (iii) Strong polyampholytes, where f+ and f- are large and approximately equal. In such sequences, electrostatic interactions between solvated side chains of opposite sign make important contributions to globule stability (50). This effect is reminiscent of work by Makhatadze and coworkers who showed that through-solvent electrostatic attractions between opposite charges on protein surfaces play an important role in stabilizing globular structures of water-soluble proteins (51, 52). To test the validity of the strong polyampholyte classification, which was not represented in the protamine inventory, we performed simulations for eight polyampholytic sequences. As expected (50), strong polyampholytes are strong globule formers. Analysis presented in the SI Appendix shows that electrostatic interactions between oppositely charged, surface-exposed side chains can contribute to the collapse of strong polyampholytes.

Connection to Theories for Polyelectrolytes and Polyampholytes in Poor Solvents.

Ha and Thirumalai (53) developed a self-consistent variational theory (54) to describe how sizes of individual polyelectrolyte chains vary in a poor solvent as a function of the net charge per monomeric unit. Their theory yields a compact expression for a quantity Xeff that measures an effective excluded volume. For a homopolymeric chain of length N, Inline graphic; Here, k1 and k2 are numerical constants and |ω2| is the magnitude of the effective two-body interaction in the absence of electrostatics. This term is negative in a poor solvent. Z is the net charge, κ-1 is the Debye screening length, b is the radius of each monomeric unit, and u = lB/b, where lB is the Bjerrum length—the length scale at which intermonomer electrostatic interactions equal thermal energy. If the net charge per monomer is small and Xeff < 0, then the chain prefers collapsed states because the term -k1|ω2|N1/2 dominates. Within a narrow range of net charge values, Xeff approaches zero. The value of the net charge per monomer for Xeff = 0 corresponds to the theta point for the polyelectrolyte in a poor solvent. For Xeff > 0, the chain expands and accesses the coil state that is congruent with the state accessed by the uncharged polymer in a good solvent. This state is distinct from the rod-like state because entropy opposes the effects of electrostatic repulsion, preventing the maximal extension necessary to attain a rod. Additionally, Xeff increases gradually with increased net charge per monomer, causing an increase in chain dimensions vis-à-vis the random coil state. The theory is also applicable to the case of weak/strong polyampholytes because the balance between collapsed and swollen states is dictated by the interplay between the first and second terms of Xeff. All aspects of our results seem to be congruent with these theoretical predictions, thereby providing a coherent explanation for our observations.

Toward a Sequence-Space Phase Diagram for Proteins.

Rooney et al. (55) noted that, although protamine sequences vary rapidly through evolution, their overall arginine content is conserved. This feature should lead to similar values for the types of properties quantified in Figs. 2–6, and might be relevant for maintenance of physiological function despite evolutionary pressures. Our results motivate a speculative generalization, which if valid would enable the prediction of polymeric phase behavior of proteins from simple sequence characteristics. Fig. 9 depicts a schematic phase diagram that summarizes the findings from previous studies (19, 21, 23–25) and those from the current investigation. The three axes denote 〈H〉, f+, and f-, respectively, and each of these parameters varies between zero and one. The line of Uversky et al. (21) is a plane separating folded proteins from IDPs. Contrary to previous assumptions (16), the phase diagram is not featureless below this plane. Sequences with low overall hydrophobicity can either be swollen coils or compact globules and the net charge per residue determines the preferred phase. An anonymous reviewer notes that the aggregation propensities of the protamines studied here decreases with increasing net charge per residue, suggesting a role for electrostatic interactions in promoting IDP solubility. These propensities may be calculated using the Zyggregator program available at http://www-vendruscolo.ch.cam.ac.uk/zyggregator.php.

Fig. 9.

Fig. 9.

Open in a new tab

Proposed schematic phase diagram for the single chain phase behavior of unbound, single domain proteins. The three-dimensional sequence space is defined by f+, f-, and mean hydropathy. The space is a pyramid instead of a cube because high hydropathy and high fractions of charged residues are mutually exclusive. The boundary separating folded proteins from IDPs is a three-dimensional rendering of the results from Uversky et al. (21). Within the intrinsically disordered region, the boundaries separating disordered globules from swollen coils are extrapolated from the results of the present study.

The results shown in Figs. 2, 4, and 7 illustrate small yet statistically significant differences between polyelectrolytes and polyampholytes, even for cases where the net charge per residue is identical. This suggests that the phase boundaries depicted in Fig. 9 may vary with f+ and f- individually rather than being a function of the net charge per residue alone.

Testing predictions of the proposed phase diagram requires quantitative studies of conformational characteristics for a wide range of IDPs. This should be tractable in light of the computational efficiency of simulations based on implicit solvation models such as ABSINTH. Indeed, the protamine simulations would not have been feasible without ABSINTH—a point underscored by comparisons between simulations using explicit and implicit solvent models for a polyarginine sequence at different salt concentrations (see SI Appendix).

Materials and Methods

Sequence Selection.

Protamine sequences were obtained from the National Center for Biotechnology Information Protein and UniProt Knowledgebase databases (June 20, 2008). An artificial polyarginine sequence of length 34 was also included. Details regarding the selection procedure may be found in the SI Appendix.

Simulations.

Markov chain Metropolis Monte Carlo simulations using the ABSINTH implicit solvation model and the OPLS-AA/L charge set were performed in the canonical ensemble (T = 298 K). Each capped sequence was enclosed in a spherical droplet of radius of at least 70 Å. We modeled explicitly represented Na+ and Cl- ions sufficient to neutralize the net polypeptide charge and mimic a 125 mM salt solution. All other details regarding the choice of sequences for simulations, the design of simulations, assessments of convergence, and the analysis of simulation results are described in the SI Appendix.

Peptide Preparation for Experiments.

Peptides were purchased from Yale University’s Keck Biotechnology Center. Each peptide has a cysteine at the N terminus to allow fluorescent labeling. Upon purification, two sets of labeled peptides were generated for each sequence by chemical modification via a through-cysteine covalent attachment of either TMR or Alexa (Molecular Probes).

Fluorescence Measurements.

All fluorescence data were collected at pH 2 to ensure that arginine side chains are always protonated. FCS measurements were performed on a Confocor II LSM system (Carl Zeiss-Evotec) with a 40× water-immersion objective. TMR-labeled samples were excited at 514 nm with an argon laser and emissions were collected in the 530–600 nm range. Alexa-labeled samples were excited at 488 nm with an argon laser and emissions were collected in the 505–550 nm range. Fluorescence anisotropy measurements were performed with TMR-labeled peptides using a PTI Quantamaster 40 L-format scanning spectrofluorometer at a temperature of 25 °C. Additional details regarding sample preparation, solution conditions, and data analysis for both sets of experiments are described in the SI Appendix.

Supplementary Material

Supporting Information
supp_107_18_8183__index.html (849B, html)

Acknowledgments.

We thank Carl Frieden and Timothy Lohman for assistance with fluorescence measurements. This work was supported by National Science Foundation (MCB 0718924), National Institutes of Health–National Institute of General Medical Sciences 5T32GM008802 (to A.H.M.), and the McKelvey Scholars program (C.L.C.).

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

This article contains supporting information online at www.pnas.org/cgi/content/full/0911107107/DCSupplemental.

References

  • 1.Wright P, Dyson J. Intrinsically unstructured proteins: Re-assessing the protein structure-function paradigm. J Mol Biol. 1999;293:321–331. doi: 10.1006/jmbi.1999.3110. [DOI] [PubMed] [Google Scholar]
  • 2.Dunker K, Brown C, Lawson D, Iakoucheva L, Obradović Z. Intrinsic disorder and protein function. Biochemistry. 2002;41:6573–6582. doi: 10.1021/bi012159+. [DOI] [PubMed] [Google Scholar]
  • 3.Dyson J, Wright P. Intrinsically unstructured proteins and their functions. Nat Rev Mol Cell Bio. 2005;6:197–208. doi: 10.1038/nrm1589. [DOI] [PubMed] [Google Scholar]
  • 4.Dosztányi Z, Chen J, Dunker K, Simon I, Tompa P. Disorder and sequence repeats in hub proteins and their implications for network evolution. J Proteome Res. 2006;5:2985–2995. doi: 10.1021/pr060171o. [DOI] [PubMed] [Google Scholar]
  • 5.Bertagna A, Toptygin D, Brand L, Barrick D. The effects of conformational heterogeneity on the binding of the Notch intracellular domain to effector proteins: A case of biologically tuned disorder. Biochem Soc Trans. 2008;36:157–166. doi: 10.1042/BST0360157. [DOI] [PubMed] [Google Scholar]
  • 6.Tóth-Petróczy Ag, Simon I, Fuxreiter M, Levy Y. Disordered tails of homeodomains facilitate DNA recognition by providing a trade-off between folding and specific binding. J Am Chem Soc. 2009;131:15084–15085. doi: 10.1021/ja9052784. [DOI] [PubMed] [Google Scholar]
  • 7.Mittag T, et al. Dynamic equilibrium engagement of a polyvalent ligand with a single-site receptor. Proc Natl Acad Sci USA. 2008;105:17772–17777. doi: 10.1073/pnas.0809222105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Ganguly D, Chen J. Structural interpretation of paramagnetic relaxation enhancement-derived distances for disordered protein states. J Mol Biol. 2009;390:467–477. doi: 10.1016/j.jmb.2009.05.019. [DOI] [PubMed] [Google Scholar]
  • 9.Borg M, et al. Polyelectrostatic interactions of disordered ligands suggest a physical basis for ultrasensitivity. Proc Natl Acad Sci USA. 2007;104:9650–9655. doi: 10.1073/pnas.0702580104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Fuxreiter M, et al. Malleable machines take shape in eukaryotic transcriptional regulation. Nat Chem Biol. 2008;4:728–737. doi: 10.1038/nchembio.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Mészáros B, Tompa P, Simon I, Dosztányi Z. Molecular principles of the interactions of disordered proteins. J Mol Biol. 2007;372:549–561. doi: 10.1016/j.jmb.2007.07.004. [DOI] [PubMed] [Google Scholar]
  • 12.Levy Y, Onuchic J, Wolynes P. Fly-casting in protein-DNA binding: Frustration between protein folding and electrostatics facilitates target recognition. J Am Chem Soc. 2007;129:738–739. doi: 10.1021/ja065531n. [DOI] [PubMed] [Google Scholar]
  • 13.Hilser V, Thompson B. Intrinsic disorder as a mechanism to optimize allosteric coupling in proteins. Proc Natl Acad Sci USA. 2007;104:8311–8315. doi: 10.1073/pnas.0700329104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Chan HS, Dill KA. Polymer principles in protein structure and stability. Annu Rev Biophys Biophys Chem. 1991;20:447–490. doi: 10.1146/annurev.bb.20.060191.002311. [DOI] [PubMed] [Google Scholar]
  • 15.Bright JN, Woolf TB, Hoh JH. Predicting properties of intrinsically unstructured proteins. Prog Biophys Mol Biol. 2001;76:131–173. doi: 10.1016/s0079-6107(01)00012-8. [DOI] [PubMed] [Google Scholar]
  • 16.Ashbaugh H, Hatch H. Natively unfolded protein stability as a coil-to-globule transition in charge/hydropathy space. J Am Chem Soc. 2008;130:9536–9542. doi: 10.1021/ja802124e. [DOI] [PubMed] [Google Scholar]
  • 17.Vitalis A, Wang X, Pappu R. Quantitative characterization of intrinsic disorder in polyglutamine: Insights from analysis based on polymer theories. Biophys J. 2007;93:1923–1937. doi: 10.1529/biophysj.107.110080. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Pappu R, Wang X, Vitalis A, Crick S. A polymer physics perspective on driving forces and mechanisms for protein aggregation. Arch Biochem Biophys. 2008;469:132–141. doi: 10.1016/j.abb.2007.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Tran H, Mao A, Pappu R. Role of backbone–solvent interactions in determining conformational equilibria of intrinsically disordered proteins. J Am Chem Soc. 2008;130:7380–7392. doi: 10.1021/ja710446s. [DOI] [PubMed] [Google Scholar]
  • 20.Vitalis A, Wang X, Pappu R. Atomistic simulations of the effects of polyglutamine chain length and solvent quality on conformational equilibria and spontaneous homodimerization. J Mol Biol. 2008;384:279–297. doi: 10.1016/j.jmb.2008.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Uversky V, Gillespie J, Fink A. Why are “natively unfolded” proteins unstructured under physiologic conditions? Proteins. 2000;41:415–427. doi: 10.1002/1097-0134(20001115)41:3<415::aid-prot130>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
  • 22.Weathers E, Paulaitis M, Woolf T, Hoh J. Reduced amino acid alphabet is sufficient to accurately recognize intrinsically disordered protein. FEBS Lett. 2004;576:348–352. doi: 10.1016/j.febslet.2004.09.036. [DOI] [PubMed] [Google Scholar]
  • 23.Crick S, Jayaraman M, Frieden C, Wetzel R, Pappu R. Fluorescence correlation spectroscopy shows that monomeric polyglutamine molecules form collapsed structures in aqueous solutions. Proc Natl Acad Sci USA. 2006;103:16764–16769. doi: 10.1073/pnas.0608175103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Möglich A, Joder K, Kiefhaber T. End-to-end distance distributions and intrachain diffusion constants in unfolded polypeptide chains indicate intramolecular hydrogen bond formation. Proc Natl Acad Sci USA. 2006;103:12394–12399. doi: 10.1073/pnas.0604748103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Mukhopadhyay S, Krishnan R, Lemke E, Lindquist S, Deniz A. A natively unfolded yeast prion monomer adopts an ensemble of collapsed and rapidly fluctuating structures. Proc Natl Acad Sci USA. 2007;104:2649–2654. doi: 10.1073/pnas.0611503104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Dougan L, Li J, Badilla C, Berne BJ, Fernandez J. Single homopolypeptide chains collapse into mechanically rigid conformations. Proc Natl Acad Sci USA. 2009;106:12605–12610. doi: 10.1073/pnas.0900678106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Walters R, Murphy R. Examining polyglutamine peptide length: A connection between collapsed conformations and increased aggregation. J Mol Biol. 2009;393:978–992. doi: 10.1016/j.jmb.2009.08.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Wang X, Vitalis A, Wyczalkowski M, Pappu R. Characterizing the conformational ensemble of monomeric polyglutamine. Proteins. 2006;63:297–311. doi: 10.1002/prot.20761. [DOI] [PubMed] [Google Scholar]
  • 29.Rubinstein M, Colby R. Polymer Physics. New York: Oxford Univ Press; 2003. pp. 99–195. [Google Scholar]
  • 30.de Gennes P-G. Scaling Concepts in Polymer Physics. Ithaca, NY: Cornell Univ Press; 1979. pp. 29–53. [Google Scholar]
  • 31.Shirvanyants D, Panyukov S, Liao Q, Rubinstein M. Long-range correlations in a polymer chain due to its connectivity. Macromolecules. 2008;41:1475–1485. [Google Scholar]
  • 32.Raos G, Allegra G. Chain collapse and phase separation in poor-solvent polymer solutions: A unified molecular description. J Chem Phys. 1996;104(4):1626–1645. [Google Scholar]
  • 33.Kaminski G, Friesner R, Tirado-Rives J, Jorgensen W. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J Phys Chem B. 2001;105:6474–6487. [Google Scholar]
  • 34.Vitalis A, Pappu R. ABSINTH: A new continuum solvation model for simulations of polypeptides in aqueous solutions. J Comput Chem. 2009;30:673–699. doi: 10.1002/jcc.21005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Kyte J, Doolittle RF. A simple method for displaying the hydropathic character of a protein. J Mol Biol. 1982;157:105–132. doi: 10.1016/0022-2836(82)90515-0. [DOI] [PubMed] [Google Scholar]
  • 36.Tanford C. Protein denaturation. Adv Protein Chem. 1968;23:121–282. doi: 10.1016/s0065-3233(08)60401-5. [DOI] [PubMed] [Google Scholar]
  • 37.Bolen W, Rose G. Structure and energetics of the hydrogen-bonded backbone in protein folding. Annu Rev Biochem. 2008;77:339–362. doi: 10.1146/annurev.biochem.77.061306.131357. [DOI] [PubMed] [Google Scholar]
  • 38.Liang J, Yang V, Vaynshteyn Y. The minimal functional sequence of protamine. Biochem Biophys Res Commun. 2005;336:653–659. doi: 10.1016/j.bbrc.2005.08.151. [DOI] [PubMed] [Google Scholar]
  • 39.Rooney AP, Zhang J. Rapid evolution of a primate sperm protein: Relaxation of functional constraint or positive Darwinian selection? Mol Biol Evol. 1999;16:706–710. doi: 10.1093/oxfordjournals.molbev.a026153. [DOI] [PubMed] [Google Scholar]
  • 40.Brewer L, Corzett M, Balhorn R. Protamine-induced condensation and decondensation of the same DNA molecule. Science. 1999;286:120–123. doi: 10.1126/science.286.5437.120. [DOI] [PubMed] [Google Scholar]
  • 41.Ward WS, Coffey DS. DNA packaging and organization in mammalian spermatozoa: Comparison with somatic cells. Biol Reprod. 1991;44:569–574. doi: 10.1095/biolreprod44.4.569. [DOI] [PubMed] [Google Scholar]
  • 42.Hatton T, Zhou S, Standring DN. RNA- and DNA-binding activities in hepatitis B virus capsid protein: A model for their roles in viral replication. J Virol. 1992;66:5232–5241. doi: 10.1128/jvi.66.9.5232-5241.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Obradovic Z, Peng K, Vucetic S, Radivojac P, Dunker K. Exploiting heterogeneous sequence properties improves prediction of protein disorder. Proteins. 2005;61(Suppl 7):176–182. doi: 10.1002/prot.20735. [DOI] [PubMed] [Google Scholar]
  • 44.Jagodzinski O, Eisenriegler E, Kremer K. Universal shape properties of open and closed polymer chains: Renormalization group analysis and Monte Carlo experiments. J Phys I. 1992;2:2243–2279. [Google Scholar]
  • 45.Dima R, Thirumalai D. Asymmetry in the shapes of folded and denatured states of proteins. J Phys Chem B. 2004;108:6564–6570. [Google Scholar]
  • 46.Imbert JB, Lesne A, Victor JM. Distribution of the order parameter of the coil-globule transition. Phys Rev E. 1997;56:5630–5647. [Google Scholar]
  • 47.García de la Torre J, Huertas M, Carrasco B. Calculation of hydrodynamic properties of globular proteins from their atomic-level structure. Biophys J. 2000;78:719–730. doi: 10.1016/S0006-3495(00)76630-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Lakowicz J. Principles of Fluorescence Spectroscopy. 3rd Ed. New York: Springer; 2006. pp. 353–381. [Google Scholar]
  • 49.Krimm S, Mark JE. Conformations of polypeptides with ionized side chains of equal length. Proc Natl Acad Sci USA. 1968;60:1122–1129. doi: 10.1073/pnas.60.4.1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Dobrynin A, Colby R, Rubinstein M. Polyampholytes. J Polym Sci. 2004;42:3513–3538. [Google Scholar]
  • 51.Gribenko A, et al. Rational stabilization of enzymes by computational redesign of surface charge-charge interactions. Proc Natl Acad Sci USA. 2009;106:2601–2606. doi: 10.1073/pnas.0808220106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Makhatadze G, Loladze V, Ermolenko D, Chen X, Thomas S. Contribution of surface salt bridges to protein stability: Guidelines for protein engineering. J Mol Biol. 2003;327:1135–1148. doi: 10.1016/s0022-2836(03)00233-x. [DOI] [PubMed] [Google Scholar]
  • 53.Ha BY, Thirumalai D. Conformations of a polyelectrolyte chain. Phys Rev A. 1992;46:R3012–R3015. doi: 10.1103/physreva.46.r3012. [DOI] [PubMed] [Google Scholar]
  • 54.Muthukumar M. Adsorption of a polyelectrolyte chain to a charged surface. J Chem Phys. 1987;86:7230–7235. [Google Scholar]
  • 55.Rooney A, Zhang J, Nei M. An unusual form of purifying selection in a sperm protein. Mol Biol Evol. 2000;17:278–283. doi: 10.1093/oxfordjournals.molbev.a026307. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_107_18_8183__index.html (849B, html)
0911107107_Appendix.pdf (9.4MB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES