Abstract
In articular cartilage, chondrocytes are surrounded by a narrow region called the pericellular matrix (PCM), which is biochemically, structurally, and mechanically distinct from the bulk extracellular matrix (ECM). Although multiple techniques have been used to measure the mechanical properties of the PCM using isolated chondrons (the PCM with enclosed cells), few studies have measured the biomechanical properties of the PCM in situ. The objective of this study was to quantify the in situ mechanical properties of the PCM and ECM of human, porcine, and murine articular cartilage using atomic force microscopy (AFM). Microscale elastic moduli were quantitatively measured for a region of interest using stiffness mapping, or force-volume mapping, via AFM. This technique was first validated by means of elastomeric models (polyacrylamide or polydimethylsiloxane) of a soft inclusion surrounded by a stiff medium. The elastic properties of the PCM were evaluated for regions surrounding cell voids in the middle/deep zone of sectioned articular cartilage samples. ECM elastic properties were evaluated in regions visually devoid of PCM. Stiffness mapping successfully depicted the spatial arrangement of moduli in both model and cartilage surfaces. The modulus of the PCM was significantly lower than that of the ECM in human, porcine, and murine articular cartilage, with a ratio of PCM to ECM properties of ∼0.35 for all species. These findings are consistent with previous studies of mechanically isolated chondrons, and suggest that stiffness mapping via AFM can provide a means of determining microscale inhomogeneities in the mechanical properties of articular cartilage in situ.
Introduction
Chondrocytes are embedded within an extensive extracellular matrix (ECM) that gives articular cartilage its functional mechanical properties. Each chondrocyte is surrounded by a narrow region called the pericellular matrix (PCM), which together with the enclosed cell is termed the chondron (1). The PCM is distinct from the ECM in its biochemical composition (1), ultrastructure (2,3), and biomechanical properties (4). Although the exact function of the PCM in cartilage is not fully understood, it is thought to play an important biomechanical role in the tissue (5), either by protecting the chondrocyte during compressive loading of the joint or by serving as a transducer of mechanical signals in the cellular microenvironment (2,6,7). Previous theoretical models (8–12) and microscopy studies of cartilage deformation under compressive loading (13) showed that the stress-strain environment in the vicinity of the chondrocyte is significantly influenced by the presence of the PCM, and highly dependent on the relative mechanical properties of the cell, PCM, and ECM.
The mechanical properties of chondrocytes (14–21) and the cartilage ECM (22–29) have been characterized extensively by multiple techniques. Recent studies have also identified the elastic and biphasic properties of enzymatically or mechanically isolated chondrons using micropipette aspiration (4,30–33). The elastic Young's modulus of the PCM was reported to be ∼40–70 kPa, an order of magnitude less than that of the surrounding ECM (4). Micropipette aspiration of canine chondrons from the surface and middle/deep zones of articular cartilage revealed zonal uniformity of the mechanical properties of the PCM (30). Enzymatic isolation was shown to result in a significant loss of mechanical properties as compared to mechanical isolation (30,34); however, the influence of mechanical isolation on PCM properties is unknown, and few studies have measured the biomechanical properties of cartilage PCM and its associated ECM in situ. In one recent study (35), the mechanical properties of the PCM were determined in situ using an inverse boundary element analysis coupled with three-dimensional confocal microscopy of chondron shape. In that study, the Young's modulus of the PCM in intact porcine cartilage was estimated to be in the range of 24–59 kPa.
Atomic force microscopy (AFM) provides a method for precise control of indentation testing that can be used to characterize samples at the nanometer length scale (36). In addition to allowing microscale measurements, a major advantage of AFM is its ability to obtain height and elasticity data simultaneously for a region of interest (37). The stiffness mapping technique, sometimes referred to as force-volume mapping (38), can be used to measure the elastic modulus of a sample at distinct points as the probe raster scans across a specified region. Stiffness mapping via AFM has been used to investigate the mechanical properties of cells (39–41) and local features in soft tissues, including the hippocampus (42), cornea (43), and cartilaginous tissues (26,27,44–46). For example, nanoindentation of rabbit articular cartilage revealed a gradient of Young's moduli increasing from the superficial zone to the calcified zone (26). Using a similar nanoscale approach, Allen and Mao (45) showed significant differences between the pericellular and interterritorial matrices of rat growth plate cartilage. Previous studies have shown that the experimental parameters chosen for mechanical testing, including probe shape and size, indentation velocity, indentation depth, and accurate representation of tip geometry in model fitting (47) are very important and impact the measured mechanical properties (27,48).
The objective of this study was to use AFM to quantify the microscale biomechanical properties of matched ECM and PCM regions of articular cartilage in situ. Specifically, we first validated the microscale stiffness mapping technique and its ability to accurately measure the spatial distribution and mechanical properties of two materials by using an elastomeric ECM/PCM model system. This indentation technique was subsequently used to measure the elastic properties of ECM and PCM in the middle/deep zones of human, porcine, and murine articular cartilage in situ.
Materials and Methods
Mechanical characterization via AFM
Elastic moduli were mapped quantitatively with the use of an atomic force microscope (MFP-3D; Asylum Research, Santa Barbara, CA). Borosilicate glass spheres (5 μm diameter) were attached to the tip of AFM cantilevers (k ∼7.5 N/m; Novascan Technologies, Ames, IA) to facilitate microscale testing. Indentation curves were sampled at 5 kHz, with a force trigger of ∼750 nN prescribing the point at which the cantilever approach was stopped and then retracted. An additional set of experiments was performed using a force trigger of ∼50 nN, but results indicated that larger indentations were necessary to evaluate macroscale-equivalent cartilage properties (see the Supporting Material). For evaluation of the PCM elastic properties, indentations (900–1600 sites/region, 15 μm/s indentation velocity) were sequentially applied over a region of interest defined by microscopic examination (Fig. 1). The ECM elastic properties were evaluated using the same technique over regions visually devoid of PCM (16 sites/region, 15 μm/s indentation velocity).
Figure 1.
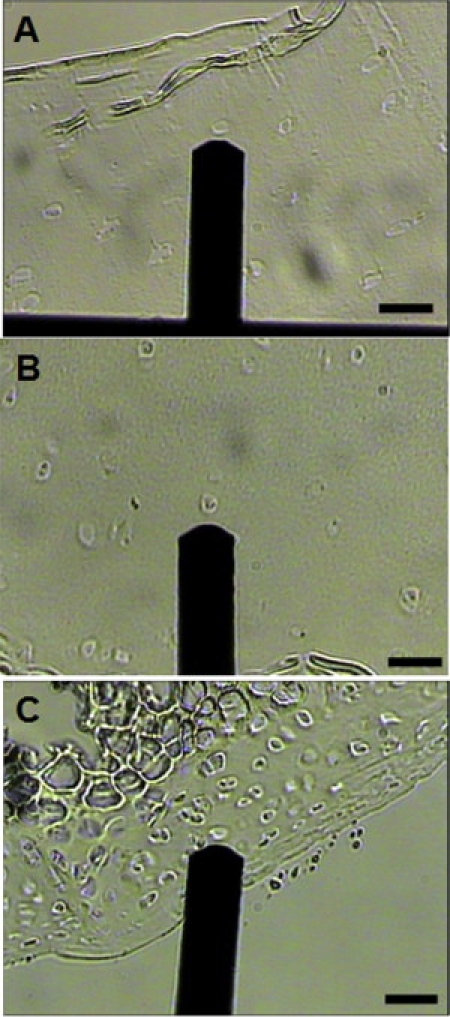
Light microscopy images illustrating testing regions in (A) human, (B) porcine, and (C) murine articular cartilage. The AFM cantilever is also shown. Murine articular cartilage exhibits the greatest cellularity of the species tested. This high cell density made it difficult to find test regions that were solely ECM in murine articular cartilage. Scale bar = 100 μm.
Elastomeric ECM/PCM model
We validated the stiffness mapping technique by probing an elastomeric model of a soft inclusion within a stiff medium. A polyacrylamide (PA) hydrogel was chosen as a model material because it has been used previously to create cell culture substrates with ECM-like stiffness (49). The gel's mechanical properties can easily be tuned over a wide range of stiffnesses by adjusting the relative amounts of acrylamide and bis-acrylamide in solution to vary the gel cross-link density (50–52). Finally, the hydrogels can be patterned using soft lithography (53,54). Here, soft lithography was used to form a higher-modulus PA mold (final acrylamide concentration of 15%, final bis-acrylamide concentration of 1.2%) with a regular pattern of holes (20 μm diameter, 12 μm depth, 50 μm center-to-center distance). These holes were then filled with lower-modulus PA (final acrylamide concentration of 8%, final bis-acrylamide concentration of 0.6%). All solutions were prepared using premixed solutions of 40% acrylamide and 2% bis-acrylamide (Bio-Rad Laboratories, Hercules, CA) with 1% v/v 1 M HEPES (pH 8.5, Gibco, Carlsbad, CA) and purified water (Sigma-Aldrich, St. Louis, MO). Polymerization was initiated with ammonium persulfate (10% w/v solution in water; Bio-Rad) and N,N,N,N-tetramethylethylene diamine (Bio-Rad). Tissue-marking dye was added to the softer PA solution to distinguish between the two materials (Fig. 2, A and B).
Figure 2.
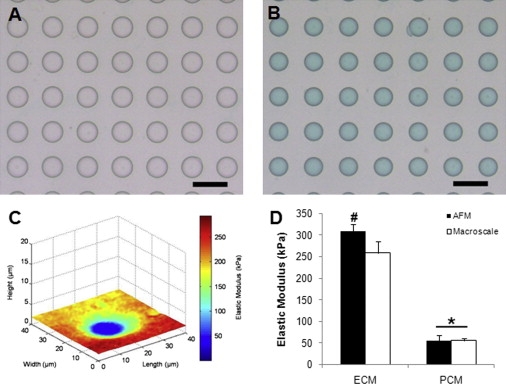
Stiffness mapping successfully depicted the spatial arrangement of moduli in PA ECM/PCM model systems. (A) Soft lithography was used to generate a mold of regularly spaced holes (20 μm diameter, 12 μm depth, 50 μm center-to-center distance) composed of stiff PA gel. (B) Holes were filled with a soft PA gel (green) to generate a soft inclusion within a stiff medium. Scale bar = 50 μm. (C) Stiffness map of model PCM showing height and calculated values of elastic moduli. (D) The elastic modulus of the stiff, outer material was fivefold higher than that of the soft, inner material (∗p < 0.0001 as compared to respective ECM, # p < 0.001 as compared to macroscale). Moduli shown as mean ± standard deviation.
A similar model surface was made using polydimethylsiloxane (PDMS) to validate testing on stiffer materials. The higher-modulus mold was comprised of a 10:1 elastomer/curing agent mixture of PDMS. Holes were filled with a 30:1 elastomer/curing agent mixture of PDMS.
The PA samples were tested in water, and PDMS samples were tested in air by AFM using the previously described protocol. Unconfined compression on a materials testing system (ElectroForce 3200; Bose-EnduraTEC, Eden Prairie, MN) was used to obtain the macroscale properties of the PA gels.
Tissue sample preparation
Articular cartilage was obtained from three different species (human, porcine, and murine) to illustrate the versatility of the microscale stiffness mapping technique. Human samples were taken from macroscopically normal regions of femoral condyles that were removed during total joint replacement surgery or from normal knee joints at autopsy. Porcine samples were collected from central regions of the medial condyle of skeletally mature knee joints with no visible signs of joint degeneration. For murine samples, entire knee joints from 3-week-old mice (C57BL/6) were harvested for evaluation purposes. All cartilage samples were wrapped in phosphate-buffered saline (PBS)-soaked gauze and frozen at –20°C for intermediate storage. To evaluate in situ matrix properties, samples were sectioned perpendicularly to the cartilage surface in 3-μm-thick slices using a cryostat microtome. Human and porcine samples were composed completely of articular cartilage. Because of size limitations, murine samples were sectioned through the entire joint to obtain a cross-section of the cartilage tissue. The samples were sectioned onto negatively charged glass slides, and the water-soluble embedding medium was washed thoroughly from all samples before AFM experiments were performed. Cartilage slices remained in PBS at room temperature for the duration of the mechanical tests.
Data evaluation
Raw data for cantilever deflection and z-piezo movement were collected and subsequently analyzed using a custom MATLAB script (The MathWorks, Natick, MA). Elastic moduli, E, were determined by fitting a modified Hertz model to force-indentation curves as described previously (14). For the elastomeric PCM model systems, the Poisson's ratio, n, was assumed to be 0.5 for PDMS (55) and 0.45 for PA (56). For articular cartilage, past studies have assumed a wide range of Poisson's ratios, but a definitive value describing the ECM and PCM at the microscale is uncertain. In this study, the local Poisson's ratio was assumed to be 0.04 for both the ECM (13,57) and PCM (22,32) based on previous experimental reports. Nonetheless, from the Hertz model, the presented modulus values can be converted from ν = 0.04 to a different assumed value of ν by multiplying by the conversion factor (1 − ν2)/(1 − 0.042). Probe-surface contact was identified using contact point extrapolation, a method that focuses on the indentation portion of the approach curve to determine where indentation begins based on the mathematical model (58). With the contact point determined, surface heights could be calculated relative to the other testing sites on the sample. Height maps were generated and overlaid with a graded coloring representative of material stiffness (see Fig. 2 C and 4, A, D, and G).
The elastic moduli for PCM regions were calculated using spatial indicators present in the stiffness maps. In brief, the thinly sliced cartilage sections provided a relatively flat, uniform surface interspersed with cell-sized holes. Voids were chosen that had no apparent cell debris or sharp contact with the underlying glass substrate in their center. Contact with the glass was readily apparent from the indentation curves and was used to define the edge of the cell voids. PCM data were included for a region extending 1 μm outward from this edge for evaluation purposes (see Fig. 4, B, E, and H), although it is possible that the PCM extends farther out than this, depending on its depth within the tissue (59).
Figure 4.
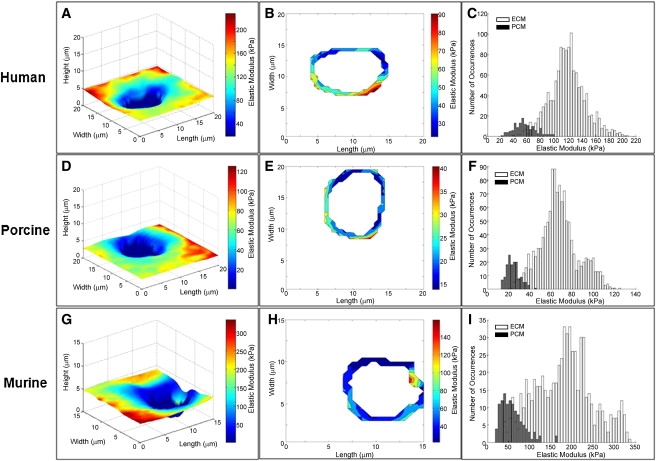
Stiffness mapping of human, porcine, and murine articular cartilage. Representative test regions are shown. (A, D, and G) Representative stiffness maps of the PCM of articular cartilage showing the height and calculated values of elastic moduli. (B, E, and H) Contour maps of the PCM. For the purposes of this study, the PCM was defined as the region extending 1 μm from cell-sized voids. Voids and ECM regions are white. (C, F, and I) Histograms of calculated elastic moduli exhibit a bimodal distribution. The low modulus peak corresponds to points within the 1 μm PCM region (black). The high modulus peak corresponds to the local ECM within each scan region (white).
Scanning electron microscopy
Cartilage sections were examined via scanning electron microscopy (SEM) to visualize tissue ultrastructure present during mechanical testing. Sectioned samples of healthy, porcine cartilage were prepared using the standard protocols of Duke University's Shared Materials Instrumentation Facility. Briefly, samples were fixed in 3.7% formaldehyde, washed with PBS, and treated with 1% OsO4 (Electron Microscopy Sciences, Hatfield, PA) for 1 h, followed by dehydration in serial gradations of ethanol. The samples were then incubated in tetramethylsilane (Electron Microscopy Sciences, Fort Washington, PA) and allowed to dry entirely before being sputter-coated with gold by means of a Desk IV sputter coater (Denton Vacuum, Moorestown, NJ). Cartilage sections were imaged using an FEI XL30 electron scanning microscope (FEI, Hillsboro, OR).
Histological staining and immunohistochemistry
For histological staining, porcine tissue sections were fixed in 10% formaldehyde for 10 min at room temperature immediately after mechanical testing. Fixed sections were rinsed with PBS and dehydrated in ethanol. Sections were stained with 0.02% aqueous fast green (Sigma-Aldrich) and Accustain Safranin-O solution (Sigma-Aldrich).
Unfixed porcine sections were fluorescently immunolabeled for type VI collagen to illustrate the presence of the PCM around cell-shaped holes using a previously described protocol (59). Specimens were labeled using a primary anti-collagen type VI antibody (RDI-6000401108; Fitzgerald Industries International, Acton, MA) followed by a fluorescein isothiocyanate-conjugated anti-rabbit secondary antibody (RDO-7111095152; Fitzgerald). Immunolabeled sections were visualized on a confocal laser scanning microscope (LSM 510; Carl Zeiss, Thornwood, NY).
Statistical analyses
Differences between the two regions for either PDMS (n = 4) or PA (n = 6) model systems were evaluated using one-way ANOVA (α = 0.05) with Fisher's least significant difference post hoc analysis to determine the level of significance. The same approach was used to analyze ECM/PCM comparisons in the middle/deep zones of human (N = 6, n = 19), porcine (N = 6, n ≥ 15), and murine (N = 6, n ≥ 15) cartilage samples. All data are presented as mean ± standard deviation.
Results
Elastomeric ECM/PCM model
Stiffness mapping successfully depicted the spatial arrangement of moduli for both control and experimental surfaces in the elastomeric model systems (Fig. 2 C). Artificial ECM/PCM structures formed with PA possessed moduli of 309 ± 16 kPa and 55 ± 12 kPa for the outer and inner materials, respectively (p < 0.0001; Fig. 2 D). For the inner material, there was no statistical difference between the microscale modulus and the macroscale value of 55 ± 5 kPa (p > 0.05). The microscale modulus of the outer material (309 ± 16 kPa) was significantly greater than the macroscale value of 259 ± 27 kPa (p < 0.001). This difference may be attributed to the local variability in acrylamide cross-linking (60). The macroscale elastic moduli were comparable to previously published values for the chosen acrylamide and bis-acrylamide concentrations (51).
The elastomeric model system was also validated for stiffer materials using a combination of high- and low-modulus PDMS. These ECM/PCM samples possessed moduli of 2.8 ± 0.5 MPa and 0.8 ± 0.3 MPa for the outer and inner materials, respectively (p < 0.0001). As for the PA samples, the microscale values measured for PDMS agreed well with the macroscale values previously reported in the literature (E = 2.8 MPa for 10:1 PDMS, E = 0.88 MPa for 30:1 PDMS) (55).
Stiffness mapping of articular cartilage
Thinly sectioned articular cartilage samples exhibited microscopic features that were consistent with the location of PCM within the tissue. Tissue within 1 μm of cell-sized voids were considered PCM, an assumption that was validated by SEM images, the higher concentration of proteoglycans in Safranin-O stained samples, and the localization of type VI collagen around the chondrocytes (Fig. 3). Topographical maps corresponded to the images created from collected data, allowing for colocalization of height and elasticity measurements throughout the tested regions (Fig. 4, A, D, and G). The Hertzian contact mechanics model provided excellent fits to the experimental data for all force-indentation curves (R2 > 0.90).
Figure 3.
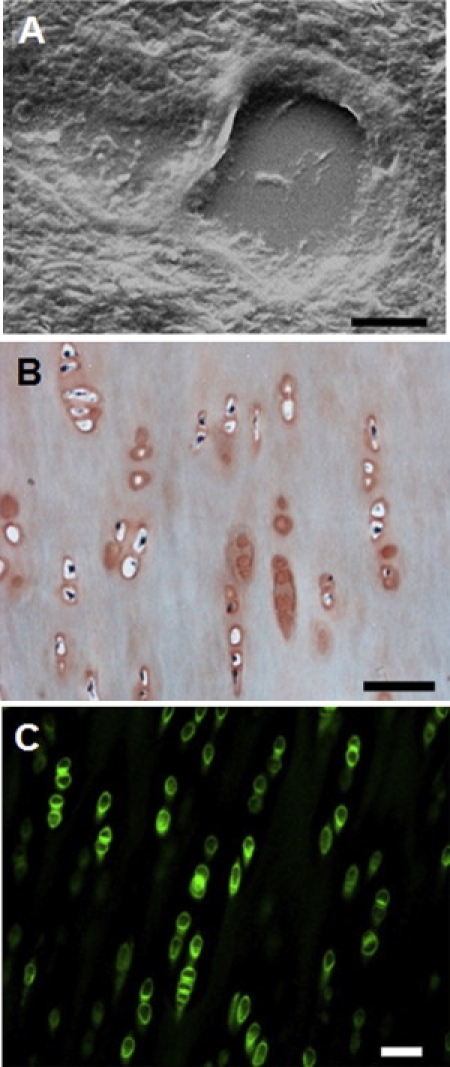
(A) SEM image of ECM/PCM in the middle/deep zones of porcine articular cartilage. The capsule-like PCM is structurally distinct from the surrounding ECM and localized around a cell-sized void in the tissue section. Magnification = 10,000×. Scale bar = 5 μm. (B) Porcine tissue sections were stained with fast green to indicate collagen fibers (green) and safranin-O to stain proteoglycans (red). Safranin-O staining is more intense in regions surrounding cell-sized voids, indicative of PCM. Scale bar = 50 μm. (C) Immunofluorescence illustrates the localization of type VI collagen to the pericellular matrix region around porcine chondrocytes. Scale bar = 50 μm.
As shown in Table 1, the elastic modulus of the ECM was significantly (p < 0.002) greater than that of the PCM for human, porcine, and murine articular cartilage. Among the three species investigated, the elastic moduli for ECM and PCM were largest in human cartilage. Porcine articular cartilage exhibited the softest mechanical properties, and the 3-week-old murine samples fell in between. Human cartilage showed similar properties whether it was obtained from macroscopically normal regions of femoral condyles removed during total joint replacement surgery (ECM = 306 ± 133 kPa; PCM = 104 ± 51 kPa) or from normal femoral cartilage from cadaver knee joints taken at autopsy (ECM = 359 ± 39 kPa; PCM = 162 ± 22 kPa). ECM regions were consistently comprised of 15–16 indentations/site, whereas PCM regions had 80–110 indentations/site. The variability for PCM measurements was associated with the cell void size, which was typically larger in human and porcine samples than in murine samples.
Table 1.
Elastic moduli of ECM and PCM regions from human, porcine, and murine articular cartilage
| Sample | ECM (kPa) | ECM range (kPa) | PCM (kPa) | PCM range (kPa) |
|---|---|---|---|---|
| Human (N = 6)n = 19, ECMn = 19, PCM | 306 ± 133 | 130–573(301 sites) | 104 ± 51 | 27–205(2062 sites) |
| Porcine (N = 6)n = 16, ECMn = 15, PCM | 81 ± 19 | 46–114(254 sites) | 30 ± 19 | 13–75(1540 sites) |
| Murine (N = 6)n = 17, ECMn = 16, PCM | 197 ± 92 | 78–391(272 sites) | 69 ± 22 | 34–110(1290 sites) |
Stiffness mapping of sectioned cartilage samples showed clear differences between the ECM and PCM regions for each species (p < 0.002). Moduli shown as mean ± standard deviation.
Discussion
Our results demonstrate that microscale stiffness mapping using AFM is a viable means of determining the site-specific mechanical properties of soft biological samples in situ. Validation of this technique in an elastomeric model system clearly illustrated the spatial arrangement of two different materials based on local micromechanical properties. For control surfaces, microscale elastic moduli showed excellent agreement with macroscale properties for all materials. Stiffness mapping of articular cartilage from human, porcine, and murine knee joints illustrated local, elastic moduli for cell-sized regions, and verified that the ECM is significantly stiffer than PCM in human, porcine, and murine tissues measured in situ, consistent with previous reports on isolated chondrons.
Previous studies of the mechanical properties of the PCM of articular chondrocytes have focused on extracting the chondron from the tissue (4,30–33) or extrapolating material parameters using inverse mathematical analyses (10,35). By allowing matrix integration between the PCM and ECM to remain relatively intact, the method presented here can provide an additional direct measure of the mechanical properties of the PCM in situ. Of importance, the moduli of the PCM and ECM were measured on the same samples (and using the same techniques), providing a means of directly comparing ECM and PCM properties. Results from all methods consistently show that the modulus of the PCM is greater than that of chondrocytes but significantly lower than that of the ECM. Human PCM values measured in this study correspond to those found using micropipette aspiration on extracted chondrons (E = 40–70 kPa (4,32)). PCM moduli for 3-week-old mice were lower than those previously reported for extracted chondrons from 1-month-old CD1 mice (E = ∼280 kPa (33)), a difference that may be related to the maturity of the cartilage or differences in the strains of mice used. Although earlier studies have reported the relationship between ECM and PCM deformation in porcine cartilage (13), this is the first study, to our knowledge, to directly measure the mechanical properties of the porcine PCM. The results for the PCM modulus in this study (E ∼30 kPa), however, are in direct agreement with a recent study that used an inverse method to match the predictions of a boundary element model of the chondron with three-dimensional confocal imaging of cell, PCM, and ECM deformation (35). Overall, the in situ mechanical properties of the PCM as measured by AFM are comparable to those measured previously for mechanically isolated chondrons, suggesting that mechanical extraction does not appear to dramatically affect the elastic properties of the PCM.
It is hypothesized that the local mechanical environment of the chondrocyte is one of many factors that regulate chondrocyte physiology. The presence of the PCM has been shown to significantly influence the mechanical and physicochemical environment of the chondrocyte (for review, see Alexopoulos et al. (9)). The mismatch between the mechanical properties of the PCM and ECM in the middle or deep zones, where the ECM is stiffer than the PCM, has been shown to result in significant strain amplification in the vicinity of the chondrocyte (8,9), which may be particularly important in the middle and deep zones where local ECM strains are lower during bulk tissue deformation (13). In this study, the ratio of PCM to ECM properties was nearly identical for all species, with values of 0.34, 0.37, and 0.35 for human, porcine, and murine cartilage, respectively. This consistency across species suggests that the mismatch in PCM and ECM properties is an intrinsic characteristic of articular cartilage, and may reflect the role of the PCM as a transducer of mechanical signals from the ECM to the chondrocyte during joint loading (1,7).
In general, the modulus values for the ECM are lower than previously reported results for macroscale properties of articular cartilage, which is also consistent with previous AFM studies (48,61). We found that the modulus value also depended on the force threshold used for the measurements. At a force threshold of ∼50 nN, the measured elastic moduli were approximately two- to fivefold lower than those measured at 750 nN (see Fig. S1). These findings are consistent with the indentation-dependent, microscale properties of articular cartilage observed by Park et al. (48). This apparently nonlinear behavior may be related to the depth- and strain-dependent behavior of articular cartilage, which is also observed at the macroscale (25,57,62). This behavior is unlikely to be due to fluid pressurization effects during loading. The time constant for interstitial fluid pressurization in cartilage during AFM-based indentation has been estimated to be less than a millisecond (48), two orders of magnitude smaller than the duration of indentation from first contact to maximum load. This suggests that fluid load support is minimal and that our technique measures the intrinsic mechanical properties of the solid matrix. Apparent softening at the microscale may also be due to the indentation of exposed proteoglycans on the cut surface of the tissue. Previous work by Dean and colleagues (63) on the compressive nanomechanics of aggrecan macromolecules illustrated that the mechanical stiffness of aggrecan increases dramatically when it is compressed at strains greater than 40%. Given that the length of aggrecan macromolecules is on the order of a micrometer (64), this strain-stiffening behavior would be observed with indentations greater than ∼400 nm, and may contribute to the indentation-dependent behavior observed in this study. Overall, our findings suggest that large indentations are required to obtain AFM-based mechanical properties representative of macroscale measurements for articular cartilage.
For this study, cartilage slices were tested in the transverse direction relative to the articular surface. In the middle/deep zones of articular cartilage, collagen fibers transition from a more random orientation in the middle zone to a highly aligned orientation perpendicular to the articular surface in the deep zone (64). Thus, measurements in this direction may yield differences in the mechanical properties as compared to the direction normal to the tissue surface. Additionally, cartilage mechanical properties have been shown to depend on the orientation of loading relative to the split-line direction (65). The split-line direction was not taken into account during sample preparation for this study, and its effect on measured mechanical properties at the microscale has yet to be determined.
The measured elastic moduli for the ECM were likely influenced by joint degeneration, maturity, and/or tissue structure in the cartilage samples. Human samples were collected from femoral condyles removed during total joint replacement surgery. Other studies have shown a decrease in the compressive stiffness of articular cartilage with age (23), as well as increasing severity of degeneration at the macroscale (23,28) and micro- and nanoscales (29). Kleeman et al. (28) recently reported that the macroscale modulus of degenerated cartilage ranges from 280–500 kPa, which is comparable to ECM moduli measured in our study.
In this work, porcine tissue was harvested from healthy, skeletally mature animals. Consistent with our results, previous reports have indicated a lower compressive modulus for porcine articular cartilage (66,67) as compared to human (24,68) or mouse tissue (33,69). Although the ECM moduli in our study are comparable to those reported for AFM indentation of the superficial zone of porcine patellar cartilage (61), they are inconsistent with macroscale values.
Murine knee joints from 3-week-old, skeletally immature mice were collected to allow for tissue sectioning without chemical treatments, such as decalcification. It is likely that skeletally immature mice do not exhibit the same mechanical properties that are characteristic of more mature animals. The average elastic modulus measured in the current study was ∼55% lower than that reported for AFM indentation of hip joint cartilage from 20-week-old mice (61). Murine articular cartilage also has a much greater cell density than that of larger animals (70). This high cellularity made it difficult to isolate testing regions that were solely ECM, resulting in lower values than would be expected (Fig. 1).
This study was aimed at characterizing the mechanical properties of articular cartilage PCM at the microscale. A recent AFM study by Stolz and colleagues (27) demonstrated that micrometer-sized indenter tips obtain elastic modulus values that better reflect macroscale measurements as compared to nanometer-sized tips. However, there are limitations to using micrometer-sized indenters for the stiffness mapping approach presented in this study. Larger tips have a larger contact area, which decreases the lateral resolution of the stiffness maps, particularly for soft materials (71). For spherical indenters, the contact radius scales with the size of the tip and indentation depth. Since measurements were conducted using a force threshold (750 nN), indentations were small in stiffer materials like the ECM but larger in softer materials like the PCM. For the softest cases, this could result in contact radii of >2.5 μm. In these cases, indenter contact with the adjacent ECM might contribute to an artificial stiffening of the measured PCM moduli. To minimize this effect, the PCM was defined as the region within 1 μm of cell-shaped voids. Since previous studies indicated that the PCM thickness varies locally around single chondrocytes (2,3), and that the PCM in the middle/deep zones of porcine articular cartilage is 3–4 μm thick (59), this 1 μm region may under- or overrepresent the extent of the PCM for any given site. Future work will investigate the micromechanical properties with smaller indenter tips to increase the lateral resolution within the PCM regions.
The results of this study suggest that stiffness mapping via AFM is a viable method for determining the site-specific mechanical properties of different regions within articular cartilage at the microscale in situ. The scale level that is accessible through AFM-based measurements facilitates more detailed investigation of the spatial distribution of PCM properties than that afforded by other techniques. This allows for the evaluation of microscale mechanical properties in small animal models, such as genetically modified mice. Furthermore, the stiffness mapping technique can be used to test neomatrix in tissue-engineered constructs at many stages of development.
Supporting Material
One table and one figure are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00370-X.
Supporting Material
Acknowledgments
We thank Poston Pritchett for his assistance in collecting human cartilage samples, and Chris Gilchrist for his assistance in preparing the PA gels.
This work was supported in part by a National Science Foundation Graduate Research Fellowship and National Institutes of Health grants AR53448, EB01630, AG15768, AR48182, AR50245, AR48852, and EB09643 (Dr. Ahmet Erdemir, PI).
Footnotes
Eric M. Darling's present address is Department of Molecular Pharmacology, Physiology, and Biotechnology, Division of Biology and Medicine, Brown University, Providence, Rhode Island.
References
- 1.Poole C.A. Articular cartilage chondrons: form, function and failure. J. Anat. 1997;191:1–13. doi: 10.1046/j.1469-7580.1997.19110001.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Poole C.A., Flint M.H., Beaumont B.W. Chondrons in cartilage: ultrastructural analysis of the pericellular microenvironment in adult human articular cartilages. J. Orthop. Res. 1987;5:509–522. doi: 10.1002/jor.1100050406. [DOI] [PubMed] [Google Scholar]
- 3.Hunziker E.B., Michel M., Studer D. Ultrastructure of adult human articular cartilage matrix after cryotechnical processing. Microsc. Res. Tech. 1997;37:271–284. doi: 10.1002/(SICI)1097-0029(19970515)37:4<271::AID-JEMT3>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- 4.Alexopoulos L.G., Haider M.A., Guilak F. Alterations in the mechanical properties of the human chondrocyte pericellular matrix with osteoarthritis. J. Biomech. Eng. 2003;125:323–333. doi: 10.1115/1.1579047. [DOI] [PubMed] [Google Scholar]
- 5.Szirmai J.A. The concept of the chondron as a biomechanical unit. In: Hartmann F., editor. Biopolymer und Biomechanik von Bindegewebssystemen. Academic Press; Berlin: 1974. p. 87. [Google Scholar]
- 6.Poole C.A., Ayad S., Schofield J.R. Chondrons from articular cartilage: I. Immunolocalization of type VI collagen in the pericellular capsule of isolated canine tibial chondrons. J. Cell Sci. 1988;90:635–643. doi: 10.1242/jcs.90.4.635. [DOI] [PubMed] [Google Scholar]
- 7.Guilak F., Alexopoulos L.G., Haider M.A. The pericellular matrix as a transducer of biomechanical and biochemical signals in articular cartilage. Ann. N. Y. Acad. Sci. 2006;1068:498–512. doi: 10.1196/annals.1346.011. [DOI] [PubMed] [Google Scholar]
- 8.Guilak F., Mow V.C. The mechanical environment of the chondrocyte: a biphasic finite element model of cell-matrix interactions in articular cartilage. J. Biomech. 2000;33:1663–1673. [PubMed] [Google Scholar]
- 9.Alexopoulos L.G., Setton L.A., Guilak F. The biomechanical role of the chondrocyte pericellular matrix in articular cartilage. Acta Biomater. 2005;1:317–325. doi: 10.1016/j.actbio.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 10.Michalek A.J., Iatridis J.C. A numerical study to determine pericellular matrix modulus and evaluate its effects on the micromechanical environment of chondrocytes. J. Biomech. 2007;40:1405–1409. doi: 10.1016/j.jbiomech.2006.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Korhonen R.K., Herzog W. Depth-dependent analysis of the role of collagen fibrils, fixed charges and fluid in the pericellular matrix of articular cartilage on chondrocyte mechanics. J. Biomech. 2008;41:480–485. doi: 10.1016/j.jbiomech.2007.09.002. [DOI] [PubMed] [Google Scholar]
- 12.Kim E., Guilak F., Haider M.A. The dynamic mechanical environment of the chondrocyte: a biphasic finite element model of cell-matrix interactions under cyclic compressive loading. J. Biomech. Eng. 2008;130:061009. doi: 10.1115/1.2978991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Choi J.B., Youn I., Guilak F. Zonal changes in the three-dimensional morphology of the chondron under compression: the relationship among cellular, pericellular, and extracellular deformation in articular cartilage. J. Biomech. 2007;40:2596–2603. doi: 10.1016/j.jbiomech.2007.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Darling E.M., Topel M., Guilak F. Viscoelastic properties of human mesenchymally-derived stem cells and primary osteoblasts, chondrocytes, and adipocytes. J. Biomech. 2008;41:454–464. doi: 10.1016/j.jbiomech.2007.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Darling E.M., Zauscher S., Guilak F. Viscoelastic properties of zonal articular chondrocytes measured by atomic force microscopy. Osteoarthritis Cartilage. 2006;14:571–579. doi: 10.1016/j.joca.2005.12.003. [DOI] [PubMed] [Google Scholar]
- 16.Trickey W.R., Baaijens F.P., Guilak F. Determination of the Poisson's ratio of the cell: recovery properties of chondrocytes after release from complete micropipette aspiration. J. Biomech. 2006;39:78–87. doi: 10.1016/j.jbiomech.2004.11.006. [DOI] [PubMed] [Google Scholar]
- 17.Trickey W.R., Lee G.M., Guilak F. Viscoelastic properties of chondrocytes from normal and osteoarthritic human cartilage. J. Orthop. Res. 2000;18:891–898. doi: 10.1002/jor.1100180607. [DOI] [PubMed] [Google Scholar]
- 18.Trickey W.R., Vail T.P., Guilak F. The role of the cytoskeleton in the viscoelastic properties of human articular chondrocytes. J. Orthop. Res. 2004;22:131–139. doi: 10.1016/S0736-0266(03)00150-5. [DOI] [PubMed] [Google Scholar]
- 19.Shieh A.C., Athanasiou K.A. Biomechanics of single zonal chondrocytes. J. Biomech. 2006;39:1595–1602. doi: 10.1016/j.jbiomech.2005.05.002. [DOI] [PubMed] [Google Scholar]
- 20.Leipzig N.D., Athanasiou K.A. Unconfined creep compression of chondrocytes. J. Biomech. 2005;38:77–85. doi: 10.1016/j.jbiomech.2004.03.013. [DOI] [PubMed] [Google Scholar]
- 21.Lee D.A., Bader D.L. The development and characterization of an in vitro system to study strain-induced cell deformation in isolated chondrocytes. In Vitro Cell. Dev. Biol. Anim. 1995;31:828–835. doi: 10.1007/BF02634565. [DOI] [PubMed] [Google Scholar]
- 22.Mow V.C., Kuei S.C., Armstrong C.G. Biphasic creep and stress relaxation of articular cartilage in compression? Theory and experiments. J. Biomech. Eng. 1980;102:73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- 23.Armstrong C.G., Mow V.C. Variations in the intrinsic mechanical properties of human articular cartilage with age, degeneration, and water content. J. Bone Joint Surg. Am. 1982;64:88–94. [PubMed] [Google Scholar]
- 24.Athanasiou K.A., Rosenwasser M.P., Mow V.C. Interspecies comparisons of in situ intrinsic mechanical properties of distal femoral cartilage. J. Orthop. Res. 1991;9:330–340. doi: 10.1002/jor.1100090304. [DOI] [PubMed] [Google Scholar]
- 25.Schinagl R.M., Gurskis D., Sah R.L. Depth-dependent confined compression modulus of full-thickness bovine articular cartilage. J. Orthop. Res. 1997;15:499–506. doi: 10.1002/jor.1100150404. [DOI] [PubMed] [Google Scholar]
- 26.Tomkoria S., Patel R.V., Mao J.J. Heterogeneous nanomechanical properties of superficial and zonal regions of articular cartilage of the rabbit proximal radius condyle by atomic force microscopy. Med. Eng. Phys. 2004;26:815–822. doi: 10.1016/j.medengphy.2004.07.006. [DOI] [PubMed] [Google Scholar]
- 27.Stolz M., Raiteri R., Aebi U. Dynamic elastic modulus of porcine articular cartilage determined at two different levels of tissue organization by indentation-type atomic force microscopy. Biophys. J. 2004;86:3269–3283. doi: 10.1016/S0006-3495(04)74375-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kleemann R.U., Krocker D., Duda G.N. Altered cartilage mechanics and histology in knee osteoarthritis: relation to clinical assessment (ICRS grade) Osteoarthritis Cartilage. 2005;13:958–963. doi: 10.1016/j.joca.2005.06.008. [DOI] [PubMed] [Google Scholar]
- 29.Stolz M., Gottardi R., Aebi U. Early detection of aging cartilage and osteoarthritis in mice and patient samples using atomic force microscopy. Nat. Nanotechnol. 2009;4:186–192. doi: 10.1038/nnano.2008.410. [DOI] [PubMed] [Google Scholar]
- 30.Guilak F., Alexopoulos L.G., Setton L.A. Zonal uniformity in mechanical properties of the chondrocyte pericellular matrix: micropipette aspiration of canine chondrons isolated by cartilage homogenization. Ann. Biomed. Eng. 2005;33:1312–1318. doi: 10.1007/s10439-005-4479-7. [DOI] [PubMed] [Google Scholar]
- 31.Guilak F., Jones W.R., Lee G.M. The deformation behavior and mechanical properties of chondrocytes in articular cartilage. Osteoarthritis Cartilage. 1999;7:59–70. doi: 10.1053/joca.1998.0162. [DOI] [PubMed] [Google Scholar]
- 32.Alexopoulos L.G., Williams G.M., Guilak F. Osteoarthritic changes in the biphasic mechanical properties of the chondrocyte pericellular matrix in articular cartilage. J. Biomech. 2005;38:509–517. doi: 10.1016/j.jbiomech.2004.04.012. [DOI] [PubMed] [Google Scholar]
- 33.Alexopoulos L.G., Youn I., Guilak F. Developmental and osteoarthritic changes in Col6a1-knockout mice: biomechanics of type VI collagen in the cartilage pericellular matrix. Arthritis Rheum. 2009;60:771–779. doi: 10.1002/art.24293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Knight M.M., Ross J.M., Poole C.A. Chondrocyte deformation within mechanically and enzymatically extracted chondrons compressed in agarose. Biochim. Biophys. Acta. 2001;1526:141–146. doi: 10.1016/s0304-4165(01)00118-0. [DOI] [PubMed] [Google Scholar]
- 35.Kim E., Guilak F., Haider M.A. An axisymmetric boundary element model for determination of articular cartilage pericellular matrix properties in situ via inverse analysis of chondron deformation. J. Biomech. Eng. 2010;132:031011. doi: 10.1115/1.4000938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ludwig T., Kirmse R., Schwarz U.S. Probing cellular microenvironments and tissue remodeling by atomic force microscopy. Pflugers Arch. 2008;456:29–49. doi: 10.1007/s00424-007-0398-9. [DOI] [PubMed] [Google Scholar]
- 37.Radmacher M., Tillamnn R.W., Gaub H.E. From molecules to cells: imaging soft samples with the atomic force microscope. Science. 1992;257:1900–1905. doi: 10.1126/science.1411505. [DOI] [PubMed] [Google Scholar]
- 38.Gad M., Itoh A., Ikai A. Mapping cell wall polysaccharides of living microbial cells using atomic force microscopy. Cell Biol. Int. 1997;21:697–706. doi: 10.1006/cbir.1997.0214. [DOI] [PubMed] [Google Scholar]
- 39.A-Hassan E., Heinz W.F., Hoh J.H. Relative microelastic mapping of living cells by atomic force microscopy. Biophys. J. 1998;74:1564–1578. doi: 10.1016/S0006-3495(98)77868-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hofmann U.G., Rotsch C., Radmacher M. Investigating the cytoskeleton of chicken cardiocytes with the atomic force microscope. J. Struct. Biol. 1997;119:84–91. doi: 10.1006/jsbi.1997.3868. [DOI] [PubMed] [Google Scholar]
- 41.Rotsch C., Braet F., Radmacher M. AFM imaging and elasticity measurements on living rat liver macrophages. Cell Biol. Int. 1997;21:685–696. doi: 10.1006/cbir.1997.0213. [DOI] [PubMed] [Google Scholar]
- 42.Elkin B.S., Azeloglu E.U., Morrison B. Mechanical heterogeneity of the rat hippocampus measured by atomic force microscope indentation. J. Neurotrauma. 2007;24:812–822. doi: 10.1089/neu.2006.0169. [DOI] [PubMed] [Google Scholar]
- 43.Last J.A., Liliensiek S.J., Murphy C.J. Determining the mechanical properties of human corneal basement membranes with atomic force microscopy. J. Struct. Biol. 2009;167:19–24. doi: 10.1016/j.jsb.2009.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hu K., Radhakrishnan P., Mao J.J. Regional structural and viscoelastic properties of fibrocartilage upon dynamic nanoindentation of the articular condyle. J. Struct. Biol. 2001;136:46–52. doi: 10.1006/jsbi.2001.4417. [DOI] [PubMed] [Google Scholar]
- 45.Allen D.M., Mao J.J. Heterogeneous nanostructural and nanoelastic properties of pericellular and interterritorial matrices of chondrocytes by atomic force microscopy. J. Struct. Biol. 2004;145:196–204. doi: 10.1016/j.jsb.2003.10.003. [DOI] [PubMed] [Google Scholar]
- 46.Lewis N.T., Hussain M.A., Mao J.J. Investigation of nano-mechanical properties of annulus fibrosus using atomic force microscopy. Micron. 2008;39:1008–1019. doi: 10.1016/j.micron.2007.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Costa K.D., Yin F.C. Analysis of indentation: implications for measuring mechanical properties with atomic force microscopy. J. Biomech. Eng. 1999;121:462–471. doi: 10.1115/1.2835074. [DOI] [PubMed] [Google Scholar]
- 48.Park S., Costa K.D., Hong K.S. Mechanical properties of bovine articular cartilage under microscale indentation loading from atomic force microscopy. Proc. Inst. Mech. Eng. [H]. 2009;223:339–347. doi: 10.1243/09544119JEIM516. [DOI] [PubMed] [Google Scholar]
- 49.Engler A.J., Sen S., Discher D.E. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–689. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 50.Pelham R.J., Wang Y. Cell locomotion and focal adhesions are regulated by substrate flexibility. Proc. Natl. Acad. Sci. USA. 1997;94:13661–13665. doi: 10.1073/pnas.94.25.13661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Peyton S.R., Putnam A.J. Extracellular matrix rigidity governs smooth muscle cell motility in a biphasic fashion. J. Cell. Physiol. 2005;204:198–209. doi: 10.1002/jcp.20274. [DOI] [PubMed] [Google Scholar]
- 52.Engelmayr G.C., Sacks M.S. Prediction of extracellular matrix stiffness in engineered heart valve tissues based on nonwoven scaffolds. Biomech. Model. Mechanobiol. 2008;7:309–321. doi: 10.1007/s10237-007-0102-1. [DOI] [PubMed] [Google Scholar]
- 53.Di Benedetto F., Biasco A., Cingolani R. Patterning polyacrylamide hydrogels by soft lithography. Nanotechnology. 2005;16:S165–S170. [Google Scholar]
- 54.Snyder P.W., Johannes M.S., Toone E.J. Biocatalytic microcontact printing. J. Org. Chem. 2007;72:7459–7461. doi: 10.1021/jo0711541. [DOI] [PubMed] [Google Scholar]
- 55.Carrillo F., Gupta S., Puttlitz C.M. Nanoindentation of polydimethylsiloxane elastomers: effect of crosslinking, work of adhesion, and fluid environment on elastic modulus. J. Mater. Res. 2005;20:2820–2830. [Google Scholar]
- 56.Engler A., Bacakova L., Discher D. Substrate compliance versus ligand density in cell on gel responses. Biophys. J. 2004;86:617–628. doi: 10.1016/S0006-3495(04)74140-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Chen S.S., Falcovitz Y.H., Sah R.L. Depth-dependent compressive properties of normal aged human femoral head articular cartilage: relationship to fixed charge density. Osteoarthritis Cartilage. 2001;9:561–569. doi: 10.1053/joca.2001.0424. [DOI] [PubMed] [Google Scholar]
- 58.Guo S., Akhremitchev B.B. Packing density and structural heterogeneity of insulin amyloid fibrils measured by AFM nanoindentation. Biomacromolecules. 2006;7:1630–1636. doi: 10.1021/bm0600724. [DOI] [PubMed] [Google Scholar]
- 59.Youn I., Choi J.B., Guilak F. Zonal variations in the three-dimensional morphology of the chondron measured in situ using confocal microscopy. Osteoarthritis Cartilage. 2006;14:889–897. doi: 10.1016/j.joca.2006.02.017. [DOI] [PubMed] [Google Scholar]
- 60.Matsuo E.S., Orkisz M., Tanaka T. Origin of structural inhomogeneities in polymer gels. Macromolecules. 1994;27:6791–6796. [Google Scholar]
- 61.Coles J.M., Blum J.J., Zauscher S. In situ friction measurement on murine cartilage by atomic force microscopy. J. Biomech. 2008;41:541–548. doi: 10.1016/j.jbiomech.2007.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Wang C.C., Chahine N.O., Ateshian G.A. Optical determination of anisotropic material properties of bovine articular cartilage in compression. J. Biomech. 2003;36:339–353. doi: 10.1016/s0021-9290(02)00417-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Dean D., Han L., Ortiz C. Compressive nanomechanics of opposing aggrecan macromolecules. J. Biomech. 2006;39:2555–2565. doi: 10.1016/j.jbiomech.2005.09.007. [DOI] [PubMed] [Google Scholar]
- 64.Mow V.C., Ratcliffe A., Poole A.R. Cartilage and diarthrodial joints as paradigms for hierarchical materials and structures. Biomaterials. 1992;13:67–97. doi: 10.1016/0142-9612(92)90001-5. [DOI] [PubMed] [Google Scholar]
- 65.Chahine N.O., Wang C.C., Ateshian G.A. Anisotropic strain-dependent material properties of bovine articular cartilage in the transitional range from tension to compression. J. Biomech. 2004;37:1251–1261. doi: 10.1016/j.jbiomech.2003.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Hennerbichler A., Rosenberger R., Hennerbichler D. Biochemical, biomechanical and histological properties of osteoarthritic porcine knee cartilage: implications for osteochondral transplantation. Arch. Orthop. Trauma Surg. 2008;128:61–70. doi: 10.1007/s00402-007-0360-5. [DOI] [PubMed] [Google Scholar]
- 67.Fermor B., Christensen S.E., Weinberg J.B. Oxygen, nitric oxide and articular cartilage. Eur. Cell. Mater. 2007;13:56–65. doi: 10.22203/ecm.v013a06. discussion 65. [DOI] [PubMed] [Google Scholar]
- 68.Magnussen R.A., Guilak F., Vail T.P. Cartilage degeneration in post-collapse cases of osteonecrosis of the human femoral head: altered mechanical properties in tension, compression, and shear. J. Orthop. Res. 2005;23:576–583. doi: 10.1016/j.orthres.2004.12.006. [DOI] [PubMed] [Google Scholar]
- 69.Cao L., Youn I., Setton L.A. Compressive properties of mouse articular cartilage determined in a novel micro-indentation test method and biphasic finite element model. J. Biomech. Eng. 2006;128:766–771. doi: 10.1115/1.2246237. [DOI] [PubMed] [Google Scholar]
- 70.Stockwell R.A. The interrelationship of cell density and cartilage thickness in mammalian articular cartilage. J. Anat. 1971;109:411–421. [PMC free article] [PubMed] [Google Scholar]
- 71.Radmacher M., Fritz M., Hansma P.K. Imaging soft samples with the atomic force microscope: gelatin in water and propanol. Biophys. J. 1995;69:264–270. doi: 10.1016/S0006-3495(95)79897-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


