Abstract
Understanding the adaptations that allow species to live in temporally variable environments is essential for predicting how they may respond to future environmental change. Variation at the intergenerational scale can allow the evolution of bet-hedging strategies: a novel genotype may be favoured over an alternative with higher arithmetic mean fitness if the new genotype experiences a sufficiently large reduction in temporal fitness variation; the successful genotype is said to have traded off its mean and variance in fitness in order to ‘hedge its evolutionary bets’. We review the evidence for bet-hedging in a range of simple plant systems that have proved particularly tractable for studying bet-hedging under natural conditions. We begin by outlining the essential theory, reiterating the important distinction between conservative and diversified bet-hedging strategies. We then examine the theory and empirical evidence for the canonical example of bet-hedging: diversification via dormant seeds in annual plants. We discuss the complications that arise when moving beyond this simple case to consider more complex life-history traits, such as flowering size in semelparous perennial plants. Finally, we outline a framework for accommodating these complications, emphasizing the central role that model-based approaches can play.
Keywords: bet-hedging, conservative, diversifying, life history, germination, flowering
1. Introduction
Temporal variation acting at a multitude of scales is a universal feature of natural environments. For example, plant species experience variation in herbivore density and rainfall from one day to the next, and the average intensity of these factors fluctuates between years, whereas disturbance processes and climate fluctuations can alter the environment over much longer time scales. Along this gradient, variation on the scale of generation time has been a consistent focus of research in evolutionary biology, because these fluctuations can lead to intergenerational variation in vital rates (Hairston et al. 1996) and, by direct implication, fitness. All else being equal, theory predicts that selection will act to reduce temporal variation in fitness (Cohen 1966). In environments that exhibit reliable cues about their future state, species may evolve mechanisms that allow them to respond appropriately to prevailing conditions via phenotypic plasticity (Via & Lande 1985). However, when reliable cues for predicting environmental variation at the intergenerational scale are unavailable, individuals are forced to apply a life-history strategy without ‘knowing’ how it will impact future fitness. Under these conditions ‘evolutionary bet-hedging’ strategies may be selected for (Slatkin 1974). Such strategies achieve a decrease in temporal fitness variation at the expense of a reduction in average fitness.
The concept of bet-hedging developed independently in fields ranging from life-history evolution (Cohen 1966; Tuljapurkar 1990a) and demography (Tuljapurkar 1989) through to population genetics (Gillespie 1974). Accordingly, the theoretical basis for understanding the evolution of bet-hedging has been established for several decades (see Seger & Brockmann 1987 and references therein) and the basic mechanism—sacrificing mean fitness for a reduction in temporal fitness variation—can be realized by a wide variety of life-history adaptations. However, with the exception of dormant life stages, there are still remarkably few studies of bet-hedging strategies in a natural setting. Since climate change is expected to lead to increasingly variable environments (Karl & Trenberth 2003), bet-hedging characteristics may be a crucial determinant of species extinction risk, and therefore warrant further research. To this end, we review the theory and empirical evidence for the evolution of bet-hedging strategies in plants. Plants have a number of characteristics that make them an attractive focus for deepening understanding of bet-hedging in an empirical setting: individuals are easy to census; individual quality and fitness are often straightforward to quantify; and life histories are frequently relatively simple (semelparous), facilitating the development of life-cycle models, which opens the way to tackle a range of questions (Childs et al. 2003, 2004; Rees et al. 2004, 2006; Ellner & Rees 2006; Evans et al. 2007; Hesse et al. 2007; Kuss et al. 2008; Williams 2009).
We start by detailing the theory underlying bet-hedging, emphasizing the distinction between conservative and diversified bet-hedging strategies. We then review the canonical and best understood example—bet-hedging in annual plants via seed dormancy—in order to highlight the types and strength of evidence derived from theoretical and empirical approaches. Finally, we consider the complications and implications for studying bet-hedging traits in a natural setting, illustrating our ideas with a second case study: flowering size in semelparous perennial plants.
2. Bet-hedging theory
In evolutionary biology, it has long been recognized that both mean and variance in fitness are key determinants of long-term evolutionary success (Dempster 1955). The term ‘evolutionary bet-hedging’ (Slatkin 1974) was coined to cement the idea that evolution may proceed via a trade-off between the expected value and the variance of fitness of a genotype or life-history strategy (Seger & Brockmann 1987; Philippi & Seger 1989). This follows from the following theoretical observation: a novel genotype may be favoured over a resident genotype with higher arithmetic mean fitness if the new type experiences a sufficient reduction in temporal fitness variation; the successful genotype is said to have traded off its mean and variance in fitness. The potential for such a trade-off is a direct consequence of the geometric mean fitness concept (Dempster 1955). When fitness is temporally variable, the appropriate measure of evolutionary success is the expected geometric mean growth rate of a genotype. This is because fitness, like population growth, is an inherently multiplicative process that is very sensitive to occasional low values. A simple limiting case makes this clear. Recall that the geometric mean of n numbers is simply the product of those n numbers raised to the power 1/n. It follows that a genotype that experiences even rare occurrences of zero fitness has an expected geometric mean of zero and is ultimately destined for extinction, no matter how high its arithmetic mean fitness. More generally, we can understand the consequences of temporal variation by considering the stochastic growth rate of a genotype (or strategy),
where λt denotes realized fitness at time t, and E[ ] the expectation. Note that ρ is simply the log of the geometric mean fitness. Since the logarithm is a concave function, Jensen's inequality (Jensen 1906) guarantees that the stochastic growth rate is less than or equal to the arithmetic mean, so that the potential for bet-hedging via a mean–variance fitness trade-off inevitably follows.
This simple definition of bet-hedging, couched in terms of temporal fitness variation, is easy enough to comprehend in light of the geometric fitness concept. However, in order for empirical work to proceed, we need to consider measurable traits (or, more broadly, life-history strategies) that ultimately mediate the mean–variance fitness relationship. In their influential review, Seger & Brockmann (1987) identified two distinct classes of bet-hedging strategy. The first of these entails individual risk avoidance, while the second involves risk spreading among related individuals. These are typically referred to as conservative and diversified bet-hedging (Philippi & Seger 1989) in the contemporary literature, and the distinction is important for understanding bet-hedging strategies.
Conservative bet-hedging results from risk avoidance at the individual level; an individual sacrifices expected fitness in order to reduce temporal variance in fitness. Examples of potential conservative bet-hedging strategies include: (i) a semelparous perennial plant initiating flowering early in life to avoid an occasional high mortality year (Rees et al. 2004, 2006), or early within the growth season to avoid the seasons' end (Simons & Johnston 2003); and (ii) an iteroparous species storing limited resources (e.g. water in arid habitat) in order to mitigate future scarcity, instead of utilizing it immediately for reproduction and growth. In either case, we can only invoke bet-hedging if the putative conservative trait reduces arithmetic fitness in addition to decreasing temporal variation in fitness. For example, storing a fluctuating resource at the expense of current reproduction could feasibly extend lifespan, reducing the variance in fitness and increasing average fitness. In this case, adopting the language of bet-hedging theory to explain the storage adaptation is inappropriate. Similarly, many species are adapted to cope with unpredictable within-generation variation in their environment. For example, long-lived plants allocate resources to structural adaptations to allow them to survive occasional extreme weather events. While this could be labelled ‘conservative’, because individuals are ‘over-engineered’ for most circumstances, it almost certainly increases arithmetic mean fitness and is therefore not a bet-hedging trait. The key message here is that bet-hedging (both conservative and diversified) cannot be understood by examining trait values alone. Instead, an analysis of bet-hedging processes must be couched in terms of the mean–variance fitness trade-off to be valid (see Rees et al. 2010 for an example and further discussion of these issues).
Diversified bet-hedging entails probabilistic risk spreading among individuals of the same genotype. A diversified strategy allows cohorts of individuals of a particular genotype to sample a range of different environments through time. If the associated sampling process is costly—as a result of elevated mortality, for example—there is potential for genuine bet-hedging via a mean–variance fitness trade-off, because diversification reduces fitness variance at the genotype level (here the term ‘genotype’ is used casually to refer to progeny derived from the same mother). The canonical example of diversified bet-hedging is seed dormancy in annual plants (Cohen 1966); in highly disturbed environments, annuals plants can reduce their variance in fitness by ensuring that only a fraction germinate in any given year (see §3). In semelparous perennial species, similar diversification may be achieved via the formation of a ‘rosette bank’, whereby individuals of one genotype initiate flowering at a range of different ages so that their seeds are dispersed in time (Baskin & Baskin 1979; Kachi 1990; Rees et al. 2006). Even though individuals are subject to increased mortality as a consequence of the delay, dormancy (or delayed flowering) is selected because it reduces fitness variation at the genotype level. An important consequence of diversified bet-hedging is that, in contrast to conservative bet-hedging, it may in some cases actually increase the variance in fitness among individuals within a generation, such that individual-level analyses can be misleading. We argue that a model-based approach that focuses on life-history strategies is often required instead. We return to this assertion below.
In both examples given above, delayed germination and flowering, diversification can be conceptualized as occurring among progeny derived from one parent during a single bout of reproduction. This is diversification within cohorts, where the term ‘cohort’ refers to a group of individuals derived from the same reproductive event. A second mode of diversified bet-hedging involves diversification among cohorts. Under this scenario, parents vary the characteristics of their progeny stochastically across reproductive bouts, such that two individuals reproducing at the same time may produce offspring distributions with very different characteristics. This second mode of diversification was originally considered in the context of ‘adaptive coin-flipping’ models of diversification (Cooper & Kaplan 1982; Kaplan & Cooper 1984); conceptually, parents flip a coin each time they reproduce in order to decide their offspring trait distribution. The offspring trait may be continuous (e.g. seed size), in which case this type of diversification generates a phenotypic polymorphism, or it may be discrete, in which case a polyphenism is observed (Walker 1986). In any case, these strategies are maintained by essentially the same mechanism as diversification within cohorts. Some cohorts have high fitness in a particular natal environment, while others perform poorly. The strategy is selected because temporal fitness variation at the genotype level is reduced, at a cost of reduced mean fitness.
Unfortunately, the term ‘adaptive coin-flipping’ is occasionally used to label among-cohort diversification as distinct from other forms of diversification (Olofsson et al. 2009). This is misleading because ‘adaptive coin-flipping’ is really just another label for diversified bet-hedging. Indeed, the originators of the term have pointed out that their model of among-cohort diversification did not preclude other diversification strategies (Kaplan & Cooper 1988). There really are only two ways to hedge your evolutionary bets: be conservative or diversify.
3. The canonical example: seed dormancy in annual plants
To illustrate these ideas, we now examine the classic example of a diversified strategy, namely seed dormancy in annual plants (Cohen 1966). We first describe the theory and then discuss the types of evidence accumulated from natural systems. Annual plants typically occur in highly disturbed environments that vary dramatically from year to year, which means that when the ‘decision’ to germinate is made, a plant has no way of ‘knowing’ what the growing conditions are going to be: the year could be good for seedling establishment and reproduction, or might be terrible, with a long drought period in which most seedlings die. Cohen (1966) suggested that ‘One obvious way to survive and reproduce in a risky environment is to spread the risk so that one failure will not be decisively harmful’. For annual plants, one way of ‘spreading the risk’ is for the seeds of an individual plant to germinate in different years even if they all experience exactly the same environment.
Consider the following simple model for an annual plant with a seed bank:
where St is the density of seeds in year t, g is the probability a seed germinates, s the probability a seed survives in the seed bank and Ft seed production in year t, which we assume fluctuates randomly from year to year about some average value. The term Ft encompasses ‘within-year’ processes such as growth and survival of germinated plants up to adulthood and subsequent production of seeds. Average fitness  increases as g increases, so complete germination maximizes average fitness. Intuitively, the reason for this is that because seed production is fluctuating about some fixed average value, delaying germination cannot increase the mean seed production of a seed that germinates; this is always the same (E[Ft]), while seeds in the seed bank suffer some mortality; so the longer a seed delays germination, the lower average fitness will be. The variance in fitness is g2 Var(Ft), so the variance in fitness also increases as g increases. Therefore, if evolution favours an intermediate value of g, then this must be a result of bet-hedging as defined in §1: plants trade off losses in mean fitness against reductions in variance.
increases as g increases, so complete germination maximizes average fitness. Intuitively, the reason for this is that because seed production is fluctuating about some fixed average value, delaying germination cannot increase the mean seed production of a seed that germinates; this is always the same (E[Ft]), while seeds in the seed bank suffer some mortality; so the longer a seed delays germination, the lower average fitness will be. The variance in fitness is g2 Var(Ft), so the variance in fitness also increases as g increases. Therefore, if evolution favours an intermediate value of g, then this must be a result of bet-hedging as defined in §1: plants trade off losses in mean fitness against reductions in variance.
The optimal germination fraction in this model is found by maximizing the stochastic growth rate (or equivalently geometric mean growth rate; Cohen 1966; Ellner 1985), which is given by
The condition for some delay in germination (g < 1) to be optimal is sE[1/Ft] > 1, which is not very transparent, but we can approximate this, arriving at the following simple condition:
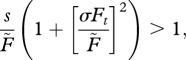 |
where σFt is the standard deviation of Ft. From this, we learn that the evolution of delayed germination is favoured by (i) high seed survival in the seed bank, which reduces the cost of delaying and (ii) high variability in the environment (σFt). In the simple case, when the environment fluctuates between good and bad, then the optimal germination fraction is equal to the probability of a good year (Cohen 1966), which means we should expect lower germination probabilities in harsh environments.
What types of evidence have been collected to determine whether bet-hedging can actually account for the evolution of delayed germination? First, long-lived seeds have been documented in plant species (Rees & Long 1993; Baskin & Baskin 1998; Grime 2002; Venable 2007), and similar life-history stages also occur in other taxa, such as insects (Hanski 1988; Gourbiere & Menu 2009) and crustaceans (Ellner & Hairston 1994). Interestingly, in these taxa, the reproductive stages are typically short-lived, and occur in ephemeral habitats, in agreement with the general theory. In plants there are at least two other possible explanations for the presence of long-lived seeds: (i) delayed germination is selected to resolve parent–offspring conflict (Ellner 1986) and (ii) seeds fail to germinate as a result of unfavourable conditions (Baskin & Baskin 1998). For the first mechanism to work, the population must be spatially structured, so competition occurs primarily between sibs. This is a possibility for plants with multi-seeded fruits; however, in general, it is unlikely to be the most important selection pressure selecting for seed dormancy. In contrast, germination is influenced by many aspects of the environment—such as light, light quality (spectral composition), temperature and temperature fluctuations, and nutrient levels (Baskin & Baskin 1998)—and the inability of seeds to germinate is undoubtedly a major factor resulting in the presence of long-lived seed banks.
Having said this, numerous studies have shown that in many species complete germination does not occur even under favourable conditions (e.g. Grime et al. 1981), suggesting an important role for bet-hedging. Moreover, many species show shifts in germination characteristics such that seeds that failed to germinate under ‘good’ conditions in their first year germinated under the same conditions in their second year (Philippi 1993). This naturally leads to the question of how parents make their offspring behave differently even when the offspring all experience the same environment. One simple mechanism is to produce seeds with varying characteristics. Again, there is abundant evidence for this; for example, there is often substantial seed mass variation within individuals (Michaels et al. 1988; Buckley et al. 2003). A more exciting possibility is that the extreme sensitivity of seeds to their environment allows individuals to achieve diversified germination strategies even in apparently homogeneous environments. Experimental studies have shown that germination is substantially influenced by the microtopography of the soil surface (Oomes & Elberse 1976) and seed orientation (Sheldon 1974), and recent work has shown that more than 30 per cent of the variation in the timing of germination is related to microgradients even within apparently homogeneous growth chambers (Simons & Johnston 2006).
Comparative analyses have also been used to explore the role of bet-hedging via delayed germination. The idea is that species with other life-history traits that ameliorate the effects of unfavourable years—such as long-lived, iteroparous adults, large seeds or efficient spatial seed dispersal—will have short-lived seeds. This idea is borne out by theoretical studies (Venable & Brown 1988; Rees 1994), and, in general, these predictions are supported by comparative studies (Thompson & Grime 1979; Rees 1993, 1996; Thompson et al. 1998). One major limitation of comparative studies is that the species are drawn from a wide range of habitats and disturbance regimes, making it difficult to separate the effects of changes in, say, adult longevity from habitat-related changes in disturbance effects (Rees 1993). In agreement with this, Thompson et al. (1998) demonstrated that habitat specialist species from stable communities such as woodlands have low seed persistence, while highly disturbed habitats, such as arable field and spoil, have high persistence.
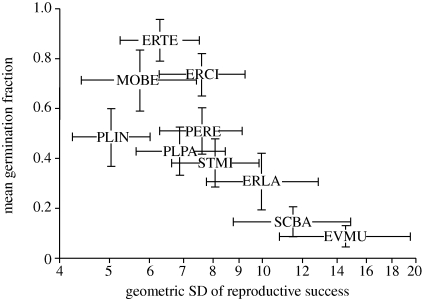
Comparative studies within habitats where fluctuations in demography have been measured are therefore much easier to interpret. Venable (2007) presents the results of a 22 year study of 10 desert annuals, and the results clearly conform to bet-hedging theory, with species that experience highly variable reproductive success having lower germination fractions (figure 1). We are only aware of two plant studies that have used a mathematical modelling approach to directly quantify the fitness consequences of delayed germination as a result of bet-hedging (Kalisz & McPeek 1993; Evans et al. 2007), and in both cases it was found that populations with delayed germination had higher stochastic growth rates than those without.
Figure 1.
Mean germination fraction of 10 species of desert annuals versus variation in per capita reproductive success. Codes indicate species names; see Venable (2007) for codes and a detailed description of the study.
4. Real-world complexities and challenges
The theoretical framework for understanding the role of diversified bet-hedging via dormant life stages has been established for over four decades, and in this time considerable evidence has accumulated to support this account of dormancy in plants and other taxa (Hanski 1988). These studies have been facilitated by the simplicity of annual species' life history. For example, there is a dominant source of temporal variation and individuals can be viewed as demographically homogeneous. In this section, we consider the challenges posed when these simplifying aspects of a life history are not present, and we broaden our discussion to include conservative bet-hedging traits, to which many of these challenges apply.
(a). Not all individuals are the same
A key assumption of Cohen's seed bank model for annual plants is that seeds are demographically homogeneous, in the sense that they experience the environment in the same way (i.e. variation in microsite availability and mortality in the seed bank are the same for all individuals). This ‘unstructured population’ assumption may be a safe approximation in many instances. When this is the case, fitness can be assayed directly by considering the mean and variance of seed production across years, and the bet-hedging trait of biological significance (seed dormancy) can be measured at the population level. However, in many settings, the assumption that all individuals are equivalent is no longer tenable. Most obviously, individuals differ in size within and among cohorts as a result of spatial and temporal variation in growth and herbivory. Typically, large individuals have higher survival and experience less temporal variation in survival than small ones (Rose et al. 2002; Metcalf et al. 2003). This in turn influences lifespan, which affects how a species responds to increases in environmental variability (Morris et al. 2008). By definition, studies of bet-hedging traits must be framed in terms of the long-term stochastic fitness of different strategies (or genotypes). Unfortunately, constructing an estimate of stochastic fitness directly from measurements of individual demography in a structured population setting is fraught with difficulties (Brommer et al. 2004), so instead we must rely on model-based approaches to quantify fitness.
(b). A single trait can mediate both types of bet-hedging response
In the context of bet-hedging theory, seed dormancy is unequivocally a diversification trait. For other traits, such unambiguous interpretation is not always possible. An explicit example, and one we will return to repeatedly, is flowering size in monocarpic (i.e. semelparous) perennial plants, henceforth referred to as ‘monocarps’. Flowering size in monocarps indirectly determines the timing of reproduction, because flowering at larger sizes implies an increased reproductive delay. This has important fitness consequences: flower too large and your risk of pre-reproductive mortality is significantly increased; flower too small and you fail to accrue the benefits of growth and increased seed production. In the context of bet-hedging theory, the key observation is that a group of individuals employing the same flowering-size strategy will flower in a range of different years, because individual growth trajectories differ. Since the variance in the age at flowering increases with flowering size, flowering at larger sizes reduces between-year recruitment variation (at the genotype level) by spreading reproduction across years, and can thus be interpreted as a diversifying strategy. However, when mortality also varies among years, delaying flowering puts individuals at risk of experiencing a high mortality year, and this selects for a conservative reduced size at flowering to reduce fitness variation. Timing of flowering may consequently mediate both conservative and diversified bet-hedging, and the evolution of this trait will be a balance between these components (Rees et al. 2004). In this example, we have assumed that adult plants make up a very small proportion of the community biomass, as is the case for the species we have studied (e.g. in Carlina vulgaris established individuals make up less than 1% of the community biomass), and so there is little direct link between their mortality and subsequent recruitment. For abundant species, years of high mortality are often followed by years of good recruitment, and in these cases variation in survival can select for delayed reproduction (Bulmer 1985; Kisdi & Meszena 1995).
(c). Multiple traits can mediate the same bet-hedging response
So far, we have considered bet-hedging in the context of a single trait (e.g. seed dormancy or delayed flowering). In reality, more than one trait may be involved in bet-hedging, even via the same pathway. In monocarps, delaying germination and delaying flowering are both examples of a diversified bet-hedging pathway, which spreads recruitment across years and reduces the variance in recruitment resulting from year-to-year fluctuations in recruitment success (Rees et al. 2006). Since both traits have essentially the same bet-hedging role, it is interesting to ask which should evolve. The answer is generally the most ‘efficient’ pathway. For example, if seed bank mortality is very high, then delaying flowering may reduce recruitment variance at lower cost to mean fitness than delaying germination (Tuljapurkar & Wiener 2000). Positive selection for two different pathways that mediate bet-hedging is also possible (e.g. selection for both iteroparity and a reproductive delay; Wilbur & Rudolf 2006), but generally reflects unusual life histories (e.g. where juvenile survival is greater than adult survival; Koons et al. 2008). Finally, it is important to recognize that in the presence of life-history trade-offs, the costs associated with a particular bet-hedging trait may be borne somewhere else in the life history. The key point is that to understand the selective role of temporal stochasticity, we must consider the complete life cycle.
(d). Stochasticity operates on multiple components of demography
Detailed analysis of Cohen's seed bank model is facilitated by the presence of a single source of temporal variation in the system (annual seed production). Once we move to consider more complex life histories, we need to account for the fact that variation operates on several components of demography simultaneously (e.g. growth, survival and recruitment), and because populations are structured by size, age and/or physiology, individual responses to this variation will differ. Stochastic variation in demographic components will increase variance in fitness (Tuljapurkar 1990b; Doak et al. 2005), which further complicates the role that particular life-cycle characteristics may play towards bet-hedging. Until now, we have focused on traits that relate to timing within the life cycle. We highlighted the idea that the optimal flowering delay in monocarps is shifted up or down by selection for diversified or conservative bet-hedging induced by variation in microsite availability and mortality, respectively. However, in addition to the selection they impose on timing traits, temporal variation and covariation among demographic components are in themselves subject to selection. Since temporal variation in these traits will typically reduce the stochastic growth rate (although see the next section), a reduction of their temporal variance is expected to evolve; a form of environmental canalization referred to as ‘demographic buffering’ (Pfister 1998). If this reduction is realized at a cost to arithmetic mean fitness, then demographic buffering can be viewed as a manifestation of conservative bet-hedging. There is an important corollary to this argument: negative covariation between stochastic fluctuations in traits may lead to selection for increased variation in particular traits (Doak et al. 2005).
(e). How variation is modelled can be critical
In Cohen's seed bank model, variation in annual seed production enters linearly. While this is typical for terms capturing recruitment variation, it is not true for other components of demography. Temporal variation in the probabilities of survival and reproduction is naturally modelled as logistic regressions, so these probabilities are nonlinear functions of time-varying regression parameters. Intuitively, we see that this nonlinearity follows from the fact that survival rates are bounded between zero and one (Morris & Doak 2004). Similar effects occur when modelling growth (Rees et al. 2004). When the relationship between a source of temporal variation and demographic rates is nonlinear, variation influences mean demographic rates through nonlinear averaging. This means that the impact of variation on both the mean and variance in fitness must be considered before any firm conclusions can be made about the role of bet-hedging. For example, life-history strategies that exhibit ‘demographic lability’ (i.e. demographic rates fluctuate freely with temporal changes in the environment) may be favoured over less labile strategies under some circumstances, because the increase in mean fitness that results from nonlinear averaging ameliorates fitness losses owing to increased temporal variation (Koons et al. 2009). Although driven by temporal environmental variation, this is clearly not evolutionary bet-hedging.
5. Accommodating real-world complexities
Given the intricacies of real-world life histories outlined above, simple verbal arguments are unlikely to help clarify the role of bet-hedging in natural systems. In the face of this difficulty, we argue that accurately parameterized population models are a crucial building block for establishing the role and relative importance of bet-hedging traits in natural populations. Appropriately constructed models naturally integrate the fitness consequences of temporal variation across the life history, including among-individual differences in variation and covariances between demographic rates (Tuljapurkar 1990b; Doak et al. 2005; Rees & Ellner 2009). With such a model in hand, we can employ standard tools from demography to quantify fitness and characterize selection on components of a life history (Metcalf & Pavard 2007). We now provide a brief overview of the modelling approaches and methods of analysis in use, and expand on approaches that have been most successful at untangling how selection for bet-hedging has shaped patterns of traits in natural systems.
In most natural plant systems, individuals vary in many ways (e.g. size, age and disease status), and this necessitates the development of a structured model. These come in several varieties, including matrix models, integral projection models (IPMs) and various types of physiologically structured models (Tuljapurkar & Caswell 1997). For each of these, there are now a wide range of tools for dissecting the impacts of temporal variation on fitness and also the evolution of traits. We illustrate this using the example of IPMs, the most suitable tool for many plant populations, since, unlike matrix models, they can accommodate continuous attributes such as size (Ellner & Rees 2006). The IPM framework is particularly powerful when demographic rates are influenced by multiple attributes, because the continuous response structure of the model facilitates simple regression modelling of trait–fate relationships.
Population growth in a stochastic IPM is most usefully characterized by the stochastic growth rate, usually denoted as log(λS), which is the structured population equivalent of the stochastic growth rate discussed earlier (Ellner & Rees 2007; Rees & Ellner 2009). Armed with this, we can characterize the stochastic population growth for populations with particular bet-hedging characteristics (for example, long or short flowering, or germination delays). Further, we can establish whether there is a particular flowering or germination strategy that, once established, cannot be invaded by any rare mutant strategies; this strategy is the evolutionarily stable strategy (ESS). ESSs identified using this approach very closely match observed flowering size and germination delays in three monocarpic plant systems (Childs et al. 2004; Rees et al. 2006; Ellner & Rees 2007).
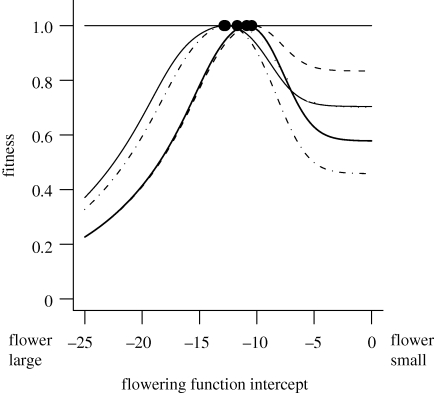
Although the match between predicted values and observed population characteristics is remarkable, the true value of this approach for understanding bet-hedging lies in the possibility of altering the strength of various components of environmental variation and exploring how this alters the ESS trait values. In essence, once a complete model for the system is available, a series of informative special cases can be developed, analysed and compared with this baseline case to tease apart the impact of different sources of stochasticity and nonlinear averaging on the ESS. For example, for C. vulgaris, a species where growth, survival and recruitment success vary from year to year, and density dependence acts primarily on recruitment, this approach reveals that different flowering strategies are affected by each component of stochasticity differently (figure 2). Detailed quantitative dissection of resulting patterns is possible: Rees et al. (2004) showed that the effects of nonlinear averaging and fluctuations in demography drive the ES flowering strategy in different directions, so the net effect of temporal variation in demography was much smaller than the absolute effect (10 versus 50%). The effect of fluctuations in recruitment is to select for larger sizes at flowering, which can be interpreted as diversifying bet-hedging, whereas fluctuations in growth and survival select for smaller sizes at flowering, which can be interpreted as conservative bet-hedging. This demonstrates that it is easy to substantially underestimate the effects of temporal variation unless all sources of variability are considered and the effects of nonlinear averaging are separated from fluctuations in demography.
Figure 2.
The fitness landscape for flowering strategies in C. vulgaris in the context of different types of environmental variation, obtained by eliminating stochastic elements from a model containing all observed sources of fluctuations (see text). Stochastic recruitment reduces the fitness of plants adopting a small-flowering strategy more than any other form of stochasticity, because small-flowering plants all flower at approximately the same age, and therefore this strategy will be least buffered against year to year fluctuations in recruitment. By contrast, stochastic variation in survival affects the fitness of small-flowering plants very little, since flowering early leaves them unexposed to many years of fluctuations. For large-flowering plants, stochastic recruitment and stochastic survival have very similar effects. See Childs et al. (2004) for a detailed description of the models. Dashed line, stochastic survival only; thin solid line, constant model; thick solid black line, fully stochastic model; dashed–dotted line, stochastic recruitment only.
6. Discussion
We believe there is now abundant empirical evidence for the role of bet-hedging in simple plant systems (annuals with seed banks and delayed flowering in monocarps). Numerous theoretical models also predict that bet-hedging should evolve in more complex life histories (Orzack & Tuljapurkar 2001), but at the moment empirical evidence for this is almost completely lacking. There is some evidence from comparative studies (Rees 1993, 1996), particularly for seed dormancy (Thompson et al. 1998). However, in many cases, interpretation is complicated by changes in habitat-specific disturbance rates. The modelling approaches we have outlined provide a possible way of bridging this gap, but there are formidable empirical and theoretical challenges. For example, in iteroparous species, in order to build sensible evolutionary models, we will have to quantify the cost of reproduction and how this influences future growth, survival and reproduction. This means that reliable measures of individual quality are required, which are notoriously difficult to obtain and are likely to change over the course of an individual's life. In such cases, rather complex system-specific statistical models may be required in order to identify the costs (Browne et al. 2007; Metcalf et al. 2009).
Even with a full demographic model encompassing individual heterogeneity, theoretically it is still not clear exactly how to identify bet-hedging in systems with complex life histories, especially when there is covariation between demographic rates (Doak et al. 2005). Such covariance might be a general feature of natural systems, acting via a range of mechanisms (e.g. years that are bad for growth of small plants might also be bad for large ones, or years that are bad for growth might also be bad for survival, or the traits might be linked by trade-offs). Linking traits to their effect on bet-hedging then becomes particularly difficult, since all the different pathways and their effect on both the mean and the variance in fitness need to be accounted for. The partitioning approach discussed above (see also Rees et al. 2006) for decomposing the effect of different sources of temporal variation on the ESS, although intuitively sensible, needs a firmer theoretical foundation. It is likely some of the approaches developed by Peter Chesson for analysing community dynamics in stochastic environments (e.g. Chesson 2003) could be adapted for this purpose, since these partition the long-term growth rate of a rare species (or, equivalently, life-history strategies) into a number of biologically meaningful terms. For discussions of the difficulties in identifying bet-hedging, even in simple systems, see Olofsson et al. (2009), Rees et al. (2010) and Ripa et al. (2010).
Recent advances in statistical approaches and the population modelling framework (Ellner & Rees 2007; Rees & Ellner 2009) provide a platform for further work precisely quantifying the evolution of reproductive delays (germination and flowering), but also reveal enormous potential for moving the focus beyond these well-known bet-hedging features to broaden the suite of traits examined. Candidate traits include: (i) vegetative dormancy, a strategy for which measurement of costs and benefits is relatively tractable, and which may be associated with diversified bet-hedging (Shefferson 2009); (ii) storage of below-ground biomass, which might operate as a conservative bet-hedging strategy in the face of unpredictable drought or herbivory (although, for the latter, difficulties associated with non-destructively measuring the trait are likely to be a serious obstacle); (iii) the evolution of growth and mortality rates (Rose et al. 2009); and (iv) offspring size—for example, Metz et al. (2010) have shown that larger-seeded species have higher mean and lower between-year variation in survival to reproduction. Beyond plant systems, evidence for diversification bet-hedging via dormant life stages is fairly well developed in insects (and echoes results on seed dormancy). However, for all other taxa, beyond speculation about the role of iteroparity and longevity (Wilbur & Rudolf 2006; Morris et al. 2008), very little is known about how bet-hedging may shape trait evolution. Many of the ideas outlined here may provide fruitful avenues of research.
Understanding which life-history settings favour diversifying versus conservative bet-hedging is a question that has largely been ignored. From a straightforward point of view diversification occurs when individuals have an opportunity to skip unfavourable years either by not germinating or flowering, or in iteroparous species reproducing multiple times. In contrast, conservative strategies are employed when the effects of environmental variability are inescapable. However, as bet-hedging strategies are explored in more complex models, this straightforward view may change and we may find that many traits, such as flowering size in monocarps, are under selection for both diversifying and conservative bet-hedging (Rees et al. 2004, 2006).
The physiological and functional mechanisms by which organisms achieve diversification are also largely unexplored. In monocarps, it is easy to see how diversification is achieved; variable growth means that individuals achieve the critical size for flowering at different ages, which automatically means that reproduction is spread across years. However, explaining why seeds that experience essentially the same environment have different germination characteristics is more difficult. All individuals should respond to reliable cues about the future environment and there is abundant evidence that seeds do this (Fenner & Thompson 2005). One simple way to ensure seeds do different things in apparently homogeneous environments is extreme germination sensitivity, and again there is a great deal of evidence for this (Baskin & Baskin 1998). One way for this to evolve is for seeds to exhibit responses to multiple environmental cues that vary over small spatio-temporal scales, but provide no information about the future environment; each seed then experiences a unique environment, which facilitates diversification. Whether this occurs in nature, or indeed is theoretically possible, are open questions.
In this review, we have highlighted the role that theoretical, comparative and, in particular, model-based approaches can play in studying bet-hedging processes in the field, and emphasized the range of challenges that must be overcome in future studies. We also outlined technical advances available to meet these challenges via model-based approaches, for which long-term data are essential. The power of such approaches lies in their ability not only to characterize variation, but also to partition its effects on traits. The techniques are general enough for application beyond plant systems—enabling the study of bet-hedging in a much wider range of systems than was previously possible (e.g. well-studied ungulates such as Soay sheep; Clutton-Brock & Pemberton 2004). This body of work will deepen our understanding of current patterns of traits in natural systems, and improve our capacity to identify characteristics that may shelter species or put them at risk in the face of increasing variation associated with changing environments.
References
- Baskin J. M., Baskin C. M.1979Studies on the autecology and population biology of the weedy monocarpic perennial, Pastinaca sativa. J. Ecol. 67, 601–610 [Google Scholar]
- Baskin C. C., Baskin J. M.1998Seeds: ecology, biogeography and the evolution of dormancy and germination. San Diego, CA: Academic Press [Google Scholar]
- Brommer J. E., Gustafsson L., Pietiainen H., Merila J.2004Single-generation estimates of individual fitness as proxies for long-term genetic contribution. Am. Nat. 163, 505–517 [DOI] [PubMed] [Google Scholar]
- Browne W. J., McCleery R. H., Sheldon B. C., Pettifor R. A.2007Using cross-classified multivariate mixed response models with application to life history traits in great tits (Parus major). Stat. Model. 7, 217–238 [Google Scholar]
- Buckley Y. M., et al. 2003Are invasives bigger? A global study of seed size variation in two invasive shrubs. Ecology 84, 1434–1440 (doi:10.1890/0012-9658(2003)084[1434:AIBAGS]2.0.CO;2) [Google Scholar]
- Bulmer M. G.1985Selection for iteroparity in a variable environment. Am. Nat. 126, 63–71 [Google Scholar]
- Chesson P.2003Quantifying and testing coexistence mechanisms arising from recruitment fluctuations. Theor. Popul. Biol. 64, 345–357 (doi:10.1016/S0040-5809(03)00095-9) [DOI] [PubMed] [Google Scholar]
- Childs D. Z., Rees M., Rose K. E., Grubb P. J., Ellner S. P.2003Evolution of complex flowering strategies: an age- and size-structured integral projection model. Proc. R. Soc. Lond. B 270, 1829–1838 (doi:10.1098/rspb.2003.2399) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Childs D. Z., Rees M., Rose K. E., Grubb P. J., Ellner S. P.2004Evolution of size-dependent flowering in a variable environment: construction and analysis of a stochastic integral projection model. Proc. R. Soc. Lond. B 271, 425–434 (doi:10.1098/rspb.2003.2597) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clutton-Brock T., Pemberton J.2004Soay sheep: dynamics and selection in an island population. Cambridge, UK: Cambridge University Press [Google Scholar]
- Cohen D.1966Optimising reproduction in a randomly varying environment. J. Theor. Biol. 12, 110–129 [DOI] [PubMed] [Google Scholar]
- Cooper W. S., Kaplan R. H.1982Adaptive coin-flipping—a decision-theoretic examination of natural-selection for random individual variation. J. Theor. Biol. 94, 135–151 (doi:10.1016/0022-5193(82)90336-8) [DOI] [PubMed] [Google Scholar]
- Dempster E. R.1955Maintenance of genetic heterogeneity. Cold Spring Harb. Sym. 20, 25–32 [DOI] [PubMed] [Google Scholar]
- Doak D. F., Morris W. F., Pfister C., Kendall B. E., Bruna E. M.2005Correctly estimating how environmental stochasticity influences fitness and population growth. Am. Nat. 166, E14–E21 [DOI] [PubMed] [Google Scholar]
- Ellner S.1985ESS Germination strategies in randomly varying environments. 1. Logistic-type models. Theor. Popul. Biol. 28, 50–79 (doi:10.1016/0040-5809(85)90022-X) [DOI] [PubMed] [Google Scholar]
- Ellner S.1986Germination dimorphisms and parent offspring conflict in seed-germination. J. Theor. Biol. 123, 173–185 (doi:10.1016/S0022-5193(86)80151-5) [Google Scholar]
- Ellner S., Hairston N. G.1994Role of overlapping generations in maintaining genetic variation in a fluctuating environment. Am. Nat. 143, 403–417 [Google Scholar]
- Ellner S. P., Rees M.2006Integral projection models for species with complex demography. Am. Nat. 167, 410–428 [DOI] [PubMed] [Google Scholar]
- Ellner S. P., Rees M.2007Stochastic stable population growth in integral projection models: theory and application. J. Math. Biol. 54, 227–256 (doi:10.1007/s00285-006-0044-8) [DOI] [PubMed] [Google Scholar]
- Evans M. E. K., Ferriere R., Kane M. J., Venable D. L.2007Bet hedging via seed banking in desert evening primroses (Oenothera, Onagraceae): demographic evidence from natural populations. Am. Nat. 169, 184–194 [DOI] [PubMed] [Google Scholar]
- Fenner M., Thompson K.2005The ecology of seeds. Cambridge, UK: Cambridge University Press [Google Scholar]
- Gillespie J. H.1974Natural selection for within-generation variance in offspring number. Genetics 76, 601–606 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gourbiere S., Menu F.2009Adaptive dynamics of dormancy duration variability: evolutionary trade-off and priority effect lead to suboptimal adaptation. Evolution 63, 1879–1892 (doi:10.1111/j.1558-5646.2009.00731.x) [DOI] [PubMed] [Google Scholar]
- Grime J. P.2002Plant strategies, vegetation processes, and ecosystem properties, 2nd edn.Chichester, UK: John Wiley & Sons, Ltd [Google Scholar]
- Grime J. P., Mason G., Curtis A. V., Rodman J., Band S. R., Mowforth M. A. G., Neal A. M., Shaw S.1981A comparative study of germination characteristics in a local flora. J. Ecol. 69, 1017–1059 [Google Scholar]
- Hairston N. G., Ellner S., Kearns C. M.1996Overlapping generations: the storage effect and maintenance of biotic diversity. In Population dynamics in ecological space and time (eds Rhodes O. E., Chesser R. K., Smith M. H.), pp. 109–145 Chicago, IL: University of Chicago Press [Google Scholar]
- Hanski I.1988Four kinds of extra long diapause in insects—a review of theory and observations. Ann. Zool. Fennica 25, 37–53 [Google Scholar]
- Hesse E., Rees M., Muller-Scharer H.2007Life-history variation in contrasting habitats: flowering decisions in a clonal perennial herb. Am. Nat. 172, E196–E213 [DOI] [PubMed] [Google Scholar]
- Jensen J. L. W. V.1906On the convex functions and inequalities between mean values. Acta Math. Djursholm 30, 175–193 (doi:10.1007/BF02418571) [Google Scholar]
- Kachi N.1990Evolution of size-dependent reproduction in biennial plants: a demographic approach. London, UK: Academic Press Limited [Google Scholar]
- Kalisz S., McPeek M. A.1993Extinction dynamics, population growth and seed banks—an example using an age-structured annual. Oecologia 95, 314–320 (doi:10.1007/BF00320982) [DOI] [PubMed] [Google Scholar]
- Kaplan R. H., Cooper W. S.1984The evolution of developmental plasticity in reproductive characteristics—an application of the adaptive coin-flipping principle. Am. Nat. 123, 393–410 [Google Scholar]
- Kaplan R. H., Cooper W. S.1988On the evolution of coin-flipping plasticity—a response to McGinley, Temme, and Geber. Am. Nat. 132, 753–755 [Google Scholar]
- Karl T. R., Trenberth K. E.2003Modern global climate change. Science 302, 1719–1723 (doi:10.1126/science.1090228) [DOI] [PubMed] [Google Scholar]
- Kisdi V., Meszena G.1995Life histories with lottery competition in a stochastic environment: ESSs which do not prevail. Theor. Popul. Biol. 47, 191–211 (doi:10.1006/tpbi.1995.1008) [Google Scholar]
- Koons D. N., Metcalf C. J. E., Tuljapurkar S.2008Evolution of delayed reproduction in uncertain environments: a life-history perspective. Am. Nat. 172, 797–805 [DOI] [PubMed] [Google Scholar]
- Koons D. N., Pavard S., Baudisch A., Metcalf C. J. E.2009Is life-history buffering or lability adaptive in stochastic environments? Oikos 118, 972–980 (doi:10.1111/j.1600-0706.2009.16399.x) [Google Scholar]
- Kuss P., Rees M., Aegisdottir H. H., Ellner S. P., Stocklin J.2008Evolutionary demography of long-lived monocarpic perennials: a time-lagged integral projection model. J. Ecol. 96, 821–832 (doi:10.1111/j.1365-2745.2008.01374.x) [Google Scholar]
- Metcalf C. J. E., Pavard S.2007Why evolutionary biologists should be demographers. Trends Ecol. Evol. 22, 205–212 (doi:10.1016/j.tree.2006.12.001) [DOI] [PubMed] [Google Scholar]
- Metcalf J. C., Rose K. E., Rees M.2003Evolutionary demography of monocarpic perennials. Trends Ecol. Evol. 18, 471–480 (doi:10.1016/S0169-5347(03)00162-9) [Google Scholar]
- Metcalf C. J. E., Stephens D. A., Rees M., Louda S. M., Keeler K. H.2009Using Bayesian inference to understand the allocation of resources between sexual and asexual reproduction. J. R. Stat. Soc. Ser. C Appl. Stat. 58, 143–170 (doi:10.1111/j.1467-9876.2008.00652.x) [Google Scholar]
- Metz J., Liancourt P., Kigel J., Harel D., Sternberg M., Tielbīger K.2010Plant survival in relation to seed size along environmental gradients: a long-term study from semi-arid and Mediterranean annual plant communities. J. Ecol. 98, 697–704 (doi:10.1111/j.1365-2745.2010.01652.x) [Google Scholar]
- Michaels H. J., Benner B., Hartgerink A. P., Lee T. D., Rice S., Willson M. F., Bertin R. I.1988Seed size variation: magnitude, distribution, and ecological correlates. Evol. Ecol. 2, 157–166 (doi:10.1007/BF02067274) [Google Scholar]
- Morris W. F., Doak D. F.2004Buffering of life histories against environmental stochasticity: accounting for a spurious correlation between the variabilities of vital rates and their contributions to fitness. Am. Nat. 163, 579–590 [DOI] [PubMed] [Google Scholar]
- Morris W. F., et al. 2008Longevity can buffer plant and animal populations against changing climatic variability. Ecology 89, 19–25 (doi:10.1890/07-0774.1) [DOI] [PubMed] [Google Scholar]
- Olofsson H., Ripa J., Jonzen N.2009Bet-hedging as an evolutionary game: the trade-off between egg size and number. Proc. R. Soc. B 276, 2963–2969 (doi:10.1098/rspb.2009.0500) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oomes M. J. M., Elberse W. T.1976Germination of 6 grassland herbs in microsites with different water contents. J. Ecol. 64, 745–755 [Google Scholar]
- Orzack S. H., Tuljapurkar S.2001Reproductive effort in variable environments, or environmental variation is for the birds. Ecology 82, 2659–2665 (doi:10.2307/2679944) [Google Scholar]
- Pfister C. A.1998Patterns of variance in stage-structured populations: evolutionary predictions and ecological implications. Proc. Natl Acad. Sci. USA 95, 213–218 (doi:10.1073/pnas.95.1.213) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philippi T.1993Bet-hedging germination of desert annuals—beyond the 1st year. Am. Nat. 142, 474–487 [DOI] [PubMed] [Google Scholar]
- Philippi T., Seger J.1989Hedging one's evolutionary bets, revisited. Trends Ecol. Evol. 4, 41–44 (doi:10.1016/0169-5347(89)90138-9) [DOI] [PubMed] [Google Scholar]
- Rees M.1993Trade-offs among dispersal strategies in British plants. Nature 366, 150–152 (doi:10.1038/366150a0) [Google Scholar]
- Rees M.1994Delayed germination of seeds—a look at the effects of adult longevity, the timing of reproduction, and population age/stage structure. Am. Nat. 144, 43–64 [Google Scholar]
- Rees M.1996Evolutionary ecology of seed dormancy and seed size. Phil. Trans. R. Soc. Lond. B 351, 1299–1308 (doi:10.1098/rstb.1996.0113) [Google Scholar]
- Rees M., Ellner S. P.2009Integral projection models for populations in temporally varying environments. Ecol. Monogr. 79, 575–594 (doi:10.1890/08-1474.1) [Google Scholar]
- Rees M., Long M. J.1993The analysis and interpretation of seedling recruitment curves. Am. Nat. 141, 233–262 [DOI] [PubMed] [Google Scholar]
- Rees M., Childs D. Z., Rose K. E., Grubb P. J.2004Evolution of size dependent flowering in a variable environment: partitioning the effects of fluctuating selection. Proc. R. Soc. Lond. B 271, 471–475 (doi:10.1098/rspb.2003.2596) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rees M., Childs D. Z., Metcalf J. C., Rose K. E., Sheppard A. W., Grubb P. J.2006Seed dormancy and delayed flowering in monocarpic plants: selective interactions in a stochastic environment. Am. Nat. 168, E53–E71 [DOI] [PubMed] [Google Scholar]
- Rees M., Jessica C., Metcalf E., Childs D. Z.2010Bet-hedging as an evolutionary game: the trade-off between egg size and number. Proc. R. Soc. B 277, 1149–1151 (doi:10.1098/rspb.2009.1541) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ripa J., Olofsson H., Jonzen N.2010What is bet-hedging, really? Invited reply. Proc. R. Soc. B 277, 1153–1154 (doi:10.1098/rspb.2009.2023) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rose K. E., Rees M., Grubb P. J.2002Evolution in the real world: stochastic variation and the determinants of fitness in Carlina vulgaris. Evolution 56, 1416–1430 [DOI] [PubMed] [Google Scholar]
- Rose K. E., Atkinson R. L., Turnbull L. A., Rees M.2009The cost and benefits of fast living. Ecol. Lett. 12, 1379–1384 (doi:10.1111/j.1461-0248.2009.01394.x) [DOI] [PubMed] [Google Scholar]
- Seger J., Brockmann J. H.1987What is bet-hedging? In Oxford surveys in evolutionary biology (eds Harvey P. H., Partridge L.). Oxford, UK: Oxford University Press [Google Scholar]
- Shefferson R. P.2009The evolutionary ecology of vegetative dormancy in mature herbaceous perennial plants. J. Ecol. 97, 1000–1009 (doi:10.1111/j.1365-2745.2009.01525.x) [Google Scholar]
- Sheldon J. C.1974Behavior of seeds in soil. 3. Influence of seed morphology and behavior of seedlings on establishment of plants from surface-lying seeds. J. Ecol. 62, 47–66 [Google Scholar]
- Simons A. M., Johnston M. O.2003Suboptimal timing of reproduction in Lobelia inflata may be a conservative bet-hedging strategy. J. Evol. Biol. 16, 233–243 (doi:10.1046/j.1420-9101.2003.00530.x) [DOI] [PubMed] [Google Scholar]
- Simons A. M., Johnston M. O.2006Environmental and genetic sources of diversification in the timing of seed germination: implications for the evolution of bet hedging. Evolution 60, 2280–2292 [PubMed] [Google Scholar]
- Slatkin M.1974Hedging ones evolutionary bets. Nature 250, 704–705 [Google Scholar]
- Thompson K., Grime J. P.1979Seasonal variation in the seed banks of herbaceous species in 10 contrasting habitats. J. Ecol. 67, 893–921 [Google Scholar]
- Thompson K., Bakker J. P., Bekker R. M., Hodgson J. G.1998Ecological correlates of seed persistence in soil in the north-west European flora. J. Ecol. 86, 163–169 (doi:10.1046/j.1365-2745.1998.00240.x) [Google Scholar]
- Tuljapurkar S.1989An uncertain life—demography in random environments. Theor. Popul. Biol. 35, 227–294 (doi:10.1016/0040-5809(89)90001-4) [DOI] [PubMed] [Google Scholar]
- Tuljapurkar S.1990aDelayed reproduction and fitness in variable environments. Proc. Natl Acad. Sci. USA 87, 1139–1143 (doi:10.1073/pnas.87.3.1139) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuljapurkar S.1990bPopulation dynamics in variable environments. London, UK: Springer-Verlag [Google Scholar]
- Tuljapurkar S., Caswell H.1997Structured-population models in marine, terrestrial, and freshwater systems. London, UK: Chapman & Hall [Google Scholar]
- Tuljapurkar S., Wiener P.2000Escape in time: stay young or age gracefully? Ecol. Model. 133, 143–159 (doi:10.1016/S0304-3800(00)00288-X) [Google Scholar]
- Venable D. L.2007Bet hedging in a guild of desert annuals. Ecology 88, 1086–1090 (doi:10.1890/06-1495) [DOI] [PubMed] [Google Scholar]
- Venable D. L., Brown J. S.1988The selective interactions of dispersal, dormancy, and seed size as adaptations for reducing risk in variable environments. Am. Nat. 131, 360–384 [Google Scholar]
- Via S., Lande R.1985Genotype–environment interaction and the evolution of phenotypic plasticity. Evolution 39, 505–522 (doi:10.2307/2408649) [DOI] [PubMed] [Google Scholar]
- Walker T. J.1986Stochastic polyphenism—coping with uncertainty. Fla. Entomol. 69, 46–62 [Google Scholar]
- Wilbur H. M., Rudolf V. H. W.2006Life-history evolution in uncertain environments: bet hedging in time. Am. Nat. 168, 398–411 [DOI] [PubMed] [Google Scholar]
- Williams J. L.2009Flowering life-history strategies differ between the native and introduced ranges of a monocarpic perennial. Am. Nat. 174, 660–672 [DOI] [PubMed] [Google Scholar]