Biophysical Coarse-Grained Modeling Provides Insights into Transport through the Nuclear Pore Complex

Abstract

The nuclear pore complex (NPC) is the gatekeeper of the nucleus, capable of actively discriminating between the active and inert cargo while accommodating a high rate of translocations. The biophysical mechanisms underlying transport, however, remain unclear due to the lack of information about biophysical factors playing role in transport. Based on published experimental data, we have established a coarse-grained model of an intact NPC structure to examine nucleocytoplasmic transport with refined spatial and temporal resolutions. Using our model, we estimate the transport time versus cargo sizes. Our findings suggest that the mean transport time of cargos smaller than 15 nm is independent of size, while beyond this size, there is a sharp increase in the mean transport time. The model confirms that kap-FG hydrophobicity is sufficient for active cargo transport. Moreover, our model predicts that during translocation, small and large cargo-complexes are hydrophobically attached to FG-repeat domains for 86 and 96% of their transport time, respectively. Inside the central channel FG-repeats form a thick layer on the wall leaving an open tube. The cargo-complex is almost always attached to this layer and diffuses back and forth, regardless of the cargo size. Finally, we propose a plausible model for transport in which the NPC can be viewed as a lubricated gate. This model incorporates basic assumptions underlying virtual-gate and reduction-of-dimensionality models with the addition of the FG-layer inside the central channel acting as a lubricant.

Introduction

All eukaryotic cells are compartmentalized by the nuclear envelope (NE) into a cytoplasm and a nucleoplasm. The exclusive pathway for the transport of cargos in and out of the nucleus is via the nuclear pore complexes (NPCs, Fig. 1) (1–3), which span the NE and perforate it such that the inner and outer nuclear membranes fuse together (4). The structural and biochemical aspects of the NPC have been recently examined in a comprehensive review by Jamali et al. (5). An exquisite example of selective transport, the NPC is one of the most complex translocational channels (6,7) and one of the largest supramolecular assemblies in eukaryotic cells (8,9). It is also suggested that the NPC is the most conspicuous structural feature of the NE (10) with the vitally important role of controlling all (supra)molecular traffic across the NE, though other roles have been investigated (11).

Figure 1.

Putative view of the NPC along with different biochemical factors. For a recent comprehensive review of biochemical and structural aspects of the NPC, see Jamali et al. (5).

A single NPC can accommodate a tremendous rate of transport: ∼1000 translocations/s, corresponding to a mass flow of ∼100 MDa/s (12). However, the exact mechanism underlying such high-throughput selective transport is a matter of debate, and several models have been proposed over the past decade (12–20). Shared by all models is the central role of natively unfolded phenylalanine-glycine (FG) repeat domains and their interactions with nuclear transport receptor (NTR). The distinction between models arises from different speculations about the nature of the FG-repeat domains and the way they interact with NTR.

While much is known about the biochemical pathways of nucleocytoplasmic transport, it seems that the role of biophysical factors has been largely underestimated in proposed models. For example, it was only recently that Lim et al. (17,21) suggested a mechanical basis for transport and that the eightfold symmetry of the spoke domains maximizes the overall bending stiffness of the NPC (22)—a fact that might be crucial for structural stability during the transport of large cargos, potentially preventing mechanical rupture of this supramolecular assembly. Biophysical factors are emerging as playing a critical role in nucleocytoplasmic transport, and we believe that a full understanding of the transport mechanism(s) cannot be achieved without considering such factors.

Various imaging techniques have revealed the architectural components of the NPC (23–26). The NPC components can be categorized based on their spatial locations into cytoplasmic, central, and nuclear region components (Fig. 2). The cytoplasmic region includes eight ∼50-nm cytoplasmic filaments and a cytoplasmic ring moiety. The central channel that is ∼90 nm in length encompasses the eightfold spoke domain, which is sandwiched between the cytoplasmic and nuclear ring. The channel exhibits an overall hourglass shape, which is ∼45–50 nm wide in the middle and expands to ∼70 nm at its edges. The nuclear part is composed of a nuclear ring featuring eight ∼75 nm rods inclined toward a distal ring to form the so-called nuclear basket (listed dimensions are for Xenopus oocytes). In addition, eight intranuclear filaments are attached at the distal ring. Although the overall dimensions of the yeast NPC are smaller than those of vertebrates, NPCs are conserved among different species in that they mostly show an octagonal shape with a strong 822 symmetry (that is, an eightfold symmetry relative to the central axis and twofold symmetry relative to the central plane) (4,27,28).

Figure 2.

Different components of the NPC along with their sizes. Cytoplasmic filaments, cytoplasmic ring, central channel, nuclear ring, nuclear basket, distal ring, and intranuclear filaments are depicted. Dimensions are for Xenopus oocyte (23,41).

The building blocks of the NPC are a family of proteins called nucleoporins (nups). Proteomic analysis has revealed ∼30 different nups for yeast and vertebrate with a total species-dependent mass of ∼44 MDa and ∼60 MDa, respectively (29). Nearly one-third of nups contain the hydrophobic, natively unfolded FG-repeat motifs (30,31), which are believed to play the key role in the transport of cargos through the NPC.

While cargos smaller than ∼5–9 nm can passively diffuse trough the NPC, larger cargos up to ∼39–40 nm actively transport through the pore (32–34), which only occurs if they are bound to a nuclear transport receptor (NTR). Inert cargos that are not small enough to passively diffuse, and lack NTRs to actively transport, are prohibited by the NPC from entering the nucleus.

Transport is a selective, signal-dependent process in which the complex of the cargo and NTR cargo-complex (also called the active cargo) bind together via a nuclear localization/export signal, respectively, for import/export. The best-known class of NTRs are soluble proteins known as the superfamily of karyopherins (35), within which importins α and β (kap-α and kap-β) have been studied extensively and are characterized better than other members of the family (13,32,35–40). Most signal-bearing cargos are carried via kap-β-family receptors (14,20). Interacting with FG-repeats, kap escorts the cargo along the pore all the way to the destination compartment, where its dissociation from the cargo is triggered by RanGTP/GAP (import/export) via a conformational change (20).

Taking into account currently known biophysical principles, in this work we present a coarse-grained model for the NPC. Our model attempts to closely incorporate experimentally observed parameters such as the dimensions (23,41) and elasticity of the NPC structure (a consequence of NE elasticity (42,43)), hydrophobic interactions between kap-β and FG-repeats (44), localization of binding spots on the convex surface of kap-β (45,46), inter-FG-repeat hydrophobic interactions in the central channel (16), the estimated density of FG-domains within the NPC (44,46), and the wormlike chain (WLC) nature of FG-repeats (47). We aim to predict the consequence of these features on cargo transport. Based on this model, we investigate roles of several biophysical factors, including cargo size, kap-FG hydrophobicity, and polymer mechanics of FG-repeats in transport selectivity and efficiency.

Materials and Methods

Based on the dimensions and mass of the Xenopus oocyte NPC (23,41), the bead-spring model (48) was employed to discretize the NPC structure (Fig. 3). The Brownian dynamics simulation was then performed, using reduced units of 1 k_BT for energy, 1 nm for length, and 0.1 ns for time (other values are reported based on these units hereafter).

Figure 3.

Initial configuration of our coarse-grained model of the NPC with FG-repeats (solid strings) attached to cytoplasmic filaments all the way to nuclear basket. (a) Magnification of a section of the cytoplasmic filament: the linear springs are depicted. A harmonic bending potential energy is also applied between each two consecutive bonds. (b) Magnification of a section of an FG-repeat: the FG-repeats are modeled as beads and series of discrete WLC springs. (Dashed line) Arbitrary configuration of the chain. The value r represents the end-to-end length of a spring.

Adjacent beads are bonded together via linear (Hookean) or nonlinear (wormlike chain) springs, depending on whether they are in the NPC backbone or FG-repeat domains. The elastic backbone of the NPC (22) is composed of linear springs with an elasticity equal to the mean value reported for the nuclear envelope, i.e., 17 kPa (43). The natively unfolded (31) filamentous (16) FG-repeat domains are modeled as discrete WLC springs with a persistence length of l_p = 0.43 nm (47), and the following force-law between neighboring beads i and j,

$$F\left(r_{ij}\right)=\frac{k_{\text{B}}T}{l_p}\left[\frac{1}{4}{\left(1-\frac{r_{ij}}{d{L}_c}\right)}^{-2}-\frac{1}{4}+\frac{r_{ij}}{d{L}_c}\right],$$ (1)

where dL_c is the contour length of the bonding spring.

The contour length of individual repeats is estimated to be between 50 nm and 200 nm (16), with longer FG-repeats supposedly localized to peripheral nups (17). In our model, we consider 50 nm FG-repeats localized to the central channel and 200 nm repeats in the peripheries. In fact, WLC springs play the role of hydrophilic linkers in FG-repeat domains.

In addition to the elastic extension between beads, the following bending potential energy is applied between consecutive bonds to take into account the bending stiffness of the NPC structure,

$$U_{ijk}^{Bend}=\frac{1}{2}b{\left[\cos \left({\theta }_{ijk}\right)-\cos \left({\theta }_{ijk}^0\right)\right]}^2,$$ (2)

where b is the bending force constant and ${\theta }_{ijk}^0$ is the equilibrium angle.

The hydrophobic cohesiveness within the central channel FG-nups (12,16,49–51), as well as the hydrophobic interaction between the cargo-complex and FG-repeats, are modeled by the long-range attractive potential energy (52) with cutoff radius 10.0,

$$U_{ij}^{hyd}=-2\gamma e^{-rij/\lambda },$$ (3)

where γ represents the hydrophobic affinity strength and λ is the characteristic length-scale. For FG-FG hydrophobic interactions, γ = 1.5 and λ = 1.0; and for kap-FG, those values are 2.0 and 1.5, respectively. Consistent with experiments (38,45,53), eight binding spots are localized to the convex surface of kap-β (Fig. 4). While it has been suggested that the various binding spots may have different affinities for FG-domains (44), we deemed it reasonable to give all sites the same affinity for simplicity of the model, given the scope of our investigation.

Figure 4.

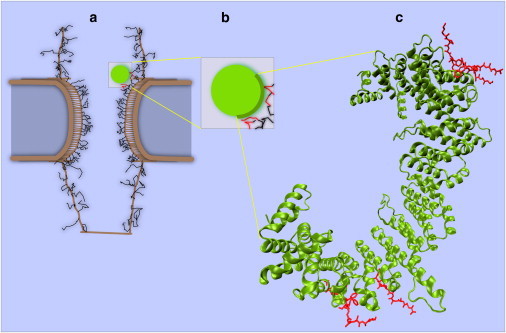
Snapshot of a cargo-complex interacting with FG-repeat domains. (a) Cargo-complex interacting with FG-repeats during transport via hydrophobic affinity between kap-β and FG-domains. Interactions are limited to the half-circle of the right side of the cargo-complex. In visualization, when a kap-FG hydrophobic interaction is active, the color of the cargo-complex becomes green and the corresponding FG-repeats become red (see Movie S1). (b) Magnification of cargo-complex along with interacting FG-repeats in its vicinity. Short-range repulsive potential energy between cargo-complex surface and FG-repeats prevents them from penetrating each other. A half-circle on the right side of the cargo-complex represents the boatlike shape of kap-β. (c) Crystal structure of the kap-β (green) interacting with FG-repeats (red) on its convex surface (1F59 in the Protein DataBank). Our supposition that kap-β is a half-circle matches well with this structure.

To take into account excluded volume effects and steric repulsions, the repulsive potential is introduced (54) as

$$U_{ij}^{rep}=\varepsilon e^{\frac{-rij}{\sigma }},$$ (4)

where ɛ = 100, σ = 1.0, and the cutoff radius is 1.35.

The Langevin equations of motion under the diffusive regime are then solved explicitly forward in time for each bead i (55) as

$${\zeta }_i\frac{dri}{dt}=F_i\left(t\right)+f_i^B\left(t\right)$$ (5)

in which the inertial term is neglected. ζ_i is the friction coefficient of bead i and is related to its hydrodynamic radius and intracellular viscosity. F_i is the total conservative force acting on bead i and f^B_i is the Brownian force with a Gaussian distribution and a zero mean (56). Integration of Eq. 6 leads to the numerical equation of motion in one direction (55),

$$x_i\left(t+\delta t\right)=x_i\left(t\right)+\frac{1}{{\zeta }_i}{F}_i^x\left(t\right)\delta t+{\Lambda }_{\mathit{i}},$$ (6)

where Λ_i is the random displacement due to the Brownian force, and δt = 0.1 (for more details of the model and the rationale behind it, see Moussavi-Baygi et al. (57)).

Results

Transport of a single cargo-complex with and without hydrophobicity

As a first step in evaluating our model, we looked into the transport of a single active cargo having a diameter of 15 nm. We carried out 150 independent simulations and took the average of the transport times. The initial conditions in all simulations are the same, and before each simulation the system is equilibrated for 80 μs. Simulation is continued until the cargo reaches the nucleus and is completely loaded in the nuclear basket. When there is no crowding of cargos in the pore, as is in our simulations, we obtained a transport time of 2.6 ± 0.22 ms (mean ± SE). (See Discussion for a comparison with experimentally reported values. Also, see Movie S1 in the Supporting Material.)

Next, we evaluated the model behavior for inert cargos, which lack affinity for FG-repeat domains. Therefore, we removed binding spots from the cargo surface and repeated the same set of simulations. We carried out 56 independent simulations, each of which was for up to 8 ms of real-time simulation. In our model, the longest time an active cargo of 15 nm needs to translocate through the NPC is 8 ms. Therefore, we continued each simulation of inert cargo up to 8 ms to investigate whether an inert cargo can pass in the same timescale as an active cargo.

Expectedly, the chance of the inert cargo entering the NPC and diffusing to reach the nucleus is dramatically reduced within this timeframe (see Movie S2). We observe that 93% of inert cargos are effectively prevented from traversing the NPC and reaching the nucleus. However, 75% can enter the NPC cytoplasmic periphery and diffuse to meet the cytoplasmic ring, but ultimately are repelled back to the cytoplasm.

Transport time increases nonlinearly with increasing cargo size

To further characterize the role of the size in transport, we varied the active cargo size and investigated its effects on the mean transport time. The minimum and maximum size of the cargo-complex are reportedly 5–9 nm and 39–40 nm, respectively (12,32–34). Therefore, we chose different diameters ranging from 5 nm to 30 nm. For every cargo size, 50 independent simulations with the same initial conditions were performed and the estimated transport times were averaged. Before each simulation, the system was equilibrated for 80 μs.

Before running simulations, it seemed reasonable to expect a continuous increase in the mean transport time with respect to the cargo size. Remarkably, we observed that for sizes up to 15 nm, the mean transport time is ∼2.7 ± 0.29 ms (mean ± SE), and is almost independent of size (Fig. 5). For larger cargo, however, we found

• 17 nm, 3.03 ± 0.34 (mean ± SE) ms,

• 20 nm, 3.30 ± 0.31 (mean ± SE) ms,

• 23 nm, 4.2 ± 0.33 (mean ± SE) ms,

• 25 nm, 4.7 ± 0.42 (mean ± SE) ms,

• 27 nm, 5.2 ± 0.60 (mean ± SE) ms, and

• 30 nm, 7.1 ± 0.60 (mean ± SE) ms.

We did not go beyond 30 nm because of the significant increase in computational cost. For cargos larger than 30 nm, it is conceivable that the NPC backbone may assist in translocation by its elastic deformation and providing more room for the cargo (58).

Figure 5.

Dependency of transport time on size of the cargo-complex (average time mean ± SE). When the cargo size exceeds 15 nm, a sharp increase in time is observed.

During transport, the cargo-complex is mainly attached to FG-repeat domains

We also measured the average time that the cargo-complex is hydrophobically interacting with FG-repeat domains during translocation. From this, the fraction of transport time that the cargo-complex is attached to FG-repeat domains can be readily calculated. Notably, it was observed that this fraction is a function of the cargo size and varies from 86% to 96% as the cargo size increases from 5 nm to 30 nm (Fig. 6). This means that during translocation, on average, a small cargo-complex is attached to FG-repeats for 86% of its total transport time while a large cargo-complex is attached for 96% of its total transport time. However, the situation within the central channel is different. Within the central channel, a small cargo-complex attaches to FG-repeats for 97% of its time, whereas a large cargo-complex attaches for 99.8% of its time (Fig. 6). This is, to our best knowledge, the first quantitative values showing what percentage of transport time a cargo-complex is engaged with FG-repeats in different zones. A typical presence contour of a 15 nm cargo-complex is shown in Fig. 7 b, while the average trajectories of cargo-complexes with different sizes are shown in Fig. 8. Both figures show that within the central channel, most of the time cargos are adhered to the wall and hence paths of their right-hand edges coincide. Note that in our model the kap-β is bound to the right-hand edge of the cargo (see Fig. 4).

Figure 6.

Attachment of the cargo-complex to FG-repeats during transport as a function of size. The red graph shows how much of the transport time, the cargo-complex is hydrophobically attached to FG-repeats. During translocation, small and large cargo-complexes are attached to FG-repeats for 86% and 96% of their transport time, respectively. The black graph shows similar information when the cargo-complex is inside the central channel. When the cargo-complex is inside the central channel, it is almost always attached to the FG-layer. Small and large cargo-complexes attach 97% and 99.8% of their time inside the channel to FG-layer, respectively. (Points) Simulation results. (Solid lines) Linear fit.

Figure 7.

Typical presence contour of an (a) inert and (b) active cargo as well as (c) FG-repeat domains in the course of simulation. The brightness is proportional to presence time. (a) Gray contour shows the typical presence of an inert cargo during ∼8 ms. To obtain this pattern, 10,000 snapshots were superimposed. The brighter the color, the more time is spent in that region. As it can be seen, inert cargo is rejected by cytoplasmic and central FG-repeats. Although it can reach the entry of the central channel, it is finally rejected (see Movie S2). FG-repeat domains are removed for the sake of clarity. Cytoplasmic filaments and nuclear rods are chosen from 20 frames during transport. (b) (Green) Contour of the active cargo presence in different locations during transport. It is obtained by superimposing of more than 3100 frames during a ∼2.7-ms import. Note that, the brighter the color, the greater the portion of transport time that is spent in that region. It can be seen that the active cargo spends more time in the central channel, especially in its upper part (see Movie S1). Sporadic detachments of cargo from the FG-domains can be distinguished by observing the dimmer protrusions from the main path. (Yellow lines, top) Wavy motions of cytoplasmic filaments from 20 frames of the same simulation. The movement of the nuclear rods of the basket is also shown (bottom), which corresponds to the same 20 frames. The central channel is shown only by one frame and FG-repeat domains are removed for the sake of clarity. (c) The area covered by FG-repeat domains in the cytoplasmic periphery, central channel, and nuclear periphery is obtained by superimposing of the same 3100 frames (shown in red). Note that the brightness of the red color shows the average presence of FG-repeats over time. FG-repeats with the help of wavy motions of cytoplasmic filaments and nuclear rods can span a wide area in the cytoplasmic and nuclear peripheries during transport, resembling a nonuniform cloud which is more dense near the filaments (and rods). This can effectively reject inert cargos while attracting active cargos. (Transparent yellow) Pliable cytoplasmic filaments and nuclear basket.

Figure 8.

Average trajectories of (a) centers-of-mass and (b) right edges of cargo-complexes with different sizes. Each trajectory is averaged over, at least, 50 independent simulations. As it can be seen, the cargo-complex, regardless of its size, is almost always attached to the channel wall. However, outside the channel, specifically in the nuclear basket, it has more fluctuations and detaches more repeatedly from the FG-repeats. Because the cargo-complex interacts with FG-repeats via its right-hand edge (see Fig. 4), in panel b) the right-hand edges' trajectories of different sizes overlap, specifically inside the central channel. The high degree of detachments inside the nuclear basket is because the cargo releases there and loses its hydrophobic affinity for FG-repeats. Cytoplasmic filaments and nuclear rods are chosen from 20 frames during a typical transport (shown in transparent gray). Central channel wall (red). FG-repeat domains are removed for the sake of clarity.

Discussion

Consistency of the model with available observations

Our model predicts that the mean transport time of a single active cargo smaller or equal to 15 nm is ∼2.7 ms. This is consistent with values of 6–10 ms reported by single molecular imaging techniques (30,59). The two- to fourfold decrease in our approximated transport time can be attributed to the cargo crowding that is absent in the model. The molecular crowdedness is shown to increase the diffusion time of macromolecules within the cytoplasm up to fourfold (60). Therefore, one can imagine that, in the absence of such effects inside the NPC, the transport time may decrease to the observed 1.5–2.5 ms here.

Inert cargos, on the other hand, do not bind to the kap and thus lack hydrophobic affinity for FG-repeats. Hydrophobic affinity is known to be a defining player in selectivity. By removing hydrophobicity from the cargo surface, our model predicts that the transport events are reduced to 7%. Strikingly, a recent single-molecule imaging with the spatiotemporal resolution of 9 nm/400 μs confirmed that inert cargos have a very low transport rate through the NPC, and only 10% of them were found on the nuclear side of the NPC (61). This is in a good agreement with a recent in vitro observation that proposes hydrophobicity of the cargo surface is sufficient to overcome the selectivity barrier across the NPC (44). In line with this, it is also shown that FG-functionalized membrane is permeable to the NTRs and NTR-bound cargos, but simultaneously much less permeable to inert cargos (62). These consistencies lend confidence in predictions made by the model.

Different biophysical factors in selectivity barrier: size, hydrophobicity, and reduction-of-dimensionality

For active cargos smaller than or equal to 15 nm, the mean transport time is almost insensitive to the size, implying that in this range, the cargo size is not a factor in transport efficiency or selectivity. Instead, kap-FG hydrophobicity is a more decisive factor. Thus, cargos without hydrophobicity are largely prevented from entering the nucleus on the same timescale. However, beyond 15 nm, transport becomes sensitive to size and a supralinear increase in the mean time is observed, indicating that the cargo size is a factor in transport efficiency for large cargos (see Fig. 5).

The increase in transport time of a large cargo-complex is partly due to its lower diffusion coefficient, which imposes a longer time on the diffusive translocation. In addition, the time increase can be attributed to the formation of a thick FG-layer on the channel wall that makes the available space limited and adds to the entropic cost that a large cargo-complex should pay to be able to pass the central channel. A small cargo-complex, however, does not encounter the limited space within the tube, and thus, it does not pay the entropic cost as a large cargo does.

To the best of our knowledge, this is the first quantitative report on the dependence of active transport time on the cargo size (see Fig. 5). Nonetheless, the mean transport time of a single cargo-complex (smaller than 15 nm) is measured to be 6–10 ms (30,59). Furthermore, Ribbeck and Görlich (49) found that large cargos drastically hinder NPC passage and thus the transport time is prolonged. Moreover, based on their in-vitro rate analysis, Lyman et al. (63) reported the bulk import rate of small and large cargos separately. In addition, based on the hypothesis of the selective phase model, Frey and Görlich (64) measured the diffusion time of inert and active cargo through an FG hydrogel. Nonetheless, none of these studies obtained an explicit pattern showing how the mean transport time varies with cargo size.

In addition, the model predicts that most often during translocation, the cargo-complex is attached to FG-repeats. This is further evidenced by a recent experimental study in which both cargo-free and cargo-bound kap-β were found mainly at channel inner wall (61). This observation is also compatible with the reduction-of-dimensionality model in which the kap-β is suggested to function as a ferry that carries cargo by sliding over a layer of FG-motifs lining the interior side of the pore (15). Our finding is, however, more comprehensive than the reduction-of-dimensionality in that it examines the cargo size effects on detachment probability in different regions of the NPC (57).

Out of 100 snapshots, a small cargo detaches, on average, 14 times from FG-repeats while a large cargo detaches only four times (see Fig. 6). This is because a small cargo diffuses faster than a large cargo in the viscous environment of the NPC and is more likely to detach. Nevertheless, within the central channel the probability of detachment from the FG-layer decreases for both small and large cargos, and they are almost always attached to the FG-layer for >95% of time. This can be attributed to the higher density of FG-repeats in the central channel compared to NPC peripheries. This higher density leads to occupation of almost all binding spots on the cargo-complex surface, and therefore, the cargo-complex is attracted by a larger hydrophobic force compared to when it is within the NPC peripheries. For other factors that might play a role in nucleocytoplasmic transport, see the Supporting Material.

A plausible mechanism for transport

In a recent study, four different models for the nucleocytoplasmic transport, i.e., reduction-of-dimensionality, virtual-gate, selective-phase, and “forest” models are compared (65). The reduction-of-dimensionality supposes that a layer of FG-motifs lines the NPC interior from cytoplasmic filaments to the nuclear face. The virtual gate suggests that the noncohesive FG-repeats form entropic bristles at the NPC peripheries. The selective phase hypothesizes that cohesive meshwork of FG-repeats constructs a channel-filling hydrogel inside the central channel, which is reversibly dissolved by NTRs, and thus, cargo-complexes can pass through it. Inert cargos, which are not bound to NTR, cannot traverse the gel. The forest model assumes that FG domains are structurally heterogeneous with two distinct conformations of collapsed-coil and extended-coil. Accordingly, FG-nups are categorized into “shrubs” having collapsed conformation and “trees” having a collapsed-coil on top of an extended-coil. This leads to formation of a central and lateral route inside the central channel, preferably for large and small cargos, respectively. In summary, discrepancies in the NPC behavior in these (14,15,18,49,65) and some other (17,20) models stem from assuming different structures formed by FG-nups.

FG-repeats in our model have some overlaps with the first three models (i.e., reduction-of-dimensionality, virtual-gate, and selective-phase) but not with the forest model. This is because for simplicity, we ignore the structural heterogeneity of FG-nups and consider homogenous FG-repeats in the peripheries as well as the central channel. Nonetheless, in our model, peripheral FG-repeats are noncohesive, which is consistent with the virtual gate, while the central FG-repeats are hydrophobically cohesive, in harmony with the selective phase. However, our model does not support formation of a channel-filling hydrogel as the selective phase does; instead, the gel is formed as a thick layer on the interior wall (see the Supporting Material for details) over which the cargo-complex diffuses. This picture is in agreement with the reduction-of-dimensionality.

Regardless of the cargo size, the main difference between an active and a passive cargo lies in their hydrophobic affinity for FG-repeat domains. Because the inert cargo lacks affinity for FG-nups, it is easily repelled near the NPC periphery by cytoplasmic filaments and FG-repeats. Thus, the inert cargo spans, randomly, a much wider area compared to the active cargo, and therefore, its chance to transport drastically decreases (see Fig. 7 a). Remarkably, consistent with this, in a recent experimental study on transport of single-molecules through the NPC with a high spatiotemporal resolution, it was found that inert cargos have a random distribution primarily in cytoplasmic periphery (61). In contrast, the active cargo sticks to FG-repeats and diffuses back and forth tens of times until it reaches its destination (see Fig. 7 b and Fig. 8) and is detached from FG-nup by RanGTP/GAP.

In effect, the same short-range repulsion is applied between the active cargo and FG-repeats as between the inert cargo and FG-repeats. However, long-range kap-FG affinity keeps the active cargo near the wall during transport and does not allow it to diffuse aimlessly. Importantly, this implies that dimension of the diffusion of the active cargo is reduced, which in turn reduces translocation time and increases the transport rate. In fact, due to the hydrophobic affinity, the active cargo is most of the time engaged with FG-repeats (see Fig. 6), which in turn speeds up the diffusion search process and makes the active cargo find its destination more quickly (66,67). This reduction-of-dimensionality can be clearly observed in Fig. 8, where the average trajectories of cargos' edges with different sizes coincide. The phenomenon of reduction-of-dimensionality was proposed long ago (68) as a mechanism to speed up reactions in biological systems and has been suggested as a plausible model for nucleocytoplasmic transport (15,46). However, for the first time (to our knowledge), our average trajectories of cargo-complexes at nanometer resolution (see Fig. 8) confirm that this phenomenon is achieved surprisingly well within the central channel.

Our model deviates from the reduction-of-dimensionality model due to the formation of a dense layer of the FG-repeats in the central channel (see Fig. 7 c). It is tempting to speculate that this dense layer of FG-repeats smoothes the translocation of the active cargo, in effect, lubricating its path. This speculation is corroborated by a study that suggests the charged polymers grafted onto a surface collectively act as a “superior lubricant” (69). Furthermore, in parallel with formation of the dense FG-layer, our model suggests that the diameter of the open tube is ∼18 nm (see the Supporting Material for details) as opposed to 8–10 nm in the reduction-of-dimensionality model (15). Perhaps this wider open tube outlines a lubricated pore for active cargos transport.

Our model also suggests that cytoplasmic filaments create an entropic barrier to inert cargos. This picture is consistent with the virtual-gate model (14). We, therefore, propose that a plausible mechanism for a high throughput, selective transport could be achieved by considering cytoplasmic filaments and peripheral FG-repeats as an entropic barrier and central FG-repeats as a “lubricating” layer. This model combines features of the virtual-gate (14) and the reduction-of-dimensionality (15) models and can be imagined as a highway in which the toll booths are located at the NPC peripheries and the charge is paid by kap-FG hydrophobic interactions. In this picture, the NPC can be viewed as a “lubricated gate”.

Conclusion

Due to its complex geometry, the functional state of the NPC cannot be directly observed in vivo, leaving plenty of room for speculation. This is particularly true for the FG-repeat domains as the key players in nucleocytoplasmic transport. Even state-of-the-art structural imaging techniques lack the resolution to detect these domains (3) or their transient binding to the cargo-complex. Hence, computational modeling is the only method capable of tracking thousands of transient interactions between cargo-complex and FG-nups during millisecond events-of-transport with refined resolutions both in spatial and temporal domains. While all-atom MD simulations of the whole NPC structure are far beyond our current capabilities, coarse-graining is the best alternative approach.

Based on polymer physics principles, we have developed an experiment-driven coarse-grained model to shed light on the biophysical principles underlying nucleocytoplasmic transport. Indeed, this technique is able to answer numerous questions previously posed due to transport being examined mostly as an input-output behavior of a black box channel. This model can track the path of a cargo-complex and its interactions inside the channel. It predicts that the mean transport time of active cargos is not sensitive to cargo size up to 15 nm. In addition, the model corroborates that kap-FG hydrophobicity is enough to overcome the entropic barrier.

Inside the central channel, FG-repeats leave an open tube and form a thick layer on the inner wall that potentially acts as a lubricant. During transport, the active cargo is almost always attached to this layer. Accordingly, we suggest that a hybrid of virtual gate (14), reduction-of-dimensionality (15) models, and our speculated lubricating FG-layer sounds a plausible mechanism for nucleocytoplasmic transport. Using the coarse-grained model proposed here, it is possible to investigate numerous interesting questions that are difficult to observe by experiments. Examples are, but not limited to, the potential effect of the channel curvature on transport efficiency, dependence of the cargo-complex diffusion pattern on the number of hydrophobic binding spots, and the role of the cargo elasticity and geometry in transport, e.g., accounting for mRNA or viral DNA cargos.