An Analysis of All the Relevant Facts and Arguments Indicates that Enzyme Catalysis Does Not Involve Large Contributions from Nuclear Tunneling

Introduction

Enzymatic reactions play a major role in controlling and performing most life processes. Thus, understanding how enzymes really work has both fundamental and practical importance. In this respect, it is crucial to understand the origin of the enormous catalytic power of enzymes, and this is currently one of the major challenges of modern biophysics^{[1, 2]}. Although many elements of this puzzle have been elucidated by biochemical and structural studies, the source of the catalytic power of enzymes has not been widely understood, and clearly remains controversial within the scientific community (see e.g. Ref. ^[3]). At the present stage, all consistent simulation studies appear to indicate that electrostatic effects play a major role in stabilizing the transition states of enzymatic reactions (for reviews of this matter, see for instance Refs. ^{[4, 5]}). However, this idea has not been generally accepted, perhaps due to the difficulties of understanding the effect and also due to general difficulties in the clarification of the nature of polar pre-organization effects^[6]. Thus, there is a great interest in exotic alternative proposals. For instance, the idea that enzyme catalysis involves special factors such as nuclear quantum mechanical (NQM) effects, and, in particular, nuclear tunneling, has gained popularity in recent years^[7–14]. Additionally, it has been suggested that transition state theory (TST) cannot be used in studies of enzyme catalysis, it has actually been demonstrated to provide an excellent tool for such studies^[15].

While there is no argument about the fact that NQM effects play a significant role in enzymatic reactions in which the rate limiting steps involves the transfer of either a proton, a hydride or hydrogen, rigorous and systematic theoretical studies have demonstrated that the NQM contributions are similar in solutions and in proteins and thus do not make a significant contribution to catalysis (where catalysis is defined as the difference between the enzymatic and the solution reactions). Additionally, is has been established that TST provides an excellent tool for quantifying enzymatic catalysis^{[16, 17]}. Nevertheless, there are still major misunderstandings remaining in the field with regards to the catalytic tunneling proposal^[18]. We would like to point out at the beginning of this paper that assessing the catalytic contributions of NQM effects must, naturally, reproduce all key experimental observations. However, it cannot be based on accepting the interpretation of experimental data as fact. Here, one needs reliable models that can actually simulate any type of experimental observations, and that allow one to dissect the overall catalytic effect in order to identify its constituent contributions. In other words, once a model is able to reproduce what is actually observed experimentally, it can then be used to separate the overall effect into its individual contributions. Since enzymes are very complex systems, the most effective models should probably be based on computational simulation approaches.

In this work, we will consider arguments that support the catalytic NQM idea, and point out the ways in which these arguments are extremely problematic (and sometimes even self-contradictory in some of the most basic cases). Our analysis aims to clarify the misunderstandings of this issue by summarizing the results of our recent studies, as well as by discussing some other relevant works. We clarify that calculations of quantized activation free energies converge much more rapidly than calculations of the temperature dependence of these quantities, and that the calculated activation free energies support our conclusions about the contribution of NQM effects to catalysis. We then proceed to clarify the difference between calculations that evaluate the temperature dependence of isotope effects by consistent microscopic simulations, and studies that reproduce such dependence by using adjustable phenomenological parameters. We point out that, at present, our studies of the temperature dependence of isotope effects are as good as (if not better than) any of the reported consistent calculations, including in the challenging case of lipoxygenase. Furthermore, we will summarize our systematic study of kinetic isotope effects (KIEs) and their temperature dependence in mutants of dihydrofolate reductase (DHFR). This study provides a unique example of the reproduction of the observed change in the trend of the temperature dependence of KIEs that is wholly based on microscopic calculations. Ultimately, our aim is to clarify the main misunderstandings in this field with simple non-polemic logical arguments. We believe that addressing the validity of the main arguments and facts in the field is the best way in order to reach a constructive scientific consensus.

I. Methods

Although many of our arguments will be based on clear and logical analyses, it is nevertheless important to provide some background information about our simulation approaches. These have been described in detail in many of our previous works, and the description below is only provided in order to establish that our argument is based on a solid and grounded scientific basis.

In order to obtain quantitative free energy surfaces, we utilized the empirical valence bond (EVB) method. This method, which has been described extensively elsewhere (e.g. in Ref. ^{[1, 19, 20]}), is particularly useful in cases of NQM calculations because long simulations are required to obtain the convergence of the corresponding free energies in such calculations (where it is helpful if the relevant potential energy surface is available in an analytical form). In this respect, the EVB approach is a very powerful tool, particularly when one is comparing activation barriers in water and in an enzyme active site, or in native and mutant enzymes.

The task we face here is to use the analytical EVB surface of the reacting system and its surrounding protein + water system in order to obtain the quantum correction to the classical activation free energy. The introduction of methods for simulating NQM effects in enzymatic reactions dates back to our works in the early nineties (see e.g. Refs. ^{[12, 14, 21, 22]}), and the use of these and alternative simulation methods has recently become quite an active field^{[2, 13, 15, 17, 23, 24]}.

Our main approach for the evaluation of NQM effects has been the quantum classical path (QCP) centroid path integral approach, that we developed in our studies of NQM effects in chemical reactions in solution and proteins^{[12, 14]}. Note that the QCP has recently been adopted by other research groups (see e.g. Refs.^[25–27]). Also, it is useful to point out that while theoretical studies of the catalytic contributions of NQM have progressed significantly (e.g. Refs. ^{[11, 13, 14, 17, 23, 24, 28, 29]}), there still remain open problems and major challenges with regards to reproducing the observed temperature effect of KIEs by actual microscopic simulations. Apparently, it is possible to account for the observed KIE and it’s temperature dependence by means of phenomenological vibronic treatments (e.g. Refs. ^{[21, 30, 31]}) in which key parameters are adjusted (as was done, for instance, in Refs. ^[11] and ^[7]). Unfortunately, vibronic treatments that have recently become very popular involve fundamental problems (see, for instance, Refs. ^[15] and ^[17] and this work), and the parameters obtained by a fitting procedure are not expected to provide a quantitative description of the reacting system. On the other hand, it is also extremely challenging to evaluate the temperature dependence by means of computational simulations that do not involve any special parameterization. In fact, with the exception of our recent works^{[23, 32]}, we are not aware of any other successful attempts to reproduce the temperature dependence of the KIEs of enzymatic reactions (where the trend changes between different mutants) in a quantitative way by means of first principle simulations, despite several attempts to do so (for instance Refs. ^{[28, 33]}).

II. Tunneling does occur in enzymes, but, the same NQM effects also occur in the corresponding solution reactions

The argument that NQM effects contribute to enzyme catalysis is based on the observation of large isotope effects in enzymatic reactions as well as other indications of nuclear tunneling (e.g. Refs. ^{[7, 18]}). These findings are both very reasonable and very important. They are also fairly consistent with the existence of nuclear tunneling, and are reproducible by simulation studies^{[23, 32]}. The problem arises from the fact that such contributions are not necessarily catalytic. That is, catalysis has to be defined relative to a reference state, and the most logical reference state to use is the rate of the same chemical reaction occurring in the enzyme when it occurs on water^[4]. Now, as we have already pointed out in several of our papers^{[4, 12, 15, 17, 23]}, the same NQM effects that occur in the enzyme also occur in the reference solution reaction and contribute in a similar way.

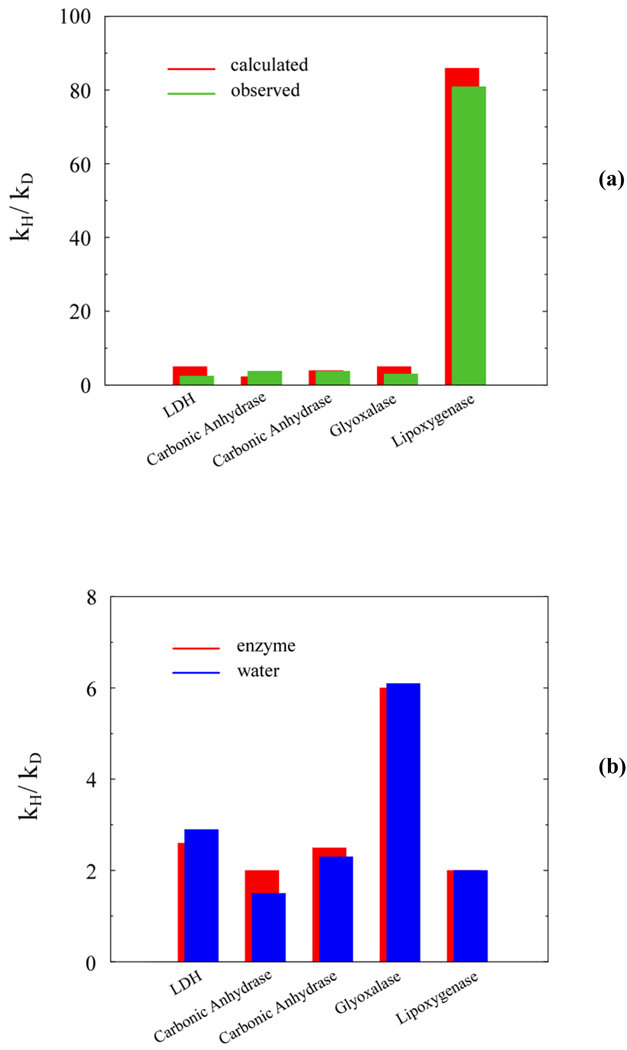
Similar findings have also been made in the several experimental studies in which the reference reaction was experimentally observed^{[34, 35]}. We should nevertheless point out that in many cases it can be hard to measure the relevant reference reaction, and computer simulations thus offer a reasonable way to explore the reference reaction^[36–42]. However, such studies are only meaningful if they can reproduce the observed catalytic effects, and, fortunately, our EVB approach (which is calibrated on ab initio solution studies) provides the needed reliability. Now, EVB studies coupled with QCP calculations of isotope effects have reproduced both the observed catalysis as well as the observed isotope effects in any systems studied by us. The same calculations also found that the isotope effects are similar in the enzymatic and solution reactions. The corresponding results are depicted in Fig. 1 (a) and (b) respectively. At this point, we would also like to mention that we are not aware of any studies that have provided different results to those reported above.

Figure 1.

A comparison between (a) the calculated and observed primary deuterium kinetic isotope effects in different enzymes and (b) the calculated primary deuterium kinetic isotope effects in these enzymes and in the relevant reference reactions in water. The data is originally presented in Ref. ^[17] (and references therein).

III. The basic assumption that enzymes increase tunneling by compressing the reacting fragments appears to be problematic

The most basic argument about the role of tunneling in enzyme catalysis starts with the idea that the enzyme compresses the distance between the donor and acceptor, thus leading to a narrower potential and to tunneling^{[18, 43–48]}. This idea, that now appears to be taught in standard undergraduate biochemistry courses, is very appealing. However, it would seem that the presumed compression leads to a reduction rather than an increase in the NQM effects.

More specifically, it is tempting to assume that enzymes catalyze reactions by means of compressing the distance between the donor and acceptor, as was done in Ref.^[49], or by the related idea of a near attack conformation (NAC), as was done in Ref.^[43] (the central problems with the NAC proposal have been clarified in Ref. ^[50]). This would mean that the enzyme leads to a change in the shape of the barrier (and, in the process, presumably enhances the contribution from tunneling to catalysis ^{[18, 43–48]}). This idea has also been used to rationalize the temperature dependence of observed KIEs^[46].

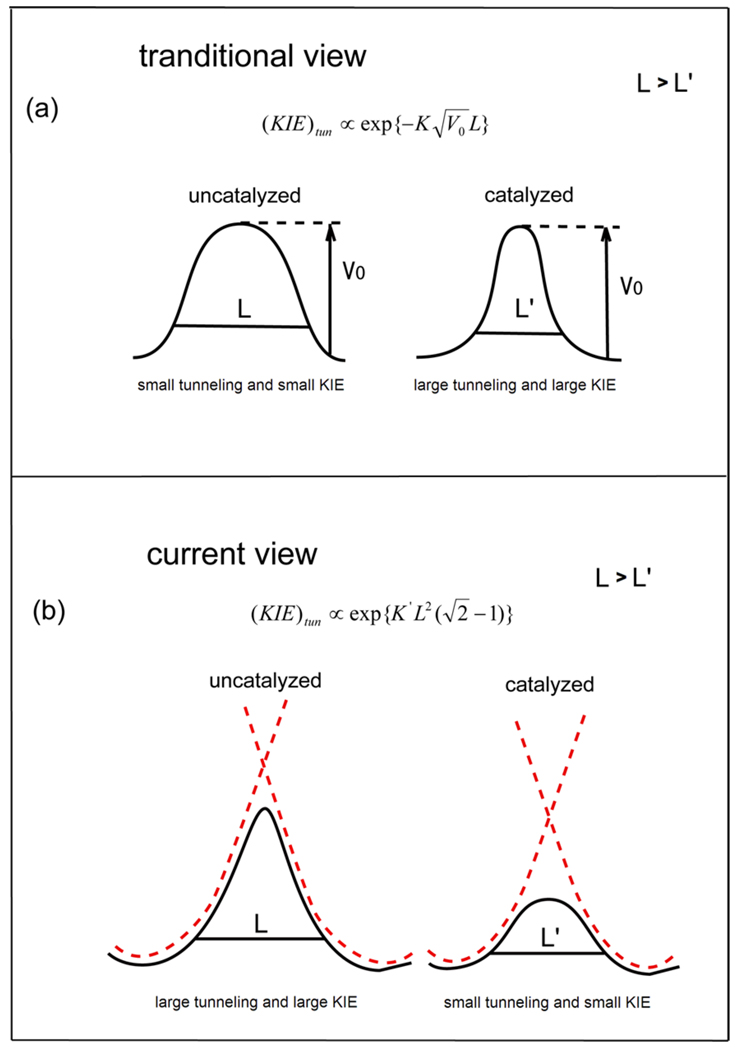
In other words, the traditional proposals of NQM contributions to catalysis^{[18, 43–48, 51]} have implied that the protein compresses the reaction fragments, which in turn leads to a narrow potential and thus to larger tunneling (Fig. 2a^[32]). In this case, one would expect a relationship of the form^[32]:

$${(KIE)}_{\mathit{\text{tun}}}\propto \text{exp}\{-K\sqrt{V_0}L\}$$ (1)

Figure 2.

The catalytic (anticatalytic effect) of the donor-acceptor distance dependence of the NQM effects in hydride transfer reactions. The traditional idea that the NQM effects increase upon compression of the donor-acceptor distance is described in Fig. 2(a). This view assumes that enzyme catalysis involves an increase in tunneling due to the compression effects. On the other hand, as shown here, the NQM effects actually increase when the donor-acceptor distance decreases (Fig. 2(b)) and thus it is hard to rationalize a relationship between NQM effects and catalysis. The figure is taken from Ref.^[32].

Where V₀ and L are the height and width of the barrier respectively. On the other hand, both us and others have recently found^{[29, 32, 52]} that even in the vibronic formulation, the isotope effect increases due to the sharp distance dependence of the zero-zero vibrational overlap (see Fig. 2b), where the tunneling contribution follows the following relationship (see Ref.^[32]):

$${(KIE)}_{\mathit{\text{tun}}}\propto \text{exp}\{K^{\text{'}}{L}^2(\sqrt{2}-1)\}$$ (2)

Thus, in the more recent view, the NQM effects decrease rather than increase upon compression. This effect is due to the fact that the tunneling in proton and hydride transfer reactions depends on the overlap between the vibrational wave functions of the reactant and product states, and this overlap in turn depends on the distance between the corresponding minima (see Ref.^[32]). The ratio between the NQM contributions of H and D changes according to Eq. 2. In fact, when the donor and acceptor are pushed to a short enough distance, the mixing between the two states makes the adiabatic surface very flat, and the tunneling effect disappears. While the above claims may sound strange to some, the simplest way to convince the reader is to point out that all key workers in this field (e.g. Refs. ^{[29, 52]}) now essentially get the dependence of Eq. 2.

Now the above analysis has, of course, a major implication with regards to the idea that NQM effects make a significant contribution to enzyme catalysis. In fact, the effects that lead to an increase in the NQM contributions appear to be anticatalytic. This is mainly due to the fact that the rate constant is smaller for larger donor-acceptor distances. Since the fact that the observation of large a large KIE reflects an increase (rather than decrease) in the distance between the donor and acceptor is a seemingly counterintuitive point, it still causes significant confusion (see Section V for further discussion of this issue).

It should be clarified here that the prediction of the vibronic formula quantizing the relationship between the KIE and the donor acceptor distance was discovered before our recent studies^{[29, 52]}. However, with the exception of the Hammes-Schiffer work^[29], we could not find any early works that realize that the increase in distance of the KIE leads to a scenario that is different from the traditionally expected scenario. Futhermore, we are not aware of any study (apart from our own^[15]) that actually established the distance dependence of the KIE by proper microscopic simulations without the use of the problematic diabatic approximation and the vibronic formula. Moreover, we could not find a clear realization of the fact that this finding makes it hard to attribute catalysis to an increase in tunneling.

IV. Temperature dependence

The temperature dependence of the NQM effects as manifested in the corresponding KIE has been a topic of significant current interest^{[7, 23, 30, 31, 52]}. Part of this interest stems from the hope that this temperature dependence can provide useful information about possible dynamical contributions to enzymatic reactions^{[7, 53]}.

We strongly believe that enzymes do not use dynamical effects in catalyzing chemical reactions, and our considerations have been summarized in several recent reviews^{[2, 17, 54, 55]}. We have also not seen any evidence that dynamical effects contribute to catalysis (see the discussion in the aforementioned reviews). However, this review focuses on the tunneling proposal, and thus, we would like to consider what information can be gleaned from the temperature effect (which is very real) about the contribution of NQM effects to catalysis.

As far as tunneling is concerned, there is a tendency to argue that the observed temperature dependence of KIEs (e.g. ^{[56, 57]}) is clear evidence for thermally activated tunneling, and thus, this can be considered support for the idea that tunneling contributes to catalysis. We have no problems with agreeing that tunneling in enzymes can be thermally activated. In fact, our simulations and formulations have long been consistent with this view^{[4, 12, 15, 17, 23]}. We have also recently succeeded in reproducing the observed temperature effect^[32]. However, our simulations have led to the conclusion that NQM effects do not help in catalysis, since the same thermally activated tunneling also exists in solution.

With the above findings in mind, we can ask what the actual meaning of the observed temperature effect is, and what it tells us about catalysis. Apparently, the studies of DHFR^[32] and lipoxygenase^[23] indicate that the KIE increases when the distance between the donor and accepter increases. This finding is somewhat counterintuitive (since it has been assumed that relative tunneling contributions increase when the distance between the donor and accepter decreases). At any rate, the temperature dependence of the KIE appears to mainly reflect the temperature dependence of the distance between the donor and accepter. Thus, the temperature dependence actually indicates that tunneling is anticatalytic (by the arguments of section IV).

An interesting recent study^[58] of SLO-1 mutants can be directly related to the discussion above. This work found that the distance mutation of I553G leads to larger KIE and to larger temperature dependence of the KIE than for the corresponding effects in the native enzyme. It was argued that this demonstrates that enzymes can make the rate of transfer via hydrogen tunneling significantly more efficient. While this is an interesting point of view, it seems to us that the experiments of Ref.^[58] simply demonstrate the key role of entropic effects in determining the temperature dependence of NQM effects (as was pointed out in our early works).

Finally, it is important to point out that while NQM effects are not likely to contribute to catalysis, the observed temperature dependence can be used to refine the potential of mean force for the donor and acceptor distance and its change due to distant mutations.

V. Arguments that tunneling occurs at a very high percent in many enzymatic reactions are fundamentally flawed

Recent works have classified reactions with a relatively small tunneling contribution^{[28, 59, 60]} (i.e. a reduction of 4% in the barriers) as proceeding predominantly by tunneling. This view is based on the fact that the NQM contribution to the rate constant is more than 50% (in one case, it is even claimed that the reaction only proceeds 1% by the classical way, i.e. 99% by tunneling^[59]). This classification seems to reflect a major misunderstanding, and is actually misleading. That is, if we had two competing pathways, one mainly with tunneling and the other without tunneling, we could have claimed that the one with tunneling contributes 99% to the reaction (if this actually were the case). Here, however, we are examining reactions with a single pathway, and thus we can best point out that the reaction barrier changes from e.g. 15 to 14 kcal/mol^[28] when we add tunneling and zero point energies. Nevertheless, it is useful to show that this assumption is problematic under any reasonable definition, for various reasons.

1. The most meaningful definition should be related to the effect of the change in the barrier relative to having no barrier. In this case, there is no need for any extended discussion, since the tunneling effect will be minor in the typical cases that will be used here for illustration purposes (for instance the barrier is reduced by a mere 1 kcal/mol from 15 to 14 kcal/mol^[28]).

2. One may say that since the rate increases by 99% with the tunneling correction added, the reaction mainly involves tunneling (despite the obvious behavior of the activation barrier that was mentioned above). The problem with this argument, however, is the fact that the rate should not be evaluated relative to the rate without tunneling, but rather relative to the basis rate when there is no classical barrier (~6 × 10¹² s⁻¹) and no correction for NQM effects. Now, with this definition, we find that the rate is 10³ s⁻¹ with only the classical barrier and 10⁴ s⁻¹ with the tunneling correction. Thus, the classical barrier reduces the rate by 109 and tunneling changes the effect by a minor factor of ~20. Apparently, the rate of the reaction is described extremely well by TST with a relative error of only 20/10⁸, such that the reaction is 99.9999% classical. Thus, it seems unjustified to us to take a care when the reaction is accelerated by a small factor of 20, (relative to a deceleration of 10⁸ due to the classical barrier), and to classify such a case as a reaction involving 99% tunneling.

3. The works that claim a large percent of tunneling give the impression that there is some theoretical basis for this quantification. However, we have failed to find any physically or mathematically consistent definition that can be used to reach the above argument. There neither is nor ever will be any formulation that correctly defines the percentage tunneling that will be physically consistent and convert a 20-fold rate enhancement.

4. If it were true that the reaction mainly occurs through tunneling, then it would have been temperature independent and would not have needed to pass through classical barrier. That is, for tunneling to hold, this means going below the classical barrier. However, none of the molecules go below the classical barrier, and, in our case, all most climb the 14 kcal/mol classical barrier. Any comment on thermal activated tunneling is therefore not so helpful, since there is no formulation that can yield this without considering the enormous effect of the classical barrier.

VI. What about other computational findings?

In recent years, there has been significant progress in the calculations of NQM effects in enzymes^{[11, 13–15, 17, 23, 24, 28, 29]}. Thus, one may wonder whether different conclusions have emerged from different studies. However, to the best of our knowledge, there are no studies that have actually evaluated the catalytic effect in a consistent way and ended up reaching different conclusions than ours (based on the calculated results). In fact, there are very few attempts to compare the NQM in enzymes and in solution except for our studies and those of the Åqvist group^[61].

In our view, the most basic “qualification” for a reliable interpretation of the meaning of observed KIEs is the ability to correctly reproduce the corresponding observed rate constants and activation barriers by microscopic simulations, without adjusting any special parameters for this purpose. Since our main interest is related to the origins of enzyme catalysis, it is crucial to reproduce the change in activation barriers relative to the corresponding barrier in water. There challenging requirements were satisfied by our studies of DHFR^[62], but, to the best of our knowledge, have not yet been satisfied in other studies. In this respect, it is important to note that the parameterization of QM/MM calculations to reproduce isotope effects (e.g. Ref.^[51]) does not necessarily satisfy the above conditions.

It is also important to clarify the fundamental difference between parameter fitting to a phenomenological formula (e.g. Ref.^[7]), and the actual microscopic simulations used here and in our previous studies. While it is almost trivial to reproduce the observed effect by means of arbitrary parameter fitting, it is extremely hard to do so by microscopic simulations. Part of the problem is associated with the difficulty of obtaining the exact PMF, and another part is associated with the general difficulties associated with capturing temperature dependent effects (such as entropic effects) by current simulation approaches (see the discussion in Ref. ^[23]).

As far as computational approaches are concerned, it is useful to consider a recent misunderstanding of this issue here. More specifically, an interesting recent study of SLO-1^[51] explored the effect of changing the width of the gas-phase potential on the calculated KIE in a model of SLO-1. It was concluded that “the decompression of the active site will result in a lower contribution to tunneling … thus indicating the importance of the proposed gating promoting modes”. However, this idea is very problematic since, as we recently discovered, decompression (or increasing the donor acceptor distance) increases rather than decreases the tunneling contribution^[17]. Unfortunately, the analysis of Ref.^[51] involved changing the width of the intrinsic potential surface (the one of the isolated substrate without the enzyme) instead of using a single potential surface for the substrate and changing the donor acceptor distance in the presence of the enzyme (as was done in Refs.^{[32, 62]}), or actually reproducing the observed effect of mutations that change the donor acceptor distance (as was done in Ref. ^[63]). Unfortunately, an arbitrary change of the width of the intrinsic potential neither addresses nor represents the proper physics of hydrogen transfer processes, since it does not converge to the proper limit at large donor-acceptor separation. More importantly, the treatment of Ref. ^[51] has not explored the effect of the protein since active site strain is not likely to cause a significant narrowing of the potential surface of the reacting atoms. Finally, it is worth mentioning that some people try to present the opposite view with regards to the change in donor acceptor distances^[63]. However, it should also be pointed out that these “calculations” show a deviation of 40–50kcal/mol from the observed barrier, and thus are not worth serious consideration.

A recent work by Schowen^[64] has addressed the classical experiment of Doll and Finke^[65], which was used to demonstrate that tunneling in the enzymatic reaction of Methylmalonyl Conenzyme A Mutase (MCM) and the reference reaction in solution are similar. Here, it was argued that Doll and Finke’s experiment is inconclusive due to their belief that the enzymatic enhancement in the rate of the tunneling reaction would produce changes in the characteristic signatures of tunneling such as the isotope effects, the isotopic A-ratios or the isotopic difference in the activation entropies. However, Schowen believes that an enzyme such as MCM may have provided such transition-state stabilization for a non-tunneling transition state that a non-tunneling mechanism would prevail for the enzyme, while tunneling would proceed as normal in the model reaction. Alternatively, Schowen argues that it was observed that the low-temperature mechanism of tunneling (with its overdependence on the temperature, which is a signature of a double search mechanism) was lost at 30° C, being replaced by a different mechanism of tunneling at higher temperature with its own signature of an underdependence on tunneling, reflecting the availability of a pre-organized tunneling state at higher temperatures. It was then concluded that tunneling in enzymes can even enhance the rate by a factor of 10². While we agree that the study with the model compound is inconclusive as the reaction in the protein is concerted^[66] and only the Co-C bond breaking was studied in the solution reaction, our detailed simulations^[66] (and to some extent those of others^[67]) have quantitatively established that the rate enhancement of ~10¹¹ is due to the electrostatic stabilization of the leaving ribose (by Glu370 and other groups), which results in transition state stabilization and reflects an almost entirely electrostatic reorganization effect. Finally, a study that attempted to address the different factors involved in this comparison and argue that the tunneling effect is crucial for catalysis^[68] (Lynn please check if they done so) did not consider the reference reaction, nor did it reproduce the enzymatic free energy surface or the catalytic effect.

One of the problematic ideas that has been connected to the tunneling proposal in recent years has been the redefinition of the pre-organization concept by Klinman and coworkers (see e.g. Ref. ^[69]). That is, the reduction in the reorganization energy by the polar pre-organization of the enzyme active site has been quantitatively established as probably the most important factor in enzyme catalysis as early as 1978^[70]. The reorganization effect has been fully quantified and expressed as a mathematical formulation in terms of the average of the protein transition state electrostatic interaction over trajectories that do not experience the substrate electrostatic potential (see e.g. Ref. ^[6]). More specifically the elctrostatic binding free energy of the TS is given by

$$\mathrm{\Delta }G(Q^{‡})=0.5({\langle U(Q=Q^{‡})-U(Q=O)\rangle }_{Q=Q^{‡}}+{\langle U(Q=Q^{‡})-U(Q=0)\rangle }_{Q=0})=0.5({\langle \mathrm{\Delta }U\rangle }_{Q=Q^{‡}}+{\langle \mathrm{\Delta }U\rangle }_{Q=0})$$ (3)

where U is the solute-solvent interaction potential, Q designates the residual charges of the solute atoms with Q^‡ indicating the TS charges and <ΔU>_Q designates an average over configurations obtained from an MD run with the given solute charge distribution. The first term in Eq. 3 is the aforementioned interaction energy at the TS, where Q=Q^‡, which is similar in the enzyme and in solution. The second term expresses the effect of the pre-organization of the environment. Or the preorgnaization effect. This is a quantitative free energy term that can be converted directly to a reduction of activation free energy (when compared to the reference reaction in water, see e.g. Ref. ^[6]). Probably the clearest explanation of the preororganization effect has been given recently in a study of KSI (here Warshel et al Biochemistry 2007) and is summarized in Fig 3 (add the figure from the attached mail) Unfortunately, Klinman and coworkers assumed that it is reasonable to consider the most important concept in enzyme catalysis as a semantic issue, and to redefine “preorganization” as the process of moving towards the catalytic configuration. Not only is this process is irrelevant to catalysis (see below), but also by this logic one can take a well defined concept with a well defined name, like for instance “free energy”, and suggest that from now on the name actually refers to the speed of moving on a freeway. Obviously it would be hard to follow the scientific philosophy (which is meant to be used to determine what is right and what is wrong) by conveniently changing the definitions of key concepts and key terms in a way that would make their discussion useless since the name that labeled the original concept would now describe another concept. This is particularly problematic when one moves from a predictive concept, i.e. the original preorganization concept, to a soft ill-defined concept of the process of searching for the ES complex. This brings us to a serious question in which it is important to realize that the search for the ES complex does not contribute to nor does it have any relation to catalysis, as long as k_on is larger than k_cat.

More specifically, the misunderstanding probably started with the idea that the chemical step in enzymes is “facilitated by a network of coupled motions that bring the donor and acceptor to the correct distance and orientation and the correct electrostatic environment”^[71]. However, the minimum of the free energy surface of the reaction in the folded enzyme that determines the positions of the reacting fragments, as well as the degree of electrostatic preorganization (please we have to have all this without pre-), and the potential surface, also determines the nature of the reactive normal modes, which are simply modes with significant projections onto the reaction path. The reverse is not true: the reactive motions do not bring the system to the pre-organized configuration. Apparently, the folded enzyme establishes the free energy surface for the catalytic reaction and the motions on this surface simply reflect the Boltzmann probability of finding the system at different points on the surface. This point is established in Fig 3. (Lynn: I am waiting for Andrei to email me the power point)(NO it is MY Power point) and discussed in ref (Hanbin Biochem 2007)

Now, in Fig. 6.4 of Ref. ^[69], Klinman considered the conformational search on the landscape as the preorganization effect. Similar misunderstanding have been expressed by other workers (e.g. put Here Shlick JACS 2007 with Wilson (show me the paper)) However, as clarified in our recent work^[72], the landscape effect may lead to some entropic contributions (which are usually small), but this is negligible as compared to the true preorganization effect, which leads to the reduction in the reorganization energy and the activation free energy. Thus, preorganization plays a major role, but this has little to do with the new definition.

VII. Concluding Remarks

Our previous computational studies have indicated that the major effect in enzyme catalysis comes from the pre-organization of the protein environment, where the enzyme plays the role of a super solvent with smaller reorganization energy than the corresponding reaction in aqueous solutions (where the solvent molecules undergo very large changes in their orientation during the reaction^[2]). However, in order to verify the observation that electrostatic effects are key to enzyme catalysis, it is crucial to demonstrate that other proposed effects to not make a significant contribution to catalysis. Demonstrating the problems with alternative proposals should not be viewed as a smear campaign, but rather, as an integral part of the scientific philosophy of excluding different proposals by examining their consistency with observed and simulated findings.

Our studies seem to indicate that tunneling effects do not make a significant contribution to catalysis (e.g. Refs. ^{[17, 23, 73]}) and enzymes do not apply strong stress that leads to a significant “compression” relative to the corresponding situation in solution (e.g. Ref.^[15]). Furthermore, our studies^{[17, 23]} and those of others^{[29, 74]} have indicated that the KIE and the relative contributions from NQM effects increase rather than decrease when the donor acceptor distance increases.

Finally, it is important to consider the idea that DHFR increases the reaction rate by optimizing the coupling between environmental dynamics and quantum tunneling (see Ref.^[75] or related ideas^[46]), as well as the implication that quantum mechanical tunneling is promoted by correlated motions^[28] and can be optimized by wild-type enzymes^[53]. In fact, tunneling is smaller in the native enzyme (where the catalysis is maximal) than in the mutant enzyme, which means that the motions that push the reacting system in the mutant enzyme to the native configuration (which can be described as moving to the NAC configuration^[43]) reduce tunneling rather than increase it.