Locating the Reference Point of Symphysis Pubis in Axial CT Images

Abstract

In this paper, we present an effective method to determine the reference point of symphysis pubis (SP) in an axial stack of CT images to facilitate image registration for pelvic cancer treatment. In order to reduce the computational time, the proposed method consists of two detection parts, the coarse detector, and the fine detector. The detectors check each image patch whether it contains the characteristic structure of SP. The coarse detector roughly determines the location of the reference point of SP using three types of information, which are the location and intensity of an image patch, the SP appearance, and the geometrical structure of SP. The fine detector examines around the location found by the coarse detection to refine the location of the reference point of SP. In the experiment, the average location error of the propose method was 2.23 mm, which was about the side length of two pixels. Considering that the average location error by a radiologist is 0.77 mm, the proposed method finds the reference point quite accurately. Since it takes about 10 s to locate the reference point from a stack of CT images, it is fast enough to use in real time to facilitate image registration of CT images for pelvic cancer treatment.

Introduction

Imaging plays a crucial role in every stage of modern cancer treatment, from screening to recovery. Especially, computed tomography (CT) imaging has played an increasingly important role in detecting the recurrence or metastasis and lesion characterization; moreover, it is the most accurate tumor detection test. Advances in cancer management using digital imaging require optimizing data acquisition, post-processing tools, and computer-aided diagnosis (CAD). Traditionally, radiologists compare the pretreatment images to post-treatment images after cancer treatment to confirm the absence, stability, progression, or spread of this disease. Subjective decision based on the interval change of size, shape, and spatial relationships of visual structures is used for monitoring the progress of cancer and the response to treatment [1].

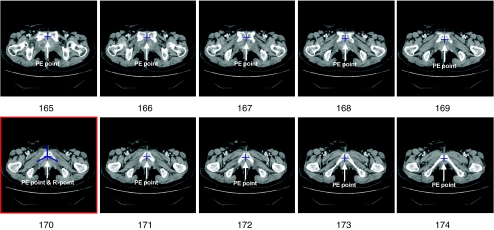
Radiologists usually make a diagnosis by comparing several pairs of CT images that correspond to anatomically identical region. In order to make a comparison, it is necessary to find the identical parts from two stacks of axial CT images that have been taken at different times in order to monitor the progress of cancer. Practically, a radiologist locates an image of interest from a stack of CT images and finds a corresponding image from another stack of CT images of the same patient. This is simple but time-consuming process, which is still conducted manually despite the advances in CAD systems. Image registration [2, 3] is essential for automatic CAD system, which find its application in the treatment of lung [4], chest [5], and brain [6, 7]. However, its application to abdominal images is still in its early stage. This is due to the relatively large movement of abdominal organs and low contrast between the lesion and surrounding soft tissues. On the other hand, the female pelvic organs such as the uterus move in a narrow range compared to the upper abdominal organs, e.g., the stomach or the liver, since they are tightly anchored to the pelvic bone by various ligaments and many organs are tightly packed in cramped space. Therefore, image registration can be relatively easily applied to the pelvic organs than other abdominal organs. For the feature-based automatic image registration of pelvic organs, the first step is to locate an anatomically characteristic point in the female pelvis. For the other image registration technique that does not rely on feature points [8, 9], the characteristic point will help to limit the search range of CT images and reduces the computational cost. For these purposes, we want to mark a particular anatomical point that can be used in CAD system for gynecological cancer management. Because the symphysis pubis (SP) in the pelvic bone structure has almost no mobility and is characterized by a high degree of contrast compared to the adjacent organs [10–12], it can be relatively accurately extracted by pattern recognition techniques. Figure 1 shows the CT images of the SP, which is the midline cartilaginous joint uniting the left and right pubic bones. In each image, the posterior end of the symphysis, which will be called as the PE point, is marked by “+.” Each image is identified by an index (or level (l)), and the lower levels corresponds to the upper parts of the body. Among the PE points, the point in the middle image (i.e., the image of level 170 in Fig. 1) can be used as an anatomical landmark to compare CT images for two axial stacks of images. Hereafter, this point will be called the reference point of SP or simply the R-point. Once the R-point is located, then it is relatively easy to find two or more additional anatomical landmark points. By using an affine transformation based on these landmark points, image registration can be performed. Therefore, the first step of the image registration is to find the R-point.

Fig. 1.

Successive CT images with the structure of SP and their levels in an axial stack

However, since no method has been proposed to locate the R-point, we will investigate how to detect the R-point in an axial stack of CT images. SP appears successively in an axial stack of CT images because of its three-dimensional structure. One of the usual practices is to select all the images that contain the SP structure from the axial CT images and to locate the R-point in the image that corresponds to middle of the selected ones, which is illustrated in Fig. 1. SP first appears in the image of level 165 and it then disappears after the image of level 174. The center image, which will be called as the R-level image, is chosen among the ten images, and has a level of 170 in Fig. 1. Then, the R-point is determined at the posterior end of the symphysis on the R-level image, which can be found at the intersection of three virtual lines shown in the image of level 170 in Fig. 1. Based on the R-point, a radiologist can be easily located the image of interest in short time.

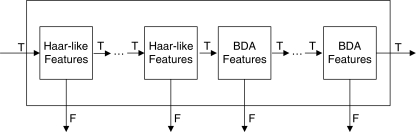
To effectively localize the R-point in SP from an axial stack consisting of several tens or hundreds of CT images, two detection procedures, coarse detection and fine detection, are successively performed as shown in Fig. 2. In the coarse detection, all the original CT images in an axial stack are resized to low resolution (128 × 128 pixels) for fast computation. More accurate results are obtained from the fine detection (256 × 256 pixels) that is focused on a limited region where the coarse detection has narrowed down. The basic element in the detection procedures is the image patches which are obtained by shifting a detection window (17 × 17 pixels in the coarse detection) in a CT image as shown in Fig. 3. Each image patch is examined to find out whether it contains the appearance of SP. If there is an SP structure in an image patch, then it will be called as an SP patch; otherwise, it will be called as a non-SP patch. SP does not appear in most image patches, which are not needed for further processing. In order to effectively remove the non-SP patches, the coarse detection makes use of three types of information, which are the location and intensity of an image patch, the SP appearance in an image, and the geometrical structure of SP. Most of the image patches, at first, are rejected based on the properties of SP patches, which are located on limited region of a few consecutive CT images and generally have more white pixels than black ones. Next, image patches that satisfy these conditions go though the classifiers connected in cascade as shown in Fig. 4 (the Haar-like and biased discriminant analysis (BDA) features in the figure will be described in the next section). The classifiers distinguish the SP patches from the non-SP patches based on SP appearance and discard the patches that are classified as non-SP patches. However, there are still some non-SP patches that have passed through these classifiers. To reject the remaining non-SP patches, these are further checked based on the geometric property of the SP structure. The coarse detection gives the rough location of the R-point from the image patches that satisfy the geometric property. Based on the result of the coarse detection, the fine detection is carried out on higher resolution CT images (256 × 256 pixels) by using a cascade detector. The R-point is then determined based on the locations of the image patches that are classified as SP patches by the fine detection.

Fig. 2.

Overall structure of the proposed method

Fig. 3.

Detection window and image patches in an image of 128 × 128 pixels

Fig. 4.

The hybrid cascade detector in the coarse detection

It is noted that when a patient receives a CT scan for the next time, the scanning conditions such as the patient positioning along the axial axis, scanning range, and slice thickness are usually made equal to the previous scanning conditions as much as possible. It is also noted that the proposed method may not work in abnormal cases where the configuration of SP is destructed due to skeletal pathology such as inflammation, infection, trauma, etc.

The rest of this paper is organized as follows. The next section provides a brief introduction of the binary classification and pattern recognition method used in this paper. The function of each block in Fig. 2 is described in “Method.” In “Experiments,” the performance of the proposed method is tested and compared to a radiologist’s decision. Finally, the last section concludes this paper.

Background

Binary Classification

As shown in Fig. 4, the cascade detector consists of several classifiers, and each classifier determines whether to send an image patch to the next classifier or not. This is a binary classification problem, in which there are two classes, positive and negative. In this paper, the SP patches are positive samples and the non-SP patches are negative samples. Let us consider N_P positive samples and N_N negative samples. Let N_TP, N_FP, N_FN, and N_TN be the numbers of samples that are true positive (TP), false positive (FP), false negative (FN), and true negative (TN), respectively. The recognition rate, , is the most typical measure of classifier performance, but it is not suitable for applications such as detection and image retrieval problems, where it is important to increase N_TP as much as possible, even at the risk of increasing N_FP. In this case, two other measures, the true positive rate (TPR or sensitivity) and the false positive rate (FPR), are usually used together.

In terms of these measures, a good classifier is required to have a high true positive rate and a low false positive rate, and such a classifier is essential to detect the R-point from a stack of axial CT images. We use nine binary classifiers in cascade for the coarse detection, and five binary classifiers in cascade for the fine detection. An image patch is classified by Haar-like features in the first four classifiers of the hybrid cascade detector in Fig. 4 and then by the features obtained from BDA in the next five classifiers. In the fine detector, only the BDA features are used in each of the five classifiers.

Haar-Like Features

Face detection in an image has been intensively studied in computer vision research, and a number of methods have been proposed. Among them, the method proposed by Viola and Jones [13] achieves good detection performance at a reasonable computational cost; therefore, it can be applied to real-time applications. Although various types of Haar-like features can be designed to distinguish facial images from non-facial images, the four types as shown in Fig. 5 are usually used in the Viola–Jones detector. Various Haar-like features from these types of features can be generated by changing their relative position or size in an image patch. Each of the Haar-like features provides a feature value f(IP) that is the difference between the sums of the pixel intensities within the white and the black regions of an image patch IP. For each feature, image patches are sorted based on f(IP). The optimal threshold θ_H for a feature can then be computed in a single pass over this sorted list and the details for determining the threshold can be found in [13]. The feature value f(IP) is compared to the optimal threshold θ_H to create a classifier h. This operation is represented as

Fig. 5.

Four types of Haar-like features

Here, p is either 1 or −1 and is determined when the threshold θ_H is determined [13]. Therefore, various binary classifiers can be constructed from the four types of Haar-like features in Fig. 5 by adjusting the size, location, threshold, and polarity. Moreover, the value of the Haar-like feature can be very efficiently computed by employing the integral image technique (see [13] for details).

Although the integral image can reduce the cost of computing the Haar-like features, it is not possible to use all feasible Haar-like features in an image patch because there can be an extremely large number of Haar-like features. For example, Viola and Jones [13] constructed about 160,000 rectangular features in a 24 × 24 image patch. Also, each classifier h that is associated with one of the Haar-like features does not usually give good results. Therefore, it is important to build a classifier with good performance by combining the best features among the various Haar-like features. This can be accomplished by using the Adaboost learning algorithm [14] that makes a strong classifier from many weak classifiers. After combining several hs by using Adaboost, a classifier with a high true positive rate and a low false positive rate can be constructed.

Biased Discriminant Analysis Features

The linear discriminant analysis (LDA) is a very popular technique [15–17] for solving classification problems. Although LDA is simple and powerful, it usually does not show good performance in one-class classification problems such as image retrieval, face, or eye detection [18]. This is because LDA tries to find a projection space in which each of the positive and negative samples is well clustered. However, this may degrade classification performance in one-class classification problems. In order to overcome this limitation of LDA, Zhou and Huang presented BDA by modifying LDA for one-class classification problems [18]. Unlike LDA, BDA tries to cluster only the positive samples and tries to place the negative samples far away from the mean of positive samples. Then, the problem is formulated to find the projection matrix 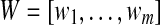that maximizes the following objective function

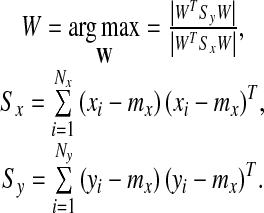1

Here, the vectors, 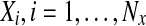and , are the positive and the negative samples, respectively, and m_x is the mean of the positive samples. The column vectors 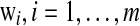can be found as the generalized eigenvectors corresponding to m largest generalized eigenvalues satisfying

If S_x is nonsingular, then w_i can be found by solving

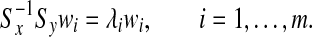2

In order to classify a sample z, the distance d_W(z, m_x) between z and m_x in the projection space is computed as

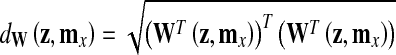3

and it is compared to a predetermined threshold θ_B. If 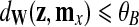, then z is classified as positive.

Usually the dimension of x corresponding to an image is much larger than the number of samples. This makes S_x singular, and w_i cannot be directly found by (2), which is called the small sample size (SSS) problem. Although several methods [18–20] have been presented to overcome this problem, the regularization method [21] is used in this paper for its simplicity. This method uses instead of S_x in the objective function in (1), where the regularization parameter μ is a small positive number and I is an identity matrix.

Method

Filtering Image Patches Based on Location and Intensity

Most of the CT images were taken with slice thickness of 2.5 mm, reconstruction increment of 2.5 mm, and 300~400 slices per scan. We use 44 axial stacks of images of 23 subjects to train the classifiers of SP detector, 21 stacks of 12 subjects for tuning the parameters of each classifiers, and 49 stacks of 25 subjects for testing. Although the size of CT images is generally 512 × 512 pixels, we resize all the images to 256 × 256 pixels to reduce computational time. Among the training images, 426 images contain the appearance of SP while the other 3,971 images do not. We will refer the 426 images as SP images (e.g., the image in Fig. 1) and the other images as non-SP images. Also, there are 183 SP images and 2,354 non-SP images in the validation set. One of the authors of this paper, who is a radiologist, located the PE point and marked in each of the SP images (e.g., see the images in Fig. 1). The PE points will be used in the fine detection. All of the CT images are further resized to 128 × 128 pixels for the coarse detection, because the computational time is still very long. In the resized image, the PE point on an SP image is located at and . An image patch IP that includes the SP appearance is then cropped to a size of 17 × 17 pixels around the PE point from the 128 × 128 SP images to make an SP patch 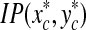, which consists of the pixels located as (x, y)s of the SP image I_SP as the following.

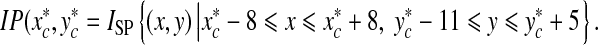4

It is noted that x and y are in the unit of a pixel. Since the upper region of the PE point contains more useful information to detect the PE point, it is positioned a little bit below the center of the SP patch. The size of 17 × 17 pixels is large enough to include the whole appearance of SP around the PE point. Figure 6 shows 20 SP patches, each of which shows the characteristic structure of SP although the appearances and the sizes are somewhat different from each other. Similarly, we define an image patch IP (x, y) with respect to the point (x, y) as in (4), and we will call (x, y) the base point of the image patch IP (x, y).

Fig. 6.

Some of the SP patches

SP patches are generally located around the center of the images which are positioned around a certain level in an axial stack. Also, SP patches have more bright pixels than dark ones. These location and intensity information make it easy to reject many non-SP patches. To establish a rejection criteria in the first stage of the coarse detection in Fig. 2, the levels l_SP(%) of the SP images and the locations of the PE points in SP images are found and also the sums of pixel intensities within SP patches are calculated. After studying the distribution of the locations of the PE points, we find that l_SP, , and the sum of all the pixel intensities in satisfy the following conditions.

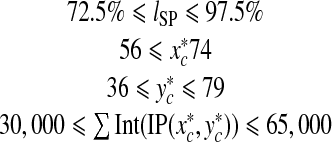5

To be an SP patch, it is necessary for an image patch IP (x, y) on level l(%) to satisfy the conditions (5), by which quite a lot of image patches can be eliminated in the beginning of the coarse detector.

However, there are still a large number of image patches that satisfy the conditions in (5) but do not include an SP structure. Therefore, we need to construct a classifier that can reject such image patches. For this, it is necessary to collect training samples to train the classifier. Among the image patches that satisfy the condition (5), 1,000 positive samples and 1,000 negative samples are randomly selected to train the first classifier in Fig. 4. In order to acquire more positive samples on SP images, some of the image patches from SP images are selected as positive samples if the distance between the PE point and their base points, i.e., is less than 2 (pixels). This gives sufficiently good positive samples considering that the side of a pixel is about 1.2 mm long. Therefore, up to nine positive samples can be cropped from an SP image. While the positive samples can be obtained in SP images, the negative samples can be extracted from non-SP images. In SP images, negative samples are also selected among the image patches whose base points are separated from the PE point by d₂  ≥  3 (pixels). Some of the negative samples are shown in Fig. 7. Compared to the SP patches in Fig. 6, the negative samples are quite different, not only from the positive ones but also from the other negative samples although they satisfy the conditions in (5). Such difference in appearance will be used to design a classifier that can differentiate between the positive and negative samples.

Fig. 7.

Negative samples

Filtering Image Patches Based on Appearance

In this subsection, we describe the hybrid detector shown in Fig. 4, which consists of binary classifiers connected in cascade. The term hybrid implies that two types of features, i.e., Haar-like and BDA features are employed in the detector. Since there are still quite a large number of non-SP patches after filtering the image patches that satisfy the conditions (5), the first few classifiers of the hybrid detector are required to reject as many non-SP patches as possible with minimum computational time. For this, the Haar-like features that employ the integral image technique are applied to the first four classifiers. Consequently, quite a few image patches that do not contain the SP structure are rejected as they go though the first four classifiers while almost all of the SP patches pass.

However, the classifier using the Haar-like features can no longer effectively discard non-SP patches after the fourth classifier because of relatively low discrimination ability. This is why the BDA features are adopted after the fourth classifier although it requires more computational time than the classifier employing the Haar-like features.

The first classifier of the cascade detector is trained with the training samples as mentioned above. After the training is completed, the classification by using the first classifier is conducted for all the image patches that have passed through the previous step. In order to train the second classifier, 1,000 positive and 1,000 negative samples are newly selected among the TP and FP samples that have passed through the first classifier (TP samples will also be called as TP patches). The next classifier is then trained similarly by using the new training samples. Since the negative samples are gathered from the FP samples, the next classifier can discard a major part of the FP samples that cannot be rejected by the current classifier. The classification criteria for TP and FP samples are that d₂ ≤ 2 (pixels) and d₂ ≥ 3 (pixels), respectively. This procedure is repeated until almost all of the non-SP patches in the training and validation images are removed. Table 1 summarizes the results after training each of the nine classifiers in the coarse detector. Note that FP patches decrease drastically compared to TP patches, and the number of FP patches after the 9th classifier are just about 20% of that of TP patches. This means that this cascade detector can pick up SP patches in a stack of images quite accurately.

Table 1.

Performance of the coarse detector

Classifier i	Number of the samples (P/N)		Feature	Number of Features	γH or θB	Performance (%)		Remaining patches after classifier i
	Training	Validation				TPR	FPR	Number of TP patches	Number of FP patches
1	1,000/1,000	1,000/1,000	Haar-like	2	0.3	96.8	29.4	1,592	103,803
2	1,000/1,000	1,000/1,000	Haar-like	10	0.56	98	47.2	1,558	42,146
3	1,000/1,000	1,000/1,000	Haar-like	13	0.92	91.8	50.6	1,418	20,223
4	1,000/1,000	1,000/1,000	Haar-like	19	0.8	98.1	47.6	1,335	7,537
5	1,000/1,000	1,000/1,000	BDA	15	12.88	100	50.7	1,335	3,725
6	1,000/1,000	1,000/1,000	BDA	15	10.2	99.6	50.1	1,330	1,889
7	1,000/1,000	1,000/1,000	BDA	20	9.52	97.3	50.2	1,298	994
8	1,000/968	1,000/944	BDA	10	6.76	95.8	50.21	1,244	474
9	1,000/258	1,000/474	BDA	10	5.06	85.1	47.05	1,053	223

The parameters in the classifiers are set so that the classifiers give the best performance for the image patches which belong to the validation set. Each classifier (i = 1,…,4) which uses the Haar-like features has two parameters to be tuned, the number of features and the parameter γ_H, which adjusts the threshold of the classifier. We evaluate the classifier performance to tune these parameters, which make the true positive rate as high as possible under the constraint that the false positive rate is less than 50% for image patches from the validation set. Table 1 shows that the first four classifiers, which use the Haar-like features, are well tuned to satisfy the performance specification.

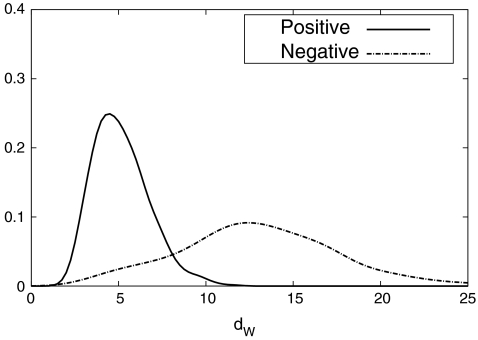
On the other hand, each of the next five classifiers using BDA features has three parameters to be tuned, i.e., the regularization parameter μ, the number of the features, and the threshold θ_B. The regularization parameter μ is always set to 0.01, and the number of the features is found among the multiples of five up to 30 to maximize the true positive rate. Then, the threshold θ_B is tuned based on the distribution of d_w in (3) for the image patches in the validation set. Figure 8 shows the distribution of d_w of the positive and negative samples in BDA space for the fifth classifier. This figure illustrates that BDA finds a subspace where the positive and negative samples are well discriminated by d_w. However, the overlapping region of the positive and negative samples increases as classification process continues, and the true positive rate of the 9th classifier goes down to 85%. From the distributions which are similar to Fig. 8, the threshold θ_B of each classifier using BDA features is set as shown in Table 1.

Fig. 8.

Distributions of d_W

The image patches satisfying the conditions (5) are gradually rejected by going through the classifiers in the cascade detector so that almost all the non-SP patches are discarded, and most of the remaining image patches are SP patches. Therefore, the cascade detector gives very high true positive rate and very low false positive rate. However, the cascade detector may reject too many SP patches, which may lead to a large error in locating the R-point. In order to avoid this, if the number of image patches that go through a classifier is less than a predetermined number, 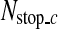, binary classification is not performed any further in the cascade detector and the next process is carried out with the remaining image patches. 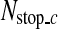is computed from the number of CT images in an axial stack. 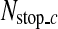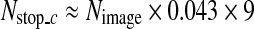In each stack, the number of SP images is about 4.3% of the number of CT images (N_image) on average, and we determine as in the coarse detector since an SP-image contains nine SP patches.

Table 1 shows that 223 non-SP patches along with 1,053 SP patches have passed through the cascade detector for the image patches in the validation set. Since these non-SP patches will contribute large errors in determining the R-level, they should be eliminated. To remove these non-SP patches, the remaining image patches are further processed by using the geometric information of SP at the end of the cascade detector.

Filtering Image Patches Based on Geometric Information

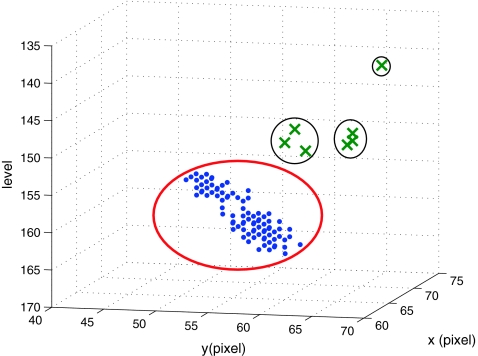
Since SP is a three-dimensional joint structure in the pelvis, the location of the PE point in an SP patch should not change abruptly as the level number increases in an axial stack of CT images. Therefore, the three-dimensional base points (x, y, l) of the TP patches that have passed the cascade detector should be in each other’s neighbor and form a cluster. By using this property, the remaining FP patches can be discarded. Therefore, a simple clustering algorithm is applied to all the base points of the remaining image patches. In the clustering, any two base points are considered to belong to the same cluster if the distance between the two points is less than θ_C (θ_C = 4 in this paper). There may exist several clusters, and in such a case, all the points are discarded except those in the largest cluster. Figure 9 shows an example of clustering, which makes four clusters. Among these clusters, only the points in the largest cluster are used to find the R-point. This example shows that the geometric information is very effective to remove the FP patches that cannot be rejected by the previous classifiers. Following a usual practice, the R-level 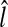is determined as the average of the smallest and the largest level numbers of the remaining base points. The location 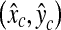of the R-point on level 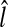is determined by averaging the base points of the remaining image patches on level 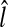. If there is no image patch remaining on , 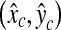is calculated as the average of all the remaining base points in the largest cluster.

Fig. 9.

Clustering of the base points. Each point denotes a base point

Fine Detection

The location of the R-point 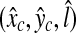has been determined based on 128 × 128 images in the coarse detection because of computational time. A further processing with higher resolution images around can improve the detection performance at small additional computational time. Here, we are interested in locating the R-point more precisely in (x, y) coordinates with the R-level fixed at 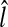. The location 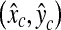on a 128 × 128 pixel image is transformed to a new location 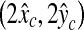on a 256 × 256 pixel image. Based on the distribution of the errors 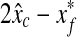and 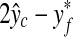of 21 stacks in the validation set, the search region for the fine detection is determined. Therefore, only the image patches around the base point (x, y) satisfying the following conditions are examined whether they are SP patches or not.

In the fine detection, the size of an image patch is 31 × 31 pixels. Among the image patches that satisfy the above conditions, positive and negative samples are selected to train the classifiers. The positive and negative samples are distinguished by the distance between the base point 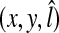and , i.e., . It is noted that l is in the unit of a level. An image patch is considered as positive if d₃ ≤ 2 whereas it is considered as negative if d₃ > 4 in the first two classifiers, and d₃ ≥ 3 in the next three classifiers. Since the number of image patches that will be classified in the fine detection is only 42, the classifier using the Haar-like features is not employed. Hence, another cascade detector that consists of five classifiers using BDA features is constructed similarly as in the coarse detector. The classification process stops when the number of image patches that go through the classifier is less than a predetermined number (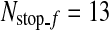in this paper). Finally, the R-point is located by averaging the base points of the remaining image patches.

Experiments

After training the classifiers described as above, we conducted experiments using 21 stacks in the validation set, the R-point obtained by the proposed method is compared to the R-point 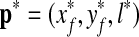determined by the radiologist for each stack. The average error 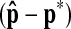and the average of absolute error 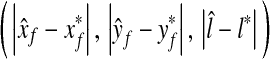are (0.42, 0.56, 0.12) and (0.87, 1.0, 0.5), respectively. Since the unit of x- and y-coordinates is a pixel (≈1.2 mm) and the unit of z-coordinate is a level (2.5 mm), the average location error is 1.88 mm. This shows that the proposed method can quite accurately detect the R-point. However, the errors in the x- and y-coordinates had more positive values than negative values, implying the results of the proposed method were positively biased. Therefore, we compensated the bias in the x- and y-coordinates, and the average of the absolute error for the x- and y-coordinates reduced to 0.79 and 0.95 pixels, respectively. Since the location of the R-point in each coordinate should be an integer, we rounded off the values found after the bias compensation to the nearest integer.

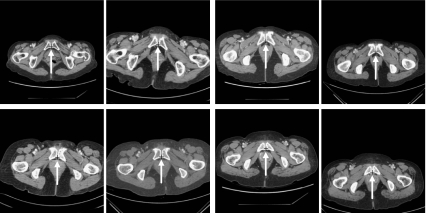
Next, experiments were conducted to detect the R-points for 49 stacks of CT images in the test set to evaluate the performance of the proposed method. Figure 10 shows some of the R-points found by the proposed method, and the points are represented by “+” in the images. Each pair of the images in Fig. 10 belongs to the same patient but was taken several months apart. Nevertheless, the R-points located in each image pair are anatomically almost identical although the SP structure appears at different locations or sizes.

Fig. 10.

The R-points detected from a pair of CT image stacks of the same patient

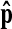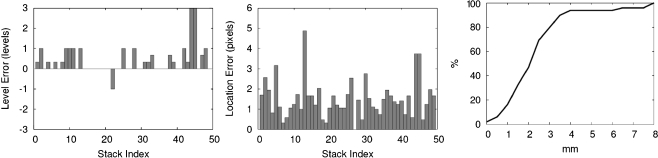
To quantitatively evaluate the performance of the proposed method, we investigated the difference between and the location located by the radiologist for 49 stacks in the test set. When the radiologist marked the R-point at different occasions, it was difficult to mark the same R-points all the time, and the marked points were at slightly different locations. Therefore, the location 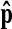found by the proposed method is compared to the average of the R-points marked by the radiologist at different occasions. The errors for each of the 49 stacks are shown in Fig. 11 after the bias compensation. The average absolute level error is 0.42 levels with the standard deviation of 0.67 levels while the average location error in the xy plane is 1.51 pixels with the standard deviation of 0.94 pixels. In three-dimensional space, these amount to the average location error of 2.23 mm with the standard deviation of 1.63 mm, whereas the average location error and the standard deviation are 0.77 and 0.45 mm for the three R-points marked by the radiologist. The last graph of Fig. 11 shows the cumulative distribution of the location error. It is noted that most of the location errors (about 94%) are smaller than 4 mm. These results imply that the proposed method can locate the R-point that is very close to the R-point that a radiologist would mark.

Fig. 11.

Errors of the 49 stacks in the test set. These figures show the level errors, the location errors in the xy plane, and the cumulative distribution of the location errors in three-dimensional space, respectively

Conclusion

In this paper, we propose a method for detecting the R-point from a stack of axial CT images. In order to reduce the computational time for real time application, the method employs the coarse detector and the fine detector. The coarse detector uses low resolution images whereas the fine detector uses high-resolution images. In coarse detection, candidates of SP patches are selected by using three types of information, which the location and intensity of an image patch, the appearance of SP, and the geometric characteristic of SP. Almost all the image patches that passed the coarse detector are SP patches. From these, the R-level is determined by averaging the lowest and the highest levels of these image patches, and the R-point is determined by averaging the base points in the image patches on the R-level. In order to locate the R-point in the xy plane more precisely, the fine detection is performed for the high resolution image patches around the R-point found in the coarse detection. The test result of 49 stacks shows that the R-point can be located with high confidence, so that it can be used as a starting point for image registration of CT images. Since it takes about 10 s to detect the R-point in an axial stack of CT images by using MATLAB on a PC (Core2 Duo), the proposed method can be used in real time applications.