Development and evaluation of a computer-aided diagnostic scheme for lung nodule detection in chest radiographs by means of two-stage nodule enhancement with support vector classification

Abstract

Purpose: To develop a computer-aided detection (CADe) scheme for nodules in chest radiographs (CXRs) with a high sensitivity and a low false-positive (FP) rate.

Methods: The authors developed a CADe scheme consisting of five major steps, which were developed for improving the overall performance of CADe schemes. First, to segment the lung fields accurately, the authors developed a multisegment active shape model. Then, a two-stage nodule-enhancement technique was developed for improving the conspicuity of nodules. Initial nodule candidates were detected and segmented by using the clustering watershed algorithm. Thirty-one shape-, gray-level-, surface-, and gradient-based features were extracted from each segmented candidate for determining the feature space, including one of the new features based on the Canny edge detector to eliminate a major FP source caused by rib crossings. Finally, a nonlinear support vector machine (SVM) with a Gaussian kernel was employed for classification of the nodule candidates.

Results: To evaluate and compare the scheme to other published CADe schemes, the authors used a publicly available database containing 140 nodules in 140 CXRs and 93 normal CXRs. The CADe scheme based on the SVM classifier achieved sensitivities of 78.6% (110∕140) and 71.4% (100∕140) with averages of 5.0 (1165∕233) FPs∕image and 2.0 (466∕233) FPs∕image, respectively, in a leave-one-out cross-validation test, whereas the CADe scheme based on a linear discriminant analysis classifier had a sensitivity of 60.7% (85∕140) at an FP rate of 5.0 FPs∕image. For nodules classified as “very subtle” and “extremely subtle,” a sensitivity of 57.1% (24∕42) was achieved at an FP rate of 5.0 FPs∕image. When the authors used a database developed at the University of Chicago, the sensitivities was 83.3% (40∕48) and 77.1% (37∕48) at an FP rate of 5.0 (240∕48) FPs∕image and 2.0 (96∕48) FPs ∕image, respectively.

Conclusions: These results compare favorably to those described for other commercial and noncommercial CADe nodule detection systems.

INTRODUCTION

Lung cancer accounts for about 28% of all cancer diagnoses in 2009.¹ The overall 5-year-survival rate for lung cancer patients is only 14%. Early detection and treatment of lung cancers are very important because the 5-year-survival rate can increase to up to 50% if the tumor is detected accurately and diagnosed at stage 1, where there is a solitary, circumscribed lung nodule.²

For detection of lung cancer at an early stage, computed tomography (CT) is considered to be a sensitive imaging modality.³ However, chest radiographs (CXRs) are used far more commonly for chest diseases because they are the most cost-effective, the most routinely available, and the most dose-effective diagnostic tool, and they are able to reveal some unsuspected pathologic alterations.⁴ Because CXRs are so widely used, improvements in the detection of lung nodules in CXRs could have a significant impact on early detection of lung cancer.

Although CXRs are the most widely used modality for lung diseases, it has been well demonstrated that detection of lung cancer at an early stage in CXRs is a very difficult task for radiologists. The difficulties in detecting lung nodules in CXRs are threefold: (1) There is a wide range of nodule sizes, (2) nodules exhibit a large variation in density in CXR, and (3) nodules can be obscured by other anatomic structures. The reasons for misdetection may be due to differences in decision techniques, lack of clinical data, and structured noise in CXRs.^{5, 6, 7} Studies have shown that up to 30% of nodules in CXRs were missed by radiologists, but nodules were visible in retrospect.^{8, 9}

Therefore, a computer-aided diagnostic (CADe) scheme^{10, 11} for nodule detection in CXRs has been investigated for assisting radiologists in improving their sensitivity in the detection of lung nodules. Detection of nodules by a CADe scheme is used as a “second opinion” for assisting radiologists’ decision-making to avoid their overlooking of subtle nodules. The feasibility and efficiency of CADe schemes were proved by Kobayashi et al.¹² and MacMahon et al.¹³ They showed that a CADe scheme could help radiologists improve their performance in the detection of pulmonary nodules. De Boo et al.¹⁴ provided a detailed review of clinical studies with CADe schemes. They reported that multiple studies had shown improvement in the detection performance of radiologists, especially of less experienced readers, with the use of CADe schemes, and that there were currently two FDA-approved systems (OnGuard, Riverain Medical and IQQA-chest, EDDA Technology) available in the market.

A wide variety of approaches in CADe schemes for nodule detection in CXRs have been developed. Giger et al.^{10, 15} developed a difference-image technique to reduce complex anatomic background structures while enhancing nodulelike structures for initial nodule candidate detection. Lo et al.^{16, 17} used a technique similar to the difference-image technique to create nodule-enhanced images, which were then processed by a feature extraction technique based on edge detection, gray-level thresholding, and sphere profile matching. Then, a convolution neural network was employed in a classification step. The CADe scheme developed by Xu et al. also employed a difference-image process, followed by feature extraction and classification processes.¹⁸ To improve the performance of the initial nodule candidate detection, Yoshida et al.¹⁹ employed the wavelet transform for detection of subtle nodules that were missed in the difference-image technique. The partial wavelet reconstruction method was used to replace the difference-image technique in the first step of the CADe scheme for enhancement of nodules while normal anatomic structures were suppressed. Vittitoe et al.²⁰ developed fractal texture characterization to improve the detection accuracy for solitary pulmonary nodules in a CADe scheme.

More recently, Carreira et al.²¹ proposed a CADe scheme based on the detection of nodule candidates with normalized cross-correlation images and classification of the candidates in curvature space. Penedo et al.²² then improved the performance of the scheme by incorporating two-level ANNs that employed cross-correlation teaching images and input images in the curvature peak space. Coppini et al.²³ developed a CADe scheme based on biologically inspired ANNs with fuzzy coding. Shiraishi et al.²⁴ incorporated a localized searching method based on anatomical classification and automated techniques for the parameter setting of three types of ANNs into a CADe scheme. Schilham et al.²⁵ proposed a new initial nodule candidate detection method based on multiscale techniques. Candidates were found by looking for local intensity maxima in the Gaussian scale space; and nodule boundaries were detected by tracing of edge points found from large scales down to the pixel scale. Campadelli et al.²⁶ improved the performance of a CADe scheme by introducing a new lung segmentation method. Hardie et al.²⁷ proposed a CADe scheme based on a weighted-multiscale convergence-index filter for initial nodule candidate detection and an adaptive distance-based threshold algorithm for candidate segmentation. Other researchers, including Mao et al., Li et al., Wei et al., and Freedman et al., reported on CADe schemes in which they incorporated various techniques for improving the performance.^{28, 29, 30, 31}

Although a great deal of work has been done by researchers to improve the performance of CADe schemes for nodule detection in CXRs, CADe schemes still produce a relatively large number of FPs. This would distract radiologists in their detection and reduce radiologists’ efficiency. A high rate of FPs would confuse radiologists by marking normal areas as suspicious, which may decrease radiologists’ specificity. In addition, radiologists may lose their confidence in the CADe scheme as a useful tool, which may result in a less improved performance by radiologists. Matsumoto et al.³² conducted an observer performance study to investigate the effect of the number of FPs on the accuracy of radiologists in detecting nodules. The study showed that if a CADe scheme had a high false-positive (FP) rate of 11∕image, radiologists’ accuracy in detecting pulmonary nodules was not improved with CADe, even though the scheme had a high sensitivity of 80%. Radiologists’ accuracy, however, was significantly improved if the CADe scheme had a simulated one FP rate with the same sensitivity. Therefore, having a low FP rate is critical for a CADe scheme to be useful. Investigators have developed various FP reduction methods. Yoshida and Keserci applied an edge-guided wavelet snake model to the extraction of a feature called a weighted overlap between the snake and the multiscale edges.^{33, 34} At the final step in their CADe scheme, the weighted overlap and morphologic features were combined by using an ANN for efficient reduction of FPs. Yoshida³⁵ proposed a method called local contralateral subtraction to remove normal anatomic structures in CXRs based on the symmetry between the left and right lung regions for FP reduction. Suzuki et al.³⁶ developed a multiple massive-training ANN to reduce the number of FPs produced by their CADe scheme.

In this research, we developed a novel CADe scheme for the detection of pulmonary nodules by using our two-stage nodule-enhancement technique combined with a support vector machine (SVM) classifier to improve the sensitivity for lung nodule detection and to reduce the FP rate. In the first stage of our two-stage nodule enhancement, gray-level morphologic nodule enhancement and a line-structure suppression technique improve the detection of the nodules overlapping ribs and clavicles in the initial nodule candidate detection. In the second stage, our nodule likelihood map improves the performance of the candidate detection further. Then, our clustering watershed method segments the detected nodule candidates accurately. Features are extracted from these segmented candidates for effectively determining the feature space, including one of the new features based on the Canny edge detector to eliminate one of the major FP sources, rib crossings. Finally, the SVM classifier with a Gaussian kernel accurately classifies the nodule candidates as nodules or non-nodules accurately.

MATERIALS AND METHODS

Databases of CXRs with nodules

Table 1 summarizes the databases used in this study. To train our CADe scheme, we collected 300 cases with nodules and 100 “normal” cases (i.e., nodule-free cases) from six medical institutions by using screen-film systems, computed radiography systems, and digital radiography systems. All nodules were confirmed by CT, and the locations of the nodules were confirmed by one of the chest radiologists. The nodule size ranged from 5 to 40 mm.

Table 1.

Databases used for training and evaluating our CADe scheme.

Database	No. of nodule cases	No. of normal cases	Descriptions
A	300	100	Training cases collected for developing our CADe scheme
BS	140	93	Subset of JSRT [14 cases with nodules in the opaque portions were excluded (Refs. 24, 27)]a
B	154	93	All nodule cases (154) and all normal cases (93) in JSRT database
C	48	0	U of C database

^aThe 14 cases were excluded because the purpose of our CADe scheme and other CADe schemes (Refs. ²⁴, ²⁷) was to detect nodules in the lung fields; therefore, the outside of the lung fields is outside our scope.

To facilitate future comparisons of our scheme with other methods, we used the JSRT database,³⁷ which is publicly available. The posteroanterior CXRs in the database were collected from 14 medical institutions by using screen-film systems over a period of 3 yr. All nodules in the CXRs were confirmed by CT, and the locations of the nodules were confirmed by three chest radiologists who were in complete agreement. The images were digitized to yield 12-bit CXRs with a resolution of 2048×2048 pixels. The size of a pixel was 0.175×0.175 mm. The original database contained 93 normal cases and 154 cases with confirmed lung nodules. The nodules were grouped into five categories, based on the degree of subtlety for detection, which may be influenced by the nodule size, occlusion by other structures, and nodule density. The subtlety categories were characterized by the average area under the receiver-operating-characteristic (ROC) curves,³⁸ determined by an observer performance study with 20 radiologists.

We created a database (denoted as database B_S) for evaluating our CADe scheme by excluding from the full JSRT database (denoted as database B) the nodules in the opaque portions of the CXR that correspond to the retrocardiac and subdiaphramatic regions of the lung because the purpose of using our CADe scheme was to detect nodules in the lung fields. As a result, 140 nodule cases were selected and included in the database (i.e., a subset of the JSRT database) for our experiments. Please note that evaluations of CADe schemes in the past studies^{24, 27} were performed without nodules in the opaque portions of CXRs for the same reason.

Table 2 shows the characteristics of the nodules in our evaluation database (database B_S). The average size of the nodules was 17.8 mm. The database contained 93 malignant nodules and 47 benign nodules, which were confirmed by histologic or cytologic examination or by follow-up imaging. Note that the resolution of internal (working) images of our CADe scheme was the same as that of the original images.

Table 2.

Characteristics of nodules in our evaluation database (database B_S) used for our experiments.

	Size (mm)			Total
	Small (5–14.9)	Medium (15–24.9)	Large (>25)
Extremely subtle	14	5	0	19 (13.6%)
Very subtle	10	13	0	23 (16.4%)
Subtle	21	19	8	48 (34.3%)
Relatively obvious	10	22	6	38 (27.1%)
Obvious	3	3	6	12 (8.6%)
Total	58 (41.4%)	62 (44.3%)	20 (14.3%)	140 (100%)

To evaluate the performance of our CADe scheme further, we collected a database (denoted as database C) containing 48 CXRs with 48 nodules, acquired with a computed radiography system (FCR 9501; Fujifilm Medical Systems, Stamford, CT) at the University of Chicago (U of C) Medical Center. These images have resolutions of 1760×1760 pixels (n=16), 2140×2140 pixels (n=8), 1760×2140 pixels (n=20), and 2140×1760 pixels (n=4), with a grayscale of 10 bits and a pixel size of 0.2×0.2 mm. This database contained 2 confirmed benign nodules, 6 suspicious malignant nodules, and 40 confirmed malignant nodules. The average size of the nodules was 31.9 mm (range: 12 mm–54 mm).

Scheme for nodule detection

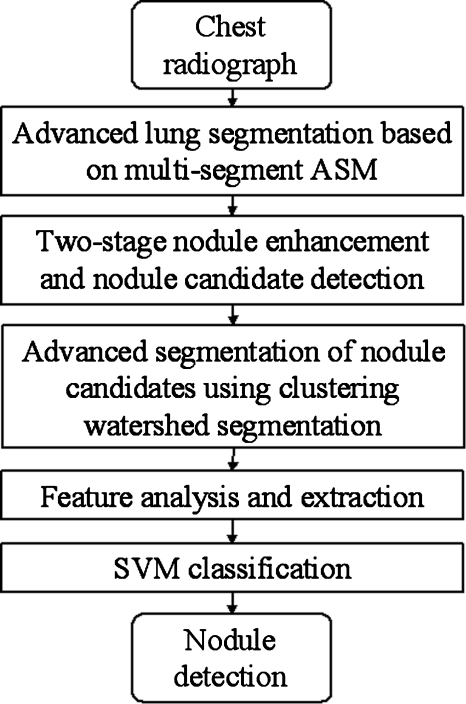
Figure 1 shows our CADe scheme for detection of lung nodules in CXRs, which consists of five major steps: (1) Segmentation of lung fields based on our M-ASM, (2) our two-stage enhancement of nodules and nodule candidate detection, (3) segmentation of the nodule candidates by using our clustering watershed algorithm, (4) feature analysis of the segmented candidates, and (5) classification of the nodule candidates into nodules or non-nodules by using a nonlinear SVM classifier.

Figure 1.

Main diagram for our CADe scheme.

Segmentation of lung fields

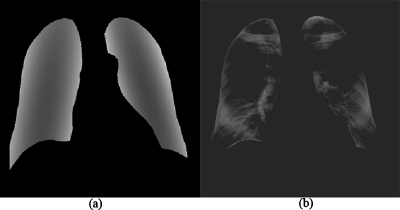
Lung segmentation is a critical component of a CADe scheme. It can prevent the occurrence of FPs outside the lung fields. Many methods have been proposed for segmenting the lungs in CXRs,³⁹ such as (1) rule-based segmentation methods, (2) pixel-based methods, (3) hybrid methods, and (4) deformable model-based methods. Because the prior information can easily be incorporated into the segmentation procedure, an active shape model (ASM) has been used for lung segmentation in CXR.^{40, 41, 42} Because a conventional ASM cannot cover changes and variations in the entire boundaries of the lungs accurately,³⁹ we developed a multisegment ASM (M-ASM) that is adaptive to each of multiple segments of the lung boundaries (which we call a multisegment adaptation approach), as illustrated in Fig. 2. Because the nodes in the conventional ASM are equally spaced along the entire lung shape, they do not fit lung shape parts with high curvatures.

Figure 2.

Lung segmentation by using an M-ASM. Each blue point represents the transitional landmarks between two boundary types (e.g., the heart and the diaphragm, the aorta, and the apex of the left lung).

In our method, the model was improved by fixating of the selected nodes at specific structural boundaries which we call transitional landmarks. Transitional landmarks identified the change from one boundary type (e.g., a boundary between the lung field and the heart) to another (e.g., a boundary between the lung field and the diaphragm). This resulted in multiple segmented lung-field boundaries where each segment is correlated with a specific boundary type (heart, aorta, rib cage, diaphragm, etc.). The node-specific ASM was built by using a fixed set of equally spaced nodes for each boundary segment.

Our lung M-ASM consisted of a total of 50 nodes for each lung boundary. The nodes were not equally spaced along the entire contour. A fixed number of nodes were assigned to each boundary segment, and they were equally spaced along each boundary (as shown in Fig. 2). For example, the boundary between the left lung field and the heart consisted of 11 points in every image, regardless of the actual extent of this boundary in the image (see Fig. 2). This allowed the local features of nodes to fit a specific boundary segment rather than the whole lung, which resulted in a marked improvement in the accuracy of boundary segmentation. In our experiment, 93 normal images from the public JSRT database were used for training of the M-ASM. From the training images, the relative spatial relationships among the nodes in each boundary segment were learned in order to form the shape model. The nodes were arranged into a vector x and projected into the principal component shape space by means of the following expression:

$$b=V^T\left(x-\overline{x}\right),$$ (1)

where V=(V₁V₂⋯V_M) is the matrix of the first M eigenvectors for the shape covariance matrix and b=(b₁b₂⋯b_M)^T is a vector of shape coefficients for the primary axes. The shape coefficients were constrained to lie in a range $\pm m\sqrt{{\lambda }_i}$ to generate only a plausible shape and projected back to node coordinates with the following expression:

$$x=\overline{x}+Vb.$$ (2)

Here, m usually has value between 2 and 3,⁴³ and it was 2.5 in our experiment.

The segmentation accuracy was computed by using the overlap measure Ω,

$$\Omega =\frac{{\text{TP}}_{\text{seg}}}{{\text{TP}}_{\text{seg}}+{\text{FP}}_{\text{seg}}+{\text{FN}}_{\text{seg}}},$$ (3)

where TP_seg was the area correctly classified as a lung field, FP_seg was the area incorrectly classified as a lung field, and FN_seg was the area incorrectly classified as the background. The mean and standard deviation of the overlap measure for all the 154 nodule images in the JSRT database were 0.913 and 0.023, respectively (including the 14 images in which nodules are in the obscured lung fields).

After the lungs were segmented, a background-trend-correction technique was applied to the segmented lung fields. A second-order bivariate polynomial function was fitted to each of the left and right lung fields individually, as illustrated in Fig. 3a, represented by

$$F\left(x,y\right)=a{x}^2+b{y}^2+cxy+dx+ey+f,$$ (4)

where a, b, c, d, e, and f are coefficients, which were calculated for each case. Subsequently, the fitted functions for the left and right lung fields were subtracted from the original image. In this way, the background trend in the lung fields as a low-frequency surface was removed, as illustrated in Fig. 3b. We call this image a preprocessed image.

Figure 3.

Background-trend-correction for the lung fields. (a) Lung fields fitted by a second-order bivariate polynomial function. (b) Preprocessed image (background-trend-corrected image).

Two-stage enhancement of nodules and nodule candidate detection

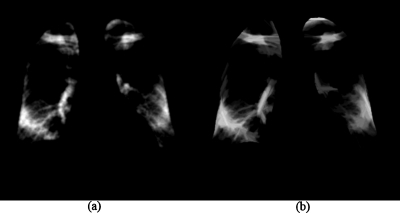
We developed a two-stage nodule-enhancement technique and applied it to the preprocessed image to obtain a nodule-enhanced image and a nodule likelihood map. The first stage of the technique was aimed at enhancing nodules and suppressing ribs, which were a major source of FPs. Two different types of gray-level morphologic opening operators⁴⁴ were used for producing a “nodule-like-pattern-enhanced” image and a “rib-like-pattern-enhanced” image.

First, a gray-level morphologic opening operator with a nodule template was applied to the preprocessed image to produce a nodule-like-pattern-enhanced image, as illustrated in Fig. 4a. A nodule is defined as a round opacity less than 3 cm in diameter seen in a chest radiograph,⁴⁵ and it is a roughly spherical object with a density comparable to that of water, which is higher than the surrounding lung parenchyma.²⁵ Therefore, we used a bivariate normal distribution as a nodule model in the nodule template, as shown in Fig. 5a. The standard deviation of the normal distribution corresponded to the scale of the target object, i.e., the average nodule size in a database. Next, several gray-level morphologic opening operators with rib templates were applied to the preprocessed image to produce a rib-like-pattern-enhanced image, as illustrated in Fig. 4b. Seven rib templates with seven different orientations, i.e., −68°, −45°, −22°, 0°, +22°, +45°, and +68°, as shown in Fig. 5b, were used for enhancing the riblike structures. The maximum value among the output of the seven operators was stored in each pixel in the rib-like-pattern-enhanced image. Finally, the rib-like-pattern-enhanced image was subtracted from the nodule-like-pattern-enhanced image to produce a nodule-enhanced image, as illustrated in Fig. 6. In the image, the nodulelike patterns have larger pixel values; the riblike patterns and other patterns have smaller pixel values. The gray-level morphologic filter can enhance a nodule effectively, as demonstrated in Fig. 7.

Figure 4.

Enhancement images by using gray-level morphologic filters with a nodule template (a) and rib templates (b). (a) Nodule-like-pattern-enhanced image. (b) Rib-like-pattern-enhanced image.

Figure 5.

Templates used for gray-level morphologic enhancement. (a) Nodule template containing a bivariate normal distribution. (b) Rib templates containing lines with seven different orientations.

Figure 6.

Nodule-enhanced image obtained by using our first-stage nodule enhancement.

Figure 7.

Nodule enhancement by using the gray-level morphologic filter. (a) ROI with a nodule. (b) Enhancement of the nodule by using the gray-level morphologic filter with the nodule (Gaussian) template. (c) Enhancement of ribs by using the gray-level morphologic filter with the rib (line) templates. (d) Nodule enhanced by subtracting (c) from (b).

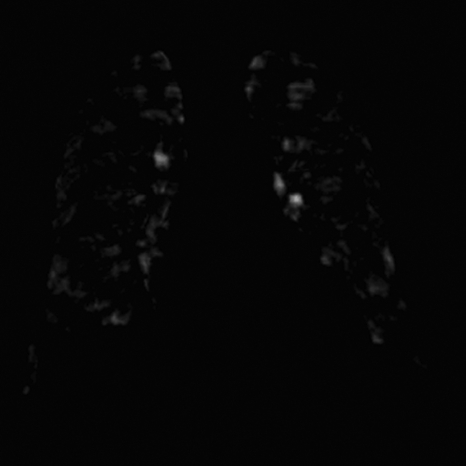
The purpose of the second stage of our nodule enhancement was to convert the nodule-enhanced image into a nodule likelihood map, as illustrated in Fig. 8. First, the nodule-enhanced image was smoothed by using a Gaussian filter in order to reduce noise. Next, the gradient magnitude M_ij and gradient direction G_ij were calculated from the noise-reduced image by using a modified Sobel operator, represented by

$$M_{ij}=\sqrt{M_{xij}+M_{yij}},G_{ij}=\text{arctan}\left(M_{yij}∕M_{xij}\right),$$$$M_{xij}=\left[\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right]\ast I_{\text{nodule-enhanced}},$$$$M_{yij}=\left[\begin{array}{ccc}1& 2& 1\\ 0& 0& 0\\ -1& -2& -1\end{array}\right]\ast I_{\text{nodule-enhanced}},$$ 5

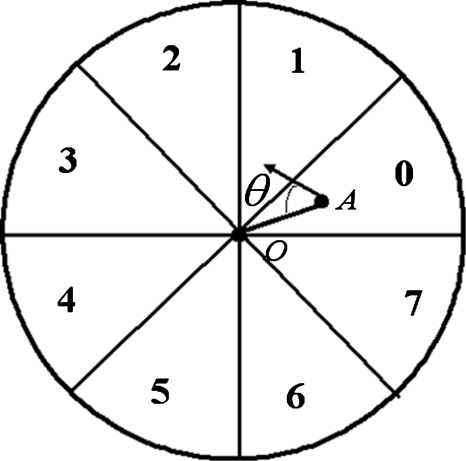
where I_{nodule-enhanced} is the nodule-enhanced image obtained by using the first-stage nodule enhancement. A nodule likelihood value was calculated at every pixel in the lung fields, as described below. A circle with its size related to the nodule template size was placed at an object pixel (i,j), as shown in Fig. 9. The circle was divided into eight sectors numbered from 0 to 7. A nodule likelihood value for section k at the object pixel (i,j) is defined by the following equation:

$$G_{ij}^k=\frac{1}{N_k}\sum _{mn∊\text{sector}k}\text{cos}{\theta }_{mn},$$$$t_1\le M_{mn}\le t_2,$$ 6

where θ is an angle between the gradient direction at a certain pixel (m,n) and a vector from the object pixel (i,j) to the pixel (m,n), t₁ and t₂ are low and high gradient magnitude thresholds, respectively, and N_k is the number of pixels in sector k. When a nodule candidate is located at the object pixel (i,j) and a certain pixel (m,n) is on the nodule candidate, cos θ should be close to 1.0. Because the gradient direction is unreliable when the gradient magnitude M is small, t₁ was utilized to prevent such an unreliable gradient direction from being used (in our experiment, t₁=5). t₂ was utilized because a pixel (m,n) may be located at a bone edge when the gradient magnitude M is large (in our experiment, t₂=150). Although some nodules have irregular shapes, the nodule likelihood values are still larger than those of ribs and other anatomic structures.

Figure 8.

Nodule likelihood map obtained by using our second-stage nodule enhancement.

Figure 9.

Schematic diagram for our nodule likelihood calculation for a point of interest O.

The final nodule likelihood combining all sectors at the object pixel (i,j) is defined by

$${\text{Likehood}}_{ij}=\frac{{\overline{G}}_{ij}}{{\sigma }_{ij}},$$ (7)

where ${\overline{G}}_{ij}$ and σ_ij are the mean and standard deviation, respectively.

Once a nodule likelihood map was calculated, local peaks in the map were detected. Because the smallest nodule in the JSRT database and the U of C database was larger than 5 mm, if the distance between any two peaks was less than 5 mm, a candidate was created only from the peak with the higher pixel value.

Coarse-to-fine segmentation of nodule candidates

After nodule candidates were detected, the boundaries of the nodule candidates had to be identified for the subsequent feature extraction. To segment the nodule candidates, we developed a “coarse-to-fine” segmentation technique based on morphologic filtering and improved watershed segmentation. First, a region of interest (ROI) in which a candidate was located at the center was extracted from the nodule-enhanced image, where the size of the ROI was larger than the largest nodule to be detected (the largest nodules in the JSRT database and the U of C database are 60 and 54 mm, respectively; in our experiment, the ROI size was 88 mm), as illustrated in Fig. 10a. Because positive values in the nodule-enhanced image are likely to be nodules, thresholding with a low positive threshold value (pixels with values less than 5 were removed) was applied to the nodule-enhanced image for extraction of nodule candidate regions, as illustrated in Fig. 10c. We applied a binary morphologic erosion operator to the nodule candidate regions to break connections between the nodule and non-nodule regions, as illustrated in Fig. 10d. The connected region that contained the nodule candidate location (as a point) determined by the initial nodule candidate detection step was retained, whereas non-nodule regions were removed, as illustrated in Fig. 10e. Next, a binary morphologic dilation operator dilated the connected region. As a result, a single connected region representing a rough nodule candidate was obtained, as illustrated in Fig. 10f.

Figure 10.

Nodule candidate segmentation by using our clustering watershed segmentation method. (a) ROI with a nodule. (b) First-stage nodule enhancement image by using background-trend correction and a gray-level morphologic filter. (c) Regions obtained by thresholding of the image (b) with a low positive threshold value. (d) Regions after erosion. (e) Connected region representing a rough nodule candidate. (f) Candidate region after dilation. (g) Inverted image. (h) Result with watershed segmentation alone. One region was divided into multiple small segments (catchment basins). (i) Nodule candidate segmented by our clustering watershed segmentation. (j) Nodule contour.

To refine the rough segmentation provided by morphologic filtering, we developed a clustering watershed segmentation technique. Peaks within the rough nodule candidate region in the nodule-enhanced image were obtained and used for initializing the watershed segmentation algorithm.⁴⁶ For the application of watershed segmentation, the grayscale of the ROI was first inverted so that the peaks became local minima, as illustrated in Fig. 10g. With the watershed segmentation, the rough nodule candidate region was divided into several catchment basins. Each minimum point was surrounded by a catchment basin associated with it; thus, there were one or more peaks, each of which was surrounded by a cluster of connected pixels that constituted a catchment basin, as illustrated in Fig. 10h. From the multiple catchment basins, a single nodule candidate region was determined by using the following clustering method: First, a primary cluster was defined as a cluster that contained the nodule candidate location (as a point) determined by the initial nodule candidate detection step. Next, clusters connected to the primary cluster were added. The connected clusters were identified by using the criterion that the minimum value between the peak in the primary cluster and each of the other peaks was larger than a threshold value, as illustrated in Fig. 11. Figure 10j illustrates a segmented nodule candidate obtained by using the clustering watershed segmentation.

Figure 11.

Criterion used for our cluster merging, where P₁ and P₂ are peak values in the corresponding clusters and min is the minimum value between the peaks.

Feature analysis and classification

We extracted features from each of the segmented nodule candidates after connected-component labeling.⁴⁷ Features in six categories (i.e., shape, gray-level, surface, gradient, texture, and a specific FP) were extracted from the segmented candidates. The shape features were defined by the following equations:

$${\text{Shape}}_1=A_{\text{region}},$$$${\text{Shape}}_2=\frac{D_{\text{major}}}{D_{\text{minor}}},$$$${\text{Shape}}_3=\frac{A_{\text{region}}}{A_{\text{convex}\text{hull}}},$$$${\text{Shape}}_4=1-\frac{d_{\text{candidate-center}}}{\sqrt{\frac{A_{\text{region}}}{\pi }}},$$ 8

where A_region is the area of a segmented nodule candidate, D_major and D_minor are the long and short axes, respectively, of an ellipse that is fitted to the segmented nodule candidate, A_{convex hull} is the area of the convex hull of the candidate, and d_{candidate-center} is the distance between the centroid of the candidate and the center of the fitted ellipse. All features were normalized so as to be independent of the magnification and resolution of the imaging system.

The gray-level features were calculated from the segmented nodule candidates and their surrounding regions in both the preprocessed image and the nodule-enhanced image. A surrounding region was produced by subtracting a candidate region from a dilated candidate region, as illustrated in Fig. 12. The gray-level features were defined as

$${\text{Gray}}_1={\mu }^{\text{region}}-{\mu }^{\text{surround}},$$$${\text{Gray}}_2={\sigma }^{\text{region}}-{\sigma }^{\text{surround}},$$$${\text{Gray}}_3={\text{min}}^{\text{region}}-{\text{min}}^{\text{surround}},$$$${\text{Gray}}_4={\text{max}}^{\text{region}}-{\text{max}}^{\text{surround}},$$ 9

where μ, σ, min, and max are the mean, the standard deviation, the minimum, and the maximum of pixel values in the preprocessed image, respectively, and the designation region and surround indicate a candidate region and its surrounding region, respectively. Gray₅, Gray₆, Gray₇, and Gray₈ were features calculated based on the above equations, but in the nodule-enhanced image (instead of the preprocessed image).

Figure 12.

(a) Nodule region. (b) Surrounding region.

The segmented candidate region in the nodule-enhanced image was fitted to a fourth-order bivariate polynomial. The principal curvatures were calculated at the point of the highest elevation in the region. Second-order derivatives of the fitted polynomial were calculated and formed the elements of a Hessian matrix. The maximum and minimum eigenvalues of the Hessian matrix, λ_max and λ_min, were the principal curvatures. The surface features were given by

$${\text{Surface}}_1={\lambda }_{\text{min}},$$$${\text{Surface}}_2={\lambda }_{\text{max}},$$$${\text{Surface}}_3={\lambda }_{\text{min}}{\lambda }_{\text{max}}.$$ 10

We used gradient in the segmented candidate region in the nodule-enhanced image to calculate gradient features, which are similar to the calculation of the nodule likelihood values in the two-stage nodule enhancement, represented by

$${\text{Gr}}^h=\frac{1}{N_h}\sum _{mn∊{\text{region}}_h}\text{cos}{\theta }_{mn},$$$$t_1\le M_{mn}\le t_2,$$ 11

where N_h is the number of pixels in the segmented nodule region h. The gradient features for the segmented nodule region were given by

$${\text{Grad}}_1=\overline{\text{Gr}}=\frac{1}{8}\sum _{k=0}^7{\text{Gr}}^h,$$$${\text{Grad}}_2=\sigma =\sqrt{\frac{1}{8}\sum _{k=0}^7{\left({\text{Gr}}^h-\overline{\text{Gr}}\right)}^2},$$$${\text{Grad}}_3=\frac{\overline{\text{Gr}}}{\sigma }.$$ 12

Texture features were calculated from the preprocessed image, the gradient magnitude image, and the gradient direction image, which were calculated by Eq. 5. The texture features were given by the following equations:

$${\text{Texture}}_1=\sum _{ij}{\left[C\left(i,j\right)\right]}^2,$$$${\text{Texture}}_2=\sum _{ij}{\left(i-j\right)}^{2}C\left(i,j\right),$$ 13

where C(i,j) is the co-occurrence matrix calculated over neighboring pixels and a summation range from the minimum to the maximum pixel value in the preprocessed image,

$$C\left(i,j\right)=\sum _{m=-1}^1\sum _{n=-1}^1\#\left\{f\left(x,y\right)=i,f\left(x+m,y+n\right)=j\right\}-\#\left\{f\left(x,y\right)=i,f\left(x,y\right)=j\right\},$$ (14)

where # is the number of elements in the set. Texture₃, Texture₄, Texture₅, and Texture₆ are features calculated based on the above equations, but in the gradient magnitude image and the gradient direction image (instead of the preprocessed image), respectively.

We developed an FP reduction feature designed to eliminate rib∕clavicle crossings, which are a major FP source. We used the Canny edge detector to find prominent edges within the lung field in the preprocessed image. Connected edge pixels then formed into chains which would correspond to rib∕clavicle edges in the image. The overlap feature was defined by

$$\text{FP}=\frac{L_{\text{overlap}}}{L_{\text{region}}},$$ (15)

where L_region is the length of the boundary of a candidate region and L_overlap is the number of pixels on the boundary that overlap the edge chains.

In addition to the above six feature categories, segmented-candidate-based features, Can.x, Can.y, Can.Cv₁, Can.Grad₁, Can.Cv₂, and Can.Grad₂, were calculated. Can.x and Can.y are the coordinates of a nodule candidate. Can.Grad₁ and Can.Grad₂ are the nodule likelihood values calculated by Eq. 7 at the detected nodule candidate location in the nodule candidate detection step in the nodule-enhanced image and the preprocessed image, respectively. Can.Cv₁ and Can.Cv₂ were calculated by using the gray-level values instead of the gradient values in Eq. 7.

Finally, a nonlinear SVM with a Gaussian kernel was employed for classification of the nodule candidates. We selected this classifier because its generalization ability is relatively high with a small number of training samples. We selected the Gaussian kernel among several kernels, including a polynomial kernel, because it achieved the best performance. The Gaussian kernel is represented by

$$k\left(x_i,x_j\right)=\text{exp}\left(-\delta {\parallel x_i-x_j\parallel }^2\right),$$ (16)

where δ is a parameter. The parameter δ in the kernel was determined to be 1.0 by empirical analysis. Note that linear SVMs were not selected because our problem is generally a nonlinear classification problem.

Classification by an SVM is realized by the solution of the following quadratic optimization problem:

$$\text{Minimize}:W\left(a\right)=-\sum _{i=1}^l{a}_i+\frac{1}{2}\sum _{i=1}^l\sum _{j=1}^l{y}_i{y}_j{a}_i{a}_{j}k\left(x_i,x_j\right),$$ (17)

$$\text{Subject}\text{to}\sum _{i=1}^l{y}_i{a}_i=0,\forall i:0\le a_i\le C,$$ (18)

where l is the number of training samples and a is a vector of l variables, each component of which, a_i, corresponds to a training sample (x_i,y_j). C was determined to be $\sqrt{{\sum }_{i=1}^l{x}_i\cdot x_i∕l}-1.0$ before training. The solution of Eq. 17 is the vector a^∗ for which Eq. 17 is minimized, while the constraints in Eq. 18 are fulfilled.

The SVM classifier was trained∕tested with a leave-one-out cross-validation test. The performance of the SVM classifier was evaluated by using free-response receiver-operating characteristic (FROC) analysis⁴⁸ and compared to that of a linear discriminant analysis (LDA) classifier.⁴⁹ Features for the LDA were selected by using the stepwise feature selection method.⁴⁹ With the selection method, we determined a single set of features from M runs of a leave-one-out cross-validation test (M is the number of features). Each feature was selected at each run after we accumulated all N results from the run (N is the number of samples).

RESULTS

In this section, we present experimental results to demonstrate the performance of our CADe scheme. We first present the results of the initial nodule candidate detection. Then, we present the overall performance of our CADe scheme for databases B_S (a subset of the JSRT database), B (the JSRT database), and C (the U of C database). Finally, we discuss comparisons with other CADe schemes.

Nodule candidate detection

The criterion for determining a TP that we adopted was that if the centroid of a detected candidate is located within the “reference-standard” nodule area, which was drawn by a radiologist, the candidate is considered as a TP. We shall call this a “region” criterion. In Sec. 4, we compare the region criterion to other criteria used in literature.

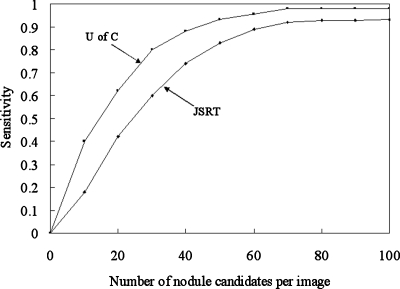
Figure 13 shows the performance of the nodule candidate detection stage in our CADe scheme for the JSRT and U of C databases. The sensitivity starts dropping when the number of nodule candidates is less than 70∕image.

Figure 13.

FROC curves indicating the performance of the nodule candidate detection part of our CADe scheme for the JSRT database and the U of C database.

The nodule candidate detection stage in our CADe scheme achieved a sensitivity of 92.1% (129∕140) with 70 candidates∕image and a sensitivity of 97.9% (47∕48) with 70 candidates∕image for databases B_S and C, respectively.

Overall performance of the CADe scheme

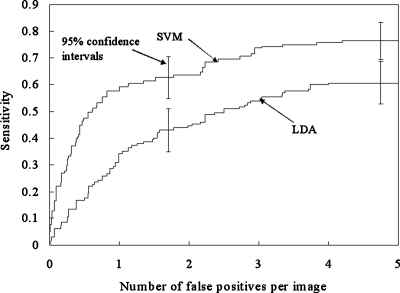
FROC curves showing the overall performance of our CADe scheme for database B_S (i.e., a subset of the JRST database) in a leave-one-out cross-validation test are shown in Fig. 14. The stepwise feature selection method selected 11 features for the LDA, as listed in Table 3. The performance of our CADe scheme with the SVM was substantially higher than that of our CADe scheme with the LDA, i.e., it achieved a sensitivity of 76.4% (107∕140) with the SVM and a sensitivity of 60.7% with the LDA at an FP rate of 5.0 FPs∕image for nodule cases in database B_S. It is interesting to note that when all 31 features were used for the LDA classifier, the sensitivity was 53.6% (75∕140) at an FP rate of 5.0 FPs∕image for the JSRT database. It is also interesting to note that if the features selected for the LDA were used for the SVM, the performance (i.e., a sensitivity of 68.6% (96∕140) with 5.0 (700∕140) FPs∕image for database B_S) was lower than the performance of the SVM with all 31 features. This would indicate that features selected for a linear classifier are not optimal for a nonlinear classifier. The SVM-based CADe scheme marked 22 more nodules than did the LDA-based CADe scheme at an FP rate of 5 FPs∕image. Most of these nodules were very subtle or extremely subtle in database B_S.

Figure 14.

FROC curves indicating the performance of our CADe scheme with SVM or LDA for the JSRT database.

Table 3.

Features selected for LDA in the two databases, i.e., databases B_S (JSRT) and C (U of C). (The asterisks indicate a selected feature.)

Extracted features	JSRT	U of C	Extracted features	JSRT	U of C	Extracted features	JSRT	U of C
Can.x	*		Gray1			Grad3	*	*
Can.y	*		Gray2			Surface1		*
Can.Grad1		*	Gray3		*	Surface2	*
Can.Cv1	*		Gray4	*		Surface3		*
Can.Grad2			Gray5	*		Texture1		*
Can.Cv2			Gray6			Texture2		*
Shape1		*	Gray7		*	Texture3		*
Shape2			Gray8	*	*	Texture4
Shape3			Grad1	*		Texture5
Shape4	*	*	Grad2	*		Texture6 FP

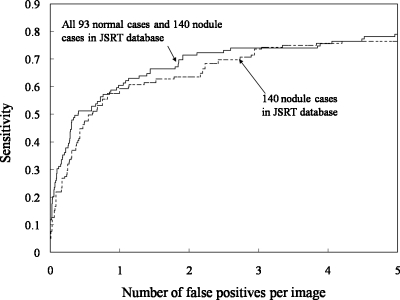
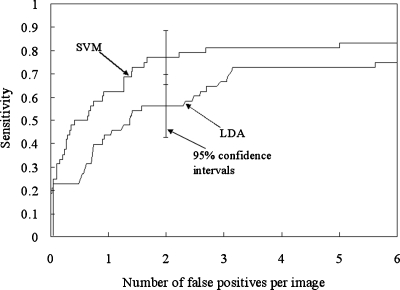
Table 4 summarizes the performance of our CADe scheme for different databases. Figure 15 compares the performance of our CADe scheme for database B_S containing all 93 normal cases and 140 nodule cases with that for the 140 nodule cases alone. The performance for database B_S was slightly higher than that for nodule cases alone. A possible reason for the higher performance is that the pessimistic bias with a leave-one-out cross-validation test was smaller when the number of cases was larger.^{50, 51} We also included in the evaluation the 14 excluded nodules in the opaque portions of the CXR that correspond to the retrocardiac and subdiaphramatic regions of the lung, i.e., database B. The sensitivity for all 154 nodule cases (i.e., database B) was lower by 9.1% (14∕154) than that for the 140 nodule cases because all of the 14 excluded nodules were outside the segmented lung fields; in other words, our CADe scheme did not process those areas, as designed. Figure 16 shows the performance of our CADe scheme for the U of C database (database C). The stepwise feature selection method selected 12 features for the LDA, as listed in Table 3. At an FP rate of 5.0 FPs∕image, the sensitivity of the SVM-based CADe scheme with all 31 features was 83.3% (40∕48), whereas that of the LDA-based scheme with the 12 selected features was 75.0% (36∕48). At an FP rate of 2.0 FPs∕image, the sensitivity of the SVM-based CADe scheme was 77.1% (37∕48).

Table 4.

Performance of our CADe scheme for different databases for which each a classifier was trained∕tested with a leave-one-out cross-validation scheme.

Databasesa	Sensitivity	FPs∕image
BS	78.6% (110∕140)	5.0 (1165∕233)
	80.0% (112∕140)b	5.0 (1165∕233)b
	71.4% (100∕140)	2.0 (466∕233)
B	71.4% (110∕154)	5.0 (1235∕247)
	64.9% (100∕154)	2.0 (494∕247)
C	83.3% (40∕48)	5.0 (240∕48)
	77.1% (37∕48)	2.0 (96∕48)

^aRefer to Table 1 for details.

^bPerformance calculated with the distance criterion of 25 mm for a direct comparison with the performance in Ref. 27. Reference ²⁴ also used the distance criterion.

Figure 15.

FROC curves indicating the performance of our CADe scheme for the JSRT database.

Figure 16.

FROC curves indicating the performance of our CADe scheme for the U of C database.

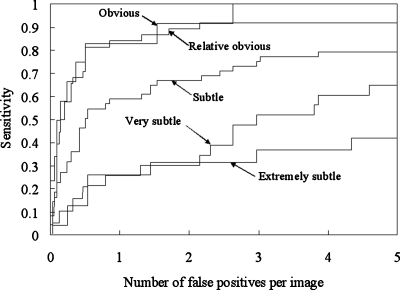
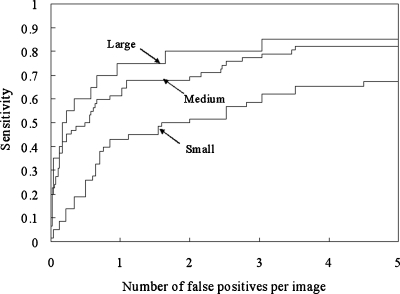
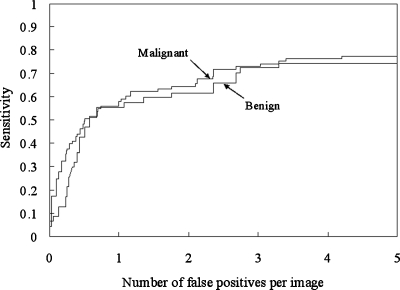
We analyzed the CADe performance according to nodule subtlety, size, and pathology, as shown in Figs. 171819 for database B_S. It should be noted that the sensitivity was calculated in each category (i.e., the sensitivity was 100% if all nodules in a particular category were marked.). Our CADe scheme marked 54.8% (23∕42) of very subtle and extremely subtle nodules with 5 FPs∕image. All obvious nodules were marked with 2.6 FPs∕image, and 91.9% (35∕38) of relatively obvious nodules were detected with 2.2 FPs∕image. Our scheme has a high performance for large- and medium-sized nodules and a relatively high performance [a sensitivity of 65.5% (38∕58) with 5.0 FPs∕image] for small nodules, as shown in Fig. 18. The sensitivities for malignant and benign nodules were comparable, as shown in Fig. 19.

Figure 17.

FROC curves indicating the performance of our CADe scheme by nodule subtlety for the JSRT database.

Figure 18.

FROC curves indicating the performance of our CADe scheme by nodule size for the JSRT database.

Figure 19.

FROC curves indicating the performance of our CADe scheme by pathology for the JSRT database.

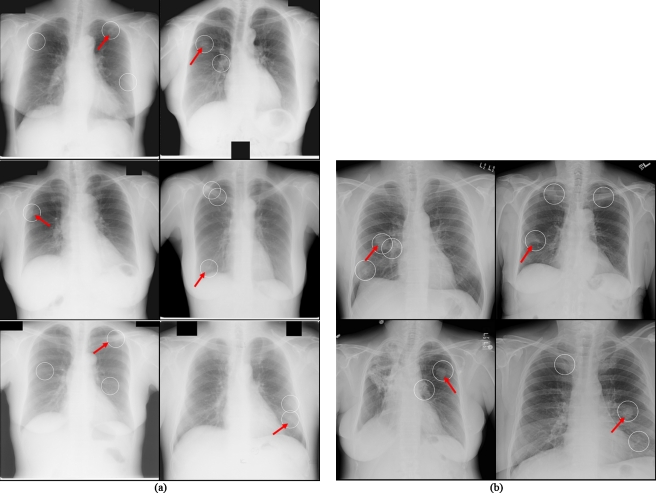
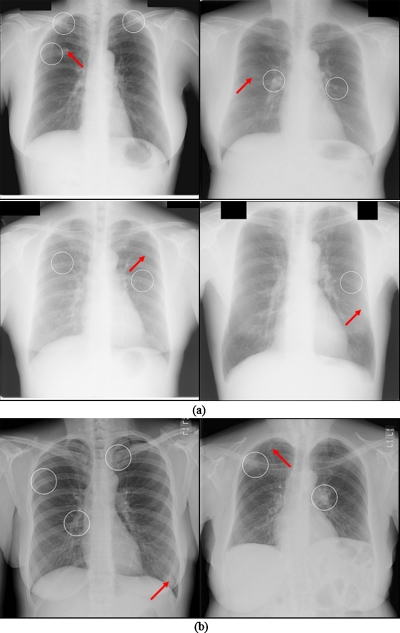
Typical examples of our CADe detection results at operating points with FP rates of 4.5 and 4.0 FPs∕image for databases B_S (i.e., the JSRT database) and C (U of C database) are shown in Figs. 20a, 20b, respectively. These examples show one TP and several FPs in each case. The FPs include an anterior and posterior rib intersection, a clavicle, and a rib intersection. Figure 21 illustrates several examples of nodules missed by our CADe scheme. We found that the missed nodules tended to be small and to have low contrast. Most of them were rated as very or extremely subtle.

Figure 20.

Illustrations of true positives (arrows) and false positives of our CADe marks (circles). (a) Cases from the U of C database. (b) Cases from the JSRT database.

Figure 21.

Illustrations of false negatives (arrows) and false positives of our CADe marks (circles). (a) Cases from the JSRT database. (b) Cases from the U of C database.

Performance comparison with other CADe schemes

It is difficult to make definitive comparisons with the previously published CADe schemes because of different databases, different TP criteria, different evaluation procedures, different optimization parameters, and different operating points.⁵² We, however, attempted to compare our performance to the performance reported in literature. We found four studies in which the publicly available JSRT database was used. Table 5 summarizes the performance comparisons among different CADe schemes in literature. Wei et al.³⁰ reported that their CAD scheme achieved a sensitivity of 80% with 5.4 FPs∕image for the JSR database. They did not mention anything about training-testing separation. Because more than 200 features (i.e., the number of freedoms) were used for training and testing which were greater than the number of nodules (i.e., the number of training samples) in the database, the reported performance should be highly biased due to the overtraining. Hardie et al.²⁷ reported that their scheme marked 80% of nodules in a subset of the JSRT database (i.e., database B_S) with 5 FPs∕image. Their performance was calculated by using the distance criterion of 25 mm for determining TP detections. Training and testing should be considered not to be independent because the authors matched the characteristics of the testing database with those of the training database. The performance (a sensitivity of 71%) of our CADe scheme was substantially higher than that (63%) of Hardie’s CADe scheme at a low FP setting (2.0∕image), which is relevant in practical use in hospitals.

Table 5.

Performance comparisons of CADe schemes that used the JSRT database for evaluation in literature.

	Sensitivity	FPs∕image	Database
Wei et al. (2002) (Ref. 30)a	80% (123∕154)	5.4 (1333∕247)	All nodule and normal cases in JSRT (247)
Coppini et al. (2003) (Ref. 23)	60% (93∕154)	4.3 (662∕154)	All nodules cases in JSRT (154)
Schilham et al. (2006) (Ref. 25)	51% (79∕154)	2.0 (308∕154)	All nodule cases in JSRT (154)
	67% (103∕154)	4.0 (616∕154)
Hardie et al. (2009) (Ref. 27)b	80% (112∕140)	5.0 (700∕140)	Nodule cases in JSRT (140)
	63% (88∕140)	2.0 (280∕140)

^aThe authors did not discuss training-testing separation. More than 200 features (i.e., the number of freedoms) were used for training and testing, which were greater than the number of nodules (i.e., the number of training samples) in the database.

^bPerformance was calculated by using the distance criterion of 25 mm for determining TP detections.

DISCUSSION

Here, we have presented a novel lung nodule CADe scheme for CXRs. A detailed performance analysis of the scheme was conducted with the use of the publicly available JSRT database (databases B_S and B) and our own U of C database (database C). We acknowledge that many experimental factors must be taken into account when comparisons are interpreted. However, we believe that the current scheme is certainly competitive and offers some useful innovations, including the two-stage nodule detection method and the watershed-segmentation-based feature extraction method. We made an interesting observation related to the choice of a classifier. We compared two classifiers and found that the nonlinear SVM generalized from a relatively small number of positive cases did better than did the LDA. For our CADe scheme, the SVM with all 31 extracted features provided a higher performance (a sensitivity of 76.4% with an FP rate of 5.0 FPs∕image) than did the LDA with selected features by the stepwise feature selection method. On the other hand, if the features selected for the LDA were used for the SVM, the performance was lower (a sensitivity of 68.6% at 5.0 FPs∕image). Thus, how to select “effective” features for a particular nonlinear classifier is an important issue in CADe research.

Different criteria for determining a TP have been used in different published studies. Research in Ref. 24 used a “distance” criterion that counts a detected candidate to be a TP if the distance between the centroid of the candidate and the reference-standard center of a nodule is less than 22 mm. A problem with this criterion is that the same distance is applied to nodules of any size. A “TP” region can be away from a small nodule. Research in Ref. 27 adopted a distance criterion with 25 mm as a threshold value. Research in Ref. 25 used an “overlap” criterion: A nodule is considered to be detected if there is any overlap between a detected candidate and the reference-standard region of a nodule. A detected candidate needs to be closer for being a TP for a smaller nodule than it does for a larger nodule. A problem with this criterion is that if a detected candidate region is large, the candidate that is not close enough to a nodule can be counted as a TP. The region criterion applied to our scheme evaluation is stricter than the distance criterion and the overlap criterion. We believe that the region criterion is more relevant scientifically because it does not have the problem with the distance criterion for small nodules or the problem with the “overlapping” criterion for large detected candidates, as described above. Because of the use of the stricter criterion, the measured performance of our CADe scheme could be lower than the performance measured with the other two criteria used in published studies. Schilham et al.²⁵ reported a sensitivity of 96.4% with 134 candidates∕image at the nodule candidate detection stage. This sensitivity was calculated based on the overlap criterion. Shiraishi et al.²⁴ reported a sensitivity of 92.5% with 60.2 candidates∕image based on the distance criterion. In our experiment, 3360 and 9800 nodule candidates were detected for the U of C database (database C) and the JSRT database (database B_S), respectively. By using our region criterion, 47 and 129 true nodules were labeled as TPs for the U of C database and the JSRT database, respectively, whereas by using the distance criterion with 25 mm, 48 and 135 nodules were labeled as TPs for the U of C database and the JSRT database, respectively. Thus, the same performance was counted as a higher performance with the distance criterion than with our region criterion. Therefore, the region criterion was a stricter criterion than was the distance criterion in our experiment.

In our experiment, the size of the nodule template for the two-stage nodule enhancement in the nodule candidate detection was fixed. Because the size of nodules in the JSRT database ranged from 5 to 60 mm, if we use nodule templates of different sizes adaptively for different-sized nodules, the performance of the initial nodule candidate detection can be improved. The development of such a method is planned for our future study.

We analyzed the false-negative nodules at the sensitivity of 76% in the JSRT database. We found that they were located either in the pulmonary trunk and artery areas or behind ribs and∕or clavicles. Because of these complex backgrounds, our scheme was not able to produce accurate segmentation of the nodules. As a result, the features computed in the subsequent step were less accurate, and this made the classification task more difficult.

In the evaluation of our CADe scheme, we used the publicly available JSRT database. A good feature of this database is that the observer performance study results for radiologists are available. The study showed that radiologists detected only 44% of the extremely and very subtle cases. At an FP rate of 5.0 FPs∕image, our CADe scheme correctly detected 55% of these cases in the same category, whereas a conventional CADe scheme, reported in Ref. 25, detected 41% of the cases. This is encouraging because our CADe scheme has a desirable characteristic, which is a high sensitivity for subtle cases. Therefore, we expect that our CADe scheme will potentially be useful for improving radiologists’ performance in the detection of subtle nodules.

The performance of our CADe scheme was higher for the U of C database than for the JSRT database. The reasons for this are threefold: (1) Nodules in the JSRT database were more subtle than those in the U of C database. There were 42 very subtle and extremely subtle nodules out of 140 nodules in the JSRT database. There are “nonactionable” nodules where all of 6 expert radiologists did not detect even when they were marked by a hypothetical CADe scheme with 100% sensitivity in an observer performance study.⁵³ (2) The average size of the nodules in the U of C database was larger than that in the JSRT database. (3) The images in the U of C database were digital images acquired with a computed radiography system, whereas the images in the JSRT database were digitized images scanned from films. Thus, the quality of images in the U of C database was better than that of the images in the JSRT database. Therefore, the “difficulty” of databases was substantially different. This substantial difference in database characteristics may have caused the different feature sets selected for LDA with the stepwise feature selection method.

How much a CADe scheme is able to improve the performance of a radiologist depends on the following factors: Radiologist’s experience, “stand-alone” performance of the CADe scheme, and the ability of the reader to distinguish a TP marking from a FP marking.¹⁴ We have developed a CADe scheme that achieved a relatively high performance. We expect that the higher stand-alone performance will be beneficial to the improvement of radiologist’s performance. We will need to carry out an observer performance study with radiologists to prove this.

The time for processing one case with our CADe scheme was about 70 s (including 25 s for nodule candidate detection and 45 s for candidate segmentation, feature extraction, and classification) on a PC-based workstation (Intel Pentium 2.4 GHz processor with a 3 GB memory). The candidate segmentation consumed about half of the entire processing time. Thus, CADe results will be obtained 70 s after the acquisition of a CXR. Therefore, at the time of the radiologist’s reading, CADe results will already be available on a viewing workstation for his∕her review.

CONCLUSION

We have developed a CADe scheme for the detection of lung nodules in CXRs. Our CADe scheme consists of an accurate lung segmentation based on the multisegment ASM, a new two-stage nodule-enhancement technique, nodule segmentation by using an improved watershed segmentation, and an SVM classifier. Our CADe scheme achieved sensitivities of 76% (107∕140) and 77% (37∕48) with 5.0 (700∕140) FPs∕image and 2.0 (96∕48) FPs∕image for a publicly available database (JSRT) and our database (U of C), respectively, in a leave-one-out cross-validation test. Therefore, we expect that our CADe scheme will be potentially useful for improving radiologist’s sensitivity in the detection of lung nodules in chest radiographs.