Delayed matching to sample: Reinforcement has opposite effects on resistance to change in two related procedures

Abstract

Effects of reinforcement on delayed matching to sample (DMTS) have been studied in two within-subject procedures. In one, reinforcer magnitudes or probabilities vary from trial to trial and are signaled within trials (designated signaled DMTS trials). In the other, reinforcer probabilities are consistent for a series of trials produced by responding on variable-interval (VI) schedules within multiple-schedule components (designated multiple VI DMTS). In both procedures, forgetting functions in rich trials or components are higher than and roughly parallel to those in lean trials or components. However, during disruption, accuracy has been found to decrease more in rich than in lean signaled DMTS trials, and conversely, to decrease more in lean than in rich multiple VI DMTS components. The present study compared these procedures with two groups of pigeons. In baseline, forgetting functions in rich trials or components were higher than and roughly parallel to those in lean trials or components, and were similar between procedures. During disruption by prefeeding or extinction, accuracy decreased more in rich signaled DMTS trials, whereas accuracy decreased more in lean multiple VI DMTS components. These results replicate earlier studies and are predicted by a model of DMTS by Nevin, Davison, Odum, and Shahan (2007).

The delayed matching-to sample (DMTS) paradigm has been used extensively in research on short-term working memory in nonhuman animals. The basic paradigm involves the presentation of one or the other of two samples, S1 or S2, in discrete trials. After sample offset, comparison stimuli C1 and C2 are presented at the end of a retention interval, and reinforcers may follow responses to the comparison that matches the sample. Data are often presented as forgetting functions relating accuracy of matching to the length of the retention interval. Several studies have used the DMTS paradigm to evaluate the effects of memorial processes such as proactive and retroactive interference (e.g., Edhouse & White, 1988; Harper & White, 1997). Other studies have addressed the effects on DMTS accuracy of drugs (e.g., Picker, White, & Poling, 1985) or brain lesions (e.g., Colombo, Swain, Harper, & Alsop, 1997).

In one way or another, the studies cited above have identified variables or processes that challenge accurate DMTS performance. The effects of such challenges may, however, depend on the conditions of reinforcement and the procedure employed. We consider two procedures that have been used to study the effects of reinforcement on DMTS performance within subjects and sessions.

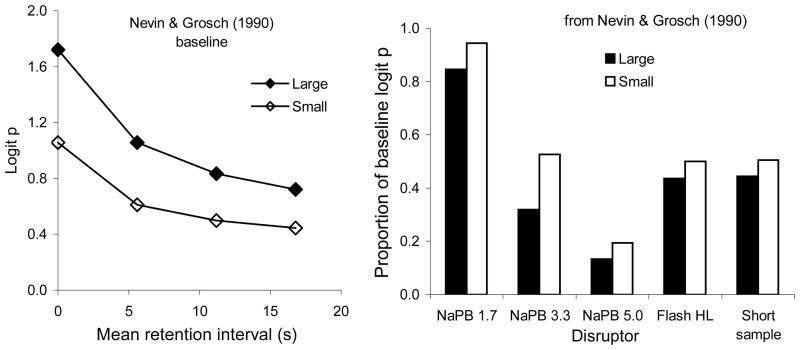
Nevin and Grosch (1990) trained pigeons on a signaled DMTS trials procedure in which an auditory stimulus presented at sample onset and continuing through the retention interval signaled whether correct matches would produce large or small reinforcers; signaled large- and small-reinforcer trials alternated irregularly, and the duration of the retention interval varied irregularly across trials. With accuracy expressed as logit p,¹ the steady-state baseline forgetting function on large-reinforcer (rich) trials was consistently higher than and roughly parallel to that for small-reinforcer (lean) trials (see Figure 1, left panel). Performance was disrupted with injections of sodium pentobarbital (NaPB) at 3 dose levels, flashing houselight during retention intervals, and reduced sample duration, with baseline recovery between disruptor tests. For every disruptor, the average proportion of baseline was greater on small- than on large-reinforcer trials (Figure 1, right panel).

Figure 1.

The left panel presents average steady-state forgetting functions obtained by Nevin and Grosch (1990) trials with signaled large-magnitude and small-magnitude reinforcers; retention intervals varied across subjects, always in the ratios 1:2:3. The right panel shows the value of logit p, averaged across retention intervals, as a proportion of average logit p for the steady-state functions at the left, during three disruptors: Injections of sodium pentobarbital (NaPB), flashing houselight during the retention interval, and reduced sample duration. Error bars are omitted because the individual data have been lost.

Comparable baseline forgetting functions have been reported by Brown and White (2005a, Experiment 1) with stimuli presented after sample offset that signaled whether correct matches would be reinforced with high (rich) or low (lean) probability in irregularly alternating DMTS trials. Thus, the effects of reinforcement on baseline forgetting functions are replicable with signals presented at sample offset rather than sample onset, and with signaled reinforcer probability rather than amount (see also Jones, White, & Alsop, 1995; McCarthy & Voss, 1995).

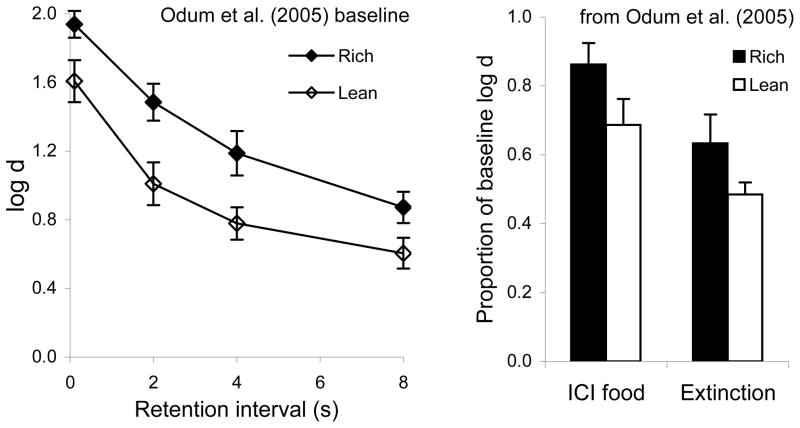
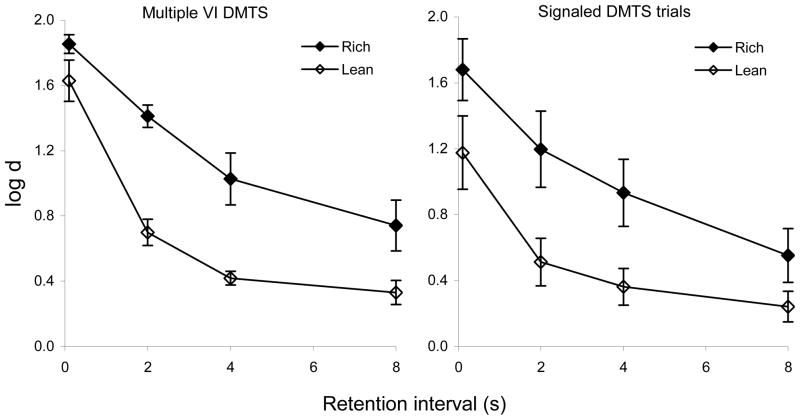
In a related procedure, Odum, Shahan, and Nevin (2005) presented DMTS trials contingent on responding according to variable interval (VI) schedules in alternating multiple-schedule components. Different reinforcer probabilities were signaled by distinctive stimuli for the entire duration of each component, comprising several successive trials with different retention intervals. This procedure, designated multiple VI DMTS and based on that of Schaal, Odum, and Shahan (2000), allows the experimenter to evaluate the effects of reinforcement on response rates as well as forgetting functions. Odum et al. found that response rate was higher in the high-probability (rich) than in the low-probability (lean) component, and that the forgetting function in the rich component was higher than and roughly parallel to that in the lean component (left panel of Figure 2, with accuracy expressed as log d¹), as in the signaled-trials procedure of Nevin and Grosch. They also found that both the rate of responding and the forgetting function in the rich component were more resistant to disruption by presentations of food during intervals separating components (ICI food) and by extinction than in the lean component (Figure 2, right panel). The opposite effects on the forgetting functions reported by Nevin and Grosch (Figure 1, right panel) may be attributable to the differences between studies in the procedures or the disruptors.

Figure 2.

The left panel presents average steady-state forgetting functions obtained by Odum et al. (2005) for VI DMTS components with high-probability (rich) or low-probability (lean) reinforcers. The right panel shows the value of log d, averaged across retention intervals and expressed as a proportion of average log d for the steady-state functions at the left, for two disruptors: Presentation of food during the ICI, and extinction. Standard errors are indicated by range bars.

Because resistance to disruption is important for effective working memory, the effects of reinforcement on the persistence of short-term remembering deserve analysis. Moreover, the opposed effects on resistance to change of rich vs. lean conditions of reinforcement in the signaled DMTS trials and multiple VI DMTS procedure, displayed in Figures 1 and 2, are predicted by a theoretical model of DMTS by Nevin, Davison, Odum, and Shahan (2007; summarized below), and need confirmation within a single experiment. Accordingly, we conducted systematic replications of the studies by Brown and White (2005a, Experiment 1) and by Odum et al. (2005) with identical retention intervals to establish comparable baseline forgetting functions, and then employed identical disruptors in both procedures.

Method

Subjects

Ten White Carneau pigeons were maintained at 80% (+/− 15 g) of free-feeding weights by post-session feeding and were individually housed in a temperature-controlled colony with free access to water under 12:12 hr light/dark cycle. Five pigeons served in the signaled DMTS trials procedure and five served in the multiple VIDMTS procedure. All pigeons had previous histories with diverse operant procedures.

Apparatus

Four Lehigh Valley Electronics pigeon chambers, 350 mm long, 350 mm high, and 300 mm wide, were used. Each front panel had three translucent plastic keys that could be lit from behind with green, red, blue, and yellow light as well as various symbols, and required a force of about 0.10 N to record a response. Keys were 25 mm in diameter and 240 mm from the floor. A lamp (28 V, 1.1 W) mounted 45 mm above the center key served as a houselight. A rectangular opening 100 mm above the chamber floor provided access to a hopper filled with pelleted pigeon chow through a 50 mm by 55 mm aperture. During hopper presentations, the opening was lighted white and the houselight and keylights were extinguished. White noise and chamber ventilation fans masked extraneous noise. Contingencies were programmed and data collected by a microcomputer located in an adjacent room using Med Associates® interfacing and software.

Procedure – Multiple VI DMTS

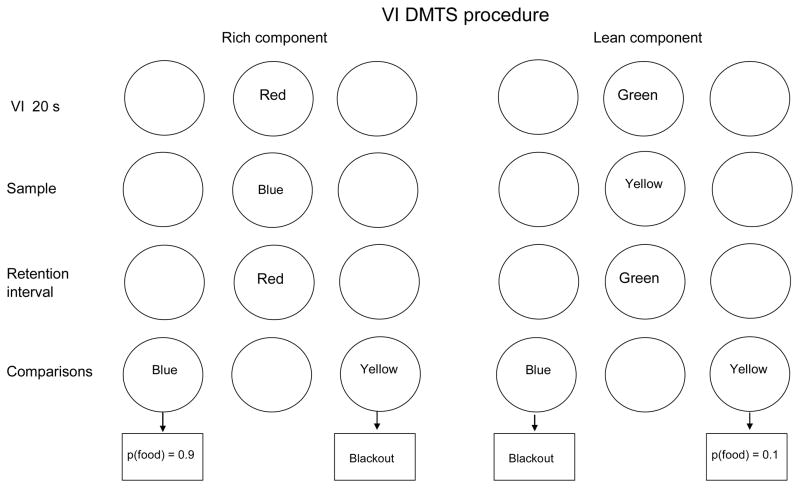
The baseline procedure was identical to that used by Odum et al. (2005). Two components of a multiple schedule, signaled by the color of the center key (either red or green), alternated. Pecks to the lit center key changed it to yellow or blue (the sample) on a VI 20-s schedule. If no peck occurred within 80 s (the longest interval duration plus 20 s), the schedule progressed to sample presentation without a key peck. The sample remained on until the first peck after 3 s or a total of 6 s had elapsed. After sample offset, the center key returned to the color present during the VI phase. Following a retention interval of 0.1, 2, 4, or 8 s, the center key was extinguished and the side keys were lit, one yellow and one blue (the comparisons). A single peck turned off the side keys and was followed by food or blackout. The procedure is diagrammed in Figure 3.

Figure 3.

The sequence of events within a trial in the VI DMTS procedure. The center key color before and after sample presentation signals the reinforcer probability. See text for complete description.

Components differed in the probability of reinforcement for pecking the color that matched the sample. In one component (rich), correct matches produced 2-s access to food with probability .9. In the other component (lean) correct matches produced 2-s access to food with probability .1. Red or green color assignments varied across birds. In both components, non-reinforced matches and incorrect choices produced a 2-s blackout. Components alternated after blocks of four trials that contained one presentation of each retention interval; their order was chosen randomly within each block. Components were separated by a 15-s ICI during which the houselight was on and the keys were dark. Experimental sessions ended after 96 trials, 48 per component, and were conducted daily at about the same time.

Procedure – Signaled DMTS trials

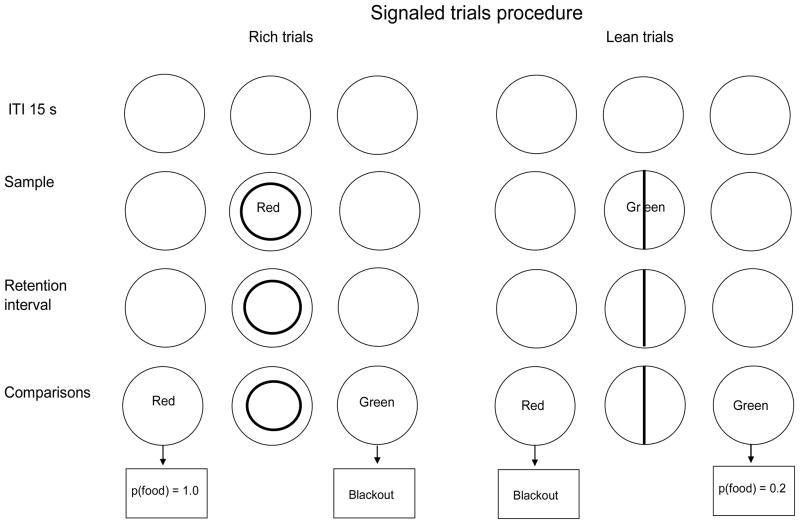
The baseline procedure was similar to that used by Brown and White (2005a), modified so that trial signals accompanied sample onset, and the range of retention intervals was the same as in the multiple VI DMTS procedure. Each session began with an intertrial interval (ITI) lasting 15 s, during which the houselight was on but all three keys were dark. After the ITI, a red or green sample was presented on the center key. The sample remained on until the first peck after 3 s or a total of 6 s had elapsed. After a retention interval of 0.1, 2, 4, or 8 s, the side keys were lit, one red and one green (the comparisons). The key that was lit with each color varied randomly across trials. A single peck turned off the side keys and was followed by food or blackout. The procedure is diagrammed in Figure 4.

Figure 4.

The sequence of events within a trial in the signaled trials procedure. The geometric figure projected on the center key throughout the trial signals the reinforcer probability. See text for complete description.

The probability of reinforcement for a correct match was signaled by a circle or a vertical line that was superimposed on the center key at the onset of the sample and remained present until a comparison was pecked. On trials with a circle, correct matches produced 2-s access to food with probability 1.0 (rich); incorrect choices produced a 2-s blackout. On trials with a line, correct matches produced 2-s access to food with probability .2 (lean); non-reinforced matches and incorrect choices produced a 2-s blackout. (These reinforcer probabilities were the same as in Brown and White (2005a, Experiment 1)). An ITI began after either food or blackout. Sessions ended after 64 trials, 32 rich and 32 lean, and were conducted daily at about the same time.

Resistance tests

To examine the resistance to change of matching accuracy, several disruptors were introduced in successive tests. Each disruptor was in effect for 10 consecutive sessions, and a minimum of 20 baseline sessions intervened between disruptors. The 10 sessions immediately preceding each disruptor constituted the baseline against which disruptor effects were evaluated. Disruptors were arranged identically across procedures. Two disruptors involved novel stimuli presented within trials, and two involved general disruptors that were in effect throughout each test session.

Sample disruption

The houselight and white side keys began flashing at sample onset and continued flashing until sample termination. The side keys and houselight flashed separately and successively every 0.2 s, rotating either clockwise or counterclockwise. On each trial, the direction of the flashing houselight and side keys was randomly selected (p=.5).

Comparison disruption

The houselight and white center key flashed on and off every 0.2 s while the comparisons were presented on the side keys.

Prefeeding

The pigeons received 30 g of pigeon chow in their home cages 30 min prior to each session.

Extinction

Correct matches were never followed by food, but were instead always followed by blackout. If no peck was made to a comparison stimulus within 20 s, the comparisons were extinguished, a blackout ensued, and that trial was not counted as correct or incorrect.

Table 1 lists the numbers of sessions and sequence of exposure to resistance tests for individual subjects in two replications of each procedure.

Table 1.

Sequence of conditions and numbers of sessions for all pigeons in both procedures

	Signaled DMTS trials (1)
	P49830	P54	P587
Baseline	50	50	50
Prefeeding	10	10	10
Baseline	50	50	50
Disrupt during samples	10	10	10
Baseline	35	35	40
Disrupt during comparisons	10	10	10
Baseline	40	35	35
Extinction	10	10	10

	Signaled DMTS trials (2)
	P11	P958
Baseline	120	120
Disrupt during samples	10	10
Baseline	20	20
Disrupt during comparisons	10	10
Baseline	18	55
Prefeeding	10	10
Baseline	20	20
Extinction	10	10

	Multiple VI DMTS (1)
	P1188	P216	P3060	P1821
Baseline*	20	20	20	20
Disrupt during comparisons	10	10	10	10
Baseline	20	20	20	20
Disrupt during samples	10	10	10	10
Baseline**	20	21	20	20
ICI food**	10	10	10	10
Baseline	20	20	20	20
Prefeeding	10	10	10	10
Baseline	20	20	20	20
Extinction	10	10	10	10

	Multiple VI DMTS (2)
	P1173
Baseline	130
Disrupt during comparisons	10
Baseline	35
Disrupt during samples	10
Baseline	76
Prefeeding	10
Baseline	3
Extinction	died

^*All four pigeons had previous experience with multiple VI DMTS so extensive baseline training was not needed.

^**ICI food results are not reported because the test was not replicated with P1173 and was not employed with signaled DMTS trials

Measures

In both procedures, accuracy is expressed as log d, the logarithm of the geometric mean of correct responses to errors on trials with samples S1 and S2, where B1 and B2 signify pecks to comparisons C1 or C2 respectively:

$$logd=0.5log[{(B1\mid S1/B2\mid S1)}^{\ast }(B2\mid S2/B1\mid S2)],$$ (1)

calculated separately for rich and lean components or trials. This measure (Davison & Tustin, 1978) has been used in many studies of conditional discrimination. Unlike per cent correct – the more traditional measure – log d has no upper bound, and is at least in principle independent of biases toward C1 or C2. Log d is not defined if any of its terms is 0, as may happen with easy discriminations at short retention intervals. Accordingly, we added 0.25 to all cells for all calculations (see Brown & White, 2005b). As a result, in multiple VI DMTS with 12 trials per session at each retention interval in rich and lean components, pooled over 10-session blocks, the maximum value of log d is 2.38. In signaled DMTS trials with 8 rich and lean trials per session at each retention interval, pooled over 10-session blocks, the maximum value of log d is 2.21.

Results

Baseline

Forgetting functions based on data pooled for the four 10-session blocks of baseline training that preceded resistance tests, averaged across pigeons, are shown in Figure 5. The left and right panels present the results for groups trained on multiple VI DMTS and signaled DMTS trials, respectively. The functions for the rich components or trials are higher than and roughly parallel to those the lean components or trials, replicating Odum et al. (2005) and Brown and White (2005a). The average levels of the rich and lean forgetting functions did not differ between procedures: A 2×2 repeated-measures analysis of variance found a main effect of rich vs lean reinforcement conditions [F(1,16) = 14.86, p = .001] but no effect of procedures [F(1,16) = 1.95, p = .182] and no interaction between reinforcement conditions and procedures [F(1,16) < 1.0]. The heights of the forgetting functions at the shortest retention interval do not differ significantly between procedures (2-tailed t tests, p > .10). Thus, differences in resistance to change between procedures cannot be ascribed to differences in baseline forgetting functions.

Figure 5.

Forgetting functions averaged over five pigeons and pooled for 10 sessions of baseline training before each of the four resistance tests for multiple VI DMTS (left panel) and signaled trials (right panel); standard errors are indicated by range bars.

Response rates in VI DMTS during baseline were higher in the rich than in the lean component for every pigeon in every replication of baseline, consistent with earlier findings (Odum et al., 2005); the data are summarized in Table 2.

Table 2.

Response rates in baseline and proportions of baseline during prefeeding and extinction for individual subjects in multiple VI DMTS.

	Responses per min Pooled Baseline		Proportions of baseline
			Prefeeding		Extinction
	Rich	Lean	Rich	Lean	Rich	Lean
P1188	116.5	53.7	0.532	0.257	0.550	0.184
P216	85.2	50.2	0.777	0.778	0.701	0.312
P3060	82.8	57.6	0.774	0.540	0.863	0.500
P1821	100.5	43.7	0.747	0.609	0.547	0.312
P1173	87.0	36.8	0.410	0.138	died

Resistance tests

Accuracy levels in baseline and disruptor test sessions were summarized by averaging log d across retention intervals separately for rich and lean components or trials for each individual. Then, for each pigeon, average values of log d during the 10 resistance test sessions were expressed as proportions of their levels during the immediately preceding 10 baseline sessions.

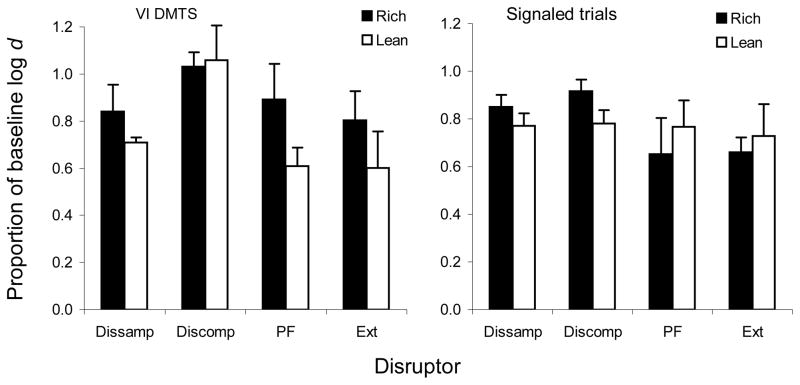
Average proportions of baseline in rich and lean components or trials are presented for each procedure and disruptor in Figure 6. The figure shows that presenting novel flashing lights during the samples had modest but similar decremental effects in both procedures, whereas flashing lights during comparisons did not reduce accuracy in multiple VI DMTS. When the data for these within-trial disruptors were expressed as differences between average proportions of baseline in rich and lean components or trials, a 2×2 repeated-measures analysis of variance found no main effects of procedures or disruptors [F(1,16) < 1.0] and no reliable interaction between procedures and disruptors [F(1,16) = 1.499, p = .23]. Accordingly, these data will not be considered further.

Figure 6.

Values of log d during resistance tests, averaged across retention intervals and expressed as a proportion of average log d for the steady-state functions in the immediately preceding baseline in multiple VI DMTS (left panel) and signaled trials (right panel) for rich and lean components or trials for all four disruptors: Dissamp = flashing lights during samples; Discomp = flashing lights during comparisons; PF = prefeeding; and Ext = extinction. Standard errors are indicated by range bars.

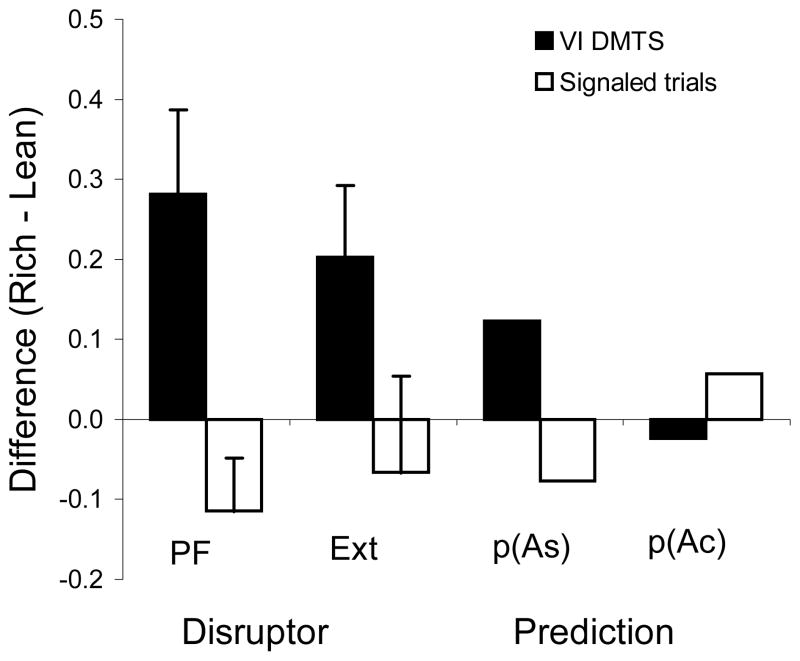
Figure 6 also shows that the general disruptors, prefeeding and extinction, reduced accuracy more in lean than in rich VI DMTS components, whereas the opposite ordering occurred in rich and lean signaled trials. By inspection, the effects of the general disruptors were more clearly differentiated between procedures than the effects of within-trial disruptors. When the data for these general disruptors were expressed as differences between average proportions of baseline in rich and lean components or trials, the difference was positive for VI DMTS and negative for signaled trials, as shown by the left-hand pairs of bars in Figure 7. A 2×2 repeated-measures analysis of variance showed that the main effect of procedures was significant: [F(1, 16) = 11.05, p = .002]; the main effect of disruptors and the interaction between procedures and disruptors were not significant [F(1,16) < 1.0]. The extinction data of P1173, which died during that phase, were replaced with the mean of the remaining four pigeons.

Figure 7.

The average differences between proportions of baseline log d in rich and lean multiple VI DMTS components and signaled trials during prefeeding and extinction (left and center-left histogram bars). Positive values signify greater resistance to disruption in rich components or trials; standard errors are indicated by range bars. The center-right and right histogram bars exhibit the differences predicted by the model of Nevin et al. (2007) when the probability of attending to the sample, p(A_s), is reduced by increasing parameter x in Equation 2 or when the probability of attending to the comparisons, p(A_c), is reduced by increasing parameter z in Equation 3; see Discussion and Appendix for explanation and calculation.

We conclude that accuracy is more resistant to general disruptors in the rich than in the lean component in VI DMTS, and that the reverse is true in signaled trials, as suggested by the difference between the effects of disruptors reported by Odum et al. (2005, Fig. 2) and by Nevin and Grosch (1990, Fig. 1).

The effects of prefeeding and extinction on response rates in VI DMTS are in accordance with the effects on accuracy. As shown in Table 2, proportions of baseline were higher in prefeeding and extinction for all pigeons except P216, prefeeding, for which there was virtually no difference. These data confirm the results of Odum et al. (2005).

Discussion

Two apparently similar procedures for the study of DMTS yielded similar forgetting functions when different reinforcer probabilities were arranged in multiple-schedule components or signaled in irregularly alternating trials. However, the effects of prefeeding and extinction differed between procedures in ways that are consistent with previous studies. Odum et al. (2005) found that accuracy in the rich component of multiple VI DMTS was less affected by presenting response-independent food between components, and by extinction, than in the lean component, where ICI food is a general disruptor analogous to prefeeding. By contrast, Nevin and Grosch (1990) found that accuracy in rich signaled trials was more affected by three doses of NaPB (a general disruptor) than in lean signaled trials. Similar results were obtained with a flashing houselight during retention intervals and with reduced sample duration (within-trial disruptors). Although Nevin and Grosch varied reinforcer magnitude rather than probability between rich and lean trials and employed different disruptors, their data resemble the signaled-trial data presented above.

In the present study, the procedures arranged for multiple VI DMTS and signaled DMTS trials differed in a number of ways. For example, different key colors were used as samples and comparisons; reinforcer probability was signaled before and after the sample in multiple VI DMTS, but during and after the sample in signaled DMTS trials; and reinforcer probabilities in multiple VI DMTS were .9 and .1 for rich and lean components, whereas in signaled DMTS trials, they were 1.0 and .2 for rich and lean trials. Because the present results replicated those of previous signaled-trial studies that also differed in a number of ways, and because baseline forgetting functions were similar, it is unlikely that the incidental differences between VI DMTS and signaled-trials procedures arranged here affected the ordinal differences in resistance to disruption.

The opposed orderings of resistance to disruption in VI DMTS and signaled DMTS trials are predicted by a model proposed by Nevin et al. (2007), which we summarize here (see Nevin et al. for a full exposition of the model’s rationale, assumptions, and applications to data).

Modeling DMTS accuracy and the effects of disruptors

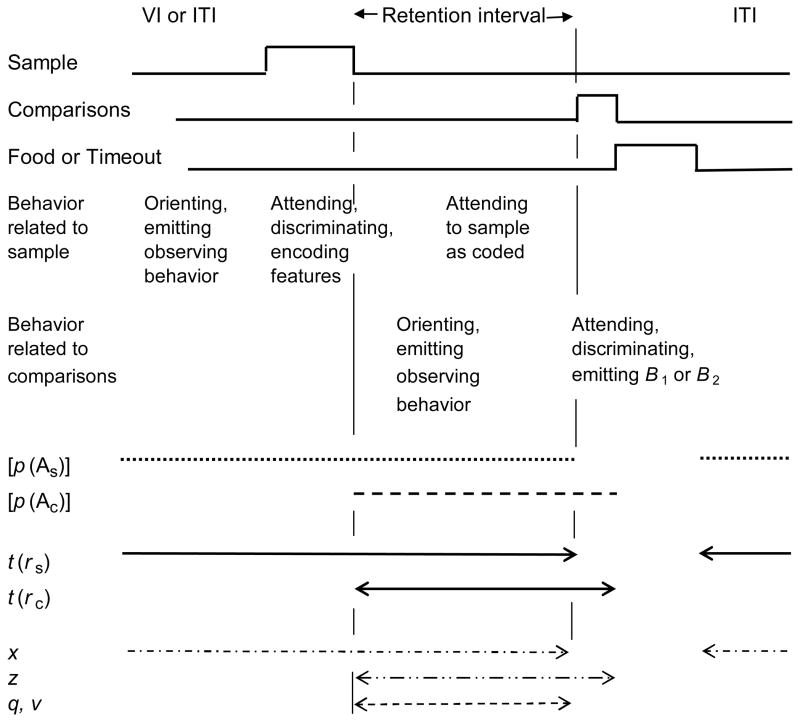
The model of Nevin et al. (2007) assumes that correct performance in DMTS requires attending to both samples and comparisons, that the probabilities of attending to the samples and comparisons in DMTS trials are independent, and that both depend directly on signaled reinforcer rates expressed relative to the context in which the stimuli appear according to equations derived from behavioral momentum theory. Attending to the samples is assumed to include observing behavior before onset of the samples, discriminative behavior in the presence of the samples, and attending to the recently encountered samples during retention intervals (rehearsal). Attending to the comparisons is assumed to include observing behavior during retention intervals and discriminative behavior in the presence of the comparisons themselves. Figure 8 portrays the sequence of events and the times during which attending to samples and comparisons is assumed to occur.

Figure 8.

Time-line diagram of experimentally arranged events within a DMTS trial, and the times during which the subject is assumed to attend to the sample and comparisons. Times during which reinforcers and disruptors are assumed to operate on attending to samples or comparisons are also indicated. (Reproduced with permission from Nevin et al., 2007.)

The probability of attending to the sample, p(A_s), is given by

$$p(A_s)=exp\left(\frac{-x-qt}{{(r_s/r_a)}^{0.5}}\right),$$ (2)

where sample-related reinforcer rate r_s (i.e., reinforcers per trial divided by the time preceding, during, and following sample presentation until onset of the comparisons in each trial) is expressed relative to the average reinforcer rate for an entire session, r_a, the overall context within which DMTS trials appear. The value of the exponent on r_s/r_a is based on fits to parametric data sets for free-operant responding and was used in all fits reported by Nevin et al. (2007). Attending to the sample may be reduced by increasing the general background disruptor x and by increasing a separate disruptor q during a retention interval of length t.

Likewise, the probability of attending to the comparisons is given by

$$p(A_c)=exp\left(\frac{-z-vt}{{(r_c/r_s)}^{0.5}}\right),$$ (3)

where comparison-related reinforcer rate r_c (i.e., reinforcers per trial divided by time from sample offset to comparison offset in each trial) is expressed relative to the reinforcer rate for attending to the samples, r_s, the context in which comparisons appear. Overall attending to the comparisons may be reduced by a general background disruptor z and by a separate disruptor v during a retention interval of length t.

In experiments with easily discriminated stimuli and with equal reinforcer probabilities for correct matches following S1 and S2, we assume that the subject always responds correctly on a given trial if it attends to both sample and comparisons. If it does not attend either to the sample or to the comparisons, it responds randomly. Thus, discrimination accuracy for a block of trials is predicted by a weighted average of trials with and without attending given by Equations 2 and 3. Specifically, proportion correct is p(A_s)*p(A_c) + 0.5*[1−p(A_s)*p(A_c)]. Proportion correct is then transformed to logit p and plotted in relation to the retention interval for comparison with empirical forgetting functions with accuracy expressed as log d. Parameters x and z determine the level of the predicted forgetting function, whereas q and v affect its slope (Nevin et al., 2007).

With the inclusion of parameters characterizing the discriminability of sample and comparison stimuli and the generalization of reinforcement across those stimuli, the model can account for the effects of differential reinforcement on the steady-state allocation of responses to the comparison stimuli (Nevin et al., 2005, 2007). However, these complexities are not critical for modeling baseline performances and their resistance to change in the present study because it employed distinctively colored samples and comparisons and arranged symmetrical reinforcer probabilities for correct responses.

Predictions for multiple VI DMTS and signaled trials

As stated above, subjects are assumed to engage in observing behavior during the VI phase or the intertrial interval (ITI) before sample presentation, to discriminate the sample while it is present, and to rehearse the recently-presented sample during the retention interval. All these activities constitute attending to the sample, and their probability p(A_s) is given by Equation 2, where the denominator is r_s/r_a. Because r_s (reinforcement associated with attending to the sample) is greater in high-probability (rich) than in low-probability (lean) VI DMTS components or signaled trials, while r_a (session-wide reinforcement) is the same, p(A_s) must be greater in rich than in lean VI DMTS components or signaled trials. However, the way in which reinforcers contribute to r_s in VI DMTS and signaled trials procedures is different. In VI DMTS, reinforcer probability is signaled throughout the VI as well as during DMTS trials. In signaled trials, by contrast, reinforcer probability is signaled only during DMTS trials, so the effective reinforcer rate during the ITI preceding a trial is based on the overall expected or average probability on rich and lean trials. As a result, p(A_s) differs more between rich and lean components in the VI DMTS procedure than between rich and lean trials in the signaled trials procedure.

The probability of attending to the comparisons, p(A_c), is assumed to depend on the ratio r_c/r_s according to Equation 3. In both procedures, the ratio of r_cRICH to r_cLEAN in rich components or trials is equal to the ratio of reinforcer probabilities. In multiple VI DMTS, the ratio of r_sRICH to r_sLEAN is also equal to the ratio of reinforcer probabilities, so r_c/r_s must be the same in rich and lean components even though its absolute value depends on VI length and trial duration. In signaled trials, by contrast, r_c/r_s must be greater in rich than in lean trials because the ratio of r_sRICH to r_sLEAN must be less than the ratio of reinforcer probabilities. The Appendix presents exact calculations for the procedures employed in the experiment reported above.

In general, p(A_s) is more differentiated between rich and lean VI DMTS components than between rich and lean signaled trials, whereas p(A_c) is more differentiated between rich and lean signaled trials than between rich and lean VI DMTS components. As a consequence, a disruptor that affects attending to samples is predicted to reduce p(A_s) less in rich than in lean VI DMTS components, and the difference should be greater than for the same disruptor in signaled trials. When p(A_s) is reduced, the predicted difference between proportions of baseline log d in rich and lean components will be positive, whereas the predicted difference between proportions of baseline log d in rich and lean signaled trials will be negative. Conversely, a disruptor that affects attending to the comparisons is predicted to have the same effect on p(A_c) in rich and lean VI DMTS components, whereas p(A_c) will be reduced less in rich than in lean signaled trials. When p(A_c) is reduced, the predicted difference between proportions of baseline log d in rich and lean components will be negative, whereas the predicted difference between proportions of baseline log d in rich and lean signaled trials will be positive. The Appendix explains these predictions in detail.

To compare the data with these predictions, we expressed the proportions of baseline for prefeeding and extinction (see Figure 6) as differences between rich and lean VI DMTS components or signaled trials (see Figure 7). Predicted differences were derived from Equations 2 and 3 by choosing values of x to reduce p(A_s), or z to reduce p(A_c), that would yield predicted proportions of baseline equal to the obtained proportions of baseline averaged over rich and lean components or trials. (Note that by using the average of rich and lean proportions of baseline to select parameter values, we did not predetermine differences between rich and lean proportions of baseline).

The right-hand pairs of bars in Figure 7 show that the predicted effect of reducing p(A_s) corresponds ordinally to the effects of the general disruptors in both procedures: Accuracy in the rich VI DMTS component is more resistant to change than in the lean component (i.e., differences are positive), whereas accuracy in rich signaled trials is less resistant to change than in lean signaled trials (i.e., differences are negative). By contrast, the predicted effect of reducing p(A_c) is ordinally opposite to the obtained differences in both procedures.

The correspondence with predictions for reducing p(A_s) suggests that general disruptors reduce attending to the sample, which includes observing behavior before sample onset (see Figure 8). As described above, the effects of the general disruptors on VI response rates, which may be construed as observing responses, are consistent with disruption of attending to the samples: Response rate, like accuracy, is more resistant to change in the rich component. The differences between the data for VI DMTS and signaled trials obtained here are similar to the differences between the VI DMTS data of Odum et al. (2005) and the signaled trials data of Nevin and Grosch (1990). Taken all in all, the data on resistance to disruption of DMTS accuracy are consistent with the ordinal predictions of the Nevin et al. (2007) model as elaborated for VI DMTS and signaled trials. However, the predicted magnitude of the difference is smaller than that obtained (see Figure 7), suggesting that the model needs revision to achieve quantitative agreement with the data; one such revision is to allow the exponent on r_s/r_a in Equation 2 to vary as a free parameter rather than being fixed at 0.5.

Alternative models of DMTS

A very different model of DMTS performance has been proposed by White and Wixted (1999). In their model, samples S1 and S2 are represented as overlapping Gaussian distributions on a dimension of stimulus value. The ordinates of these distributions are multiplied by reinforcer probabilities to yield distributions of expected reinforcers associated with each point on the stimulus value dimension. When a subject encounters a particular stimulus value on a given trial, its choice of C1 or C2 is assumed to match the ratio of expected reinforcers at that value.

Because the model’s predictions are based on reinforcer ratios, it cannot account for the effects of absolute reinforcer probabilities on forgetting functions such as those illustrated in Figures 1, 2, and 5. In order to account for the enhancement of accuracy by more frequent reinforcement, Brown and White (2009) added a term for unmeasured extraneous reinforcers by assuming that the relative effects of reinforcers R1 and R2 explicitly arranged for correct choices of C1 or C2 are, in effect, diluted by extraneous reinforcers. Thus, choices at each point along the stimulus value dimension are given by

$$B_1/B_2=(R_1+R\text{e})/(R_2+R\text{e}),$$ (4)

where Re represents extraneous reinforcers. Brown and White (2009) varied reinforcer probabilities in successive experimental conditions and showed that the effects on the level of the forgetting function could be explained by a single value of parameter Re.

Brown and White (2009) also showed that the effects of explicit alternative reinforcers could be treated similarly. Brown and White (2005c) arranged DMTS trials where center-key pecks were reinforced with food according to VI schedules during retention intervals, and found that the level of the forgetting function decreased as the frequency of food provided by the VI schedule increased, while the slope remained about constant. These results are consistent with those of Jans and Catania (1980), who found that presenting food throughout the retention interval reduced accuracy to near-chance levels; the VI schedules used by Brown and White (2005c) could be expected to have similar but less drastic effects. The results are also consistent with predictions based on Equation 4: Replacing hypothetical extraneous reinforcers Re with explicit reinforcers Ro, it is clear that as Ro increases, the B1/B2 ratio must decrease and approach 1.0 as Ro becomes large.

In addition, Brown and White (2009) showed that Brown and White’s (2005c) data could be explained by the Nevin et al. (2007) model by allowing the disruption parameters x, q, z, and v to increase. This makes sense because added reinforcers during the retention interval are readily construed as disruptors, as suggested by Jans and Catania (1980). Brown and White (2009) noted that the effects of Re in Equation 4 depend on the absolute values of R1 and R2. Thus, if R1 and R2 are large relative to Re, as in rich components or trials, reductions in accuracy due to increases in Re will be smaller than if R1 and R2 are small, as in lean components or trials. If Re is assumed, not unreasonably, to increase relative to R1 and R2 during prefeeding and extinction, the augmented White-Wixted model predicts that these general disruptors will have a smaller decremental effect on accuracy in the rich component, as found for multiple VI DMTS. However, decremental effects on accuracy were greater in rich signaled trials, and it is not obvious how the White-Wixted model can be adapted to account for opposed results in closely related DMTS procedures. Although the White-Wixted and Nevin et al. (2007) models are equally effective in accounting for steady-state forgetting functions in relation to the conditions of reinforcement despite their structural differences, tests of resistance to change such as those reported here can differentiate between them.

Appendix

Here we illustrate the calculation of reinforcer terms r_a, r_s, and r_c in Equations 2 and 3, which we repeat for convenience:

Within each trial, the probability of attending to the sample, p(A_s), is given by

$$p(A_s)=exp\left(\frac{-x-qt}{{(r_s/r_a)}^{0.5}}\right),$$ (2a)

and the probability of attending to the comparisons is given by

$$p(A_c)=exp\left(\frac{-z-vt}{{(r_c/r_s)}^{0.5}}\right),$$ (3a)

We begin by calculating reinforcer terms for VI DMTS.

The overall average reinforcer rate r_a programmed in an experimental session is given by summing all available reinforcers and dividing by session time. For the VI DMTS procedure with the parameters employed here, there were 96 trials, 4 trials per component with reinforcer probabilities .9 or .1, so there were 48 reinforcers available per session. Components were separated by 15 s. An average trial lasted 20 s for the VI, 3-s sample duration, and 4 equally likely retention intervals averaging 3.525 s, plus an assumed 1-s latency to respond to the comparisons, totaling 27.525 s. Thus, r_a for a complete session is:

$${[48/({27.525}^{\ast }96+{15}^{\ast }24)]}^{\ast }3600=57.55\text{reinforcers}/\text{hr}$$

The reinforcer rate for attending to the sample, r_s, is defined as reinforcers per trial divided by the time preceding, during, and following sample presentation until onset of the comparisons in each trial, which includes the particular retention interval on that trial. Time for the VI preceding a trial is 20 s, plus 3-s sample duration, plus the retention interval (0.1, 2, 4, or 8 s), plus an assumed 1-s latency to respond to the comparisons, totaling 24 s plus the retention interval t in effect on that trial. Thus, r_s for a given trial in the rich component is [.9/(24+t)]*3600 reinforcers/hr. In the lean component, r_s is [.1/(24+t)]*3600. On trials with 2-s retention intervals, for example, r_s = .9/(20+3+2)*3600 = 129.6 reinforcers/hr in the rich component and .1//(20+3+2)*3600 = 14.4 reinforcers/hr in the lean component. Because the value of r_a is the same for both components, the ratio of r_sRICH/r_a to r_sLEAN/r_a is 9, which is the same as the ratio of reinforcer probabilities.

The reinforcer rate for attending to the comparisons, r_c, is defined as reinforcers per trial divided by time from sample offset to comparison offset in each trial. Thus, on trials with a 2-s retention interval and an assumed 1-s latency to respond to the comparisons, r_c = .9/(2+1)*3600 = 1080 reinforcers/hr (rich) and .1/(2+1)*3600 = 120 reinforcers/hr (lean). Thus, the ratio of r_cRICH/r_sRICH to r_cLEAN/r_sLEAN is 1, regardless of the reinforcer probabilities or retention interval length.

We now repeat the process for signaled trials with the parameters employed here. There were 64 trials with equally likely reinforcer probabilities 1.0 and .2, so there were 38.4 reinforcers available per session. Trials were separated by 15 s, sample duration was 3 s, the 4 equally likely retention intervals averaged 3.525 s, and a 1-s latency to respond to the comparisons was assumed, so the total time for each trial was 22.525 s. Thus, r_a for a complete session is 38.4/(64*22.525)*3600 = 96 reinforcers/hr.

As in VI DMTS, r_s is defined as reinforcers per trial divided by the time preceding, during, and following sample presentation until onset of the comparisons in each trial, which includes the particular retention interval on that trial. Because the reinforcer probability is not known until trial onset, the expected reinforcer probability is .6 during the 15-s s ITI, and 1.0 or .2 during the 3-s sample plus the retention interval. If the retention interval is 2 s, the value of r_s on rich trials is (.6*15/20 + 1.0*5/20)/20*3600 = 126 reinforcers/hr, and on lean trials it is (15*.6 + 5*.2)/20*3600 = 90 reinforcers/hr. Note that the ratio of r_sRICH/r_a to r_sLEAN/r_a is 1.4, which is substantially smaller then the ratio of reinforcer probabilities.

Also as in VI DMTS, r_c is reinforcers per trial divided by time from sample offset to comparison offset in each trial. Thus, on trials with a 2-s retention interval and an assumed 1-s latency to respond to the comparisons, r_c on rich trials is 1.0(2+1)*3600 = 1200 reinforcers/hr (rich) and r_c on lean trials is .2/(2+1)*3600 = 240 reinforcers/hr. As a consequence, the ratio of r_cRICH/r_sRICH to r_cLEAN/r_sLEAN is (1200/126)/(240/90) = 3.57

The r_s/r_a and r_c/r_s ratios – i.e., the denominators of Equations 2a and 3a – in rich relative to lean VI DMTS components and signaled trials are summarized in the following matrix, assuming a 2-s retention interval as in the examples above:

	VI DMTS	Signaled trials
(rsRICH/ra)/(rsLEAN/ra)	9.0	1.4
(rcRICH/rsRICH)/(rcLEAN/rsLEAN)	1.0	3.57

The asymmetry of these reinforcer ratios across procedures is responsible for the asymmetry in the predicted effects of reducing p(A_s) by increasing x in Equation 2a, or reducing p(A_c) by increasing z in Equation 3a.

Table 1a presents the obtained baseline values of log d and the proportions of baseline predicted when x is increased to 0.15 or when z is increased to 0.50. The differences between proportions of baseline log d for VI DMTS and signaled trials are depicted in Figure 7. Readers can set up a worksheet following the layout in Table 1a to confirm these predictions and explore the effects of alternative parameter values; an electronic copy, in Microsoft Excel 2003^™, is available from the first author.

Table 1a.

Calculation of predicted differences in log d during disruption

						Fitted parameter values
Baselines						x	q	z	v	VAC
VI DMTS						0.02	0.07	0.06	0.00	0.97
	ra	rs	rc	rs/ra	rc/rs	p(As)	p(Ac)	p(corr)	log d
Rich	57.6	129.6	1080	2.25	8.33	0.904	0.980	0.943	1.219
Lean	57.6	14.4	120	0.25	8.33	0.739	0.980	0.862	0.797
Sig trials						0.00	0.00	0.20	0.11	0.89
	ra	rs	rc	rs/ra	rc/rs	p(As)	p(Ac)	p(corr)	log d
Rich	96	126	1200	1.31	9.52	1.000	0.874	0.937	1.174
Lean	96	90	240	0.94	2.67	1.000	0.776	0.888	0.899

Increase x to 0.15						x	q	z	v
VI DMTS						0.15	0.07	0.06	0.00
	ra	rs	rc	rs/ra	rc/rs	p(As)	p(Ac)	p(corr)	log d	prop BL	diff	average
Rich	57.6	129.6	1080	2.250	8.333	0.827	0.980	0.905	0.979	0.803	0.123	0.742
Lean	57.6	14.4	120	0.250	8.333	0.565	0.980	0.777	0.542	0.680
Sig trials						0.15	0.00	0.20	0.11
	ra	rs	rc	rs/ra	rc/rs	p(As)	p(Ac)	p(corr)	log d	prop BL	diff	average
Rich	96	126	1200	1.313	9.524	0.877	0.874	0.884	0.880	0.750	−0.024	0.762
Lean	96	90	240	0.938	2.667	0.856	0.776	0.832	0.696	0.774

Increase z to 0.5						x	q	z	v
VI DMTS						0.02	0.07	0.50	0.00
	ra	rs	rc	rs/ra	rc/rs	p(As)	p(Ac)	p(corr)	log d	prop BL	diff	average
Rich	57.6	129.6	1080	2.250	8.333	0.902	0.841	0.879	0.862	0.707	−0.077	0.746
Lean	57.6	14.4	120	0.250	8.333	0.733	0.841	0.808	0.625	0.784
Sig trials						0.00	0.00	0.50	0.11
	ra	rs	rc	rs/ra	rc/rs	p(As)	p(Ac)	p(corr)	log d	prop BL	diff	average
Rich	96	126	1200	1.313	9.524	1.000	0.794	0.897	0.939	0.800	0.057	0.772
Lean	96	90	240	0.938	2.667	1.000	0.646	0.823	0.668	0.743