A genetic instrument for Mendelian randomization of fibrinogen

Abstract

Mendelian randomization studies on fibrinogen commonly use a single genetic variant as an instrument, but this may explain only a small proportion of the total phenotypic variance. We examined the contribution of multiple common single nucleotide polymorphisms (SNPs) and haplotypes in the entire fibrinogen gene cluster to plasma fibrinogen levels in two prospective cohorts, for use as instruments in future Mendelian randomization studies. Genotypes for 20 SNPs were determined in 2,778 middle-age (49–64 years) men from the Second-Northwick-Park-Heart Study (NPHS-II). These were replicated in 3,705 men from the Whitehall-II study (WH-II). Plasma fibrinogen levels were determined six times in NPHS-II and three times in WH-II. The minor alleles of four SNPs from the FGB gene, two from the FGA gene, and one from the FGG gene were associated with higher plasma fibrinogen levels. SNP rs1800790 (−455G >A) commonly used in Mendelian randomization studies was associated with R² = 1.22% of the covariate adjusted residual variance in fibrinogen level. A variable selection procedure identified one additional SNP: rs2070011 (FGA) altogether explaining R² = 1.45% of the residual variance in fibrinogen level. Using these SNPs no evidence for causality between the fibrinogen levels and coronary heart diseases was found in instrumental variables analysis. In the replication cohort, WH-II, the effects of the two SNPs on fibrinogen levels were consistent with the NPHS-II results. There is statistical evidence for several functional sites in the fibrinogen gene cluster that determine an individual’s plasma fibrinogen levels. Thus, a combination of several SNPs will provide a stronger instrument for fibrinogen Mendelian randomization studies.

Introduction

The Mendelian randomization approach has been advanced as a methodological tool to strengthen causal inferences in observational studies of modifiable risk factors with known genetic determinants. It is postulated to reduce problems encountered in observational epidemiology studies, such as residual confounding, reverse causation and selection bias, and is predicated upon the random assortment of alleles at the time of gamete formation, which leads to population distributions of genetic variants that are, generally, independent of the environmental exposures commonly confounding risk factor–disease associations. These unconfounded genetic differences in risk factor levels should translate into genuine differences in disease occurrence if the exposure is truly a causal risk factor.

Plasma fibrinogen is a potentially suitable target for Mendelian randomization analyses. Observational studies show that an increase of 1 g/L of plasma fibrinogen is associated with more than a two-fold increase in coronary heart disease (CHD), stroke, and vascular mortality [1]. However, plasma fibrinogen levels are also known to be affected by various potential confounding factors, such as age, gender, smoking, body mass index (BMI), plasma lipid concentration and alcohol consumption. The mature fibrinogen protein is made up of two chains of each of three different polypeptides called alpha, beta, and gamma, which are encoded by three genes located in a cluster of 51 kb on chromosome 4 at q23–q32 [2]. Multiple single nucleotide polymorphisms (SNPs) have been identified in the genes. Some of the SNPs are located in the promoter region of the fibrinogen beta chain (FGB) gene, the transcription of which is believed to be the rate limiting step in fibrinogen synthesis [5–7]. These SNPs have been strongly and consistently associated with differences in plasma fibrinogen levels [3–5], but their association with CHD is less clear, with the reported associations often not being replicated by others [6–9].

A crucial step for using Mendelian randomization to assess the effect of fibrinogen on disease risk is the extent to which the selected genetic variants explain measured fibrinogen levels; a weak association can lead to unreliable estimates (known as the weak instrument bias) [10, 11]. At least two studies [12, 13] have used a Mendelian randomization approach and concluded that elevated fibrinogen levels are not causal for CHD, although we have argued that this result should be interpreted with caution [12]. In those studies, a single SNP has been used to determine the association between the genetic component of fibrinogen, the trait and the disease. Since one SNP explains only a small proportion of the total phenotypic variance, it is likely that one or more un-genotyped SNPs will also contribute to the association and can potentially provide more information on the relationship between fibrinogen levels and CHD. For example, polymorphisms in the fibrinogen alpha chain (FGA) and fibrinogen gamma chain (FGG) genes are under-studied, while fibrinogen haplotypes have been reported to influence plasma fibrinogen levels [13, 14]. In this study, we therefore evaluated the contribution of multiple common SNPs and haplotypes, in the entire fibrinogen gene cluster, to plasma fibrinogen levels, and used these in a Mendelian randomization study in two prospective cohorts of healthy middle-aged men with repeated measures of fibrinogen levels. We discuss our results in the context of whether one SNP is enough to represent the association between fibrinogen gene cluster and plasma fibrinogen levels for Mendelian randomization.

Materials and methods

Study subjects and data collection

The NPHS-II study

The prospective Second Northwick Park Heart Study (NPHS-II) commenced in 1989, and 3052 middle-aged men (49–64 years) were recruited from nine general medical practices in the UK. Participants were free of unstable angina, myocardial infarction, evidence of silent infarcts, coronary surgery, anti-coagulant drugs (including aspirin), cerebrovascular disease, malignancy and any condition or disease preventing the attainment of written, informed consent or long-term follow-up. Information on lifestyle habits, height, weight, and blood pressure was recorded at baseline and on subsequent prospective follow-up. Details of recruitment, measurements, follow-up and definitions of incident disease described elsewhere [15]. A blood sample was processed as described elsewhere [16, 17]. Fibrinogen concentration was measured by a thrombin-clotting method [18] and expressed in terms of a World Health Organization standard (code label 89/644). DNA was obtained from 2,778 men at the time of recruitment. Interviews and repeat measurements were conducted annually for surviving participants. CHD end points up to 15 years follow-up were as follows: (1) acute CHD events: sudden coronary death, fatal acute myocardial infarction, and nonfatal acute myocardial infarction (details of possible events were obtained through medical practices, hospitals, and coroners’ offices; the clinical history, ECGs, cardiac enzymes, and pathology were assessed by independent review according to World Health Organization criteria [19]; and normal limits for cardiac enzymes were those for the reporting laboratory); (2) a new major Q wave on the ECG after 5 years of follow-up (Minnesota codes 1₁, 1_2.1–1_2.7, and 1_2.8 plus 5₁ or 5₂) [20]; and (3) surgery for angina pectoris with CHD angiographically demonstrated.

Sixteen SNPs were genotyped using an Illumina GoldenGate candidate gene chip [21] shown in supplementary Table S1. Tagging SNPs for the three fibrinogen genes were selected with Tagger [22] using the CEU panel of HapMap, applying an r² threshold of 0.8 and a minor allele frequency threshold of 0.04. The tagSNPs were optimized for the Illumina platform by preferentially selecting the SNP with the highest genotyping success rate in each block as a tag and re-evaluating the r² in the sample. Additionally, 4 SNPs were previously genotyped by RFLP methods [23, 24].

The WH-II study

The Whitehall-II study (WH-II) recruited 10,308 participants (70% men) between 1985 and 1989 from 20 London-based Civil service departments [25, 26]. Blood samples for DNA were collected in 2002–2004 from more than 6,000 participants [26]. Fibrinogen was measured in phases 1 (1985–1988), 3 (1991–1993) and 5 (1997–1998) by an automated Clauss assay in a MDA-180 coagulator (Organon Teknika) using the manufacturer’s reagents and the International Fibrinogen Standard [27]. Thirteen SNPs were genotyped 2003–2004 using the HumanCVD Bead-ChipI llumina [28] shown in supplementary Table S1 with more information shown in Talmud et al. 2009 [26].

Statistical analysis

Hardy–Weinberg equilibrium (HWE) was assessed using a Chi-square test in STATA release 10 (Stata Corp., College Station, Texas, USA). Pairwise linkage-disequilibrium (LD) between the SNPs was calculated from the genotype data and measured as both D′ and r² with the software Haploview (http://www.broad.mit.edu/mpg/haploview). Haplotypes were inferred using PHASE [29–31]. Missing SNPs genotypes were imputed though haplotypic reconstruction using the PHASE algorithm [29–31] that has been shown to be accurate for imputation of missing genotypes among unrelated individuals [32]. Is has been previously demonstrated that haplotype inference programs such as PHASE can infer phasing information with high accuracy, thereby minimizing errors in subsequent imputation attributable to these inferred haplotypes [29, 32, 33]. In addition, the observed minor allele frequency (MAF) and the LD was identified in the NPHS-II and in WH-II cohorts. The average fibrinogen was used as the phenotype of interest, representing the mean of the available measurement for each individual. Measurement error or within-person variability (regression-dilution bias) in fibrinogen concentration and the other risk factors can lead to miss-estimation of risk [34]. Instead of using the regular methods of correction for regression dilution bias, such as repeated measure [35] or long-term average concentration from serial measurements [34], the fibrinogen concentration value used was estimated as the mean of all the available annual measurements for each individual in the 6 years follow-up period in NPHS-II and three available measurements in WH-II. Eighty-eight percent of the subjects had more than three measurements of fibrinogen levels in NPHS-II and eighty percent of the subjects had more than three measurements of fibrinogen levels. In addition, follow-up started after the last measurements of fibrinogen levels, with measures made after any early event excluded from the mean levels. The results using longitudinal models are remarkably similar with the results presented as a mean of all the available annual measurements for each individual in the 6 years follow-up period in NPHS-II and three available measurements in the WH-II study. The levels of fibrinogen concentration were logarithmically transformed. The concentrations shown are after back-transformation to the original scale of measurement. All regression models included adjustment for age, clinic and current smoking in the NPHS-II study and age and smoking in WH-II. The subset of SNPs providing the best fit to the data, among all the possible models, was selected using a number of criteria (Akaike information criterion (AIC), Bayesian information criterion (BIC), Mallows Cp, Residual Mean Square (RMS), a leave-one-out Cross-validation, R², and conditional analysis as commonly used in GWAS) in R (http://www.r-project.org). To check how sample size affect the results we randomly selected a proportion (25%, 50%, 75%) of our original dataset to apply the stepwise AIC procedure used in the main analysis and repeated the procedure a 1,000 times. General linear models were fitted to determine relationships of individual tagSNPs variant alleles in additive models (coded 0/1/2 indicating the number of copies of the variant allele) with the continuous outcome measures of plasma fibrinogen levels using Stata software. Additive genotypic models were used in the absence of knowledge about the true mode of inheritance [36]. In the haplotype analysis the most frequent haplotype was used as reference. Effect sizes were estimated in terms of the regression coefficients and partial R² were computed to assess the impact of each variable in the model on the total variance of fibrinogen levels. The weighted genetic score was computed as the sum of the genotypes multiplied by the effect size (coded as 0/1/2 indicating the number of copies of the rare allele). The SNPs were incorporated as instrumental variables to examine the association between plasma fibrinogen and CHD [11, 37]. We used the methods described in [38] using maximum quasi-likelihood estimator (qvf command in Stata) [38, 39]. Cox proportional hazards models were used to estimate hazard ratios (HR), and logistic regression analysis was used to estimate Odds Ratio (OR) and 95% confidence intervals (95% CI) for the associations of SNPs and haplotypes with risk of CHD events in the NPHS-II and WH-II studies, respectively.

Results

Allele frequencies and pair-wise LD structure at the fibrinogen gene cluster

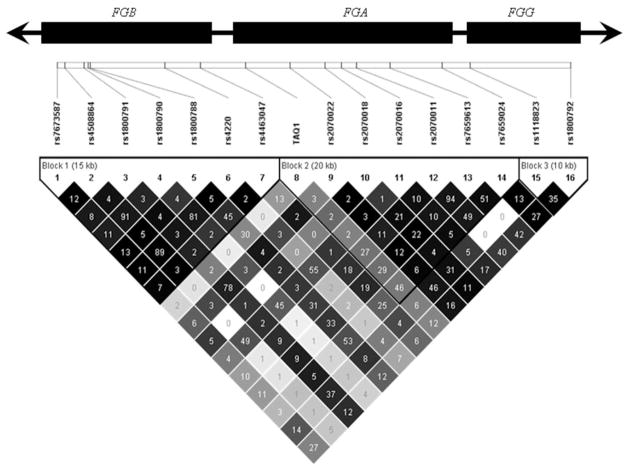
Table 1 shows the baseline characteristics of the NPHS-II sample. Subjects were genotyped for 20 SNPs, 16 using the Illumina platform and four by an RFLP method. SNPs rs2070025 and rs2066870 were monomorphic in our sample and were not considered further, while the frequencies of the rare alleles for the rs6054 and rs2066860 SNPs were 1 and 3%, respectively and were subsequently dropped from the analysis. All polymorphisms genotyped were in Hardy–Weinberg equilibrium (supplementary Table S1). The LD structure, expressed as D′ and r², is shown in Fig. 1 (supplementary Figure S1). There is high LD between many of the SNPs within the fibrinogen gene cluster.

Table 1.

Baseline characteristic [Mean (SD) or N (%)] of the subjects in the NPHS-II and WH-II studies

	NPHS-II (n = 2,778)	WH-II (n = 3,705)
Age (years)	58.5 (3.45)	52.0 (5.85)
BMI (kg/m2)	26.6 (3.50)	25.0 (3.08)
SBP (mmHg)	135 (16)	122 (13)
DBP (mmHg)	83 (10)	81 (9)
Current smokers (%)	28.1	12.5
Diabetes mellitus (%)	2.5	0.6
CHD (%)	10.2	8.3
Average fibrinogen (g/L)	2.84 (0.43)	2.61 (0.50)
Lipoprotein and apolipoprotein
TC (mmol/L)	5.65 (0.88)	6.45 (1.11)
LDL-C (mmol/L)	3.09 (1.01)	4.42 (0.98)
apoB (g/L)	0.90 (0.26)	1.30 (0.29)
TG (mmol/L)	2.05 (1.10)	1.54 (1.17)
HDL-C (mmol/L)	1.71 (0.59)	1.33 (0.35)
apoAI (g/L)	1.63 (0.32)	2.06 (0.32)

n, Sample size; BMI body mass index, CHD coronary heart disease, SBP systolic blood pressure, DBP diastolic blood pressure, TC total cholesterol, LDL-C LDL cholesterol, apoB apolipoprotein B, TG triglyceride, HDL-C HDL cholesterol; apoA, apolipoprotein AI

Fig. 1.

Pair-wise linkage disequilibrium structure represent as a D′ (different colour intensities) and r² values (numbers) in the NPHS-II study. The rs numbers and the relative physical distance between the SNPs are shown above (gene are the larger rectangular boxes). The colour gradient indicates relative level of LD from black complete to white no LD

Association between fibrinogen genes SNPs and plasma fibrinogen levels

Genotype frequencies and results from the univariate analysis for the association of the fibrinogen cluster SNPs with plasma fibrinogen levels are presented in Table 2. The minor alleles of five SNPs (FGB: rs4508864, rs1800790 (−455G >A), rs4220; FGA: rs2070016; FGG: rs1800792) were associated with higher average plasma fibrinogen levels, while two SNPs (FGB: rs1800788; FGA: rs2070011) were associated with lower average plasma fibrinogen levels. SNP rs4508864 was associated with the largest effect, with a per-allele difference of 3.04% in average fibrinogen levels.

Table 2.

The association between fibrinogen FFB/FGA/FGG genotypes and mean average fibrinogen levels in the NPHS-II and WH-II studies

Cohort
Gene	SNPs	MAF	Effect size (β), g/L	R2 (%)	P value
NPHS-II
FGB	rs4508864	0.19	0.082	1.223	3.10E – 09
	rs1800790	0.19	0.081	1.220	3.24E – 09
	rs1800788	0.20	−0.032	0.176	1.52E – 02
	rs4220	0.17	0.084	1.206	3.96E – 09
FGA	rs2070016	0.15	0.083	1.002	7.54E – 08
	rs2070011	0.39	−0.036	0.359	9.28E – 04
FGG	rs1800792	0.45	0.031	0.252	4.69E – 03
WH-II
FGB	rs4508864	0.19	0.079	0.774	4.85E – 08
	rs1800790	0.19	0.079	0.772	5.03E – 08
	rs1800788	0.20	−0.065	0.579	2.09E – 06
	rs4220	0.17	0.066	0.475	1.60E – 05
FGA	rs2070016	0.14	0.055	0.266	9.73E – 04
	rs2070011	0.38	−0.030	0.152	9.96E – 03
FGG	rs1800792	0.44	0.027	0.121	1.92E – 02

MAF minor allele frequency, Effect size (β coefficients) per-allele effect adjusted for age, clinic (only NPHS-II), and smoking

Model selection methods

The SNPs considered were not completely independent of each other, with LD ranging from an r² value of<0.001–0.95 (Fig. 1). A model using all of the SNPs as explanatory variables will account for the between-SNP associations, but would also lead to over fitting. To determine a parsimonious set of SNPs accounting for the association of the fibrinogen gene cluster with fibrinogen levels, we used a number of criteria of fit, with both stepwise and best-subset methods as described previously [40]. Table 3 presents all the criteria used and the SNPs in the best model in each case. The Bayesian information criterion (BIC) was the most conservative, choosing only the rs4508864 SNP. The Akaike information criterion (AIC), adjusted R², Mallows Cp, Residual Mean Square (RMS), and the leave-one-out cross-validation scheme, selected a model containing two SNPs: the “historical” FGB rs1800790 SNP, and the FGA rs2070011 SNP. The conditional analysis supported the idea that more than a single SNP is required but in addition to the rs2070011 SNP it selected the rs4508864 instead of the “historical” SNP. Ranking the SNPs by P value shows that SNP rs4508864, also chosen by BIC, was the top-ranking SNP, while the most commonly selected rs1800790 and rs2070011 SNPs were ranked as second and fifth, respectively. Stepwise regression using AIC stopped at the same two SNPs as the best-subset method. The P-value based stepwise regression, selected the same two SNPs, when a P value of 0.1 was used as a cut-off.

Table 3.

Comparison of different model selection approaches with all the SNPs in the NPHS-II study

Gene	SNPs	Mean log of fibrinogen	Rank of P value	Conditional regression analysis	Adjusted R2	Mallows’ Cp	RMS residuals	AIC	AICc	BIC	Cross- validation	Stepwise regression using AIC	Stepwise regression using P = 0.1a
FGB	rs7673587	−0.0066	12
	rs4508864	0.0300****	1	X						X
	rs1800791	−0.0020	16
	rs1800790	0.0297****	2			X	X	X	X		X	−2768.462	2.01e – 08
	rs1800788	−0.0120*	8
	rs4220	0.0307****	3
	rs4463047	−0.0095	11
FGA	Taq1	−0.0093*	9
	rs2070022	−0.0031	15
	rs2070018	−0.0077	13
	rs2070016	0.0304****	4
	rs2070011	−0.0135****	5	X	X	X	X	X	X		X	−2773.900	0.006
	rs7659613	−0.0124**	6
	rs7659024	−0.0094*	10
FGG	rs1118823	−0.0042	14
	rs1800792	0.0114**	7

The best-subset models cross (X) denotes inclusion in the best model

AIC Akaike’s information criterion, BIC Bayesian information criterion; RMS root mean square; AIC given;

^aP value are shown;

^*<0.05;

^**<0.01;

^***<0.001;

^****<0.0001

Using the baseline fibrinogen levels in the model selection methods, instead of the average of the six measures changed the best model selected by AIC, Mallows Cp, RMS Residuals, and leave-one-out Cross-validation to a model containing, in addition to the two previous SNPs (rs1800790, rs2070011), SNP rs4463047, which did not, however, show association with fibrinogen levels (Data not shown).

To check how sample size affects the results of variable selection procedure we randomly selected a proportion of our original dataset to apply the stepwise AIC procedure used in the main analysis and repeated the procedure a 1,000 times (presented in Table S4). The median number of selected SNPs was two for all proportions tested and was thus similar to the results obtained in the entire sample. The mean number of variables selected increased slightly with sample size, suggesting that more than two SNPs might provide a slightly better prediction, as the sample size is increasing, but the SD of the solutions decreased sharply with increasing sample size, signifying the increasing accuracy with which the best model is selected.

In considering the two best model (Table 4), the first model containing the “historical” FGB rs1800790 SNP and FGA rs2070011 explained 1.45% (AIC = −2773.900) of the residual variance in average fibrinogen levels when adjusted for age, clinic, and current smoking (which explained 14.7% of the variance), i.e. an increase of 19% over the single SNP effect of 1.22%. In the second model, the P value top-ranking SNPs found in the BIC selected model the FGB rs4508864 and FGA rs2070011 SNPs explained 1.44% (AIC = −2773.644) of the residual variance in average fibrinogen levels when adjusted for age, clinic, and smoking.

Table 4.

Multivariate regression with the two selected SNPs and the independent contributions of covariates to plasma average fibrinogen levels in the NPHS-II and WH-II studies

Model	Dependent variable	Independent variable	Effect size (β), g/L	P value for variables	F statistic, P value (all model)	P value for R2 change	Adjusted R2 (AIC)	P value between the models (model 1 reference)
NPHS-II
Model 1	Fibrinogen	rs1800790	0.081	3.24E – 09	35.26, 3.24E – 09	–	1.22 (−2768.462)	–
Model 2	Fibrinogen	rs1800790	0.077	2.01E – 08	–	–	–	–
		rs2070011	−0.030	6.42E – 03	21.39, 6.03E – 10	0.006	1.45 (−2773.900)	0.006
Model 3	Fibrinogen	rs4508864	0.078	2.29E – 08	–	–	–	–
		rs2070011	−0.029	7.76E – 03	21.26, 6.85E – 10	0.008	1.44 (−2773.644)	0.007
WH-II
Model 1	Fibrinogen	rs1800790	0.079	5.03E – 08	28.83, 5.03E – 08	–	0.77 (−1920.360)	–
Model 2	Fibrinogen	rs1800790	0.077	1.14E – 07	–	–	–	–
		rs2070011	−0.026	2.43E – 02	17.47, 2.81E – 08	0.024	0.88 (−1923.437)	0.024
Model 3	Fibrinogen	rs4508864	0.077	1.10E – 07	–	–	–	–
		rs2070011	−0.026	2.44E – 02	17.50, 2.73E – 08	0.023	1.00 (−1923.498)	0.023

Effect size (β coefficients) per-allele effect adjusted for age, clinic (only NPHS-II), and smoking; AIC Akaike’s information criterion

Association between haplotypes of the fibrinogen gene cluster and plasma fibrinogen levels

The haplotypes examined were based on the variable selection results that account for the presence of three LD blocks, and two SNPs selected FGB: rs1800790, and FGA: rs2070011. The common haplotypes for the FFB/FGA/FGG gene cluster and their association with plasma average fibrinogen levels are presented in Table 5. Four haplotypes were observed, and compared to the most common haplotype (A1 frequency 45.5%), only A3 (frequency 16.4%) was associated with a significant per allele raising effect of 3.0% (P <0.001) in average plasma fibrinogen level (Fig. 2). Fitting a model through either all haplotypes or only A3 (under an additive model) and covariates (age, clinic, and smoking) accounted for 0.66 and 1.37%, respectively of the variation in average plasma fibrinogen levels.

Table 5.

Common haplotypes estimated for the FFB/FGA/FGG cluster and association with plasma average fibrinogen levels in the NPHS-II and WH-II studies

Haplotype	rs1800790	rs2070011	Freq. (%)	Effect size (β), g/L	P value	Total R2 (AIC)
NPHS-II
A1	1	1	45.5	Ref.	–	–
A2	1	2	35.2	−0.019	0.111	–
A3	2	1	16.4	0.081	2.42E – 07	–
A4	2	2	2.9	0.027	0.394	0.66 (−5506.520)
Only A3
A3	–	–	–	0.094	1.32E – 18	1.37 (−5548.332)
WH-II
B1	1	1	46.6	Ref.	–	–
B2	1	2	35.0	−0.018	0.141	–
B3	2	1	15.5	0.072	1.32E – 05	–
B4	2	2	3.0	0.071	0.035	0.39 (−3813.541)
Only B3
B3	–	–	–	0.081	8.18E – 13	0.68 (−3836.525)

1, Major allele; 2, Minor allele; Freq., frequency; Effect size (β coefficients) per-allele effect adjusted for age, clinic, and smoking; AIC, Akaike’s information criterion; Only A3/B3, Non-carrier, Heterozygote, Homozygote for haplotype A3/B3

Fig. 2.

The association between haplotype A3 and B3 and average fibrinogen levels in the NPHS-II and WH-II studies

Association between SNPs/haplotypes of the fibrinogen gene cluster and tertiles of plasma fibrinogen levels

The association between fibrinogen FFB/FGA/FGG genotypes and the highest tertile of fibrinogen levels is presented in Table 6. The odds ratio (OR, 95% confidence interval) of being in the highest tertile of plasma fibrinogen levels (over 2.99 g/l) was 1.54 (95% CI: 1.30–1.82, P = 3.72E – 07) per allele of SNP rs1800790. As expected, the SNP rs2070011 had a protective per allele effect of OR = 0.79, (95% CI: 0.69–0.90, P = 5.14E – 04). The combinations of these two SNPs together in a weighted genetic score or haplotype analysis increased the risk of an individual being in the highest tertile of fibrinogen levels. The weighted genetic score had an OR = 2.48 (95% CI: 1.83–3.36, P = 5.46E – 09) per increasing allele and the OR for carrying haplotype A3 was 1.80 (95% CI: 1.58–2.05, P = 5.88E – 14).

Table 6.

The association between SNPs/haplotypes of the fibrinogen gene cluster and tertiles of plasma fibrinogen levels in the NPHS-II and WH-II studies

Tertile of fibrinogen	NPHS-II OR (95% CI), P value	WH-II OR (95% CI), P value
rs1800790	1.54 (1.30–1.82), 3.72E – 07	1.35 (1.16–1.56), 7.26E – 05
rs2070011	0.79 (0.69–0.90), 5.14E – 04	0.87 (0.78–0.98), 2.46E – 02
Weighted genetic- score*	2.48 (1.83–3.36), 5.46E – 09	2.59 (1.70–3.94), 9.18E – 06
Haplotype	Ref.	Ref.
A1/B1	0.83 (0.72–0.96), 0.013	0.90 (0.80–1.02), 0.098
A2/B2	1.60 (1.33–1.94), 9.72E – 07	1.27 (1.07–1.50), 6.00E – 03
A3/B3	1.13 (0.77–1.66), 0.519	1.38 (0.99–1.92), 0.060
A4/B4	1.80 (1.58–2.05), 5.88E – 14	1.33 (1.19–1.50), 1.12E – 06
Only A/B 3
A3 or B3

OR odds ratio; CI confidence interval 95%; models adjusted for age, clinic, and smoking in NPHS-II study and age, smoking in WH-II;

^*Highest tertile of weighted genetic-score; 11, Only A/B 3, Non-carrier, Heterozygote, Homozygote for haplotype A3 or B3

Associations of fibrinogen SNPs with potential confounding factors

We found no consistent associations of the fibrinogen SNPs with potential confounding factors in either cohort, such as age, smoking, recruiting center, BMI, total cholesterol, LDL-C, ApoB, triglycerides, HDL-C, ApoAI, systolic blood pressure, diastolic blood pressure, and CRP (supplementary Table S3).

Effects of fibrinogen levels and fibrinogen SNPs/ haplotypes on CHD

A linear relationship between average plasma fibrinogen levels and CHD events was seen in the NPHS-II study (P-for trend = 7.58E – 05). Individuals in the highest tertile of plasma fibrinogen levels (2.99–5.31 g/L) had a Hazard Ratio (HR) of 1.85 (95% CI: 1.39–2.46, P = 2.91E – 05) compared to those in the lowest tertile (1.52–2.63 g/L). Adjustment for age, clinic, BMI, and smoking reduced this estimate to HR = 1.68 (95% CI: 1.19–2.36, P = 0.003). Only one SNP (rs4463047: HR = 0.74, 95% CI: 0.56–0.98, P = 0.038) was found to be associated with CHD risk (Supplementary Table S2).

Association between genetic markers of fibrinogen and CHD

The distribution of both SNPs and haplotypes was not different between the CHD event and non-event group. Neither the SNPs nor the haplotypes, showed any associations with risk of CHD before or after adjustment for other CHD risk factors. The incidence of CHD in the NPHS-II and WH-II studies was less than 11 and 9%, respectively, resulting in a limited statistical power (~30 and, ~20% for individual SNPs and haplotypes, respectively) to detect modest effects, such as those observed here, for the association between genetic variability at this locus and disease. Our power calculation assumes a fibrinogen-CHD association equal to the observed association, which means that the actual power could be even lower, if unmeasured confounding were to cause an over-estimation of the odds ratio between fibrinogen and CHD observed.

Instrumental variable regression

The first stage F-statistic for instrumental variables analysis suggested that the SNPs were a sufficiently strong genetic instrument. The F-value was F(1, 2773) = 35.26 for SNP rs1800790, and F(1, 2773) = 10.99 for SNP rs2070011. When both SNPs were included as instruments the F-value was F(2, 2772) = 21.39, while combining them in a weighted gene score resulted in an F of F(1, 2773) = 42.45. The second stage instrument variable regression in all cases, suggested that there is no causal effect between fibrinogen levels and CHD in our sample (P = 0.726 SNP rs1800790, P = 0.126 SNP rs2070011 as an instrument; P = 0.321 for multiple SNPs rs1800790 and SNP rs2070011 and P = 0.135 for weighted genetic score used as the instrument). The over-identification test showed no strong evidence against the joint use of the two SNPs as multiple instrument (P = 0.184).

Replication study WH-II

Association between fibrinogen genes SNPs and plasma fibrinogen levels

Genotypes for 13 SNPs were determined in WH-II. The minor alleles of five SNPs (FGB: rs4508864, rs1800790 (−455G >A), rs4220; FGA: rs2070016; FGG: rs1800792) were associated with higher average plasma fibrinogen levels, while two SNPs (FGB: rs1800788; FGA: rs2070011) were associated with lower average plasma fibrinogen levels (Table 2). Again, SNP rs4508864 was associated with the largest effect, with a per-allele difference of 3.12% in average fibrinogen levels and a R² of 0.77% after adjusted for age and smoking which explained 4.96% of the variance. During variable selection, when the FGB rs1800790 and FGA rs2070011 SNPs were forced into the model, none of the other SNPs were able to minimize AIC further (Table 3). These two genotypes explained 0.88% (AIC = −1923.437) of the residual variance in average fibrinogen level adjusted for age, and smoking i.e. an increase of 14% over the single SNP effect.

Association between haplotypes of the fibrinogen cluster and plasma fibrinogen levels

Again, haplotypes were inferred using SNPs rs1800790 and rs2070011. All four possible haplotypes were observed and subsequently compared to the most common haplotype (B1 frequency 46.6%). As was seen in NPHS-II, only B3 (frequency 15.5%) was associated with a per allele raising effect on average plasma fibrinogen levels of 2.86% (P = 1.32E – 05) (Table 5). The overall model including all haplotypes, or only B3 and covariates (age and current smoking) accounted for 0.39 and 0.68%, respectively of the variation in average plasma fibrinogen levels.

Association between SNPs/haplotypes of the fibrinogen cluster and tertiles of plasma fibrinogen levels

The OR (95% confidence interval) of being in the highest tertile of plasma fibrinogen levels was 1.35, (95% CI: 1.16–1.56, P = 7.26E – 05) per allele of SNP rs1800790 (Table 6). As expected, SNP rs2070011 had a lowering per allele effect of OR = 0.87, (95% CI: 0.78–0.98, P = 2.46E – 02). The combination of these two SNPs, in a weighted genetic score or haplotype, increased the risk of having fibrinogen levels in the highest tertile. The weighted genetic score was associated with an OR per allele of 2.59, (95% CI: 1.70–3.94, P = 9.18E – 06) while the OR for carrying haplotype B3 was 1.33 (95% CI: 1.19–1.50, P = 1.12E – 06).

Effects of fibrinogen SNPs/haplotypes upon CHD and instrumental variable regression

Two of the SNPs considered were found to be associated with CHD risk (rs2070011: OR = 1.23, 95% CI: 1.04–1.46, P = 0.017 and rs7659613: OR = 1.22, 95% CI: 1.03–1.45, P = 0.020). The F-value in the first-stage instrumental variables analysis was F(1, 3703) = 29.83 for SNP rs1800790 and F(1, 3703) = 6.65 for SNP rs2070011 and F(2, 3702) = 18.45 for multiple SNPs (rs1800790 and rs2070011), while combining them in a gene score resulted in an F of F(1, 3703) = 34.78. The second stage instrument variable regression in all cases, suggested that there is no causal effect between fibrinogen levels and CHD in our sample (P = 0.536 SNP rs1800790, P = 0.066 SNP rs2070011 as an instrument; P = 0.708 for multiple SNPs rs1800790 and SNP rs2070011 and P = 0.586 weighted genetic score used as the instrument).

Discussion

In this paper we have shown that more than one SNP is required to maximize the association between the fibrinogen gene cluster and plasma fibrinogen levels. We have found that two SNPs, rs1800790 and rs2070011, are adequate to capture the common functional variation of the gene cluster, although the precise functional SNPs are not known. In addition, we show that the use of these two SNPs will increase statistical power to identify if a causal relationship between plasma fibrinogen levels and CHD exist. One of the main strengths of the study is that repeated measures of plasma fibrinogen over time were available for both studies, all assayed in the same laboratory for each study and under standardised conditions, which considerably enhances the ability to detect modest effects associated with genotypes and haplotypes. In terms of Mendelian randomization, we were not able to identify a causal link between fibrinogen levels and CHD. The relatively small number of CHD events (284 and 308 in NPHS-II and WH-II studies, respectively) and the small percentage of the phenotypic variance explained by the markers considered, preclude a reliable examination of the association between fibrinogen SNPs and CHD. This second stage analysis will require a major collaborative effort, as has been put together for example for CRP [9].

Although, of the 20 SNPs examined, seven FGB, FGA and FGG SNPs had effects on the average plasma fibrinogen levels in univariate analysis, only two SNPs were retained in the most parsimonious model obtained from the model selection methods. One SNP is in the FGB promoter (rs1800790), and the other (rs2070011) in the FGA promoter. These associations were consistent and replicated in the WH-II sample although overall, genotype explained a smaller proportion of the variance than in the NPHS-II. Several SNPs showed a high degree of LD with the “historical” SNP (rs1800790 or −455G >A), commonly used in Mendelian randomization studies [8, 9, 12], including SNP rs2070011, selected from the variable selection procedure. This SNP when added to the model, improved the explained residual variance and AIC by more than ~0.15% compared to the model with only the “historical” SNP.

This finding was supported by the instrumental variable analysis. The F statistic is considered as a metric for the strength of the instrument, with higher values signifying a better instrument [10, 11, 37, 41]. In our case the first stage F increased from 35.26 for the single “historical” SNP to 42.45 for the two SNPs grouped in a weighted genetic score in NPHS-II. Similarly in WH-II the F statistic increased from 29.83 for the single “historical” SNP to 34.78 for the combination of the two SNPs. The use of multiple instruments potentially increases the finite sample (weak instrument) bias, something that has not received prominence in Mendelian randomization studies. When the instrumental variable is only weakly correlated with the exposure, the IV estimator will be imprecise with large standard error, and biased when either the sample size is small or one of the assumptions is only slightly violated [10, 37, 41]. In our study, the variable selection methods consistently chose the same two SNPs, so the association for both instruments is strong. The partial R² and F statistic of the identified instruments in the first stage provide information on the quality of the SNPs as IV [10, 11].

Multiple testing can indeed be a problem in this kind of studies and spurious combinations can arise. The use of a second, completely independent study does provide unbiased estimates for the increase in the variance explained by the combination of the two SNPs compared to the single commonly used SNP. Using both SNPs in variable selection in the WH-II study (the replication study) we confirmed that the Bayesian information criterion (BIC) was the most conservative, choosing only the rs1800790 SNP, while the Akaike information criterion (AIC), adjusted R², Mallows Cp, Residual Mean Square (RMS), and the leave-one-out cross-validation scheme, all selected a model containing the two SNPs selected in NPHS-II (the derivation study), that is the “historical” FGB rs1800790 SNP, and the FGA rs2070011 SNP. In addition, the genetic effects underlying complex traits and disorders are small, and their detection requires comprehensive typing of single nucleotide polymorphisms (SNPs) in large samples [42, 43]. Many previous genetic association studies have been underpowered [44, 45] and even very large biobanks [46] may not individually provide conclusive results for certain outcomes.

The most widely studied fibrinogen polymorphism is the −455G >A (rs1800790) change in the promoter region of the β fibrinogen (FGB). There is strong LD between SNPs at the α, β, and γ fibrinogen loci, with several common SNPs that alter amino acids in either the α gene (A312T, rs6050) or the β chain (−148C >T, rs1800787) show varying degrees of LD with the “historical” SNP [12, 13]. Interestingly, SNP rs4508864, in the upstream promoter region of FGB (C/T), had the largest effect in the univariate analysis and was included in the best model when the −455G >A SNP (rs1800790) was not forced at the start, due to the almost complete LD between the two (r² = 0.91 in NPHS-II and r² = 0.99 in WH-II). Using a purely statistical approach, it is not possible to confirm whether either or both of these SNPs are themselves functional, or whether they are acting simply as markers for another SNP(s) with which they are in LD. One SNP showing strong LD with both SNPs is rs4220 (coding, non-synonymous) where the sequence change alters the R448 K amino acid in the beta chain, and has been previously associated with fibrin gel formation [24, 47]. In contrast, the C >T sequence change due to rs4508864 is located −3093 bp from the start of transcription of the FGB gene and has not been studied in previous reports [13, 48–50] since this region was not covered in the sequencing analysis used. This sequence change is close to a putative X box (located at positions −3110 to −3092), and a putative SP1/GC element (located at positions −3112 to −3091), so it is possible that it may be influencing transcription of the gene directly through altering binding of such activators. The second SNP chosen, rs2070011, is in the alpha gene promoter, (−58G >A) which has been reported to affect transcription [51].

In all models considered, we included adjustment for a number of covariates including age, smoking habit and differences between recruiting centers in NPHS-II. Compared to these covariates it is clear that the genotypes at this locus are explaining, at best, only a very small proportion of the between-individual differences in fibrinogen levels. Similar modest effects versus covariates have been reported in a number of other studies [52, 53]. To reduce the impact of measurement error and within-person variability in fibrinogen concentration as well as other factors such as inflammation and infection that can lead to mis-estimation of the association, multiple measures of fibrinogen in the two cohorts was used.

Haplotypes were used to account for the genetic architecture at this locus. We chose to construct haplotypes using only the two selected SNPs as a balance between information captured and “noise” introduced from inclusion of non-informative SNPs. In both NPHS-II and WH-II studies, the third most frequent haplotype, A3 and B3 respectively, was associated with a raising effect on average fibrinogen levels compared to the most common haplotype. Mannila et al. have reported an association between FGG-FGA and FGG-FGB haplotypes and MI risk [13, 54, 55]. However their results did not confirm other studies that examined single SNPs, or haplotypes in the gene cluster with risk of MI or CHD [14, 49, 50, 56, 57].

Another way to explore whether more than one SNP is useful to be included in the model is by examining the likelihood of individuals with different genotypes to be in the highest tertile of fibrinogen levels. The results including the two SNPs together as a weighted genetic score or haplotype showed strong association to the highest tertile of fibrinogen levels in NPHS-II and WH-II studies, and pooled estimates across the two studies.

To summarize, we found that there was a difference between the model including the two SNPs, selected from the variable selection procedure, and the model including only the single historical SNP. Adding the second SNP in the model was able to modestly improve the variance of fibrinogen levels explained, increasing the variance by 19% in NPHS-II and by 14% in WH-II, although in neither study was the genetic effects large, suggesting that there are likely to be other genes elsewhere in the genome yet to be identified. Our data clearly suggest that there is more than one functional site in the fibrinogen gene cluster that determines an individual’s plasma fibrinogen levels. We conclude that a single SNP is not adequate to represent the association between fibrinogen gene cluster and plasma fibrinogen levels, and that future Mendelian randomization studies to explore the potential causality of elevated fibrinogen levels in causing CHD should include this second SNP.