Abstract
In clinical trials with time-to-event outcomes, it is common to estimate the marginal hazard ratio from the proportional hazards model, even when the proportional hazards assumption is not valid. This is unavoidable from the perspective that the estimator must be specified a priori if probability statements about treatment effect estimates are desired. Marginal hazard ratio estimates under non-proportional hazards (NPH) are still useful, as they can be considered to be average treatment effect estimates over the support of the data. However, as many have shown, under NPH the “usual” unweighted marginal hazard ratio estimate is a function of the censoring distribution, which is not normally considered to be scientifically relevant when describing the treatment effect. In addition, in many practical settings, the censoring distribution is only conditionally independent (e.g., differing across treatment arms), which further complicates the interpretation. In this paper, we investigate an estimator of the hazard ratio that removes the influence of censoring and propose a consistent robust variance estimator. We compare the coverage probability of the estimator to both the usual Cox model estimator and an estimator proposed by Xu and O’Quigley (2000) when censoring is independent of the covariate. The new estimator should be used for inference that does not depend on the censoring distribution. It is particularly relevant to adaptive clinical trials where, by design, censoring distributions differ across treatment arms.
Keywords: Multiplicative hazards model, Partial likelihood, Time-varying effects, Weighted estimator
1. Introduction
Randomized clinical trials are usually conducted to provide an objective and reproducible basis for selecting the better of two (or more) treatments. For this reason the statistical analysis is usually specified a priori, and must define the within-group measure of treatment effect and the between-group comparison measure. For example, with censored time-to-event outcomes such as overall survival or progression-free survival, it is common to quantify the within-group survival distribution with the instantaneous hazard function, and the treatment effect by the average hazard ratio. With a priori specification the choice of these measures should be governed by the scientific and clinical questions of interest rather than questions regarding model fit. In this context, it is entirely possible (in fact, likely) that the treatment effects are not proportional; however, the challenge is to use analytic methods that assure consistent estimation of the underlying hazard ratio as opposed to post-hoc adjustments for model misspecification.
When we are interested in treatment effects as measured by the hazard ratio, consistent inference in the presence of non-proportionality is a function of the underlying censoring distribution as defined by the total observed support and intermittent censoring [1]. The implication of this result is that the usual unweighted Cox estimator will be consistent for a parameter that is dependent upon patient accrual and dropout patterns that bear no relevance to the scientific objectives of a clinical trial. Xu and O’Quigley [2] (hereafter XO) and van Houwelingen et al. [3] describe a re-weighted estimate of the hazard ratio to a standard censoring distribution in the setting where the censoring distribution is independent of the treatment group or covariate level. However, in some practical applications, the assumption of independent censoring is not reasonable.
The objective of the work described below is to obtain a robust estimator of the hazard ratio and its variance in the presence of conditionally independent censoring where the observed accrual or dropout pattern differs by treatment arm. The resulting estimator applies to all clinical trials with censored time-to-event endpoints where consistent inference (relative to a pre-specified censoring distribution) is desired. While not commonly investigated, differential censoring patterns may arise in multiple clinical trial settings via intentional design-based strategies or due to unintended treatment effects. As examples, conditionally independent censoring is generally inherent among clinical trials that utilize historical data, trials in which levels of stratification variables are added as the trial proceeds, as in the case of many international trials where new continents or countries may be added to the study over time, and trials that incorporate outcome adaptive randomization.
In adaptive randomization trials, the randomization allocation is initialized at a ratio, commonly 1:1, and then changes over time depending on an estimate of the treatment effect (via, eg, the log-rank statistic). The idea with such an allocation is to bias the treatment assignment in favor of the “winning” treatment so that patients have a higher chance of receiving the best treatment. At the end of the trial, the administrative time censoring distributions are therefore, by design, treatment group specific. When the adaptive randomization is based on the hazard ratio estimate or the log-rank statistic, the randomization ratio over time will be dependent on the censoring in the presence of non-proportional hazards; the interplay between the allocation rule and the treatment effect estimate is a complex one in these settings, and does not appear to have been acknowledged in the references on adaptive randomization [4, 5, 6, 7].
As noted above, another setting where conditionally independent censoring is likely to arise includes historical control trials as described by the International Conference on Harmonization E10 document [8]. For an example, we will consider study RT-008, a phase 2 trial conducted to estimate the activity of the agent efaproxiral when used as an adjunct to whole brain radiation therapy (WBRT) for the treatment of patients with brain metastases [9]. The study enrolled 69 patients from February 26, 1998 to June 3, 1999. An external control dataset, based on a larger randomized trial in the same patient population for patients treated with WBRT alone, was also available for comparison. Recognizing the limitations of comparing data from different studies, it was nevertheless of interest to make this comparison to aid in the decision as to the direction for future clinical trials. In this example, the treatment and comparison arms have very different censoring distributions; thus, consistent estimation of the hazard ratio is only possible when the censoring distributions are standardized to a common reference.
In the next section we describe the setting and formally define conditionally independent censoring. Section 3 presents the re-weighted estimator and establishes its asymptotic distribution. In Section 4 we present simulation studies to evaluate the estimator relative to the usual Cox estimator and the independent censoring re-weighted estimators in cases where censoring differs by treatment arm and stratification variables. We apply the proposed estimator to data from the RT-008 trial in Section 5 and discuss further applications and implications of these results in Section 6.
2. Setting
With censored time-to-event outcomes, it is common to measure treatment effects by the rate of failure in some interval (t, t + h) conditional on survival to time t. In the limit, this conditional failure rate defines the hazard function λ(t) = limh↓0 P(t ≤ T < t + h|T ≥ t)/h.
It is also common to measure the effects of the p × 1 covariate vector Z on the hazard function by the multiplicative hazards model λ(t) = λ0(t)g (β(t)Z(t)), where λ0(t) denotes the baseline hazard and g(Z) is a relative risk function. A special case of the multiplicative hazards model was proposed by Cox [10], in which g(·) = exp(·) and λ(t) = λ0(t) exp(β(t)Z(t)). For the treatment group contrast in randomized clinical trials, the indicator for group affiliation is not typically a function of time, in which case the Cox model simplifies to
| (1) |
In the two group setting (Z ∈ {0, 1}), (1) is sufficiently flexible to handle any type of survival data as long as β is allowed to vary with time. Although others [11] have considered (1) as a prediction problem, in clinical trials (in the absence of existing pilot data to suggest otherwise) it is common to pre-hypothesize a model with a constant treatment effect, β, satisfying:
| (2) |
and proceed with estimation by maximizing the partial likelihood. This simpler model is rarely if ever correct, but is commonly specified and can be interpretable as a contrast of clinical interest for measuring treatment effects. Specifically, when (1) holds the resulting estimand by assuming (2) and maximizing the partial likelihood is the result of an integral of β(t) through time with respect to some measure that integrates to 1. In extreme cases where the hazard functions cross with large differences before and after the crossing time point, it may be better to consider effects by time period. Even in such cases, these extreme effects would need to be anticipated at the design stage, which is difficult in most applications.
In survival analysis it is common to assume that the random variable representing the time to censoring, C, is independent of the random variable representing the time to failure, T. Under this assumption a functional on the distribution of T (e.g., the hazard) can be estimated without parameterizing the relationship between T and C. In randomized clinical trials where a binary indicator Z is the only covariate of interest, it is also common to assume that the distribution of C is independent of Z. We refer to these two assumptions in tandem as independent censoring. The introduction presents examples in which fully independent censoring cannot be assumed, and instead it is reasonable to assume that the censoring and survival times are independent conditional on the covariate. We will refer to this scenario as conditionally independent censoring.
More formally, let Xi = min{Ti, Ci}, δi = I(Ti ≤ Ci), fT(t) be the density function, FT(t) the cumulative distribution function and ST(t) = 1 − FT(t) be the survival distribution function. Conditionally independent censoring is defined as P(X > t|Z) = P(T > t, C > t|Z) = P(T > t|Z)P(C > t|Z), and independent censoring is defined as P(X > t|Z) = P(T > t)P(C > t). In either case, the likelihood for the independent observations (Xi, δi, Zi), i = 1, …, n is given by
with score function
| (3) |
which forms an estimating equation for β when λ(X) is parameterized as a function of β as in (2).
The use of (3) requires full specification of the survival density; however, for clinical trials, we seek estimators that are robust to misspecification of the survival distribution, but retain efficiency properties when the distribution is correctly assumed. One such estimator is obtained by using the partial likelihood; setting the resulting score equation equal to zero leads to the usual estimating equation for β from the Cox model [10] which can be expressed as the stochastic integral
| (4) |
where , and Ni(t) denotes a counting process that counts the number of events in the interval (0, t) for the ith individual.
Struthers and Kalbfleisch [1] show that the solution to (4) (which we denote by β̂PH) is consistent for the value of β solving
| (5) |
where ST(·) and SC(·) denote the survival functions for the failure and censor times, respectively, and expectation is over Z. Under independent censoring, SC(t|Z) ≡ SC(t), so that (5) simplifies to
| (6) |
showing that β̂PH depends on SC(t) only through weights that apply to the difference in brackets. In the special case where T and Z are independent, DiRienzo and Lagakos [12] have shown that the usual Cox model estimator for β will on average go to zero as the sample size increase. When data follow (1) with conditionally independent censoring, then (5) does not simplify. Thus, for non-proportional treatment effects on the hazard, β̂PH has the undesirable property of changing with the censoring distribution. We also note that this dependence on the censoring distribution has additional consequences; for example, Gillen and Emerson [13] show that the log-rank test depends on the censoring distribution, and therefore lacks transitivity.
3. Re-weighted estimators and their variance
3.1. Re-weighted estimators
We seek a modification to the usual estimating equation to remove the dependency of the estimator on the observed censoring distribution. Consider the weight function indexed by subject j and time t:
and the re-weighted estimating equation given by
| (7) |
where , and Wj(t) is the inverse of the left-continuous version of the Kaplan-Meier estimate of the censoring distribution for group Zj at time t.
It follows from (5) that the solution to (7), which we denote β̂CIC, is consistent for βCIC defined as the solution to:
| (8) |
which removes the dependence on the censoring distribution. Similarly, under independent censoring, the weight function constructed from the combined censoring distribution:
with corresponding estimating equation:
| (9) |
modifies (6) to remove dependence on the censoring distribution. These latter estimates, which we denote β̂IC, are the same as those proposed by Xu and O’Quigley [2].
Although the integration of equations (7) and (9) is over the full support of t, a trial only provides information over its observed support; thus, the above re-weighted estimators will be consistent for the marginal hazard ratio calculated through the shorter of the maximal event times in each arm. Since the maximal event time is a random variable, it might be prudent in clinical trials to instead select a reference time, say τ, for reporting the marginal inference; thus, all data beyond τ would be censored. This can be viewed as standardizing inference to a reference censoring distribution defined by τ with cumulative distribution function: FC(t) = It>τ (t ≥ 0; τ > 0). It can be achieved by redefining the above weights to include an indicator function that defines the reference interval. Equivalently, the integrals of equations (7) and (9) can be over (0, τ) as opposed to (0, ∞).
3.2. Robust variance for the re-weighted estimators
Under suitable regularity conditions (see Appendix), the variance of the Cox estimator obtained by solving the Cox model score equation (4) in a correctly specified model can be consistently estimated via the inverse of the second derivative of the log-partial likelihood [14]. However, as noted by Lin and Wei [15] this method does not provide a consistent variance estimator when the proportional hazards assumption is violated. As we are primarily concerned with the use of the proposed β̂CIC estimator under departures from proportional hazards it is necessary to consider the variance of the estimator when the proportional hazards assumption fails to hold.
To derive a variance estimator for β̂CIC, we begin by defining A = −limn→∞ n−1∂U(β)/∂β|β=β̂ and note that (7) can be written as:
where . Expanding about , and ÑW·(t) = limn→∞ n−1NW·(t), (7) is asymptotically equivalent to
| (10) |
consisting of independent and identically distributed mean zero terms. Thus n−1/2U*(β) is asymptotically zero-mean normal with covariance matrix
and the asymptotic variance of β̂CIC is given by limn→∞ n−1A−1BA−1.
To estimate the variance of β̂CIC note that the ith component of (10) can be estimated by the quantity
| (11) |
Further, when Z = 0 or 1, a consistent estimate of A is given by
| (12) |
Putting (11) together with (12), a robust variance estimator for β̂CIC is given by
| (13) |
where . Note also that (13) could be used as a variance estimator for β̂IC as well since it is a special case of β̂CIC with Wi(Xj) = 1 for i ≠ j.
The large sample properties of the proposed estimator for βCIC using (7) are established in the following theorem:
Let β̂CIC denote the solution to (7), where the true data are generated from the possibly misspecified model given by (1). Then β̂CIC is asymptotically normally distributed with mean βCIC and variance V(βCIC) consistently estimated by (13). Further, under the proportional hazards model in (1), β̂CIC is asymptotically normally distributed with mean β and variance A−1(β) where A(β) is consistently estimated by (12). [Proof: see Appendix.]
4. Simulations
Simulation results are divided into three subsections: Section 4.1 compares the coverage probabilities of the estimators β̂PH, β̂IC, or β̂CIC for β from model (2) under (a) independent censoring and (b) conditionally independent censoring schemes for various types of data from model (1). Section 4.2 considers the performance of the proposed estimator in a stratified analysis when the censoring distribution differs from one stratum to the next. Section 4.3 evaluates the small sample properties and asymptotic convergence of V̂(β̂CIC) as defined in (13).
We consider the standard context for clinical trials in which our a priori measure of treatment effect is the marginal hazard ratio from (2) but acknowledge that the true underlying model is specified by (1). Further, we assume that the pre-specified target of inference is the marginal hazard ratio in the absence of any censoring prior to time τ > 0; i.e., the cumulative reference censoring distribution is FC(t) = It>τ (t ≥ 0; τ > 0). In the following simulations, we take τ = 4.
For all simulations, survival data were generated from model (1) via a piecewise exponential distribution with hazard function given by
| (14) |
where Z is the covariate value taking values 0 (control) or 1 (active treatment), t0 = 0.5, β0 = 0, and β1 = 3. Censoring times were specified by a “powered uniform” distribution given by:
| (15) |
Here, r(Z, S) controls the rate of censoring, which can differ by covariate value Z and stratum Z (if only 1 stratum exists then the notation is taken to be indexed by only Z as in r(Z)). As an example, in many clinical trials, there is a ramp up time while sites are initiated and patient enrollment begins, causing a lag in the enrollment rate and pushing relatively early censoring in the survival curves. Such a scenario corresponds to r > 1.
Simulations were written in the R software language. For β̂PH, we used the robust variance estimator proposed by Lin and Wei [15]. For β̂CIC, the robust variance estimator V̂(β̂CIC) defined in (13) was used, and for β̂IC an analogous variance estimator was formed by replacing β̂CIC with β̂IC in (13). These model-based standard errors (SE) are presented along with the standard deviation of the simulated estimates (SD) in each table. It should be recognized that the robust variance estimator of Lin and Wei for the usual Cox model is not often used in practice. Choosing the usual variance estimator would likely skew the results of the simulations even more in favor of the weighted estimators, but would not, strictly speaking, be a fair comparison, since we are assuming model misspecification in the simulations.
Coverage probabilities are the percentage of confidence intervals, based on the estimates plus or minus 1.96 times the model-based standard errors, that contain the true parameter value. All three estimation techniques are applied to the same dataset simulated each time for a total of 1,000 simulated datasets. The reference contrast, which is the estimate of the hazard ratio from (4) with no censoring prior to τ = 4, is also presented.
4.1. Simulation results under independent censoring and conditionally independent censoring
Tables 1 and 2 present the results of the simulations for the independent censoring and conditionally independent censoring scenarios with no stratification. For the conditionally independent censoring simulations (Table 2), the r(1) parameters could be interpreted as the censoring distribution in a single-arm trial which is compared with an external control with complete follow-up through τ (denoted by r(0) = ∞). In keeping with the reference censoring distribution, values beyond τ are censored at τ. In all cases, the coverage probability of the unweighted estimator is different from the nominal level. This is mostly driven by the bias of the estimate, which in some cases is extreme. It is worth repeating that this is the estimator most commonly used in practice.
Table 1.
Simulation results under independent censoring. Results are based on 1,000 simulated data sets for each scenario.
| % Censoring | n | Estimator | β | Estimate | SE | SD | CP |
|---|---|---|---|---|---|---|---|
| 20% | 100 | β̂PH | −0.60 | −0.543 | 0.163 | 0.167 | 0.934 |
| β̂IC | −0.60 | −0.595 | 0.171 | 0.171 | 0.953 | ||
| β̂CIC | −0.60 | −0.595 | 0.177 | 0.169 | 0.958 | ||
| 500 | β̂PH | −0.60 | −0.545 | 0.073 | 0.074 | 0.882 | |
| β̂IC | −0.60 | −0.600 | 0.078 | 0.079 | 0.952 | ||
| β̂CIC | −0.60 | −0.599 | 0.082 | 0.078 | 0.960 | ||
| 40% | 100 | β̂PH | −0.60 | −0.442 | 0.188 | 0.194 | 0.841 |
| β̂IC | −0.60 | −0.581 | 0.210 | 0.208 | 0.951 | ||
| β̂CIC | −0.60 | −0.583 | 0.216 | 0.206 | 0.954 | ||
| 500 | β̂PH | −0.60 | −0.448 | 0.084 | 0.081 | 0.543 | |
| β̂IC | −0.60 | −0.596 | 0.098 | 0.093 | 0.963 | ||
| β̂CIC | −0.60 | −0.597 | 0.102 | 0.091 | 0.974 |
n = number of individuals per group, β = true time-averaged treatment effect when there is no censoring through τ = 4, SE is the mean of the model-based standard errors, SD is the empirical standard error, and coverage probability (CP) is the percentage of SE-based confidence intervals that contain β. Censoring times were generated from (15) with r(0) = r(1) = 2.20 to give 20% censoring and r(0) = r(1) = 0.73 to give 40% censoring.
Table 2.
Simulation results under conditionally independent censoring. Results are based on 1,000 simulated data sets for each scenario.
| % Censoring | n | Estimator | β | Estimate | SE | SD | CP |
|---|---|---|---|---|---|---|---|
| 20% | 100 | β̂PH | −0.60 | −0.540 | 0.166 | 0.168 | 0.924 |
| β̂IC | −0.60 | −0.602 | 0.172 | 0.176 | 0.940 | ||
| β̂CIC | −0.60 | −0.596 | 0.173 | 0.167 | 0.948 | ||
| 500 | β̂PH | −0.60 | −0.545 | 0.074 | 0.075 | 0.882 | |
| β̂IC | −0.60 | −0.611 | 0.077 | 0.080 | 0.948 | ||
| β̂CIC | −0.60 | −0.599 | 0.078 | 0.075 | 0.963 | ||
| 40% | 100 | β̂PH | −0.60 | −0.427 | 0.264 | 0.273 | 0.849 |
| β̂IC | −0.60 | −0.478 | 0.250 | 0.284 | 0.874 | ||
| β̂CIC | −0.60 | −0.595 | 0.269 | 0.296 | 0.925 | ||
| 500 | β̂PH | −0.60 | −0.440 | 0.117 | 0.119 | 0.658 | |
| β̂IC | −0.60 | −0.498 | 0.110 | 0.125 | 0.806 | ||
| β̂CIC | −0.60 | −0.604 | 0.121 | 0.129 | 0.926 |
n = number of individuals per group, β = true time-averaged treatment effect when there is no censoring through τ = 4, SE is the mean of the model-based standard error, SD is the empirical standard error, and coverage probability (CP) is the percentage of SE-based confidence intervals that contain β. Censoring times are generated from (15) with r(0) = ∞ and r(1) = 1.2 to give 20% censoring, and r(0) = ∞ and r(1) = 0.17 to give 40% censoring.
In the independent censoring case, the simulations suggest that either re-weighted estimator performs well with respect to bias and coverage probability. However, in the conditionally independent censoring case (Table 2), both the unweighted estimator and the re-weighted estimator that assumes independent censoring result in estimates that are biased, which in turn affects their coverage probability. The percentage censoring accounts for the total amount of censoring, which includes the truncation at τ. Thus, when censoring on (0, τ) is minimal, such as the case when there is 20% total censoring, the bias of the independent censoring estimator is not of much concern. The magnitude of the bias is much larger when censoring increases to 40% overall. However, the group-specific re-weighted estimator continues to perform well. Other settings for the underlying hazard function relationships have also been explored and have yielded similar results (data not shown).
4.2. Simulation results for robust estimation in stratified analyses
Usually additional analyses are conducted after the conclusion of a trial to investigate whether treatment effects differ across levels of other factors (e.g., stratification factors). In the special case where censoring is independent of the stratum given the treatment group, and the there is no effect of the treatment group on the time to event, the estimator from the standard Cox model is consistent [12]. More generally such analyses may need to consider conditionally independent censoring. As an example, consider a multinational study with stratified randomization by country which opens at different times in different countries. In this example it is likely that the censoring distribution will differ by stratum. Even if the true treatment effect is homogeneous across strata, under non-proportional hazards the stratum-specific treatment effect estimates could differ due to differences in censoring distributions. Furthermore, pooling across strata would give an estimated treatment effect that is conditional on the censoring distribution observed within each stratum. To remove this dependency, β̂CIC can be extended to include stratification factors by first re-weighting the treatment effect estimate within each stratum and then pooling the estimates in the usual fashion. Formally, for K strata, the stratified estimate is the solution to
| (16) |
where U(k)(β) denotes the estimating equation (7) applied in stratum k. The stratified robust variance estimator is based on equation (13):
Table 3 displays the results comparing the stratified estimator (16) with the usual stratified Cox model estimator. Use of the usual estimator gives estimates from stratum 3 that are different on average than those from strata 1 and 2, since the censoring distribution differs in stratum 3. The proposed re-weighted estimator corrects this.
Table 3.
Stratified Parameter Estimates, Powered Uniform Censoring Scheme, Treatment Group Independent but Stratum Dependent
| % Censoring | n | Estimator | β | Estimate | SE | SD | CP |
|---|---|---|---|---|---|---|---|
| 32% | 100 | β̂PH | −0.60 | −0.568 | 0.102 | 0.098 | 0.944 |
| β̂CIC | −0.60 | −0.624 | 0.111 | 0.103 | 0.955 | ||
| 500 | β̂PH | −0.60 | −0.563 | 0.046 | 0.046 | 0.845 | |
| β̂CIC | −0.60 | −0.622 | 0.052 | 0.049 | 0.951 | ||
| 45% | 100 | β̂PH | −0.60 | −0.501 | 0.113 | 0.109 | 0.865 |
| β̂CIC | −0.60 | −0.607 | 0.125 | 0.117 | 0.968 | ||
| 500 | β̂PH | −0.60 | −0.500 | 0.051 | 0.052 | 0.474 | |
| β̂CIC | −0.60 | −0.612 | 0.059 | 0.058 | 0.959 |
n = number of individuals per group per stratum (3 levels of stratification factor), β = true time-averaged treatment effect when there is no censoring through τ = 4, SE is the mean of the model-based standard error, SD is the empirical standard error, and coverage probability (CP) is the percentage of SE-based confidence intervals that contain β. Censoring times were generated from (15) with r(0, 1) = r(0, 2) = r(1, 1) = r(1, 2) = 4 and r(0, 3) = r(1, 3) = 0.5 to give 32% censoring and r(0, 1) = r(1, 1) = 4, r(0, 2) = r(1, 2) = 0.4 and r(0, 3) = r(1, 3) = 0.5 to give 45% censoring.
4.3. Small sample performance and asymptotic convergence of V̂(β̂CIC)
The variance estimator given in (13) is asymptotic, so we investigated the convergence of the estimator over various sample sizes. Table 4 provides the results of the variance estimates for increasing sample sizes for one type of censoring and non-proportional hazards data scenario. For this example, the model-based SE tends to overestimate the true standard error slightly until n = 10, 000.
Table 4.
Convergence of Robust Variance Estimator
| n | SE | Empirical SD | Ratio |
|---|---|---|---|
| 100 | .1940 | .1808 | 1.073 |
| 500 | .0866 | .0829 | 1.045 |
| 1000 | .0613 | .0597 | 1.027 |
| 5000 | .0274 | .0270 | 1.013 |
| 10000 | .0194 | .0194 | 1.000 |
Censoring times were generated from random exponential with mean 3. Survival times were generated from λ(T|Z) = I(T < 0.5) + 3ZI(T ≥ 0.5). Any observed survival times greater than 3 were truncated at 3 and scored as censored. The scheme results in approximately 31% censoring at each sample size.
5. Application to brain metastases data
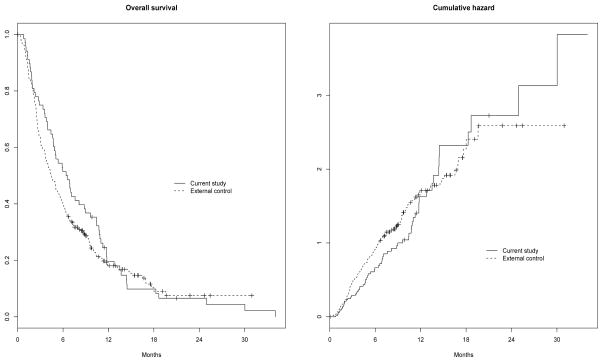
In the brain metastasis trial described above, survival data from a single arm trial were compared with data from the control arm in a different randomized clinical trial. The single-arm trial enrolled 69 subjects, and at the time of analysis median survival time was 6.4 months with 11.6% censoring. The external control data set was comprised of data on 267 subjects for which a median survival time of 4.5 months and 17.2% censoring were observed. Overall survival and cumulative hazard figures are provided in Figure 5; some non-proportionality is evident.
Suppose that our objective is to report consistent inference of the marginal hazard ratio calculated through 30 months without conditioning on the observed censoring distribution; i.e., inference relative to the reference censoring distribution: Fc(t) = It>30 (for t ≥ 0). Table 5 compares the various estimators that might be applied in this setting. The first, the standard Cox estimate (β̂PH) over restricted (30-month) support, illustrates estimates that might be reported in a standard analysis. The remaining rows compare three alternative estimators over the 30-month support. The first (β̂PH) uses the robust variance estimator of Lin and Wei [15], which recognizes the potential for model misspecification but does not standardize to the reference censoring distribution. The second and third are the re-weighted estimators described above: the Xu-O’Quigley estimate assuming independent censoring (β̂IC), and the estimate assuming conditionally independent censoring (β̂CIC). This example illustrates that the different approaches provide different estimates, and that some can differ substantially. Furthermore, in this example it is interesting to note that the standard error from the robust variance estimator for β̂PH is smaller than the standard error normally used with the standard Cox model estimator. In an additional simulation where the example was resampled and increased in sample size (results not shown), a similar observation was noted for the adjusted estimators. The relative magnitude of the variance of the estimators is a function of the particular nature of the censoring distribution, and the behavior in any particular data set should be interpreted with caution. The trade-off between bias and variance is evaluated in Section 4. Given its robustness to all forms of conditionally independent censoring, we recommend the use of β̂CIC in order to assure consistent point estimates and nominal coverage probability for interval estimates.
Table 5.
Hazard Ratio Estimates for Brain Metastasis Trial
| Estimator | Estimate | SE | HR (95% CI) |
|---|---|---|---|
| β̂PH | −0.142 | 0.144 | 0.87 (0.65, 1.15) |
| β̂PH* | −0.142 | 0.131 | 0.87 (0.67, 1.12) |
| β̂IC | −0.074 | 0.118 | 0.93 (0.74, 1.17) |
| β̂CIC | −0.104 | 0.144 | 0.90 (0.68, 1.19) |
All subjects surviving beyond 30 months are censored at 30 months.
Indicates robust variance estimator used.
6. Discussion
Randomized clinical trials are often conducted to provide an objective and reproducible basis for selecting the better of two (or more) treatments with respect to a time-to-event outcome. When one is interested in treatment effects as measured by the censoring-free average hazard ratio, consistent inference in the presence of non-proportionality requires estimating the censoring distribution [1]. The implication of this result is that the usual Cox estimator will be consistent for a parameter that is dependent upon patient accrual and dropout patterns that bear no relevance to the scientific objectives of a clinical trial. Here we have proposed an estimator that is robust to conditionally independent censoring and is easy to implement in practice. Furthermore it results in little increased variability relative to the semi-parametric efficient estimator of Cox in the case of a correctly specified proportional hazards model. Under covariate-independent censoring, our simulation studies indicate that the proposed estimator behaves similarly to the covariate-independent estimator of Xu and O’Quigley (such behavior is analogous to the unequal variance t-test performing well even when variances are equal). It may therefore be prudent to report inference using the proposed estimator in all settings rather than speculate about unknown elements of the censoring mechanism.
Throughout we have focused on problems motivated by the two-group clinical trial setting and have shown that the proposed censoring adjusted estimator generalizes to the case of k > 2 levels of a discrete covariate in a straight-forward fashion. In the case of continuous covariates, factoring out the effect of the censoring distribution would require a further assumption on the relationship between the censoring mechanism and the particular values of the covariate (see, eg, [12]). In this situation one would need to consider an analogous weighted estimator based on a rich class of predictive models for the underlying censoring distribution.
Others have studied similar re-weighted estimators in a different context. For example, Bednarski [16] and Marzec and Marzec [17] considered covariate-robust estimators; however, we note that estimators robust to covariate outliers are not of concern for our setting because the covariate of interest is an indicator for treatment group. Robins and Finkelstein [18] investigate the case where survival and censoring times are dependent, and apply the inverse probability of censoring weighted estimator to recover survival times after correcting for assumed relationships between observed time-dependent prognostic factors and the survival and censoring times. In a related work, DiRienzo and Lagakos [12] considered adjustments to the score test under model misspecification and conditionally independent censoring. They proposed a similar adjustment to the score equation, but their weight function was defined differently. They also acknowledged the weight function proposed here as a potential adjustment to the score function. Their work focused on hypothesis testing rather than estimation, so robust sandwich variance estimators were not considered. Similarly, O’Quigley [19] provides a comprehensive investigation of proportional hazards regression, including an estimator similar to the one we provide, though the variance is left as an open problem.
In the current work, we derived the asymptotic variance of the proposed estimator assuming known weights. However, in practice the weights must be estimated because the true underlying censoring distribution for each comparison group is unknown. As such, the derived variance estimator may lead to slightly conservative large-sample inference in practice. However, we have demonstrated reasonable coverage probability of asymptotic confidence intervals and observed convergence of the proposed estimator via simulation, minimizing any concerns.
Finally, we note that dependence on the underlying censoring distribution is not unique to the Cox estimator. Indeed, alternative semi-parametric estimation methods such as the accelerated failure time model can result in censoring-dependent estimators under a misspecified model. Thus attention to the censoring pattern is also of concern when using semi-parametric estimation techniques for the accelerated failure time model. This is an area of current research.
Figure 1.
Overall survival and cumulative hazard curves for the brain metastasis data
Acknowledgments
Contract/grant sponsor: Supported by NIH/NCRR Colorado CTSI Grant Number UL1 RR025780. Contents are the authors’ sole responsibility and do not necessarily represent official NIH views.
The authors would like to thank Allos Therapeutics, Inc. for permission to use the brain metastasis data.
Appendix
Let β0 denote the true value of β. Let Xi = min(Ti, Ci), Ni(t) = I(Xi ≤ t, δi = 1), a right-continuous counting process, and Yi(t) = I(Xi ≥ t) be the left-continuous at-risk process for the ith individual. Also, note that the process Wi(t) = (SC(t|Zi))−1 is left-continuous, and denote the history process (filtration) as , Zi: i = 1, …, n; 0 ≤ u < t}. We take (Ti, Ci, Zi), i = 1, …, n to be independent, identically distributed replicates where Ti and Ci are conditionally independent given Zi. Define for r = 0, 1, 2, E(β, t) = S(1)(β, t)/S(0)(β, t), and s(r)(β, t) = ES(r)(β, t). We may write S(r)(β, t) as S(r) for conciseness when it can be done so without introducing ambiguity.
Theorem 5.3 of Kalbfleisch and Prentice [20] provides the conditions under which Rebolledo’s theorem applies, which are listed here.
There exists an open neighborhood
 of β0 and functions s(r)(β, t), r = 0, 1, 2 defined on
of β0 and functions s(r)(β, t), r = 0, 1, 2 defined on
 × [0, τ] which satisfy the following:
× [0, τ] which satisfy the following:
as n → ∞;
s(0)(β, t) is bounded away from 0 for t ∈ [0, τ];
For r = 0, 1, 2, s(r)(β, t) is a continuous function of β uniformly in t ∈ [0, τ] and s(1) = ∂s(0)/∂β and s(2) = ∂2s(0)/∂β2;
is positive definite for all β ∈
 ;
;Zi are bounded for all t ∈ [0, τ];
.
To prove Theorem 1 it is therefore sufficient to demonstrate that the conditions 1. – 6. stated above hold for our model. In order to do so we assume P(Yi(τ) > 0) > 0, which essentially requires us to have stability at τ. This assumption implies 2. and 6. holds. The assumption of iid observations together with boundedness of the covariates implies that the S(r) are comprised of independent terms so that by the strong law of large numbers S(r) converges to s(r). Assume P(Xi ≥ t|Zi) is continuous in t. That there exists a neighborhood
 such that with probability one the convergence is uniform on the set
such that with probability one the convergence is uniform on the set
 × [0, τ] follows since s(r) must be continuous in t (boundedness convergence theorem) and, for any t ∈ [0, τ], the strong law of large numbers implies with probability 1 that S(0) → s(0) as n → ∞. We thus have a sequence S(r) of bounded monotonic functions (indexed by n) converging pointwise to the bounded monotonic functions s(0), implying the convergence must be uniform. This implies condition 1. The boundedness of Zi together with the Dominating Convergence Theorem [21] imply condition 3. The positive definiteness required in condition 6. is assumed to hold.
× [0, τ] follows since s(r) must be continuous in t (boundedness convergence theorem) and, for any t ∈ [0, τ], the strong law of large numbers implies with probability 1 that S(0) → s(0) as n → ∞. We thus have a sequence S(r) of bounded monotonic functions (indexed by n) converging pointwise to the bounded monotonic functions s(0), implying the convergence must be uniform. This implies condition 1. The boundedness of Zi together with the Dominating Convergence Theorem [21] imply condition 3. The positive definiteness required in condition 6. is assumed to hold.
All that remains is to establish that our estimating equation can be written as
for some predictable process Gi(t) and martingale Mi(t) (both with respect to
 ). Define Gi(t) = Zi − E(Zi). Since Z is assumed bounded this quantity is predicable w.r.t.
). Define Gi(t) = Zi − E(Zi). Since Z is assumed bounded this quantity is predicable w.r.t.
 . The compensator of Wi(t)Ni(t) is
, giving
as a mean-zero martingale with respect to the filtration
. The compensator of Wi(t)Ni(t) is
, giving
as a mean-zero martingale with respect to the filtration
 . We can thus express our estimating equation as
. Thus, the ith term of U is a sum of a stochastic integral of a predictable process with respect to a martingale, implying U is a mean zero martingale with respect to
. We can thus express our estimating equation as
. Thus, the ith term of U is a sum of a stochastic integral of a predictable process with respect to a martingale, implying U is a mean zero martingale with respect to
 . Then
is a martingale with predictable covariation process
. Generlizing the convergence result to the misspecified model is a direct application of White [22]. Let (Xi, Zi) have some distribution G, and suppose there exists a unique point β0 such that EG(U(X, Z; β0)) = 0. Then under standard regularity conditions the solution β̂CIC to U(β) = 0 is asymptotically normally distributed with mean β and covariance matrix consistently estimate by V̂(β̂CIC) in (13).
. Then
is a martingale with predictable covariation process
. Generlizing the convergence result to the misspecified model is a direct application of White [22]. Let (Xi, Zi) have some distribution G, and suppose there exists a unique point β0 such that EG(U(X, Z; β0)) = 0. Then under standard regularity conditions the solution β̂CIC to U(β) = 0 is asymptotically normally distributed with mean β and covariance matrix consistently estimate by V̂(β̂CIC) in (13).
References
- 1.Struthers CA, Kalbfleisch JD. Misspecifed proportional hazard model. Biometrika. 1986;73:363–369. [Google Scholar]
- 2.Xu R, O’Quigley J. Estimating average regression effect under non-proportional hazards. Biostatistics. 2000;1:423–439. doi: 10.1093/biostatistics/1.4.423. [DOI] [PubMed] [Google Scholar]
- 3.van Houwelingen HC, van de Velde CJH, Stijnen T. Interim analysis on survival data: its potential bias and how to repair it. Statistics in Medicine. 2005;24:2823–2835. doi: 10.1002/sim.2248. [DOI] [PubMed] [Google Scholar]
- 4.Wei LJ, Durham SD. The randomized play-the-winner rule in medical trials. J Am Stat Assoc. 1978;73:840–843. [Google Scholar]
- 5.Rosenberger WF, Lachin JM. The use of response-adaptive designs in clinical trials. Control Clin Trials. 1993;14:471–484. doi: 10.1016/0197-2456(93)90028-c. [DOI] [PubMed] [Google Scholar]
- 6.Rosenberger WF. Randomized play-the-winner clinical trials: Review and recommendations. Control Clin Trials. 1999;20:328–342. doi: 10.1016/s0197-2456(99)00013-6. [DOI] [PubMed] [Google Scholar]
- 7.Zhang L, Rosenberger WF. Response-adaptive randomization for survival trials: the parametric approach. JRSS-C. 2007;56:153–165. [Google Scholar]
- 8.International Conference on Harmonisation - Harmonised Tripartite Guideline: Choice of Control Group and Related Issues in Clinical Trials E10; 2000. [Google Scholar]
- 9.Shaw E, Scott C, Suh J, Kadish S, Stea B, Hackman J, Pearlman A, Murray K, Gaspar L, Mehta M, Curran W, Gerber M. RSR13 plus cranial radiation therapy in patients with brain metastases: Comparison with the Radiation Therapy Oncology Group Recursive Partitioning Analysis Brain Metastases Database. Journal of Clinical Oncology. 2003;21:2364–2371. doi: 10.1200/JCO.2003.08.116. [DOI] [PubMed] [Google Scholar]
- 10.Cox DR. Regression models and life tables (with discussion) Journal of the Royal Statistical Society B. 1972;34:187–220. [Google Scholar]
- 11.Haneuse S, Rudser K, Gillen D. The separation of timescales in Bayesian survival modeling of the time-varying effect of a time-dependent exposure. Biostatistics. 2008;9:400–410. doi: 10.1093/biostatistics/kxm038. [DOI] [PubMed] [Google Scholar]
- 12.DiRienzo AG, Lagakos SW. Bias correction for score tests arising from misspecified proportional hazards regression models. Biometrika. 2001;88(2):421–434. [Google Scholar]
- 13.Gillen DL, Emerson SS. Nontransitivity in a class of weighted logrank statistics under nonproportional hazards. Statistics & Probability Letters. 2007;77:123–130. [Google Scholar]
- 14.Anderson PK, Gill RD. Cox’s regression model for counting process: a large sample study. The Annals of Statistics. 1982;10:1100–1120. [Google Scholar]
- 15.Lin DY, Wei LJ. The robust inference for the Cox proportional hazards model. Journal of the American Statistical Association. 1980;84:1074–1078. [Google Scholar]
- 16.Bednarski T. Robust estimation in Cox’s regression model. Scandinavian Journal of Statistics. 1993;7:215–228. [Google Scholar]
- 17.Marzec L, Marzec P. Generalized martingale-residual processes for goodness-of-fit inference in Cox’s type regression models. Annals of Statistics. 1997;25(2):683–714. [Google Scholar]
- 18.Robins JM, Finkelstein DM. Correcting for noncompliance and dependent censoring in an AIDS clinical trial with inverse probability of censoring weighted (IPCW) log-rank tests. Biometrics. 2000;56:779–788. doi: 10.1111/j.0006-341x.2000.00779.x. [DOI] [PubMed] [Google Scholar]
- 19.O’Quigley J. Non-proportional hazard regression. Springer; New York: 2008. [Google Scholar]
- 20.Kalbfleisch J, Prentice R. The Statistical Analysis of Failure Time Data. Wiley; New York: 2002. [Google Scholar]
- 21.Rudin W. Principles of Mathematical Analysis. 3. McGraw-Hill; New York: 1976. [Google Scholar]
- 22.White H. Maximum likelihood estimation of misspecified models. Econometrica. 1982;50:1–25. [Google Scholar]