Generator localization by current source density (CSD): Implications of volume conduction and field closure at intracranial and scalp resolutions

Abstract

The topographic ambiguity and reference-dependency that has plagued EEG/ERP research throughout its history are largely attributable to volume conduction, which may be concisely described by a vector form of Ohm’s Law. This biophysical relationship is common to popular algorithms that infer neuronal generators via inverse solutions. It may be further simplified as Poisson’s source equation, which identifies underlying current generators from estimates of the second spatial derivative of the field potential (Laplacian transformation). Intracranial current source density (CSD) studies have dissected the “cortical dipole” into intracortical sources and sinks, corresponding to physiologically-meaningful patterns of neuronal activity at a sublaminar resolution, much of which is locally cancelled (i.e., closed field). By virtue of the macroscopic scale of the scalp-recorded EEG, a surface Laplacian reflects the radial projections of these underlying currents, representing a unique, unambiguous measure of neuronal activity at scalp. Although the surface Laplacian requires minimal assumptions compared to complex, model-sensitive inverses, the resulting waveform topographies faithfully summarize and simplify essential constraints that must be placed on putative generators of a scalp potential topography, even if they arise from deep or partially-closed fields. CSD methods thereby provide a global empirical and biophysical context for generator localization, spanning scales from intracortical to scalp recordings.

1. Neuroanatomical basis of brain electrical potentials

Evoked potentials (EPs) provide an anatomical method that yields time-locked indices of information processing by, and transfer through, neural structures. Early applications of EPs gave insights into functional neuroanatomy by mapping activity through well-defined pathways from the sense organs through the central nervous system (CNS) in anesthetized animals (e.g., Marshall, Woolsey and Bard, 1937; Mountcastle and Henneman, 1952; Rose and Woolsey, 1949). Beyond the sensory and motor systems, this approach allowed the systematic visualization and parsing of neuroanatomical processing, as evidenced by transit times and response morphology following electrical or sensory stimulation. These same anatomical considerations are preserved when the approach is generalized as the event-related potential (ERP), which incorporates a myriad of sensory, motor and cognitive paradigms (cf. Kayser and Tenke, 2005; Luck, 2005; Picton et al., 2000). However, even when the anatomical underpinnings of an ERP provide a characteristic electrical pattern (signature) in its waveform (timing), these properties may be obscured by the overlap in time and space from simultaneous activity within multiple neuronal regions and networks. Moreover, since electrical measurements are potential differences (i.e., voltages), the resulting ambiguity may be further exacerbated when the voltage measured at one electrode contact actually originates from activity near the “indifferent” recording reference (i.e., the ubiquitous reference problem; e.g., Kayser and Tenke, 2010; Luck, 2005; Nunez and Srinivasan, 2006a; Wolpaw and Wood, 1982; Yao, 2001). In view of the desirability of a common set of methods, models and analysis strategies capable of spanning from intracranial investigations of neuronal activity within narrowly-defined regions of cortical tissue to macroscopic, grossly-sampled electrical activity at the scalp, an examination of the impact of these measurement scales on the recorded EEG is of considerable importance.

2. Volume conduction: From current generator to measured voltage

The passive transmission of electric fields through biological tissue from an underlying electrical current generator is known as volume conduction. Although volume conduction follows Maxwell’s equations, for the case of the low-frequency activity characteristic of the EEG (i.e., below 1 kHz) in a conductive medium, it can be efficiently simplified by neglecting the capacitive component of tissue impedance, as well as induction and the related electromagnetic propagation (Plonsey, 1982). The result is a linear (or piecewise-linear) relationship that parallels Ohm’s Law (V = IR), which expresses the well-known proportionality between the potential difference (voltage; V) across a conductor with a given resistance (R) in an electrical circuit and the current (I) that flows through it.

Inasmuch as current represents the rate of change of charge over time, a quasistatic model of volume conduction through a conductive medium may be proposed, with properties that precisely parallel those of a point charge in free space (Freeman and Nicholson, 1975). The voltage potential O produced by a point current source I thereby takes the form of:

$$\mathrm{\Phi }(d)=I/(4\pi \sigma d)$$ Eq. 1

where the potential at a radial distance (d) from the generator is directly proportional to the injected current (I), and inversely related to a resistive impedance term related to the conductivity of the medium (σ; analogous to permittivity in free space; cf. Nicholson and Freeman, 1975, Eq. 1).

Fig. 1 shows the implications of Eq. 1 for the potential produced by a current dipole consisting of a point current source (current injected into medium, yielding positivities) and sink (current removed from medium, yielding negativities). For any recording contact, the potential may be computed as a linear summation of the two contributions. For more complex configurations of sources and sinks, the recorded potential is the linear summation (i.e., volume integration) of all such contributions. Although this example clearly shows that the fall-off from each individual point source (sink) is inversely related to distance (also see Eq. 3.6, Nunez and Srinivasan, 2006a), it can readily be shown that the corresponding fall-off from a radially-distributed set of sources and sinks (i.e., a sheet or layer of multiple source-sink pairs) approximates a linear function as the radius of the set increases (cf. Tenke et al., 1993).

Figure 1.

Left. Volume conduction from a fixed point sink at 950 μm depth, 50 μm lateral offset, and source at 450 μm, 50 μm lateral offset, shown in two dimensions. The recording electrode axis corresponds to the path of a single recording contact as it is inserted into the conductive medium at different depths. This track is aligned 50 μm lateral to each of the two poles. Although the electrode can only sample the potential on this axis (i.e., lateral offset = 0), the source and sink yield predictable potentials throughout the medium. Isopotential contours are indicated for positive (nearer to source; <700 μm depth) and negative (nearer to sink; >700 μm depth) curves. These potentials are sampled at eight distinct equidistant depths (large dots on recording electrode axis at multiples of 200 μm), producing the potential profile on the right. Using the electrode at 600 μm depth as an example, the potential measured at the recording contact (circled positive potential) may be directly computed from Eq. 1 as the sum of contributions from the sink (I is negative; d = length of arrow from sink) and source (I is positive; d = length of smaller arrow from source) contributions. This simplistic model may be generalized to compute forward solutions from any number, area, or volume of known generators in (piecewise) homogeneous media.

The charges in electrostatic theory may independently exist at any location in space, but the current sources and sinks of Eq. 1 imply movement of charges through space (i.e., current). The source and sink shown in Fig. 1 may therefore be considered as generators of the fields shown. A physical mechanism underlying the injection into and removal of current from the medium is not required for this hypothetical dipole, nor are there any constraints on the distance between the two poles. In contrast, the currents underlying a real neuronal generator originate in the balance between intra- and extracellular processes associated with the neuronal resting potential, but are only evidenced by flow of current into (depolarization; extracellular sink and negativity) and out of (hyperpolarization; extracellular source and positivity) the cell from the extracellular medium. The necessary circuit closure for these currents is through the intracellular compartment, but is not generally visible to a recording contact in the extracellular medium.

Eq. 1 provides a useful description of what is already known, but cannot be used empirically to detect and measure unknown current generators. First, it is rigidly structured, based on the location and intensity of individual generators. Second, the resulting potential is expressed with reference at infinity. Finally, the direction of local current flow in the medium (i.e., orthogonal to the isopotential lines in Fig. 1) is ignored. The end result of these shortcomings is that, even though potential differences can be measured empirically, an unknown generator remains unknown.

These three problems may be resolved by a vector interpretation of Ohm’s Law:

$$J=\sigma E$$ Eq. 2

where J is the current density (e.g., referred to as current flow density by Nicholson and Freeman, 1975), E is the electric field, and σ is the conductivity tensor for the medium. This equation concisely describes the directional properties of the current flow through the medium, independent of any recording reference. Unfortunately, it is not expressed as a measurable voltage potential, which makes it unsuitable for probing the fields shown in Fig. 1, much less those from an EEG.

Clinical EEG standards frequently rely on bipolar montages (i.e., sequentially changing the reference as opposed to relying on a fixed, single reference) to help localize electrographic abnormalities associated with seizures (e.g., Osselton, 1965). This intuitive approach may be generalized by noting that the electric field (E) is a vector quantity defined as the negative gradient (i.e., spatial slope) of the field potential (−∇Φ). The direction of the electric field corresponding to the point source and sink shown in Fig. 1 is normal to the isopotential lines at any location (for additional intuitive and mathematical implications, see Schey, 1997). The use of the gradient, which, at least in theory, represents a continuous difference potential pointing in the direction of greatest potential decrease (i.e., downhill), sidesteps the longstanding controversy over the optimal (or universal) recoding reference for scalp-recorded EEG or ERP. Another notable property of the field potential gradient is that it is approximately constant as large or distributed current generators are approached (i.e., field potential fall-off is approximately linear above a cortical generator; cf. Tenke et al., 1993).

Substituting for E in Eq. 2 provides a (vector) measure of J based on voltage, but still does not represent the point current generators in Eq. 1. However, a subsequent divergence operation (i.e., spatial differentiation to quantify the divergence of current flow at each point) transforms the vector field J into a scalar current source density (CSD), or I_m following the nomenclature of Nicholson and Freeman (1975):

$${\text{I}}_m=\nabla ·(\sigma (-\nabla \mathrm{\Phi }))$$ Eq. 3

where the subscript m is used to indicate that the current is injected into the extracellular medium across the cell membranes (m) of neurons within the tissue. If tissue impedance may further be considered to be spatially invariant (or approximately so), the tensor σ may be replaced by scalar constant σ to yield the scalar relationship:

$${\text{I}}_m=-\sigma {\nabla }^2\mathrm{\Phi }$$ Eq. 4

This definition of CSD is Poisson’s source equation, relating the measured voltage to the amplitude of the underlying current generators. Inasmuch as the Laplacian operator (∇²) is a second spatial derivative, Eq. 4 may be intuitively understood as a spatial analog of F = ma, the well known relationship from classical physics that defines the proportionality between an object’s acceleration (second temporal derivative of location) and the time course of a force applied to it.

3. Impact of spatial scale on CSD implementations

By virtue of Eq. 4, CSD methods have been widely applied to identify and measure the current generators underlying the local field potential (LFP) of intracranial recordings (LFP depth profile). For the same reason, CSD methods have been successful for revealing neuronal current generators underlying EEG scalp topographies. Although a similar computational approach is used, the vast differences in scale make the implementations quite distinctive. In view of the history of the approach and the intuitive correspondence between the neuronal generators and the computed CSD, we will first explore the development and implementation of multicontact intracranial methods specialized for measuring LFPs in laminated tissue (e.g., cortical structures). The application of these methods to EEG scalp topographies will then be described in the context of the volume conduction model.

3.1. Empirical considerations for linear (one-dimensional) intracranial recordings

Nicholson (1973) derived a CSD implementation for recordings through laminated tissue (e.g., cerebellar or cerebral cortex). The derivation posits an arbitrary closed surface area bounding a volume of tissue that contains neuronal core conductors, each characterized by transmembrane currents reflecting neuronal polarization due to resting- and activity-related processes. Eq. 4 therefore defines I_m as the volume-dependent CSD that it “smoothed out” over the volume implicit in the divergence operation. In the case of an orthogonal penetration through laminated tissue, and assuming sufficient radial invariance (i.e., isopotential lines are radial to the recording axis in the region sampled), current flows normal to the lamination, suggesting a one-dimensional model obeying:

$$\mathrm{\Phi }(x^l)=\underset{0}{\overset{C}{\int }}G(x^l,z)I_m(z)dz$$ Eq. 5

where x^l is the depth orthogonal to the uniform generator, depth C encompasses all active generators, and G is a weighting function relating the geometry and impedance of the tissue to the recording site. This one-dimensional model may be interpreted as a spatial convolution integral (Nicholson, 1973), and expresses a simplified forward solution for reconstructing laminar field potential profiles represented by the CSD.¹

The scalar simplification expressed in Eq. 3 and the applicability of Eq. 5 require a computational method as well as empirical validation. The general approach recognizes that intracranial fields must inevitably be sampled at discrete locations. This is illustrated in Fig. 1 (right) by the correspondence between the potential sampled by the recording electrode contacts (200 μm separation) and the continuous potential it represents. A slope (first derivative) can be computed for any adjacent pair of observations, and serve as an estimate for the curve between these points. Although the dipole that is illustrated is neither physiological nor adequately sampled, it is evident that the slope of the measured potential increases as the source is approached, inverting when it is passed. In contrast, a second derivative (i.e., change of slope) requires a minimum of three consecutive observations and serves as an estimate of the middle observation, but cannot be computed at the boundaries (0 and 1400 μm depths for the electrode shown in Fig. 1).

The computation of the spatial derivative for a linear (or stepwise) penetration of tissue originally proposed by Freeman and Nicholson (1975) was a local “slope-of-slope” measure, estimated as the potential at any location minus half the potential at each of the two neighboring sites (an alternative, 5-point smoothed estimate was also suggested). As the method was developed, the anisotropy of the tissue impedance was also explored (Nicholson, 1973). However, for one-dimensional applications, small impedance variations between laminae were generally ignored, while efforts to preserve the available spatial resolution without introducing computational noise proved to be a greater concern (Freeman and Nicholson, 1975; Mitzdorf, 1985; Tenke et al., 1993). Even though small sampling-related irregularities may be magnified in local CSD estimates, smoothing carries the risk of obscuring or misrepresenting reproducible, physiologically meaningful laminar processes.

The intracranial, one-dimensional CSD has been empirically validated as a method for identifying ERP generators at an sublaminar scale (Mitzdorf, 1985; Schroeder et al., 1995). In addition to cortical generators, a one-dimensional CSD is directly applicable to other laminated structures as well (e.g., inferior colliculus, Muller-Preuss and Mitzdorf, 1984; lateral geniculate nucleus, Schroeder et al., 1989). In all cases, CSD sinks indicate local depolarization (current removed from the extracellular medium), while sources indicate local return currents and neuronal hyperpolarization (current injected into the extracellular medium).

3.1.1. The cortical dipole and field closure

The notation of a “cortical dipole” arose to explain observed surface-to-depth EEG polarity inversions in neocortex based on its well-known histological properties. Lorente de No (1947) proposed that the asymmetry and local alignment of projection cells in various regions (i.e., not simply cortical laminae, but various nuclei as well) can result in a pattern of activation that produce an “open field,” which can volume conduct over distance. In contrast, radially-symmetric or disorganized cellular alignments result in local cancellation of the potential field, identifying it as a “closed field.” The concept of field closure may be generalized to refer to those properties of a neuronal generator that result in cancellation, sculpting, or spatial distortion of a field potential between local and macroscopic scales. These properties are a direct result of the geometry (pattern) of the generator that, in turn, reflects both the cytoarchitecture and the gross anatomy of the active tissue.

Fig. 2A exemplifies the cortical dipole produced by the inversion of the earliest cortical responses to clicks (N8 of Steinschneider et al., 1992; P12 and P24 of Arezzo et al., 1975) within primary auditory cortex in the monkey (cf. Liégeois-Chauvel et al., 1994, for suspected homologs in human). The depths indicated are displacements below the ipsilateral frontal dura during an intracranial penetration of the superior temporal plane from a trajectory approximately orthogonal to the cortical surface within the Sylvian fissure (adapted from Tenke et al., 1987; cf. Steinschneider et al., 1992). At a depth of 5 mm, a dual positivity (P12/24) is seen following the auditory brainstem response (ABR) and an initial negativity (N). At great distances from the generator, the auditory evoked potential (AEP) is a low amplitude response, with a very shallow gradient (e.g., from 5–17 mm) and a stable morphology. Although the field potential amplitude noticeably increases with increased proximity to primary auditory cortex (at about 22 mm), it is only within the generating tissue (i.e., 23–24 mm) that amplitudes and spatial gradients become quite large, whereupon the morphology of the waveform is transformed, and cleanly inverts below the cortical generator (i.e., 25–26 mm). The comparability and polarity-inverted AEPs above and below the generator (e.g., compare waveforms at 20 mm and 26 mm) provide the informal basis for the notion of a cortical dipole.

Figure 2.

Auditory click-evoked potentials (AEP) recorded from 16-channel multicontact stainless steel electrodes (25 μm diameter, 100 μm intercontact spacing; Barna, Arezzo and Vaughan, 1981) during a transcortical penetration through primary auditory cortex of the monkey (subcutaneous needle electrode recording reference anterior to contralateral ear; >200 trials/average), with a trajectory approximately orthogonal to the surface of the superior temporal plane (from Tenke et al., 1987). A. Cortical dipole. AEP waveforms at sequential depths below the ipsilateral frontal dura reveal a cortical dipole, with depths indicated at left. At a shallow depth of 5 mm, the auditory brainstem response (ABR), initial negativity (N), and dual positivity (P12, P24) are all visible (see inset; positive up). Although the surface-to-depth AEP inversion across the cortex is simple (compare waveforms at 20 mm and 26 mm), the inversion sequence is complex within the generating tissue. B. Concurrent multicontact AEP, CSD (3-point algorithm) and multiunit activity (MUA; 500–10,000 Hz bandpass, rectified) at intracortical sites surrounding the AEP inversion (22.3–24.0 mm). The activity pattern for the waveforms marked in gray at 23.3 mm and 23.4 mm is consistent with thalamocortical activation of layer IV. The early sink in layer IV and subsequent sinks in supragranular layers (23 and 22.9 mm) arise from distinct cellular populations, with open- and closed-field properties evident for each in the balance of concurrent sources.

An intracortical view of the AEP inversion, shown in Fig. 2B, reveals the limitations of the cortical dipole as an explanatory concept at high local resolutions. At this scale, the simplistic model of dipole sheet or layer must be recast as the superposition of layers and/or regions composed of extracellular current sources and sinks, each element contributing to the field potential throughout the conductive medium. Much of the activity is locally cancelled (i.e., closed) and cannot be precisely anticipated from distant recordings; however, the resultant field potential typically inverts in polarity across the cortical mantle. In the case shown in Fig. 2B, the initial negativity of the AEP increases with depth through the middle cortical layers, inverting in subgranular layers and white matter (23.8–24.0 mm; cf. Steinschneider et al., 1992). A comparison of concurrent AEP, CSD and multiunit activity (MUA) implicates direct contributions to the initial negativity from the thalamocortical afferent volley, immediately followed by postsynaptic activation. This is evidenced by early CSD sinks in middle cortical layers (lamina IV waveforms; 23.3–23.4 mm), corresponding in timing and location to multiple high amplitude MUA peaks. Despite the prominence of the early sink and its time-locking with local MUA, its impact on the volume-conducted field potential is largely cancelled by adjoining, field-closing sources. These sources are found both in supra- and subgranular laminae (immediately above and below the channels labeled as lamina IV), reminiscent of the closed-field pattern observed for the flash-VEP in lamina 4 of striate cortex (Kraut et al., 1985; Schroeder et al., 1995; Tenke et al., 1993). In the same manner, the large source that follows the early sink (lamina IV CSD waveforms from 20 to 55 ms) occurs in association with a MUA reduction below baseline, and is likely to reflect local postsynaptic inhibition (i.e., it is an active source), with somewhat shallower, circuit-closing sinks above and below (immediately above and below channels labeled as lamina IV). In contrast to the early negativity, the positive components invert more superficially, corresponding to sequential supragranular activation (CSD sinks at 22.8–23.0 mm), with uncancelled sources in superficial laminae. However, the morphology of the AEP shifts dramatically as the corresponding active sinks are approached.²

Although scalp-recorded activity necessarily implies an open field (i.e., uncancelled activity), field closure must always be viewed quantitatively. Real ERPs are always the result of the summation (i.e., volume integration) of interrelated cortical processes, most of which are locally cancelled, and invisible at the scalp (i.e., the fields are largely closed). Tenke et al. (1993) simulated open- and closed-field laminae composed of distributed point sources and sinks, as described by Eq. 1. Layers of paired source and sink generators (“dipoles”) resulted in an open field, characterized by a linear potential gradient outside the lamina, and a simple inversion profile inside. In contrast, the addition of “inverted dipoles” led to partial or complete field closure, identifiable from a nonlinear inflection of the field within the “closed” edge of the lamina. Even a small bias in an otherwise closed filed lamina was found to effectively open the field, and consequently, even symmetric neurons (e.g., stellate cells) can contribute to the volume-conducted field. These simulations also demonstrated a somewhat counterintuitive finding: although the precise localization of focal activity may require a high-resolution CSD, open field activity may be best characterized (quantified) by a downsampled (or spatially filtered) CSD, even if it occurs within a largely cancelled profile³ (Tenke et al., 1993).

3.1.2. Representative intracranial CSD applications to sensory physiology

Following-up on the pioneering efforts of Nicholson, the definitive work on the application and interpretation of CSD methods to intracranial recordings was performed by Mitzdorf (1985), drawing from evidence based on micropipette recordings in cat. By careful evaluation of the biophysical properties of action potentials (fiber, dendritic, and somatic), excitatory postsynaptic potentials (EPSPs), and inhibitory postsynaptic potentials (IPSPs), she presented convincing evidence that intracranial CSD profiles disproportionately identify membrane depolarization arising from EPSPs.⁴ This property anchors the interpretation of CSD profiles firmly in the lineage of classical EP methods by identifying their time course and laminar specificity with ascending and intracortical processes.

The sequential activation of granular and supragranular laminae evidenced by CSD profiles for the unimodal auditory response to clicks (Fig. 2; Steinschneider et al., 1992) and tones (Fishman et al, 2001b) supports the a view of temporal and spectral processing by auditory cortical regions that follows directly from conventional anatomical reasoning (Mitzdorf, 1985).

Schroeder et al. (1991, 1998) used laminar CSD profiles in response to diffuse light and pattern stimuli to identify the sequential activation pattern corresponding to information processing and transfer via visual regions (i.e., lateral geniculate nucleus, V1, V2 and V4). In each case, the most prominent early cortical response is in and near the thalamorecipient laminae, with a subsequent response in extragranular laminae. Both granular and subsequent supragranular responses reflect neuronal excitation, typically identifiable by the co-localization of extracellular sinks with concurrent MUA increases. The intracortical dynamics of these distinct processes may be differentially biased. Local infusions of the competitive GABA antagonist bicuculline lead to an elaboration of the flash-evoked supragranular sink, which grows to massive proportions in concert with the local MUA (Schroeder et al., 1990). A similar laminar pattern has also been observed for interictal spikes (Ulbert et al., 2004). In a nonpathologic form, the supragranular response may also be overlaid by convergent multisensory (Lakatos et al., 2007) and attentional processes (Lakatos et al., 2008). Feed-forward processing is also evidenced by CSD patterns across regions (Givre et al., 1994; Schroeder et al., 1998). However, recordings from the ventral visual stream show a laminar pattern suggesting modulatory processes, in which the initial response originates in multiple laminae simultaneously, and CSD components are associated with no changes in MUA, or even MUA suppression (Schroeder et al., 1998).

3.1.3. Intracranial CSD caveats

There is no a priori assurance that a scalp-recorded EP/ERP component structure will be mirrored by local intracranial CSD components or the LFPs from which they are derived. This caveat is particularly relevant to prominent late components, such as the auditory N1, which have their own literature based on the summation (volume integral) of generators with overlapping time courses and anatomical localizations (Fishman et al., 2001a; Godey et al., 2001; Liegeois-Chauvel et al., 1994). An appropriate interpretation of the corresponding CSD profiles necessarily requires an appraisal of the scale of the measurement as well. For example, if the purpose of a study is only to identify generators of globally-recorded field potentials (e.g., the scalp-recorded EP/ERP), highly localized patterns of neuronal activity (e.g., processes limited to the scale of a single cortical column) that are largely cancelled (i.e., closed) may be of minimal interest, due to their negligible contributions to the distant field. Conversely, these same patterns may be of considerable interest to an understanding of local neuronal processing. Because of these divergent needs, CSD estimates based on spatial high- and low-resolution sampling (compared to the width of the laminae) may differentially serve as tools for identifying closed- and open-field contributions, respectively (Tenke et al., 1993).

A CSD is not a measurement per se, but rather an estimate based on the available spatial data.⁵ In particular, it is a composite of spatial and electrical measurements with unique properties that should not be confused with those of the field potentials from which they are derived. The goal of an intracranial CSD is not to accurately represent a continuous second spatial derivative of the LFP, but rather to match the resulting estimates to known anatomical and physiological properties of the tissue. A coarse, but interpretable measure of the underlying (ensemble) current generators has greater empirical value than a “more precise” estimate that is unintelligible. Although the underlying ERP generators may be traceable to the molecular scale of ion channels (cf. Nunez and Srinivasan, 2006a), a CSD model is not appropriate for such microscopic potential gradients. The CSD method necessarily depends on a presumed divergence volume, and the original one-dimensional derivation (Nicholson, 1973) assumed that the resulting volume estimate would reflect the laminar properties of the tissue.

It is generally unfeasible to compute a true, three-dimensional CSD because the extensive penetration would certainly compromise the integrity of the neuronal elements underlying it, rendering the exercise futile. The theoretical limitation of the standard one-dimensional CSD is the assumption that current flows only in the dimension sampled (i.e., across laminae), but not orthogonal to it. This implies that the CSD is invariant within region, making it a suitable approach for the study of generators that are distributed across a region or cytoarchitectonic field, and consistent with an intuitive view of the cortical dipole. However, the CSD will be variable or inconsistent for penetrations through small gyri, near regional boundaries, or for oblique penetrations through highly localized fields (e.g., confined to one or a few columns), because volume conduction through a conductive medium is not directional, and there is no reason to assume that field closure is limited to a single dimension.⁶

Another caveat is the collapse of impedance to a scalar in Eq. 4, making anisotropy (e.g., impedance differences across laminae) a possible source of error. In practice, the lamination of the tissue provides landmarks for interpreting CSD findings, but distortions arising from impedance irregularities exacerbate errors arising from the precise localization of the recording contacts. Inasmuch as the potential difference between adjacent electrodes is generally smaller in a closely-spaced, high-resolution compared to a low-resolution profile (i.e., the magnitude of the measured potential differences is reduced), the former is more susceptible to electrode-spacing errors and noise (both physiological and nonphysiological).

A final consideration for the adequacy of the CSD is related to the properties of the recording contacts themselves. Recordings from large (mm scale), low impedance disks are integrated over the electrode surface, rendering it impossible to resolve finer details. Conversely, high impedance tips (μm scale) may inadvertently isolate unit discharges, thereby making it impossible to continuously map (or differentiate) the LFP. These considerations are also important for inferences about the recordability of the LFP at a distance, such as the presumption that high frequency activity recorded from macroelectrodes over scalp and muscles bear a simple relationship to neuronal activity recorded from subjacent intracortical microelectrodes.

3.2. The surface Laplacian, volume-conduction and CSD

A surface Laplacian reflects the application of a Laplacian operator that has been restricted to a two-dimensional surface topography. Although the general volume-conduction relationship indicated in Eq. 3 may be simplified for one-dimensional intracranial implementations by the proportionality indicated in Eq. 4, the volume implied by a spherical (or more complex) three-dimensional model is clearly not represented by the surface Laplacian. However, the Laplacian operator retains its usefulness for any spatial data set, providing an efficient filter that reliably sharpens images by enhancing edges (e.g., Chanda and Majumder, 2006). Coupled with the reference-independence of the measure, these advantages attracted considerable interest when CSD was first popularized, whether it be the capacity to localize visual (Srebo, 1985) or somatosensory processes (Crammond et al., 1985) or to simplify the topography of EEG rhythms (Koles et al., 1989; Law et al., 1993a; Tenke and Kayser, 2005). The same properties also make the surface Laplacian attractive as a solution to practical problems common in brain computer interfaces (BCI; Babiloni et al., 2001; Cincotti et al., 2003; Pfurtscheller, 2003; Pineda et al., 2003; Wolpaw and McFarland, 1994).

The application of a Laplace operator to a montage of field potential waveforms does not necessarily prodecu a valid or interpretable CSD measure, a point that was implicit in Nicholson’s original derivation of the method, and emphasized by the distinctions noted by Nunez and Srinivasan (2006a). Even the defense of a one-dimensional CSD estimate for intracranial data hinges on a specific application for orthogonal penetrations through laminated tissue, leaving it open whether the reduced-dimensional solutions or conductivity simplifications required to produce Eq. 4 are universally appropriate. The suitability of a surface Laplacian as a measure of underlying current generator patterns must likewise rest on the plausibility and empirical value of the approach.

If we attempt to bridge between the intracranial CSD and the scalp, a three-dimensional volume-conduction model may be posited that also complies with Eq. 2. This model may then be expanded to include extraneural dura-bone-scalp transitions common to all inverse models, such as three- and four-shell models used in Brain Electrical Source Analysis (BESA; Scherg, 1990) and similar methods that fit isolated equivalent dipoles (i.e., oriented point dipoles that serve as replacement for physically-separated sources and sinks) to a scalp topography via forward solutions. Impedance transitions at gross anatomical landmarks (e.g., gyrus patterns, ventricles, etc.) may also be incorporated, and even those associated with the local microstructure (including cyto- and fiberarchitectonic patterns). Not coincidentally, the volume-conduction model is also critical to the definition and implementation of low resolution brain electromagnetic tomography (LORETA; Pascual-Marqui et al., 1994), local autoregressive averages (LAURA; Grave de Peralta Menendez, 2004), and similar inverse models. Although a discussion of the strengths and limitations of each of these methods is beyond the scope of this paper, it is sufficient to distinguish between a generator that is empirically identified from an intracranial CSD estimate using Eq. 4 and one that is asserted by an inverse solution that is consistent with Eq. 2.

The scalp-based surface Laplacian is distinguished from a three-dimensional CSD, being limited to the external surface that encompasses the complete volume-conduction model. In fact, Nunez and Srinivasan (2006a) have urged against unifying implementations of an intracranial CSD and a surface Laplacian, arguing that a “different principle” is involved, because the accuracy and utility of scalp-based surface Laplacian depends on the “focusing of cortical currents by the high-resistivity of the skull.” Despite these distinctions, Eq. 4 still reflects Poisson’s source equation for scalp data. The surface Laplacian therefore identifies the locations at which current is injected into the measurement space (i.e., the scalp recording montage) from the underlying multi-shelled conductive media.

3.3. Empirical considerations for planar (two-dimensional) scalp-recorded EEG

In marked contrast to an intracranial CSD, a surface Laplacian computed from a scalp montage clearly does not reflect neuronal generators within that surface (i.e., the scalp), but rather the currents that impinge on the scalp radially from the brain (e.g., Perrin et al., 1989; Giard et al., 1990). This implies that the surface Laplacian provides a coarse, but noninvasive, image of the subdural generators that have an effect on the montage from below, a simplification supported by the observed similarity of surface Laplacian waveforms and direct (invasive) recordings of field potentials at the dural surface (Junghöfer et al., 1997; Nunez et al., 1994), or by spatial deconvolution to that predicted at the dural surface (e.g., deblurring; Le and Gevins, 1993). The surface Laplacian may thereby be considered as a conservative description of essential constraints required of any proposed generator, in that even a precisely localized generator inferred from an inverse model is not plausible unless it is consistent with a Laplacian topography (cf. discussions in Tenke et al., 2010). Thus, a Laplacian topography reveals the spatial topography of underlying neuronal current generators, whereas this generator pattern is typically obscured in a surface potential topography. Of crucial importance for any CSD estimate, whether intracranial or scalp, is the need to interpret the observed pattern with regard to the known functional neuroanatomy, a limitation that equally applies to other localization methods (e.g., inverse models).

The local Hjorth algorithm⁷ (Hjorth, 1975) applies the nearest neighbor strategy of the linear intracranial CSD to a two-dimensional surface (i.e., subtracting the linearly-weighted potential of the nearest neighbors). Such local estimates fail at the edges of a two-dimensional montage (cf. Tenke et al., 1998), effectively reducing the number of channels with available CSD data. Likewise, just as the consecutive points in a one-dimensional calculation may be smoothed across additional points (e.g., 5-point smoothing; Freeman and Nicholson, 1975), a wider spatial filter may be applied to a two-dimensional array as well. At this point it becomes intuitively apparent that smoothed scalp Laplacian estimates will begin to fail when smoothed across long distances if the curvature of the scalp is not accounted for, and conversely may be improved or stabilized (i.e., filtered) by various spline-fitting methods (e.g., Koles et al., 1989; Carvalhaes and Suppes, 2011). The impact of activity at more distant sites is greater when estimates are fit using a rigid spline, while local influences will increase with a flexible spline. Likewise, a spherical geometric model provides both a parsimonious simplification (Perrin et al., 1989; Law et al., 1993a, 1993b) and consistent estimates across all channels of the EEG montage.

Le and Gevins (1993) arrived at a similar solution using a completely different approach. Eq. 2 was defined for scalp-recorded potentials, but based on a multiple shell model of the head, whereby the CSD generators of interest were posited to exist below the skull on the dural surface. Just as Nicholson identified Eq. 5 as a convolution integral by which a CSD source (or sink) imposes a field potential profile across the conductive medium, a dural source (sink) produces a field potential topography across the scalp. Given approximate thicknesses and impedances of the scalp and skull, the weighting function can be estimated and the scalp potential image deblurred (i.e., deconvolved) to regain the image at the dura. Nunez et al. (1994) reported that the image produced by the scalp Laplacian compared favorably with one produced by deblurring. Not surprisingly, Junghöfer et al. (1997) noted a relationship between deblurring methods, including CSD and cortical mapping, and the inverse problem. Another application of this approach has been proposed by Yao (2001) to yield an estimate for reference-free field potentials termed reference electrode standardization technique (REST). Yao’s REST approach posits a radial dipole layer below the skull that is only used indirectly as a means to compute a theoretical reference at a point of infinity, although simpler alternatives may yield similar solutions (Ferree, 2006; Kayser and Tenke, 2010; Thuraisingham, 2011). These approaches provide advantages over standard reference schemes when a field potential topography is desired, or when there is concern over the loss of volume integration constants that occurs when the Laplacian is computed (Qin et al., 2010; Yao et al., 2005, 2007).

3.3.1. Surface Laplacian applications

In electrophysiology, the surface Laplacian has found use in applications in which sharp localization is expected, as is the case for ERP generators associated with neuronal activation in well-defined motor or sensory structures. For instance, the auditory N1 provides a well-studied model of historic relevance to the electrophysiologic study of functional localization. MEG and intracranial methods suggest multiple generators in Heschl’s gyrus and the planum temporale (Godey et al, 2001). However, the human AEP N1 component occurs much later than the initial response of primary cortex, its generators are not as sharply localized to Heschl’s gyrus (Liegeois Chauvel et al., 1994), and subdural electrode grids identify a corresponding maximum over posterior portions of the Sylvian fissure and upper superior temporal gyrus (Neelon et al., 2006). Despite these caveats, the auditory N1 component is particularly well-suited to showcase the merits of CSD methods.

Fig. 3 illustrates the scalp field potentials (nose-referenced ERP) and CSD topographies at the peak latency of N1 produced to a number of different auditory stimuli. All nose-referenced ERP topographies show the distributed, midline-frontal negativity described for N1/P2 by Vaughan and Ritter (1970). The corresponding CSD topographies are readily distinguished from the corresponding ERP topographies by their regional specificity and the absence of a midline maximum. In place of a midline topography, the auditory N1 CSD includes sinks immediately anterior to, and sources posterior to, the Sylvian fissure, aligned in proximity to primary auditory cortex. This generator pattern is repeatedly obtained for frequent nontargets and distractors in various auditory oddball tasks, but is readily distinguishable from that of a slightly later, overlapping pattern of activity identified with sinks over the lateral surface of the temporal lobe (temporal N1; Kayser and Tenke, 2006a; Tenke et al., 1998, 2008, 2010).

Figure 3.

Nose-referenced ERP [μV] and CSD [μV/m²] topographies for different EEG montages (71, 67, or 31 channels) at the peak latency of N1 evoked by different auditory stimuli (spherical spline interpolations using constants of m = 4 for flexibility, λ = 10⁻⁵ for smoothing, and 50 iterations; cf. Perrin et al., 1989). A. Brief binaural tones (40 ms; 1000 Hz) presented during a loudness-dependency paradigm (no behavioral response required) as a function of stimulus intensity (60–100 dB; N = 127; number of trials/condition, M = 85 ± 11). B. Frequent binaural (300 ms; 1000 Hz; 85 dB; pure tones; N = 98; number of trials/condition, M = 222 ± 25; data from Tenke et al., 2010) and dichotic (250 ms; 444 or 485 Hz; 72 dB; complex tones; N = 64; number of trials/condition, M = 120 ± 34; data from Tenke et al., 2008) nontargets presented during oddball tasks. C. Infrequent binaural nontargets (100–400 ms; 85 dB; environmental sounds; N = 98; number of trials/condition, M = 30 ± 6; data from Tenke et al., 2010).

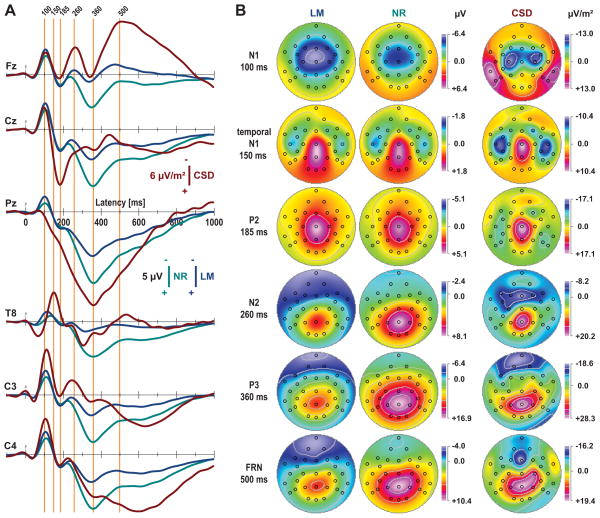
The capacity of a surface Laplacian to separate individual components based on differences in topography and time course is exemplarily shown for an auditory oddball task in Fig. 4, comparing CSD waveforms and topographies to their surface potential counterparts for two commonly-used EEG reference schemes. At its typical peak latency (100 ms) for surface potentials, N1 is larger for a linked-mastoids compared to a nose reference at the depicted midline and lateral sites (first perpendicular orange line at 100 ms in Fig. 4A), while the corresponding topographies (Fig. 4B, top row) verify that the difference is due to the shift in the zero point from nose to mastoids. The CSD topography indicates that the origin of this shift is the proximity of the mastoids, but not the nose, to the sources that characterize N1. Moreover, volume-conduction renders a midline FCz maximum for both surface potential topographies (i.e., over an area without underlying cortical tissue), whereas the bilateral N1 sink-source patterns correctly identify two separate dipoles spanning the Sylvian fissure over each hemisphere, with sink maxima over mid-lateral sites (C3/4).

Figure 4.

Comparison of surface potentials and surface Laplacian for auditory ERPs (complex tones) to targets (right-hand button press) during an auditory oddball paradigm (N = 66; number of trials, M = 26.3 ±5.5; data from Kayser and Tenke, 2006a). A. ERP waveforms [μV] referenced to linked mastoids (LM; TP9/10) or nose tip (NR) and current source density (CSD) waveforms [μV/m²] at selected midline (Fz, Cz, Pz) and lateral (T8, C3, C4) sites. Perpendicular lines (orange) indicate peak latencies of prominent deflections in these ERP and/or CSD waveforms typically associated with distinct ERP components (e.g., N1, P2, N2, P3; negative up). B. Scalp field potential (LM, NR) and surface Laplacian (CSD) topographies (31-channel EEG montage; top view of scalp, nose at top; radial 2-D projection by linear extension of spherical spline interpolation [m = 2, no smoothing; cf. Perrin et al., 1989]) corresponding to the peak latencies (ERP components) indicated in A. Note the different scales for each component (symmetric for N1, temporal N1, and P2; optimized for range for N2, P3, and frontal response-related negativity [FRN]).

Temporal N1 (150 ms) is clearly distinguished from N1 by the progression and spread of the pre-Sylvian CSD sink onto the convexity of the temporal lobe. At the temporal N1 peak, this sink obliterates the earlier post-Sylvian source, and a vertex source forms and reaches a maximum at the peak of P2. However, the temporal N1 component is prominent only for the CSD waveform over the convexity of the temporal lobe (see CSD waveform at site T8 in Fig. 4A), where the ERPs show a (reference-dependent) low-amplitude peak of variable latency. Despite this volatility, ERP evidence for this component takes the form of a topographic shift of the residual N1 across the temporal lobe that is quite consistent with the CSD (Fig. 4B, second row), and that disappears by the time of the midline positive peak (CSD source) corresponding to P2 (185 ms).

Although the nature and significance of the later components is beyond the scope of this paper, the CSD also offers clear advantages over ERPs for the late, condition-dependent components (i.e., prominent for rare targets requiring a right hand response compared to frequent nontargets). First, the sinks corresponding to N2 (260 ms) and the frontal response-related negativity (FRN; 500 ms) are considerably more prominent and topographically distinct in the CSD waveforms and topographies than are the negativities in either of the reference-dependent ERPs. Second, the well-defined P3 source (360 ms in Fig. 4A) contrasts with the marked differences between nose- and mastoid-referenced ERPs at all locations. Third, the localization and asymmetry of the late response-related components are most distinctive for the CSD (cf. Fz, C3, C4 in Fig. 4A), revealing a robust, persistent negativity over, but not confined to, the left motor cortex (i.e., contralateral to the response hand) and a robust, focal mid-frontal sink at the approximate time of the button press. Furthermore, the response-related, contralateral negativity is superimposed on P3, revealing a characteristic source asymmetry over central sites, that is barely notable in the ERP topographies (Fig. 4B, row 5). All of these distinctions are even more striking when viewed as concurrent animations for stimulus and response types (http://psychophysiology.cpmc.columbia.edu/mmedia/kayser2003b/cn2003csd.html). It should also be noted that comparable components have been described for CSD waveforms stemming from different computational methods (local Hjorth vs. spherical spline) and different montage densities (Kayser and Tenke, 2006b), resulting in comparable findings even when using different methods of component quantification (window averages vs. principal components analysis; Tenke et al., 1998; Kayser and Tenke, 2006a).

CSD methodology has been successfully applied in other sensory modalities and for other components as well. For example, the advantage of reference-independence of CSD topographies (Nagamine et al., 1992) and their superiority over field potentials in localizing electrical activity (Tomberg, 1991) have been noted for the somatosensory evoked response. Likewise, striate and extrastriate activity has been separated by the surface Laplacian for the pattern onset VEP (Manahilov et al., 1992). As an incomplete list of other examples, CSD methods have been applied with equal success to study event preparation (Tandonnet et al., 2003), event-related desynchronization (Pfurtscheller, 1988; Babiloni et al., 2004), novelty detection (Friedman and Simpson, 1994; Yago et al., 2003; Tenke et al., 2010), episodic and working memory (Kayser et al., 2006, 2007, 2009, 2010a), error processing (Allain et al., 2004; Cavanagh et al., 2009), resting EEG (Tenke and Kayser, 2005; Tenke et al., 2011), early visual processing (Kayser et al., in press), and even olfactory function (Kayser et al., 2010b).

3.3.2. CSD as a conservative description of neural current generators

The redundancy and linearity that is implicit in Eq. 2 provides multiple paths to the identification of the neuronal generators underlying a scalp topography. In a number of circumstances, these solutions partially or completely converge with results obtained using other methods that vary widely in their assumptions, constraints, or underlying theoretical models. Cincotti et al. (2004) argued that a surface Laplacian and a distributed inverse model may both be useful as deblurring methods in a clinical context. Foffani et al. (2004) went even further, noting that an alternative decomposition method (independent component analysis) compared favorably with scalp Laplacians computed using realistic scalp models. This degree of convergence validates the presumption that neural processes are separable and quantifiable in multiple ways. Conversely, if results diverge, the model most parsimonious with regard to known biophysical processes must be preferred.

Practical inverse solutions must necessarily be constrained by simplifications of the general model. In addition to structural nuances (e.g., number and geometry of shells or compartments between the neuronal generators and the scalp), dipole inverses require the identification of a set (i.e., one or more) of generator locations with predictable forward solutions (i.e., locations, magnitudes as well as orientations). Even a dipole at a plausible location may be inconsistent with known physiology if it requires an inexplicable orientation.

Alternative approaches to the inverse problem assume that neuronal tissue is continuous over sufficient distances and may therefore not be suited to a single dipole solution. One such model, termed low resolution brain electromagnetic tomography (LORETA; Pascual-Marqui et al., 1994), requires the alignment (i.e., low-resolution smoothing) of current density contributions (vector J in Eq. 2) through contiguous brain regions. From an idealized tomographic map of the gray matter, putative generators are inferred by the localization of high current densities. However, LORETA also does not restrict the direction of current flow, so that the inferred vectors fields have no relationship to the orientation of neurons and laminae within the region.⁸ These properties impart both strengths and limitations to the approach that complement or counter those of dipole inverse models. For these reasons, it is incorrect to assert that activity in a given region is “measured” by that model, even though it may be appropriate to refer to results as being consistent with activity in an anatomical region based on a particular inverse model. This is not a trivial distinction, because such strong statements implying functional neuroanatomy require convergent findings from carefully designed intracranial and scalp recordings aimed at convincingly piecing together a volume-conduction model that spans the two domains.

The defining role of volume conduction in the topography of N1 was demonstrated by Scherg and von Cramon (1985), who identified and localized pairs of equivalent dipoles to the vicinity of auditory cortex (one tangential and one radial). The CSD topography of N1 is likewise consistent with a tangential generator within the Sylvian fissure, while the temporal N1 is consistent with an overlapping radial generator on the convexity of the temporal lobe. Both approaches represent reference-free simplifications of the field potential topography, and the dipole solution is quite useful and appropriate for specific, localized generator configurations. In the case of auditory N1, they both represent informal properties of the cortical dipole as well: surface-to-depth polarity inversions, regional composite generators, and dipolar elements aligned with the axis of the cortical projection cells. However, whereas an equivalent dipole model requires these simplifications, a CSD topography does not. Conversely, an equivalent dipole may be used to simplify a field potential topography even when it does not accurately represent the neuroanatomical generators that produce it. As sharply concluded by Fishman et al. (2001a), intracranial data “render untenable the often used assumption that auditory cortical organization can be elucidated by modeling auditory cortical activity as a single dipole generator situated within the superior temporal gyrus.” In contrast, a CSD topography can accurately describe the pattern of radial currents impinging on the skull from an ensemble of generators, even though their number and locations remain unknown. For these reasons, the sink/source CSD pairs representing N1 may be considered to be essential constraints on the flow of radial currents corresponding to these dipoles.

With these cautions in mind, it is nevertheless instructive to compare CSD topographies with inverse-based simplifications. Fig. 5 illustrates the field potential topography corresponding to a single equivalent dipole located in the vicinity of the left primary auditory cortex, placed manually to approximate the group-averaged N1 topographies shown in Fig. 3. The topography was produced by Dipole Simulator (Berg, 2006), a forward-solution using the same volume-conduction model used by BESA, referenced to the estimated potential mean over the surface of the sphere. The resulting current sinks immediately anterior to the Sylvian fissure and sources posterior to it are not surprising for this austere model, because the generator was positioned to approximate this characteristic topography. The resulting source topographies are also represented in the corresponding sLORETA solution, although an uncritical interpretation of the sLORETA solution might suggest a contribution from the cortical gray matter throughout the temporal lobe.

Figure 5.

Dipole forward solution manually positioned to approximate unilateral current source density (CSD) topography of an auditory N1 (cf. Fig. 3). A. Dipole location, orientation, and nose-referenced topography (Dipole Simulator; Berg, 2006; time course is arbitrary). B. Corresponding surface potential (SP [μV]) and Laplacian (CSD [μV/m²]) topographies, with maximal sink at site C3, and corresponding source maximal over inferior temporal sites. C. This surface potential topography is similarly mapped using sLORETA (v2008-11-04; Pascual-Marqui, 2002), which yields an inverse solution that approximately matches the surface Laplacian.

4. Additional considerations of empirical relevance

Several computational aspects affect the properties of the surface Laplacian, which in turn affect the usefulness and interpretability of CSD measures in the context of an empirical research objective. This section will discuss selected, but nevertheless important, issues unique to the CSD computation, which have not been adequately acknowledged in the literature.

4.1. CSD at multiple resolutions

In recognition of the spatial filter properties of a surface Laplacian CSD, the approach is commonly identified as high-resolution EEG, in contrast to the spatially-smoothed field potentials produced by standard, reference-dependent EEG recordings. Nunez et al. (1994) noted that the conventional EEG often has a spatial resolution of considerably worse than 5 cm, but that surface Laplacian and cortical imaging methods could achieve a resolution of 1–3 cm. Although we have noted that Laplacian methods may be appropriate for mid-to-low density montages (i.e., 32-channels or less; Kayser and Tenke, 2006a,2006b; Tenke and Kayser, 2005; Tenke et al., 2011), the empirical merits for a given montage must clearly be supported for each application, and are therefore beyond the scope of the present report. However, for any given montage, the CSD may itself provide a multiresolutional⁹ measure if the properties of the CSD computations are altered, such as the spline flexibility, or the number or spacing of nearest neighbors used to compute a local Hjorth.

A local Hjorth is a close computational analog to the simplest intracranial CSD algorithm for the scalp-recorded EEG, and has been reported to yield similar results to other Laplacian estimates (Tandonnet et al., 2005; Tenke et al., 1998). In principle, the CSD estimate may be optimized at different resolutions to focus on the different scales for different applications, components or regions (Tenke et al. 1993; Tenke and Kayser, 2005). A multiresolutional approach for scalp data could be based on multiple submontages, whereby a local Hjorth estimate may be computed at multiple resolutions (e.g., nearest-neighbor vs. next-nearest-neighbor). Alternatively, multiple smoothing parameters may be used for a given montage.

A local Hjorth Laplacian is ideally suited for intracranial electrode grids on the dural surface, because volume conduction allows current closure not only orthogonal to the cortical surface (i.e., across laminae), but tangentially (within cortical or across columns) as well. Field closure would be evidenced by sharply localized radial sources (sinks), with smaller sinks (sources) identifiable as computational artifacts that will shift in location with changes in resolution (Tenke et al., 1993). Depending on the stimuli used and the comparisons made across conditions (e.g., random drift patterns in visual regions), this approach could help to isolate and interpret measures of local activity when local cancellation and field closure dominate the available data. Conversely, the omission of field closure as a consideration in LFP studies may contribute to findings that suggest an unexpectedly strong attenuation of field potentials over space, and that thereby challenge known properties of volume conduction (e.g., Katzner, 2009; Linden et al., 2011). Although assertions that the LFP may be restricted in scale to a few hundred microns have been countered using one-dimensional CSD methods (e.g., Kajikawa and Schroeder, 2011), the integration of findings based on different scales and methods into a single cohesive model would be a timely addition to the field.

Even though the surface Laplacian is identified with high-resolution EEG, CSD estimates using a reduced montage are often surprisingly stable, particularly for group averages (Kayser and Tenke, 2006b; Tenke et al., 2011). Fig. 6A shows auditory N1 ERP and corresponding CSD topographies from a 71-channel montage, as well as subsets as sparse as 16-channels. The overall topography of N1 is quite stable, as is the amplitude and location of the N1 sink. The corresponding source topography is also surprisingly preserved, even when it is poorly represented in the montage. However, the spatial resolution of a spline estimated CSD can also be directly varied. Fig. 6B illustrates the impact of spline flexibility on the spatial resolution of a common spherical spline Laplacian (Perrin et al., 1989; Kayser, 2009). All topographies show a common generator pattern consisting of a current sink anterior to the Sylvian fissure, coupled with a current source posterior to it. With a stiffer spline (i.e., larger m constant; cf. Eq. 2 in Kayser and Tenke, 2006a; Perrin et al., 1989), the sink is coarsely localized, while a more flexible spline (smaller m) localizes it more precisely. However, for a 71-channel montage, the N1 sink topography is clearly overresolved for the most flexible spline (m = 2). With high-density montages, the precision of each electrode placement and the reproducibility and size of the electrode-scalp interface must also be considered (Tenke and Kayser, 2001; Greischar et al., 2004) before computing and interpreting a Laplacian based on this variability. With this in mind, a flexibility of m = 4 is frequently chosen for scalp ERPs (cf. Perrin et al., 1989), resulting in consistent CSD topographies for group averages using high- or low-density montages (Fig 6A; cf. Kayser and Tenke, 2006a,b). However, a flexibility of m = 3 is well-considered for application to motor processes with a stable, known localization (e.g., Burle et al., 2008). Likewise, a flexibility of m = 5 may stabilize the topography resulting from less consistent or variably localized processes (but see Carvalhaes and Suppes, 2011, for limitations).

Figure 6.

Implications of spatial density and spline flexibility on CSD topography of auditory N1 to 100 dB tones shown in Fig. 3A. A. Nose-referenced ERP [μV] and CSD [μV/m²] topographies at N1 peak latency for different montage densities (71-channel and 30, 24, or 16-channel subsets; m = 4, λ = 10⁻⁵, 50 iterations for all CSD maps). B. CSD topographies at N1 peak latency (cf. 71-channel ERP topography in A), computed using different spline flexibilities (m = 2–5).

4.2. The problem of field closure for scalp-recorded EEG

By definition, brain activity that is volume-conducted to the scalp must be open field activity. However, even within a laminated cortical structure populated by asymmetric projection cells, considerable activity is locally cancelled (cf. CSD profile in Fig. 2B), making the notion of a closed field a relative concept. Ahlfors et al. (2010) also recognized the need to analyze the cancellation effects for distributed EEG and MEG generators. Caution must therefore be exercised when attempting to attribute ERP generators to regions identified by imaging methods that are not constrained by the properties of volume conduction. A non-electrical measure may identify activity corresponding to a predominantly closed field, phasic inhibitory activity, or patterned activity that is not represented by the scalp potential. Moreover, even when local intracranial activity appears to correspond to that recorded at the scalp, the different properties of intracranial and scalp electrodes must be carefully evaluated (e.g., contact size, impedance, and the tissue interface).

An example of the discontinuity between the scalp and intracranial literatures is presented by the novelty P3 ERP component. The midline topography of this component suggests a generator in midline cortex, and the localization of an equivalent dipole in anterior cingulate cortex led to widespread acceptance of the solution (e.g., Dien et al., 2003; Debener et al., 2005). These results have been replicated using location constraints based on fMRI (Crottaz-Herbette and Menon, 2006). Similar arguments have also been made for the midline generation of error-related negativity and anterior midline theta, leading those who consider the properties of volume conduction to conclude that the effective generators “must” lie in the banks of the cingulate fissure. Unfortunately, the intracranial fields contributing to such generators have not been adequately probed, leaving the regional and laminar generator patterns that might give rise to this equivalent dipole solution poorly understood (Tenke et al., 2010). As a result, seasoned, but cautious, investigators have questioned the adequacy of these solutions (e.g., Verleger et al., 2006; Mathalon et al., 2003). Although the nature and anatomical distribution of the generators of novelty P3 are beyond the scope of this review, the biophysical properties of hypothetical cortical generators within the longitudinal fissure can serve as a heuristic example of the implications of field closure on the scalp-recorded EEG.

Consider as an example a bilateral cortical generator deep within the longitudinal fissure (Fig. 7A). The alignment of superficial sources and deep sinks results in extensive cancellation of the intracranial field, with an uncancelled residual remaining at the scalp that is reminiscent of a laminar closed field observed using one-dimensional intracranial methods (cf. Fig. 3 of Tenke et al., 1993). A reasonable simplification of this generator configuration is a pair of opposed dipole generators (i.e., a linear quadrupole), symmetrically positioned within midline gyral cortex and oriented normal to the cortical surface (corresponding to “cortical dipoles” with superficial sources; Figure 7C, D). This generator configuration results in a summation of midline sources, yielding a sharply localized source on the midline scalp. The remaining uncancelled activity, corresponding to the deep sinks, is projected onto the lateral cortical surfaces. The more superficially the generator is positioned within the longitudinal fissure, the larger is the midline positivity (compare waveforms at site FCz in Fig. 7E and F), and the smaller the displacement of the negative maximum from the midline (maximal at FC3/4 in Fig. 7F vs. FC5/6 in Fig. 7E). The corresponding surface Laplacian topographies show similar, but more sharply localized, differences (Fig. 7G).

Figure 7.

A, B. Coronal section through a bilateral cortical generator located deep or superficially within the longitudinal fissure (dotted line). Within each hemisphere, equivalent planar current sources (+) and sinks (−) are distributed according to the lamination of the tissue within each hemisphere, resulting in local dipolar configurations radial to the local cortical surface (i.e., tangential to the scalp). Although this geometry results in extensive local field potential cancellation between hemispheres, an uncancelled residual positivity remains at the dorsal midline (large plus sign at surface), with the corresponding negativities preserved diffusely across lateral sites (smaller minus signs). The uncancelled residual positivity at the dorsal midline is larger for the shallow than the deep generator, and the corresponding negativities are closer to the midline. C, D. Deep and shallow generators are simplified as a pair of symmetric dipoles in the midline cortex of left and right hemispheres, with isopotential lines shown for each on the dorsal surface of the scalp. E, F. Field potentials (temporal waveforms; positive down; spherical average reference estimate [cf. Berg, 2006]) at 19 selected sites resulting from the deep or shallow generator consist of a midline positivity accompanied by adjacent negativities. Compared to the deep generator, the shallow generator produces a more focal midline positivity, maximal at frontocentral sites, which is surrounded by negativities on the surface of the frontal lobe, whereas negative maxima are displaced to the lateral surface of the frontal lobe for the deep generator. G. Surface potentials (SP) and current source density (CSD) topographies for deep (row 1) and shallow (row 2) closed field generator models, displayed using spherical spline interpolation without smoothing (top view of scalp; nose at top; radial 2-D projection by linear extension; scalp positivities/sources shown in red, negativities/sinks in blue; scales optimized for pairwise comparisons of generator depth). The deep closed field CSD topography (framed) is also displayed using the ellipsoid interpolation model of BESA (right), showing that the lateral displacement of the sinks is simply and geometrically related to the location and orientation of the dipoles composing the generator. Corresponding SP and CSD topographies for deep (row 3) and shallow (row 4) open field generator models were created by eliminating the left hemisphere dipoles.

As should be self-evident, bilateral midline generator configurations, depicted in Fig. 7C and D, are inconsistent with any single dipole inverse solution, and no single dipole can account for the variance of the topography. Solutions based on linked, symmetric bilateral dipoles can represent the orientation of the simulated dipoles, their locations being displaced from the midline according to the regularization parameter (not shown). However, the heuristic value of blindly submitting these topographies to a single-dipole model is to emphasize that ERP fields that match a single, radially-oriented midline dipole are inconsistent with the intracranial currents implied by a deep bilateral midline generator. As indicated in Fig. 8A, no single-dipole localization was possible for the deep bilateral generator (row 1), but the shallow bilateral generator (Fig. 8A, row 2) was localized to the midline (albeit at an implausibly superficial location). Of course, solutions for unilateral, open-field generators, each simulated by a single dipole, closely replicate the orientations and locations of the original simulation (Fig. 8A, rows 3 and 4).

Figure 8.

Inverse solutions for generator configurations modeled in Fig. 7. A. BESA single dipole fits. For the deep closed field (row 1), the dipole aligns with one of the sinks on the lateral surface, and thereby fails to represent the underlying intracranial generator. A midline radial dipole is identified for the superficial closed field (row 2), although it aligns at an implausible location (i.e., above the brain). These solutions are thereby inconsistent with radial dipole solutions fit reported for empirical data. In contrast, single dipoles are accurately localized for open fields (unilateral dipoles) at both deep (row 3) and superficial (row 4) locations. B. sLORETA source tomographies (v2008-11-04; Pascual-Marqui, 2002). For the deep closed field (row 1), the generator is localized to regions essentially identical to those identified for a superficial closed field (row 2). In contrast, the inverses for deep (row 3) and superficial (row 4) open fields suggest plausible generators.

In contrast to dipole-based inverse models, sLORETA (Pascual-Marqui et al., 1994) solutions are based on a low-resolution model, in which a concurrence of local activity (i.e., smoothed current density) is presumed. As such, regional generators are not overresolved. To the contrary, unilateral dipoles are blurred (Fig. 8B, rows 3 and 4). Consequently, the structure of the proposed midline closed field generator is fundamentally inconsistent with the presuppositions of this inverse method. However, even after the reduction or elimination of regularization (smoothing), closed fields generators (both superficial and deep) are localized to the dorsal cortical surface (Fig. 8B, rows 1 and 2), with displacements from the midline that coarsely parallel those the sinks of the surface seen for the corresponding CSD solutions (Fig. 7G). Despite the markedly divergent anatomical inferences that might be drawn from the two approaches, sLORETA and surface Laplacian solutions were again (cf. Fig. 5) compatible, thereby supporting the use of such inverses as a deblurring method (Cincotti et al., 2004). The advantage of the surface Laplacian is its generality, in that it is unencumbered by the presuppositions of any particular source model.

Although novelty P3 (Dien et al., 2003 Debener et al., 2005), no-go P3 (Verleger et al., 2006), error-related negativity (Burle et al., 2008) and other activity in this family (e.g., frontal midline theta; Luu et al., 2004) may have similar generator properties to these heuristic closed fields (cf. Kayser et al., 2007), they are merely intended to serve as an illustration of how inverses and CSD measures may lead to different conclusions. These simulations omit radial contributions from sulci within the longitudinal fissure (e.g., cingulate sulcus), as well as activity on the basal cortical surface, both of which are likely contributors to various midline scalp-recorded phenomena (cf. Tenke et al., 2010). However, any real bilateral midline generator is likely to include a continuum of adjoining cortical regions, and is thereby likely to incorporate both closed- and open-field activity in unknown proportions.

This distinction between open- and closed-field contributions becomes particularly problematic when different measures with distinctive properties are combined, such as electrical and metabolic indices, or field potentials recorded from macroscopic and microscopic electrode contacts. Such convergent solutions cannot rely on more sophisticated inverse models or independent imaging data, but require an extensive mapping of the intracranial field. Finally, none of these approaches can be applied without an intimate understanding of both the method and the neuronal processes involved. As succinctly stated by Nunez and Silberstein (2000) in their abstract (p. 79):

“Each experimental measure of brain function is generally sensitive to a different kind of source activity and to different spatial and temporal scales. Failure to appreciate such distinctions can exacerbate conflicting views of brain function that emphasize either global integration or functional localization.”

4.3. Limitations of the surface Laplacian: Caveats and empirical implications

The attributes that provide the surface Laplacian with its advantages in sharpening a topography and eliminating redundancy may become limitations as well. These concerns have become so well known by the research community (for a concise and terse summary, see Nunez and Srinivasan, 2006a) that they are often expressed categorically, and without regard for the specific application in question. From their empirical data, Hjorth and Rodin (1988) specifically proposed the use of a local Laplacian CSD as a means of parsing the contributions of superficial from deep generators of scalp-recorded seizure activity. Although quantitatively correct, simulations readily discount the strict, qualitative dichotomy implied by this approach (Turetsky and Fein, 1991; also cf. Figures 7 and 8). Moreover, coherence estimates from scalp potentials and Laplacians have been shown to be sensitive to different spatial bandwidths, which led Srinivasan et al. (1998) to recommend using the two measures in parallel.

Computationally, the Laplacian suppresses volume-conducted contributions by eliminating the potential accounted for by the recording reference, as well as associated linear spatial trends. Because of this property, an active generator in surface cortex could also be strongly attenuated if it is broadly-distributed (e.g., diffusely synchronized). Likewise, the generators of EEG activity that is transmitted via local wave-propagation across contiguous cortical regions will also be difficult to identify using simple CSD methods if they result in traveling or standing waves (Robinson, 2003; Nunez and Srinivasan, 2006b).

A final concern that warrants consideration is the geometry of the skull and brain case model. A local Hjorth Laplacian does not imply a particular head shape, but rather a piecewise-planar surface. In contrast, spline interpolations are invariably limited by their capacity to adequately match the curvature of the skull and scalp (Carvalhaes and Suppes, 2011). With these concerns in mind, Babiloni et al. (1995) examined the performance of a various surface Laplacian estimates, suggesting that the choice of a measure could be matched to the particular clinical or research need. They also identified systematic errors for high-resolution montages (> 64 channels) that were related to the anatomical imprecision of the head model. A related concern is that topographic CSD features may be misrepresented, or even missed altogether, if inadequately sampled (e.g., using an extremely low-density montage, or one for which the spatial density grossly changes across the sampled scalp surface; cf. Tucker, 1993). Likewise, some localized generators may be difficult or impossible to identify if they vary across subjects with respect to bony landmarks (unless supported by imaging methods). Despite these concerns, we note from our experience with grouped data that these problems have not been apparent for standard ERP components (e.g., Kayser and Tenke, 2006 a,b) or regional EEG alpha (Tenke and Kayser, 2005; Tenke et al., 2011), both of which have yielded stable results across studies and montage densities. Moreover, the same concerns apply to the detection of localized activity by reference-dependent scalp potentials, where spatial nuances are subject to greater attenuation by volume conduction. The capacity to consistently identify CSD waveforms and topographies may be valuable even if they are shown to be quantitatively imprecise.

The aforementioned concerns also illustrate frequently misunderstood properties of volume conduction in general, and the surface Laplacian in particular: 1) a surface Laplacian can detect deep generators, despite a relatively greater attenuation than field potentials (compare bottom two rows of Fig. 7G); 2) a surface Laplacian topography can provide a valuable and interpretable indication of the structure, location and orientation of intracranial generators, even though they are derived from estimates of radial scalp currents; 3) despite its nominal identification as high-resolution EEG, a Laplacian derived from a low density montage can yield group summaries and statistics that are useful, stable, and closely comparable to those derived from a high density solution (Kayser and Tenke, 2006 a,b); 4) high density measures (not only Laplacians) may themselves be subject to greater spatial noise, owing to greater relative variability in the placement of electrodes (i.e., small scale EEG gradients require greater spatial precision, but closely spaced electrodes are more prone to the spread of electrolyte, and even to electrolyte bridges between electrodes; Tenke and Kayser, 2001; Greishar et al., 2004); and 5) some open-field generator configurations may be better described using low- than high-density Laplacian estimates (Tenke et al., 1993).

5. CSD as an integrated approach

The present report has developed intracranial and surface Laplacian CSD methods as distinct, but compatible, applications of Poisson’s source equation aimed at identifying the generators of volume-conducted activity arising from the injection of current into, or removal from, the extracellular medium across the neuronal membrane. For an appropriately recorded intracranial field potential profile, these sources and sinks may be directly matched to the corresponding cyto- and fiberarchitecture of the region recorded, while for scalp-recorded EEG, the surface Laplacian identifies the resultant currents that enter and leave the skull and scalp from the subjacent dura.

Intracranial CSD profiles through generator regions are frequently characterized by substantial amounts of activity that is locally cancelled (closed), which may be difficult or impossible to identify at a distance. Such closed-field properties reflect the local structure of the tissue, rather than the emergence of an unforeseen spatial horizon for detecting the LFP. Incongruous findings must always be interpreted in the context of the volume-conduction model. A surface Laplacian CSD may likewise identify field cancellation on a larger scale, thereby providing a conservative standard (analogous to a intracranial dural image) against which more refined hypotheses and inverse models may be compared. CSD methods are also applicable to the study of network processes at all scales. The reduction of signal coherence (e.g., Pascual-Marqui, 1993) is an obvious advantage for spectral and time-frequency EEG applications that have been plagued by confounds from spurious correlations between signals. Compatible approaches have already been suggested for scalp (Tenke and Kayser, 2005) and intracranial resolutions (Maier et al., 2011).

Regardless of the location, orientation, number, or extent of the regions of active neural tissue, a CSD topography provides a conservative description of the neuronal generator patterns contributing to scalp-recorded EEG. CSD provides insights into the anatomical origins of the scalp potentials, while avoiding the pitfalls of overinterpretation common to inverse models. A CSD topography also identifies essential properties that must be reproduced by putative inverse solutions, particularly when the sharp gradients associated with field closure are suspected. CSD methodology thereby provides a global empirical and biophysical context for generator localization, spanning scales from cortical laminae to scalp topographies.

Highlights.

1. Current source density (CSD) methodology represents a common bridge between scalp-recorded EEG and intracranial local field potential recordings.

2. CSD reduces the redundancy, ambiguity, and reference-dependency of volume-conducted EEG measures at all observational scales.

3. CSD scalp topographies identify essential constraints on plausible neuroanatomical generators.