Sensitivity of the discrete-time Kaplan-Meier estimate to nonignorable censoring: Application in a clinical trial

Abstract

Untestable assumptions about association between survival and censoring times can affect the validity of estimates of the survival distribution, including the Kaplan-Meier (KM) nonparametric MLE. This article explores the sensitivity of the KM curve to nonignorable censoring by extending the index of local sensitivity to nonignorability (ISNI) (Troxel et al. 2004, Zhang and Heitjan 2006) to the case of a nonparametric survival model. The method involves first specifying a coarse-data selection model to describe the association between the failure and censoring processes, then evaluating the slope of the nonparametric survival MLE ordinate with respect to a nonignorability parameter in the neighborhood of the ignorable model. We define the nonparametric MLE of the survival curve for a fixed value of the nonignorability parameter, and show in a simulation that ISNI analysis effectively captures local sensitivity to nonignorability. The method measures sensitivity in the sense of identifying functionals of the nonparametric MLE that nonignorability, if present, can affect substantially. We demonstrate the method with an application to a trial comparing mechanical assistance to optimal medical management in the treatment of end-stage heart failure.

1. Introduction

Right censoring is a type of data coarsening [1] commonly encountered in survivorship studies. Although it is well known that association between failure and censoring times can distort likelihood-based inferences, data analysts often accept without scrutiny an assumption of ignorable censoring. This is at least partly because it is well known that there is little information in most data sets to permit a robust assessment of the censoring mechanism.

Random censorship gives rise to data of a competing-risks structure, and consequently partakes of the identifiability issues associated with such data [2, 3]. Peterson [4] proposed an approach to evaluating the sensitivity to nonignorable censoring, deriving bounds for the survivor function across the range of possible censoring mechanisms. These bounds evaluate the impact of nonignorable censoring on survival estimates in extreme cases, and therefore can be regarded as a form of global sensitivity analysis. Although sharp, they are unfortunately too wide to be of practical value in many applications.

If one is willing to restrict the set of survival and censoring distributions somewhat, one can derive proper inferences by jointly estimating the survival and censoring distributions using either likelihood methods or estimating equations. Fitting such models is not trivial, but the approach is sound when one has confidence that the assumptions are valid [5].

A less ambitious approach is to execute a sensitivity analysis by assuming a parametric model for the censoring mechanism and evaluating the limits of possible inferences for the survival model as the degree of nonignorability varies across its range. Scharfstein and colleagues [6, 7, 8, 9] developed methods for estimating survival curves under informative censoring, using estimating equations weighted by the inverse of the probability of censoring. To determine the weights, they proposed a “censoring bias function” that contains a nonidentifiable/sensitivity parameter to capture the dependence of failure time on censoring after adjusting for measured factors. Evaluating the dependence over a range of plausible values for the sensitivity parameter, their methods allow for a point-wise sensitivity analysis of nonignorable censoring. Shardell et al. [10] described an approach that involves the solicitation of medical expert opinion for determining the plausible range of the sensitivity parameter.

Another approach is to evaluate the sensitivity of inferences to small departures from ignorability; that is, to conduct a local sensitivity analysis. The method of Siannis et al. [11, 12] assumes a parametric survival/censoring model in which the distribution of the censoring time, given the survival time, depends on the parameter of the survival model and a nonignorability parameter. Under this model, likelihood estimation must account for the censoring mechanism even if no data are censored. An alternative approach is that of Zhang and Heitjan [13], who derived an index of local sensitivity to nonignorability (ISNI) [14] for a general parametric model of survival and censoring. This method is also likelihood-based and yields a true index of sensitivity that declines to zero together with the fraction of censored observations. Yet the need to specify a parametric survival model limits the applicability of these methods to situations where such an assumption is tenable.

The Kaplan-Meier (KM) estimate of the survival curve is valid without parametric assumptions on the underlying distribution but not without an assumption of ignorability of the censoring mechanism. Taking advantage of its interpretation as a nonparametric maximum likelihood estimate (NPMLE), however, one can apply the same local sensitivity analysis previously developed for parametric models. In this paper we develop such an approach. Our method has several advantages over previous methods: First, it avoids specification of a parametric survival model. Second, unlike point-wise sensitivity analysis, it does not require repeatedly estimating a nonignorable model and so potentially avoids arduous computations. Third, it provides a valid index of sensitivity which, in the spirit of likelihood inference and of the Peterson bounds, vanishes when censoring is absent. And fourth, although we do require a model for the censoring process, it is possible to specify such a model with only weak assumptions.

Nonignorable censoring is a concern in clinical trials, where failure and censoring times may be correlated as a consequence of time trends in treatment effects or association of enrollment time with the health of entering patients. [13, 15] Although censored and missing data are both special cases of the coarse-data model, there are important differences between them with respect to sensitivity analysis. With a trial that is subject to potentially nonignorably missing observations, if the nonignorable mechanism and the fraction of missing observations are equal across arms, comparisons between arms are insensitive to nonignorability. [16] This is not the case with nonignorable censoring, because the incompleteness of the data is a consequence of both the censoring mechanism and the survival distribution. The latter may well differ between arms even if the former does not.

The REMATCH trial [17], which compared mechanical assistance to optimal medical therapy in the treatment of advanced heart failure, provides an instructive example. Investigators had grounds to anticipate differential trends in survival between arms, as the device arm involved novel surgical and medical interventions that were difficult to master and still evolving as the trial began, whereas the medical arm involved only the administration of commonly used drugs. Thus one could anticipate some correlation of survival and censoring times in the device arm. As expected, there was a strong treatment effect, with the device arm having much better survival and therefore a larger fraction of censoring. This would induce sensitivity even if there was a common nonignorable censoring mechanism that affected both arms equally. A previous analysis based on parametric survival distributions found moderate sensitivity, but results varied to some extent by the model being estimated. [15] Thus in this article we seek to evaluate the sensitivity of inferences that are less reliant on parametric assumptions.

The paper is organized as follows: In Section 2, we review the coarse-data model and ISNI. In Section 3, we derive ISNI for KM and for functions of the survival curve such as moments and quantiles. In Section 4, we illustrate the method with simulated data, and in Section 5, we apply it to REMATCH. Section 6 concludes with further discussion.

2. ISNI in the Coarse-Data Model

2.1. Notation and the coarse-data model for right censoring

Let T be a discrete failure time and C its corresponding right censoring time, both taking values on a common, finite support 𝕋 = {t₍₁₎, … t_(m)} with 0 < t₍₁₎ < ⋯ < t_(m). If the supports for T and C differ, we let 𝕋 be their union. Let $p_{\theta }^T$ be the probability mass function of T, where θ is the governing parameter. Adopting a nonparametric perspective, we can think of θ as a vector θ = (θ₁, …, θ_m)^⊤where θ_k ≥ 0 is the probability mass on t_(k) ∈ 𝕋, and ${\sum }_{k=1}^m{\theta }_k=1$. We denote the survival and hazard functions by S(t) = Pr(T ≥ t) and λ(t) = S(t)⁻¹ Pr(T = t). Our interest is in estimating S(t) or λ(t), but we are concerned that a nonignorable right censoring mechanism may distort our estimates. Note that the survival function is a step function with jumps only at {S(t), t ∈ 𝕋}, and the hazard function is 0 except for taking values λ(t) at t ∈ 𝕋. Thus we henceforth represent the two functions using the coordinates S = (S₁, ⋯ ,S_m)^⊤ and λ = (λ₁, ⋯ ,λ_m)^⊤ where S_k = S(t_(k)) and (λ_k = (λ(t_(k)).

In the case of random censorship, where we do not know the censoring time except when a subject’s event time is actually censored, the right censoring is a data-coarsening process on failure time, and similarly the mortality is a data-coarsening process on the censoring time. [1] Mathematically, the two simultaneous coarsening processes can be expressed by

$$Y(T,C)=\{\begin{array}{cc}\left\{T\right\}\hfill & T\le C\hfill \\ \mathbb{𝕋}\cap (C,\infty )\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$

and

$$G(C,T)=\{\begin{array}{cc}\left\{C\right\}\hfill & T>C\hfill \\ \mathbb{𝕋}\cap [T,\infty ]\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$

where (Y, G) are observable set outcomes. For data collected from n independent subjects, the (Y_i, G_i) pairs are independent copies of the observed, coarsened version of the (T_i, C_i) pairs for i = 1, … n.

Under general assumptions, the distribution of (Y, G) does not uniquely determine the failure time distribution $p_{\theta }^T$; this is the so-called “nonidentifiability” problem. Thus except in certain special cases, to obtain a correct estimate of θ we must take into account the censoring mechanism. Throughout this paper, we use a selection model to describe the censoring mechanism

$$C\mid T\sim p_{\gamma }^{C\mid T},$$

where $p_{\gamma }^{C\mid T}$ denotes the conditional distribution of censoring time C for a given failure time T, and γ is assumed to be distinct from θ in the sense of Rubin [18]. We further assume that γ can be decomposed as γ = (γ₀, γ₁)^⊤, where γ₀ is a nuisance parameter (possibly a vector), and (γ₁ is a sensitivity parameter that satisfies the following three conditions:

• γ₁ controls the magnitude of the nonignorability in the censoring mechanism;

• it is not identified by the data; and

• supplying a value of γ₁ allows the rest of the parameters to be identified.

In the sequel we refer to γ₁ as the nonignorability parameter. Moreover we assume that when γ₁ = 0 the censoring mechanism is ignorable in the sense that the random censoring times can be treated as if they are fixed prior to the study and independent of the failure times.

Given a censoring model, the likelihood of θ and γ conditional on the observable (Y = y, G = g) is [19]

$$L(\theta ,\gamma )=\sum _{t\in y}\left\{p_{\theta }^T\left(t\right)\sum _{c\in g}{p}_{\gamma }^{C\mid T}(c\mid t)\right\}.$$ (1)

When γ₁ = 0, the likelihood inference for θ based on (1) is exactly the same as that based on

$$L_{ign}\left(\theta \right)=\sum _{t\in y}{p}_{\theta }^T\left(t\right).$$ (2)

This ignorable likelihood is the likelihood that one uses in applications that disregard the stochastic nature of the censoring mechanism.

2.2 Review of ISNI

The index of local sensitivity to nonignorability (ISNI) [13, 14] is a measure of the extent to which small deviations in the nonignorability parameter around the ignorable value γ₁ = 0 affect likelihood-based inferences on the parameter of interest. We give here a brief review of the method. Throughout the paper, we will use $\widetilde{.}$ (tilde) to denote the maximum likelihood estimate under the complete data likelihood (1) for a given γ₁, and $\widehat{.}$ (hat) to denote the maximum likelihood estimate under the ignorable likelihood (2).

For ease of illustration, assume for the moment that γ₁ is a scalar. When γ₁ is sufficiently small, the log of the correct likelihood (1) ℓ(θ, γ₀, γ₁) = log L(θ, γ₀, γ₁) can be approximated using the Taylor expansion

$$\begin{array}{cc}\hfill \ell (\theta ,{\gamma }_0,{\gamma }_1)& \approx \ell (\theta ,{\gamma }_0,0)\hfill \\ \hfill & +(\theta -\widehat{\theta },{\gamma }_0-{\widehat{\gamma }}_0,{\gamma }_1)\frac{\partial \ell }{\partial {(\theta ,{\gamma }_0,{\gamma }_1)}^{\top }}{\mid }_{(\widehat{\theta },{\widehat{\gamma }}_0,0)}\hfill \\ \hfill & +\frac{1}{2}(\theta -\widehat{\theta },{\gamma }_0-{\widehat{\gamma }}_0,{\gamma }_1)\frac{{\partial }^2\ell }{\partial (\theta ,{\gamma }_0,{\gamma }_1)\partial {(\theta ,{\gamma }_0,{\gamma }_1)}^{\top }}{\mid }_{(\widehat{\theta },{\widehat{\gamma }}_0,0)}{(\theta -\widehat{\theta },{\gamma }_0-{\widehat{\gamma }}_0,{\gamma }_1)}^{\top }\hfill \end{array}$$

where $\widehat{\theta }$ and ${\widehat{\gamma }}_0$ are the MLEs assuming the ignorable model. We differentiate the right hand side with respect to θ for fixed γ₁ and then solve for θ, and after some manipulation obtain

$$\tilde{\theta }\left({\gamma }_1\right)\approx \widehat{\theta }-{\mathcal{I}}_{ign}^{-1}\frac{{\partial }^2\ell }{\partial \theta \partial {\gamma }_1}{\mid }_{(\widehat{\theta },{\widehat{\gamma }}_0,0)}{\gamma }_1,$$

where $\tilde{\theta }\left({\gamma }_1\right)$ is the maximum likelihood estimate of θ given the data and assuming fixed γ₁, and

$${\mathcal{I}}_{ign}=-\frac{{\partial }^2\text{log}{L}_{ign}}{\partial \theta \partial {\theta }^{\top }}{\mid }_{\widehat{\theta }}$$

is the observed information for the ignorable likelihood. This expression motivates the definition of ISNI [14] as

$$\text{ISNI}\left(\widehat{\theta }\right)={\mathcal{I}}_{ign}^{-1}\frac{{\partial }^2\ell }{\partial \theta \partial {\gamma }_1}{\mid }_{(\widehat{\theta },{\widehat{\gamma }}_0,0)}.$$ (3)

In the neighborhood of the ignorable model (i.e., where γ₁ = 0), $\tilde{\theta }\left({\gamma }_1\right)\approx \widehat{\theta }+{\gamma }_1\text{ISNI}$, so ISNI is the rate of change of the MLE $\tilde{\theta }$ as γ₁ varies around the ignorable model. Thus ISNI measures the local sensitivity of the parameter estimate to departures from ignorability. A large value of ISNI implies that the ignorable likelihood estimator is sensitive to modest departures of the censoring model from ignorability, whereas a small value suggests that the estimator is locally robust. ISNI is typically easy to compute and avoids the requirement to repeatedly maximize L(θ, γ) under a range of nonignorable models.

When γ₁ is a q-dimensional vector, Xie and Heitjan [16] proposed an alternative definition of ISNI as

$$\text{ISNI}\left(\widehat{\theta }\right)=\sqrt{q}{\Vert \frac{\partial \tilde{\theta }}{\partial {\gamma }_1^{\top }}{\mid }_{(\widehat{\theta },{\widehat{\gamma }}_0,0)}\Vert }^{1∕2},$$

which approximates the maximal sensitivity when the vector-valued nonignorability parameter lies on a ball of radius $\sqrt{q}$ around the origin; i.e., $\text{ISNI}\approx {\text{max}}_{\Vert {\gamma }_1\Vert =\sqrt{q}}(\tilde{\theta }-\widehat{\theta })$.

2.3 Local sensitivity assessment

Because ISNI refers to the derivative of the MLE with respect to the nonignorability parameter, and the nonignorability parameter depends on the measurement scale of T, the interpretation of ISNI also depends on the measurement scale. To avoid such dependence, Troxel et al. [14] defined the statistic

$${\gamma }_1^{\ast }=\mid \frac{\text{SE}\left(\widehat{\theta }\right)}{\text{ISNI}\left(\widehat{\theta }\right)}\mid ,$$ (4)

where the numerator is the standard error (SE) of $\widehat{\theta }$ under the ignorable model. This ${\gamma }_1^{\ast }$ is approximately the value of γ₁ that can cause a one-SE change in $\widehat{\theta }$. If ${\gamma }_1^{\ast }$ is implausibly large, then we would require an implausibly large amount of nonignorability to change inferences substantially, and therefore we deem the estimation insensitive to nonignorability. If ${\gamma }_1^{\ast }$ is a plausible value of the nonignorability parameter for the data at hand, we conclude that $\widehat{\theta }$ is sensitive to nonignorable censoring.

3. Evaluating Sensitivity of KM

To derive ISNI for the KM survival estimate, we use the fact that KM is also an MLE, albeit a nonparametric MLE in a model with a parameter of potentially high dimension. In the following, we commit a slight abuse of our notation 𝕋 by letting it also denote the set of unique ordered failure and censoring times that are observed. We first derive ISNI for the KM hazard estimates, which turns out to be straightforward. We then derive ISNI for the KM survival estimates by using the one-to-one mapping between survival and hazard.

3.1. ISNI for the hazard estimate

Let d_k and r_k be the numbers of subjects dead and at risk, respectively, at time t_(k) ∈ 𝕋. The KM hazard estimate at t_(k) is ${\widehat{\lambda }}_k=d_k∕r_k$, which is also the NPMLE under the ignorable likelihood

$$L_{ign}\left(\theta \right)\propto \prod _{i=1}^n\left(\sum _{t_{\left(k\right)\in y_i}}{\theta }_k\right)=\prod _{k=0}^m{\lambda }_k^{dk}{(1-{\lambda }_k)}^{r_k-d_k}.$$

The first factor in the definition of ISNI (3) is the inverse information under the ignorable likelihood, which for the hazard estimate is

$${\mathcal{I}}_{ign}^{-1}=\text{Diag}\{r_0^{-1}{\widehat{\lambda }}_0(1-{\widehat{\lambda }}_0),\cdots ,r_m^{-1}{\widehat{\lambda }}_m(1-{\widehat{\lambda }}_m)\}.$$ (5)

For d_j = 0 we adopt the convention 0 · ∞ = 1 to avoid ambiguities in calculating the matrix inverse.

To derive the second factor in (3), we write out the log of the correct likelihood (1) as the sum of log likelihoods for observed and censored death times

$$\ell (\theta ,\gamma )=\sum _{{\delta }_i=0}\left[\text{log}\left\{p_{\theta }^T\left(t_i\right)\sum _{c\in g_i}{p}_{\gamma }^{C\mid T}(c\mid t_i)\right\}\right]+\sum _{{\delta }_i=1}\left[\text{log}\left\{\sum _{t\in y_i}{p}_{\theta }^T\left(t\right)p_{\gamma }^{C\mid T}(c_i\mid t)\right\}\right],$$

where δ_i = 1(t_i > c_i) indicates whether a right censoring occurs. When taking the second-order derivative $\frac{{\partial }^2}{\partial \theta \partial {\gamma }_1}$, the first term vanishes with the assumption that θ and γ are distinct. [18] Consistent with our intuition, for local sensitivity what really matters is the sum of the log-likelihood for censored failures. With some algebra, we find that

$$\frac{{\partial }^2\ell }{\partial {\lambda }_k\partial {\gamma }_1}{\mid }_{{\gamma }_1=0,\lambda =\widehat{\lambda }}=-\sum _{c_i<t_{\left(k\right)}}\left[\frac{{\delta }_i{A}_{\gamma 0}\left(c_i\right)}{p_{{\gamma }_0}^C\left(c_i\right)}\sum _{j\ge k}\frac{(t_{(j+1)}-t_{\left(j\right)})\prod _{c_i<t_{\left(l\right)}\le t_{\left(j\right)}}(1-{\widehat{\lambda }}_l)}{1-{\widehat{\lambda }}_k}\right],$$ (6)

where $A_{{\gamma }_0}\left(c\right)=\frac{\partial p_{\gamma }^{C\mid T}}{\partial \left({\gamma }_{1}t\right)}{\mid }_{{\gamma }_1=0}$ and $p_{{\gamma }_0}^C\left(c\right)=p_{\gamma }^{C\mid T}(c\mid t;{\gamma }_1=0)$, which does not depend on t. Now, bringing (5) and (6) into (3), we obtain the ISNI for the KM hazard estimates as

$$\text{ISNI}\left(\widehat{\lambda }\right)={(\text{ISNI}\left({\widehat{\lambda }}_1\right),\cdots ,\text{ISNI}\left({\widehat{\lambda }}_m\right))}^{\top },$$

where

$$\text{ISNI}\left({\widehat{\lambda }}_k\right)=\frac{{\widehat{\lambda }}_k}{r_k}\sum _{c_i<t_{\left(k\right)}}\left[\frac{{\delta }_i{A}_{{\widehat{\gamma }}_0}\left(c_i\right)}{p_{{\widehat{\gamma }}_0}^C\left(c_i\right)}\sum _{j\ge k}\left\{(t_{(j+1)}-t_{\left(j\right)})\prod _{c_i<t_{\left(l\right)}\le t_{\left(j\right)}}(1-{\widehat{\lambda }}_l)\right\}\right].$$

3.2 ISNI for KM

The KM ordinates are given by ${\widehat{S}}_j={\prod }_{k=0}^j(1-{\widehat{\lambda }}_k)$. To simplify the derivation, consider logs of the survival function,

$$\text{log}{S}_k=\sum _{j=1}^k\text{log}(1-{\lambda }_j)\Rightarrow \frac{\partial \text{log}{S}_k}{\partial {\lambda }_l}=\{\begin{array}{cc}-\frac{1}{1-{\lambda }_l},\hfill & l\le k;\hfill \\ 0,\hfill & \text{o.w.}\hfill \end{array}\phantom{\}}$$

By the chain rule, the ISNI of KM is

$$\begin{array}{cc}\hfill \text{ISNI}\left({\widehat{S}}_k\right)& ={\left\{\frac{\partial \left(\text{log}{S}_k\right)}{\partial S_k}{\mid }_{S_k={\widehat{S}}_k}\right\}}^{-1}{\left\{\frac{\partial \left(\text{log}{S}_k\right)}{\partial \lambda }{\mid }_{\lambda =\widehat{\lambda }}\right\}}^{\top }\text{ISNI}\left(\widehat{\lambda }\right)\hfill \\ \hfill & ={\widehat{S}}_k\sum _{l=1}^k\left\{\frac{dl}{r_l^2}\sum _{c_i<t_{\left(l\right)}}\left[\frac{{\delta }_i{A}_{{\widehat{\gamma }}_0}\left(c_i\right)}{p_{{\widehat{\gamma }}_0}^C\left(c_i\right)}\sum _{j\ge l}\frac{(t_{(j+1)}-t_{\left(j\right)})\prod _{c_i<t_{\left(z\right)}\le t_{\left(j\right)}}(1-d_z∕r_z)}{1-d_l∕r_l}\right]\right\}.\hfill \end{array}$$ (7)

This expression suggests that the KM curve is insensitive up to the time of the first censoring event. After that, its sensitivity depends on the fraction of data censored, and as KM approaches 0, its sensitivity declines to 0 again because the upper and lower bounds of the survival function limit the effect of nonignorability.

3.3. Example for a specified $p_{\gamma }^{C\mid T}$

In the preceding section, we derived ISNI for KM with a general nonignorable model. Here we show that the nonignorable model $p_{\gamma }^{C\mid T}$ can have a semiparametric form such that we only need to explicitly specify the part that involves the interaction of γ₁ and the survival time.

Our example assumes that the censoring time, conditional on the failure time, follows a proportional hazards model ${\lambda }^{C\mid T}(c\mid t)={\lambda }_0^C\left(c\right)\text{exp}\left({\gamma }_{1}t\right)$. With this setup, the nuisance parameter is the baseline hazard of censoring ${\gamma }_0=\{{\lambda }_0^C\left(c\right),c\in \mathbb{𝕋}\}$, which can be left unspecified. Further we can derive the selection model as $p_{\gamma }^{C\mid T}(c\mid t)={\lambda }_0^C\left(c\right)\text{exp}\left({\gamma }_{1}t\right){\prod }_{t_{\left(j\right)<c}}[1-{\lambda }_0^C\left(t_{\left(j\right)}\right)\text{exp}\left({\gamma }_{1}t\right)]$, and calculate the following term of (7) for this selection model:

$$\frac{A_{{\gamma }_0}\left(c\right)}{p_{{\gamma }_0}^C\left(c\right)}=\frac{\partial \left\{\text{log}{p}_{\gamma }^{C\mid T}(c\mid t)\right\}}{\partial \left({\gamma }_{1}t\right)}{\mid }_{{\gamma }_1=0}=1-\sum _{t_{\left(j\right)}<c}\frac{{\lambda }_0^C\left(t_{\left(j\right)}\right)}{1-{\lambda }_0^C\left(t_{\left(j\right)}\right)}.$$ (8)

We can estimate the nuisance parameter $\{{\lambda }_0^C\left(c\right),c\in \mathbb{𝕋}\}$ by the KM hazard estimator, treating censoring as an “event” that can be censored by an event. By substituting (8) for the corresponding term in (7), we readily obtain $\text{ISNI}\left({\widehat{S}}_k\right)$ for this model.

3.4. ISNI for statistics derived from KM

Because ISNI is simply a derivative, once one has computed it for a particular parameter, one can apply the chain rule to compute it for any function of that parameter. In this sub-section we derive ISNI for three scalar functions of the survival curve that are relevant in applications.

Mean Survival Time

An estimate of mean survival is the area under the survival curve, ${\widehat{\mu }}_T={\sum }_{j=1}^m{\widehat{S}}_{j-1}(t_{\left(j\right)}-t_{(j-1)})$. It follows immediately that

$$\text{ISNI}\left({\widehat{\mu }}_T\right)=\sum _{j=1}^m\text{ISNI}\left({\widehat{S}}_{j-1}\right)(t_{\left(j\right)}-t_{(j-1)}).$$

That is, ISNI for mean survival is just a linear combination of the ISNI values computed at each survival time.

Restricted Mean Survival

When late censoring is substantial or failure time is highly skewed, it may be preferable to consider τ-restricted mean survival, defined as the mean lifetime among a subpopulation who experience failure before τ. Karrison [20] proposed the estimator $\widehat{\mu }\left(\tau \right)={\sum }_{t_{\left(j\right)\ge \tau }}{\widehat{S}}_j{\varphi }_j$, where ${\varphi }_j=({\varphi }_j^{\ast }+{\varphi }_{j-1}^{\ast })∕2$ with ${\varphi }_0^{\ast }=0$ and ${\varphi }_j^{\ast }=t_{(j+1)}-t_{\left(j\right)}$. ISNI for the τ-restricted mean life is therefore

$$\text{ISNI}\left(\widehat{\mu }\left(\tau \right)\right)=\sum _{t_{j\le \tau }}\text{ISNI}\left({\widehat{S}}_j\right){\varphi }_j.$$

ISNI for a Quantile

Another parameter of potential interest is the median survival, denoted by T_0.5, or more generally the wth quantile of survival T_w. In the Appendix, we show how to calculate ISNI for the estimated wth quantile when failure time T is continuous. When 𝕋 is discrete, there is ambiguity in the definition of the wth quantile. Henceforth we take the following definition:

$$T_w=\frac{t_{(j^{\ast }+1)}(S_{j^{\ast }}-w)+t_{\left(j^{\ast }\right)}(w-S_{j^{\ast }+1})}{S_{j^{\ast }}-S_{j^{\ast }+1}},$$ (9)

where j* = j : Pr(T < t_(j)) ≤ w < Pr(T < t_(j+1)). This is equivalent to regarding the survival function as continuous with linear interpolations between successive distinct survival probabilities over 𝕋,

$$\stackrel{‒}{S}\left(t\right)=\sum _{j}1(t\in [t_{(j-1)},t_{\left(j\right)}))\frac{(t_{\left(j\right)}-t)S_{j-1}+(t-t_{(j-1)})S_j}{t_{\left(j\right)}-t_{(j-1)}}.$$ (10)

Note that definition (10) implies a probability density function

$$\stackrel{‒}{f}\left(t\right)=\sum _{j}1(t\in [t_{(j-1)},t_{\left(j\right)}))\frac{S_{j-1}-S_j}{t_{\left(j\right)}-t_{(j-1)}},$$

and it is easy to check that the definition in (9) can be expressed as $t_w={\stackrel{‒}{S}}^{-1}\left(w\right)$.

We can estimate ${\widehat{T}}_w$ by bringing the KM estimates into (9). Applying (15) (from the Appendix), we obtain that when ${\widehat{T}}_w\notin \mathbb{𝕋}$,

$$\text{ISNI}\left({\widehat{T}}_w\right)\approx \frac{({\widehat{T}}_w^{+}-{\widehat{T}}_w)\text{ISNI}\left({\widehat{S}}_w^{-}\right)+({\widehat{T}}_w-{\widehat{T}}_w^{-})\text{ISNI}\left({\widehat{S}}_w^{+}\right)}{{\widehat{S}}_w^{-}-{\widehat{S}}_w^{+}},$$ (11)

and when ${\widehat{T}}_w\in \mathbb{𝕋}$,

$$\text{ISNI}\left({\widehat{T}}_w\right)\approx \{\begin{array}{cc}\frac{({\widehat{T}}_w-{\widehat{T}}_w^{-})\text{ISNI}\left({\widehat{S}}_w\right)}{{\widehat{S}}_w^{-}-{\widehat{S}}_w},\hfill & \text{ISNI}\left({\widehat{S}}_w\right){\gamma }_1<0;\hfill \\ \frac{({\widehat{T}}_w^{+}-{\widehat{T}}_w)\text{ISNI}\left({\widehat{S}}_w\right)}{{\widehat{S}}_w-{\widehat{S}}_w^{+}},\hfill & \text{ISNI}\left({\widehat{S}}_w\right){\gamma }_1>0\hfill \end{array}\phantom{\}}$$ (12)

where ${\widehat{T}}_w^{-}\left({\widehat{T}}_w^{+}\right)$ is the largest (smallest) value in 𝕋 less (greater) than ${\widehat{T}}_w$, and ${\widehat{S}}_w^{-}\left({\widehat{S}}_w^{+}\right)$ is the KM ordinate at ${\widehat{T}}_w^{-}\left({\widehat{T}}_w^{+}\right)$.

4. Simulation

We conducted a simulation to evaluate the ability of ISNI to approximate the impact of small departures from ignorability on the MLE. We generated 5,000 independent failure times from the exponential distribution with mean 10, and discretized the data by taking the ceiling (⌈·⌉]) of each outcome, i.e.

$$U\sim \text{EXP}\left(10\right)\text{and}T=\lceil U\rceil .$$

We simulated the corresponding censoring times from the nonignorable censoring mechanism

$$V\mid T\sim \text{EXP}\left(10\text{exp}(-{\gamma }_{1}T)\right)\text{and}C=\lceil V\rceil .$$

We generated the data assuming a value of the nonignorability parameter γ₁ = 0.4.

Results appear in Figures 1, 2 and 3. In Figure 1, the KM curve for the simulated data is the gray line, and the true survival curve is the thin solid black line. With γ₁ > 0, people with long survival times have short censoring times and people with short survival times have long censoring times. Thus shorter survival times are over-represented in the data set, and the KM curve underestimates survival, as can be seen in every panel of Figure 1.

Figure 1.

Estimated survival curves for the simulated data. The thick gray lines are the KM curves and the thin black lines are the underlying true survival functions; these are the same for all six plots. The thick black lines are the estimated SC curves assuming different values of γ₁.

Figure 2.

ISNI for the simulated data. The circles connected by the solid lines are the SC ordinates assuming γ₁ = −0.01, 0, … , 0.04 at times 1, 3, … , 11. The circles at γ₁ = 0.04 are the true survival probabilities. The solid lines have intercepts equal to the KM survival estimates and slopes equal to the corresponding ISNI.

Figure 3.

ISNI of KM across time for the simulated data. Upper plot: the KM curve with the Peterson bounds; lower plot: ISNI over time.

Also in Figure 1, we present the self-consistent (SC; see Appendix) estimate of the survivor function as the dark solid lines along the KM and true survival curves, for the range of values of the nonignorability parameter γ₁ = −0.01, 0, 0.01, 0.02, 0.04, 0.06. That is, the thick black lines represent estimates of the survival curve assuming fixed values of the nonignorability parameter. Therefore when γ₁ = 0 we are assuming ignorability and the SC curve equals the KM curve. When we assume γ₁ = 0.04, the nonignorable model is correctly specified and the SC curve closely matches the true survival curve.

Figure 2 plots the SC survival probability estimates (shown as circles) against the values of γ₁ at times 1, 3, … , 11. The dashed lines have intercepts equal to the survival probabilities evaluated at γ₁ = 0 (the KM estimates) and slopes equal to ISNI, indicating that ISNI successfully approximates the impact of 71 on survival estimates in the neighborhood of γ₁ = 0.

Figure 3 plots the ISNI values for the KM ordinates together with the KM curve and the estimated Peterson bounds. The ISNI “curve” begins at 0 and is right-continuous, as suggested by (7). The absolute value of ISNI has a maximum around t = 20 and then decreases to 0 for larger times, showing that the middle part of the survival curve is relatively more sensitive to nonignorability. Prior to time 2 (the observed event time after the first censoring), overlapping of the upper and lower Peterson bounds suggests that KM is completely insensitive. This well agrees with ISNI, which is also 0 before time 2. As time increases, both the lower Peterson bound and the survival curve converge to 0, suggesting that later survival estimates are insensitive to nonignorability, if only in one direction. ISNI also converges to 0, suggesting a complete lack of sensitivity for large t.

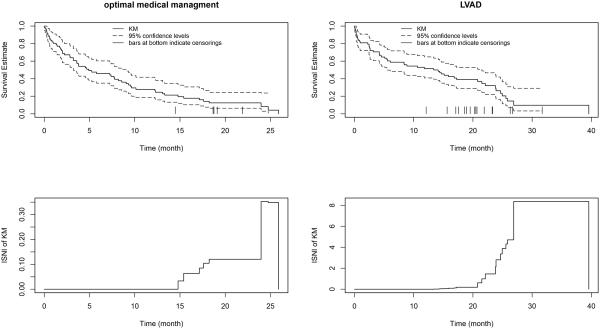
5. Application to REMATCH

The REMATCH trial [17] evaluated the long-term survival benefit of a surgically implanted left ventricular assist device (LVAD) in heart failure patients who were ineligible for cardiac transplantation. The study enrolled 129 patients and randomized them to either LVAD (n = 68) or optimal medical management (OMM) (n = 61). Five patients on OMM and 16 on LVAD were censored as of the closing date for our data set. To assess the impact of right censoring on survival estimates in REMATCH, we considered the following model for each arm: V|T ~ EXP(exp(γ₀ + γ₁T)) and C = ⌈V⌉, allowing the parameters γ₀ and γ₁ to differ between arms.

Figure 4 shows the KM survival estimates, 95% confidence limits, and KM ISNI curves for the OMM and LVAD arms of REMATCH. The KM curves suggest that LVAD has a substantially better survival rate. Only the later portions (after the smallest censoring times) of the KM curves are subject to the impact of possible nonignorable censoring. Local sensitivity for the KM estimate is much greater for the LVAD arm than for the OMM arm, because the proportion of censored events for the LVAD arm is higher.

Figure 4.

The KM curve with 95% confidence levels and ISNI for the REMATCH data.

Table 1 summarizes the mean survival (assuming that after the last observation the survival curve declines to 0), the restricted mean survival for τ = 18 months, the median survival, and four landmark survival probabilities, together with their ISNI assessment. For comparison of the two arms, we calculated ISNI using the method of Xie and Heitjan [16] for vector-valued γ₁, assuming the two arms have distinct values of this parameter. By the definition of ${\gamma }_1^{\ast }$, $\text{log}\left(12{\gamma }_1^{\ast }\right)$ is the hazard ratio of staying in the trial, for two people whose survival times differ by one year, that can cause one SE change in the estimate of the parameter of interest. In REMATCH, we think that this hazard ratio is plausibly no more than 2. Transformed back to the scale of γ₁, the critical figure is 0.06. By this criterion, the mean, restricted mean, median, and their comparisons between arms are insensitive to nonignorability. Compared with mean survival, the restricted mean and median survival are more locally robust. The survival estimate in the LVAD arm at 24 months and the difference between the two arms at 24 months are potentially sensitive to nonignorability, whereas the survival estimates at the other landmark times are robust. These results agree well with previous analyses by Zhang and Heitjan [15], who assumed parametric distributions for the survival times.

Table 1.

Sensitivity analysis for the mean, restricted mean (τ = 18 months), median, and survival probabilities at months 6, 12, 18 and 24 in the REMATCH data. The standard errors (SEs) for the mean, restricted mean and median were calculated using a bootstrap with 1,000 resamples.

	mean	restricted mean (τ = 18)	median	landmark survival (mo)
				6	12	18	24
OMM
Estimate	8.13	7.12	4.80	0.46	0.28	0.14	0.08
ISNI	0.35	0.07	0	0	0	0.10	0.35
SE/ISNI $\left({\gamma }_1^{\ast }\right)$	2.82	11.6	∞	∞	∞	0.44	0.13
LVAD
Estimate	14.5	10.4	13.3	0.60	0.51	0.39	0.26
ISNI	14.7	0.12	12.3	0	0	0.19	2.81
SE/ISNI $\left({\gamma }_1^{\ast }\right)$	0.11	7.41	0.28	∞	∞	0.31	0.02
Difference: (LVAD — OMM)
Estimate	6.38	3.30	8.53	0.14	0.24	0.25	0.18
ISNI	20.8	0.19	17.4	0	0	0.31	4.00
SE/ISNI $\left({\gamma }_1^{\ast }\right)$	0.09	6.07	0.21	∞	∞	0.24	0.02

6. Discussion

Nonignorability of the random censoring mechanism has the potential to spoil estimates of the survival curve. In this paper we describe a local sensitivity method to assess the impact of nonignorable censoring on the discrete-time KM survival estimate. Using the self-consistent estimates for a simulated data set, we show that our method performs satisfactorily as a measure of local sensitivity. Previous authors have considered sensitivity analyses that assume parametric models for survival and censoring. [11, 12, 15] In this paper, we apply the local sensitivity method of Troxel et al. [14] to a model that entirely avoids parametric assumptions about the survival distribution.

Our method has several advantages over other available procedures: First, because sensitivity assessment via ISNI does not require estimation of the nonignorable censoring mechanism, it allows sensitivity analyses to be performed with little effort under a range of nonignorable models. As we showed in Section 3.3, one can apply a general censoring model such as a semiparametric proportional hazards model, reducing concerns about misspecification. Moreover, we can readily extend analysis from the KM curve itself to derived quantities such as the mean, restricted mean, median and other quantiles, not all of which may be equally sensitive to nonignorability.

We emphasize that the purpose of our method is to measure the sensitivity of the KM curve, in its guise as an NPMLE, to potential nonignorability in the censoring mechanism. The underlying idea is that when faced with random coarsening, the preferred option is always to assume that the coarsening is ignorable. This is because the standard statistical approach of nesting the ignorable model within a nonignorable model, then testing for adequacy of fit, can be impracticable even when the coarsening mechanism is assumed “known” up to parameters. Thus sensitivity measures such as ISNI do not attempt to estimate the nonignorability but to evaluate whether modest departures from ignorability would substantially affect estimates. Moreover ISNI is Bayesian in spirit in that it applies to the data at hand rather than to long-run averages including other data sets that might have been observed but were not. So for example when substantial censoring is present only in the far right tail of the distribution, ISNI will show that sensitivity is modest for KM ordinates at short survival times. In this sense ISNI diagnostics are similar to regression diagnostics that identify parameters whose estimation may be sensitive to departures from the assumed model at one or more points in the observed data.

A potential limitation of the method is its continued reliance on model assumptions, however weak, regarding the censoring mechanism. Because we typically have little prior information about the censoring mechanism, it is advisable to conduct sensitivity analyses under a plausibly broad range of assumptions. Evidently the only alternative to making some kind of assumption is to resort to Peterson’s bounds, which are unacceptably wide in many applications.

The derivation of ISNI for KM takes advantage of the fact that right censoring falls under the rubric of the Heitjan-Rubin coarse-data model. [1, 19] In a strict sense, this model requires that the sample space be discrete, because the likelihood function is the integral of the underlying density over the set of possible values of the complete data that could have given rise to the observed, coarsened data. With a continuous model, a perfectly observed data point (in REMATCH, an observed death) therefore contributes a factor of 0 to the likelihood. It is possible to extend the coarse-data model to underlying continuous sample spaces, [21] but the analysis is complex. In any event, the discrete model more accurately represents real-world data, which we can never measure with infinite precision. We argue that models assuming continuous random variables are merely approximations that one should eschew when they add no value to the analysis.

A next obvious step in the research is to develop measures for sensitivity of parameters in nonparametric or semiparametric survival regression models such as the Cox model.

Appendix

Nonparametric survival MLE with informative censoring

In our simulation study (Section 4), we proposed a self-consistent (SC) procedure to estimate the survival curve for a fixed value of γ₁. To derive the SC procedure, we first write out the complete-data likelihood (1) using survival coordinates,

$$L(\theta ,\gamma )\propto \prod _{j=1}^m\left[{\left\{(S_{j-1}-S_j)\sum _{k\ge j}{p}_{\gamma }^{C\mid T}(t_{\left(k\right)}\mid t_{\left(j\right)})\right\}}^{d_j}{\left\{\sum _{k>j}(S_{k-1}-S_k)p_{\gamma }^{C\mid T}(t_j\mid t_k)\right\}}^{r_j-d_j}\right].$$

Solving the score equations for a fixed γ₁ and requiring that 1 = S₀ ≥ S₁ ≥ ⋯ ≥ S_m leads to the following equations:

$${\tilde{S}}_j=\frac{\sum _{k>j}{d}_k^{\prime }}{\sum _{k\ge j}{d}_k^{\prime }}{\tilde{S}}_{j-1},\text{for}j=1,2,\dots ,m,$$ (13)

where $d_j^{\prime }=d_j+1(j>1){\sum }_{k<j}{d}_{jk}^{\ast }$ and $d_{jk}^{\ast }=1(j>k)\frac{(r_k-d_k)({\tilde{S}}_{j-1}-{\tilde{S}}_j)p_{\gamma }^{C\mid T}(t_{\left(k\right)}\mid t_{\left(j\right)})}{{\sum }_{l>k}({\tilde{S}}_{l-1}-{\tilde{S}}_l)p_{\gamma }^{C\mid T}(t_{\left(k\right)}\mid t_{\left(l\right)})}+1(j\le k)\frac{d_j{p}_{\gamma }^{C\mid T}(t_{\left(k\right)}\mid t_{\left(j\right)})}{{\sum }_{l\ge j}{p}_{\gamma }^{C\mid T}(t_{\left(l\right)}\mid t_{\left(j\right)})}$, and the nuisance parameter ${\tilde{\gamma }}_0$ must satisfy

$$\frac{\partial \left\{\sum _j\sum _k{d}_{jk}^{\ast }\text{log}{p}_{\gamma }^{C\mid T}(t_{\left(k\right)}\mid t_{\left(j\right)})\right\}}{\partial {\gamma }_0}{\mid }_{{\gamma }_0={\widehat{\gamma }}_0}=0.$$ (14)

Simultaneously solving (13) and (14) for $\left\{{\tilde{S}}_j\right\}$ and ${\tilde{\gamma }}_0$ is not straightforward, but one can readily solve the equations with a self-consistency algorithm [22], which in this case is equivalent to an EM algorithm [23]. The idea is based on Turnbull [24, 25] and is similar to that of Link [26].

Having chosen a starting value (KM for {S_j} and any reasonable guess for γ₀ will serve), one solves the equations using the following steps: 1. Compute $\left\{d_{jk}^{\ast }\right\}$ and $\left\{d_j^{\prime }\right\}$; 2. with ${\tilde{S}}_0=0$, compute $\left\{{\tilde{S}}_j\right\}$ using (13); 3. compute $\left\{d_{jk}^{\ast }\right\}$ and $\left\{d_j^{\prime }\right\}$ with the updated $\left\{{\tilde{S}}_j\right\}$ from Step 2; 4. and solve for ${\tilde{\gamma }}_0$ using (14). Cycle through 1–4 until convergence.

If censoring is ignorable (i.e., if γ₁ = 0), the SC curve equals the KM curve. Although the SC curve can serve as the basis of a sensitivity analysis, the computation is laborious and may be impractical in many situations.

ISNI for an estimated quantile when T is continuous

Consider the case of continuous T with estimated survival function $\tilde{S}\left(t\right)$ that is differentiable at the wth estimated quantile ${\tilde{T}}_w$. Taking derivatives on both sides of the equation, $\tilde{S}\left({\tilde{T}}_w\right)=1-w$, with respect to γ₁, we have

$$\frac{\partial \tilde{S}\left(t\right)}{\partial {\gamma }_1}{\mid }_{t={\tilde{T}}_w}-\tilde{f}\left({\tilde{T}}_w\right)\frac{\partial {\tilde{T}}_w}{\partial {\gamma }_1}=0,$$

where $\tilde{f}$ is the estimated density function of T. Rearranging, we obtain the ISNI for the wth estimated quantile as

$$\text{ISNI}\left({\widehat{T}}_w\right)=\frac{\partial {\tilde{T}}_w}{\partial {\gamma }_1}{\mid }_{{\gamma }_1=0,{\gamma }_0={\widehat{\gamma }}_0}=\frac{\text{ISNI}\left(\widehat{S}\left(t\right)\right)}{\widehat{f}\left(t\right)}{\mid }_{t={\widehat{T}}_w}.$$ (15)