Combining Boundary-Based Methods With Tensor-Based Morphometry in the Measurement of Longitudinal Brain Change

Abstract

Tensor-based morphometry is a powerful tool for automatically computing longitudinal change in brain structure. Because of bias in images and in the algorithm itself, however, a penalty term and inverse consistency are needed to control the over-reporting of nonbiological change. These may force a tradeoff between the intrinsic sensitivity and specificity, potentially leading to an under-reporting of authentic biological change with time. We propose a new method incorporating prior information about tissue boundaries (where biological change is likely to exist) that aims to keep the robustness and specificity contributed by the penalty term and inverse consistency while maintaining localization and sensitivity. Results indicate that this method has improved sensitivity without increased noise. Thus it will have enhanced power to detect differences within normal aging and along the spectrum of cognitive impairment.

I. Introduction

Detecting biological change in longitudinal pairs of magnetic resonance imaging (MRI) brain images is a challenging task. Accurate estimations of change are confounded by many factors. Some factors are inherent in the images themselves such as scanner induced geometric distortion, intensity nonuniformities, and artifacts due to movement. Others are intrinsic to the methods used, such as the inevitable effects of partial volume induced by image realignment, biases inherent in computational algorithms and lack of definitive approaches for modeling biological change. Additionally, the veracity of all methods is difficult to determine due to limitations of current methods for simulating atrophy [1].

A major issue in brain change quantification is whether to model change in terms of strong deformations at region boundaries that attenuate quickly with distance from the boundary [2], or milder deformations that are more evenly distributed throughout the adjacent region [3]-[5]. The former may provide more sensitive and localized measurement, but requires an explicit definition of region boundaries (i.e., edges) and may misrepresent highly localized artifacts (noise) that masquerade in follow-up images as true change. Conversely, the latter approach typically uses a regularization or “penalty” function which counteracts too-abrupt movement, enhancing robustness to noise. The strength of the regularization term is adjusted by a weighting factor, but this does not vary by location (it is not spatially adaptive) and thus the method may be less sensitive to actual subtle, localized changes.

In this paper we will employ the terms sensitivity and specificity in a way consistent with the statistical concepts of binary classification rates, but referring here to tracking differences in serial images that represent real brain changes. An ideal method would possess high sensitivity (i.e., identifying image differences due to actual brain changes), high localization (i.e., representing change in regions conforming to where differences actually occur), and high specificity (i.e., minimizing the effect of image differences due to noise or other artifacts).

The goal of this work is to combine the localization and sensitivity advantages of boundary-based approaches with the specificity of smoother region-based approaches.

We focus on tensor-based morphometry (TBM), a commonly used and evolving technique [5]-[14] that computes a deformation field between a pair of images and then uses the log-Jacobian determinants to map local volume change. TBM starts with vector “force fields” derived from voxel intensity mismatch functions, adds a penalty term to discourage excessive deformation, and solves for velocity “flow fields” which drive the deformation.

Recent work has shown that in addition to noise sensitivity, TBM algorithms also possess an inherent bias that overstates volume change [3]-[5]. This problem is particularly evident when TBM methods are applied to longitudinal images with short intervals between scans, in which no actual brain atrophy should be expected [5]. Log-Jacobian images of such warps should be uniformly close to zero, yet patterns of nonzero volume “changes” typically appear at tissue boundaries and also in homogeneous brain regions. The skewness of the log-Jacobian field distribution was hypothesized to be one reason for this overestimation and a novel method has been developed to counteract its effect [4], [5] by penalizing the Kullback–Liebler divergence [15] of the log-Jacobian determinants from the identity distribution. The effect of an additive Kullback–Liebler penalty term (called R_KL) is to smooth the Jacobian fields, especially in homogeneous brain regions remote from areas of high tissue contrast [16].

A recent debate in the literature [14], [17] has also pointed out that even in the presence of the Kullback–Liebler penalty, significant inherent bias toward indicating nonbiological differences in images remains. This apparent bias, however, can be significantly reduced by imposing inverse consistency [18]—the simultaneous calculation of forward and backward deformations that are constrained to be inverses of one another.

Thus penalty terms and inverse consistency are each indispensible. But in addition to reducing bias, each of these also reduces sensitivity to real differences between successive images. By spreading change over larger areas, the penalty term diminishes localized sensitivity even as it enhances specificity. By reducing magnitudes the inverse-consistency constraint also may contribute to under-reporting of real change. As a result the TBM method may either fail to record change or attribute change too broadly throughout the image, leading to estimates that do not reflect actual differences.

This raises the question whether sensitivity and localization can be maintained without losing specificity. We propose to incorporate a notion of tissue boundary location from an established boundary-based technique [2] into the energy functional for an inverse-consistent TBM, so that deformations near a boundary are allowed to be large while deformations away from boundaries are dampened. Force fields due to mismatch and penalty terms are each locally modified by the likelihood of edge presence. Our hypothesis is that the combination of boundary terms and R_KL penalty will enhance sensitivity and localization while retaining specificity.

This hypothesis is illustrated in Fig. 1, an experiment on change within synthetic images that will be described fully in the data analysis and results sections. The results of this experiment suggest that it is indeed possible to record localized real change while retaining reasonable robustness against noise and algorithm bias.

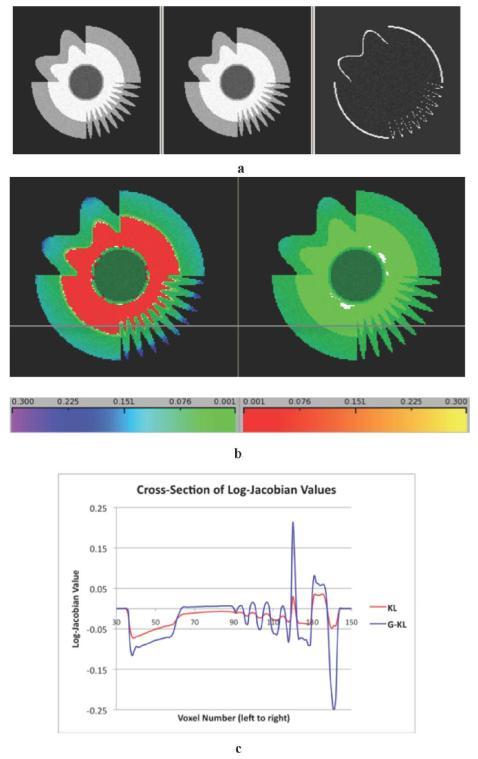
Fig. 1.

(a) Synthetic “longitudinal” image pair in which the second “time point” has cortical atrophy of about 3%. Both synthetic images have additive Gaussian noise with magnitude 4.67% of underlying white matter intensity. The right panel shows the extent of “atrophy.” (b) Comparison of log-Jacobian fields computed by KL (right panel)—incorporating the R_KL penalty term, against our proposed method G-KL (left panel) incorporating R_KL plus prior boundary information. Log-Jacobian values are displayed in translucent color allowing underlying tissue structure to be visible. Same color scales apply to both images. Contractions (“atrophy”) are in cool colors (left color bar) and expansions in warm (right color bar). Jacobian values outside the image have been suppressed. Left panel: G-KL. Right: KL. (c) Cross section of log-Jacobian values along the horizontal line drawn in Fig. 1(b). Intensities for G-KL are in blue, those for KL in red. G-KL shows increased boundary discrimination and increased sensitivity to change over small structures.

To summarize, this paper presents our method for change detection, called G-KL, and compares it to a TBM method having no boundary information (KL). Each method is so named because it incorporates the R_KL penalty term while G-KL also uses additional boundary information. We test the hypothesis that boundary-based information can improve the sensitivity-localization versus specificity tradeoff. We compare estimates of brain change from KL and G-KL with prior estimates from independent methods of automatic brain segmentation and manual delineation. We further compare change detection between KL and G-KL in subjects having normal cognition, mild cognitive impairment and Alzheimer’s disease, using data obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI). Results suggest that our proposed method is able to obtain good specificity while maintaining localization and sensitivity, out-performing the method that uses only the penalty term.

II. Theory—Incorporating Boundary Information Into TBM

A. Problem Formulation

Let Ω be a bounded 3-D image space. T₁ and T₂ are real valued intensity functions on Ω representing our images at time 1 and time 2, respectively. The images T₁ and T₂ have been pre-aligned using an optimized linear transformation. To compute a deformation of T₂ onto T₁ , we compute an inverse-consistent deformation g : Ω → Ω such that for each location x in Ω, T₁(g(x)) should equal T₂(x). The deformed imageis therefore T₁ ° g. Let u(x) be the displacement from a position in the deformed image back to its source in T₂. Then g(x) = x − u(x). Matching T₁ and T₂ means finding an optimal g or equivalently an optimal u for the deformation between the images.

B. Outline of the Standard TBM Algorithm

The usual TBM algorithm optimizes an energy functional E to generate a matching u between the images. E has the format

$$E({\mathrm{T}}_1,{\mathrm{T}}_2,\mathbf{u})=M({\mathrm{T}}_1,{\mathrm{T}}_2,\mathbf{u})+\lambda R\left(\mathbf{u}\right)$$ (1)

where M is an image dissimilarity term and R is a regularizing penalty term, both dependent on the deformation u. Common image dissimilarity metrics are mutual information (MI) [5], [8] or least squares [19]. For our experiment, we use a dissimilarity term consisting of cross-correlation (CC) because this is easy to compute and robust in the presence of noise. It is maximized when the image intensity arrays lie along a regression line [20] and this is appropriate for registering images of the same MRI modality. The adaptation for our G-KL method inserts a voxel-varying weighting factor based on probabilistic estimates of boundary locations into the CC formula, creating a new dissimilarity functional G-CC. These dissimilarity functionals will be fully defined below in (11) and (14). They are integral to the two methods (KL and G-KL) which we will be comparing.

For KL the penalty term will be R_KL and for G-KL we will define a modified term G–R_KL which also makes use of the boundary estimates. We present details below. The parameter λ governs the strength of the penalty term.

The algorithm solves the Euler–Lagrange equation ∂_uE = 0, at least approximately, obtaining a u to optimize E [21]. The variational derivative of the matching term M takes the form

$${\partial }_{\mathbf{u}}M=m({\mathrm{T}}_1,{\mathrm{T}}_2,\mathbf{u})\nabla {\mathbf{T}}_1\left(\mathbf{g}\right(\mathbf{x}\left)\right)$$ (2)

where m is a scalar function and ▽T₁(g(x)) is the intensity gradient of T₁ at the location specified by g(x) (in our implementation T₁ is the target image). The variational derivative of M has an inherent asymmetry because it depends explicitly only on the gradients of T₁. We will explain below how our proposed method partially balances this asymmetry by introducing terms derived from the gradient of T₂. Additionally, inverse consistency restores symmetry in the sense that it solves for deformations in both directions, with each the inverse of the other; the “backward direction” deformation depends on ▽T₂.

The combined variational derivative of E is a force field ∂uE = F₁ + λF₂, with F₁ and F₂ being the variational derivatives of the matching term and penalty term, respectively. F₁ is a force generated by intensity mismatch of the two images at each voxel, driving the solution toward image matching. F₂ is a force driving the solution to reduce the penalty term.

1) The Fluid Flow Method

Instead of solving the Euler–Lagrange equation by gradient descent, fluid flow methods [5], [6], [8] solve for the flow velocity field v, then use it to update the deformation u iteratively over small time interval increments via Euler integration

$$\mathbf{u}(\mathbf{x},\mathrm{t}+\Delta \mathrm{t})=\mathbf{u}(\mathbf{x},\mathrm{t})+(\mathbf{v}-\mathbf{v}\cdot \nabla \mathbf{u})\Delta \mathrm{t}.$$ (3)

This formula is based on a discrete approximation to the total time derivative of u [6]. The size of the time increment Δt is often varied so that a maximal u displacement is not exceeded at each iteration [5], [8].

The velocity v is derived in [6] by using successive over-relaxation (SOR) to solve the Navier–Stokes partial differential equation

$$\mu {\nabla }^2\mathbf{v}+(\mu +\nu )\nabla (\nabla \cdot \mathbf{v})=-\mathbf{F}(\mathbf{x},\mathbf{u}).$$ (4)

Citing the computational complexity of the Navier–Stokes equation, other authors [5], [8] prefer obtaining v as a convolution of the force term by a Gaussian

$$\mathbf{v}=G_{\sigma }\ast \mathbf{F}.$$ (5)

In sum, the fluid flow method consists of iterated steps, each step generating v from the current force field, updating u and checking to see whether a termination condition is satisfied.

2) The Kullback–Liebler Penalty Term

Yanovsky et al. [5] use a fluid-flow implementation in which the matching term is MI, the velocity v is computed by Gaussian convolution, and the penalty term R_KL is based on the Kullback–Liebler divergence metric [15] for the log-Jacobian distributions. R_KL is a measure of the divergence between probability densities P_id and Pg, the identity distribution and log-Jacobian distribution for g, respectively. Since R_KL penalizes deviation from a uniform distribution, it tends to homogenize the Jacobian field in the absence of strong mismatch forces. R_KL is expressed as

$$R_{KL}={\int }_{\Omega }\log \mid \mathrm{D}\mathbf{g}\left(\mathbf{x}\right)\mid d\mathbf{x}.$$ (6)

Thus, the total energy functional has the form

$$E({\mathrm{T}}_1,{\mathrm{T}}_2,\mathbf{u})=M({\mathrm{T}}_1,{\mathrm{T}}_2,\mathbf{u})+\lambda R_{KL}\left(\mathbf{u}\right).$$ (7)

3) Fluid Flow Incorporating Boundary Information

In this study, the “baseline” (KL) method has the R_KL penalty term, uses CC for its matching function, and computes the velocity v using SOR to solve the Navier–Stokes PDE. Our proposed method G-KL is the same as KL except that its energy functional incorporates spatially varying a priori estimates for the likelihood of tissue edge presence at each location x, based on intensity gradient magnitudes. Because T₂ does not move while T₁ is iteratively pulled toward it by g, we use T₂ to generate these estimates. To assess edge likelihood, we create a probabilistic map of edge locations in T₂ from the cumulative distribution function (CDF) of slightly smoothed T₂ intensity gradient magnitudes. The function GradCDF(x) is defined as the percentile of the gradient magnitude of T₂ at location x in this CDF. High values, close to 1, occur at locations of strong gradients and almost always at edges. The GradCDF image appears very similar to an intensity gradient magnitude image, but the values between 0 and 1 indicate probabilities of edge proximity rather than the actual magnitude of the intensity gradient.

The respective forces for KL and G-KL are defined here and summarized in Table I. Define

$$\begin{array}{cc}\hfill F_1=& {\partial }_{\mathbf{u}}CC({\mathrm{T}}_1,{\mathrm{T}}_2,\mathbf{u})\hfill \\ \hfill F_2=& {\partial }_{\mathbf{u}}{R}_{KL}\left(\mathbf{u}\right)\hfill \end{array}$$ (8)

to be the mismatch and penalty forces in the KL implementation. The formula for F₂ is provided in [5].

TABLE I.

Summary of Force Adjustments for Various Methods

Method	Description	Mismatch Force	Penalty Force
NF	No corrections	F1, = ∂uCC(T1,T2,u)	0
KL	Kullback-Leibler penalty	F1, = ∂uCC(T1,T2,u)	F2 = ∂u Rkl(u)
G-KL	Gradient correction to both F1, and KL penalty	GF1 = ∂uG-CC(T1,T2,u)	GF2 = ∂uG-Rkl = (l-GradCDF)F2

To derive corresponding forces fields for G-KL, we will define energy functionals G-CC and G–R_KL which contain the GradCDF multipliers at appropriate positions as voxel-based weighting terms. Then the corresponding forces will be

$$\begin{array}{cc}\hfill {\mathrm{GF}}_1=& {\partial }_{\mathbf{u}}G-CC({\mathrm{T}}_1,{\mathrm{T}}_2,\mathbf{u})\hfill \\ \hfill {\mathrm{GF}}_2=& {\partial }_{\mathbf{u}}G-R_{KL}\left(\mathbf{u}\right).\hfill \end{array}$$ (9)

a) Derivation of Mismatch Forces for KL and G-KL

For simplicity of computation we internally set the means of T₁ and T₂ to zero before starting the solution. Since the working version of T₁ changes as it is iteratively pulled toward T₂, its mean intensity also changes at each iteration, but in practice these deviations from zero are small (on the order of 1% of the maximum intensity at most) and are ignored. Then the formulas for CC and G-CC can be expressed as follows.

Define

$$\begin{array}{cc}\hfill {\mathrm{v}}_{12}=& {\int }_{\Omega }{\mathrm{T}}_1\left(\mathbf{g}\right(\mathbf{x}\left)\right){\mathrm{T}}_2\left(\mathbf{x}\right)d\mathbf{x}\left({\mathrm{covariance}\mathrm{of}T}_1\text{and}{\mathrm{T}}_2\mathrm{intensities}\right)\hfill \\ \hfill {\mathrm{v}}_1=& {\int }_{\Omega }{\mathrm{T}}_1^2\left(\mathbf{g}\right(\mathbf{x}\left)\right)d\mathbf{x}\left(\mathrm{variance}\text{of}{\mathrm{T}}_1\right)\hfill \\ \hfill {\mathrm{v}}_2=& {\int }_{\Omega }{\mathrm{T}}_2^2\left(\mathbf{x}\right)d\mathrm{x}\left(\mathrm{variance}\text{of}{\mathrm{T}}_2\right).\hfill \end{array}$$ (10)

Then

$$CC={\mathrm{v}}_{12}^2∕\left({\mathrm{v}}_1{\mathrm{v}}_2\right).$$ (11)

Using the rules for variational derivatives [21] which in this situation parallel the usual quotient, product and chain rules

$$\begin{array}{cc}\hfill {\partial }_{\mathbf{u}}\mathrm{CC}=& (2{\mathrm{v}}_1{\mathrm{v}}_2{\mathrm{v}}_{12}{\partial }_{\mathbf{u}}{\mathrm{v}}_{12}-{\mathrm{v}}_{12}^2{\mathrm{v}}_2{\partial }_{\mathbf{u}}{\mathrm{v}}_1)∕{\left({\mathrm{v}}_1{\mathrm{v}}_2\right)}^2\hfill \\ \hfill =& 2\left({\mathrm{T}}_2\right(\mathbf{x}){\mathrm{v}}_1{\mathrm{v}}_2{\mathrm{v}}_{12}-{\mathrm{T}}_1(\mathrm{g}\left(\mathbf{x}\right)\left){\mathrm{v}}_{12}^2{\mathrm{v}}_2\right)∕{\left({\mathrm{v}}_1{\mathrm{v}}_2\right)}^2\times \nabla T_1\left(\mathbf{g}\right(\mathbf{x}\left)\right).\hfill \end{array}$$ (12)

This gives the mismatch force for KL. Now define G-CC as follows, using similar notation as for CC but with modified formulas:

$$\begin{array}{cc}\hfill {\mathrm{gv}}_{12}=& {\int }_{\Omega }\mathrm{GradCDF}\left(\mathbf{x}\right){\mathrm{T}}_1\left(\mathbf{g}\right(\mathbf{x}\left)\right){\mathrm{T}}_2\left(\mathbf{x}\right)d\mathbf{x}\left(\text{weighted}{\mathrm{covariance}\mathrm{of}T}_1\text{and}{\mathrm{T}}_2\right)\hfill \\ \hfill {\mathrm{gv}}_1=& {\int }_{\Omega }\mathrm{GradCDF}\left(\mathbf{x}\right){\mathrm{T}}_1^2\left(\mathbf{g}\right(\mathbf{x}\left)\right)d\mathbf{x}\left(\text{weighted}\mathrm{variance}\text{of}{\mathrm{T}}_1\right)\hfill \\ \hfill {\mathrm{gv}}_2=& {\int }_{\Omega }{\mathrm{T}}_2^2\left(\mathbf{x}\right)d\mathbf{x}\left(\mathrm{variance}\text{of}{\mathrm{T}}_2\right).\hfill \end{array}$$ (13)

Then

$$\mathrm{G}-\mathrm{CC}={\mathrm{gv}}_{12}^2∕\left({\mathrm{gv}}_1{\mathrm{gv}}_2\right).$$ (14)

Since GradCDF(x) is derived solely from T₂ and is therefore constant with respect to g, the variational derivatives become

$$\begin{array}{cc}\hfill {\partial }_{\mathbf{u}}\mathrm{G}-\mathrm{CC}=& (2{\mathrm{gv}}_1{\mathrm{gv}}_2{\mathrm{gv}}_{12}{\partial }_{\mathbf{u}}{\mathrm{gv}}_{12}-{\mathrm{gv}}_{12}^2{\mathrm{gv}}_2{\partial }_{\mathbf{u}}{\mathrm{gv}}_1)∕{\left({\mathrm{gv}}_1{\mathrm{gv}}_2\right)}^2\hfill \\ \hfill =& 2\mathrm{GradCDF}\left(\mathbf{x}\right)\left({\mathrm{T}}_2\right(\mathbf{x}){\mathrm{gv}}_1{\mathrm{gv}}_2{\mathrm{gv}}_{12}-{\mathrm{T}}_1(\mathrm{g}\left(\mathbf{x}\right)\left){\mathrm{gv}}_{12}^2{\mathrm{gv}}_2\right)∕{\left({\mathrm{gv}}_1{\mathrm{gv}}_2\right)}^2\nabla T_1\left(\mathbf{g}\right(\mathbf{x}\left)\right).\hfill \end{array}$$ (15)

Thus, formally ∂_uG–CC resembles “GradCDF(x) times ∂_uCC” but the correspondence is not exact because the constants gv₁₂ and gv₁ are not equal to their counterparts v₁₂ and v₁. Nonetheless the resemblance is instructive because it shows that the mismatch force magnitudes are explicitly modulated by GradCDF.

b) Derivation of Penalty Forces

The derivation of the penalty forces for G–R_KL is simpler. We define

$$\mathrm{G}-R_{KL}={\int }_{\Omega }(1-\mathrm{GradCDF}(\mathbf{x}\left)\right)\log \mid \mathrm{D}\mathbf{g}\left(\mathbf{x}\right)\mid d\mathbf{x}.$$ (16)

Then as with the mismatch forces, since GradCDF is independent of g

$$\begin{array}{cc}\hfill {\partial }_{\mathbf{u}}\mathrm{G}-R_{KL}=& (1-\mathrm{GradCDF}(\mathbf{x}\left)\right){\partial }_{\mathbf{u}}{\int }_{\Omega }\log \mid \mathrm{D}\mathbf{g}\left(\mathbf{x}\right)\mid d\mathbf{x}\hfill \\ \hfill =& (1-\mathrm{GradCDF}(\mathbf{x}\left)\right){\partial }_{\mathbf{u}}{R}_{KL}\left(\mathbf{u}\right)\hfill \end{array}$$ (17)

in other words

$${\mathrm{GF}}_2=(1-\mathrm{GradCDF}(\mathbf{x}\left)\right){\mathbf{F}}_2$$ (18)

where, as above, F₂ is the penalty force vector field for KL.

In G-KL the multiplier functions GradCDF and 1 – GradCDF guide the warp using anatomical knowledge of T₂, based on the following considerations. Mismatch forces F₁ occurring at or near tissue boundaries are more likely to represent real biological change [2] and should be preserved. On the other hand, F₁ forces at a distance from edges are more probably due to noise and should be attenuated. The formula of GF₁ at each voxel accomplishes both these aims since GradCDF will be close to 1.0 near edges and lower away from them. Likewise the penalty force should be dampened near edges while allowing its full effect away from them, and this is accomplished by (1 − GradCDF)F₂.

We note that G-KL partially redresses the asymmetry of the original Euler–Lagrange equation resulting from the presence of only T₁ gradients. Gradient-derived information from both of the images, i.e., ▽T₁(g(x)) from T₁ and GradCDF(x) from T₂, is now present in G-KL, although they are not in the same form. Rather than being an actual gradient, GradCDF is a scalar multiplier related to the boundary mask concept described by Freeborough and Fox. [2].

4) Inverse Consistency

We have implemented inverse-consistency based on work by Leow et al. [22] and summarized in [14]. We present a brief outline here and refer the reader to these references for a fuller explanation. Let g and h be deformations in the forward and backward directions, respectively, with corresponding displacement fields u and w.

We optimize the energy functional

$$\begin{array}{cc}\hfill E({\mathrm{T}}_1,{\mathrm{T}}_2)=& E_F({\mathrm{T}}_1,{\mathrm{T}}_2,\mathbf{u})+E_B({\mathrm{T}}_2,{\mathrm{T}}_1,\mathbf{w})\hfill \\ \hfill =& M_F({\mathrm{T}}_1,{\mathrm{T}}_2,\mathbf{u})+\lambda R\left(\mathbf{u}\right)+M_B({\mathrm{T}}_2,{\mathrm{T}}_1,\mathbf{w})+\lambda R\left(\mathbf{w}\right).\hfill \end{array}$$ (19)

The subscripts “F” and “B” refer to the forward and backward directions. In this setting M_F and M_B are formally the same but the roles of T₁ and T₂ are opposite, and M_F depends on u while M_B depends on w.

The algorithm calculates g and h concurrently, imposing the constraint that at each iteration the composition of the current g and h, incorporating the updates being computed at this iteration, must to second order equal the identity function [14].

The derivatives ∂_uE and ∂_wE are each a sum of two variational terms because of the summation E_F of and E_B. Updates to the forward deformation g come from solutions to the Navier–Stokes equation (4) for ∂_uE = ∂_uE_F = ∂_uE_F + ∂_uE_B, while updates to h come from solutions for ∂_wE. It is straightforward to compute ∂_uE_F and ∂_wE_B, as described above in (12) or (14), but the dependences of E_F and E_B on their “opposite” deformations are not explicitly known, so the derivatives ∂_wE_F and ∂_uE_B are inferred by imposing the identity constraint mentioned above. The result of this constraint is a pair of linear equations involving the Jacobians Dg and Dg⁻¹, by which we solve for ∂_wE_F and ∂_uE_B in terms of the already computed ∂_uE_F and ∂_wE_B [22]. This avoids the necessity of actually inverting g and provides the updates for both g and h at the current iteration.

For inverse-consistent versions of our two methods, we use M_F = M_B = CC and R = R_KL for KL, with M_F = M_B = G–CC and R = G–R_KL for for G-KL.

5) Summary

In summary, we compare our method G-KL that involves gradient information from both images against a baseline method KL that is identical except for lacking the T₂-based GradCDF factors. These estimators are built into the energy potential of G-KL, producing local attenuation of mismatch or penalty forces, depending on the estimation of edge likelihood.

III. Data Analysis

A. Change in Synthetic Images

Our first experiment used synthetically generated images with simple tissue structure (simulated gray, white and CSF) and fine detail cortical “gyri” to illustrate the performance of our TBM methods with and without tissue boundary information (G-KL and KL, respectively). These are designed to simulate gray matter “atrophy” in serial images where ground truth is known so that performance can be accurately evaluated. Each image includes additive gaussian noise having magnitude 4.67% of white tissue intensity. Fig. 1(a) shows “baseline” (left panel), “time 1” (middle), and the difference (right) depicting about 3% volume loss in the outer gray matter rim.

B. Longitudinal Image Data

Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (www.loni.ucla.edu/ADNI). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies, and nonprofit organizations, as a $60 million, five-year public-private partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 adults, ages 55–90, to participate in the research—approximately 200 cognitively normal older individuals to be followed for three years, 400 people with MCI to be followed for three years, and 200 people with early AD to be followed for two years.

We tested each of our TBM algorithms in several warping experiments. All ADNI images were subjected to a correction protocol described by Jack et al. [11]. This included 1) the Grad-Warp correction procedure for gradient nonlinearity [23], 2) a “B1-correction” adjusting for intensity inhomogeneities due to B1 nonuniformities [11], 3) “N3” bias field correction [24], and 4) geometric scale adjustment using a phantom scan acquired with each image [11].

We used two sets of data in our experiments. The first consisted of a developmental data set with a “no-change” group of 12 subjects having two scans made on the same day, and a second “change” group of 20 subjects diagnosed with Alzheimer’s disease having scans approximately one year apart. Demographic characteristics of the “change” subjects are shown in Table II(a). The developmental dataset tested our fundamental hypothesis that G-K reduces noise and bias almost as much as KL for images in which no biological change is expected.

TABLE II.

(a)Demographic Characteristics of the Development Group “Change”Subjects. All Are AD Subjects With Two Scan Dates One Year Apart, (b) Demographic Characteristics of the Validation Group Subjects

	AD
No (F/M)	20(8/12)
Age, y	78.2 ± 6.0
Educ	14.3 ± 2.6
MMSE	21.3 ± 4.4

	CN	MCI	AD
No (F/M)	106 (52/54)	93 (34/59)	65 (31/34)
Age, y	75.7 ± 5.4	73.4 ± 7.2	75.8 ± 7.6
Educ	15.8 ± 2.7	15.6 ± 3.1	14.9 ± 3.2
ApoE4%	32	51	74
MMSE	29.2 ±0.8	27.0 ± 1.7	23.2 ± 1.8
ADAS- Cog	5.8 ± 2.9	11.3 ± 4.9	18.4 ± 5.6

The second group was a validation dataset. It consisted of a larger number of subjects having repeated imaging separated by one year with varied degrees of cognitive ability at baseline. This dataset included 106 normal (CN), 65 AD, and 93 mild cognitive impairment (MCI) subjects. The subjects of the validation dataset did not overlap with any of the AD subjects in the developmental data set. Among the validation dataset, CSF measures of beta-amyloid were available for four CN, 48 AD, and 93 MCI, and we used these to test voxel-wise correlations of log-Jacobians with levels of beta-amyloid. Finally, we also used a subset of 50 AD, 38 MCI, and 37 normals to measure cumulative longitudinal changes over time intervals of six, 12, and 24 months. Demographic characteristics of the validation group are shown in Table II(b).

C. Statistical Analyses

1) Group Comparisons

All group analyses were based upon log-Jacobian images of the deformations. Group analyses required a deformation of all subjects onto a “minimal deformation template” (MDT) constructed to be minimally distant from images in the group [25]. We used an MDT made from 29 clinically normal individuals 60 years of age or older. Each subject T₂ image (on which the Jacobian change maps were computed) was warped to the MDT using a cubic B-spline warp [26], [27]. Such a warp is standard procedure in cross-sectional image registration, where a more powerful large-deformation warp like fluid-flow would inappropriately crush together structures in regions of topological mismatch with the template. The native Jacobian determinant change maps were then deformed into MDT space to facilitate group analysis.

2) Comparison of Methods on No-Change Images

In order to compare the performance of KL and G-KL on our dataset of no-change images we compared distributions of log-Jacobian values between KL, G-KL, and an inverse-consistent TBM algorithm without penalty term (called NF for “no filter”).

3) Significance Testing of Voxel Log-Jacobian Values

To assess locations of significant change in the log-Jacobian images in template space, we performed permutation testing for correction of multiple comparisons [28]. There were several contexts in which we used this technique. We used permutation testing on the log-Jacobian values to compute significant change within a group, to find group-difference t-values for the log-Jacobians in order to compute areas of significant differences between diagnostic groups, and finally to test for significant regression associations between log-Jacobians and metadata such as MMSE or CSF amyloid-beta. We used permutation testing for voxel-wise significance of Jacobian values as well as size significance for contiguous clusters of Jacobian values above or below a preassigned threshold. In all our tests we performed 10 000 permutations.

4) Statistical ROIs and Power Analysis

We use statistically defined ROIs [29], [30] as another measure of statistical power. The statistically defined ROI (statROI) is intended to focus measurements to a brain region most strongly associated with change in a given method [29], and therefore statROIs differ for each method. We defined our statROI for each method following Hua et al. [30] using voxel-wise t-values for the log-Jacobians

$$\mathrm{t}\left(\mathbf{x}\right)=\surd \mathrm{n}{\mu }_{\log J}\left(\mathbf{x}\right)∕{\sigma }_{\log J}\left(\mathbf{x}\right)$$ (20)

where μ_logJ(x) and σ_logJ(x) are the mean and variance, respectively, over all subject log-Jacobian values at x.

The statROI for a given method consisted of voxels in brain tissue for which the voxel-wise t-probability over the 20 “change” images was p ≤ 0.001 (uncorrected). Thus in each method the statROI represents regions of change strongly recorded by that method for the one-year change images in the developmental dataset.

We used the statROI for each method to perform a power analysis in the validation dataset, distinct from the images on which it was generated. As described in Hua et al. [14], mean change and standard deviation for log-Jacobians over the statROI yield the minimum sample size needed to detect 25% change with 80% power at α = 5% significance level, according to the formula

$$n80=\frac{2{\sigma }^2{(z_{1-\alpha ∕2}+z_{\text{power}})}^2}{{\left(0.25\mu \right)}^2}.$$ (21)

Here the z_b variables refer to thresholds in the standard normal distribution such that P[Z < z_b] = b; μ is the log-Jacobian mean over the statROI and σ is its standard deviation. We have implemented this formula slightly differently, however, following recommendations of Holland et al. [31] to use change differences between the target group and normal subjects, rather than total mean change in a group. The concept is that of measuring reduction in potentially treatable effects, i.e., effects due to pathology beyond those of normal aging. Thus, for the AD group as an example, our μ is the log-Jacobian mean of that group minus the corresponding mean of the normal group over the statROI for a given method. These are termed age corrected rates by Holland et al. [31].

5) Bias Toward Nonzero Intercept for Change in Multiple Time Points

Thompson and Holland pointed out [17] that algorithmic bias can exist in which change appears proportionally higher over a smaller time interval than over a larger interval that includes it, such as baseline to six months as compared with baseline to one year. This manifests as a nonzero intercept for a line fitted to change estimates over two or more time points. Inverse-consistency largely corrects this bias, as reported in [14]. We tested G-KL and KL by computing change over statROIs for each method in populations of AD, MCI and Normals at six, 12, and 24 months, comparing the sizes of their nonzero intercepts to those reported for the inverse-consistent methods in [14].

6) Correlation of Change With Cognitive or Clinical Data

We examined voxel level and statistical ROI correlations with clinical data as a heuristic assessment of the biological relevance for our method. We performed voxel-based regressions of log-Jacobians with cognitive data (MMSE one-year change) and clinical biomarkers (CSF beta-amyloid). At each voxel we set up a regression model involving the log-Jacobian values for subjects in a group and their corresponding clinical data. We measured the significance of the associations using permutation tests as described above. In addition, we analyzed associations for the mean Jacobian of each method statROI on a variety of clinical tests including longitudinal differences in cognitive performance.

7) Diagnostic Group Difference Testing

A final statistical test measured the ability of log-Jacobians to distinguish clinical diagnostic groups. For a given method we compute the t-value of log-Jacobian difference at each voxel for two clinical groups (for example AD minus CN). We use permutation tests to evaluate the null hypothesis of no difference by randomly varying the assignments to the two groups. We also assessed the ability of each method to detect group differences using average Jacobians from their respective statROIs. Differences in the methods were further assessed by their ability to discriminate MCI subjects who converted to dementia from nonconverters.

IV. Results

In this section, we present the results of several experiments testing the properties of G-KL in comparison to KL. The value of λ= 4 used in both G-KL and KL was determined heuristically by looking at the quality of image detail in no-change and change images (Fig. 2(b) and Fig. 3). Higher values of λ suppress noise better in the no-change images, but also reduce sensitivity and localization in the change images. We determined that this value was a reasonable compromise for both methods.

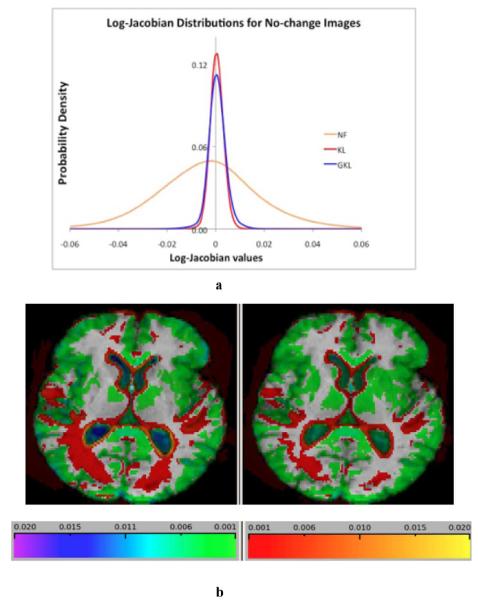
Fig. 2.

(a) Intensity PDF for log-Jacobians corresponding G-KL (blue), KL (red), and TBM (“NF” or no filter) having no penalty corrections (orange). G-KL and KL are symmetric about y-axis with G-KL showing slightly greater variance than KL. NF is very wide and asymmetric to the left, demonstrating the inherent bias in the uncorrected log-Jacobians as explained in the text. (b) Average log-Jacobian values for each method displayed in cool colors for contractions and warm colors for expansions. Most values are low in magnitude (in the range of 0.001–0.005 magnitude; 0.1%–0.5% change), but are higher at the edges for G-KL as would be expected through reduction of R_KL penalty at tissue boundaries. Left panel: G-KL. Right: KL.

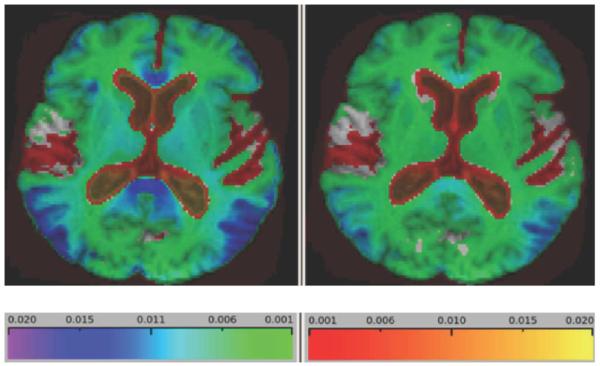
Fig. 3.

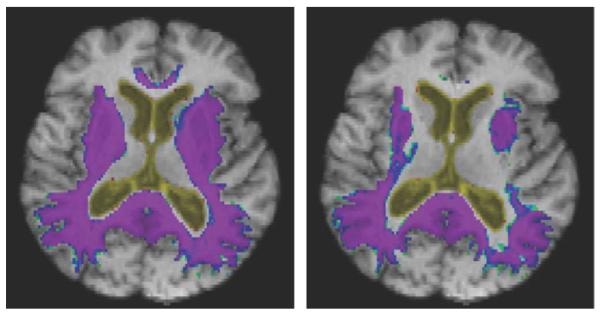
Average log-Jacobian values over 20 one-year AD “change” images. This figure shows that increased magnitude of brain change as evidenced by higher Jacobian values, particularly in the posterior temporal lobes, genu, splenium, as well as broader lower-level changes in subcortically. Left panel: G-KL. Right: KL.

Experimental results can be summarized as follows: A) synthetic image changes; B) bias and noise evaluation in no-change images; C) estimates of change in 20 one-year AD images, including generation of statROIs for each method; D) bias analysis of nonzero intercepts from trajectories of change over three time points; E) minimum sample size computations (power analysis) for each method; F) validation of reported change in the full ADNI data set of 106 normal, 93 MCI, and 86 AD subjects, by comparison of each method with applicable results in the literature.

A. Synthetic Image Changes

Fig. 1 illustrates our experiment with synthetic longitudinal images. Fig. 1(a) shows the image pair including a profile of “loss” at “time 2.” Fig. 1(b) shows the log-Jacobians of G-KL compared with those using KL. Fig. 1(c) provides a log-Jacobian intensity cross section for each method, graphing the relative sensitivities to longitudinal change. These figures illustrate the greater localization of change inherent in G-KL. Table I gives log-Jacobian estimates of tissue change for these synthetic images compared to the ground truth values. The G-KL method captures almost all the actual change in the “cortical gray” layer as compared to KL, which records about half the change. G-KL also more accurately estimates the zero change in white matter, while overstating the zero change in CSF by about 0.1%.

Fig. 1 and Table III illustrate the interaction of the R_KL and boundary information terms. The R_KL term alone (KL method, Fig. 1(b), right panel) smoothes the Jacobian images and spreads out estimated change, even across tissue boundaries as seen in the consistent green colorization over the image. This indicates diffuse contraction throughout the image, not only over the gray layer where the actual atrophy occurs. And it leads to an overestimate of losses in the neighboring white matter. In contrast, the boundary information interacting with R_KL (G-KL, left panel) retains smoothness within tissue layers but prevents contraction from crossing tissue boundaries, as evidenced by the blue-green coloration restricted to the outer gray only. Localized areas of large change in the gyral “fingers” are more faithfully rendered by G-KL while the overall estimate of gray matter loss (Table I) is very close to ground truth. White matter change (which should be zero) is also more accurately captured by G-KL because contraction from the gray atrophy has not “bled” across into the white. There is, however, a small price to pay using the G-KL approach. By containing the smoothed change within tissue boundaries, the boundary information induces a sign change across tissues in which no actual change occurred. In the current example, this produces less of an error in the white matter than the residual smoothness from the KL method, but it contributes to a slightly worse estimate in the central CSF.

TABLE III.

Ground Truth Tissue Change Values for Synthetic Images Compared to G-KL and KL Estimates. For Each Tissue, the Most Accurate Jacobian Estimates of Actual Change Are in Bold

Method	CSF (% change)	Gray (% change)	White (% change)
Ground Truth	0	−12.52	0
G-KL	−1.06	−10.79	+0.19
KL	−0.19	−6.88	−0.34

B. Assessments of Bias in G-KL Compared to KL on No-Change Images

Fig. 2 summarizes voxel patterns of KL and G-KL for the twelve subjects in the no-change dataset. Fig. 2(a) shows histograms of log-Jacobian values over the average Jacobian images for KL, G-KL and also, for comparison, fluid flow having no penalty correction (NF). The histogram of NF is left-skewed while those for KL and G-KL are more symmetric, with peaks close to zero. The leftward skew of NF results from the non-negativity of the Kullback–Liebler divergence metric (KLDiv). As shown in [3], the integral of the log-Jacobian is the negative Kullback–Liebler divergence [15] between the probability density functions of the identity distribution and the Jacobian field of the deformation, and hence is nonpositive

$$\underset{\Omega }{\int }\log \left(J\right(x\left)\right)dx=-\mathrm{KLDiv}(pd{f}_{id},pd{f}_J)\le 0.$$ (22)

Here, the nonpositive inequality on the right follows from Gibbs’ Inequality, which has a corollary that KLDiv(pdf_id, pdf_j) = 0 if and only if J(x) = 1 at all voxels [15]. This implies that any uncorrected nonconstant Jacobian field will necessarily be negatively skewed. The R_KL penalty term is designed to correct this skew [3], [5]. The zero peaks for both KL and G-KL in Fig. 2(a) suggest that the correction is effective and is not weakened by the presence of boundary terms in G-KL. Thus G-KL and KL are equally free from the bias expressed by (22).

Regarding noise suppression, the histogram for G-KL is slightly wider than KL, for values above about 0.01. The images of log-Jacobians in Fig. 2(b) show the occurrence of higher edge values in G-KL, principally at ventricle boundaries. Magnitudes there are 0.01–0.02. Similarly, higher negative values occur in the ventricles in reaction to the higher expansions at the edges. These each account for the slightly wider right and left tails of the G-KL histogram. In sum, the histograms of KL and G-KL are similar, though G-KL has a slightly wider distribution. Both are considerably narrower than the histogram of the uncorrected TBM, suggesting that G-KL achieves almost as much noise reduction as KL on this dataset.

From Fig. 2(a) and (b) we conclude that on no-change images G-KL and KL have comparable lack of bias as in (24) and comparable reduction of Jacobian magnitudes except near edges and inside ventricles. We address the source of these differences and possible future solutions in the discussion section.

C. Estimates of Change in 20 One-Year AD Images. Creation of StatROIs

Fig. 3 shows patterns of log-Jacobian change in the 20 one-year AD subjects. Both methods show extensive cortical and subcortical loss throughout the brain, but G-KL identifies more localized change visible in the splenium, cingulate, and temporal-parietal cortices.

Fig. 4 shows the statROIs constructed as described previously for G-KL and KL. Comparing Figs. 3 and 4, we see that the patterns of heightened cortical and subcortical atrophy in G-KL (Fig. 3) are reflected in the extended areas within the statROIs of G-KL as compared to KL (Fig. 4). These include higher and more extensive Jacobian values in the retrosplenial area, thalamus, basal ganglia and striatum, genu and anterior cingulate, and frontal cortex.

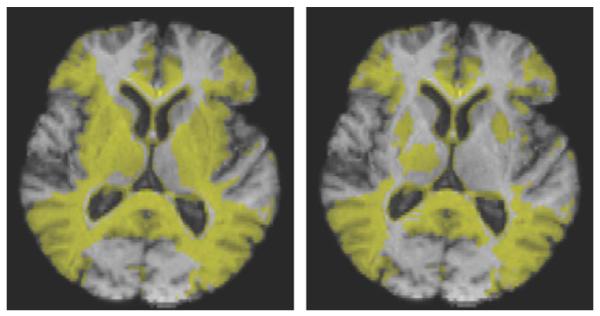
Fig. 4.

StatROIs for G-KL (left panel) and KL (right). Yellow areas show voxels with t-value p < 0.001 (uncorrected). These ROIs differ mainly with G-KL showing more extensive areas of significant change in the striatum and subcortical nuclei.

The results from sections A, B, and Fig. 3 of C suggest that G-KL has increased sensitivity to localized changes while losing only a small amount of specificity, mainly within and at the edges of the ventricles in the no-change images. Because of these results suggesting greater localization for G-KL, it may seem paradoxical that its statROI is more extensive (less localized) than that of KL (Fig. 4). In cortical areas or ventricle edges having tissue boundaries (gray-CSF or gray-white) the statistically significant changes of G-KL are due to stronger log-Jacobian values. We have seen in section A that change values are spread throughout homogeneous areas of the synthetic image by the penalty term, but do not cross strong tissue boundaries. In the brain the periventricular regions are relatively homogeneous and experience this spreading effect. These account for most of the greater extent in the G-KL statROI.

D. Bias Analysis of Nonzero Intercepts From Trajectories of Change Over Three Time Points

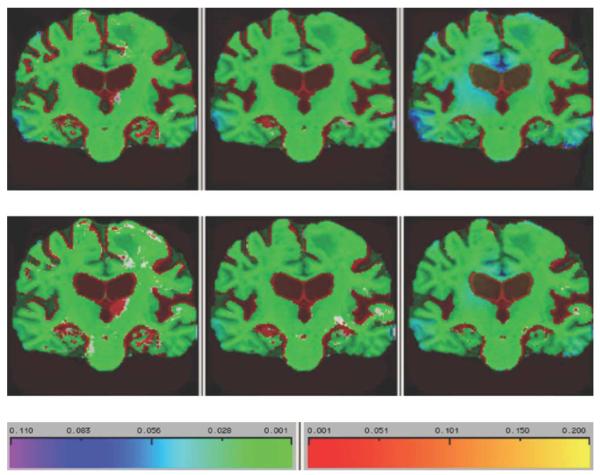
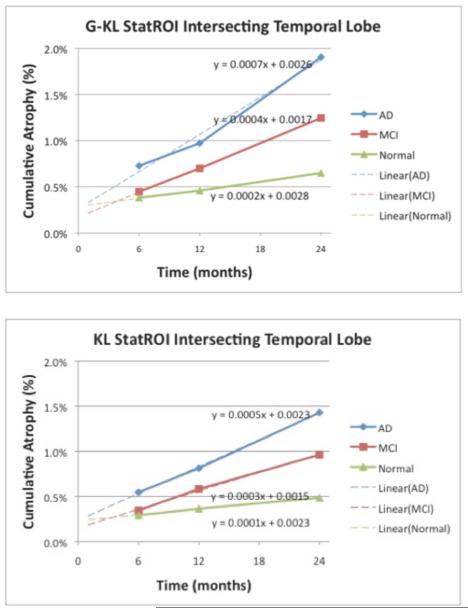
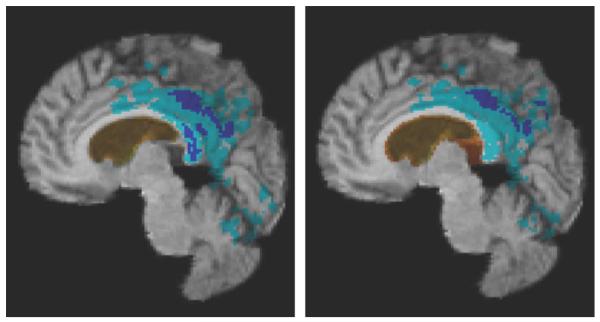
Fig. 5 shows log-Jacobian fields of a single AD subject for each method, over intervals of six, 12, and 24 months. This illustrates the relative ability of each method to record localized changes and increasing atrophy over longer intervals. G-KL displays enhanced ability to depict atrophy in small structures such as temporal and cingulate gyri as well as more broadly in the thalamus. Fig. 6 shows trajectories of change over periods of baseline to six, 12, and 24 months, derived from mean change estimates at each time point in populations of 50 AD, 38 MCI, and 37 normals. Jacobians were averaged over the statROI of each method intersected with the temporal lobe, following the method reported by Hua et al. [14].

Fig. 5.

Single-subject log-Jacobian image of an AD subject over (left to right) 6, 12, and 24 months scan intervals, showing patterns of increasing atrophy. This figure illustrates enhanced ability of G-KL to capture greater differences in regions expected to change with the disease. Top row: G-KL. Bottom row: KL.

Fig. 6.

Change trajectories for each method, computed for three time intervals, averaged over 50 AD, 38 MCI, and 37 normals. Slope and intercept values of fitted trend lines are also displayed. Intercepts of fitted lines of the two methods are similar. Range of intercepts for both methods, from 0.15% to 0.28%, is also similar to the range of intercepts for statROIs reported by Hua et al., [14]. Top panel: G-KL. Bottom: KL.

Trend lines were regressed against the three change values. Fitted lines all have small nonzero intercept values (in the range of 0.1%–0.3%) that are almost identical in each diagnostic group across the methods. The range of these intercepts coincides with that reported in Fig. 5 of Hua et al. [14] and is considerably lower than the corresponding intercepts for noninverse-consistent TBM as reported in [14] and [17]. The trajectories of G-KL have slopes that are consistently higher than their counterparts in KL, but corresponding intercepts are still almost the same in both methods. This suggests that the presence of boundary information in G-KL does not introduce new bias in reporting longitudinal differences.

E. Minimum Sample Size Computations (Power Analysis) for Each Method

Table IV gives n80 minimum sample calculations using (21) for MCI and AD groups by each method over its statROI for six, 12, and 24 month time intervals. Mean changes inserted into (21) are the difference values or age corrected rates described by Holland et al. [31], i.e., mean AD or MCI minus mean normal changes. For each time interval and group, the smaller sample size of the two methods is printed in boldface. We see that G-KL has smaller sample sizes for all times except MCI at 12 months. G-KL shows a marked decrease compared to KL for AD at six months and smaller decreases for AD at 12 and 24 months. Sample sizes for both methods are also comparable or smaller than age corrected sample sizes reported in Holland et al. [31] (Tables II and III).

TABLE IV.

Minimum Size Calculations (Rounded to Nearest Integer) by Method and Diagnostic Group, Using StatROI for Each Method. Group Sizes: MCI (N = 48), AD (N = 61). At Each Time Point and Group, the Smaller of the Minimum Sample Estimates Is in Bold

Method	MCI 6 Months	MCI 12 Months	MCI 24 Months	AD 6	AD 12	AD 24
G-KL	1900	551	279	285	135	104
KL	1959	433	286	356	151	110

F. Validation of Reported Change in Full ADNI Data Set

This section reports outcomes from exploring whether G-KL has increased power for detecting biological results in the full ADNI validation dataset. These experiments are summarized as follows: 1) comparison of change estimates for G-KL and KL with prior published longitudinal results; 2) voxel-based differences of each method between clinical diagnostic groups; 3) differences between clinical groups in the statROIs; 4) voxel-based regressions of log-Jacobians against clinical data.

Demographics of the subjects in the validation group are summarized in Table 2(b). In general, our subset of subjects was similar to published baseline data for the entire ADNI dataset. The age of the MCI group was slightly lower than the CN and AD subjects whereas the AD subjects had substantially less educational achievement. The percentage of ApoE4 genotype carriers in our CN and AD groups were, however, slightly higher than the entire cohort.

1) Comparison of Change Estimates With Prior Results

We computed volumetric change factors for KL and G-KL over a set of brain ROIs representing anatomical structures for which previous longitudinal change values are available. Results are displayed in Table V along with comparable results from other previously published studies. Our goal was to evaluate whether KL and G-KL appear to compute “reasonable” levels of change by reference to what has already been reported.

TABLE V.

ROI Change Values for Normal Subjects (% Change Yearly) for KL and G-KL, Compared to Previously Published Results. Values in First Two Columns Are Derived From Jacobian Values Computed by KL and G-KL. For the Columns Showing Previous Studies, Percent Changes Given Over Period of N Years in the Study Are Converted to Annual Changes by the 1/N Root of the Changes Described in That Study. Boldface Results in the Columns of KL and G-KL Indicate Matches Within 20% of a Previously Published Value

	KL	G-KL	Walhovd 20111	Walhovd 20052	Raz 20103	Raz 20054	Gonoi 20095
Lat Vent	+1.28	+1.86	+1.92	+2.20	--	--	--
CC	−0.03	−0.13	--	--	−0.46	--
Striatum Gray	0.00	−0.04	−0.38	−0.25	−0.42	−0.79	--
Thalamus	−0.11	−0.16	−0.40	−0.38	--	--	--
Frontal G+W	−0.16	−0.24	--	--	--	--	−0.42
Templ G+W	−0.21	−0.29	--	--	--	--	−0.36
Cerebrum Gray	−0.24	−0.35	−0.45	−0.42	--	--	--
Cerebrum White	−0.15	−0.21	−0.35	−0.27	--	--	--
Cerebellum Gray	−0.29	−0.37	−0.31	−0.38	--	--	--
Cerebellum White	−0.25	−0.40	−0.34	−0.36	−0.72	−0.66	--

Notes on individual studies:

¹Values computed from [35] Table 3 giving mean volumes of structures by decade of age. Calculated annualized change from first decade to last, using N = 62 years.

²Values computed from [34] Table 6 that gives adjusted ICV (intra-cranial volume) percent changes from age 20 to 90, N = 70 years.

³Values computed from [33] Table 3 showing longitudinal change (N = 1.25 years) for mean volumes adjusted by ICV. Change is for δ12 only.

⁴Values computed from [32] Table 1 that gave mean volumes at two intervals (N = 5 years).

⁵Values computed from Gonoi et al. [36] using estimated volumes from their Fig. 2 regression plots by gender, right and left side, annualized using N = 55 years, then averaged for an overall value.

Selected ROIs included cerebral gray and white masks, corpus callosum, thalamus, striatum (gray tissue) consisting of caudate, putamen and globus pallidus, lateral ventricles, frontal and temporal lobar regions and cerebellum gray and white masks. For each ROI we obtained the average change over the 106 normal subjects in the validation group. These percentage changes appear in the left-most columns of Table V. We gathered comparable data from other studies. Two studies [32], [33] examined changes in healthy normal subjects using hand-drawn ROIs on native subjects to measure volumes at different times. Three others [34]-[36] also used normal subjects but the ROIs were generated by automatic labeling techniques: the first from the Center for Morphometric Analysis [37], the second by atlas-based template matching, and the third using FreeSurfer (http://surfer.nmr.mgh.harvard.edu). Details of the time intervals and number of subjects for these studies are given in the caption of Table V.

The results show that the volume change percentages for G-KL are consistently larger than those of KL and also appear to be in the same range as many of those from the automatic labeling studies. For lateral ventricles the G-KL value is within 10% of Walhovd et al. [35]. In cerebral and cerebellar gray and white, G-KL is within 10%–20% of the corresponding values in an earlier study [34]. KL is within 10% of cerebellar gray measured by [35]. Frontal and temporal lobar values are larger in G-KL than in KL. The G-KL temporal volume change is within 20% of that in the atlas-based study [36].

In summary, Table V shows that results from G-KL are similar to previously reported findings for change in ventricular CSF, temporal lobe, cerebral gray matter and cerebellar gray and white matter. For each of these regions, G-KL estimates of change were within 20% of previously published values. Conversely, KL meets similar approximation only for change in cerebellar gray matter (Table V, boldfaced values). The table also indicates that both methods tend to under-report changes in subcortical brain structures compared to previous automated or hand-traced measurements, though in these regions G-KL consistently shows greater similarity to the other methods than does KL.

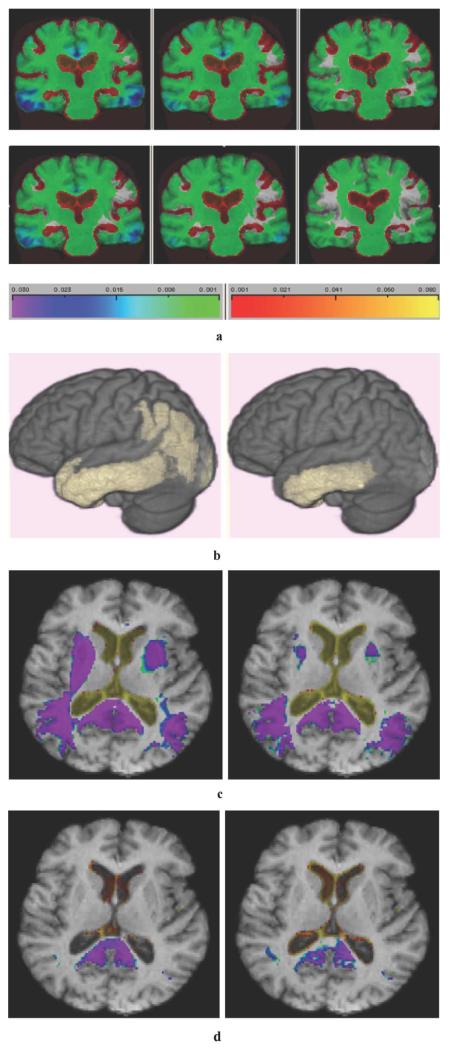
2) Clinical Group Differences in the Validation Dataset

Fig. 7(a) shows average changes over each group by method. Little difference is visible between G-KL (top row) and KL (bottom) for CN (right column) but in MCI and AD, G-KL shows increasingly larger loss estimates in temporal and cingulate regions. Fig. 7(b) depicts contiguous clusters of cortical loss exceeding 1% in AD subjects. Clusters are significant (p < 0.05 for size, corrected by permutation analysis [28]). G-KL (left panel) shows more extensive patterns including parietal loss not recorded in KL.

Fig. 7.

(a) Average patterns of change recorded by method for each diagnostic group, for 65 AD (left panels), 93 MCI (middle), and 106 CN subjects (right). Upper row: G-KL. Lower row: KL. (b) 3-D display of significant cortical atrophy by method over AD group of 65 subjects. Clusters aresignificant by size (p < 0.05, corrected) for log-Jacobian values less than −0.01. Left panel: G-KL. Right: KL. (c) Voxel locations of significant difference between AD and CN. Significant voxel differences (p < 0.05, corrected) for clinical diagnostic groups by method. Warm colors denote positive differences (greater expansion of group 1 compared to group 2); cold colors denote significant contractions. AD or MCI has significantly greater brain loss than CN, signified by cold colors, and greater CSF expansion, signified by warm colors. There were no significant voxel-based differences between AD and MCI. Left panel: G-KL. Right: KL. (d) Voxel locations of significant difference between MCI and CN. Same color scales as Fig. 7(c). Left panel: G-KL. Right: KL.

Fig. 7(c)-(d) shows group difference analyses for KL and G-KL. We generated voxel t-values for the mean log-Jacobian differences between pairs of groups: AD-CN, AD-MCI (not shown), and MCI-CN. We analyzed these t-images for voxel-wise significance (correcting for multiple comparisons using 10 000 permutations).

Fig. 7(c) shows voxel level results for the AD-CN comparison and 7(d) shows results from the MCI-CN comparison. All colored voxels are significant to p < 0.05 (corrected) for voxel t-value. No significant voxel differences were found for AD-MCI.

For the AD-CN comparison, each method shows extensive regions of greater brain tissue loss and CSF space expansion in AD. The G-KL method, however, depicts more extensive and more significant p-values in the striatal and retrosplenial areas. The G-KL also identifies significant differences in the anterior cingulate, not seen with the KL method. For the MCI-CN comparison the G-KL voxel images show greater localized splenium and retrosplenial differences.

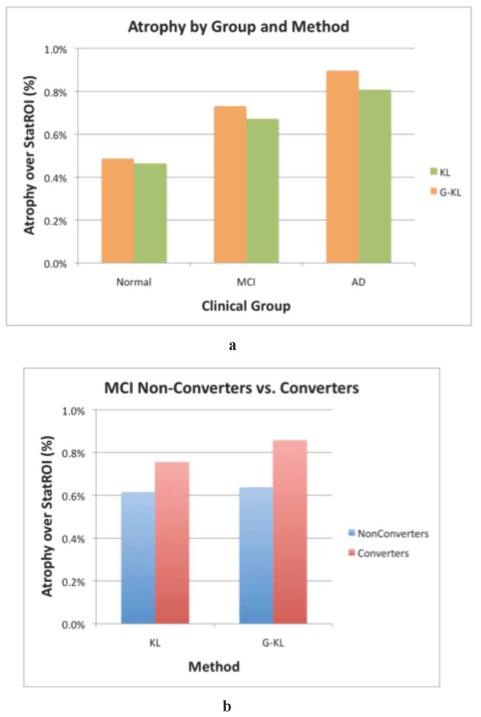
3) Clinical Group Differences in the StatROIs

Fig. 8(a) summarizes the results of diagnostic group analyses by method (G-KL versus KL) showing mean log-Jacobian over the statROI for each method. Using repeated measures MANOVA, there was a significant main effect of clinical group (p < 0.0003) indicating significant differences in volume change according to baseline clinical diagnosis, a significant effect of method (p < 0.0001) indicating that the G-KL method measured greater rates of change on average as compared to the KL method, and a significant interaction of group × method (p < 0.0003) indicating that the differences in method varied by group. Differences in Jacobian estimates between methods varied substantially according to diagnostic category. For example, mean Jacobian difference (G-KL versus KL) was only 5% for cognitively normal individuals, but 9% and 11% for MCI and AD subjects respectively indicating that sensitivity to change increased with degree of expected difference.

Fig. 8.

(a) Mean Jacobian differences according to baseline clinical diagnosis. Using MANOVA, there was a significant main effect of diagnosis and method as well as a significant method by diagnosis interaction (see text for details). Paired t-tests identified significant differences between methods for each diagnostic category. The magnitude of the between-method differences increases with increasing cognitive severity (Normal = 5%, MCI =9% and AD= 11%). (b) Mean Jacobian differences according to conversion status (MCI to AD) among 88 MCI subjects during 24 months of the ADNI study. There was no significant difference by method for Jacobian rate of change measures among the nonconverters. Method related differences, however, were highly significant (p = 0.0004) among those converting to dementia within 24 months.

Recognizing that MCI is a clinically heterogeneous group [38], we performed further analysis to assess group differences in rate of statROI change comparing those who converted to dementia to those who did not over 24 months. Of the 88 MCI subjects included in this study, 38 (43%) converted to dementia over the 24-month period of the ADNI study with an average time of conversion of 19.8 months. Fig. 8(b) summarizes the results of mean Jacobian differences at one year comparing converters to nonconverters for both methods. Using repeated measures MANOVA, there was a significant main effect of conversion status (p < 0.013), a significant effect of method (p < 0.0001) and a significant interaction of conversion status × method (p = 0.015) indicating that converters had significantly greater Jacobian differences in the G-KL method but not with KL. Direct comparison by method also showed that mean Jacobian values in the statROI for converters were significantly different (p = 0.0004) by method type, but a similar comparison of methods for nonconverters was not statistically significant.

4) Regressions of Log-Jacobians Versus Clinical Data

We conducted two sets of regressions for each TBM method. One regression model included one-year change in MMSE as the outcome variable with voxel-wise log-Jacobian as the predictor variable. This regression had 271 subjects. The other regression model examined the outcome of CSF beta-amyloid as predicted by voxel-wise log-Jacobian. This regression had 159 subjects.

a) MMSE One-Year Change Versus Log-Jacobian

Voxel-wise significance results for the MMSE change regressions are shown in Fig. 9. Both algorithms show extensive areas of association between brain tissue loss, ventricle expansion and change in MMSE (all p < 0.05, corrected for voxel-wise multiple comparisons). However, G-KL identified significant associations in anterior cingulate and striatal/putamen regions, not detected by KL.

Fig. 9.

Voxelwise significance images of correlation between one year change in MMSE versus log-Jacobian values. Cool colors (magenta, blue) indicate significant associations (p < 0.05, corrected) between brain atrophy and MMSE. Warm colors (yellows) indicate significant associations (p < 0.001, corrected) of CSF expansion and MMSE. Left panel: G-KL. Right: KL.

b) CSF Beta-Amyloid Versus Log-Jacobian Values

The associations between CSF beta-amyloid and log-Jacobians, shown in Fig. 10, were modest. No significant voxels existed after correction for multiple comparisons; therefore Fig. 10 shows cluster analyses. Both methods show significant clusters (p < 0.05 by cluster size, corrected) posteriorly of relatively weak association (t-thresholds at −3 and −4) between CSF beta-amyloid and brain tissue loss. The principal difference is that G-KL shows stronger associations in the medial retrosplenial area as illustrated in Fig. 10. Both methods also show significant associations of ventricular expansion with lower CSF levels of beta-amyloid.

Fig. 10.

Voxelwise cluster significance images for the association between baseline CSF A-β and log-Jacobian values by method. Individual clusters at thresholds of t = −3 (light blue), t = −4 (dark blue), and t = +4 (orange) are displayed. All clusters are significant to p < 0.05 (corrected). Cool colors indicate association of brain loss with levels of CSF A-β . Warm indicates association of CSF expansion versus CSF A-β . Left panel: G-KL. Right: KL.

5) Clinical Correlations With StatROIs

Table VI summarizes age, education, and gender adjusted associations between cognitive and CSF measures. In general, both methods were highly associated with these various measures.

TABLE VI.

Comparison of Statistical ROI Relations for G-KL Versus KL Methods, Adjusting for Age, Gender, and Education. For Cognitive Measures, the StatROI Was An Independent Variable, Whereas for the CSF Measures, StatROI Was the Dependent Variable

Method	Variable	Beta ± se	T-statistic	p-value
G-KL	MMSE	−348 ± 42	−8.3	<0.0001
	ADAS-Cog	637 ± 95	6.7	<0.0001
	CDR-sum of boxes	150 ± 21	7.0	<0.0001
	Trails B	5343 ± 983	5.4	<0.0001
	Delayed Story	−206 ± 75	−2.7	0.0070
	CSF ABeta	−2.5×10−5 ± 4.0×10−6	−6.3	<0.0001
	CSF Tau	1.2×10−5 ± 5.1×10−6	2.3	0.019
	CSF Tau/ABeta	0.002 ± 0.0005	3.8	0.0002
KL	MMSE	−463 ± 55	−8.4	<0.0001
	ADAS-Cog	876 ± 123	7.1	<0.0001
	CDR-sum of boxes	195 ± 28	7.0	<0.0001
	Trails B	6938 ± 1271	5.5	<0.0001
	Delayed Story	−267 ± 99	−2.7	0.008
	CSF ABeta	−2.0×10−5 ± 3.0×10−6	−6.7	<0.0001
	CSF Tau	8.2×10−6 ± 3.9×10−6	2.1	<0.04
	CSF Tau/ABeta	0.0015 ± 0.0004	3.7	0.0002

V. Discussion

We have described a new inverse-consistent method of brain change detection that combines TBM methods for computing spatially-smooth and specific deformation fields [5] with edge information akin to the boundary mask concept [2] for localizing change to region boundaries.

We hypothesized that this approach would improve the inevitable tradeoff between smoothness and localization. We tested this hypothesis in a pair of synthetic “serial” images for which simulated atrophy of the cortical gray layer was known. Results showed that G-KL had superior sensitivity, localization and specificity when compared to KL. We then compared G-KL and KL on test-retest “no-change” brain images and on images where real change is expected. A perfect algorithm should report zero log-Jacobians on the no-change images, while being sensitive to even small longitudinal differences in images expected to change. We found that the no-change image histograms of G-KL and KL are both narrow and also free of the bias in the Kullback–Liebler divergence inequality (22). We also found that G-KL shows increased sensitivity to change in one-year AD subjects (Fig. 3) by comparison with KL. We next confirmed that there is low bias for both methods in trajectories of cumulative atrophy over six, 12, and 24 month scans. G-KL and KL have comparably low nonzero intercepts for trend lines fitted to these trajectories, and these intercepts are also in the range of previously reported inverse-consistent methods [14]. We also conducted power analyses for log-Jacobian change in each method over groups of MCI and AD subjects, using age-corrected rates of change. G-KL had smaller minimum sample size estimates in all but one case.

These results suggest that adding boundary terms has caused only a slight degradation of performance for G-KL in no-change images while improving its performance in images where change is expected. Nevertheless, comment is required for the better noise suppression of KL at the ventricle edges in the no-change images. This is a direct consequence of attenuating the R_KL penalty term in G-KL at tissue edges. Results from the validation dataset suggest that this may not be a serious issue in images of real change. For example, G-KL shows increased ability to distinguish clinical diagnostic groups, including more subtle expected differences in rates of change for MCI subjects converting to dementia versus those who do not over a two-year interval [Fig. 8(a) and (b)]. As another example, G-KL’s computed rates of volume change over selected brain ROIs are in accord with published results from automated brain segmentation techniques (Table V). The corresponding change rates for KL are consistently lower than G-KL and do not agree as closely with published values. For the ventricles in particular, G-KL’s rates of expansion are in excellent agreement with previously published values, suggesting that edge-based error seen in no-change images has not resulted in over-reporting of real change. These comparisons also indirectly validate the statROI of G-KL. Regions such as the striatum and thalamus fall within the G-KL statROI but not that of KL. And estimated change in these regions is larger for G-KL, therefore closer to published estimates.

The issue of noise at tissue boundaries is important and requires further discussion. By using intensity gradient vector fields as the basis of mismatch force vectors [(12) and (15)], TBM is susceptible to errors at edges where these vectors are large. Interpolation during preprocessing—before TBM is applied—creates intensity discrepancies between longitudinal images, even for same-day scans. This introduces differences at corresponding edges even though no biological change is present. Such differences could possibly be reduced by modifications in our preprocessing pipeline to eliminate asymmetry inherent when one image is aligned onto the other [39]. In any case, future research should be aimed at quantifying likely residual edge-centered errors, so that models might be developed to discount these without also diminishing mismatch forces from differences representing actual brain changes.

In conclusion, our findings suggest that G-KL has benefited from the positive features of both bias-correction and boundary localization while mitigating their limitations. The Kullback–Liebler penalty by itself creates a smooth Jacobian field with reduced sensitivity and localization at edges. The boundary shift approach requires careful user-delineated brain masks in order to correctly locate edges and computes brain volume change only within the edge masks. G-KL, combining these approaches, is by contrast completely automatic and regains edge sensitivity without loss of much specificity.

Our derivation has indicated how a family of energy functionals may be constructed by incorporating prior image information. The functional G-CC in the G-KL method is one example. Future research will explore how functionals such as this—using improved edge detection or other information together with models of spurious change—may restore even more sensitivity without losing specificity.