The ingenious Mr Hughes: Combining forced, flat, and reverse perspective all in one art piece to pit objects against surfaces

Abstract

The artist Patrick Hughes has ingeniously painted rows of stacked Brillo boxes in Forced into Reverse Perspective. The geometry is in reverse perspective, predicting only one type of illusory motion for each planar surface for moving viewers. He “broke” these surfaces into objects by painting the boxes in three types of perspective (planar, forced, and reverse). Our experiments confirmed that he succeeded in eliciting different types of illusory motion, including “differential motion” between boxes for most viewers. In some sense, this illustrates the superiority of secondary (painted) over primary (physical) cues.

In 1964, Patrick Hughes introduced the idea of reverse perspectives, or “reverspectives” (Slyce 1998; Wade and Hughes 1999). Reverspectives are 3D paintings, comprising prisms (and/or truncated pyramids) protruding from the wall with apices closer to the observer. They are cleverly painted with linear perspective so that physically nearer features appear to be farther away than the base, provided that viewers are at an adequately large distance. As a result of the construction and the painted scene, reverspectives appear in reverse depth. In contrast, “proper (forced) perspectives,” typically used in theater stages, are constructed so that far surfaces are smaller than their near counterparts. Finally, linear perspective is used mostly on conventional flat paintings (“planar perspective”). Note that proper and reverse perspectives are formed by non-planar combinations of planar surfaces, whereas planar perspectives are based on a single flat surface.

The painted scene elicits a depth percept that is just the reverse of the physical depth in reverspectives; thus the depth cues of stereoscopy, motion parallax, vergence, and accommodation compete against cues provided by the painted scene. This causes reverspectives to appear to move as viewers move in front of them (Papathomas 2007; Rogers and Gyani 2010). Forced perspectives appear stable (stationary) to a moving viewer. Planar perspectives are somewhere in between. Their flat surface, although in disagreement with the 3D depth suggested by the painted cues, does not have the opposite 3D arrangement, as in reverspectives. Nevertheless, the juxtaposition of the flat surface and the painted scene produces certain shape distortions (Kubovy 1986 has a review); in some cases, the depicted scene appears to move, albeit much less than in reverspectives (Papathomas et al 2010).

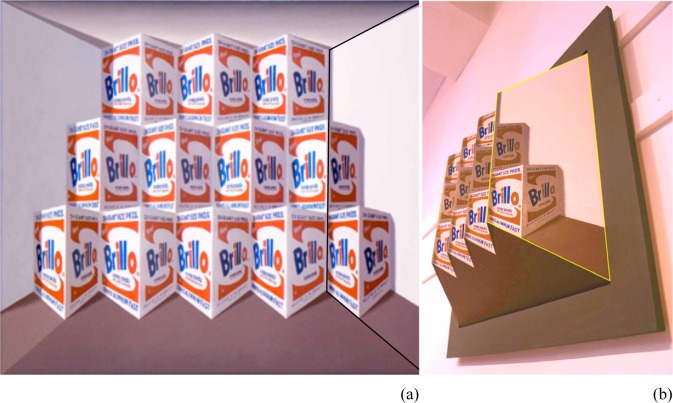
This paper highlights an ingenious piece of art, Forced into Reverse Perspective (2008), in which Hughes combined all three forms of perspective (flat, forced, and reverse). Figure 1a is a front view of a replica that was used in our experiments; Figure 1b is an oblique view of the original art piece. Orthographic projections are in Figure 2. If one ignores the painted objects, one recognizes that the overall 3D shape is a reverspective: edges that are closest to the viewer (such as AB) are smaller than edges that are farther away (CD), which in turn are smaller than the edges that are farthest (EF). Thus, if a viewer moves in front of the unpainted piece, the trapezoid surfaces (such as ABDC) appear to move even though the perspective information of the outline is minimal. Hughes's ingenuity is to break surfaces into objects—Brillo boxes—through the use of slanted lines (such as GH). Thus, the three middle boxes of the bottom row and top-row boxes form reverse perspectives, whereas the middle-row boxes form proper perspectives. Deviously, the two outside boxes in the bottom row are painted entirely on a flat–non-frontoparallel surface (planar perspective).

Figure 1.

(a) Front view of a replica. (b) Oblique view of the original art piece. In both views, the edges of the rightmost planar surface are highlighted to emphasize that this is, indeed, a planar trapezoid; compare with trapezoid ABFE in Figure 2.

Figure 2.

Orthographic front, side and plan views. Black thick solid and dashed-dotted lines indicate 3D physical edges. Red dashed lines indicated painted, non-physical, box edges (shown only on the front view). Trapezoid ABFE is highlighted in Figures 1a and 1b.

If the painter's intentions are realized and the 3D boxes are individuated as observers move in front of the artwork, they should experience strong illusory counter-rotation for the reverspective boxes (top row and three middle boxes in bottom row) (Papathomas 2007; Rogers and Gyani 2010), possibly a weaker illusory counter-rotation for the two planar perspective boxes (two outer boxes in bottom row) (Papathomas et al 2010), and no illusory motion for the forced-perspective boxes (middle row). This means that viewers would see differential motion between the boxes (ie, different rows moving in different directions). As a corollary, when the art piece is rotated, stationary observers would still see this differential motion of the objects. Seventeen subjects with normal acuity took part in Experiments 1 and 2 to test these predictions.

In Experiment 1, we produced four animation sequences involving the art piece on a Dell Studio Laptop; the images were 15.2 cm wide × 12.1 cm tall and were viewed binocularly from a distance of 58 cm. The animations were produced by rotating the art piece as follows: (a) Clockwise (CW) as seen from above (Movie 1); (b) Counterclockwise (CCW) (Movie 2); (c) Upward (UP), ending with a position where the ceiling plane was parallel to the line of sight (appeared as a single line) (Movie 3); (d) Downward (DN), ending with the floor plane appearing as a single line (Movie 4). Videos started from the straight-ahead position that lasted for 1 second; each animation lasted for 5 seconds. We showed each animation four times (four trials) in random sequences. Observers reported (i) what direction (CW/CCW or UP/DN) they perceived boxes in the bottom row to rotate in one trial. (ii) They repeated the process for the middle row in another trial and (iii) again for the top row. (iv) They also rated the perceived motion of one of the outer bottom boxes relative to the middle bottom box; the magnitude indicated the relative strength (maximum 10) and the +/− sign indicated that the outer box was perceived to rotate in the same/opposite direction as the middle bottom box. It must be noted that, displaying the animations on a flat screen is an impoverished viewing condition because observers rely on just perspective and motion for recovering 3D shape, whereas the binocular disparity signals specify a flat surface.

Movie 1.

Animation rotated clockwise (CW) as seen from above.

Movie 2.

Animation rotated counterclockwise (CCW).

Movie 3.

Animation rotated upward (UP), ending with a position where the ceiling plane was parallel to the line of sight (appeared as a single line).

Movie 4.

Animation rotated downward (DN), ending with the floor plane appearing as a single line.

In Experiment 2, we presented two stationary artworks (both 91 cm wide × 71 cm tall × 25 cm deep) in a random sequence at a viewing distance of 2.62 m: (a) The art piece of Figure 1 and (b) a variant in which thin vertical stripes were painted between the boxes—1.5 cm wide, same colour as the wall—to facilitate distinguishing the boxes from each other. Observers viewed the stimulus monocularly and reported whether they saw differential motion between the boxes as they (the observers) moved left-right through approximately 30 cm.

Results: There was great inter-observer variability in both experiments; nevertheless, the majority of observers obtained the percepts intended by the artist. Specifically, for Experiment 1, the number of observers who perceived the differential motion for CW, CCW, UP, and DN rotations were 10, 13, 11, and 6, respectively; for the same rotations, the number who perceived the planar boxes to move in the same direction as the center bottom box were 11, 9, 13, and 13, respectively, with an average relative strength of +7.10 among those who saw same-direction motion; the overall average was +3.00. For Experiment 2, the addition of the “dividing lines” between boxes increased the number of observers who perceived the differential motion from 9 to 14. However, we found the results to be different for small viewing distances (≤ 2.5 m) as readers may observe.

Overall, the results indicate that Patrick Hughes's intuition was correct. He managed to enable the painted objects to dominate over the physical surfaces in this art piece, illustrating the superiority of secondary over primary cues. Parenthetically, this is not the only art piece of its kind. “Day-dreaming 2008” is a more complex reverspective that contains the geometry of Figure 2 as a subset. It depicts houses that are much better distinguished from each other than the Brillo boxes, hence likely to produce better results (http://www.patrickhughes.co.uk/gallery/daydreaming08.htm). These art pieces offer examples for which Donald Norman's quotation (Neal 2007) so aptly applies: “It's often the case that artists are ahead of scientists. What scientists do is notice what the artists have done, and then try to understand it.”

Biography

Thomas Papathomas received his BS, MS, and PhD from Columbia University in electrical engineering and computer science. He is the Director of the Laboratory of Vision Research in the Center for Cognitive Science at Rutgers University, Professor in the Department of Biomedical Engineering, and serves as the Busch Campus Dean. He has designed several exhibits on stereopsis in science museums, and he won third prize in the 2008 International Best Illusion contest (http://www.youtube.com/watch?v=0QgoX78q-0Y). His research interests are in the perception of 3D faces, objects, and scenes, and the interactions between science and art. For more information: http://ruccs.rutgers.edu/∼papathom/index.html.

Nicholas Baker is a Cognitive Science major at Johns Hopkins University. He is currently in his second year and has a particular interest in vision sciences, as well as in studying other perceptual systems.

Arielle Yeshua is an undergraduate at Rutgers University School of Arts and Sciences Honors Program, pursuing a degree in Genetics and Psychology. She is conducting research for Prof. Papathomas in the Laboratory of Vision Research at Rutgers University on the perception of 3D faces, objects, and scenes.

Xiaohua Zhuang received her BS in Psychology from Peking University, China; and recently obtained her MS in Statistics, MS and PhD in Cognitive Psychology from Rutgers University, USA. She currently works as a Postdoctoral Research Associate in the Department of Ophthalmology and Visual Sciences at the University of Illinois at Chicago and her career goal is to become an independent researcher in vision science. Her research interests include retinal visual processing, visual attention, and interactions between higherorder cognitive and early visual processing.

Andrew Ng is a senior at High Technology High School in Lincroft, NJ. A competitive chess player, he has won several national and international awards. He worked as a student researcher at the Laboratory of Vision Research at Rutgers University during the summer of 2011, conducting research in the perception of 3D faces and scenes. He plans to study computer engineering and computer science in college.