Simple Moment-Closure Model for the Self-Assembly of Breakable Amyloid Filaments

Abstract

In this work, we derive a simple mathematical model from mass-action equations for amyloid fiber formation that takes into account the primary nucleation, elongation, and length-dependent fragmentation. The derivation is based on the principle of minimum free energy under certain constraints and is mathematically related to the partial equilibrium approximation. Direct numerical comparisons confirm the usefulness of our simple model. We further explore its basic kinetic and equilibrium properties, and show that the current model is a straightforward generalization of that with constant fragmentation rates.

Introduction

As a typical self-assembly phenomenon, the amyloid fibrous aggregation caused by protein misfolding or (partially) unfolding has been proved to be an intrinsic feature of many different kinds of proteins. It can occur in various biosystems (cells and tissues) and is directly related to several types of well-known neuron-degenerative diseases (1–3), including Alzheimer’s, Parkinson’s, and prion diseases. Thus, elucidating the fibrillation mechanisms of amyloid proteins will not only help us gain a better understanding of how and why amyloidosis arises and proceeds in vivo (4,5), it will also aid in the medical diagnosis and treatment of amyloid-related diseases, and drug development (6).

Among the various experimental, computational, and theoretical methods used in this field, modeling based on mass-action equations appears to be a successful approach (7,8). In this approach, the basic processes of fiber formation are modeled by chemical reactions with empirical reaction rates, and the time evolution of each chemical component (amyloid proteins or fibrils) is formulated according to the law of mass action. Mass-action equations have been widely used due to their special advantages for quantitatively characterizing the kinetic procedure of amyloid fiber formation, theoretically relating various kinetic quantities (e.g., lag time and apparent fiber growth rate) with model parameters (e.g., protein concentration and reaction rate constant), and directly interpreting experimental data with high precision.

The first notable adaptation of the above approach to this field was made in 1959 by Oosawa et al. (9), who investigated how native-state G-actin proteins transform into F-actin. In Oosawa’s model, the conformational transition between ordinary polymers and helical polymers was recognized as a key step for actin growth. The importance of protein conformational transition in fiber formation was subsequently confirmed for many other amyloid proteins (10,11). In 1971, Eisenberg (12) proposed the mechanism of subsequent monomer addition for the polymerization of glutamate dehydrogenase. In 1974, Hofrichter et al. (13) combined the classical homogeneous nucleation (or primary nucleation) with subsequent monomer addition in a study of sickle-cell hemoglobin gelation. This provided the basic modeling framework for most subsequent studies (14,15). In addition, Ferrone et al. (16) suggested a new heterogeneous nucleation mechanism (monomer-dependent secondary nucleation) to account for the extreme autocatalysis phenomenon observed in the sickle-cell hemoglobin gelation induced by photolysis. In contrast to homogeneous nucleation, heterogeneous nucleation occurs on the surface of existing fibrils and thus depends on the concentrations of both monomeric proteins and fibrils (17,18). In 1975, Oosawa and Asakura (7) introduced further steps of filament fragmentation and association for breakable amyloid filaments, which can effectively produce new fiber seeds in the absence of monomeric proteins. Recently, quantitative analysis of this monomer-independent secondary nucleation has received much attention (8,19,20) and is the main focus of this work. In addition, many researchers have made great contributions to our understanding of random polymerization (21), on- and off-pathway competition (22), autocatalytic surface growth (23), branching (24), and lateral association (25,26). These works have largely enhanced our understanding of amyloid fiber formation and revealed important connections among theoretical modeling, experimental data fitting, and prediction.

Although they have shown great success in modeling and application, mass-action equations suffer from an intrinsic bottleneck. In principle, the models involve infinitely many equations if we distinguish filament species with different lengths. Even for the realistic cases, the number of the species is quite large (from thousands to hundreds of thousands). Faced with such a high-dimensional system of ordinary differential equations (ODEs), it is definitely difficult to perform direct calculations or analyses.

An often-adopted method is to define some macro-measurable statistical quantities, such as number concentration $P\left(t\right)$ (zeroth-order moment of filament length) and mass concentration $M\left(t\right)$ (first-order moment of filament length) of filaments, and then derive their time-evolution equations from the original mass-action equations (8). (Similar ideas have been widely applied to other problems, such as turbulence and neuron networks (27).) If the time-evolution equations are closed (e.g., for models with primary nucleation and elongation, the time-evolution equations for $P\left(t\right)$ and $M\left(t\right)$ can be shown as closed if boundary terms are neglected), we can obtain the desired answer. However, if high-order moments or more complicated fibrillation mechanisms (such as fragmentation) are considered, it seems impossible for the resulting equations to be closed.

To deal with this problem, in this work we introduce a general moment-closure method (28). Precisely, we define a free energy for systems in a model that includes primary nucleation, elongation, and fragmentation. By taking the minimization of the free energy under proper constraints, we derive a closed system of two time-evolution equations for number concentration $P\left(t\right)$ and mass concentration $M\left(t\right)$ of filaments. Numerical comparisons and direct fitting of experimental data show that this simple system is a quite good approximation of the original mass-action equations. We also point out several basic kinetic properties of the two-equation system that may be useful for further studies and applications.

Materials and Methods

Modeling the kinetic processes of amyloid fiber formation

Mass-action equations

To quantitatively account for the formation of breakable amyloid filaments, the general model under consideration (8) includes three basic processes--primary nucleation, elongation, and fragmentation (see Fig. 1):

$$\begin{array}{l}{n}_c{A}_1\underset{k_n^{-}}{\overset{k_n^{+}}{\rightleftharpoons }}{A}_{n_c},\\ A_1+A_i\underset{k_e^{-}}{\overset{k_e^{+}}{\rightleftharpoons }}{A}_{i+1},(i\ge n_c)\\ A_{i+j}\underset{k_f^{-}(i,j)}{\overset{k_f^{+}(i,j)}{\rightleftharpoons }}{A}_i+A_j,\left(i,j\ge n_c\right)\end{array}$$ (1)

where the critical nucleus size is $n_c\ge 2$;$A_1$ stands for monomeric proteins; $A_i$ are filaments of size $i$; and $k_n^{+},k_e^{+},k_f^{+}\left(i,j\right)$ and $k_n^{-},k_e^{-},k_f^{-}\left(i,j\right)$ are the forward and backward reaction rate constants for fiber nucleation, elongation, and fragmentation, respectively.

Figure 1.

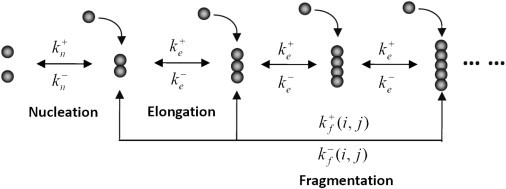
Illustration of primary nucleation, elongation, and fragmentation processes in the formation of breakable amyloid filaments.

According to the law of mass action, the time-evolution equations for $\left[A_i\right]$,the molar concentration of filament of size i, can be written as

$$\{\begin{array}{l}\frac{d}{dt}\left[A_1\right]=-n_c{k}_n^{+}{\left[A_1\right]}^{n_c}+n_c{k}_n^{-}\left[A_{n_c}\right]-2k_e^{+}\left[A_1\right]\sum _{j=n_c}^{\mathrm{\infty }}\left[A_j\right]+2k_e^{-}\sum _{j=n_c+1}^{\mathrm{\infty }}\left[A_j\right],\\ \frac{d}{dt}\left[A_i\right]=2k_e^{+}\left[A_1\right](\left[A_{i-1}\right]-\left[A_i\right])-2k_e^{-}(\left[A_i\right]-\left[A_{i+1}\right])+2\sum _{j=n_c+i}^{\mathrm{\infty }}{k}_f^{+}(i,j-i)\left[A_j\right]-\sum _{j=n_c}^{i-n_c}{k}_f^{+}(j,i-j)\left[A_i\right]-2\sum _{j=n_c}^{\mathrm{\infty }}{k}_f^{-}(i,j)\left[A_i\right]\left[A_j\right]+\sum _{j=n_c}^{i-n_c}{k}_f^{-}(j,i-j)\left[A_j\right]\left[A_{i-j}\right]+\left(k_n^{+}{\left[A_1\right]}^{n_c}-k_n^{-}\left[A_i\right]-2k_e^{+}\left[A_1\right]\left[A_{i-1}\right]+2k_e^{-}\left[A_i\right]\right){\delta }_{i,n_c}.(i\ge n_c)\end{array}$$ (2)

This is our mass-action equation. Thanks to the conservation law of mass, we also have $\left[A_1\right]+{\sum }_{i=n_c}^{\mathrm{\infty }}i·\left[A_i\right]=m_{tot}$. Note that similar equations can be found elsewhere (8,14), but backward reactions were usually neglected for simplicity in previous works.

Moment-closure method

It is easy to see that for the above choices of $k_f^{+}(i,j)$ and $k_f^{-}(i,j)$, Eq. 2 generally cannot lead to closed equations for $P\left(t\right)={\sum }_{i=n_c}^{\mathrm{\infty }}\left[A_i\right]$ and $M\left(t\right)={\sum }_{i=n_c}^{\mathrm{\infty }}i·\left[A_i\right]$.

To solve this problem, we adopt the moment-closure method (28) in the kinetic theory. For this purpose, we construct the free energy function as

$$F={\epsilon }_n\sum _{i=n_c}^{\mathrm{\infty }}\left[A_i\right]+{\epsilon }_e\sum _{i=n_c}^{\mathrm{\infty }}\left(i-n_c\right)·\left[A_i\right]+k_{B}T\left[\left(\left[A_1\right]\ln \left[A_1\right]-\left[A_1\right]\right)+\sum _{i=n_c}^{\mathrm{\infty }}\left(\left[A_i\right]\ln \left[A_i\right]-\left[A_i\right]\right)\right].$$ (3)

where ${\epsilon }_n>0$ represents the free energy associated with the nuclei region of a fiber (i.e., the boundary energy penalty), ${\epsilon }_e<0$ captures the averaged monomeric free energy gained from various interactions and conformational constraints (e.g., hydrogen bonds, hydrophobic interactions, and side-chain packing), $k_B$ is the Boltzmann constant, and T denotes the temperature. The last term in Eq. 3 comes from the mixing entropy of different filament species as in the Flory-Huggins theory (29). Note the resemblance between the Boltzmann factors $\exp [-{\epsilon }_n/\left(k_{B}T\right)]$, $\exp [-{\epsilon }_e/\left(k_{B}T\right)]$ and the two parameters $\sigma$(for helix nucleation) and s (for helix propagation) in the helix-coil transition theory (30), except that ${\epsilon }_n$ and ${\epsilon }_e$ are for β-structures (31). Furthermore, according to the well-known relation between the Gibbs free-energy change for a reaction and the equilibrium constant (32), we can correlate the energetic parameters in Eq. 3 and the reaction rate constants introduced in Eq. 1 as ${\epsilon }_n=-k_{B}T\ln \left(k_n^{+}/k_n^{-}\right)$ and ${\epsilon }_e=-k_{B}T\ln \left(k_e^{+}/k_e^{-}\right)$.

It is easily seen that the free energy thus defined is convex with respect to the distribution $\left(\left[A_1\right],\left[A_{n_c}\right],\left[A_{n_c+1}\right],\dots \right)$. Therefore, we consider the minimization of the free energy under proper constraints:

$$\min F\left(\left[A_i\right]\right)$$ (4)

$$\text{s.t.}\sum _{i=n_c}^{\mathrm{\infty }}\left[A_i\right]=P,\sum _{i=n_c}^{\mathrm{\infty }}i·\left[A_i\right]=M,\left[A_1\right]+\sum _{i=n_c}^{\mathrm{\infty }}i·\left[A_i\right]=m_{tot}.$$ (5)

The first two constraints in Eq. 5 are based on the targeted macroquantities $P\left(t\right)$ and $M\left(t\right)$, and the last one is from the conservation law of mass.

Because the free energy is convex, the above constrained optimization problem can be solved simply by taking the variation

$$\frac{\delta }{\delta \left[A_i\right]}\left[\frac{F\left(\left[A_i\right]\right)}{\left(k_{B}T\right)}-{\lambda }_1\left(\sum _{i=n_c}^{\mathrm{\infty }}\left[A_i\right]-P\right)-{\lambda }_2\left(\sum _{i=n_c}^{\mathrm{\infty }}i·\left[A_i\right]-M\right)-{\lambda }_3\left(\left[A_1\right]+\sum _{i=n_c}^{\mathrm{\infty }}i·\left[A_i\right]-m_{tot}\right)\right]=0,$$ (6)

with Lagrangian multipliers ${\lambda }_1,{\lambda }_2,{\lambda }_3$ corresponding to three constraints. From this, it follows directly that

$$\{\begin{array}{l}\left[A_1\right]=\exp \left({\lambda }_3\right)\\ \left[A_i\right]=\frac{k_n^{+}}{k_n^{-}}{\left(\frac{k_e^{+}}{k_e^{-}}\right)}^{i-n_c}\exp ({\lambda }_1+i{\lambda }_2+i{\lambda }_3).(i\ge n_c)\end{array}$$ (7)

Moreover, it is not difficult to express the multipliers ${\lambda }_1,{\lambda }_2,{\lambda }_3$ in terms of $P\left(t\right),M\left(t\right),m_{tot}$:

$$\{\begin{array}{l}{\lambda }_1=\ln \left[\frac{k_n^{-}}{k_n^{+}}\frac{P^2}{M-\left(n_c-1\right)P}\right]-n_c·\ln \left[\frac{k_e^{-}}{k_e^{+}}\frac{M-n_{c}P}{M-\left(n_c-1\right)P}\right],\\ {\lambda }_2=\ln \left[\frac{k_e^{-}}{k_e^{+}}\frac{M-n_{c}P}{M-\left(n_c-1\right)P}\right]-\ln \left[m_{tot}-M\right],\\ {\lambda }_3=\ln \left[m_{tot}-M\right].\end{array}$$ (8)

Note that generally there is some freedom in the choice of free-energy function (Eq. 3) for the moment-closure method. Different forms of free energy intrinsically correspond to different assumptions regarding the system (i.e., which kinds of interactions and motions are considered) and will lead to different approximate fiber length distributions (Eqs. 7 and 8). In this work, we choose the free energy according to Lee (33) and Schmit et al. (34), which leads to a single exponential distribution of form $\left[A_i\right]\propto e^{-gi}$(g is a constant). Fortunately, this choice accounts perfectly for the assumption of fast equilibrium in the fiber elongation process. (There is a small difference between our free energy (Eq. 3) and Hill’s free energy (reformulated with our notation):

$$\frac{F}{\left(k_{B}T\right)}=-\ln \left(\frac{k_f^{+}}{k_f^{-}}\right)\sum _{i=n_c}^{\mathrm{\infty }}\left[A_i\right]-\ln \left(\frac{k_e^{+}}{k_e^{-}}\right)\sum _{i=n_c}^{\mathrm{\infty }}i·\left[A_i\right]+\left(\left[A_1\right]\ln \left[A_1\right]-\left[A_1\right]\right)+\sum _{i=n_c}^{\mathrm{\infty }}\left(\left[A_i\right]\ln \left[A_i\right]-\left[A_i\right]\right)-n\sum _{i=1}^{\mathrm{\infty }}\ln i·\left[A_i\right].$$

If we set $k_n^{+}/k_n^{-}{\left(k_e^{+}/k_e^{-}\right)}^{-n_c}=k_f^{+}/k_f^{-}$, then the only difference from our expression (Eq. 3) is the last term, $n{\sum }_{i=1}^{\mathrm{\infty }}\ln i·\left[A_i\right]$. This term accounts for the translational and rotational freedoms of a fiber in solution. The latter will lead to a distribution function of fiber length in the form of $\left[A_i\right]\propto i^n{e}^{-gi}$ corresponding to the partial equilibrium approximation on fiber fragmentation process. Considering that elongation is usually much faster than fragmentation in realistic amyloid fiber systems, our current free energy is expected to give better results than Hill’s.)

Moment-closure equations

For the length-dependent reaction rate constants for filament fragmentation and association, we refer to Hill’s theoretical calculations (36) and take them as

$$\{\begin{array}{l}{k}_f^{+}(i,j)=\frac{k_f^{+}{\left(ij\right)}^{n-1}\left(i\ln j+j\ln i\right)}{{\left(i+j\right)}^{n+1}},\\ k_f^{-}(i,j)=\frac{k_f^{-}\left(i\ln j+j\ln i\right)}{\left[ij\left(i+j\right)\right]},\end{array}$$ (9)

where n represents the degrees of freedom of a filament in the solution. For several typical amyloid fiber systems (see Fig. 3 D), we find $n=1\sim 3$, which means they are in a partially mobile state. (According to Hill’s argument (36), the value of index n accounts for the translational and rotational degrees of freedom for a filament moving in solution. In principle, the contribution from translation is 3/2, the contribution from two-dimensional rotation of a rigid rod is 3, and the contribution from rotation about the axis of a rigid rod is 1/2. Thus $n\approx 4\sim 6$ when a filament has completely free motion in solution. On the contrary, $n\approx 0$ for the immobile case. For several typical amyloid fiber systems shown in Fig. 3 D, we found $n\approx 1\sim 3$. We expect this is caused by some degrees of freedom for the filament motion becoming frozen due to filaments cross-linking, bundling, and so on. Thus, the filaments in these systems will lie in a state between freely mobile and immobile, which we describe as partially mobile.)

Figure 3.

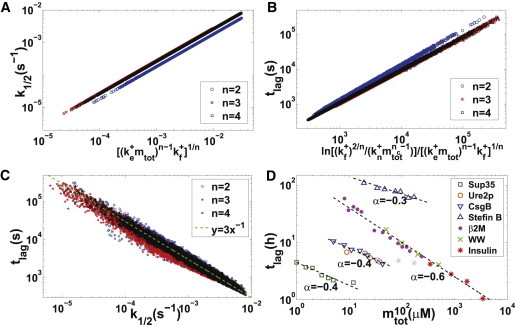
(A–C) Scaling relationships among apparent fiber growth rate, lag time, and model parameters. For parameter $n=2,3,4$, 10,000 data points are generated separately with reaction rate constants randomly chosen in $m_{tot}=0.1-100\mu M$, $k_n^{+}={10}^{-9}-{10}^{-6}{M}^{-1}{s}^{-1}$, $k_e^{+}={10}^3-{10}^6{M}^{-1}{s}^{-1}$, $k_f^{+}={10}^{-8}-{10}^{-5}{s}^{-1}$ for $n=2$, $k_f^{+}={10}^{-13}-{10}^{-10}{s}^{-1}$ for $n=3$, $k_f^{+}={10}^{-15}-{10}^{-12}{s}^{-1}$ for $n=4$, $k_f^{-}=k_n^{-}=k_e^{-}=0$, $n_c=2$. (D) Scaling relationship between lag time and protein concentration ($t_{lag}\propto m_{tot}^{\alpha }$). Data are shown for Sup35 NW region (dark green squares) (14), Ure2p (brown circles) (48), CsgB_trunc (blue downward triangles) (49), Stefin B (purple upward triangles) (50), β2-microglobulin (pink dots) (51), WW domain (light green crosses) (44), and insulin (red stars) (52). Black dashed lines denote the best fitting curves for each data set, with the slope numbered beside the line. For scaling exponents $\alpha =-0.3,-0.4,-0.6$, the corresponding model parameters are $n=1.4,1.7,2.5$, respectively.

Then, using the distribution function in Eq. 7, we derive our simple model (or moment-closure equations) from Eq. 2 as

$$\{\begin{array}{l}\frac{dP}{dt}=k_n^{+}{\left(m_{tot}-M\right)}^{n_c}-k_n^{-}\left(1-\theta \right)P+k_f^{+}\left(1-\theta \right)P{\theta }^{n_c}{\Xi }_{n-1}-k_f^{-}{\left(1-\theta \right)}^2{P}^2{\Lambda }_1,\\ \frac{dM}{dt}=n_c{k}_n^{+}{\left(m_{tot}-M\right)}^{n_c}+2k_e^{+}\left(m_{tot}-M\right)P-2k_e^{-}P-\left(n_c{k}_n^{-}-2k_e^{-}\right)\left(1-\theta \right)P,\end{array}$$ (10)

where $\theta \equiv \left(M-n_{c}P\right)/\left[M-\left(n_c-1\right)P\right]\in [0,1)$. In Eq. 10, the functions

$${\Xi }_{n-1}=\frac{n_c^n}{2^n}\left[\frac{\ln n_c}{n_c^2{(-\ln \theta )}^2}+\frac{\left(n-2\right)\ln n_c+1}{n_c^3{(-\ln \theta )}^3}+\frac{(3n-5)(n-4)\ln n_c+6(n-3)}{4n_c^4{(-\ln \theta )}^4}+\dots \right]$$

and

$${\Lambda }_1=\frac{\ln n_c}{n_c^2{(-\ln \theta )}^2}$$

are derived from the infinite summations in Eq. 2 through integration by parts. In practice, to account for all positive contributions in the summations, only one term is needed for filament association (${\Lambda }_1$), and $n-1$ terms (${\Xi }_{n-1}$) are required for filament fragmentation. Note that ${\Xi }_{n-1}$ is an asymptotic series and may diverge as $\theta \to 1$ (though $\left(1-\theta \right){\Xi }_{n-1}$ still converges).

To our knowledge, this is the first work to obtain closed-form equations for the moments $P\left(t\right)$ and $M\left(t\right)$ when general length-dependent fiber fragmentation processes are considered. For models without fragmentation ($k_f^{+}(i,j)=0$), exact solutions have been obtained by Oosawa and Asakura (7), Lomakin et al. (38), and Cohen et al. (39). For models with length-independent fragmentation ($k_f^{+}(i,j)=k_f^{+}$), closed-form equations for $P\left(t\right)$ and $M\left(t\right)$ can be derived by neglecting unimportant boundary terms. Furthermore, approximate solutions with high accuracy have been obtained through fixed-point analysis (8,40,41). However, for models with length-dependent fragmentation, self-closure of moment equations is usually an illusion. In these cases, our moment-closure method provides a general solution framework regardless of what kinds of real forms for fiber fragmentation are taken.

Relation with partial equilibrium approximation

The moment-closure method used here has a strong physical basis: the minimization of the system free energy under given constraints ($P\left(t\right)$, $M\left(t\right)$, and $m_{tot}$ for the present case). Furthermore, we can show that this moment-closure method is equivalent to the partial equilibrium approximation on fiber elongation in mathematics, and thus clarify the applicable range of our method.

A notable aspect of the original mass-action equations is that the fiber elongation processes alone satisfy the principle of detailed balance whenever they are reversible. In fact, for any given positive numbers ${\left[A_1\right]}^{\ast }$ and ${\left[A_{n_c}\right]}^{\ast }$, we can easily find positive numbers ${\left[A_i\right]}^{\ast }={\left[A_{n_c}\right]}^{\ast }{\left(k_e^{+}{\left[A_1\right]}^{\ast }/k_e^{-}\right)}^{i-n_c}$ ($i>n_c$), such that

$$k_e^{+}{\left[A_1\right]}^{\ast }{\left[A_i\right]}^{\ast }=k_e^{-}{\left[A_{i+1}\right]}^{\ast }.$$ (11)

Coincidently, with the constraints ${\sum }_{i=n_c}^{\mathrm{\infty }}{\left[A_i\right]}^{\ast }=P$ and ${\sum }_{i=n_c}^{\mathrm{\infty }}i·{\left[A_i\right]}^{\ast }=M$, the filament length distribution ${\left[A_i\right]}^{\ast }={\theta }^{i-n_c}(1-\theta )P$ ($i\ge n_c$) can be derived from Eq. 11. It is exactly the same as that obtained by the moment-closure method in Eqs. 7 and 8. This connection suggests that in the current case, the moment-closure method is equivalent to the partial equilibrium approximation on fiber elongation.

To further discuss the mathematical foundation for the partial equilibrium approximation, we set $X\left(t\right)\equiv {\left(\left[A_1\right],\left[A_{n_c}\right],\left[A_{n_c+1}\right],\dots \right)}^T$. Then the mass-action equations Eq. 2 can be rewritten into a vector form:

$$\frac{d}{dt}X=\frac{1}{{\tau }_n}{R}_n\left(X\right)+\frac{1}{{\tau }_e}{R}_e\left(X\right)+\frac{1}{{\tau }_f}{R}_f\left(X\right),$$ (12)

where $R_n\left(X\right)$, $R_e\left(X\right)$, and $R_f\left(X\right)$ represent the terms from primary nucleation, elongation, and fragmentation, respectively, and ${\tau }_n$, ${\tau }_e$, and ${\tau }_f$ characterize the timescales of the corresponding processes. In addition, one can directly verify that

$$\{\begin{array}{l}(0,1,1,\dots )R_e\left(X\right)\equiv 0,\\ (1,n_c,n_c+1,\dots )R_e\left(X\right)\equiv 0,\end{array}$$ (13)

which means that $P\left(t\right)$ and $m_{tot}$ are two conservative quantities for fiber elongation.

Assume that the elongation processes are much faster than others, i.e., ${\tau }_n$ and ${\tau }_f$ are moderate and ${\tau }_e=\tau$ is small. Under this assumption, $1/{\tau }_e{R}_e\left(X\right)$ can be regarded as a stiff term. Because elongation processes obey the principle of detailed balance, we know from the singular perturbation theory (42,43) that the solution $X^{\tau }$ of Eq. 12 possesses the following property: as $\tau$ tends to zero, $P^{\tau }\left(t\right)=\left(0,1,1,\dots \right)X^{\tau }\left(t\right)$ and $m_{tot}^{\tau }\left(t\right)=\left(1,n_c,n_c+1,\dots \right)X^{\tau }\left(t\right)$ converge to the solutions of the following equations uniformly for t in any given bounded time interval:

$$\{\begin{array}{l}\frac{d}{dt}P=\left(0,1,1,\dots \right)\left[\frac{1}{{\tau }_n}{R}_n\left(X^0\right)+\frac{1}{{\tau }_f}{R}_f\left(X^0\right)\right],\\ \frac{d}{dt}{m}_{tot}=(1,n_c,n_c+1,\dots )\left[\frac{1}{{\tau }_n}{R}_n\left(X^0\right)+\frac{1}{{\tau }_f}{R}_f\left(X^0\right)\right],\end{array}$$ (14)

Here $X^0$ is the unique solution to

$$\{\begin{array}{l}{R}_e\left(X\right)=0,\\ (0,1,1,\dots )X=P,\\ (1,n_c,n_c+1,\dots )X=m_{tot}.\end{array}$$ (15)

To some extent, this argument provides a mathematical basis for the partial equilibrium approximation, as well as the moment-closure method proposed here. However, for general applications, the underlying connections between the moment-closure method and partial equilibrium approximation still need further clarification.

Results

Numerical comparison and data fitting

According to our above mathematical argument, as long as the reaction rate for fiber elongation is much larger than that for other processes (e.g., primary nucleation, fragmentation, and corresponding backward reactions), the moment-closure equations will provide a reasonable approximation in the calculation of $P\left(t\right)$ and $M\left(t\right)$ compared with the original mass-action equations. This is further confirmed by the numerical calculations shown in Fig. 2, A and B. In contrast, large deviations in the filament length distribution can be observed due to the presence of the fragmentation process (see Fig. 2 C). It is fair to say that Eq. 7 captures an average tendency of the realistic filament length distribution, whereas the moving peaks in filament length distribution produced by fragmentation are totally neglected. In principle, if more macroquantities (such as high-order moments of filament length) are considered as constraints in the minimization problem, one can expect better results for the filament length distribution. However, one must aware that the corresponding computational complexity will be dramatically increased.

Figure 2.

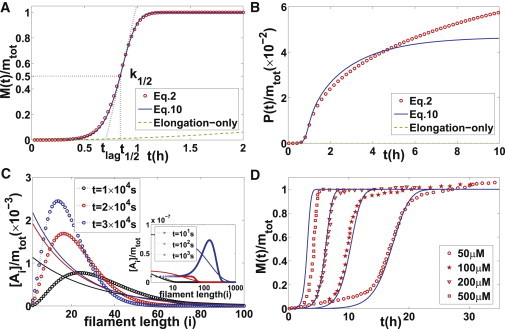
(A and B) Comparisons of mass-action Eq. 2 (red circles), elongation-only model (green dashed lines), and moment-closure Eq. 10 (blue solid lines) in the calculation of $P\left(t\right)$ and $M\left(t\right)$ with $m_{tot}=50\mu M$, $k_n^{+}={10}^{-4}{M}^{-1}{s}^{-1}$, $k_e^{+}=5\times {10}^3{M}^{-1}{s}^{-1}$, $k_f^{+}=5\times {10}^{-7}{s}^{-1}$, $k_f^{-}={10}^2{M}^{-1}{s}^{-1}$, $k_n^{-}=k_e^{-}=0$, $n_c=2$, $n=3$. Three major kinetic quantities are represented by black dotted lines. (To highlight the significant roles of fragmentation, we plot the results of the elongation-only model (38,39) (by simply neglecting the fragmentation process $k_f^{+}(i,j)=0$) for comparison. It can be clearly seen that the elongation-only model is only applicable to the very initial stage, in correspondence with the fact that elongation is much faster than fragmentation. Actually, when the long-time behaviors are concerned, the slow processes (fragmentation in this case) play a major role. This is expected mathematically. From a biological point of view, fragmentation can provide more fiber seeds (even their reaction rate constants look very small compared with other processes), which will greatly affect the formation of amyloid fiber.) (C) Comparison of exact fiber length distribution (calculated from Eq. 2 and shown by dots) and approximate fiber length distribution (obtained in Eq. 7 and shown by solid lines) at different time. (D) Experimental data fitting for polymerization of the WW domain measured by Ferguson et al. (44). Red circles indicate experimental data under different initial protein concentrations $m_{tot}=500,200,100,50\mu M$, respectively; blue solid lines indicate numerical solutions of moment-closure equations (Eq. 11) with $k_n^{+}=8\times {10}^{-9}{M}^{-1}{s}^{-1}$, $k_e^{+}=1\times {10}^5{M}^{-1}{s}^{-1}$, $k_f^{+}=1.7\times {10}^{-13}{s}^{-1}$, $k_f^{-}=1\times {10}^3{M}^{-1}{s}^{-1}$, $k_n^{-}=k_e^{-}=0$, $n_c=2$, $n=3$. (Knowles et al. (8) performed a similar fitting for models with length-independent fragmentation. However, their reaction rate constant for fragmentation appears to be much larger than ours due to their oversimplified assumption of length dependence.)

In contrast to the extremely long time required for a consistent calculation of the original mass-action equations, our moment-closure equations offer great simplicity for model analysis, numerical calculations, and experimental data fitting. In general, the performance is improved by at least 10,000-fold (from days to seconds). In Fig. 2 D, we apply our simple model to study the polymerization data of the WW domain measured by Ferguson et al. (44). By choosing appropriate reaction rate constants (the extraction of model parameters from the experimental data follows the procedure described in Hong et al. (20)), we can fit all four kinetic curves under different protein concentrations simultaneously. This is a critical test of the moment-closure equations (Eq. 10).

Basic model properties

We further explore the basic kinetic and equilibrium properties of the moment-closure equations. To quantitatively characterize the kinetic curves for $M\left(t\right)$, two often-studied quantities are the apparent fiber growth rate $k_{1/2}\equiv \dot{M}\left(t_{1/2}\right)/m_{tot}$ (defined as the normalized rate for mass concentration changes at the half-time of fibrillation $M\left(t_{1/2}\right)=m_{tot}/2$) and the lag time $t_{lag}\equiv t_{1/2}-1/\left(2k_{1/2}\right)$. Through mathematical analysis (at the half-time of fiber formation, we usually have $M\gg P$, thus, $\theta \approx 1$ and $-\ln \theta \approx 1-\theta$; putting these relations into the first formula of Eq. 2 and keeping the leading term of ${\Xi }_{n-1}$, we get $dP/dt\sim k_f^{+}{M}^{n-1}/P^{n-2}$; combining the sigmoidal curve of M with the definition of apparent fiber growth rate $k_{1/2}$, we have $P\sim {\left(k_f^{+}/k_{1/2}\right)}^{1/(n-1)}{m}_{tot}$; then, using the formula $dM/dt\sim k_e^{+}{m}_{tot}P$, we get $k_{1/2}\sim k_e^{+}{\left(k_f^{+}/k_{1/2}\right)}^{1/(n-1)}{m}_{tot}$, which predicts the relation $k_{1/2}\propto {\left[{\left(k_e^{+}{m}_{tot}\right)}^{n-1}{k}_f^{+}\right]}^{1/n}$) and numerical experiments, we find the following elegant relations (see Fig. 3, A–C):

$$k_{1/2}\propto {\left[{\left(k_e^{+}{m}_{tot}\right)}^{n-1}{k}_f^{+}\right]}^{1/n},$$ (16)

$$t_{lag}\propto \frac{\ln \left[{\left(k_f^{+}\right)}^{2/n}/\left(k_n^{+}{m}_{tot}^{n_c-1}\right)\right]}{{\left[{\left(k_e^{+}{m}_{tot}\right)}^{n-1}{k}_f^{+}\right]}^{1/n}},$$ (17)

provided that the fragmentation is more efficient in producing new seeds than primary nucleation at the half-time of fiber formation ${\left[{\left(k_e^{+}{m}_{tot}\right)}^{n-1}{k}_f^{+}\right]}^{1/n}\gg {\left(k_n^{+}{k}_e^{+}{m}_{tot}^{n_c}\right)}^{1/2}$, which can be easily verified. (This condition can be verified for all data sets used in Fig. 3 as follows: for n = 2, ${\left[{\left(k_e^{+}{m}_{tot}\right)}^1{k}_f^{+}\right]}^{1/2}={10}^{-6}-{10}^{-3/2}\gg {\left(k_n^{+}{k}_e^{+}{m}_{tot}^2\right)}^{1/2}={10}^{-15}-{10}^{-9}$; for n = 3, ${\left[{\left(k_e^{+}{m}_{tot}\right)}^2{k}_f^{+}\right]}^{1/3}={10}^{-7}-{10}^{-2}\gg {\left(k_n^{+}{k}_e^{+}{m}_{tot}^2\right)}^{1/2}={10}^{-15}-{10}^{-9}$; and for n = 4, ${\left[{\left(k_e^{+}{m}_{tot}\right)}^3{k}_f^{+}\right]}^{1/4}={10}^{-27/4}-{10}^{-3/2}\gg {\left(k_n^{+}{k}_e^{+}{m}_{tot}^2\right)}^{1/2}={10}^{-15}-{10}^{-9}$). The above relations confirm that the model with constant filament fragmentation rates (8,20) can be regarded as a special case of the length-dependent one with $n=2$ (when $n=2$, $k_f^{+}(i,j)/k_f^{+}\sim O(\ln \left(i\right)+\ln \left(j\right))$, thus it can be roughly regarded as length independent). Furthermore, we see that the universal inverse relationship $k_{1/2}\propto t_{lag}^{-1}$ between the apparent fiber growth rate and lag time mentioned in the literature (47) holds only approximately (see Fig. 3 C).

Note that the $(n-1)/n$-law ($k_{1/2}\propto m_{tot}^{(n-1)/n},t_{lag}\propto m_{tot}^{-(n-1)/n}$) obtained above is different from the $(n_c+1)/2$-law (7) for the classical nonbreakable filament model (primary nucleation) and the $(n_2+1)/2$-law (18) for the heterogeneous nucleation model (also nonbreakable). Our simple model may provide an explanation for the observed weak dependence (scaling exponent < 1) between the apparent fiber growth rate (or lag time) and initial protein concentration for many amyloid proteins (8,20) (see also Fig. 3 D). More importantly, these different scaling behaviors offer an effective way to extract the underlying mechanisms from experimental data and choose the correct model for a given amyloid fiber system.

From Eqs. 16 and 17, we get a rough idea that the major kinetic behaviors of $M\left(t\right)$ are determined by three forward reaction rate constants (primary nucleation, elongation, and fragmentation). However, when the equilibrium values of $P\left(t\right)$ and $M\left(t\right)$ are concerned, backward reaction rate constants cannot be neglected. In fact, it is not difficult to deduce from our simple model (Eq. 10) that

$$m_{tot}-M\left(\mathrm{\infty }\right)\sim \frac{k_e^{-}}{k_e^{+}},$$ (18)

$$P\left(\mathrm{\infty }\right)\sim {\left(\frac{k_f^{+}{m}_{tot}^{n-1}}{k_f^{-}}\right)}^{1/n}.$$ (19)

Therefore, the nonzero value of $k_e^{-}$ guarantees a measurable concentration of monomers in the equilibrium (53), and the presence of $k_f^{-}$ is necessary for a reasonable equilibrium value of $P\left(t\right)$. If $k_f^{-}=0$, the predicted average length of filaments ($\sim n_c$) will be much smaller than experimental values (from hundreds to tens of thousands) (20,42,43). This point did not receive enough attention in previous studies (8,54,55).

Discussion

In addition to the two often-studied quantities, the zeroth-order moment $P\left(t\right)$ and first-order moment $M\left(t\right)$, high-order moments have recently attracted much interest in theoretical analysis (54) and experimental measurements (e.g., the light intensity in static light scattering is proportional to the second-order moment of filament length (15)). High-order moments can be computed by using available low-order moments; for example, in the current case the qth-order moment can be computed as ${\sum }_{i=n_c}^{\mathrm{\infty }}{i}^q·\left[A_i\right]={\sum }_{i=n_c}^{\mathrm{\infty }}{i}^q·{\theta }^{i-n_c}(1-\theta )P$. However, this method may not guarantee good accuracy. Another approach is to introduce the targeted high-order moments as new constraints in the minimization problem. Quantitative comparisons of two different approaches are in progress.

An interesting question is, why does the moment-closure method work so well? Physically, the method is based on the principle of minimum free energy under certain constraints, so it seems reasonable. Mathematically, however, no theoretical support is available in the literature. For the present case, we have pointed out the mathematical relation between the moment-closure method and the partial equilibrium approximation, which to our best knowledge is the first justification for the mathematical correctness of this method. However, for general applications, it is still an open problem.

Another interesting question is, how well does this approach compare with other methods? Wang et al. (56) compared several closure methods by means of numerical experiments and claimed that the current method is the best. However, for mass-action equations, quantitative conclusions require further clarification.