Misplaced helix slows down ultrafast pressure-jump protein folding

Abstract

Using a newly developed microsecond pressure-jump apparatus, we monitor the refolding kinetics of the helix-stabilized five-helix bundle protein λ*YA, the Y22W/Q33Y/G46,48A mutant of λ-repressor fragment 6–85, from 3 μs to 5 ms after a 1,200-bar P-drop. In addition to a microsecond phase, we observe a slower 1.4-ms phase during refolding to the native state. Unlike temperature denaturation, pressure denaturation produces a highly reversible helix-coil-rich state. This difference highlights the importance of the denatured initial condition in folding experiments and leads us to assign a compact nonnative helical trap as the reason for slower P-jump–induced refolding. To complement the experiments, we performed over 50 μs of all-atom molecular dynamics P-drop refolding simulations with four different force fields. Two of the force fields yield compact nonnative states with misplaced α-helix content within a few microseconds of the P-drop. Our overall conclusion from experiment and simulation is that the pressure-denatured state of λ*YA contains mainly residual helix and little β-sheet; following a fast P-drop, at least some λ*YA forms misplaced helical structure within microseconds. We hypothesize that nonnative helix at helix-turn interfaces traps the protein in compact nonnative conformations. These traps delay the folding of at least some of the population for 1.4 ms en route to the native state. Based on molecular dynamics, we predict specific mutations at the helix-turn interfaces that should speed up refolding from the pressure-denatured state, if this hypothesis is correct.

Temperature and pressure are excellent perturbations when comparing experimental folding kinetics with molecular dynamics (MD) simulations (1). Fast temperature-jumps (T-jumps) and pressure-jumps (P-jumps) are relatively easy to simulate by MD. Typical temperature changes required to cross the protein folding transition are 5–20 K, easily implemented with laser T-jumps (2). Typical pressure changes required to cross the folding transition are 1–5 kbar, previously achieved only with millisecond time resolution (piezo methods are limited to ΔP < 100 bar) (3, 4). We recently reported a P-jump instrument capable of >1-kbar P-drops with ∼1-μs dead time (5).

Folded proteins have a larger partial molar volume than pressure-denatured proteins (by about 10¹–10² mL/mol) (6). The fractal dimension of their folded state is less than 3 because voids occur whenever a connected chain made from a finite amino acid alphabet is packed into a compact structure (7, 8). Such imperfections in packing, which disappear when small water molecules solvate the polypeptide chain, lead to protein unfolding under pressure (9). Pressure unfolding is a slow process because the positive activation volume is unfavorable at high pressure (10).

Here, we study the much faster process of protein refolding at 1 bar and room temperature, starting from the pressure-denatured ensemble. We chose λ*YA, the Y22W/Q33Y/G46,48A mutant of λ-repressor fragment 6–85, as our model protein (11, 12). Tryptophan W22 provides a fluorescent probe (11). Based on the crystal structure, tyrosine Y33 enhances the fluorescence lifetime difference between folded and unfolded states by contact quenching W22 when the protein is folded (13). The glycines-to-alanines substitution stabilizes helix 3 of the protein (Fig. 1); thus, helices 1, 3, and 4 have high stability (14). Stable helical structure in small peptides is difficult to pressure-denature (15), even though secondary structure, whose stability is assisted by tertiary contacts, denatures easily when the tertiary contacts are disrupted (16). With the high stability of helices 1, 3, and 4 in λ*YA, we expect a relatively helix-rich unfolded coil on P-denaturation of λ*YA, even in the 2.4 M guanidine hydrochloride (GuHCl) buffer we use to poise the protein at the unfolding transition.

Fig. 1.

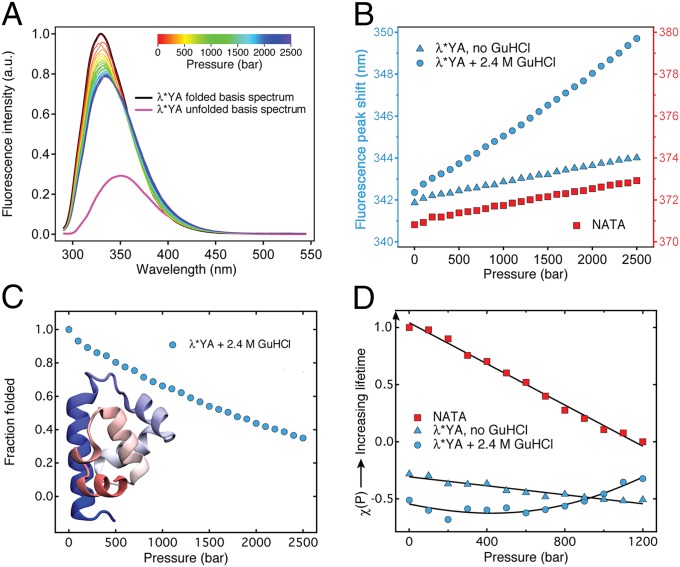
Pressure denaturation of λ*YA probed by fluorescence spectroscopy of a 200-μM sample (A–C) and fluorescence lifetime analysis of a 300-μM sample (D). (A) Fluorescence spectra of λ*YA in guanidine (pH 7) at 100-bar intervals from 1 to 2,500 bar (rainbow gradient). The basis spectrum of the folded state is shown in black, and that of the fully unfolded state is shown in purple (SI Appendix). a.u., arbitrary units. (B) Fluorescence peak shift (centroid) as a function of pressure. λ*YA in 2.4 M GuHCl shows a much larger 0.0032-nm/bar shift than λ*YA in buffer (native state model) or NATA (denatured state model). (C) Fraction folded was calculated by fitting the spectra in A to a linear combination of the folded and unfolded basis spectrum (two-state model; SI Appendix); at 1,200 bar (initial condition for P-jumps), ∼40% of the protein is unfolded. The crystallographic structure of λ*YA obtained from the PDB (ID code 3KZ3) is shown. (D) Scaled fluorescence lifetime change relative to NATA (1 at 1 bar, 0 at 1,200 bar). NATA and λ*YA in 0 M GuHCl lifetimes decrease linearly with pressure, whereas λ*YA in 2.4 M GuHCl shows the onset of pressure denaturation (χ for proteins was shifted up by +3 because NATA has a much longer lifetime; SI Appendix, Fig. S4).

We find that pressure-denatured λ*YA is very different from temperature-denatured λ*YA, offering an opportunity to study the effect of the initial denatured state on refolding. Pressure unfolding induces a mix of helix and coil conformations, and it is reversible at all pressures used in our high-pressure experiments. In contrast, high temperature causes aggregation or populates extended (β-like) structure at high denaturant concentration (17). Our microsecond resolution P-jump refolding experiment reveals a 1.4-ms “slow” phase, in addition to a microsecond “burst” phase. Based on residual helical structure in the pressure-denatured state as measured by IR spectroscopy, we assign the slowdown to a trap with nonnative helix, which does not exist in the temperature-denatured state.

To investigate the plausibility of this assignment further, we calculated over 50 μs of explicit solvent MD trajectories using four different force fields. First, λ*YA was denatured at high temperature and pressure in silico. With CHARMM27 and 22* force fields, refolding trajectories after a downward P-jump reveal a likely culprit for the slow phase: misplaced helical structure where there should be loops connecting helices in the native state. Such nonnative helix forms rapidly via local interactions and then traps the protein in compact states because incorrect loops lead to incorrect packing of the native-like helices. By identifying loop regions with nonnative helix propensity, we predict mutation sites that could reduce the slow recovery from the misplaced helix traps. CHARMM36 and AMBER99-SB do not rapidly form compact helix-rich states after the P-jump. The initial state before the jump is not to blame: CHARMM27 and 22* form helical traps even when they start out with initial conditions from AMBER-99SB.

Nonnative transient helix en route to the native state has been observed many times under cryogenic conditions (18–20), but it can be studied in our experiments at room temperature and 1 bar. Although helix overshoots in MD simulations may be due to force field bias (21), our results highlight that misplaced helical structure may occur experimentally also. Microsecond P-jump studies can contribute to the continued calibration and improvement of force fields by providing an alternative initial ensemble to temperature denaturation.

Results

We used λ*YA as a model system to study the behavior of a fast folder by P-denaturation and microsecond P-jump kinetics. We used two different probes in our experiments, fluorescence of tryptophan W22 and IR absorbance of the peptide bond in the amide I′ region of the IR spectrum. W22 fluorescence was used previously to study fast folding of λ*YA by T-jumps (12, 13). Thus, our pressure experiments can be directly compared with the T-jump results. The motivation to use IR absorbance as a complementary structural probe came from recent computational and experimental reports indicating the presence of transient β-sheet formation in λ*YA at high temperature (17, 22, 23). It was unknown what type of residual secondary structure would exist in λ*YA at high pressure.

Equilibrium Pressure Denaturation Probed by Fluorescence.

λ*YA was prepared just shy of denaturation in 2.4 M GuHCl (SI Appendix, Fig. S2). Subsequent pressure denaturation of λ*YA was monitored by tryptophan fluorescence spectra and fluorescence decay lifetimes of 200–300 μM λ*YA in 50 mM K₃PO₄ buffer (Methods and Fig. 1). Decay lifetime (and also intensity) is sensitive to tryptophan quenching by tyrosine 33, which was used as the probe in our P-jump. The peak shift of the spectra is sensitive to solvent exposure (redder = more exposed).

Without denaturant, the small shift of the spectrum to longer wavelengths (Fig. 1B) is very similar to that observed for the tryptophan derivative N-acetyl-tryptophanamide (NATA). Like NATA’s lifetime, the lifetime of λ*YA decreases linearly with pressure in the absence of denaturant (Fig. 1D). Pressure denaturation of λ*YA in 2.4 M GuHCl (Fig. 1) shows a much larger wavelength shift and a nonlinear lifetime increase. By fitting the fluorescence spectra in Fig. 1A, we estimate ≈40% denatured population at 1,200 bar, the starting point for our P-jump experiments. It is common for pressure-induced protein denaturation to have low cooperativity (5, 24–26), and this is also the case for λ*YA in Fig. 1.

Fast P-Jump Kinetics.

We induced relaxation of λ*YA from the denatured state to the native state by means of a large microsecond P-drop. We extended the capabilities of our recently reported P-jump instrument (5) further: Mechanical damping and optical isolation make the triggering more reliable, and up to 5 ms of data can be collected (0.5 ms previously). The protein solution is placed into a 1-mm dimple machined into a sapphire cube, which is optically transparent at wavelengths greater than 280 nm for laser excitation and fluorescence detection (Fig. 2). We monitored pressure denaturation of λ*YA via tryptophan lifetime (Fig. 1D) by slowly increasing the pressure of the sample to 1,200 bar.

Fig. 2.

P-jump instrument. The sample is pipetted into a dimple in a sapphire cube. The dimple is covered with mylar-coated aluminum foil and pressurized by pumping ethanol into a pressure fitting. A current burst into a copper electrode bursts the upper steel membrane and releases the pressure. Sample fluorescence is excited by a 280-nm pulsed laser every 12.5 ns and is collimated by a UV light guide onto a photomultiplier. The digitized raw data consist of a train of fluorescence decays, whose lifetime and intensity monitor the refolding of the sample after the sudden P-drop at t = 0.

The pressure was then jumped down to 1 bar with a microsecond dead time by resistively heating and puncturing a steel burst membrane (Fig. 2). To monitor kinetics, the sample was excited by 280-nm UV pulses every 12.5 ns. Tryptophan fluorescence decays were detected every 12.5 ns with a 100-ps time resolution. To monitor how the fluorescence lifetime relaxes to equilibrium, we applied linear two-state fitting to the decays to scale the lifetime change from χ = 0 (before P-jump) to χ = 1 (5 ms after P-jump) (Methods). The <3-μs dead time of the P-jump instrument was calibrated by performing pressure jumps on NATA (SI Appendix, Fig. S1).

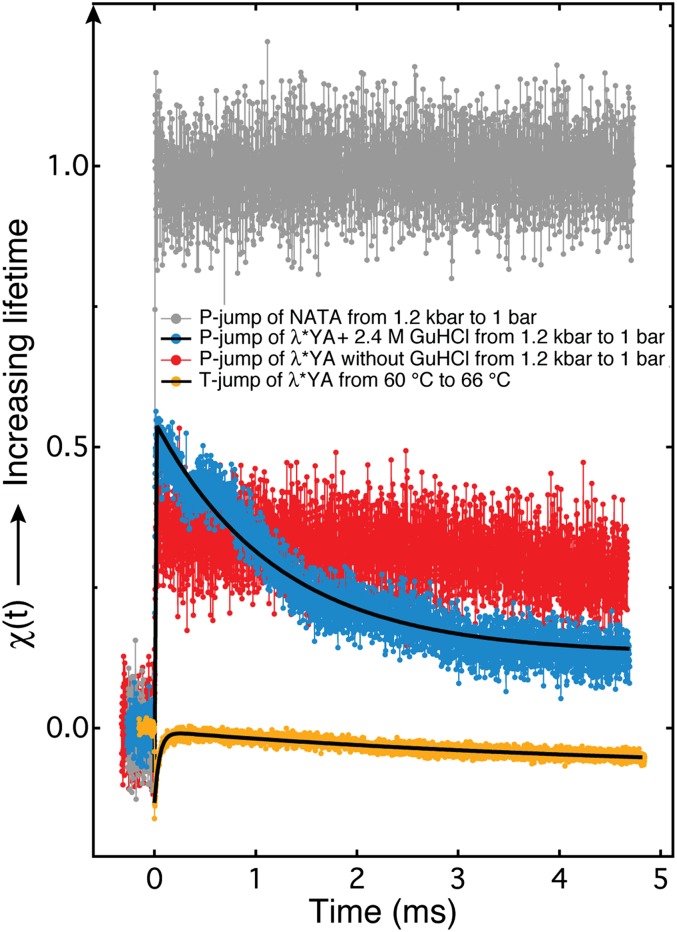
Fig. 3 shows the refolding kinetics of λ*YA on a 1,200→1-bar P-jump at 295 K in buffered 2.4 M GuHCl. Two phases are observed: a fast microsecond phase during which the W22 lifetime increases relative to the value before the P-jump and a slower millisecond phase during which the W22 lifetime decreases. The fast phase could not be resolved within the dead time. For reference, we also measured the P-jump kinetics of λ*YA without denaturant, our model for folded protein (Fig. 1). The net burst phase is the difference between the blue and red curves at t = 0 (Fig. 3). On the relative scale of the NATA fluorescence lifetime change (0 at 1,200 bar, 1 at 1 bar), the net amplitude of the burst phase is +0.2 and the amplitude of the ms phase is −0.4 (absolute changes in fluorescence decays are shown in SI Appendix, Fig. S4). The fast phase associated with protein refolding has a relaxation time τ_f ≤ 3 μs, and the slower phase fits to a single-exponential lifetime of τ_s = 1.4 ± 0.2 ms. The T-jump unfolding relaxation kinetics from Prigozhin and Gruebele (23) at 339 K are also shown for comparison. A ≈60-μs phase of increasing lifetime was observed in that case, followed by a small millisecond phase attributed to a β-sheet-rich trap in the studies by Bowman et al. (22) and Prigozhin and Gruebele (23).

Fig. 3.

P-jumps (300-μM sample) and T-jumps (200-μM sample) of λ*YA and NATA, probed by tryptophan fluorescence decays. Tryptophan lifetime change was normalized for NATA so that χ = 0 corresponds to the decay lifetime before the jump (1,200 bar) and χ(t) = 1 corresponds to the decay lifetime 5 ms after the jump (1 bar). The rest of the jumps were analyzed using the lifetime decays from the P-jump of NATA for direct comparison. Solid black curves are the double-exponential fits of the data with relaxation times τ_f = 3.8 ± 0.4 μs and τ_s = 1.4 ± 0.2 ms for the P-jump and τ_f = 63 ± 2 μs and τ_s = 2.17 ± 0.02 ms for the T-jump.

These observations are consistent with two scenarios. In one scenario, separate microsecond- and millisecond-folding populations start out from two slowly interconverting pressure-denatured states and proceed to the native state, where W22 is quenched by Y33. Slow interconversion is not implausible at high pressure, given the potentially large activation volume between compact denatured states. In the other scenario, the entire denatured protein population is trapped in a partially folded state within 3 μs, from which it escapes to the native state within 1.4 ms. In both scenarios, it is also possible that transient aggregation contributes to the slow millisecond phase.

Pressure Denaturation Probed by IR Absorption.

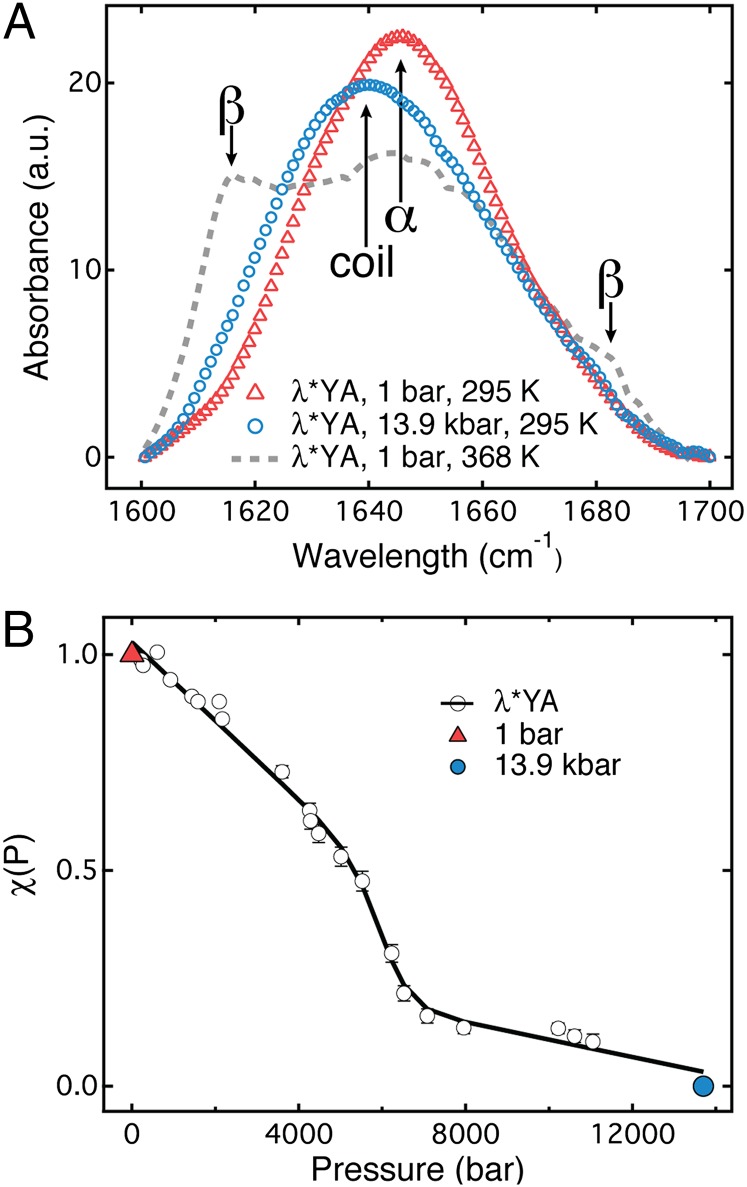
To relate the slow phase on P-drop refolding of λ*YA to secondary structure, we used IR absorption spectroscopy. IR spectroscopy has been successfully applied in the past to resolve the secondary structure content of proteins under high pressure (16). We carried out equilibrium pressure denaturation of λ*YA in a diamond anvil cell. We monitored pressure-induced changes in the amide I′ region (prime denotes measurements in D₂O solvent) from 1,600 to 1,700 cm⁻¹. This region contains vibrational information about the carbonyl group in the amide bonds, which depends on the dihedral angles of the backbone, and therefore the secondary structure of the protein. The crystallographic state of λ*YA is 71% helical [Protein Data Bank (PDB) ID code 3KZ3 (13)]. The IR spectrum of a helix in the amide I′ region contains a single band with a peak wave number at ∼1,650 cm⁻¹. Under pressure, the protein is expected to lose at least some of its helical content in favor of the random coil structure. The spectrum of a random coil exhibits a characteristic maximum at ∼1,640 cm⁻¹.

Fig. 4A shows IR spectra of λ*YA in the absence of denaturant, one recorded at 1 bar and the other recorded at 13.9 kbar. The absorption maximum shifts from 1,650 cm⁻¹ (helix) toward 1,640 cm⁻¹ (coil) on pressure denaturation. The two spectra were used as basis functions to fit a sequence of λ*YA spectra as a function of pressure. A linear combination of these two basis functions fitted data at all pressures within measurement uncertainty (SI Appendix, Fig. S5). Fig. 4B shows the pressure denaturation curve, along with a two-state thermodynamic fit (27). The data without denaturant show a transition midpoint at 6.0 ± 0.2 kbar. Helix-coil denaturation is also observed in 0.5 M guanidine deuteriochloride (GuDCl) by IR spectroscopy, and the absence of aggregation can be verified in 2.4 M GuDCl (SI Appendix, Fig. S7).

Fig. 4.

Equilibrium denaturation of λ*YA by pressure and temperature, probed by IR spectroscopy (1.7-mM sample). (A) IR absorbance spectra of λ*YA in the amide I′ region measured at 295 K. Triangles indicate 1 bar, and circles indicate 13.9 kbar. These spectra were used as basis functions for the analysis of the entire pressure denaturation curve (Methods and SI Appendix). The IR absorbance spectrum of λ*YA in the amide I′ region measured at 1 bar and 368 K is shown as a gray dashed line. (B) Denaturation of λ*YA as a function of pressure [χ(P) = 1 means the 1-bar basis function contributes 100% of the signal, χ(P) = 0 means the 13.9-kbar basis function contributes all the signal]. A thermodynamic two-state fit of the data is shown as a solid black curve, and the error bars are the residuals (SI Appendix, Fig. S5). The midpoint of pressure denaturation, P_m, is equal to 6.0 ± 0.2 kbar in the absence of denaturant.

Temperature denaturation produces an entirely different result. The gray curve in Fig. 4A is the IR spectrum at 1 bar and 368 K. At 335 K, the protein undergoes a cooperative thermal denaturation. Two shoulders at 1,618 cm⁻¹ and 1,680 cm⁻¹ appear, due to formation of extended [β-sheet or left-handed polyproline helix (PP-II)] structure at high temperature. Extended structure in temperature/GuHCl-denatured λ-repressor can occur in the monomeric protein (17). Indeed, at the protein concentration of 2.5 μM, temperature denaturation is reversible (SI Appendix, Fig. S3). However, the IR measurement was taken at a much higher concentration (1.7 mM), and above 50 μM, denaturation is irreversible and aggregates form (SI Appendix, Fig. S3).

In contrast, SI Appendix, Fig. S6 shows full reversibility of pressure denaturation at the protein concentration used for our pressure jumps, and Fig. 4A shows no evidence of β-sheet structure. Thus, the pressure-denatured state of λ*YA is very different from the temperature-denatured state. The denatured state preceding the downward P-jump in Fig. 3 is a helix-coil state, rather than a β-rich state as proposed for high-temperature kinetics (22, 23). Without any evidence at all of equilibrium pressure-dependent aggregation with or without denaturant (SI Appendix, Fig. S6), we also think that transient aggregation is unlikely to dominate the slow 1.4-ms phase in the two scenarios described above, but we cannot rule out transient interactions of the helix-coil states during folding.

P-Denaturation and P-Jump Refolding Probed by MD Simulation.

To probe fast protein refolding on downward P-jump with atomistic detail, we carried out all-atom MD simulations in explicit solvent with four force fields: CHARMM27, CHARMM22*, CHARMM36, and AMBER99-SB (28–33) (Methods).

Initial denatured structures at 325 K and 5 kbar were created by a 0.3-μs heating/pressurization protocol (Methods, SI Appendix, Fig. S8, and Movie S1). The protocol differs in three important aspects from experiment. No denaturant is included in the simulation. MD pressure unfolding was assisted by high temperature because pressure unfolding alone is very slow. Finally, refolding was studied at 325 K instead of 295 K because the melting point of λ-repressor is too high in CHARMM27 and CHARMM22*; thus, 325 K in silico correlates with a lower experimental temperature (31).

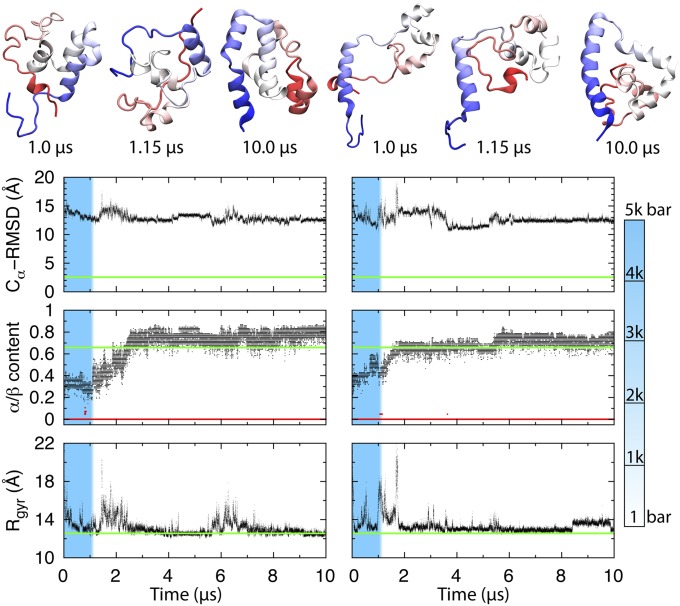
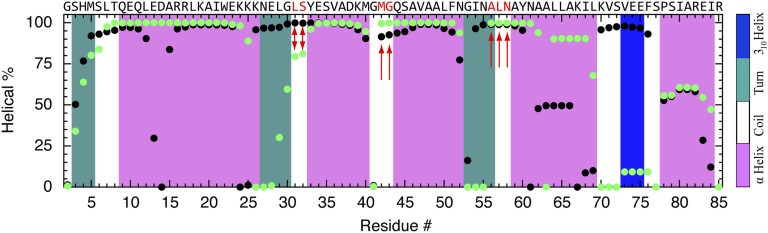
Two fast pressure drops were simulated with CHARMM27 (Fig. 5). Analogous results for CHARMM36 and AMBER99-SB are shown in SI Appendix, Fig. S10. The two refolding trajectories in Fig. 5 collapse rapidly into structures with near-native radii of gyration, making occasional excursions to a larger size in the search for the native state. Both accumulate nonnative helical structure within 2 μs after the P-jump (SI Appendix, Fig. S9). The first trajectory yields a compact helical globule. The second trajectory produces a conformation much closer to the native state (SI Appendix, Movie S2), with helices 1–3 formed and packed into the correct native orientation (SI Appendix, Fig. S9 and Movie S3). However, helix 4 is threaded through the ring formed by helices 1–3, creating a knotted conformation (Fig. 5, Upper Right). In Fig. 6, the α-helical propensity for each residue is given based on the time percentage spent in α-helical conformation in the last 8 μs of each simulation. Both trajectories form nonnative helix, where there should be turns or loops in the native state (red arrows in Fig. 6). A compact trap with helix misplaced into loops that persists for >10 μs is consistent with the experimental data of a slowly (1.4 ms) refolding state formed from a helix-coil-rich denatured state right after the P-jump.

Fig. 5.

CHARMM27 simulation of λ*YA during P-drop. (Upper) Structures from the two trajectories. The high-pressure simulations start with 1 μs at 325 K and 5 kbar (blue zone), followed by a 0.15-μs P-drop to 1 bar (white zone). (Lower) Refolding (8.85 μs) was simulated at 1 bar and 325 K. Central carbon atom root mean square displacement values were calculated relative to the crystal structure (PDB ID code 3KZ3) (13). The fraction of residues in α (gray) and β (red) conformations is shown. R_gyr is the unsolvated radius of gyration. The native mean values (green solid lines, except red for β-fraction) are from a 150-ns equilibrium simulation of the native structure at T = 325 K and P = 1 bar.

Fig. 6.

Residue-specific α-helical propensity of the simulations in Fig. 5 (black, first simulation; green, second simulation). The helical percentage was defined as the time percentage each residue spent in α-helical conformation during the last 8 μs of refolding simulation. The secondary structure of the crystal structure is shown as a color-coded background, and the sequence at the top, together with the red arrows, highlights turn/coil residues with >75% helix content in both simulations.

MD Simulations Using Different Force Fields.

Protein dynamics in MD simulations depends on the underlying force field. CHARMM27 with correction map (30) has a bias toward helical structure (e.g., ref. 21). In contrast, our CHARMM36 and AMBER-99SB simulations with the exact same protocol produce virtually no helix in the initial denatured structure (SI Appendix, Fig. S8), nor do they produce any native-like structure or a helical trap on P-drop (SI Appendix, Fig. S10).

We examined if the initial configuration of the protein is responsible for inability of helical structure to form rapidly. We started with the AMBER-99SB denatured structures from SI Appendix, Fig. S8 and then simulated the P-drop with CHARMM27 and CHARMM22* force fields at T = 325 K and P = 1 bar (SI Appendix, Fig. S11). The CHARMM22* force field has both folded helical-rich protein and β-rich protein (34). Although there is almost no helix left in the initial configuration, the helix recovered to near-native value in less than 1 μs with CHARMM27. In a 10-μs simulation using CHARMM22*, helix content becomes significant, although it never exceeds the native value. Like CHARMM27, CHARMM22* exhibits a nonnative helical propensity in several turn/coil residues (M42, G43, A56, L57, and N58 in SI Appendix, Fig. S12).

CHARMM22* and CHARMM27 are thus most consistent with our experimental data. Although there is a strong helical bias in the CHARMM27 force field, another variant of λ-repressor was folded successfully in a high-temperature enhanced sampling MD simulation using CMARMM27 force field (35). The high temperature used in the current study likely compensates for the helical bias in the force field to match up best with the experiment.

Discussion

Fast-folding experiments and simulation have converged to the point where several small proteins’ folding equilibria have been observed in silico and validated by kinetic, structural, and thermodynamic experimental data (34–36). The same small model proteins, under the right conditions, now offer the opportunity to study delays in folding caused by a frustrated free energy landscape or transient aggregation. The advantage of these model proteins is that their misfolding processes can also be quite rapid, and are thus amenable to simulation (22).

The formation of helical secondary structure requires only local i to i + 4 contacts. Thus, it is not surprising that helical intermediates that trap proteins en route to the native state have been reported for a wide variety of proteins (18–20). However, these excess helix traps have generally been observed under cryogenic conditions.

Here, we provide experimental and computational evidence that the five-helix bundle λ*YA can get trapped transiently in states with misplaced helix at room temperature and 1 bar, when folding is initiated from the pressure-denatured state. Pressure unfolding experiments reveal a highly reversible denatured ensemble with helix-coil composition (Fig. 4 and SI Appendix, Fig. S6), and ultrafast P-jump refolding from this ensemble detects a 1.4-ms phase in addition to a microsecond phase (Fig. 3). All-atom MD simulations show that after a P-jump, refolding trajectories can get stuck in structures with helix misplaced into loops for >8 μs. MD results for CHARMM27 and CHARMM22* are consistent with some fraction of the λ*YA population being trapped in a state containing nonnative helix within ≤3 μs, from which it recovers in ∼1.4 ms according to experiment (possibly slowed further by transient aggregation). This refolding pathway is very different from refolding out of the thermally denatured state; in that state, the protein folds in <100 μs (12) and, if not, it either aggregates irreversibly or is trapped in a state with extended (β-like) structure, based on simulation (22) and thermal titrations (17) (SI Appendix, Fig. S3).

Even for a helix bundle such as λ_6–85, there can be too much of a good thing. When nonnative helix encroaches on turns, it renders them unable to align the secondary structure elements so that they can assemble into the proper native tertiary structure. The “knotted” state in Fig. 5 is a good example. Fig. 6 highlights in red the turn/coil regions of λ*YA that are particularly prone to forming nonnative helix. In both simulations, L31, S32, M42, G43, A56, L57, and N58 exhibit ≥80% average helical populations. According to the scale of Pace and Scholtz (37), the helical propensity for these residues is A>L≈M>S>N>G. Thus, we propose that helix-breaking mutations L31G, M42G, A56G, and L57G in particular could reduce the transient trapping of λ-repressor fragment when it refolds from the P-denatured state.

Pressure denaturation of fast folders could provide a rich test bed for calibrating force fields against experimental data, by looking at transient nonnative structure in addition to native structure. The advantage of small fast folders in this regard is that such nonnative structures can form and dissolve on time scales accessible to full atom simulation, enabling comparisons of mechanism beyond rate coefficients, stability, or native structure.

Methods

Protein Expression and Purification.

λ*YA was expressed as described previously (27). GuHCl, deuterium oxide 99.9% (D₂O), and NATA were obtained from Sigma–Aldrich and used without further purification.

P-Jumps.

P-jumps with a home-built apparatus are described in detail elsewhere (5). Briefly, 300 μM protein solution was pipetted into an ∼8-μL hemispherical dimple machined in-house into an optical grade 3/8-inch sapphire cube (Esco Products). The dimple was then covered with a double-layer of mylar-coated aluminum foil to prevent mixing of the sample with ethanol, which served as the pressurization fluid. The cube was inserted into a pressurization clamp as described elsewhere (5), and the sample was pressurized to 1.2 kbar using a hydrostatic pump (High Pressure Equipment Company). We used 0.007-inch-thick stainless-steel burst membranes and 95 V (∼10-kA current) to burst the membrane.

The sample was excited by a Ti:sapphire laser (KMLabs). The laser emission at 840–860 nm was frequency-tripled to 285 ± 3 nm. The laser was adjusted to a pulse rate of 80 MHz. Tryptophan fluorescence decay was collected by means of an optical waveguide (Oriel) every 12.5 ns and passed through a B370 band-pass filter (Hoya) onto a photomultiplier (R7400U-03; Hamamatsu Corp.). The fluorescence decays were recorded by a DPO7254 digitizer (Tektronix) with 2.5-GHz bandwidth, locked to the 80-MHz laser cavity to avoid aliasing. Each kinetic trace contained 400,000 fluorescence decays. Each fluorescence decay was sampled at 10 GHz (125 points per decay). The amplitude of the fluorescence signal was 100–250 mV.

The data were analyzed using custom code written in LabView (National Instruments), MATLAB (MathWorks), and IGOR Pro (Wavemetrics). One hundred raw fluorescence decays were binned into average decays every 1.25 microseconds, reducing the time resolution to a value comparable to the dead time of the P-jump. To assign a single lifetime parameter to each fluorescence decay, we fitted them to the linear combination of a prejump and postjump fluorescence decay. We averaged the first 100 decays of the time trace to get a representative decay f₁ before the P-jump and the last 100 decays at 5 ms to get a representative decay f₂ after the P-jump. Decays between these two P-jumps were fitted by f = a₁f₁ + a₂f₂, and the fraction contributed by the second decay was calculated as χ = a₂/(a₁ + a₂). Thus, a decay with the same lifetime as before the jump yields χ = 0, and a decay with the same lifetime as at 5 ms yields χ = 1. We fit the resulting time trajectory to a double-exponential function A_fexp(−t/τ_f) + A_sexp(−t/τ_s).

Fluorescence Thermodynamics Under Pressure.

Fluorescence spectra were measured using a Cary Eclipse fluorescence spectrophotometer (Varian). Excitation and emission slit widths were 5 nm each, excitation wavelength was 280 nm, and the scan rate was 120 nm/min. Sample concentration was 200 μM. The sample was pressurized with a high-pressure cell (ISS). We used a rectangular quartz cuvette with a path length of 4 mm. Spectrophotometric grade ethyl alcohol (95.0%, A.C.S. reagent; Acros Organics) was used as pressurization fluid. The center of the spectral mass in Fig. 1B is the weighted average 〈I〉=∫dλ λ I(λ)/∫dλ I(λ) of the fluorescence intensity in Fig. 1A (6).

IR Thermodynamics Under Pressure.

Lyophilized protein was dissolved in 50 mM K₃PO₄ buffer in D₂O (Sigma), and D₂O exchange was allowed to proceed for 2 h at room temperature and then overnight at 4 °C. The protein was then lyophilized again. For the measurement, the protein was dissolved in 50 mM K₃PO₄ buffer in D₂O at pD = 7.1 to the final concentration of 1.7 mM. pH of deuterium (pD) was adjusted using DCl. Approximately 10 μL of the sample was then placed in a diamond anvil cell equipped with type IIa diamonds (High Pressure Diamond Optics). The sample was held in a stainless-steel gasket (overall diameter = 12.5 mm, center pinhole diameter = 0.45 mm, thickness = 0.050 mm). The gasket was secured in the diamond anvil cell using gum from Faber–Castell (127020). A small amount of BaSO₄ was placed in the chamber with the sample. IR spectra were collected using a Nicolet Magna IR 550 spectrometer equipped with a nitrogen-cooled mercury cadmium telluride (MCT) detector. The sample chamber within the instrument was purged with dry CO₂-free air. The IR beam was focused onto the pinhole of the diamond anvil cell. Spectra were collected from 400 to 4,000 cm⁻¹ using 256 accumulations and a resolution of 1 cm⁻¹. Pressure was increased using the spring-loaded screw of the diamond anvil cell assembly. Changes in the pressure were quantified by monitoring the stretching vibration of the calibrant, BaSO₄. Its peak was at 983.6 cm⁻¹ at 1 bar and shifted linearly with pressure toward larger wave numbers.

All-Atom MD Simulations.

All-atom MD simulations were performed in explicit solvent using the TIP3P water model (38). The simulations were carried out both on general-purpose supercomputers using NAMD 2.8 (39) and on the special-purpose supercomputer Anton (40). All simulations were carried out with periodic boundary conditions in constant particle number, temperature and pressure ensemble. More details of the simulations are given in SI Appendix.

To generate two initial states for P-drop simulations, we started with λ*YA constrained to the PDB structure (PDB ID code 1LMB) (41) at 325 K. The pressure was increased from 1 to 5 kbar in 0.15 μs. The temperature was then ramped to 525 K for another 0.15 μs to unfold the protein more extensively (SI Appendix, Fig. S8). Finally, the simulation was returned to 325 K and 5 kbar to yield the initial states for the P-drop simulations.