Structure and Dynamics of Urea/Water Mixtures Investigated by Vibrational Spectroscopy and Molecular Dynamics Simulation

Abstract

Urea/water is an archetypical “biological” mixture, and is especially well known for its relevance to protein thermodynamics, as urea acts as a protein denaturant at high concentration. This behavior has given rise to an extended debate concerning urea’s influence on water structure. Based on a variety of methods and of definitions of water structure, urea has been variously described as a structure-breaker, a structure-maker, or as remarkably neutral towards water. Because of its sensitivity to microscopic structure and dynamics, vibrational spectroscopy can help resolve these debates. We report experimental and theoretical spectroscopic results for the OD stretch of HOD/H₂O/urea mixtures (linear IR, 2DIR, and pump-probe anisotropy decay) and for the CO stretch of urea-D₄/D₂O mixtures (linear IR only). Theoretical results are obtained using existing approaches for water, and a modification of a frequency map developed for acetamide. All absorption spectra are remarkably insensitive to urea concentration, consistent with the idea that urea only very weakly perturbs water structure. Both this work and experiments by Rezus and Bakker, however, show that water’s rotational dynamics are slowed down by urea. Analysis of the simulations casts doubt on the suggestion that urea immobilizes particular doubly hydrogen bonded water molecules.

I. INTRODUCTION

The urea/water system has attracted much attention over the last few decades for several reasons. First, urea is well-known for its ability to denature proteins at high concentrations. Second, urea is of more general biological importance,¹ and a thorough understanding of concentrated urea/water mixtures should aid the attempt to understand more complex, crowded biological solutions. Finally, urea is an important test case for the aqueous solvation of a neutral species with mixed hydrophilic and hydrophobic character, since the oxygen and hydrogen atoms offer hydrogen-bonding sites, while the carbon and nitrogen atoms are not involved in such strong, short-range interactions and instead behave as hydrophobic centers.^2–4

A number of studies suggest that urea is a remarkably non-perturbative solute in water. It is well-known that urea’s activity coefficient is essentially constant over its entire solubility range on the molar scale;^5,6 this indicates that urea-water energetic interactions are very well-balanced with water-water and urea-urea interactions. The relative ideality of urea/water mixtures is also supported by NMR,⁷, THz absorption,⁸ calorimetry,⁹ and dielectric spectroscopy.¹⁰ From a microscopic perspective, simulation^2,11–14 and neutron scattering¹⁵ have found urea to have little effect on metrics such as the water-water hydrogen-bond angle and the three-dimensional distribution of first solvation shell water around a central water. Accordingly, the so-called “indirect model” for protein denatura-tion, in which urea acts as a water “structure-breaker” and causes protein-water interactions to become relatively more favorable by weakening water-water interactions,^16,17 has fallen out of favor, particularly in light of mounting evidence for a “direct model” based on favorable urea-protein interactions.^5,9,18–41

In an attempt to rationalize the ideality of urea/water mixtures, it has been suggested that urea can substitute for a water dimer in water’s hydrogen bond network.⁴² However, a comparison of the urea and water partial molar volumes measured by densitometry⁴³ indicates that each urea molecule replaces about 2.45 water molecules, rather than 2, as this hypothesis implies. It is, indeed, natural to suppose that urea cannot be truly neutral towards water structure, and claims linger that urea acts as a slight structure-breaker^14,44,45 or structure-maker^46,47 in water, and that indirect effects might be relevant for denaturation.^{14,44,47–51} To cite a few examples, urea has been called a structure-breaker (or “structure disrupter”) on the basis of simulations showing its negative impact on the tetrahedrality of the water oxygen network⁴⁵ and of neutron diffraction results revealing a disordering of the second coordination sphere of water around water.^15,52 It has also been called a slight structure-maker on the basis of thermodynamic (Kirkwood-Buff) analysis showing that urea-water interactions become relatively slightly less favorable as the urea concentration increases.⁴⁶ We note here that the first two examples employ a geometric, and the final example an energetic, criterion for structure-breaking and structure-making.

Due to its sensitivity to the details of molecules’ local environment and dynamics, vibrational spectroscopy holds promise as a means for resolving some of these questions.⁵³ For example, by measuring the OH-stretch absorption spectrum of water as a function of urea concentration, one can hope to learn about how urea perturbs water’s local structure. Such an experiment, however, is complicated by OH-stretch coupling,⁵⁴ which delocalizes the vibrational eigenstates and renders the spectroscopic probe less local. To overcome this difficulty, one can study dilute HOD in H₂O (D₂O), in which case the significant mismatch between OH- and OD-stretch frequencies makes the coupling ineffective, so that the OD (OH) stretch functions as a local chromophore. For example, Sharp et al. measured the OH-stretch absorption spectrum of relatively dilute (10%) HOD in D₂O in the absence and presence (at 5 M) of urea-D₄ and concluded from the lack of significant change in the spectrum that the structure of the water network is almost unaffected by urea.¹¹

An alternative is to measure CO-stretch spectroscopy of urea, as a function of urea concentration. (As urea is present at lower concentration, vibrational coupling is probably less important in this case, and there is less need to isotopically label the C and/or O atoms of urea.) To this end, Grdadolnik and Maréchal⁵⁵ measured spectra of urea-H₄ in H₂O and urea-D₄ in D₂O, as a function of urea concentration. The spectra in the CO-stretch region for the H₂O solution is complicated by the presence of, and coupling to, the NH₂ bends, while in the D₂O solution the ND₂ bends are shifted to significantly lower frequency, leading to cleaner CO-stretch spectra. In the latter case, the CO-stretch spectrum hardly changes with increasing urea-D₄ concentration, again suggesting that urea does not significantly perturb water structure.

To our knowledge, only one ultrafast spectroscopic study has focused on the dynamics of urea/water mixtures.⁴² In this experiment, Rezus and Bakker examined the OD stretch of relatively dilute (8%) HOD in H₂O for urea concentrations ranging from 0 to 7.8 M. They measured the pump-probe anisotropy, which in the dilute-HOD limit reflects single-molecule rotational relaxation, and found that the reorientation of water is significantly slowed by concentrated urea. The results were explained via a two-component model in which a fraction of water molecules had drastically slowed rotations due to forming simultaneous hydrogen bonds with urea oxygen and hydrogen, while most molecules had bulk-like dynamics.⁴² (A similar division between unperturbed and strongly bound water molecules has also been invoked in the interpretation of results from THz absorption⁸ and dielectric spectroscopy.¹⁰)

Although a large number of molecular dynamics simulation studies have focused on the structure, dynamics, and thermodynamics of urea/water mixtures,^{3,4,11,45,47,56–66} we are not aware of any theoretical studies of vibrational spectroscopy for this system. In this paper, we develop a theoretical approach for studying the CO-stretch spectroscopy of urea in aqueous solution. We present theoretical results for CO-stretch absorption line shapes of urea-D₄ in D₂O as a function of urea concentration. We also use our existing methods^67,68 to calculate absorption and 2DIR OD-stretch spectra of dilute HOD in H₂O, as a function of urea concentration. For this same system, we also calculate the anisotropy decay,^69,70 and compare directly to the experiments of Rezus and Bakker.⁴²

In order to provide experimental comparisons for some of these calculations, we measure experimental absorption line shapes for urea-D₄ in D₂O (as mentioned above, similar experiments were performed by Grdadolnik and Maréchal,⁵⁵ but not at the urea concentrations we have simulated). We also measure absorption line shapes for dilute (2%) HOD in H₂O at different urea concentrations (recall that Sharp et al.¹¹ have measured similar spectra, but for HOD in D₂O, and at a higher chromophore concentration, where residual coupling effects may be evident).

For the absorption spectra, theory and experiment are in reasonable agreement, and show only a weak dependence on urea concentration, consistent with the idea that urea does not appreciably perturb water structure. Our anisotropy decay results are also in reasonable agreement with experiment,⁴² and our theoretical 2DIR spectra show a similar slow-down (in this case for spectral diffusion, which is related to hydrogen-bonding dynamics) with increasing urea concentration. Thus, while urea may not perturb the structure of water, it does indeed perturb its dynamics.

II. METHODS

A. Simulation Details

Although a number of urea (OPLS,⁷¹ KBFF,⁶⁰ CHARMM,⁷² AMBER*^73,74) and water (SPC/E,⁷⁵ TIP4P,⁷⁶ TIP3P⁷⁶) potentials are reasonable choices for study, here we consider only the KBFF-SPC/E pair, since this potential has been found to reasonably model urea/water mixtures in previous studies,^4,60,63 and since we have already developed substantial spectroscopic infrastructure for use with the SPC/E potential.^67,68 (“KBFF” stands for “Kirkwood-Buff Force Field”; this model was designed to reproduce the experimental Kirkwood-Buff integrals, which are related to the degree of urea aggregation and the urea activity coefficient.⁶⁰) Parenthetically, we mention here that have also examined the OD-stretch spectroscopy of the OPLS-TIP4P pair using our methods for TIP4P water^77,78 (results not shown). The results were generally inferior to those for KBFF-SPC/E; the linear spectra exhibited a significant blue-shift with urea concentration, and little slow-down was seen in the anisotropy and 2DIR.

For the OD-stretch spectroscopy of dilute HOD in H₂O, we actually simulated urea-H₄ in pure H₂O, and tagged one or more water H atoms to be the putative OD chromophores.⁷⁹ For the urea spectroscopy, we simulated urea-D₄ in D₂O. All simulations were performed using GROMACS-4.5.3.⁸⁰ Initial configurations were built by randomly placing first urea, then water molecules in a cubic simulation box with edge length 4.05 nm, using the genbox utility of GROMACS. Due to the typically high potential energy of these initial configurations, systems were first equilibrated under NVT conditions (T = 298 K) for 20 ps using a 0.2 fs time step and a very fast (τ = 0.001 ps) Berendsen thermostat. Systems were then further equilibrated under NPT conditions for 2 ns using a 1 fs time step, PME for electrostatics, a 1.8 nm cutoff for dispersion interactions, and a Berendsen thermostat (τ = 0.05 ps) and barostat (τ = 1.0 ps). (The equilibration time required to achieve proper mixing has been discussed at length by Sokolić et al.;⁵⁹ their results indicate that 2 ns should be more than adequate.) Production runs were then carried out under NPT conditions for 2 ns (1 ns for pure water simulations) using a 1 fs timestep, PME for electrostatics (Fourier grid spacing 0.076 nm), a 1.8 nm cutoff for dispersion interactions, a Nosé-Hoover thermostat (τ = 2 ps, T = 298 K), and a Parrinello-Rahman barostat (τ = 6 ps, P = 1.01325 bar, β = 2.755×10⁻⁵ bar⁻¹). Configurations were output every 5 fs. For further simulation details, see Table I.

TABLE I.

Selected simulation details for KBFF-SPC/E runs.

Nominal urea concentration (M)	Actual urea concentration (M)	N (urea)	N (water)	Average box length (nm)
0	0.00	0	2213	4.0494
0.5	0.52	21	2163	4.0508
4	4.02	161	1818	4.0510
8	8.03	321	1420	4.0493

The box lengths of the four NPT simulations shown in Table I are all very similar. Therefore, one can easily see for example that for the 0.5 M solution, 21 urea molecules replace 50 water molecules, or each urea molecule replaces 2.38 water molecules (on average). This is in quite good agreement with the experimental value of 2.45.⁴³ Moreover, at higher urea concentration, urea’s molar volume increases slightly, as in experiment.⁴³

B. Calculation of Spectroscopic Observables

The calculation of linear IR,^68,81,82 2DIR,^67,81,83 and anisotropy decay^69,70,84 observables within the mixed quantum-classical approximation has been described in previous publications. For example, for the linear absorption spectrum of an isolated chromophore we use

$$I(\omega )~\text{Re}{\int }_0^{\infty }dt{e}^{i\omega t}\langle {\mu }_{10}(0){\mu }_{10}(t)\text{exp}[-i{\int }_0^{t}d\tau {\omega }_{10}(\tau )]\rangle e^{-t/2T_1},$$ (1)

where the angular brackets denote an average over the ensemble in the classical simulation, and T₁ is the vibrational lifetime: 1.8 ps for HOD/H₂O⁸⁵ and 0.29 ps for urea (from pump-probe results, not shown). ω₁₀(t) is the chromophore’s fluctuating 1-0 transition frequency, and µ₁₀(t) is the projection of the fluctuating transition dipole onto a lab-fixed unit vector (the polarization of the light electric field).

To determine a chromophore’s transition frequency from a simulation snapshot we use electric-field maps.^67,86 For the OD chromophore of SPC/E water, the relevant electric field is at the D atom and projected along the OD bond, and the frequency formula⁸⁷ is given in Table II. For the urea CO stretch, we base our map on our previous work for acetamide⁸⁶ (a molecule similar to urea, but with one NH₂ group replaced by CH₃). In that case, the map involved the electric fields on the C and N atoms and in the CO bond direction. Here, we simply extend the map by adding the same contribution for the second NH₂ group, as shown in Table II. (Note that because this map was parameterized for use with SPC water, SPC point charges were used for the frequency calculation, although the simulations were still performed with SPC/E water. For both maps, the electric field of urea is calculated using the KBFF point charges.)

TABLE II.

Mapping relations for calculation of spectroscopic observables. For HOD, E is the electric field (in atomic units) at the D atom and along the O-D bond; for urea, E_C is the electric field at the C atom and along the C=O bond, and E_Ni is the electric field on N atom i and in the C=O bond direction. ω₁₀ and ω₂₁ are the vibrational frequencies in cm⁻¹, µ′ is the dipole derivative (in atomic units), and x₁₀ and x₂₁ are the position matrix elements (in atomic units).

SPC/E water OD stretch

ω10 = 2762.6 – 3640.8E – 56641E2

ω21 = 2695.8 – 3785. 1E – 73074E2

µ′ = 0.1333 + 14.17E

x10 = 0.16627 – 2.0884×10−5ω10

x21 = 0.23228 – 2.8822×10−5ω21

Urea CO stretch

ω10 = 1714 + 2154EC + 3071(EN1 + EN2)

For HOD, we take the transition dipole to point along the OD bond, and use an electric-field map to describe the non-Condon effect (the magnitude of the transition dipole depends on the molecular environment).⁸⁸ µ₁₀ is therefore given by

$${\mu }_{10}=\mu \prime x_{10}\widehat{u}\cdot \widehat{\epsilon },$$ (2)

where û is the OD unit vector and ε̂ is a unit vector in an arbitrary lab-fixed direction. The maps⁸⁹ for µ′ and x₁₀ are given in Table II. For the CO stretch we make the Condon approximation (the magnitude of the transition dipole is constant).⁸⁶

For 2DIR calculations, we additionally require the 2-1 transition frequency, and x₂₁ (for the dipole for this transition),⁶⁹ which are also given in Table II for the OD stretch. For the anisotropy decay calculations for a finite fraction of OD chromophores, we also need to include intramolecular and intermolecular vibrational coupling, as described previously^68,89 Theoretical expressions for calculating 2DIR spectra and (frequency-integrated) anisotropy decay are given elsewhere.^69,70,83

C. Samples

Urea (ACS reagent grade) was purchased from EMD Chemical, and urea-D₄ (98+ atom %D) and D₂O (99.9 atom %D) were purchased from Sigma-Aldrich; all were used without further purification. H₂O was obtained from an in-house filtration system. For water OD-stretch spectra, 5 µL of the appropriate solutions were transferred to a CaF₂ infrared cell with a 56 µm Teflon spacer. For urea-D₄ CO-stretch spectra, 5 µL of the appropriate solutions were transferred to a CaF₂ infrared cell without a spacer. Samples were kept under dry air to prevent hydrogen exchange with ambient water vapor.

D. Measurement and Processing of Linear Absorption Spectra

Spectra were collected over the range 400–4000 cm⁻¹ and at 1 cm⁻¹ resolution using a Thermo Scientific Nicolet iS10 spectrometer with a dry air-purged sample chamber. All spectra were measured in absorbance mode but were subsequently converted to line shape via the relation:

$$I(\omega )~\frac{A(\omega )}{\omega (1-e^{-\beta \hslash \omega })},$$ (3)

where I(ω) is the line shape, A(ω) the absorbance, ω the frequency, and β = 1/kT. For water spectra, the contribution from the OD stretch was found via subtraction of the pure H₂O spectrum from the 2% HOD spectrum at the same urea concentration. For urea spectra, a baseline correction was applied, and spectra were smoothed using a 40-point FFT filter, to minimize the absorption lines of residual water vapor in the sample chamber.

III. RESULTS AND DISCUSSION

A. Linear IR Spectra of the Water OD Stretch

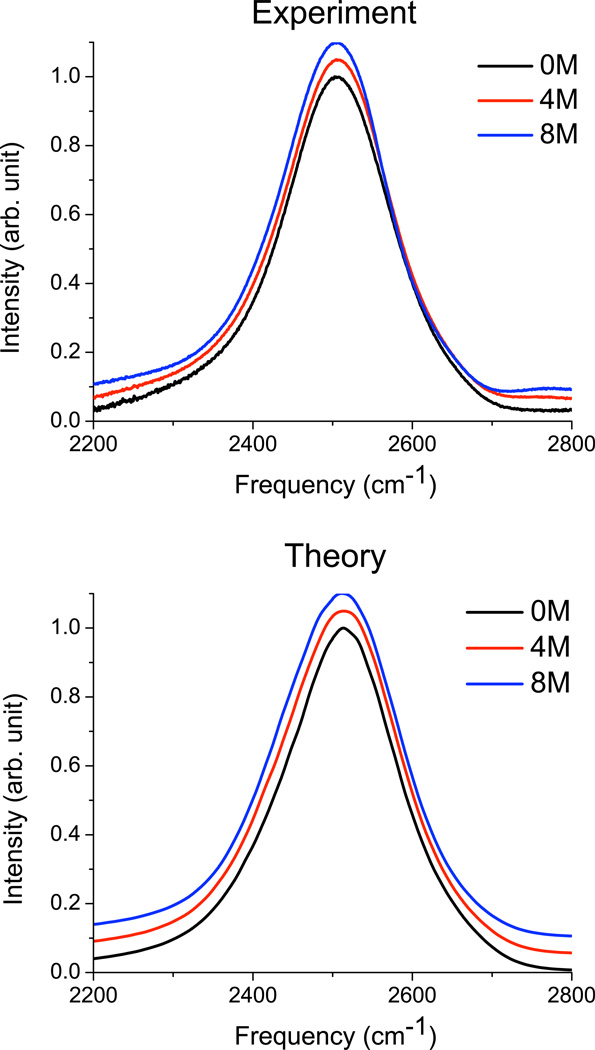
Experimental and theoretical spectra for dilute HOD in urea-H₄/H₂O at 0, 4, and 8 M urea are presented in Figure 1; peak positions and line widths are given in Table III. The experiment is at ∼2% HOD, while the calculated spectra are for a single HOD in an otherwise protonated solution. For the experimental spectra, there is a possible complication due to the fact that the urea ND stretching mode is expected to absorb in a similar region to water OD.⁵⁵ However, subtraction of the 0 M spectrum from that at 8 M did not reveal any significant peaks in the OD-stretch region. In addition, fitting the data at each concentration to a sum of two Lorentzian line shapes yields an excellent fit at each concentration (r² > 0.9999), with the peak positions remaining essentially unchanged with concentration (though the relative amplitudes change considerably); the emergence of a distinct urea ND peak is not discernible. Thus, it seems that the urea ND absorption must either be significantly shifted from the water OD, or else essentially overlapped. In the latter case, it is possible that the experimental spectral narrowing is actually due to the growth of a narrower urea band, as concluded by Sharp et al.¹¹

FIG. 1.

Experimental and theoretical spectra for OD stretch of dilute HOD in H₂O, as a function of urea concentration. Spectra are peak normalized. For clarity, spectra at 4 M urea are offset by 0.05, and spectra at 8 M urea are offset by 0.12.

TABLE III.

Comparison of spectroscopic parameters for water OD stretch (peak position and full-width at half maximum in cm⁻¹).

[urea] (M)	ωpeak, theory	ωpeak, exp	FWHM, theory	FWHM, exp
0	2514.3	2506.3	171.3	160.8
4	2514.3	2506.9	179.0	157.8
8	2512.0	2505.8	180.8	151.6

Agreement between theory and experiment is very good. Table III shows that the peak position in both theory and experiment is essentially independent of urea concentration, and the width changes only slightly (although it actually decreases slightly in experiment, and increases slightly in the theory). Through careful analysis not presented in detail here, one can show that the lack of change in the spectrum is actually due to the cancellation between a small (∼1 cm⁻¹/M urea) blue-shift due to the relative weakness of the urea NH-water OD interaction as compared to the water OH-water OD interaction, and a similarly sized red-shift due to a slight favoring of linear hydrogen bond geometries in urea’s first solvation shell. These effects are quite small, however, and we conclude, in agreement with the complementary HOD/D₂O experiments of Sharp et al.,¹¹ that water’s structure is essentially unchanged by the presence of urea (up to 8 M). It is also satisfying that the electric-field maps developed for neat water appear to work well even for a quite concentrated urea solution.

B. Linear IR Spectra of the Urea CO Stretch

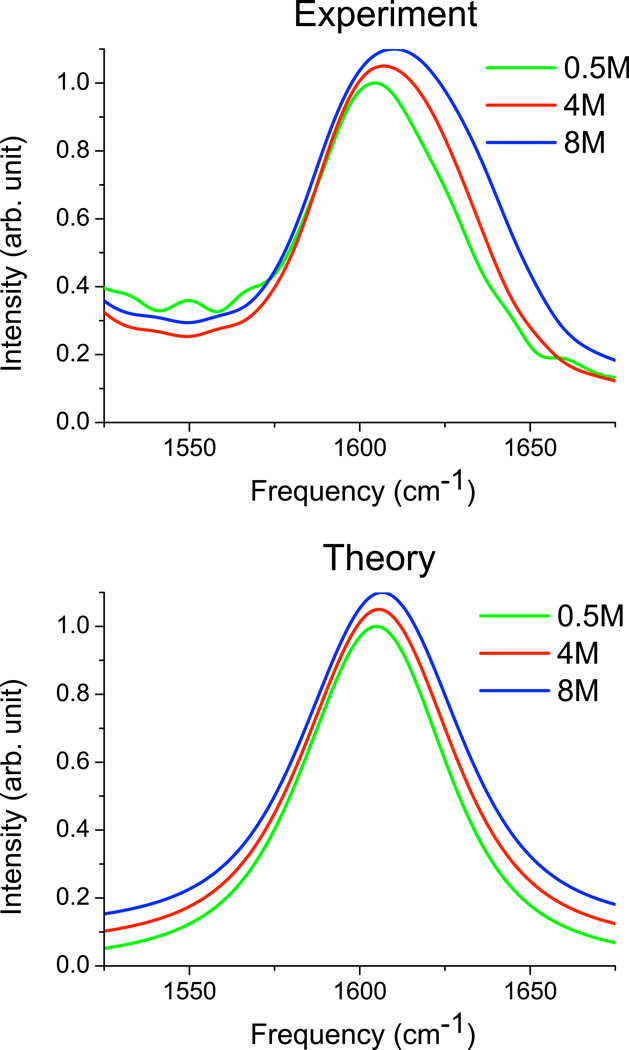
Experimental and theoretical IR spectra for the CO stretch of urea-D₄ in D₂O are shown in Figure 2; peak positions and line widths are listed in Table IV. The experimental spectra are very similar to those measured by Grdadolnik and Maréchal,⁵⁵ and suffer from a peak overlap with the C-N anti-symmetric stretching mode, which is centered at ∼1490 cm⁻¹.⁵⁵ This lower-frequency peak is not included in the theory. Aside from this issue, theory and experiment are again in reasonable agreement, showing, perhaps surprisingly, that the simple modification of the acetamide map works very well for urea in aqueous solution. Both theory and experiment show a slight blue-shift and broadening with increasing urea concentration. The experimental broadening is modestly larger than in theory, possibly as a result of intermolecular CO stretch coupling interactions (which were neglected in the theory). Overall, however, we see that the urea line shapes do not change much with urea concentration. The simplest interpretation of this is that urea causes only minor structural perturbations of water, consistent with the interpretation of the OD line shapes discussed above. (If urea did distort its first solvation shell, then the spectrum would be expected to change at high urea concentration, where different solvation shells overlap.)

FIG. 2.

Experimental and theoretical spectra for CO stretch mode of urea-D₄ in D₂O. Spectra are peak normalized. For clarity, spectra at 4 M urea are offset by 0.05, and spectra at 8 M urea are offset by 0.1.

TABLE IV.

Comparison of spectroscopic parameters for urea CO stretch (peak position and full-width at half maximum in cm⁻¹).

[urea] (M)	ωpeak, theory	ωpeak, exp	FWHM, theory	FWHM, exp
0.5	1605.0	1604.2	49.6	51.6
4	1605.6	1607.3	51.2	53.3
8	1606.6	1610.0	53.3	59.9

C. Anisotropy Decay of Water

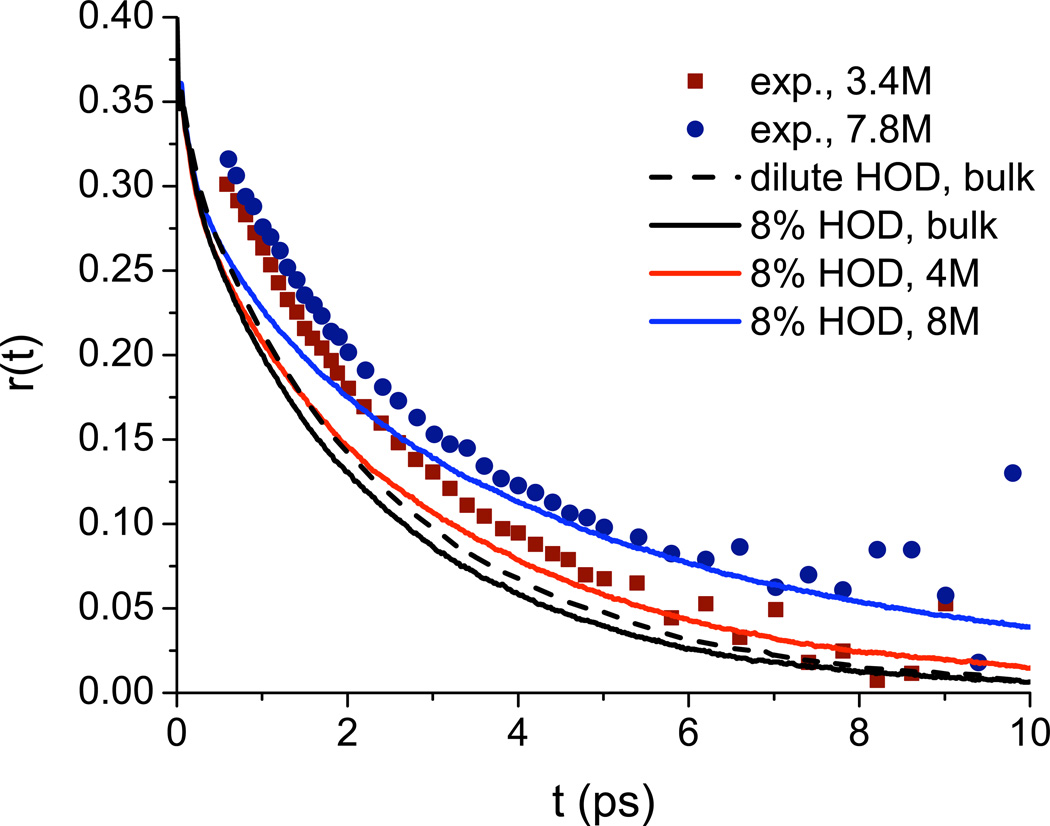
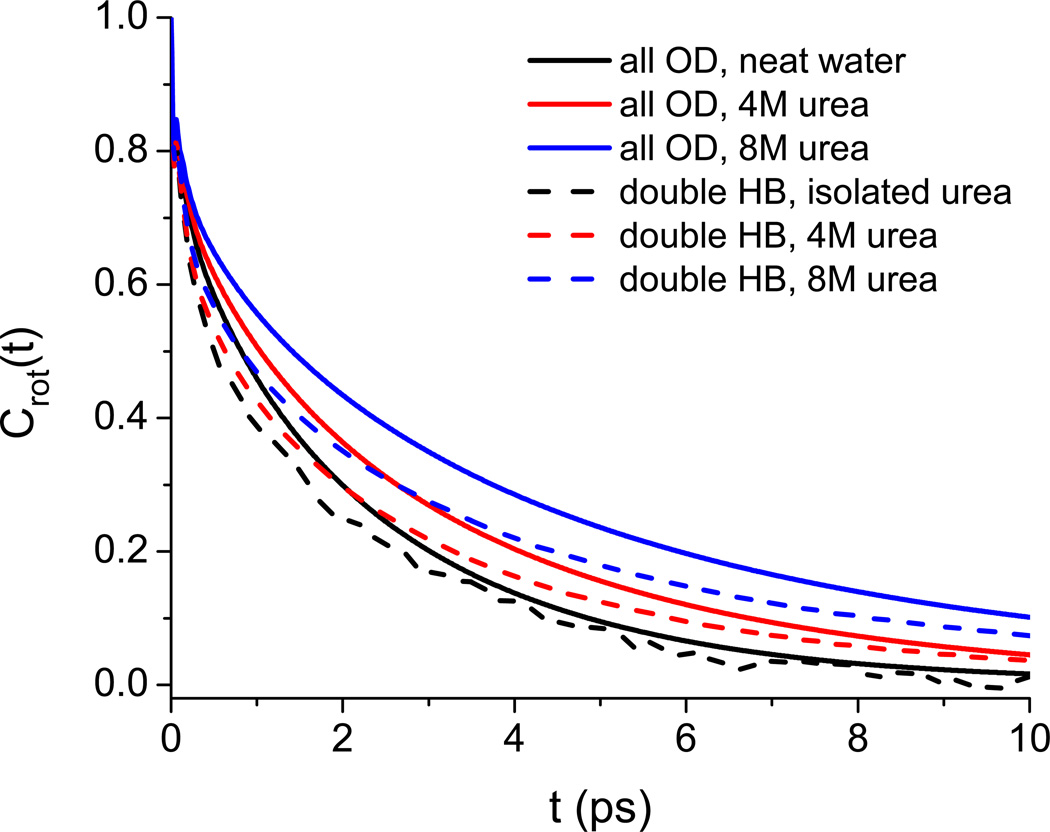
Rezus and Bakker⁴² have measured the anisotropy decay for the OD stretch of 8% HOD in mostly protonated urea solution; their results at 3.4 and 7.8 M are shown in Figure 3. These results are frequency-resolved at 2500 cm⁻¹, but it is stated that the results are insensitive to the probe frequency.⁴² The anisotropy decay is slower at higher urea concentration. These results were interpreted by fitting the data to a single exponential with a variable offset. This approach provided good fits, and the offset increased with increasing urea concentration. For all urea concentrations, the decay time of the exponential was found to be 2.5 ps, roughly the same as that for bulk HOD/H₂O.^90,91 These results led to the conclusion that most of the water in the urea solvation shell is unperturbed, but that a small fraction, corresponding to about one OH per urea molecule, is essentially immobilized on the experimental timescale (10 ps). It was hypothesized that these immobilized water molecules were doubly hydrogen-bonded to urea through the O and one of the H atoms.

FIG. 3.

Anisotropy decay of water OD for 8% HOD in H₂O for 3.4 M and 7.8 M urea solutions. Experimental values (symbols) were taken from the study by Rezus and Bakker.⁴² Theoretical results are shown for isolated HOD in bulk water (dashed line) and for 8% HOD in bulk water and in 4 M and 8 M urea (solid lines).

Theoretical results for the anisotropy decay in 4 and 8 M urea for 8 % HOD in proto-nated solution are also shown in Figure 3. Note that although these results are frequency-integrated, previous work has found little difference between theoretical frequency-resolved and frequency-integrated decays.^69,70 Also note that these calculations include the effects of OD-OD energy transfer due to the finite concentration of OD oscillators. Theory and experiment are in reasonable agreement at the longer times, but theory decays too quickly at short times. Likely, this discrepancy would mostly disappear if we convoluted our results with finite-width pump and probe pulse envelopes. Also shown are theoretical results for 8% HOD in H₂O without urea, and for HOD at (nearly) infinite dilution in H₂O (dashed line). Comparison between these two shows the relatively small effect of OD-OD energy transfer at 8 % HOD (which does, however, become somewhat more substantial at high urea concentration), while comparison between the curves for 0 and 4 M urea shows the more significant change induced by the addition of urea.

Assuming that the reasonable agreement between theory and experiment allows us to comment about the mechanism of the urea-induced slow-down, we can ask the following questions from the simulations: 1) on average, how many water molecules per urea molecule are doubly hydrogen bonded to urea oxygen and hydrogen (as shown schematically in Figure 5 of Reference⁴²)?; 2) how quickly do such molecules reorient? Using simple distance-only hydrogen-bond cut-offs of 2.5 Å (which correspond roughly to the first minima of the relevant radial distribution functions), we find that the answer to the first question ranges from ∼0.06 in 8 M urea to ∼0.08 in dilute urea. This is significantly smaller than the roughly one doubly hydrogen bonded molecule per urea suggested by Rezus and Bakker.⁴² To answer the second question, in Figure 4 we show the P2 rotational time-correlation function

$$C_{rot}(t)=\langle \frac{3{[\widehat{u}(0)\cdot \widehat{u}(t)]}^2-1}{2}\rangle ,$$ (4)

where û is the OD unit vector, and where the average is considered both over all OD groups and over only OD groups that formed hydrogen bonds to the O and H of a single urea molecule at t = 0. The results show that the rotation of these doubly hydrogen bonded molecules is, if anything, a little faster than average. Both of these results cast doubt on the existence of a significant fraction of immobilized water molecules.

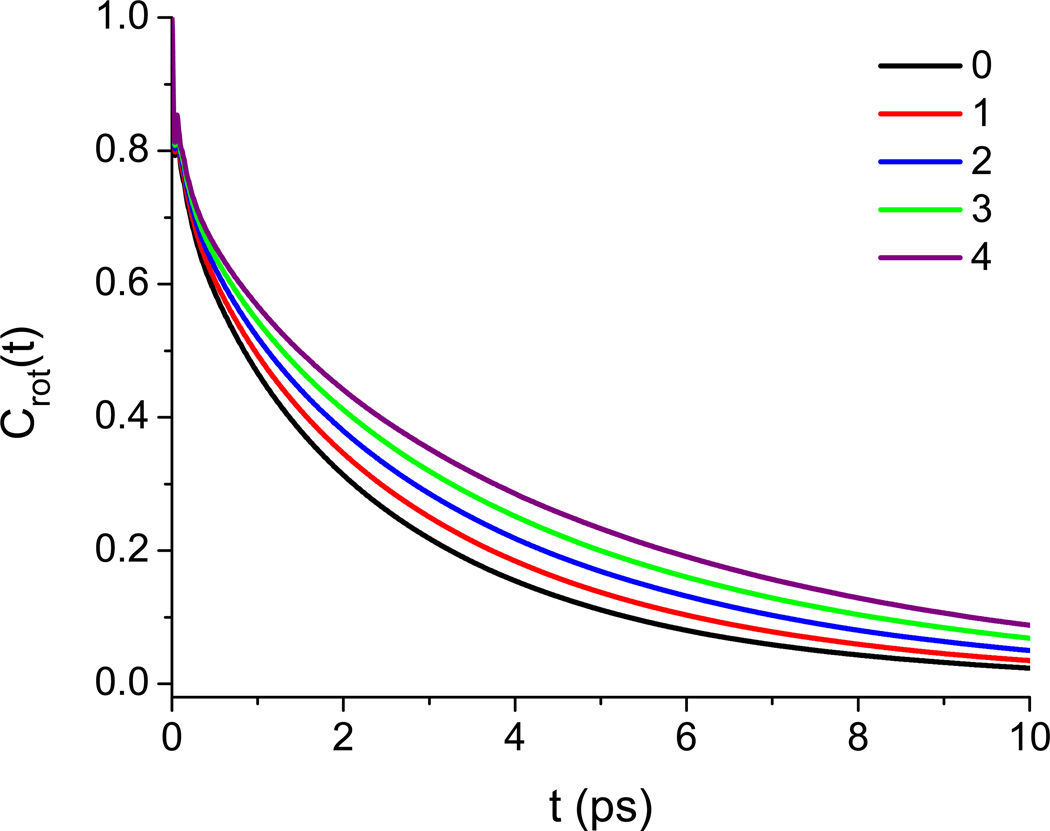
FIG. 5.

P2 rotational OD-bond time-correlation functions at 4 M urea as a function of the number of urea molecules solvated by a given water at t = 0. Urea solvation is defined using a urea carbon–water oxygen cutoff of 5.5 Å.

FIG. 4.

P2 rotational OD-bond time-correlation functions, averaged either over all OD’s in the simulation (solid lines) or over only OD’s initially doubly hydrogen bonded to urea.

Instead, we posit that the urea-induced slow-down is more homogeneous and arises because urea’s excluded volume blocks possible avenues for the reorientation of its solvation water, as described by Laage and Hynes.^92,93 We illustrate this idea by calculating C_rot(t) separately for water molecules in different urea solvation environments. A water molecule is defined to be in the solvation shell of a urea if its oxygen is within 5.5 Å of the urea carbon (the first minimum of the appropriate radial distribution function). Populations are then defined based on the number of urea molecules solvated at t = 0. In figure 5, we present results based on the 4 M solution for water molecules solvating up to four urea molecules. As can be seen, there is a steady slow-down in the decay of C_rot(t) as more urea molecules are solvated.

D. 2DIR of Water

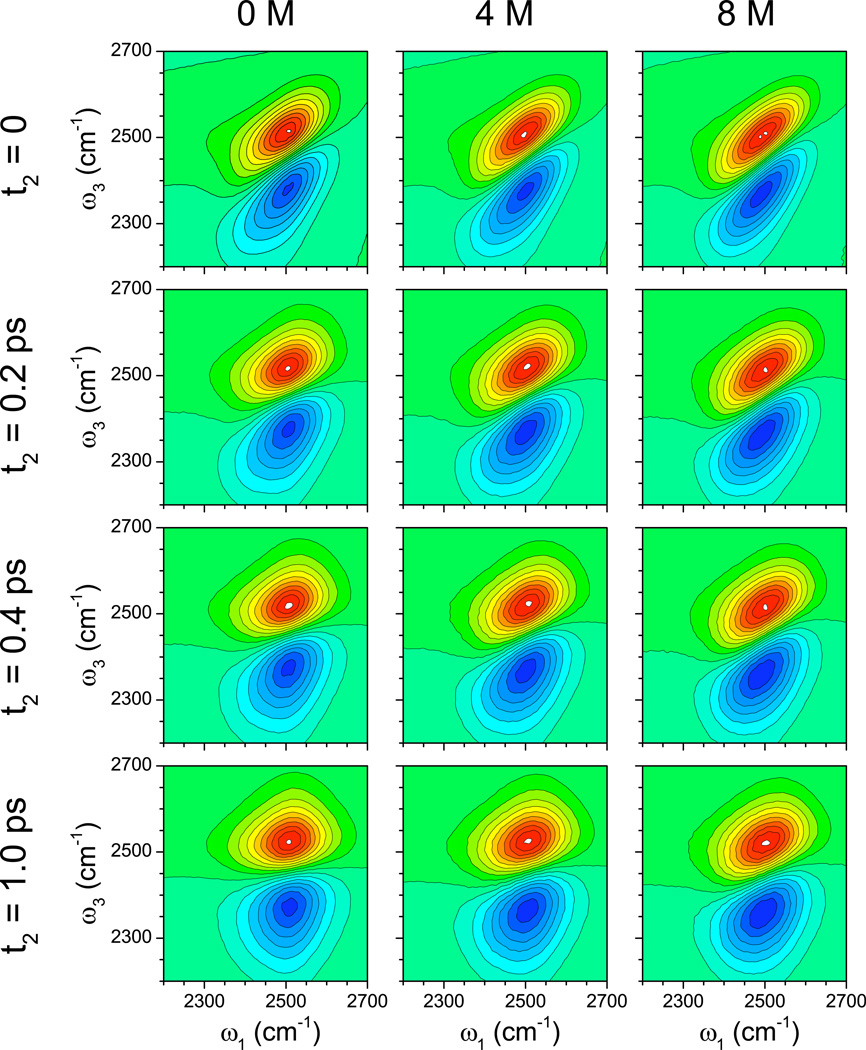
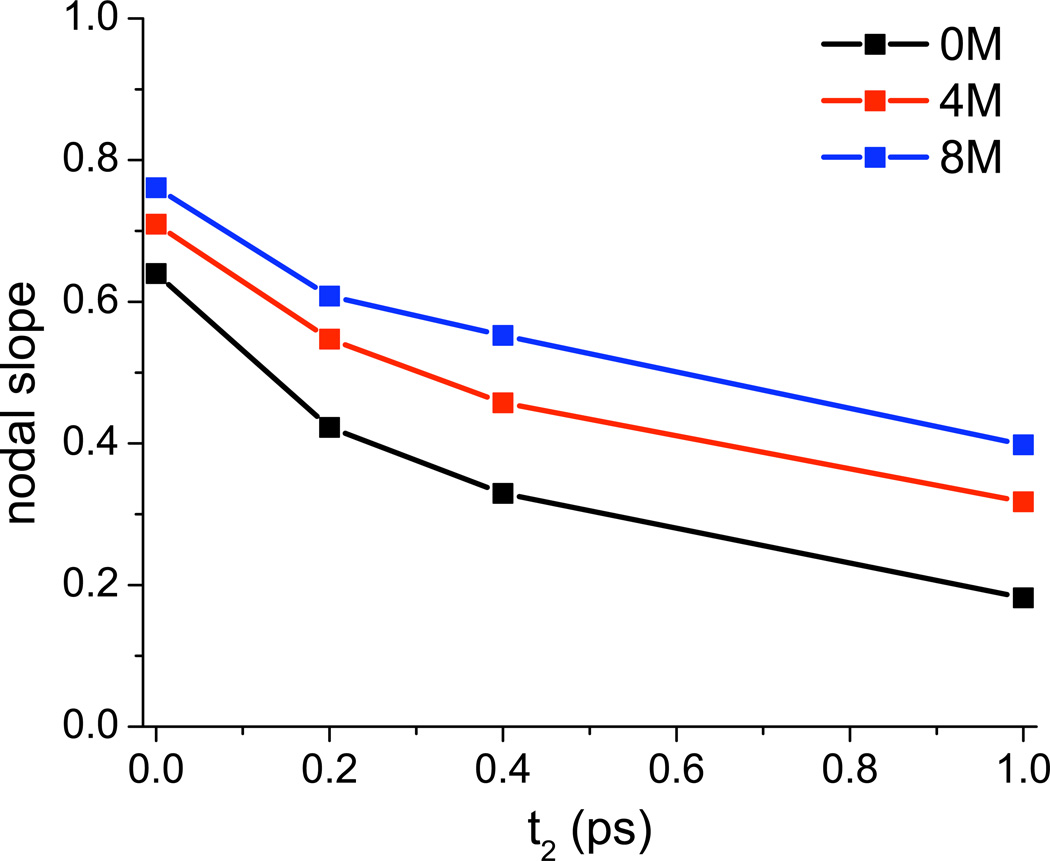
2DIR spectra of isolated chromophores in aqueous solution produce excellent measures of spectral diffusion, which describes the rate at which a chromophore loses frequency memory. For the water OD stretch, spectral diffusion is closely related to hydrogen-bond rearrangement dynamics.⁹⁴ Experimental 2DIR spectra for dilute HOD in H₂O (or any other isotopic mixture) as a function of urea concentration have not been reported. Nevertheless, in Figure 6 we provide the calculated 2DIR spectra as a function of waiting time (t₂) for 0, 4, and 8 M urea. The rounding of the spectra with increased waiting time provides clear evidence of spectral diffusion on a 1 ps time scale. A number of metrics have been proposed to quantify spectral diffusion; here we choose one, the nodal slope, and plot that as a function of waiting time in Figure 7. One sees that spectral diffusion slows down modestly, but significantly, as the urea concentration is increased. (Note that besides the vertical shift of the nodal slope with increasing urea concentration—indicative of a more heterogeneous distribution of enviroments at higher concentration—the decay of the nodal slope is also slightly slower at higher concentration.)

FIG. 6.

Theoretical OD-stretch 2DIR spectra for HOD/H₂O as a function of urea concentration. Spectra are normalized to the 1-0 peak intensity. Red regions are positive; blue regions are negative.

FIG. 7.

Nodal slopes from OD-stretch 2DIR spectra for HOD/H₂O as a function of delay time for various urea concentrations. Nodal slope is determined over a range of 60 cm⁻¹, centered on the 1-0 peak.

Again, it seems possible to explain these results in terms of the restricted dynamics of water in the solvation shell of urea. In Figure 8, we show the frequency-frequency correlation function (FFCF), which is closely related to the decay of the 2DIR nodal slope,^81,95

$$C_{\omega }(t)=\frac{\langle \delta \omega (t)\delta \omega (0)\rangle }{\langle \delta \omega {(0)}^2\rangle },$$ (5)

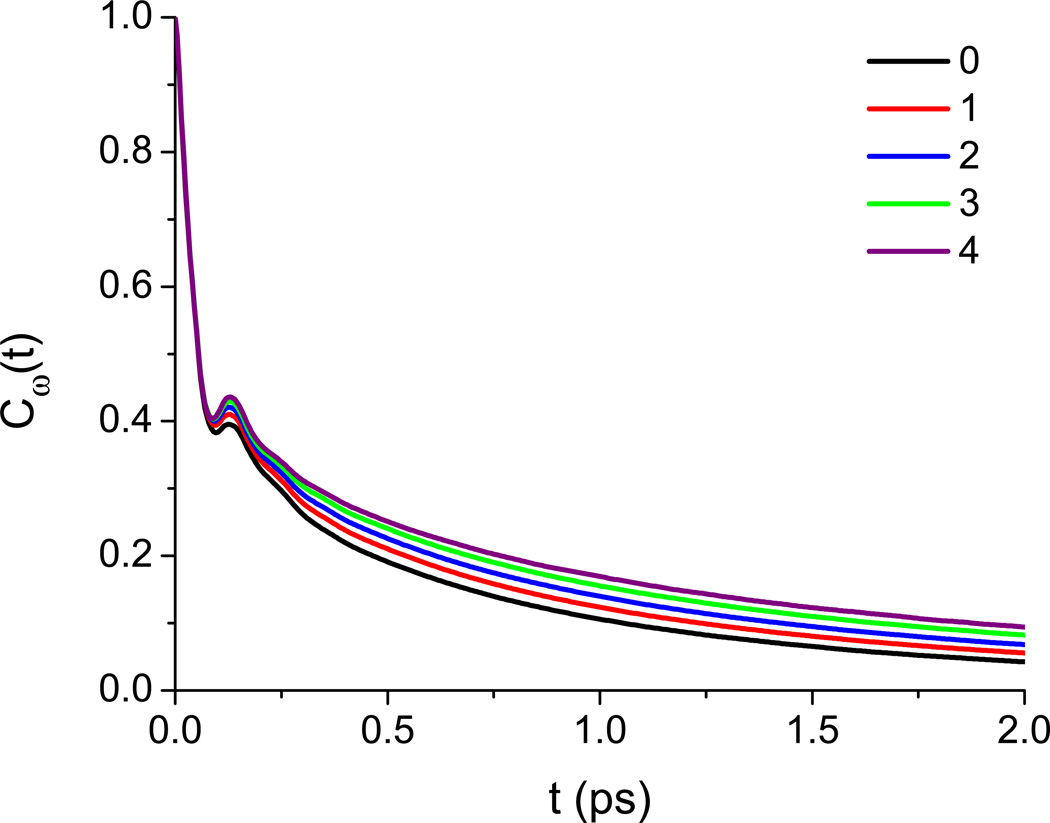
where δω(t) = ω(t) – 〈ω〉 (t) is the instantaneous difference of the water OD-stretch frequency from its average value. We display C_ω(t) separately for water molecules which solvate different numbers of urea molecules at t = 0 (solvation being defined as above), and define 〈ω〉 (t) as the average frequency at time t for water molecules which at t = 0 solvated some number of urea molecules. All results are for 4 M urea. The FFCF consists of three primary features: a fast initial drop, a recurrence at ∼0.15 ps due to the water’s intermolecular hydrogen-bond stretch, and a long-time decay related to hydrogen-bond reorganization dynamics.⁸¹ It can be seen that increasing the degree of urea solvation slows down the decay of the FFCF with respect to the two slower processes, indicating that the slowed decay of the nodal slope arises from a general rigidification of the water network around urea.

FIG. 8.

Water OD-stretch frequency-frequency time-correlation functions at 4 M urea as a function of the number of urea molecules solvated by a given water at t = 0. Urea solvation is defined using a urea carbon–water oxygen cutoff of 5.5 Å.

IV. CONCLUSIONS

In this paper, we have explored what infrared spectroscopy can tell us about the structure and dynamics of urea/water mixtures, both from the perspective of urea through its CO stretch, and of water through the OD stretch of HOD probe molecules. As is typical for the IR spectra of aqueous solutions, the line shapes are inhomogeneously broadened and report mainly on structure, not dynamics. We have measured IR spectra for urea-D₄ in D₂O, and for dilute HOD in D₂O, both as a function of urea concentration. We find, as have others before us, that these spectra are remarkably insensitive to urea concentration, reinforcing the idea that the urea molecule has little effect on the structure of liquid water. We also calculate these spectra theoretically. For HOD, we use our previously developed techniques,^54,96 and for urea, we propose a simple modification of our previous frequency map developed for acetamide.⁸⁶ Our spectra are in good agreement with experiment for all urea concentrations.

In order to investigate dynamics, we can turn to ultrafast experiments such as pump-probe anisotropy decay and 2DIR. Experiments on the OD stretch of HOD/H₂O as a function of urea concentration have already been performed by Rezus and Bakker,⁴² who found that the anisotropy decay slows as the urea concentration increases, a conclusion well-captured by our calculations. This effect was hypothesized by Rezus and Bakker to arise from immobilized water molecules that are doubly hydrogen bonded to urea. Analysis of our simulations shows that this is not the case (within the simulation model); rather, the slow-down seems to result from a more generic excluded-volume effect, as discussed by Laage and Hynes.⁹³ In addition, we have calculated 2DIR spectra of dilute HOD in H₂O for several urea concentrations. We find a similar, albeit smaller, slow-down for spectral diffusion as the urea concentration increases.

Inasmuch as thermodynamics is related to structure, from line-shape studies we would conclude that urea is neither a structure-maker nor a structure-breaker, and that urea’s effect on thermodynamic properties like protein stability are therefore due to the direct mechanism of urea interacting with the protein. Nonetheless, it is noteworthy that urea influences water’s dynamics. The consequences of this for biology are unclear at present.

Looking forward, the urea frequency map proposed and validated herein will presumably be useful for theoretical calculations of urea vibrational spectroscopy in urea/water/peptide ternary mixtures. In particular, two-color 2DIR experiments involving any two of the water OH stretch, urea CO stretch, and peptide amide I, promise to shed light on the interactions between different components in these important systems.