Unexpected variations in the triple oxygen isotope composition of stratospheric carbon dioxide

Abstract

We report observations of stratospheric CO₂ that reveal surprisingly large anomalous enrichments in ¹⁷O that vary systematically with latitude, altitude, and season. The triple isotope slopes reached 1.95 ± 0.05(1σ) in the middle stratosphere and 2.22 ± 0.07 in the Arctic vortex versus 1.71 ± 0.03 from previous observations and a remarkable factor of 4 larger than the mass-dependent value of 0.52. Kinetics modeling of laboratory measurements of photochemical ozone–CO₂ isotope exchange demonstrates that non–mass-dependent isotope effects in ozone formation alone quantitatively account for the ¹⁷O anomaly in CO₂ in the laboratory, resolving long-standing discrepancies between models and laboratory measurements. Model sensitivities to hypothetical mass-dependent isotope effects in reactions involving O₃, O(¹D), or CO₂ and to an empirically derived temperature dependence of the anomalous kinetic isotope effects in ozone formation then provide a conceptual framework for understanding the differences in the isotopic composition and the triple isotope slopes between the laboratory and the stratosphere and between different regions of the stratosphere. This understanding in turn provides a firmer foundation for the diverse biogeochemical and paleoclimate applications of ¹⁷O anomalies in tropospheric CO₂, O₂, mineral sulfates, and fossil bones and teeth, which all derive from stratospheric CO₂.

For most materials containing oxygen, the relative abundances of its three stable isotopes (¹⁶O, ¹⁷O, and ¹⁸O) fall on a “mass-dependent” fractionation line (1) with a ln¹⁷O-ln¹⁸O three-isotope slope^† near 0.5, which is well-predicted by statistical thermodynamics (3) and chemical reaction rate theories (4). In other words, ¹⁷O is usually one-half as depleted or enriched as ¹⁸O when measured relative to ¹⁶O and relative to those same ratios in an international standard. Discoveries of large deviations from a mass-dependent slope of 0.5 in meteorites (5) and ozone (6, 7), resulting in nonzero ¹⁷O anomalies (i.e., Δ¹⁷O = ln¹⁷O − 0.52 ln¹⁸O ≠ 0), have led to many applications tracing the histories and inventories of materials throughout the solar system (1), despite continuing debate about their chemical or physical origins (e.g., refs. 1, 8).

For ozone, the non–mass-dependent enrichments in ¹⁷O and ¹⁸O have a three-isotope slope of 0.65–1.0 (e.g., ref. 9) and have been traced to anomalous kinetic isotope effects (KIEs) in O₃ formation:

where M is any collision partner (10–12). Although much progress has been made in understanding ozone’s non–mass-dependent isotopic composition (12–14), the theoretical basis in chemical physics is still unresolved (15–17). In addition, whether ¹⁷O anomalies in other species––such as CO₂, N₂O, sulfates, and nitrates (e.g., ref. 18)––result solely from transfer from O₃ or from additional anomalous KIEs remains unclear. Stratospheric CO₂, for example, attains at least part of its observed non–mass-dependent isotopic composition (19–24) via reactions 2–3b (25–28):

The observed three-isotope slope for stratospheric CO₂ ranges from ∼1.2 to 1.7, much larger than for O₃. To explain the difference, non–mass-dependent isotope effects beyond O₃ formation have been postulated (19, 29), including a coincidental near-resonance for ¹⁷O¹²C¹⁶O₂* or a nuclear spin/spin-orbit coupling effect in [3a]. In addition, three-isotope slopes for CO₂ measured in laboratory mixtures of UV-irradiated O₂ or O₃ and CO₂ (29–32), slopes calculated from photochemical models of laboratory experiments (30) and the stratosphere (27, 28), and slopes from observations show remarkable disagreements. For example, three-isotope slopes for CO₂ in laboratory experiments typically vary from about 0.8 to 1.0 (29, 30, 32) not the value of 1.7 that has come to be expected for the stratosphere (22, 33). Although one laboratory study has yielded a slope up to 1.8 (31), the experiment was performed at unrealistically high O₃/CO₂ ratios and shows unusual behavior relative to all other published experiments. Experiments under nearly identical conditions but longer irradiation times (32) yielded a slope near 1, suggesting that the higher slope in the high O₃/short irradiation time experiments likely results from non–mass-dependent isotope effects in O₃ photodissociation due to O₃ self-shielding, which is not relevant for atmospheric conditions; thus, the apparent agreement with previous stratospheric observations is arguably fortuitous, as discussed further below. In addition, ln¹⁷O was measured directly in only one previous laboratory study (32), whereas it was inferred from mass balance in all others, which adds additional uncertainty (e.g., if unknown ¹³C isotope effects might affect the results due to the isobaric interference between ¹³C¹⁶O¹⁶O and ¹²C¹⁷O¹⁶O in mass spectrometry measurements). Finally, Liang et al. (27, 28) calculate a three-isotope slope of 1.5 for CO₂ in their model at latitudes >25°N that shows little temporal or spatial variation in the lower and middle stratosphere. The current level of disagreement between experiments, atmospheric observations, and atmospheric modeling shows that isotope exchange between O₃ and CO₂ is still not well understood.

Here, we report measurements of ln¹⁷O and ln¹⁸O of stratospheric CO₂ that reveal much larger three-isotope slopes than expected and their systematic variation with latitude, altitude, and season. We also report time-dependent laboratory and modeling results that demonstrate that anomalous KIEs in O₃ formation alone quantitatively account for the triple isotope composition of CO₂ in the laboratory. Combining laboratory and stratospheric results, we show that differences in temperature, relative rates of mass-dependent reactions, and vertical versus quasihorizontal transport rates can plausibly explain differences in the ln¹⁷O-ln¹⁸O relationships between the laboratory and stratosphere and within the stratosphere. The results thus provide a deeper understanding of contemporary stratospheric CO₂ isotope variations, the underlying isotope chemistry, and a sounder foundation for the biogeochemical, paleoclimate, and paleoatmospheric applications of ¹⁷O anomalies in materials that derive their signals from stratospheric CO₂ (34–40).

Stratospheric CO₂ was separated cryogenically from whole air samples collected by National Aeronautics and Space Administration (NASA) ER-2 aircraft (41) in winter 1999–2000 during the SAGE III Ozone Loss and Validation Experiment (SOLVE) (42) and a September 2004 balloon flight (43) at 34°N. The isotopic composition was measured on a Finnigan MAT 252 isotope ratio mass spectrometer using the CeO₂ equilibration technique (44). Additional sampling and measurement details are provided in Materials and Methods and SI Appendix. Results are shown in Fig. 1 and SI Appendix, Tables S1–S4. Samples of high-latitude air (>55°N) determined to be in the polar vortex from nitrous oxide (N₂O) and potential temperature (θ) measurements (45) (SI Appendix, Fig. S1) exhibit a three-isotope slope from a bivariate linear least-squares regression of 2.22 ± 0.07(1σ). Samples collected at midlatitudes (25–55°N) and in “midlatitude-like” (i.e., nonvortex) air at high latitudes (based on N₂O and θ) yield a three-isotope slope of 1.95 ± 0.05. These slopes are significantly larger (Table 1) than the expected value of 1.71 ± 0.03 from Lämmerzahl et al. (22), with homogeneity of regression tests demonstrating that these differences with respect to the Lämmerzahl data are both significant at the 99% confidence interval (SI Appendix, Table S5). If only the new lower stratospheric (<21 km) samples are included in our midlatitude regression, the slope is 1.7 ± 0.2, closer to expectations but more variable. We believe this increased variability in the lower stratosphere is real (see below), although additional uncertainty from a smaller regression range may also contribute.

Fig. 1.

Stratospheric CO₂ observations. Three isotope plot for the balloon (34°N) and “SOLVE” aircraft (24–83°N) samples, with previous observations: Thiemens (19) and Zipf and Erdman (20) are rocket samples from ∼34°N. Lämmerzahl (22) are balloon samples from 44° and 68°N. Alexander (21) are balloon samples from 68°N. Kawagucci (24) are balloon samples from 39° and 68°N. Data from Boering et al. (23) are not shown because of an earlier analytical mass-dependent artifact that affected ln¹⁷O and ln¹⁸O but not Δ¹⁷O. The mass-dependent fractionation line with slope 0.528 (red) and a hypothetical end member mixing line (black) with slope 1.7 (SI Appendix, Table S6) are also shown. The overall 1σ uncertainties for the SOLVE and Balloon 2004 data including both external precision and accuracy are ±0.1% for ln¹⁸O and ±0.5% for ln¹⁷O.

Table 1.

Summary of three isotope slopes for stratospheric CO₂

Source	Dates	Region	Altitude, km	N	Slope, ±1σ
SOLVE	12/99–3/00	High latitude/vortex	11–20	24	2.22 ± 0.07
SOLVE	12/99–3/00	High latitude/nonvortex and midlatitude	11–20	11	1.7 ± 0.2
SOLVE + balloon	12/99–3/00, 9/04	High latitude/nonvortex and midlatitude	11–33	20	1.95 ± 0.05

Additional insight into the regional differences in slope is gained by examining Δln¹⁷O/Δln¹⁸O (i.e., the slope of a line defined by two points: the ln¹⁷O and ln¹⁸O isotopic composition of a sample and the isotopic composition of tropospheric CO₂ with ln¹⁷O = 21.1% and ln¹⁸O = 40.2%) for individual datapoints from the rocket (19) and 2004 balloon datasets. Vertical profiles of CH₄, N₂O, and θ suggest the influence of air transported from more equatorial regions (SI Appendix, Figs. S2 and S3 and Table S3). The Δln¹⁷O/Δln¹⁸O values for these tropically influenced samples are typically larger than for samples with more midlatitude-like character based on CH₄, N₂O, and θ. These differences suggest that even larger slopes may be observable in the deep tropics and that transport and mixing of tropical air to 34°N contributes to the Δln¹⁷O/Δln¹⁸O variability in these profiles.

These systematic variations in Δln¹⁷O/Δln¹⁸O and three-isotope slopes with latitude, altitude, and season are not inconsistent with the previous observations of Lämmerzahl et al. (22) at 44°N and 68°N. The narrow range in slope of 1.71 ± 0.03 they measured has been considered the “standard” against which other measurements and model predictions should match (22, 33). However, the Lämmerzahl flights, based on their timing, would have likely always intercepted nonvortex extratropical air, yielding a relatively homogeneous three-isotope slope not necessarily representative of other regions, similar to how the long-lived tracers CH₄ and N₂O exhibit homogeneous nonvortex extratropical slopes distinct from tropical and vortex slopes. Satellite measurements of CH₄ and N₂O show CH₄:N₂O relationships that are compact (i.e., homogeneous) and distinct between three regions: the tropics, the extratropics, and the polar vortices after significant descent has occurred (46). In contrast, the region at 25 ± 10°N exhibits CH₄:N₂O correlations that are much less compact, consisting of inhomogeneous mixtures of tropical and midlatitude air (46). The CO₂ isotopic composition is also a long-lived tracer (23, 27, 28) because the lifetime for isotope exchange with O₃ is always at least an order of magnitude longer than stratospheric transport timescales, even at 45 km where O(¹D) peaks (27, 28); thus, transport and mixing affect the CO₂ isotopic composition similarly to CH₄ and N₂O. By analogy, homogeneous three-isotope slopes for CO₂ can be observed poleward of 35°N except in Arctic vortex air in January–March (42); the tropical and late vortex three-isotope slopes can be distinct from the nonvortex/extratropical relationships; and the 25 ± 10°N “mixed region” would be an inhomogeneous mixture, as observed. These variations in three-isotope slopes thus appear to be explicable and robust across high-precision CO₂ datasets.

These systematic variations with latitude and season we observe may also account for at least some of the variability in what have been considered to be the noisier datasets shown in Fig. 1 (20, 21, 24). For example, the dataset of Alexander et al. (21) consists of six samples that were collected in or near the polar vortex and which indeed show a higher three-isotope slope of 2.1 ± 0.6(1σ, n = 6), although the variability is high and the uncertainty in slope means it is not statistically different from the previous, lower slope datasets. It is not clear whether the variability is due to the small number of samples and real atmospheric variability (such as moving in and out of vortex air) or to possible measurement artifacts. Our vortex data and interpretation presented here suggest that at least some of the variability may be real. Similarly, some of Kawagucci et al.’s datapoints (24) overlap with our larger slope datapoints, but they report themselves that a linear fit to their data yields a slope of 1.63 ± 0.05(1σ, n = 58) and that their slope and data in general are not statistically nor characteristically different from the Lämmerzahl et al. dataset. If additional unpublished trace gas data and geophysical parameters are available for their samples, it may be possible to investigate their outliers at larger or smaller Δln¹⁷O/Δln¹⁸O values. Otherwise, whether these outliers are explained by atmospheric variability or by a lower measurement precision for their online CuO equilibration isotope ratio mass spectrometry (IRMS) technique (as the much more scattered relationship between their Δ¹⁷O of CO₂ and N₂O mixing ratio measurements may suggest (SI Appendix, Fig. S4) is unclear. Homogeneity of regression tests demonstrate that the differences in slope between our “vortex” and the Kawagucci data and between our “midlatitude” and the Kawagucci data are statistically significant at the 99% and 95% confidence intervals, respectively (SI Appendix, Table S5). Finally, the rocket dataset reported by Zipf and Erdman (20), which also lacks information on other long-lived tracer and potential temperature data, overlaps with our dataset, showing a curvilinear ln¹⁷O–ln¹⁸O relationship that links our lower and middle stratospheric data with the middle and upper stratospheric rocket data reported by Thiemens et al. (19); this dataset is thus also consistent with the idea that we put forth here that a linear ln¹⁷O–ln¹⁸O relationship of 1.7 with a small SD of <0.1 cannot represent the entire stratosphere, in contrast with the now widely held assumption that it does.

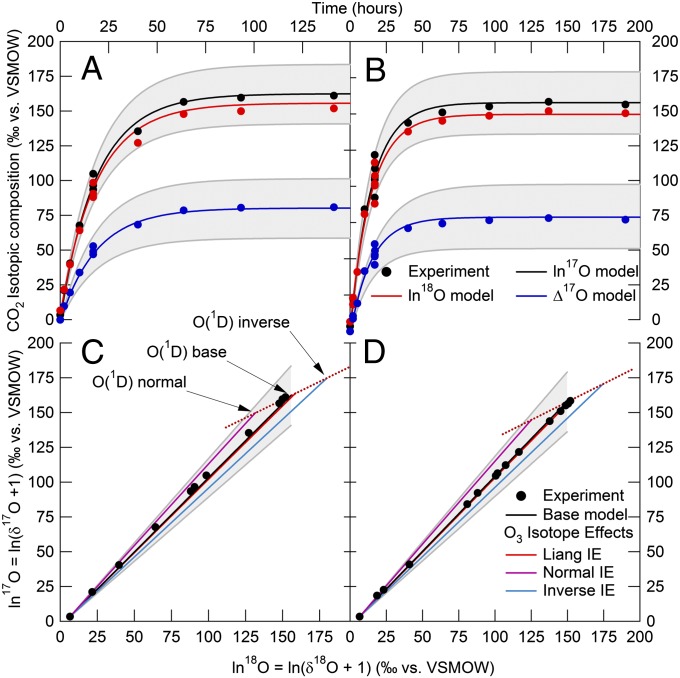
To investigate processes that could lead to the larger Δln¹⁷O/Δln¹⁸O values and three-isotope slopes we observe, O₂ and CO₂ mixtures near atmospheric mixing ratios were irradiated with UV light (Materials and Methods and SI Appendix). The CO₂ isotopic composition was measured (SI Appendix, Table S7) and compared with results from a time-dependent photochemical kinetics model we developed using KINTECUS software (SI Appendix, Tables S9 and S10). The model accurately predicts both the time dependence and the steady-state values for ln¹⁷O, ln¹⁸O, and Δ¹⁷O of CO₂ (Fig. 2 and Table 2). These results demonstrate that anomalous KIEs in O₃ formation can quantitatively explain the triple isotope composition of CO₂ in the laboratory at atmospherically relevant O₂, O₃, and CO₂ mixing ratios without invoking additional anomalous KIEs or other unknown effects to account for the data. Importantly, the model uses molecular level rate coefficients without using empirical or phenomenological parameterizations of how the transfer of the anomaly from CO₂ to O₃ occurs at steady state used in previous work (28, 32). These results also demonstrate that slopes close to 1 are to be expected in most laboratory experiments using mercury lamps at atmospherically relevant O₂/CO₂ ratios and pressures below 150 torr. Indeed, even the very high O₃/CO₂ experiments of Shaheen et al. performed for long irradiation times (32) resulted in an experimental slope near 1, as did our photochemical model run under conditions similar to theirs, unlike the slope of 1.8 measured at very high O₃/CO₂ mixing ratios for short irradiation times (31). The short irradiation times combined with the narrow lines of a Hg lamp, large reactor volume, and very high amounts of O₃ in the Chakraborty and Bhattacharya experiments (31) suggest that their 1.8 slope for CO₂ results from non–mass-dependent isotopic self-shielding by O₃ during O₃ photodissociation and subsequent transfer to CO₂ (32) rather than to processes simulating stratospheric isotope photochemistry in their experiment. In other words, isotopic self-shielding by O₃ does not occur at the O₃/CO₂ levels in the atmosphere or in the near-atmospheric mixing ratio laboratory experiments, or even at the longer irradiation times in the high O₃/CO₂ experiments of Shaheen et al.; thus the apparent agreement between the three-isotope slope for CO₂ of 1.8 with the previously expected value of 1.7 is likely fortuitous.

Fig. 2.

Experimental versus model results. Time evolution of the CO₂ isotopic composition for the 50 torr (A) and 100 torr (B) UV irradiation experiments (symbols) and predictions from a photochemical kinetics model (lines). Shaded area shows uncertainty in the base model predictions, dominated by a conservative estimate of the uncertainty in k_asymmetric for ¹⁷O¹⁶O¹⁶O formation. (C and D): Same as A and B in a three-isotope plot. Also included in different model scenarios (SI Appendix, Table S10) shown here are theoretical mass-dependent (“MD”) isotope effects in O₃ photolysis at 254 nm (48); and large, hypothetical “normal” and “inverse” MD O₃ photolysis isotope effects to illustrate how the three-isotope slope for CO₂ is increased (normal) or decreased (inverse) along a mass-dependent line of slope 0.528 (red dotted line) as the MD isotope effects change the isotopic composition of O₃ and O(¹D), while leaving Δ¹⁷O (Table 2) essentially unchanged (to within small differences in the MD coefficients, λ, in Δ¹⁷O = ln¹⁷O−λln¹⁸O, which can range from 0.500 to 0.529; ref. 2). Under these laboratory conditions, there is only one O(¹D) isotopic composition, so the CO₂ isotopic composition evolves along a straight line connecting the O(¹D) isotopic composition with that of the initial CO₂.

Table 2.

Isotopic compositions from photochemistry experiments and kinetics modeling at 50 torr

	CO2*				O3†
Description	ln17O	ln18O	Slope	Δ17O‡	ln17O	ln18O	Slope	Δ17O‡
Experiment	160 ± 1	151 ± 1	1.075 ± 0.004	80.7 ± 1.3	114 ± 7	138 ± 8	0.83 ± 0.07	41 ± 6
Model: base scenario	163	156	1.067	80.3	113	139	0.81	39.2
Liang photolysis IE§	164	159	1.056	80.2	110	134	0.82	39.3
Normal photolysis IE	150	132	1.172	80.4	119	151	0.79	39.2
Inverse photolysis IE	175	180	0.989	79.7	107	127	0.84	39.5
Tropopause O2 and CO2	161	153	1.24	80.4	111	136	0.82	39.4
Trop O2, CO2, 250 K	140	124	1.41	74.5	96	117	0.83	34.8
Trop O2, CO2, 220 K	126	105	1.61	70.7	87	104	0.83	31.8
Trop O2, CO2, 200 K	117	92	1.84	68.0	80	95	0.84	29.7

Isotopic compositions are reported in ‰ on the Vienna Standard Mean Ocean Water scale. The modeled O(¹D) isotopic composition is identical to that for CO₂ because isotope effects in the O(¹D) + CO₂ isotope exchange reaction were not included in these model scenarios. Results for 100 torr are shown in SI Appendix, Table S11.

^*Experimental results for CO₂ are an average (n = 2, ±1σ) of the measured values at isotopic steady state.

^†Experimental results for O₃ are an average (n = 2, ±1σ combined error) of previous results at 50 torr (54, 57).

^‡Δ¹⁷O = ln¹⁷O − 0.528 ln¹⁸O.

^§Theoretical mass-dependent O₃ photolysis isotope effect at 254 nm (48).

The three-isotope slopes near 1.1 in experiments without isotopic self-shielding artifacts, however, are still much smaller than stratospheric observations. To investigate the possible origins of the laboratory–stratosphere differences in Δln¹⁷O/Δln¹⁸O values, we tested the sensitivity of the photochemical model to various inputs and processes (Fig. 2 and Table 2). Initializing the model with the tropospheric isotopic compositions of O₂ and CO₂ increases the slope from 1.067 to 1.24, a sensitivity previously noted (28, 31, 32). As the model temperature decreases to stratospheric values, the modeled slope increases further, to 1.84 at 200 K, based on several temperature-dependent O₃ KIE measurements (47) and our estimates of others not yet measured (SI Appendix). The temperature decrease changes the predicted magnitudes of the O₃ formation KIEs, which in turn alter the non–mass-dependent isotopic compositions of O₃ and O(¹D) and hence both the three-isotope slope and Δ¹⁷O of CO₂. Introduction of mass-dependent isotope effects in any number of reactions can also change the three-isotope slope but leaves Δ¹⁷O effectively unchanged (Fig. 2 C and D and Table 2). For example, a mass-dependent O₃ photolysis isotope effect at the experimental wavelength of 254 nm that isotopically depletes the remaining O₃ (48, 49) will mass-dependently enrich O(¹D) and CO₂ and thus decrease the three-isotope slope. Similarly, but with opposite effect, a hypothetical mass-dependent isotope effect that isotopically enriches O₃ will deplete O(¹D) and CO₂, thereby increasing the three-isotope slope. Broadband O₃ photolysis in the stratosphere appears to mass-dependently enrich the remaining O₃ (9), which would increase the slope for CO₂. [Note that the existence of non–mass-dependent isotope effects in ozone photolysis has been proposed (50), but subsequent analysis (51) of those experimental results demonstrated that ozone formation was in fact responsible for the non–mass-dependent enrichments observed.] These experimental and modeling results support the hypothesis (18, 32) that temperature dependence of the O₃ formation KIEs and mass-dependent O₃ photolysis isotope effects likely cause the laboratory–stratosphere differences in the three-isotope slope for CO₂, although differences in the importance of other mass-dependent isotope effects between the laboratory and stratosphere leading to isotopic depletions in O(¹D) or CO₂ cannot be ruled out.

Because the modeled ln¹⁷O–ln¹⁸O relationship for CO₂ depends on temperature and O₃ photolysis wavelengths and rates, which vary with altitude and latitude, these variables are the likely origin of the observed regional differences in stratospheric ln¹⁷O–ln¹⁸O relationships. Indeed, the O₃ isotopic composition in the upper stratosphere shows regional differences attributed to UV photolysis (9), which was estimated to contribute 25–30% of the total enrichments in tropical O₃ versus only 20–25% at midlatitudes. Our model sensitivities suggest that larger tropical O₃ enrichments would increase the three-isotope slope of tropical CO₂ relative to the extratropics, consistent with inferences from our mixed region observations.

With larger three-isotope slopes in upper tropical CO₂, transport and mixing (which are much faster than CO₂–O₃ isotope exchange) then redistribute this tropical signal to other regions yet keep the slopes distinct, as for the CH₄:N₂O slopes. The larger tropical Δln¹⁷O/Δln¹⁸O values are transported into the mixed region at 25 ± 10°N at 25–40 km and will decrease as mixing into extratropical air proceeds (see below). Similarly, transport of this tropical upper stratospheric air by the residual circulation into the polar vortex generates the high Δln¹⁷O/Δln¹⁸O values there, similar to the winter buildup of O₃ at high latitudes from the tropics (42). Because little photochemistry and vertical mixing occurs in the vortex, and a dynamic barrier at the vortex edge blocks most mixing with midlatitude air, the larger Δln¹⁷O/Δln¹⁸O tropical values are maintained in the vortex. When the vortex breaks up in spring, vortex and midlatitude air mix, decreasing the slope to the extratropical value. For example, apparent vortex remnants sampled in May 1998 at 22 km show a slope of 1.7 (22). Tracer measurements in similar vortex remnants in 1997 demonstrate that such remnants have mixed extensively with midlatitude air by May–June (42, 52). End member mixing of high-N₂O and low-N₂O air produces a mixing line of slope 1.7 (Fig. 1; SI Appendix, Table S6) using two samples with ranges of N₂O concentrations similar to air that mixed during and after the 1997 vortex breakup (42, 52) and, more generally, similar to the mixing of low-N₂O and high-N₂O air that occurs on much larger spatial and temporal scales that are known to result in different CH₄:N₂O relationships in the tropics and extratropics (46).

Transport and mixing can also explain the larger scatter in slope in the lower stratosphere noted above. For example, Δln¹⁷O/Δln¹⁸O values for N₂O < ∼220 parts per billion by volume (ppbv) are >1.7, but for N₂O > ∼220 ppbv they vary between ∼0.5 and 1.7, are roughly inversely correlated with N₂O, and increase with increasing Δ¹⁷O (Fig. 3). Moreover, the few outliers to the Δ¹⁷O and inverse N₂O trends can be explained by (i) the degree of mixing of lower-N₂O air from higher altitudes with higher-N₂O air at lower altitudes, or (ii) the fact that the samples are from the lowermost stratosphere (θ< 380 K), which is a mixture of stratospheric air with air recently transported from the troposphere. These characteristics suggest that such lower stratospheric mixing creates real atmospheric variability in Δln¹⁷O/Δln¹⁸O values ranging between the entry (tropospheric) value of ∼0.5 to values ≥1.7 (also SI Appendix).

Fig. 3.

Variations in Δln¹⁷O/Δln¹⁸O of CO₂. (A) Δln¹⁷O/Δln¹⁸O of CO₂ versus N₂O mixing ratio and (B) Δln¹⁷O/Δln¹⁸O of CO₂ versus Δ¹⁷O of CO₂; Δln¹⁷O/Δln¹⁸O = 1.7 is shown (dashed line) for reference. In general, the Δln¹⁷O/Δln¹⁸O values increase from a tropospheric, near–mass-dependent value to >1.6 as (A) N₂O decreases and (B) Δ¹⁷O of CO₂ increases, explaining at least part of the larger observed variability in Δln¹⁷O/Δln¹⁸O in the lower stratosphere where “younger,” high N₂O air mixes with “older,” lower N₂O air. Note that, for these samples, the trends in Δln¹⁷O/Δln¹⁸O are still apparent (even though the values change) even if we assume that the entry value for ln¹⁸O of CO₂ entering the stratosphere from the troposphere can vary by ±0.5, either by applying the same offset for every point or by mimicking a seasonal variation within the dataset, and even though the overall 1σ uncertainty in the ln¹⁷O measurements including both accuracy and precision is ±0.5%.

In summary, we have shown that room temperature laboratory measurements of CO₂–O₃ isotope exchange near an atmospheric O₂/CO₂ mixing ratio can be quantitatively predicted with a first principles photochemical model and results in a linear ln¹⁷O–ln¹⁸O relationship for CO₂ of 1.2 (starting with tropospheric O₂ and CO₂ isotopic compositions), whereas the ln¹⁷O–ln¹⁸O relationship for stratospheric CO₂ can vary systematically with latitude, altitude, and time, ranging up to 2.2 in a sometimes curvilinear manner. Model sensitivities suggest that the laboratory–stratosphere and regional stratospheric differences originate from differences in mass-dependent isotope fractionation in O₃ photolysis and in temperature due to the temperature dependence of the non–mass-dependent isotope effects in O₃ formation. The latitude, altitude, and seasonal dependence of the observed three-isotope slopes suggests that stratospheric transport and mixing act to redistribute air with higher Δln¹⁷O/Δln¹⁸O values for CO₂ from the tropical source region to the subtropics and into the polar vortex and then homogenize these higher values to the extratropical background of 1.7. Additional CO₂ isotope measurements in the tropics could validate our hypothesis that the three-isotope slopes are greater there and provide additional constraints on photolysis isotope effects and the temperature dependence of the O₃ formation KIEs, which also need further laboratory investigation. Also, 2D and 3D atmospheric models that include the latitude and altitude dependencies of the isotope chemistry inferred here and that can simulate realistic transport barriers are needed. For ¹⁷O anomalies in tropospheric CO₂ (34), in O₂ on short (35, 36) and glacial–interglacial (37, 38) timescales, in ancient mineral sulfates (39), and in fossilized bioapatite (40), we note the following: On one hand, productivity estimates for the current terrestrial and oceanic biospheres are on sounder footing because the isotope chemistry is no longer mysterious. Furthermore, these large three-isotope slopes do not affect previous estimates of the annual mean flux of Δ¹⁷O of CO₂ to the troposphere because Δ¹⁷O is still similarly well-correlated with N₂O in the lower stratosphere (SI Appendix, Fig. S4) (23). Importantly, the magnitude of Δ¹⁷O matters more than the magnitude of the three-isotope slopes, a point which is often overlooked. On the other hand, a sensitivity of Δ¹⁷O of CO₂ to the temperature dependence of the anomalous O₃ KIEs represents a possible caveat for longer timescale variations in Δ¹⁷O of O₂, mineral sulfates, and bioapatite. Although Luz et al. (37) already elucidated the need to consider past changes in O₃ and CO₂ levels on Δ¹⁷O of O₂, variations in stratospheric temperatures as climate changes may also affect Δ¹⁷O anomalies, especially if the temperature dependencies of the O₃ KIEs are larger than estimated here.

Materials and Methods

Atmospheric Samples.

Air samples were collected between 24°N and 83°N and 11 and 20 km by the Whole Air Sampler instrument during the SOLVE mission (42) in January–March 2000 and at 34.5°N between 27 and 33 km by the Cryogenic Whole Air Sampler instrument aboard a high-altitude scientific balloon (43) launched from Fort Sumner, NM, in September 2004. Mixing ratios of trace gases in the samples were measured at the University of Miami or the National Center for Atmospheric Research, including N₂O and CH₄ using an HP5890 II+ series GC, before shipment to University of California Berkeley (UC Berkeley). At UC Berkeley, CO₂ was separated from air and any residual water in a series of five liquid N₂ and −75.5 °C ethanol–LN₂ traps, respectively. The resulting aliquots of 30–60 μmol of CO₂ were flame sealed into glass ampoules for subsequent IRMS analysis. Several samples exhibited water levels higher than stratospheric air [typically <10 parts per million by volume (ppmv)], indicating the sampler manifolds may have been temporarily contaminated with water. To eliminate potential artifacts from isotope exchange between CO₂ and H₂O either in the sample canisters or during the cryogenic separation that could increase Δln¹⁷O/Δln¹⁸O values, samples with residual water > 20 ppmv have been eliminated from analysis (SI Appendix).

Laboratory Experiments.

Mixtures of O₂ (Scott Specialty Gases, 99.999%) and CO₂ (Scott Specialty Gases, 99.998%) close to the atmospheric ratio (O₂/CO₂ ∼ 450) were introduced into a 2.2-L borosilicate glass bulb fitted with a fused quartz (Heraeus-Amersil, Inc.) “finger” extending into the interior of the bulb. A low-pressure Hg/Ar pen lamp (Oriel Instruments) with major emission lines at 184.9 and 253.7 nm was placed in the quartz finger to irradiate the bulb from the center. After irradiation for 0–190 h, the CO₂ and resulting O₃ were separated cryogenically from O₂ using liquid nitrogen and were transferred to a sample tube containing nickel shavings. After heating at 60 °C for 15 min to decompose O₃, the CO₂ was separated cryogenically from the resulting O₂ with liquid nitrogen and then measured by IRMS. In some experiments, the isotopic composition of O₃ was determined by measuring the O₂ from O₃ decomposition at m/z values of 32, 33, and 34 by IRMS.

IRMS Measurements.

The triple oxygen isotope composition of CO₂ was measured on a Finnigan MAT 252 IRMS at UC Berkeley using the CeO₂ equilibration technique (44) on 12–18-μmol aliquots of the purified CO₂ from the whole air samples or the purified CO₂ from the laboratory experiments. Corrections to the IRMS signals for the presence of N₂O in the stratospheric CO₂ samples before CeO₂ equilibration were made using measurements of the mixing ratio and isotopic composition of N₂O made directly on the stratospheric whole air samples. External 1σ measurement precisions (n = 104 over 2 y) for ln¹⁸O, ln¹⁷O, and Δ¹⁷O of CO₂ were ±0.05%, ±0.2%, and ±0.2%, respectively, where Δ¹⁷O = ln¹⁷O−0.528 ln¹⁸O. Including accuracy (SI Appendix) yields overall 1σ uncertainties of ±0.1%, ±0.5%, and ±0.5%, respectively.

Photochemical Kinetics Model.

The isotope-specific reaction kinetics occurring in the laboratory reaction bulb was predicted with KINTECUS software (53) using the Modified Bader–Deuflhard integrator to solve the system of stiff differential equations. The model is based on a previous model of O₂–O₃ isotope photochemistry (51) modified to include reactions relevant for CO₂. In the “base model,” only KIEs in O₃ formation and O + O₂ isotope exchange were included, as measured or derived in earlier studies (10, 11). The pressure dependence of the O₃ formation KIEs was derived from the O₃ formation KIEs at low pressure and the pressure dependence of the O₃ isotopic enrichments (54–56). In the model runs investigating sensitivity to temperature, the temperature dependence of the O₃ formation KIEs was based on a combination of measurements of the temperature dependence of the KIEs for formation of the ¹⁸O-containing O₃ isotopomers (47) and the temperature dependence of the ¹⁸O and ¹⁷O enrichments in O₃ (9, 47) In model runs investigating sensitivity to possible isotope effects in O₃ photolysis, a theoretical value at 254 nm from Liang et al. (48, 49) was used, as well as hypothetical limiting values for normal and inverse isotope effects. See SI Appendix for more details regarding the measurements and calculations.