Improving Low-Dose Blood-Brain Barrier Permeability Quantification Using Sparse High-Dose Induced Prior for Patlak Model

Abstract

Blood-brain-barrier permeability (BBBP) measurements extracted from the perfusion computed tomography (PCT) using the Patlak model can be a valuable indicator to predict hemorrhagic transformation in patients with acute stroke. Unfortunately, the standard Patlak model based PCT requires excessive radiation exposure, which raised attention on radiation safety. Minimizing radiation dose is of high value in clinical practice but can degrade the image quality due to the introduced severe noise. The purpose of this work is to construct high quality BBBP maps from low-dose PCT data by using the brain structural similarity between different individuals and the relations between the high- and low-dose maps. The proposed sparse high-dose induced (shd-Patlak) model performs by building a high-dose induced prior for the Patlak model with a set of location adaptive dictionaries, followed by an optimized estimation of BBBP map with the prior regularized Patlak model. Evaluation with the simulated low-dose clinical brain PCT datasets clearly demonstrate that the shd-Patlak model can achieve more significant gains than the standard Patlak model with improved visual quality, higher fidelity to the gold standard and more accurate details for clinical analysis.

1. Introduction

As the first leading cause of long-term disability in the United States, stroke imposes a substantial economic burden on individuals and society, with an annual direct and indirect costs totaling US$69 billion in 2006 (Lloyd-Jones et al., 2009). Stroke may be ischemic or hemorrhagic and for the former case, intravenous rtPA(alteplase) is an effective treatment widely adopted in clinical practice (Clark et al., 2000). However, hemorrhagic transformation (HT) is a serious and potentially fatal complication in patients with acute ischemic stroke, especially for those treated with rtPA (Lopez-Yunez et al., 2001). This complication has been and is the hindrance to the administration of the rtPA for this condition (Jaillard et al., 1999; Su et al., 2008). Blood-brain barrier (BBB) breakdown due to ischemia before reperfusion therapy is considered one of the contributing factors to HT in acute ischemic stroke patients (Lin et al., 2007). Early detection of a damaged BBB with increased blood-brain barrier permeability (BBBP) could be a valuable tool to identify patients who are more likely to suffer from HT after acute reperfusion therapy, and assist evaluation of the benefits/risks of this treatment (Bisdas et al., 2007).

Perfusion computed tomography (PCT) imaging has been advocated to quantify the rate of BBBP (Cianfoni et al., 2006) from the enhanced time series CT images, with the Patlak model (Patlak et al., 1983). The standard Patlak model states that a steady-state of contrast levels must be achieved before BBBP assessment, and therefore a delayed PCT acquisition of 240 seconds (Dankbaar et al., 2008) is required to accurately assess BBBP. The associated excessive radiation exposure of the standard PCT scanning protocol in cine mode for about 1 minute has already raised significant concerns on radiation safety (Frush et al., 2003; Imanishi et al., 2005; Wintermark and Lev, 2010), let alone the prolong protocol for BBBP assessment. While effective radiation dose reduction in PCT is an important arena of continuing research efforts, minimizing the reasonable radiation dose for BBBP assessment is a relatively new topic drawing accumulating research attention.

Up to now, many efforts to reduce radiation dose in PCT have been performed to optimize PCT scanning protocol (Fleischmann et al., 2000; Wintermark et al., 2000; Wiesmann et al., 2008; Yu et al., 2009; Jia et al., 2010; Badea et al., 2011). Among these techniques, lowering the milliampere-seconds (mAs) is a straightforward and cost-effective method to reduce the radiation dose in PCT. However the associated increased noise in the sinogram will unavoidably lead to quality degradation and image artifacts in the reconstructed image series and hemodynamic parameter maps. Numerous approaches have been proposed to reduce the noise in the low-dose PCT data, including denoising the sinogram and/or reconstructed image series (Mendrik et al., 2011; Ma et al., 2011, 2012; Saito et al., 2008; Lin et al., 2001) and regularizing the residue functions in the deconvolution process (Calamante et al., 2003; Nathan et al., 2008; Andersen et al., 2002; Wong et al., 2009; He et al., 2010; Fang et al., 2012, 2013). However most of these approaches are not addressing the optimization of BBBP map specifically. The interweaving nature of temporal information in the Patlak model and the spatial correlation with the neighborhood tissue is also not effectively utilized.

The standard Patlak model analyzes each voxel in the region of interest independently when a steady-state phase is reached between reversible compartments. It also assumes that the radiation dosage and tracer concentration are high enough to generate high-quality, nearly noise-free tissue density curves (TDC) in the cine-mode scanning. However the noise in the PCT data due to the reduced radiation dose will unavoidably disturb the linearity between the variables in the steady-state phase for Patlak model analysis, thus degrade the accuracy of the permeability calculation. To mitigate the noise issue associated with the standard Patlak model, in this paper, we develop a spatial-temporal formulation that interweaves the temporal relationship between TDCs of the artery and the tissue, with the spatial similarity between the high- and low-dose BBBP maps. This is achieved by constructing a dictionary from the repository of high-dose BBBP maps available in the clinical database and imposing a sparsity prior to select a few atoms in the dictionary for the restoration of the low-dose map. In spite of the recent research that bridges the gulf between high- and low-dose perfusion maps such as CBF with a learned dictionary (Fang et al., 2013), to the best of our knowledge, it is the first attempt to enhance the BBBP map at low radiation dose by improving the standard Patlak model.

The novelty of sparse high-dose induced Patlak model (shd-Patlak) model is three-fold. First, shd-Patlak explores the similarity in the brain structure across patients and the specific anatomy at each region of the brain by constructing a location adaptive dictionary from the high-dose maps of different patients. Second, a sparsity term is imposed to the optimization problem in producing the high-dose induced prior as a strategy to select the proper patches for reconstruction. Third, an iterative process with steepest descent algorithm is proposed to optimize the the current shd-Patlak model. Qualitative and quantitative evaluations were carried out on the scans of clinical patients in terms of different evaluation metrics.

2. Related Work

Since sparsity prior is used in the optimization of our paper, we review the relevant work on the theoretical background and the application of sparsity prior.

Sparsity approach has inspired much research in recent years. It dates back to 2006 when Donoho (2006) and Candés et al. (2006) showed that with high probability a sparse signal could be reconstructed from a small number of its linear measurements. Since then, numerous greedy algorithms have been developed to address the sparsity optimization problem. These algorithms include orthogonal matching pursuit (OMP) (Chen et al., 1989), matching pursuit (Mallat and Zhang, 1993), basis pursuit (BP) (Chen et al., 2001) and stagewise OMP (stOMP) (Donoho, 2006). Besides the greedy algorithms which solve the L₀ norm problem, relaxation to L₁ norm which is convex has been explored (Candès et al., 2006; Kim et al., 2007; Figueiredo et al., 2007), leading to optimization algorithms including LARS-Lasso (Tibshirani, 1996), interior-point (Kim et al., 2007), etc.

Sparsity prior have been widely applied to computer vision, multimedia processing and medical imaging communities. In the natural image domain, the applications range from the natural image and video denoising (Elad and Aharon, 2006; Protter and Elad, 2009), image super-resolution (Yang et al., 2008), image demosaicing and inpainting (Mairal et al., 2008), robust face recognition (Wright et al., 2009), automatic image annotation (Zhang et al., 2012a). In the medical image domain, sparsity prior has shown its advantage in shape modeling (Zhang et al., 2012b), deformable segmentation (Zhang et al., 2012c), MR reconstruction (Lustig et al., 2007; Huang et al., 2011), etc.

3. Background: Patlak Model

Patlak model, first described by Patlak et al. (Patlak et al., 1983; Patlak and Blasberg, 1985), is a theoretical model of blood-brain exchange. When a steady-state phase is reached between the reversible (arterial) intravascular and the irreversible extravascular (in this case the brain parenchyma) compartments, transfer of tracer is assumed to be unidirectional. The Patlak plot is a graphical representation of the Patlak model. The rate of transfer between the two compartments is computed from the slope of the linear part of the plot.

The Patlak model is derived from the idea that the total attenuated contrast of a current voxel or region of interest could be represented as a sum of the tracer in the intravascular and extravascular compartments at a specified time t as:

$$T(t)=\mathit{CBV}·c_{iv}(t)+p{\int }_0^t{c}_{iv}(\tau )d\tau =\text{Intravascular}+\text{Extravascular}$$ (1)

where T(t) is the tissue density curve or tracer at time t, and c_iv(t) is the intravascular concentration of the voxel at time t, CBV is the cerebral blood volume. The multiplication of c_iv(t) and CBV would yield the total amount of tracer residing in the intravascular component. For the extravascular component, ${\int }_0^t{c}_{iv}(\tau )d\tau$ represents the total amount of tracer that perfused the intravascular component from time 0 up till time t, and p is the permeability constant, which is the target of Patlak analysis. The total amount of tracer that leaks from the intravascular to the extravascular component is proportional to the permeability and could be computed via the multiplication of p with ${\int }_0^t{c}_{iv}(\tau )d\tau$.

In practice, arterial input function AIF (t) is used as a substitute of c_iv(t) since the voxels in the artery contains only an intravascular component. Eq. 1 now becomes

$$T(t)=\mathit{CBV}·\mathit{AIF}(t)+p{\int }_0^t\mathit{AIF}(\tau )d\tau$$ (2)

By dividing AIF (t) from both sides, the equation yields an easily plotable line in which the slope is p:

$$\frac{T(t)}{\mathit{AIF}(t)}=\mathit{CBV}+p·\frac{{\int }_0^t\mathit{AIF}(\tau )d\tau }{\mathit{AIF}(t)}$$ (3)

By setting

$$y=\frac{T(t)}{\mathit{AIF}(t)}\text{and}x=\frac{{\int }_0^t\mathit{AIF}(\tau )d\tau }{\mathit{AIF}(t)}$$ (4)

we get

$$y=\mathit{CBV}+p·x$$ (5)

The slope of a regression line fit to the linear part of the Patlak plot is an approximation of p (the rate of transfer) at time t. The value indicates the amount of accumulated tracer in relation to the amount of tracer that has been available in the plasma and BBBP is expressed in mL×100g⁻¹×min⁻¹. The y-axis intercept equals CBV. To correct the overestimation of BBBP due to delayed arrival of tracer in the current voxel compared to AIF (t) (Dankbaar et al., 2008), we shift the time-enhancement curve in each parenchymal voxel to match the arrival time of tracer in the artery (Schneider et al., 2011):

$$c_{iv}(t)=\mathit{AIF}(t-[\mathit{TTP}(T)-\mathit{TTP}(\mathit{AIF})])$$ (6)

where TTP is the time to peak of a curve. The new c_iv(t) replaces the AIF (t) for all delay-corrected calculation.

4. Sparse High-dose Induced Patlak Model

4.1. Basic Idea

Our key assumption is that image information lost in the low-dose BBBP map due to severe noise could be recovered from the corresponding anatomical regions from the high-dose BBBP maps in the clinical repository. The similarity in the human brain structure and perfusion mechanism makes restoration of missing information of one patient from other individuals possible.

Up till now the BBBP computation with Patlak model is voxel-independent, neglecting the contextual information embedded in the neighboring voxels in the same BBBP map and the similarity between high- and low-dose BBBP maps of different patients. Thus we propose to impose a regularization prior R(P) to the linear regression problem in Eq. 5 to improve the quality of BBBP maps, especially at low-dose. In this paper, following the line of the previous studies for sparsity-based perfusion deconvolution for cerebral blood flow (CBF) map (Fang et al., 2013) and residue function (Fang et al., 2012) regularization, we propose a sparse high-dose induced prior for Patlak model (“shd-Patlak”) with location adaptive dictionaries constructed from corresponding anatomical regions in the high-dose maps from the existing repository, and an EM style algorithm to solve the maximum a posterior (MAP) optimization. The flowchart of the shd-Patlak model is summarized in Fig. 1.

Figure 1.

The flowchart of the low-dose map enhancement framework which consists of three modules: location adaptive dictionary construction, sparsity imposed prior estimation and MAP optimization. Using the high-dose repository, high-quality parameter maps are computed as training data from which we are able to construct location adaptive dictionaries. Then an iterative process consisting of prior estimation and MAP optimization is applied to enhance the low-dose map.

4.2. Construction of Location Adaptive Dictionary

The structural similarity between the brains of different individuals motivates us to explore the connections between the high- and low-dose BBBP maps of distinct patients. While patch-based dictionary learning is widely adopted in computer vision for image denoising and super-resolution (Elad and Aharon, 2006; Mairal et al., 2008; Yang et al., 2010), a global dictionary is usually learned from hundreds of thousands of patches to achieve a universal representation of all the possible patches with enough accuracy. However, the large computational demand in the reconstructed process to evaluate every patch in the global dictionary and the existence of the unnecessary patches in the global dictionary for reconstruction of the patch of interest make us turn to location adaptive dictionaries.

Assuming that the space of a low-dose BBBP map P has been divided into overlapping patches, we use p_i, a column vector to denote the intensity values of a patch at location i. The search for patches to be included in the location adaptive dictionary is based on a search-window S_i surrounding the location i in the high-dose maps. For each high-dose map H_j for training, we extract with respect to p_i a L × m dictionary matrix $D_j=[p_j^1,\dots ,p_j^m]$, where L is the length of p_i, and m is the number of patches to select from each high-dose map. The search process is repeated for all available high-dose maps j (j = 1, …, n) to build the final L ×M dictionary matrix D = [D₁, …, D_M], where M = mn. The location adaptive dictionary relaxes the need for accurate registration via its patch-based search mechanism, and saves the computational demand at restoration. The concept of the location adaptive dictionary is shown in Fig. 2.

Figure 2.

Construction of location adaptive dictionaries for a low-dose map P (red) from the high-dose repository (blue). Search bounding box is adaptively determined for each patch P (such as the purple box p_i or the orange box p_j) by using the location of the current patch as reference. After determining the bounding box (dashed line S_i and S_j) for the current patch, a certain number of patches across different training samples are selected into the dictionary D.

4.3. Sparse High-dose Induced Prior

Without loss of generality, the BBBP measurement can be approximately expressed as a linear regression problem:

$$Y=\mathit{CBV}+X\otimes P$$ (7)

where P in R^N×1 is the vector of BBBP values to be estimated by stacking the pixels in the 2-D map vertically. Y, X and CBV in R^T×N are the dependent, the independent variables and the intercept derived from Eq. 5 for all pixels in P. The operator ⊗ indicates that the column i in X is multiplied by the i^th value in P. The goal of blood-brain barrier permeability computation is to estimate the parameter P according to the measurement model in Eq. 7.

Direct linear regression for each pixel independently may lead to unreliable outcome given the noisy sinogram data at low-dose PCT with various artifacts. To address this problem, we propose a penalized least square approach based on the MAP estimation criterion by adding a priori term R(P) to the least square form of the problem:

$$P\ast =\underset{P\ge 0}{argmin}{\Vert Y-V-X\otimes P\Vert }_2^2+\beta R(P)$$ (8)

The priori term R(P) plays an important role for reliable BBBP estimation in low-dose condition. Here based on the previous studies using sparse and redundant dictionaries for sinogram denoising in regular CT (Shtok et al., 2011) and cerebral blood flow map enhancement (Fang et al., 2013) in perfusion CT, a sparse high-dose induced prior (named shd prior) is proposed:

$$R(P)={\Vert P-\mathit{shd}(P)\Vert }_2^2$$ (9)

where shd(P) represents a sparse high-dose induced reconstruction.

Upon obtaining the corresponding location adaptive dictionary D_i for patch p_i in the low-dose BBBP map P, the denoised version of p_i is assumed to be formulated as a linear combination of a few patches in the dictionary D_i as p_i = D_iα, where α is a M × 1 column weight vector to choose the appropriate dictionary atoms.

$$\mathit{shd}(p_i)=\underset{p_i}{argmin}{\Vert p_i-D_i\alpha \Vert }_2^2\text{subject}\text{to}{\Vert \alpha \Vert }_0<K$$ (10)

where || · ||₀ represents the L₀ norm which constrains the number of atoms to combine the reconstructed patch to less than K.

The sparsity constraint in Eq. 10 is necessary in two ways. First the noise may be perfectly reconstructed if any combination can be used. Second, the solution to the problem may not be unique when the dictionary D is overcomplete (M > L). Sparsity constraint has been shown effective in various scenarios, including natural image denoising, image super-resolution, video denoising, MR reconstruction, etc. (Elad and Aharon, 2006; Yang et al., 2010; Protter and Elad, 2009; Huang et al., 2011), by imposing a regularization term that limits the number of examples to select from the training repository. Another important advantage of the sparse L₀-based constraint over the L₂-based constraint is that the L₀ constraint is less sensitive to the outliers, which in image processing applications indicates sharp edges.

The constraint in Eq. 10 is not directly tractable due to non-convexity of the L₀ norm. Greedy algorithms can be used to solve this NP-hard L₀ norm minimization problem. Yet there is no guarantee to find the global minima. Generally, no known algorithms can search for the sparsest solution more efficiently than exhausting all possible subsets of α. Fortunately, the recent development in the sparse representation theory (Donoho, 2006) proves that L₁ norm can be applied to impose sparsity while making the problem convex. So Eq. 10 is relaxed to

$$\mathit{shd}(p_i)=\underset{p_i}{argmin}{\Vert p_i-D_i\alpha \Vert }_2^2+\lambda {\Vert \alpha \Vert }_1$$ (11)

where ||α||₁ stands for the sum of the absolute values of the components of α.

The sparse high-dose induced prior of BBBP map P can thus be reconstructed by overlapping the reconstructed patches from Eq. 11. And the final cost function to optimize is

$$P^{\ast }=\underset{P\ge 0}{argmin}{\Vert Y-\mathit{CBV}-X\otimes P\Vert }_2^2+\beta {\Vert P-\mathit{shd}(P)\Vert }_2^2$$ (12)

The cost function composes of two terms: the temporal linear regression model from the Patlak assumption, and the spatial regularization term of sparse reconstruction induced from the high-dose maps. The interweaving of the temporal and spatial information can overcome the high noise sensitivity of the Patlak model with sole temporal term and pave the way for a robust model for low-dose BBBP estimation.

4.4. Problem Reformulation

Given that the weight vector α in Eq. 11 is a function of the objective map P, solving the cost function in Eq. 12 is not straightforward. Therefore an iterative approach is adopted to optimize the cost function, which automatically adjust the weight vector α in Eq. 11 according to the current estimation P^t at t^th iteration and the location adaptive dictionaries during each iteration. To solve the objective function with the operator ⊗ in Eq. 12, we first reformulate it to conventional matrix multiplication. The Patlak model in Eq. 7 can be expressed as

$$\overline{Y}=X·\mathit{diag}(P)=\overline{X}P$$ (13)

where Ȳ in R^TN×1 is formed by stacking the columns of Y − CBV vertically. X̄ is a TN × N matrix formed by positioning the columns of matrix X on the diagonal of the new matrix X̄, so that

$$\overline{X}=\left(\begin{array}{cccc}{X}_{.,1}& 0& \cdots & 0\\ 0& X_{.,2}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & X_{.,N}\end{array}\right)$$ (14)

Now the objective function in Eq. 12 becomes

$$P^{\ast }=\underset{P\ge 0}{argmin}{\Vert \overline{Y}-\overline{X}P\Vert }_2^2+\beta {\Vert P-\mathit{shd}(P)\Vert }_2^2$$ (15)

4.5. MAP Optimization Framework

The shd-Patlak algorithm optimizes the estimated low-dose BBBP map by an EM style MAP algorithm, which iterates the following two steps:

1. shd prior estimation. Given the current map estimation P^t and the high-dose map repository, location adaptive dictionaries are built for each patch $p_i^t$ in P^t. Eq. 11 can be solved by multiple algorithms and we use Lasso (Tibshirani, 1996) in this paper. The regularization term R(P) is then obtained in Eq. 9.

2. Steepest descent optimization. The steepest descent optimization is applied to Eq. 15 to generate the new map estimation. The updated estimation of BBBP map, i.e. P^t+1, can be expressed as:

   $$P^{t+1}=P^t+{\gamma }^{t+1}({\overline{X}}^T(\overline{Y}-\overline{X}P))$$ (16)
   where γ^t+1 indicates the gradient step-size which can be computed adaptively following the estimator (Sullivan and Chang, 1991)

   $${\gamma }^{t+1}=\frac{Q^{T}Q}{{(\overline{X}Q)}^T(\overline{X}Q)}\text{where}Q\equiv {\overline{X}}^T(\overline{X}{P}^t-\overline{Y})$$ (17)

   The updated P^t+1 is put back to step 1 again to obtain the new shd prior estimation.

The optimization framework of the algorithm is detailed in Algorithm 1. We observe that our results are quite stable with respect to the local random perturbations of the subject space (e.g. the initialization). This shows that slight differences of the initial estimation algorithm do not affect the final results.

Algorithm 1.

The iterative optimization framework to solve Eq. 15

Input: Location adaptive dictionaries Di∈I ∈ RL×M (I is the set of all possible patch locations), input low-dose BBBP map P ∈ RN. Independent and dependent parameters in Patlak model X̄ ∈ RTN×N and Ȳ ∈ RTN×1.

Output: Updated low-dose BBBP map Pt ∈ RN.

R(P) = 0.

repeat

for i = 1, 2, …, |I| do

Compute the sparsity-induced prior using Lasso

$$\mathit{shd}(p_i)=\underset{p_i}{argmin}{\Vert p_i-D_i\alpha \Vert }_2^2+\lambda {\Vert \alpha \Vert }_1$$ (18)

end for

Update regularization prior $R(P^t)={\Vert P^t-\mathit{shd}(P^t)\Vert }_2^2$

Update Pt using steepest descent optimization

$$P^{t+1}=P^t+{\gamma }^{t+1}({\overline{X}}^t(\overline{Y}-\overline{X}P))$$ (19)

where ${\gamma }^{t+1}=\frac{Q^{T}Q}{{(\overline{X}Q)}^T(\overline{X}Q)}$, Q ≡ X̄T (X̄ Pt − Ȳ)

until Stop criteria

5. Experiment Setup

5.1. Data Acquisition

To evaluate the performance of the proposed shd-Patlak algorithm on BBBP map computation in PCT, clinical brain PCT images were acquired with GE Pro-16 scanners (General Electric Medical Systems, Milwaukee, WI) located at NewYork-Presbyterian Hospital at Weill Cornell Medical College in New York City, NY. First, 45 mL of non-ionic iodinated contrast was administrated intravenously at 4.0 mL/s using a power injector. Then with a 5 s delay, the cine (continuous) enhanced high-dose scan was performed at tube voltage of 80 kVp, tube current of 190 mA, 1 rotation per second for duration of 45 s. The scanning volume of 2.0 cm consists of 4 slices at 5.0 mm thickness with its inferior extent selected at the level of basal ganglia, above the orbits, to minimize radiation exposure to the lenses. The source-to-detector distance was 946 mm, and the source-to-patient distance was 538 mm. CT dose index volume (CTDI-vol) was 725.21 mGy, and the dose-length product was 1450.42 mGy-cm.

5.2. Low-dose Data Simulation

Repetitive scanning of the same patient at different radiation doses is unethical. So instead of scanning the patients twice, researchers simulate low-dose CT images from the acquired high-dose data with noise models of varying complexity (Britten et al., 2004; Veldkamp et al., 2009; Zauner et al., 2006; Florie et al., 2007; Frush et al., 2002; Hanai et al., 2006; Massoumzadeh et al., 2009; Tack et al., 2005). Among these techniques, we use the approach described by Britten et al. (2004), which demonstrated that low-dose scan can be simulated by adding spatially coherent statistical noise to the reconstructed CT images (before processing to generate perfusion maps), for its simplicity and effective low-dose simulation.

Quantum noise is linearly related to the square root of the absorbed dose in the detector. The absorbed dose is proportional to the tube current level multiplied by the X-ray exposure time, mAs. When the X-ray exposure time is fixed, the noise standard deviation σ and the tube current I (mA) has an inverse relationship as below:

$$\sigma =\frac{K}{\sqrt{I}}$$ (20)

Let’s define I₀ as the original high-dose tube current level in mA, I the desired low-dose tube current level. σ₀ and σ are the corresponding standard deviation of the pixels in the reconstructed CT images at the above tube current levels. The distribution of the noise is independent, so the standard deviation σ_G of the added Gaussian noise can be derived from

$${\sigma }_G^2={\sigma }^2-{\sigma }_0^2=(I_0/I-1){\sigma }_0^2=K^2(1/I-1/I_0)$$ (21)

To generate the spatially correlated statistical noise, we first measure the spectral properties of CT noise from the phantom data and then calculate the noise power spectrum for each tube current setting. The shape of the normalized noise power spectra is stable at different mAs, so the same spectrum model is used for all cases and noise levels. Following the practice in (Britten et al., 2004), we generate the noise autocorrelation function (ACF) from these data and choose the 11 × 11 window around the autocorrelation peak as a convolution filter for producing colored noise in subsequent experiments.

The autocorrelation function is convolved with the white Gaussian noise to simulate noise with a proper power spectrum then the convolved noise is scaled to the desired standard deviation σ_G. The noise image is masked by a filter of valid pixels in the PCT data and is added to the same image. The noise spectrum of any simulated noise added to any image by this procedure is guaranteed to have the spectral properties observed in an actual CT scan of the phantom on this scanner.

In this study, the constant K in Eq. 20 is calibrated with 22 patients under I₀ = 190 mA and the average value of K is 103.09 mA^1/2. The reduced tube current I is chosen to represent the ultra-low dose at 15 mAs to match previously published techniques highlighting ultra-low exposure in lung CT perfusion examinations (Yu et al., 2009). However it is important to note that the technique introduced in that work enhances the reconstructed CT images instead of the perfusion maps and is based on the nonlinear filtering of the difference image between the low-dose scan and the previous normal dose scan. This technique can be incorporated with our proposed spatio-temporal method to achieve further dose reduction and quality improvement.

5.3. Performance Evaluation Metrics

We adopted the following three metrics to evaluate the noise reduction for the quantitative comparison:

1. Local signal to noise ratio (LSNR)

   $$\mathit{LSNR}=\frac{\frac{1}{N}{\sum }_{i=1}^{N}P(i)}{\sqrt{\frac{1}{N}{\sum }_{i=1}^N{(P(i)-\frac{1}{N}{\sum }_{i=1}^{N}P(i))}^2}}$$ (22)
2. Root-mean-square error (RMSE)

   $$\mathit{RMSE}=\sqrt{\frac{1}{N}\sum _{i=1}^N{[P(i)-P_{hd}(i)]}^2}$$ (23)

   where P (i) is the permeability value at voxel i in the low-dose map, N is the total number of voxels in the region of interest (ROI). P_hd(i) is the permeability value at voxel i in the corresponding high-dose map.

3. Structural similarity index (SSIM) (Wang et al., 2004)

   $$\mathit{SSIM}(x,y)=\frac{(2{\mu }_x{\mu }_y+C_1)(2{\sigma }_{xy}+C_2)}{({\mu }_x^2+{\mu }_y^2+C_1)({\sigma }_x^2+{\sigma }_y^2+C_2)}$$ (24)
   where μ_x, μ_y are the expectation (mean) of image x and y, σ_x and σ_y are the unbiased standard deviation of image x and y. σ_xy is estimated as

   $${\sigma }_{xy}=\frac{1}{N-1}\sum _{i=1}^N(x_i-{\mu }_x)(y_i-{\mu }_y)$$ (25)

   C₁ = (K₁L)², and C₂ = (K₂L)², where L is the dynamic range of the pixel values, and K₁ = 0.01, K₂ = 0.03 are used in this paper.

5.4. Statistical Analysis

The hypothesis for the quantitative evaluation of the BBBP maps was that each low-dose permeability maps enhanced using the proposed shd-Patlak model had no change in terms of above mentioned three metrics compared with the maps estimated by Patlak model, first across designated ROIs, and second over the whole brain region, while the maps estimated at high-dose 190 mA were regarded as golden standard for metric computation. The metric values were computed for each patient individually. Therefore, it was considered statistically appropriate to analyze these quantitative data by using the paired t-test. All P values were 2-sided, and P < .05 was considered statistically significant.

5.5. Implementation Details

The implementation of the Patlak and shd-Patlak models was conducted on a MacBook Pro with 2.80 GHz Intel Core i7 processor with dual cores and 4 GB of RAM memory in MATLAB 2013a environment (The Math Works Inc., Natick, MA). BBBP maps using Patlak model on the high-dose 190 mA scan served as gold standard for the testing cases. A trained neuroradiologist (P.S.) with 12 years of experience reviewed permeability maps of all high-dose datasets and identified regions with visual perfusion deficits, defined as focal areas with elevated BBBP.

The training cases for location adaptive dictionary construction in Section 6 except Section 6.6 include the BBBP maps processed by Patlak model on the 190 mA scan of 10 cases (5 with brain deficits and 5 normal). For Section 6.6, 10 cases of pathological patients and 10 cases of healthy controls were used respectively for two experimental settings. No additional smoothing was performed in BBBP map estimation.

The related parameters in the implementation were selected as follows:

1. The size of the search-window S_i was 11 ×11. Since there was no registration performed, for the voxels on the boundary of the test image, the search space might consist of only background from the training data. Thus search window was moderately expanded based on the percentage of background voxels in the current patch on the boundary.

2. The patch size L was 5 × 5 with a overlap of 3.

3. The number of patches extracted from each training image m was 5.

4. The sparsity weight λ was 0.05.

5. The weighting parameter of high-dose induced prior β was 0.3. The choice of the parameters will be detailed in Section 6.7.

6. Results

6.1. Clinical BBBP Maps

Fig. 3 shows the cerebral BBBP maps computed from the high-dose 190 mA and simulated low-dose PCT data at different exposure levels (mAs) (50 mA, 25 mA and 15 mA) using different computation methods. In the BBBP map computed by Patlak model from the simulated low-dose 15 mA and 30 mA PCT data, serious noise-induced artifacts can be observed, which obscure the permeability information. In the low-dose BBBP maps computed by shd-Patlak model, the clearly delineated signal with clear-cut edges in the shd-Patlak images are better reproduced than those from the Patlak model with independent computation of each voxel.

Figure 3.

Cerebral BBBP maps computed by different methods from simulated low-dose PCT data at different exposure levels (mAs). The 1st column is the BBBP map estimated from high-dose 190 mA data (gold standard). The 2nd column is the BBBP maps estimated using Patlak model at simulated low-dose. Dose reduction, achieved through tube current reduction, primarily results in increased image noise, demonstrated as increased “graininess” in the map of the simulated low-dose scan. The 3rd column is the enhanced low-dose BBBP maps using shd-Patlak model. The 1st row is at tube current 50 mA (σ_G = 12.51), 2nd row at 25 mA (σ_G = 17.27), and 3rd row at 15 mA (σ_G = 25.54). The display window option: width is 5 HU, level is 2.5 HU. (Color image)

6.2. Vertical Profiles

Fig. 4 depicts the vertical profiles of the BBBP maps shown in Fig. 3, where the profile from the high-dose map is regarded as a reference standard. The profiles from the shd-Patlak model matches better with that from the reference standard than the profile from the standard Patlak mode. In other words, the gains from the present shd-Patlak model are more noticeable than those from the Patlak model.

Figure 4.

Vertical profiles of the BBBP map at high-dose and simulated at tube current of 15 mA in Fig. 3 at (a) x=320 using Patlak model, (b) x=320 using shd-Patlak model, (c) x=220 using Patlak model and (d) x=220 using shd-Patlak model. Profile between y=101 and 420 is shown and used for quantitative evaluation. The ‘dash line’ is from Patlak model or the shd-Patlak model. The ‘solid line’ is from the high-dose map which acts as the ground-truth for comparison.

To quantitatively measure the consistency between the vertical profiles from the high-dose BBBP map and the vertical profiles from the simulated low-dose maps computed by the Patlak model and the shd-Patlak model, Table 1 lists the Lin’s concordance correlation coefficients (Lawrence and Lin, 1989) of the two vertical profiles indicated by the white lines in Fig. 4. The results demonstrated that in profiles (a) and (b), Lin’s concordance correlation coefficients from the low-dose Patlak maps are below 0.7 while the corresponding Lin’s concordance correlation coefficient from the BBBP maps by the present shd-Patlak model is higher than 0.9, with all lower bounds of the 95% confidence interval of the concordance correlation coefficients higher than 0.9. In other words, the results may suggest a significant agreement between the profiles from the shd-Patlak maps and the high-dose maps.

Table 1.

Lin’s concordance correlation coefficient between the vertical profiles from the high-dose map and from the low-dose maps computed by the Patlak model and the shd-Patlak model.

Profile	Methods	Sample size	Lin’s concordance correlation coefficient	95% confidence interval of concordance coefficient	P -value of significance level
a	Patlak	320	0.6810	(0.6791, 0.6829)	P < 0.0001
	shd-Patlak	320	0.9033	(0.9026, 0.9291)	P < 0.0001
b	Patlak	320	0.6846	(0.6826, 0.6865)	P < 0.0001
	shd-Patlak	320	0.9247	(0.9242, 0.9253)	P < 0.0001

6.3. Visual Analysis

Fig. 5 shows the BBBP parameter maps calculated from the original high-dose images and the low-dose images computed by different methods from the noisy data, which is 15 mA, about one-twelfth radiation dose of the high-dose scan. The BBBP maps have a relatively small dynamic range compared to other hemodynamic parameter maps such as cerebral blood flow (CBF) and mean transit time (MTT), so that the errors in the low-dose maps are not as significant in its absolute value as those in other maps. We could still observe that the BBBP maps derived from the shd-Patlak model is similar to that derived from the original high-dose images. The shd-Patlak model can yield sharper edges and higher contrast between gray and white matter than the standard Patlak model. To further show the performance of the present shd-Patlak model, the zoomed ROIs of the BBBP maps are shown in Fig. 6. The results clearly demonstrate that the shd-Patlak model has more gains than the standard Patlak model in preserving dynamic detail information (as indicated by the arrows in Fig. 6), which further indicates more reliable cerebral permeability parameter.

Figure 5.

BBBP maps of 3 patients calculated from the different brain PCT images. Every row contains BBBP maps of one patient at different exposure and computation methods. The first column was calculated from the high-dose 190 mA images using Patlak model (the gold standard); the second and third columns were calculated from the simulated low-dose images by the Patlak model and the shd-Patlak model, respectively. The radiation dose in the low-dose data simulated is 15 mA, which equals to a 92% reduction of radiation exposure compared to the high-dose. Three ROIs of size 50 × 50 pixels are selected for all patients and quantitative evaluation is shown in Section 6.4. ROI2 is enlarged and displayed on the lower right corner of the maps. The first two patients are normal, while the third patient has brain deficit in the right middle cerebral artery (RMCA).

Figure 6.

Zoomed regions of the BBBP maps shown in Fig. 5. The first column was calculated from the high-dose 190 mA images using Patlak model (the gold standard); the second and third columns were calculated from the simulated low-dose images by the Patlak model and the shd-Patlak model, respectively. The radiation dose in the low-dose data simulated is 15 mA, which equals to a 92% reduction of radiation exposure compared to the high-dose. The arrows highlight the tissue and blood vessels which are enhanced in the simulated low-dose maps.

6.4. Quantitative Analysis

Table 2 lists the LSNR, RMSE and SSIM metrics of three ROIs and the whole brain from the low-dose PCT by two different methods. The results from shd-Patlak model exhibits significant gains over the standard Patlak model in terms of the three metrics. On average, the shd-Patlak model performs better than Patlak model. On ROI1, the performance of shd-Patlak has 58.58%, 49.37% and 54.17% gain over Patlak model in terms of LSNR, RMSE and SSIM. Experimental results on other two ROIs and the whole brain also further demonstrate better performance of the present shd-Patlak approach. P-values from the paired t-test show that our proposed method shd-Patlak consistently and significantly improve the performance of permeability computation at low-dose in three different metrics.

Table 2.

Image quality metrics of 16 patients on the three ROIs indicated by the squares in Fig. 5 and on the whole brain. Each section divided by a horizontal line is the metric values for one patient. The first row in each section is the results using Patlak model, and the second row is these using the shd-Patlak model. The best performance in the average value for each metric and region is highlighted with bold font.

ID	ROI1			ROI2			ROI3			Brain
	LSNR	RMSE	SSIM	LSNR	RMSE	SSIM	LSNR	RMSE	SSIM	LSNR	RMSE	SSIM
1	0.93	0.73	0.47	1.20	0.83	0.46	1.13	0.83	0.46	0.78	0.69	0.60
	1.54	0.36	0.76	2.10	0.39	0.79	2.09	0.38	0.78	1.03	0.34	0.84
2	1.05	0.20	0.44	1.11	0.20	0.48	1.14	0.20	0.48	0.81	0.16	0.61
	1.62	0.09	0.74	1.59	0.10	0.76	1.64	0.10	0.74	1.04	0.08	0.83
3	0.73	0.62	0.74	1.15	0.67	0.67	0.82	0.69	0.72	0.80	0.59	0.70
	0.82	0.36	0.90	1.52	0.36	0.89	0.92	0.48	0.91	0.94	0.31	0.91
4	1.18	1.12	0.39	1.23	1.16	0.43	1.20	1.16	0.38	0.95	1.03	0.48
	2.50	0.53	0.68	1.86	0.47	0.76	1.89	0.53	0.68	1.32	0.46	0.75
5	1.04	0.86	0.43	1.18	0.92	0.45	1.27	0.94	0.52	0.87	0.80	0.53
	1.85	0.42	0.70	1.98	0.45	0.73	2.22	0.44	0.77	1.19	0.40	0.76
6	0.76	0.64	0.53	1.11	0.75	0.54	1.08	0.72	0.56	0.86	0.65	0.59
	0.95	0.35	0.74	1.73	0.39	0.77	1.60	0.39	0.76	1.15	0.35	0.80
7	0.87	0.61	0.44	1.15	0.75	0.50	1.19	0.73	0.44	0.87	0.64	0.52
	1.43	0.31	0.71	1.57	0.35	0.78	1.78	0.35	0.75	1.14	0.30	0.79
8	1.27	0.85	0.35	1.58	0.90	0.41	1.35	0.86	0.38	1.09	0.80	0.46
	2.22	0.38	0.68	2.49	0.38	0.75	2.55	0.38	0.69	1.42	0.35	0.74
9	0.86	0.72	0.41	1.43	0.91	0.49	1.14	0.85	0.46	0.87	0.74	0.59
	1.43	0.38	0.66	2.48	0.45	0.74	2.38	0.43	0.72	1.15	0.37	0.81
10	1.03	0.99	0.55	1.57	1.10	0.51	1.27	1.10	0.58	1.08	0.98	0.57
	1.23	0.61	0.76	2.61	0.54	0.76	1.54	0.58	0.79	1.33	0.50	0.79
11	0.84	0.85	0.59	1.09	0.97	0.60	0.94	0.88	0.65	0.81	0.81	0.65
	1.10	0.44	0.82	1.60	0.47	0.84	1.28	0.44	0.86	1.10	0.42	0.86
12	1.04	0.95	0.76	1.02	0.98	0.75	1.06	0.99	0.76	0.63	0.78	0.82
	1.31	0.48	0.92	1.39	0.53	0.91	1.29	0.55	0.91	0.78	0.52	0.93
13	0.88	0.80	0.37	1.39	0.96	0.45	1.03	0.87	0.46	0.85	0.76	0.56
	1.25	0.41	0.63	2.17	0.44	0.74	1.41	0.41	0.73	1.09	0.35	0.79
14	0.95	0.67	0.54	1.20	0.78	0.53	1.00	0.70	0.52	0.80	0.63	0.63
	1.44	0.36	0.77	1.91	0.40	0.79	1.48	0.38	0.77	1.06	0.34	0.82
15	1.22	1.13	0.44	1.50	1.23	0.44	1.30	1.22	0.50	1.14	1.11	0.47
	1.79	0.55	0.71	2.55	0.57	0.74	1.58	0.57	0.77	1.52	0.52	0.74
16	1.15	0.85	0.31	1.13	0.83	0.36	1.17	0.87	0.45	0.84	0.73	0.51
	2.45	0.41	0.62	2.70	0.40	0.63	1.78	0.42	0.72	1.16	0.35	0.73
Mean	0.99	0.79	0.48	1.25	0.87	0.50	1.13	0.85	0.52	0.88	0.74	0.58
	1.56	0.40	0.74	2.01	0.42	0.77	1.72	0.43	0.77	1.15	0.37	0.81
Std	0.16	0.22	0.13	0.18	0.24	0.10	0.14	0.23	0.11	0.13	0.21	0.09
	0.50	0.12	0.08	0.44	0.11	0.07	0.42	0.11	0.07	0.18	0.11	0.06
P	< 0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001

6.5. Correlation Analysis

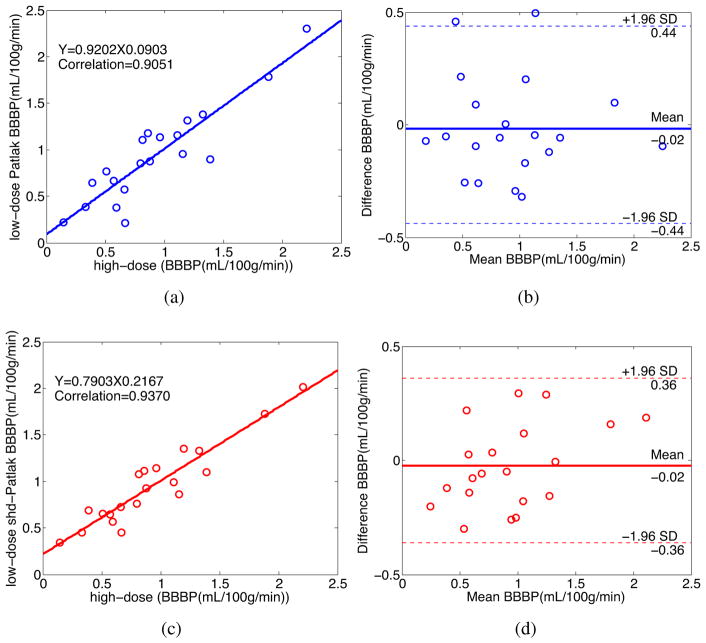
To further demonstrate the merits of the present shd-Patlak model quantitatively, we manually select 20 specific ROIs of size 3 × 3 pixels from the second and third subjects in Fig. 5 which exclude the areas that contain major blood vessel branches and suspected abnormal signs. The ROIs are located at both hemispheres in basal ganglia, gray matter and white matter. Fig. 7 and 8 illustrate the regression equation, Pearson correlation coefficients and the corresponding Bland-Altman plots of BBBP values under different conditions for the these two patients in Fig. 5. It can be observed that the correlation coefficients derived from the high- and the low-dose maps computed by the shd-Patlak model are consistently higher than those from the low-dose maps of the Patlak model, whereas the difference in the ordinate axis on the Bland-Altman plot is smaller. For the BBBP parameters shown in Fig. 7 the bias from the shd-Patlak model is also less than that from the Patlak model. These figures suggest that the shd-Patlak model can achieve noticeable performance in low-dose PCT map estimation with the accuracy of diagnostic physiological parameters.

Figure 7.

The correlation (left column) and Bland-Altman plot (right column) between the BBBP values computed from the high-dose images and the low-dose images by different methods for the patient in the second row in Fig. 5. Plots (a) and (b) represent the results obtained from the high-and low-dose by the Patlak model. Plots (c) and (d) represent the corresponding results obtained from the high- and low-dose by the shd-Patlak model.

Figure 8.

The correlation (left column) and Bland-Altman plot (right column) between the BBBP values computed from the high-dose images and the low-dose images by different methods for the patient in the third row in Fig. 5. Plots (a) and (b) represent the results obtained from the high- and low-dose by the Patlak model. Plots (c) and (d) represent the corresponding results obtained from the high- and low-dose by the shd-Patlak model.

6.6. Evaluation of Training Data

To evaluate the impact of pathological and normal training data on the low-dose enhancement results, we choose 6 patients with brain deficits among the 16 patients and enhance them by training on only the healthy controls or the pathological cases. Each of the 6 low-dose testing cases has brain deficits due to subarachnoid aneurysmal hemorrhage (SAH) at one or more regions from the following: right anterior cerebral artery (RACA), left anterior cerebral artery (LACA), right middle cerebral artery (RMCA), left middle cerebral artery (LMCA). The pathological training cases include deficits caused by SAH in all of the above mentioned regions. The healthy controls do not have any deficit in the BBBP maps. Fig. shows the BBBP maps of Patient 8 at different experimental settings. Visual inspection indicates that while the BBBP maps estimated by both shd-Patlak models (either trained on cases with deficits or normal controls) outperform the maps generated by the standard Patlak model at low-dose 15 mA, there is no obvious visual differences between the maps estimated by the two shd-Patlak models. The abnormalities in the brain of the testing data are well preserved by using shd-Patlak model in both cases. Table lists the LSNR, RMSE and SSIM metrics of LMCA, RMCA and the whole brain region from the 6 pathological testing cases at low-dose exposure by three approaches: Patlak model, shd-Patlak trained on pathological and shd-Patlak trained on normal cases. Both shd-Patlak models significantly outperform the standard Patlak model in terms of three metrics on two regions and the whole brain area (P1 and P2). The hypothesis for P3 is that the permeability maps enhanced using the shd-Patlak model trained on healthy controls have no change in terms of three metrics compared with the maps enhanced by shd-Patlak trained on pathological cases. Paired t-test demonstrates that in terms of RMSE and SSIM, in general the two approaches are not statistically different. For LSNR, the two approaches are statistically different. Further one-tail t-test shows that shd-Patlak model trained on cases with deficits yields higher LSNR compared to that trained on normal controls for low-dose enhancement of pathological cases.

6.7. Evaluation of Convergence and Parameter Sensitivity

We also conducted experiments of the convergence rate and parameter sensitivity (Fig. 10). The cost function in Eq. 15 drops fast and usually converges after 2 or 3 iterations, as shown in Fig. 10(a). In our framework, five parameters should be selected manually, namely the patch-size L, the search-window S_i, the atom number m, the weighting parameters λ and β, which controls the sparsity the coefficient α and the importance of the regularization term. It is worthwhile to mention that all the related parameters are likely dependent on the application in practice. In general, the performance was stable for all parameters, and the optimum parameters were chosen for the above mentioned experiments. From Fig. 10(a), the optimal patch size of 5 × 5 was adequate for effective noise and artifact suppression while retaining computational efficiency. The search-window S_i should be sufficiently large to acquire more similarity information while minimizing the influence of the mismatched tissues. The size of the search window will also influence the searching time. To find sufficient similar patches in reasonable time, based on the analysis in Fig. 10(b), we chose a search window of 11 × 11. For the parameters λ and β, in this paper, we briefly fixed the sizes of the search-window and patch-size, and compared the results estimated with a broad range of parameter values in term of visual inspection and quantitative measurements. The atom number from each training sample m depends on the size of the training dataset, and for the current experiment setting, m = 5 generated sufficient training patches. The sparse weight λ should not be too large, otherwise it will produce over-smoothed results and we found that λ = 0.05 generates satisfactory results for the cases in general. The weighting parameter β reflects the importance of the sparse high-dose induced prior and β = 0.3 was adequate for the reconstruction. More theoretical analysis in optimizing the parameters are necessary, which may be a topic for future research.

Figure 10.

Convergence rate and parameter sensitivity of patch size, search window size, training samples per image, λ and β. A set of parameter values is tested. The cost function drops fast and usually converges after 2 or 3 iterations. Generally the performance is stable and the optimum values are chosen in the following experiments.

7. Discussion

In this paper, we present a high-dose induced prior for the low-dose blood-brain barrier permeability estimation in cerebral PCT. The experimental results show that the present shd-Patlak model can yield more significant performance gains than the existing Patlak model in terms of different measurement metrics and visual quality.

The penalty prior reflects the information of the desired BBBP map. The traditional image prior to tackle the inverse problems relies on some simplifying assumptions. These assumptions include local spatial smoothness, sparsity in the transformed domain and low/max-entropy, etc. In general, given that these assumptions are in accordance with the properties of the desired BBBP maps with a low noise level, these priors might work well. On the other hand, given that the noise level is relatively significant and the image information is deteriorated by the high noise level in the low-dose map, these priors would tend to produce the over-smoothed regions. More importantly, such condition is misleading in clinical scenarios because the related over-smoothed effect may average the neighboring pixels with the abnormal tissue and lead to neglect of the abnormality.

In PCT imaging, scans performed at higher tube current following the outdated and current protocols are available in the clinical data repository at hospitals. The high-dose high-quality BBBP maps provide strong a priori information of the general brain structure and permeability pattern. It would be a natural choice to use the high-dose BBBP maps to induce low-dose BBBP map estimation from the measured noisy data. However, the patient distinction and the tissue deformation make such application challenging. Thus to fully use the high-dose permeability maps of different patients, dedicated image registration techniques are needed. Sparse high-dose induced prior may be a good candidate to use the high-dose maps for the current patient BBBP estimation because it does not heavily depend on the accuracy of the image registration due to its patch searching mechanism. Consequently, an important novelty of the present shd-Patlak model in this paper is the utilization of the existent high-dose maps without the need of accurate image registration. In other words, the shd-Patlak model can relax the need for accurate image registration processing through its patch-based search mechanism during construction of the location adaptive dictionaries and selection of a sparse set of useful atoms from the dictionary during the reconstruction process.

The enhanced BBBP maps with abnormalities trained on healthy controls or the subjects with abnormalities are not statistically different in terms of RMSE and SSIM, while those trained on subjects with abnormalities have slightly higher LSNR. Visual inspection by neuroradiologists indicates that no significant difference can be found between the two cases and both of them significantly outperform the results using the standard Patlak model. Since RMSE and SSIM reflect the differences between the enhanced images and the gold standard, while LSNR is a metric that reflects the relationship of the signal value and the variance of the enhanced test image itself, the former two metrics reflect the fidelity between the enhanced low-dose image and the gold standard. When the patch size is sufficiently small (much smaller than the size of the abnormalities), the patches from the training data can represent the tissue structures at the corresponding anatomical regions of the test data despite of the differences in subjects and types of deficits. Hence, an important advantage of the proposed shd-Patlak model is the independence between the abnormalities in the training and the testing data. In another word, the shd-Patlak model does not strictly require the same pathologies to be seen in the training data for reliable enhancement of the corresponding abnormalities in the testing cases.

Visual inspection on the enhanced low-dose BBBP maps by using shd-Patlak model shows minor loss of spatial resolution and color contrast. To address this, a neuroradiologist with 12 years of experience (P.C.S.) reviewed the simulated low-dose BBBP maps estimated using the standard Patlak model and shd-Patlak model in pairs while using the high-dose 190 mA BBBP maps as the reference. It shows that the minor loss of spatial resolution and color contrast in the BBBP maps of 16 cases did not significantly hamper the clinical diagnosis, while the severe noise (or “graininess”) in the low-dose maps did hinder the accurate diagnosis of brain abnormality, especially at vessel boundaries and lobes. Further subjective evaluation by the neuroradiologists on clinical diagnosis could be a future research direction.

The EM-style algorithm converges fast, as shown in Fig. 10(a) and usually converges in 2–3 iterations. Every step in the EM algorithm decreases or maintains the global energy without increasing it, leading to convergence in the end. Although there is no theoretical guarantee of the global optimum for this iterative algorithm, local random perturbations of the initialization yields stable optimization results. With good initialization using the BBBP map estimated using the standard Patlak model from the low-dose PCT data, the cost function generally converges to ideal solution. With proper parameter setting, the present shd-Patlak model takes 40 s to process a PCT dataset of 512×512×119 voxels, while the Patlak model takes 20 s in the same experimental setting. Considering the improved qualitative and quantitative results, the extended computation time is worthwhile. Obviously with faster computers, dedicated hardware and implementation of the algorithm in C++ environment would boost up the execution time and make the processing time clinically acceptable.

8. Conclusion

In this paper, we propose an approach to restore the missing information in the low-dose BBBP maps generated from PCT with Patlak model. The standard Patlak model based PCT requires excessive radiation exposure, which raised attentions on the radiation safety. The proposed method constructs high quality BBBP maps from low-dose PCT by using the brain structural similarity between different individuals and the relations between high- and low-dose maps.

The proposed approach first builds a high-dose induced prior for the Patlak model with a set of location adaptive dictionaries obtained from the corresponding anatomical regions in the high-dose maps from the repository, followed by an optimized estimation of BBBP map with the prior regularized Patlak model.

The shd-Patlak model was validated on a series of high-dose brain PCT datasets and the corresponding low-dose images simulated from the high-dose images. Evaluations were performed with visual inspection, profile comparison, three quantitative performance evaluation metrics and correlation analysis. The impact of abnormalities in the training data and parameter sensitivity were also analyzed.

Currently our efforts were focused on the noise suppression in BBBP estimation using an iterative algorithm with a sparse high-dose induced prior. For future work, besides noise, bias and data corruption are also important problems in the low-dose PCT imaging which are worth future study. In clinics, the present algorithm can be applied to other spatial-temporal medical data and applications in which high-quality prior image is available and subsequent acquisition is performed, such as radiotherapy and magnetic resonance perfusion. Thus the present model can be adapted to the associated application for radiation dose reduction, opening another topic for future research.

Figure 9.

BBBP maps of Patient No. 8 at different experimental settings. (a) A frame from the PCT data of Patient 8, who has RACA deficit due to ventriculostomy catheter and the blood in the brain vessel flows into the skull. (b) Map calculated using Patlak model at 190 mA. (c) Map calculated using Patlak model at 15 mA. (d) Map calculated using shd-Patlak model at 15 mA and trained on deficit cases. (e) Map calculated using shd-Patlak model at 15 mA and trained on normal cases. Left and right middle cerebral arteries (LMCA and RMCA) are enlarged below the map.

Table 3.

Image quality metrics of 6 patients with brain deficits on either RMCA or LMCA indicated by the rectangles in Fig. 9 and on the whole brain. Each section divided by a horizontal line is the metric values for one patient. The first row in each section is the results using Patlak model. The second row is these using the shd-Patlak model trained on cases with brain deficits in the BBBP maps. The third row is these using the shd-Patlak model trained on cased with normal brain BBBP maps. The best performance in the average value for each metric and region is highlighted with bold font. P1 is the p-value for comparison between Patlak and shd-Patlak trained on deficit cases. P2 is the p-value for the comparison between Patlak and shd-Patlak trained on normal cases. P3 is the p-value for the comparison between shd-Patlak model trained on the deficit cases and shd-Patlak trained on normal cases.

ID	Method	RMCA			LMCA			Brain
		LSNR	RMSE	SSIM	LSNR	RMSE	SSIM	LSNR	RMSE	SSIM
2	Patlak	1.21	0.20	0.52	1.18	0.20	0.51	0.88	0.17	0.58
	shd (defcit)	1.63	0.10	0.79	1.68	0.10	0.78	1.11	0.09	0.82
	shd (normal)	1.58	0.10	0.81	1.66	0.10	0.78	1.09	0.08	0.83
4	Patlak	1.27	1.16	0.40	1.30	1.18	0.38	0.87	0.97	0.52
	shd (defcit)	2.03	0.51	0.71	2.32	0.52	0.71	1.17	0.44	0.77
	shd (normal)	1.94	0.53	0.69	2.18	0.52	0.71	1.15	0.44	0.77
6	Patlak	1.19	0.74	0.55	1.24	0.76	0.54	0.82	0.62	0.63
	shd (defcit)	1.91	0.39	0.78	2.00	0.39	0.77	1.07	0.33	0.82
	shd (normal)	1.88	0.40	0.78	1.84	0.38	0.79	1.05	0.33	0.83
8	Patlak	1.59	0.91	0.39	1.38	0.88	0.37	1.01	0.77	0.48
	shd (defcit)	2.52	0.39	0.72	2.41	0.39	0.69	1.28	0.34	0.76
	shd (normal)	2.43	0.40	0.72	2.29	0.40	0.69	1.27	0.35	0.75
9	Patlak	1.35	0.91	0.48	1.22	0.86	0.46	0.81	0.71	0.61
	shd (defcit)	2.17	0.42	0.77	2.20	0.41	0.74	1.06	0.35	0.82
	shd (normal)	2.02	0.42	0.78	2.07	0.41	0.76	1.04	0.35	0.83
10	Patlak	1.62	1.11	0.49	1.49	1.11	0.49	1.01	0.94	0.59
	shd (defcit)	2.52	0.54	0.75	2.10	0.53	0.76	1.21	0.47	0.81
	shd (normal)	2.49	0.55	0.74	2.07	0.55	0.75	1.20	0.48	0.80
Mean	Patlak	1.37	0.84	0.47	1.30	0.83	0.46	0.90	0.70	0.57
	shd (defcit)	2.13	0.39	0.75	2.12	0.37	0.74	1.15	0.34	0.80
	shd (normal)	2.06	0.40	0.75	2.02	0.39	0.75	1.13	0.34	0.80
Std	Patlak	0.19	0.35	0.06	0.12	0.35	0.07	0.09	0.29	0.06
	shd (defcit)	0.35	0.16	0.03	0.26	0.16	0.04	0.09	0.13	0.03
	shd (normal)	0.35	0.16	0.04	0.23	0.16	0.04	0.09	0.14	0.03
P	P1	<0.001	<0.01	<0.001	<0.001	<0.01	<0.001	<0.001	<0.01	<0.001
	P2	<0.001	<0.01	<0.001	<0.001	<0.01	<0.001	<0.001	<0.01	<0.001
	P3	0.01	0.04	1.00	0.01	0.47	0.36	<0.001	0.61	0.69

1. Interweaving the standard Patlak model with sparse high-dose induced prior.

2. Construct location adaptive dictionary based on anatomical structure of the brain.

3. Learn sparse high-dose induced prior from different patients without the need of accurate registration.

4. Propose EM style iterative optimization for sparse high-dose induced Patlak model.

5. Outperform Patlak model in low-dose BBBP estimation in terms of different metrics.