An adaptive coarse graining method for signal transduction in three dimensions

Abstract

The spatio-temporal landscape of the plasma membrane regulates activation and signal transduction of membrane bound receptors by restricting their two-dimensional mobility and by inducing receptor clustering. This regulation also extends to complex formation between receptors and adaptor proteins, which are the intermediate signaling molecules involved in cellular signaling that relay the received cues from cell surface to cytoplasm and eventually to the nucleus. Although their investigation poses challenging technical difficulties, there is a crucial need to understand the impact of the receptor diffusivity, clustering, and spatial heterogeneity, and of receptor-adaptor protein complex formation on the cellular signal transduction patterns. Building upon our earlier studies, we have developed an adaptive coarse-grained Monte Carlo method that can be used to investigate the role of diffusion, clustering and membrane corralling on receptor association and receptor-adaptor protein complex formation dynamics in three dimensions. The new Monte Carlo lattice based approach allowed us to introduce spatial resolution on the 2-D plasma membrane and to model the cytoplasm in three-dimensions. Being a multi-resolution approach, our new method makes it possible to represent various parts of the cellular system at different levels of detail and enabled us to utilize the locally homogeneous assumption when justified (e.g., cytoplasmic region away from the cell membrane) and avoid its use when high spatial resolution is needed (e.g., cell membrane and cytoplasmic region near the membrane) while keeping the required computational complexity manageable. Our results have shown that diffusion has a significant impact on receptor-receptor dimerization and receptor-adaptor protein complex formation kinetics. We have observed an “adaptor protein hopping” mechanism where the receptor binding proteins may hop between receptors to form short-lived transient complexes. This increased residence time of the adaptor proteins near cell membrane and their ability to frequently change signaling partners may explain the increase in signaling efficiency when receptors are clustered. We also hypothesize that the adaptor protein hopping mechanism can cause concurrent or sequential activation of multiple signaling pathways, thus leading to crosstalk between diverse biological functions.

1. Introduction

To respond to the complexities of their external environment, living cells have evolved complex signal transduction pathways, most of which surpass the complexity of modern processing units. The cellular signaling machinery represents a robust multiscale system with a large range of time (from sub-seconds for biomolecular complex formation to hours and days for transcription and translation (Kholodenko, Demin et al. 1999; Bonneau, Reiss et al. 2006)) and length (nanometers to tens of micrometers) scales. It is understood that the effects of signal transduction go far beyond the signaling pathway itself, leading to cell-fate decisions such as cell migration, tissue reorganization, inflammation, cell growth, and apoptosis. Due to this fundamental role, understanding the mechanisms and modulations that regulate cell signaling is of utmost importance and an intrinsically multiscale problem.

The Toll-like receptor (TLR) signal transduction system deciphers pathogen patterns and responds with the appropriate cellular response thus initiating the transition from innate to adaptive immunity (Janssens and Beyaert 2003; McCoy and O’Neill 2008; Tanaka, Oh-Hashi et al. 2008). The physiological consequences of TLR activation have the potential to devastate the host cell with activation of apoptotic pathways; therefore the TLRs are tightly regulated and expressed at very low levels (Regueiro, Moranta et al. 2009). In addition to the regulation by changes in expression levels, dynamics and signaling properties of TLRs (and other similar receptor systems) are also regulated physically by the structure and organization of the cell membrane since these receptors are membrane bound. The spatial landscape of the plasma membrane has been shown to determine signaling efficiency (Tian, Harding et al. 2007), orchestrate receptor co-localization and clustering, and serve as a mechanism for receptor spatio-temporal regulation. Compounding this complexity is how the membrane proteins such as TLR interact with cytosolic species which, through sequential protein-protein interactions convey the external cues received by the membrane proteins to the interior of the cell. How and which adaptor proteins interact with each other defines the intracellular signaling patterns. Efficiency of the interactions between cytosolic proteins and receptors are inadvertently affected by the membrane structure. Because of such effects on molecular properties, it is of critical importance to understand how receptor diffusion, spatial organization of cell signaling and receptor-adaptor protein interactions are affected by the organization of the cell membrane.

Since the paradigm shift in the concept of the plasma membrane from a two-dimensional continuum fluid model as described in the seminal work of Singer-Nicolson (Singer and Nicolson 1972) to the understanding that the plasma membrane is an inhomogeneous surface with possible functional domains (Kusumi, Nakada et al. 2005), scientists are just beginning to realize the profound ways that inhomogeneities of the plasma membrane may impact receptor dynamics and that protein diffusivity may have on downstream signal transduction. For example, the underlying actin cytoskeleton constrains lipid and protein diffusivity in a picket-fence manner where proteins are immobilized in pickets on the extracellular surface (Kusumi, Suzuki et al. 1999; Ritchie and Kusumi 2004). The actin cytoskeleton can thus enhance receptor encounters by corralling receptors into microdomains where the probability of receptor dimerization is higher, and such an increase in the signal transduction capacity was observed when receptors were clustered (Costa, Radhakrishnan et al. 2009). Similarly, self-organizing lipids rafts can restrict receptor diffusivity and act as hubs of signal transduction (Dietrich, Yang et al. 2002; Chen, Yang et al. 2004). In addition, endocytotic structures clathrin and caveolae can impact complex formation patterns by co-localizing the receptors or affect receptor mobility and degradation patterns through trafficking (Resat, Ewald et al. 2003; Shankaran, Wiley et al. 2007).

Many mathematical models have been developed to understand the dynamic behavior of signal transduction pathways (Kholodenko, Demin et al. 1999; Sasagawa, Ozaki et al. 2005; Shankaran, Wiley et al. 2006). Unfortunately, most models neglect the significance of receptor spatial organization by assuming the well-mixed condition which is inherent to ordinary differential equation (ODE) models or their stochastic versions (Resat, Costa et al. 2011). Here we have taken a different approach and developed a multiscale stochastic platform to study spatio-temporal properties of signal transduction networks in pseudo three dimensions. This study extends our coupled spatial non-spatial algorithm CSNSA, which combined a spatially resolved Monte Carlo lattice approach for receptor interactions and the Gillespie algorithm for the dynamics of cytoplasmic proteins (Costa, Radhakrishnan et al. 2009), where the intracellular environment is now treated as a spatially organized, non-homogeneous system. Since spatial-temporal models are computationally intensive, it is not be feasible to model spatial temporal interactions of all proteins. Therefore, our new approach employs a computationally less intensive hybrid approach instead, and it extends the adaptively coarse-grained Monte Carlo (ACGMC) method (Chatterjee, Snyder et al. 2004; Chatterjee, Katsoulakis et al. 2005; Chatterjee, Vlachos et al. 2005; Collins, Chatterjee et al. 2008; Collins, Stamatakis et al. 2010) to three dimensions. This extension made it possible to obtain spatial-temporal resolution of proteins spanning multiple time and length scales by appropriately partitioning the system according to desired resolutions. We have applied the new approach to study cellular signaling in three dimensions. Our results imply that adaptor protein hopping, i.e., sequential binding of the adaptor proteins to multiple receptors, may be a plausible mechanism exploited by pathogens to alter the signaling patterns of their hosts.

2. Adaptively coarse-grained Monte Carlo algorithm

2.1. Simulation System Setup

Multiresolution coarse graining offer solutions to some of the computational bottlenecks encountered in multiscale systems. Arguably the most direct way to implement coarse graining is to use multiple lattices where different sections of the system have different resolutions that are assigned according to the intrinsic properties of the studied biological problem. In this report, as an application of our new method, we address how receptor co-localization and complex formation with adaptor proteins may impact downstream signal transduction. We therefore were mostly interested in receptor-receptor interactions on the plasma membrane and in receptor-cytosolic species reactions at the plasma membrane/cytoplasm interface. Reactions that occur in the cytoplasm further away from the membrane can be expected to occur homogeneously, and therefore, do not need to be tracked individually. To accommodate these requirements into the simulation set-up, we apply coarse-graining along the z-axis to define three regions with different levels of resolution (Figure 1):

Figure 1.

Schematic layout of the coarse grained simulation framework representing the fine spatial resolution near the plasma membrane and coarse-graining in the cytoplasm where the resolution of the regions decreases in successive steps as moved away from the cell surface.

1. High resolution region. Lattice layers i=1–7 represent the plasma membrane and the adjacent cytosol region. These layers have a z-lattice spacing of 10 nm. The first layer represents the plasma membrane and it is the only layer that is accessible to the receptors. Layers #2–#7 form the 60 nm thick cytosol region that is modeled at a high (10 nm) spatial resolution.

2. Intermediate resolution region. Lattice layers i=8 and 9 represent the intermediate cytosol region that act as a two-tiered buffer region between the near membrane and the bulk cytoplasm regions. These lattices have a z-lattice spacing of 50nm, which the medium resolution level in the simulated system.

3. Low resolution region. Last layer i=10 has a 100 nm z-lattice spacing and it represents the deeper parts of the cytosol away from the membrane.

The x-y dimensions were described using a 50×50 lattice mesh with 10 nm spacing and periodic boundary conditions. We note that this spacing and the highest resolution along the z-direction was chosen according to the typical size of membrane-bound receptors, which is ~10 nm (Carpenter and O’Neill 2009; Lin, Lo et al. 2010). With this choice, a single lattice site of layer #1 can only contain one receptor, i.e., the lattice site is considered fully occupied when it contains a receptor. Similarly, receptor dimerization results in the occupancy of two adjacent sites. Being smaller in size, it was assumed that the adaptor proteins occupy the same lattice site of the receptors that they are bound to. With these assumptions, in our set-up receptors and receptor dimers reside on layer #1. Adaptor proteins bound to a membrane receptor also reside on layer #1 and they diffuse as part of a receptor complex on the plasma membrane. Upon dissociation from the receptors, adaptor proteins are placed at layer #2.

2.2. Dynamics in the high resolution region

Diffusion at the plasma membrane layer

In the top layer of the high resolution region (layer #1), which represents the plasma membrane, the diffusional translational motion of proteins were modeled as hopping between adjacent lattice sites with a microscopic diffusion rate of ${\mathrm{\Gamma }}_{i\to j}^{\mathit{diff}}=\frac{1}{m}{\mathrm{\Gamma }}^{\mathit{diff}}{\sigma }_i(1-{\sigma }_j)$ where σ_i is the occupancy factor of the site i. Factor m is equal to the 2 × dimensionality of the system, i.e., m=4 for 2-D and 6 for 3-D motion. Since each lattice site can hold at most one receptor or one receptor-adaptor protein complex in this high resolution layer (Section 2.1), σ_i is either one or zero for this layer. Thus, the σ_i (1−σ_j) factor in the formula ascertains that receptor hopping can only occur from an occupied lattice site to an unoccupied one. With the choice ${\mathrm{\Gamma }}^{\mathit{diff}}=\frac{m{D}_c}{a^2}$, where D_c is the molecular diffusion coefficient and a is the grid spacing (=10 nm), hopping motion on a rectangular grid represents the diffusive motion (Berg 1993).

Diffusion near the cell surface

Diffusion of the proteins in the other parts of the high resolution region (layers #2–#7, part of the cytosol adjacent to the plasma membrane) are modeled in the same way as the diffusion in layer #1 by choosing the dimensionality factor as m=6 because the proteins can jump in between different layers as well in that region.

Biochemical reactions

The association-dissociation and chemical reactions between receptors, cytosolic proteins, and receptor-cytosolic species were dependent on the state of the neighboring lattice sites, and they were modeled using the stochastic simulation algorithm (SSA) (Gillespie 1977; Resat, Wiley et al. 2001) in the high resolution region. In SSA, every reaction is associated with a probability that specifies the rate at which that reaction may occur. For our system, the rates of the involved reactions and molecular transitions were computed as follows: The transition rate for the receptor dimerization between receptors in adjacent lattice sites R_i+R_j→C_ij was ${\mathrm{\Gamma }}_{i,j}^{\mathit{dimer}}=\frac{k{\sigma }_i{\sigma }_j}{2}$. Similarly, the transition rate for biomolecular reactions A_i+B_j→C was ${\mathrm{\Gamma }}_{ij}^{\mathit{reac}}=\frac{k{\sigma }_i{\sigma }_j}{6}$. Unimolecular reactions A→C, which only takes place when ligand binds to its receptor on the plasma membrane and the dissociation reactions (C_ij →R_i+R_j or C→ A_i+B_j) were described with a transition rate of ${\mathrm{\Gamma }}_i^{\mathit{uni}}=k{\sigma }_i$. In these expressions k is the is the ordinary rate constant of the reaction.

2.3. Dynamics in the coarse-grained lattices

The coarse-grained region occupies the volume formed by layers #8–#10. In these layers, each coarse grained site C_k is characterized with the number of microscopic sites q_k that it contains. The number of microscopic sites in C_k is given as $q_k=a_k^x{q}_k^y{q}_k^z$, where $q_k^l$ is the microscopic partitioning along the l^th axis (l=x,y, or z, and $q_k^l$ is the size ratio of the resolutions of the coarse grained unit and the highest resolution region along axis l). In other words, q_k corresponds to the number of microscopic sites of the highest resolution lattice that fits into a site of the coarse-grained lattice. With this notation, the occupancy of a coarse-grained lattice site C_k would be η_{k = Σp∈Ck} σ_p, corresponding to a fractional coverage of $\overline{{\eta }_k}={\eta }_k/q_k$. In our set-up, the resolution along the x-y plane was 10 nm in all the layers, so $q_k^x=q_k^y=1$.

Diffusional hopping and biochemical reactions in the coarse-grained lattices can be defined in a similar way to the expressions for the highest resolution lattice (Chatterjee, Vlachos et al. 2004; Chatterjee, Katsoulakis et al. 2005; Chatterjee, Vlachos et al. 2005; Chatterjee and Vlachos 2007): The diffusion rate from a high resolution lattice site to a coarse cell or coarse-cell to another coarse-cell q_i → q_j in terms of the underlying microscopic diffusion rate is ${\mathrm{\Gamma }}_{i\to j}^{\mathit{diff},\mathit{coarse}}=\frac{{\eta }_i(n-{\overline{\eta }}_j)}{q_i(q_i+q_j)}{\mathrm{\Gamma }}_{i\to j}^{\mathit{diff}}$. In the limit of the diffusion from the coarse grained lattice #8 to high resolution lattice #7, this expression becomes ${\mathrm{\Gamma }}_{i\to j}^{\mathit{diff},c}=\frac{{\eta }_i(1-{\eta }_j)}{q_i(q_i+1)}{\mathrm{\Gamma }}_{i\to j}^{\mathit{diff}}$.

As in the case of the high-resolution lattice (Section 2.2), the rates of the biochemical reactions occurring in the coarse-grained lattices can be defined analogously to the diffusional hopping expressions. In this case, $\overline{{\eta }_J}$ in the rate expressions represents the fractional occupancy of the encountered reactant B, $\overline{{\eta }_{B,J}}={\eta }_B/q_j$. Further details of these rate expressions and their derivation for the adaptive coarse graining can be found in (Chatterjee, Vlachos et al. 2004; Chatterjee, Katsoulakis et al. 2005; Chatterjee, Vlachos et al. 2005; Chatterjee and Vlachos 2007). The diffusion and reaction rates are computed a priori for each lattice and are updated throughout the simulation as required by the occupancy of neighboring lattice sites and the state of species at these sites.

3. Algorithm implementation and simulation details

3.1. Stochastic Monte Carlo simulation

The Monte Carlo simulation requires the selection of the location (which lattice site) and the type of the reaction that may occur next. To do this, first the total transition rate of all the diffusion and biochemical reaction transitions Γ _tot,lat,i that may take place on layer i was computed (cf., Section 2; i=#1–#10). Then the total transition rate of the reactions that may occur in the whole system Γ _tot is the sum Γ _tot,lat,i over the constituent lattice layers. The probability for selecting a reaction occurring in a given layer is then the ratio of the total transition rate for that lattice layer divided by the total transition rate, P_lat,i = Γ_tot,lat,i/Γ_tot. A random Monte Carlo selection was used to select the lattice layer for the next reaction according to the computed lattice layer probabilities. Once a lattice layer has been selected, a lattice site from that two-dimensional layer was chosen using a uniform random selection. Picked site is the location of the next potential reaction in the system. Occupancy information and protein species states were indexed for all neighboring lattice units of the selected reaction site. A Monte Carlo null based approach is used to determine the event (diffusion, reaction, or null) to implement (Costa, Radhakrishnan et al. 2009). When a diffusion or biochemical reaction event was selected, whether it actually occurred was decided by comparing the ratio of the propensity of the event Γ _i→j to the “local maximum propensity” Γ _max with a uniform random number r1 in the [0:1] range, i.e., the event was accepted to occur if r₁< Γ_i→j/Γ_max. Otherwise a null event was chosen. Choosing ${\mathrm{\Gamma }}_{\mathit{max}}={\sum }_{j\in n.n.}{\mathrm{\Gamma }}_{i\to j}^{\mathit{diff}}+\mathit{max}\left\{{\mathrm{\Gamma }}_{i\to j}^{\mathit{bioreac}}\right\}$ ensured that the selection probability was less or equal to 1 in this scheme. First sum in the definition of Γ_max corresponds to the propensities of diffusion (hopping) out of the selected lattice site, and the second term is the propensity of the biochemical reaction (dimerization, association, etc.) with the largest propensity that could occur in the chosen unit. Thus, Γ_max is the maximum propensity that any of the reactions that could possibly occur in the chosen lattice site i, and therefore, Γ_i→j ≤ Γ_max condition is always satisfied.

Execution of the algorithm detailed above superposes the kinetics in all lattices into a single Monte Carlo trajectory. Correspondingly, time is updated in a combined manner from the total transition rate for all events in the system as Δt = log (r₂)/Γ_tot where r₂ is a uniformly selected random number. This selection ensures that the reaction times are exponentially distributed (Gillespie 1977; Resat, Wiley et al. 2001). The algorithm was validated by comparing the results with the ODE solution when the diffusion coefficient was large. Allowing the biomolecules to move with large diffusion coefficients made it possible to mimic the “well-mixed” system conditions of the ODE simulations in control and validation studies. Obtained results (not shown) showed agreement between the ACGMC and the ODE solutions.

3.2. Simulation flowchart

Steps of the ACGMC algorithm are summarized in Figure 2:

Figure 2.

Workflow of the presented adaptive coarse-grained Monte Carlo method.

1. Randomly populate the lattice grid units according to the initial concentrations of the proteins, and compute the transition rates and probabilities for each event.

2. Compute the total transition rate and probabilities for each of the ten lattice layers.

3. Randomly select a lattice layer based on the total transition probability distributions of the layers.

4. Randomly select an occupied grid unit among the sites on the chosen two-dimensional lattice layer.

5. Obtain information regarding the occupancy and protein species state for the neighboring lattice sites.

6. Calculate the probabilities for each event (diffusion, reaction, or null) based on the state of the lattice units; randomly select the event type.

7. If the selected event was not a null event, execute the event and update species concentration and/or the state of the lattice units; otherwise repeat from step 4.

8. Compute transition rates in adjacent lattice layers both before and after the event.

9. Update the transition rates for all lattice sites and dependent neighboring lattice site positions.

10. Compute the total transition rate and update time.

11. Check if time has met or exceeded the maximum time. If so terminate, otherwise repeat from Step 3.

The simulation software is written in Fortran 90, compiles under Microsoft Visual Studio, and is available upon request.

3.3. Model parameters

We have previously shown that decreased diffusion within the lipid raft could lead to receptor clustering (Hsieh, Yang et al. 2010). To further simulate this process with our improved method, we have pursued simulations for homogeneous and inhomogeneous receptor distributions caused by lipid rafts where overcrowding may lead to slower diffusion of biomolecules. Receptor diffusion kinetics and their aggregation in lipid rafts was modeled by assigning a 200 nm size patch to be the raft in which receptor diffusion constant was reduced (Pralle, Keller et al. 2000; Kusumi, Ike et al. 2005). Receptor diffusion constant within the lipid raft was assumed to be D_c=10⁻⁴ μm²/s while it was 10⁻² μm²/s outside the raft, i.e., a slow down by a factor of 100 (Pralle, Keller et al. 2000; Kusumi, Ike et al. 2005). We assumed diffusivity of the cytosolic proteins, which are typically smaller than the transmembrane receptors, to be 10 times greater than the receptor diffusivity, i.e. D_c was 10⁻¹ μm²/s (Kholodenko 2006; Kholodenko and Kolch 2008; Kholodenko, Hancock et al. 2010). Although the diffusion constant depends on the size and shape of the molecules, such details are not directly relevant to the purpose of our study and were ignored to keep the number of model parameters to a minimum.

Although our major interest is the TLR pathway, the lack of quantitative experimental data and reaction parameters makes it difficult to develop a valid model for the TLR system. Therefore, we employ a hypothetical receptor signaling system to demonstrate the conditions that can give rise to regulation by diffusivities of receptors and cytosolic species. We are not interested in predictions which can arise from parameter variability but rather the role of diffusion on signal transduction properties. For this reason, we chose the initial concentrations and kinetic parameters to be in the ranges for the growth factor receptor signaling pathway, arguably the most studied receptor signaling system(Schlessinger 2000). Biochemical reactions forming the signaling pathway model that were included in our study and their kinetic rates were taken directly from Table II in (Kholodenko, Demin et al. 1999) without any modifications. Therefore, the model parameters are not repeated here and can be found in (Kholodenko, Demin et al. 1999). Even though the rates could somewhat differ between the signaling pathways, involved time scales would be comparable and this choice would not significantly alter the derived conclusions about the role of spatial inhomogeneities on diffusion and of the trends in receptor dynamics.

4. Results

We tested the effects of receptor clustering on signaling by comparing the results for the homogeneous diffusion condition with the results of the inhomogeneous diffusion conditions that were imposed by lipid rafts. We initially distributed the receptors on the plasma membrane randomly at a density of 204 receptors/μm² (~2.5×10⁵ receptors/cell), and allowed receptors to equilibrate. In the simulations employing the lipid raft domains, receptors clustered within 10 ms as detected by the Hopkins statistics test (Jain, Hamper et al. 1988); a statistical measurement of the significance of spatial organization. After this equilibration step, ligand was added to stimulate the signaling pathway. The dynamics of the system, i.e., how the activated receptors form dimers and associate with cytosolic species were then followed in time.

We have previously shown that receptor clustering increases downstream signaling (Costa, Radhakrishnan et al. 2009). The current study concentrated on determining what mechanism might be leading to signal enhancement. For this, we analyzed the number of receptor dimerization and adaptor protein-receptor association events. As shown in Fig. 3, there is only a slight increase in the number of dimerization events per second for receptors which cluster in rafts while there is a large increase in the number of associations with the adaptor proteins when receptors are clustered.

Figure 3.

Cumulative counts of (A) receptor dimerization and (B) adaptor protein-receptor association events when receptors are clustered (cyan) and uniformly distributed (magenta) in the plasma membrane. The x-axis indicates elapsed time of the simulation and the y-axis shows number of occurred events (dimerization or association).

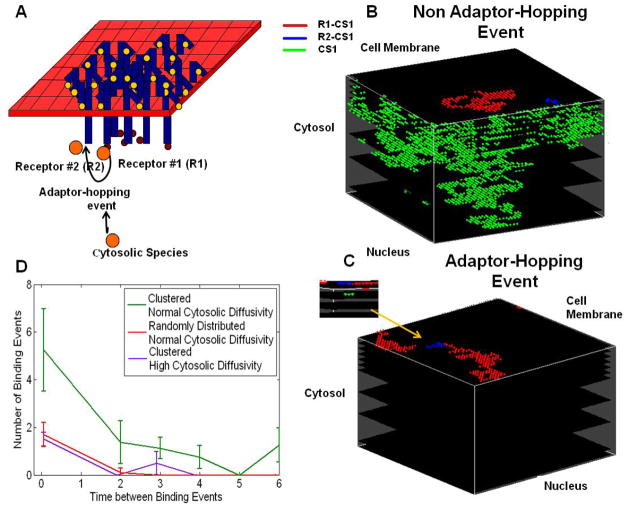
After observing a substantial increase in the number of receptor-adaptor protein association for roughly the same number of receptor dimerization occurrence, we hypothesized that receptor clustering enhances signal transduction through sequential binding of cytosolic species to neighboring receptors. This ‘adaptor protein hopping’ mechanism is schematically illustrated in Figure 4A: When it encounters a cluster of ligand-bound receptors, a cytosolic adaptor protein may associate with one of the receptors (R1) in cluster. Upon disassociation from R1, close proximity of neighboring receptors increases the probability of the adaptor protein forming a new complex with another receptor (R2) instead of diffusing into the cytosol. This frequent rebinding of the adaptor protein to the receptors could enhance the signaling potential by allowing a limited number of adaptor proteins to retrieve and convey the signal from a large number of membrane receptors to the downstream signaling elements. Hence, the adaptor protein hopping could be an efficient sampling mechanism of the receptor activation states by the cell using only a limited number of relay proteins.

Figure 4.

3D single particle tracking of cytosolic species (CS1) in the simulations, diffusing in the cytoplasm (green), diffusing on the plasma membrane while bound to receptor 1, R1-CS1 (red) or bound to receptor 2, R2-CS1 (blue). (A) Schematic illustration of the adaptor protein hopping mechanism. (B) Simulation of a rebinding event which is not an adaptor hopping event. (C) Simulation of an adaptor-hopping rebinding event. Inset shows the event’s projection onto the x-z plane. (D) Statistical distribution of the adaptor protein-receptor rebinding event counts as a function of the time (in second units) between rebinding events.

Binding events were classified as either adaptor-hopping or non-adaptor-hopping events by monitoring the rebinding times. Figures 4B&C report the trajectory of cytosolic adaptor proteins (CS) during a simulation run. The location is marked green when CS was freely diffusing in the cytosol and in red (R1) or blue (R2) when bound to receptors. Figure 4B illustrates a typical trajectory when hopping is rare; the CS disassociates from R1 and enters the cytoplasm where it diffuses for ~30 s in a well mixed pool before rebinding R2. In contrast Figure 4C shows rebinding via the adaptor protein-hopping mechanism; the CS disassociates from R1 and rapidly (~80 ms) binds to R2.

Adaptor protein hopping is a random event which depends on the factors that affect detainment of the protein near the receptors, such as receptor density and diffusion rate of the protein. As shown above, adaptor protein hopping is more dominant in rafts where the receptor concentration is much denser. It is also expected that adaptor protein hopping decreases with increasing cytosolic diffusivity because it allows the protein to move away from the receptors before re-binding occurs. Figure 4D compares the statistical distribution of the rebinding times in seconds for adaptor protein hopping events under different conditions. It was computed by counting the number of times a protein dissociated from a receptor complex and then re-attached to the same complex and the time it took to rebind. When receptors were clustered (i.e., in rafts) and adaptor protein diffusion constant D_c=10⁻¹ μm²/s (green line), the number of quick (< 500 ms) rebinding events were the most common. In contrast, the distribution of the rebinding times were more uniformly distributed when a) receptors were randomly distributed and D_c was still 10⁻¹ μm²/s (red line) or b) receptors were clustered and cytosolic diffusivity was higher D_c=10² μm²/s (purple line). We also note that the rebinding time distribution difference is statistically significant, p-values are 0.001, 0.01 and 0.002 at the first three time points, respectively, as evaluated by t-test between the results for clustered vs. uniformly distributed receptor cases (i.e., green vs. red curves in Fig. 4D). These results confirm the expected conditions for frequent adaptor protein-receptor rebinding.

5. Discussion and Conclusion

Using our spatially-resolved ACGMC algorithm, we observed that adaptor protein hopping mechanism can increase signal transduction efficiency through sequential binding of adaptor proteins to clustered receptors. The adaptor protein hopping mechanism may help to explain previous experimental findings about spatially regulated cellular signaling (Kempiak, Yip et al. 2003; Reynolds, Tischer et al. 2003; Xavier, Rabizadeh et al. 2004; Tian, Harding et al. 2007). Reynolds et al., describe a bistable state in the EGFR receptor tyrosine kinase (RTK)/protein tyrosine phosphatase (PTP) model that shows a high proportion of phosphorylated receptors are maintained in plasma membrane regions that are not exposed to ligand (Reynolds, Tischer et al. 2003). In a study investigating Ras nanoclusters, Tian et al., concluded that signal transduction is dependent on the spatial-organization of Ras and abrogated if nanoclustering is disrupted (Tian, Harding et al. 2007). Xavier et al., showed that Dlg1 is recruited upon activation to cortical actin and forms complexes with adaptors and this process is necessary for T cell activation (Xavier, Rabizadeh et al. 2004). Suggesting that differing spatial scales of signaling are supportive of models of chemotaxis; Kempiak et al., showed that EGF-induced actin polymerization remains localized following receptor overexpression. Finally, Suenaga et al., showed though Molecular Dynamics (MD) simulations that the binding affinities of EGFR-phospho peptides bind with significantly more strength to unphosphorylated Shc compared with phosphorylated Shc (Suenaga, Hatakeyama et al. 2009). These studies emphasize the importance of spatial regulation of receptors and the spatial scales of scaffolding adaptor proteins.

The in silico prediction of this new regulatory mechanism was made possible by the use of our new approach that provided multiscale spatio-temporal resolution. The ability to capture receptor-cytosolic signaling partnering dynamics and reactions in three-dimensions is a significant advancement to understand signal transduction. The more popular modeling methods such as ordinary differential equations (ODEs) cannot provide the required spatio-temporally resolved description of signal transduction within the cell. Multiscale models such as the one presented in this study can be powerful tools to aid systems biology efforts by providing a mechanistic understanding of cellular events which are not easily feasible experimentally. Our study shows the power of model development to identify novel mechanisms that have not been considered previously with an example. In addition, our hypothesis about the possible regulatory role of adaptor protein hopping can in principle be validated in optical microscopy experiments that can track single molecules (Andrews, Lidke et al. 2008; Kelly, Kober et al. 2009).

Although our study provides evidence for adaptor protein hopping mechanism, it should be noted that it was observed only when adaptor protein diffusion constant is low ~10⁻¹ μm²/s, which is 2–3 orders of magnitude lower than the experimentally measured protein diffusion in the cytoplasm (Phillips 2009). The probability of cytoplasmic protein rebinding to a nearby receptor decreases steeply as diffusion becomes faster. This is due to the fact that proteins that disassociate from receptors enter the 3D cytoplasmic volume and easily diffuse away from the membrane surface thus drastically reducing their probability of re-association with the receptors. However, the diffusion rates at the membrane-cytoplasm interface are likely to be significantly lower due to the slowing effects of the membrane layer and the underlying membrane cytoskeleton structure (Konopka, Shkel et al. 2006). These are challenging experiments, but our multiscale simulations have pointed to this as a critical phenomenon for developing a deeper understanding of signal transduction and it regulation.