Contact between rough surfaces and a criterion for macroscopic adhesion

Significance

Macroscopic objects rarely stick together, yet the van der Waals interactions between surface atoms produce attractive pressures that are orders of magnitude larger than atmospheric pressure. This “adhesion paradox” has been linked to surface roughness, which reduces the area of intimate atomic contact to summits on the rough landscape. This paper presents a parameter-free theory that captures the interplay between elasticity, interatomic attraction, and surface roughness. It predicts how adhesion changes contact area and when surfaces are sticky. The results offer a simple explanation for why tape sticks to our desktops but a sheet of paper does not, and may aid in the design of adhesives and in engineering surface roughness to enhance or eliminate adhesion.

Abstract

At the molecular scale, there are strong attractive interactions between surfaces, yet few macroscopic surfaces are sticky. Extensive simulations of contact by adhesive surfaces with roughness on nanometer to micrometer scales are used to determine how roughness reduces the area where atoms contact and thus weakens adhesion. The material properties, adhesive strength, and roughness parameters are varied by orders of magnitude. In all cases, the area of atomic contact is initially proportional to the load. The prefactor rises linearly with adhesive strength for weak attractions. Above a threshold adhesive strength, the prefactor changes sign, the surfaces become sticky, and a finite force is required to separate them. A parameter-free analytic theory is presented that describes changes in these numerical results over up to five orders of magnitude in load. It relates the threshold adhesive strength to roughness and material properties, explaining why most macroscopic surfaces do not stick. The numerical results are qualitatively and quantitatively inconsistent with classical theories based on the Greenwood−Williamson approach that neglect the range of adhesion and do not include asperity interactions.

Surfaces are adhesive or “sticky” if breaking contact requires a finite force. At the atomic scale, surfaces are pulled together by van der Waals interactions that produce forces per unit area that are orders of magnitude larger than atmospheric pressure (1). This leads to strong adhesion of small objects, such as Gecko setae (2, 3) [capillary forces may also contribute to Gecko adhesion in humid environments (4, 5)] and engineered mimics (6), and unwanted adhesion is the main failure mechanism in microelectromechanical systems with moving parts (7). Although tape and gecko feet maintain this strong adhesion at macroscopic scales, few of the objects we encounter are sticky. Indeed, our world would come to a halt if macroscopic objects adhered with an average pressure equal to that from van der Waals interactions.

The discrepancy between atomic and macroscopic forces has been dubbed the adhesion paradox (8). Experiments show that a key factor underlying this paradox is surface roughness, which reduces the fraction of surface atoms that are close enough to adhere (8–11). Quantitative calculations of this reduction are extremely challenging because of the complex topography of typical surfaces, which have bumps on top of bumps on a wide range of scales (12, 13). In many cases, they can be described as self-affine fractals from a lower wavelength of order nanometers to an upper wavelength in the micrometer to millimeter range (10, 14).

The traditional Greenwood−Williamson (GW) (15) approach for calculating nonadhesive contact of rough surfaces approximates their complex topography by a set of spherical asperities of radius R. The distribution of asperity heights is assumed to be either exponential or Gaussian, and the long-range elastic interactions between different asperities are neglected. This approach is analytically tractable and provided a simple explanation for the observation that the area of contact between nonadhesive elastic surfaces is proportional to the normal force or external load pushing them together. Later generalizations (9, 16) considered the effect of adhesion between surfaces. These theories predict that adhesion depends on the ratio of the root-mean-squared (rms) variation in surface separation h_rms to a length that characterizes the strength of adhesion. The calculated force needed to separate surfaces drops rapidly as increases.

In the last decade, there has been great progress in studies of nonadhesive contact between self-affine rough surfaces. Persson has developed a scaling theory that includes an approximate treatment of asperity interactions (17, 18). At the same time, large-scale numerical calculations of contact between rough surfaces have become feasible (19–23). Both approaches reveal limitations in the GW treatment of nonadhesive surfaces. For example, the definition of R is ambiguous (24), the predicted range of linear scaling between area and load is orders of magnitude too small (25), and predictions for the geometry of individual contacts and the spatial correlations between them are qualitatively wrong (18, 19). As shown below, these geometrical features determine the effect of adhesion.

In recent work, Persson has extended his theory to include adhesion and presented numerical solutions of his equations for several cases (26–30). The results indicate a general trend with increasing adhesion (29). At first, adhesion leads to an increase in the ratio of contact area to load. Above a threshold adhesive strength, there is a finite contact area at zero load, and the surfaces become sticky. This powerful approach has not yet led to simple analytic predictions for general surfaces or been tested against extensive numerical simulations of adhesive contact.

Here, we use an efficient Green’s function approach to calculate adhesive contact of surfaces with roughness from subnanometer to micrometer scales for a wide range of surface roughness, adhesive interactions, and material properties. The numerical results are clearly inconsistent with expressions based on the GW approximation. They also indicate the importance of parameters that have not yet been explicitly included in Persson’s theory. We use insights obtained from these calculations to develop a simple, parameter-free equation that predicts the effect of adhesion on contact.

Results

In continuum theory, contact between two rough, elastic surfaces can be mapped to contact between a flat elastic substrate and a rigid rough surface (31). The combined compliance of the surfaces determines the elastic modulus of the substrate, and the height profile of the rigid surface matches their changing surface separation. Our simulations take advantage of this mapping to reduce the parameter space.

Fig. 1A shows the geometry of the simulations. There is a rigid upper surface with self-affine roughness between lower and upper wavelengths and (see Methods). This implies that the rms change in surface height over a lateral distance r scales as r^H for . H is called the Hurst exponent and is between 0 and 1 (13). One additional parameter is needed to characterize how rough the surface is. A convenient choice is the rms gradient or surface slope (Fig. 1G) at small scales ,

Fig. 1.

Geometry of surfaces and contacting regions. (A) A rigid surface with a self-affine fractal height profile is pushed down on an elastic substrate by an external load N. The substrate is initially flat with atoms spaced by a₀. Substrate deformations produced by a typical adhesive contact are shown with height variations magnified to show on the scale of the figure. (B−E) Surface map of atoms that feel repulsive (orange) and attractive (black) forces at a fixed contact area . Nonadhesive results for the entire system are shown in B, and expanded views of the region indicated by a square in B are shown in C−E for the indicated . (F) Magnified view of an wide region of E. The mean diameter d_rep is obtained by averaging the distance across A_rep. (G) Vertical slice through a contact patch showing the rigid rough (gray) surface and the deformed elastic substrate. The root-mean-square slope, , is the rms average of the local height gradient, , as indicated on the right. The attractive length d_att is the distance from the contact perimeter at which the surface separation equals the interaction range . The separation rises as a 3/2 power of the distance from the perimeter for nonadhesive surfaces, leading to the 2/3 exponent in Eq. 6.

The elastic substrate is the (100) surface of an fcc crystal with atomic spacing a₀. The interactions within the substrate are chosen so that it responds like an isotropic solid with Young’s modulus E and Poisson ratio v (see Methods). The effective modulus that controls the response to contact forces is .

The interactions between surfaces determine the work of adhesion, w, which is defined as the free energy gained per unit contact area. There is no need to separately consider the effect of w and because they always enter as a ratio with dimensions of length: . As described in Discussion, is typically much less than unity and we use it to quantify the relative strength of adhesion. The value of is increased by increasing both the range over which attractive forces are significant and the characteristic attractive pressure pulling surfaces together, . In the following discussion, we assume that attractive forces vanish at separations greater than , but general equations for long-range potentials are given in SI Text, section S-I. In general, is of the order of the equilibrium spacing between surfaces . The latter length was used to estimate the range of adhesion in Tabor’s early theory of adhesion by a single spherical asperity (32).

The surfaces are brought together under an external load N. We identify regions where atoms feel a repulsive force (Fig. 1) with the true contact area A_rep (see Methods). The total force on these atoms is N_rep. The corresponding area and force associated with regions where there is an attractive interaction are A_att and . The external load .

Fig. 1B shows the complex spatial distribution of A_rep for nonadhesive interactions . Analytic and numerical studies find that A_rep is much smaller than the nominal area A₀ and rises linearly with the external load N pushing the surfaces together for small A_rep (15, 17, 18, 20–23). This implies a constant mean repulsive pressure p_rep in contacting regions. Steeper and stiffer surfaces are harder to bring into contact, and both numerical and analytic calculations find (15, 17, 18, 20–23)

where is a dimensionless constant that is close to 2. This behavior is illustrated by the gray line in Fig. 2.

Fig. 2.

True contact area A_rep as a function of external normal load N for different adhesive interactions. For nonadhesive contact, A_rep rises approximately linearly with N with dimensionless prefactor (Eq. 2). As the strength of adhesion increases, the area rises more rapidly with load. Straight lines show linear fits at small A_rep whose slopes give the renormalized values of κ (Eq. 3). The value of κ initially rises with adhesion (blue lines) and diverges at the onset of stickiness (green line). The red line shows a sticky case where and the pull-off force is nonzero. Results shown are for a surface with Hurst exponent , root-mean-square slope , and lower wavelength cutoff .

Figs. 1 B−E and 2 show how adding adhesion affects the distribution of contacting and attracting regions and the relation between load and true contact area A_rep. Our first finding is that there is always a linear relation between the external load N and the area in intimate repulsive contact at low A_rep (Fig. 2):

where κ is renormalized from its nonadhesive value . As the strength of adhesion increases, κ and the ratio of A_rep to load rise. Eventually, the ratio diverges, and the surfaces become sticky when κ changes sign. A negative κ leads to an elastic instability that pulls surfaces into contact. A pull-off force equal to the magnitude of the most negative load (Fig. 2) is then needed to separate them.

A quantitative model for the changes in κ can be derived by analyzing how adhesion affects the geometry of interacting areas and the associated forces. Fig. 1 C−E illustrates how the geometry changes with increasing adhesion strength . The external load is adjusted to hold the total contact area A_rep constant, and the figures demonstrate that attractive forces have little effect on the detailed morphology of A_rep. The corresponding repulsive force N_rep and mean pressure are also nearly unchanged, which means that N_rep and A_rep continue to be related by Eq. 2. Fig. 3 Upper Inset shows that this relation holds for all systems and contact areas studied. The observation that adhesion produces little change in the surface deformation indicates that we are in the Derjaguin−Muller−Toporov (DMT) limit (33). As discussed in SI Text, section S-I, this is consistent with direct evaluation of the Tabor (32) and Maugis (16) parameters.

Fig. 3.

Plots showing the linear relationships between repulsive and attractive areas and forces, and between perimeter and area for the wide range of parameters indicated by the symbols defined below. Over five orders of magnitude in both quantities, the ratio between N_att and A_att is equal to the mean adhesive pressure (Eq. 4). (Upper Inset) For the same parameters, N_rep and the contact area A_rep follow the linear relation predicted by Eq. 2, showing that adhesion does not change the mean repulsive pressure in the contact. (Lower Inset) Plot showing that the contact area A_rep is proportional to the length of its perimeter P. The plot is normalized to show that the proportionality constant (Eq. 9). Deviations by up to a factor of 2 from this expression for d_rep are responsible for the spread in the figure. For a given system, changes in d_rep with A_rep are less than 25% over 2–3 decades in A_rep. All plots show multiple contact areas for each realization of a surface. Results are shown for (triangles), 0.5 (squares), and 0.8 (circles) and (black), 0.005 (blue), and 0.05 (red). Closed and open symbols are for and 0.3, respectively. The symbol size increases as increases from 4 to 64 in powers of 2.

The main change from Fig. 1C to Fig. 1E is that the total area feeling an attractive force, A_att, spreads around the periphery of A_rep as is increased by extending the range of adhesive forces, (Fig. 1 F and G). As shown in Fig. 3, the total force from the attractive region N_att is just A_att times the mean attractive pressure ,

The fact that the mean pressures in the repulsive and attractive regions are constant (Fig. 3) allows us to write the external load as . From Eqs. 2−4, we find with and

The remaining unknown is the ratio of repulsive to attractive area, which we now show is independent of load.

If , it can be approximated by where P is the length of the perimeter of A_rep and d_att is the average lateral distance from the perimeter where the surface separation reaches the interaction range (Fig. 1G). Using a general relation between area and perimeter, we can write , where d_rep is the mean diameter (see Fig. 1F and SI Text, section S-II). For ordinary 2D objects like a circle, the perimeter and diameter are proportional and increase as the square root of the area. This behavior is assumed in conventional theories of contact between rough surfaces that ignore long-range elastic interactions between individual contacting asperities, such as the previously discussed GW (15) and related adhesive (9, 16, 34) models. Including elastic interactions leads to qualitative changes in contact geometry (18–20). The contact area becomes a fractal with the same fractal dimension as the perimeter (20) [a true “monster” (13)]. We find that d_rep is then nearly independent of contact area, load, and adhesive strength and present an analytic expression for it below.

We calculate d_att using continuum theory for nonadhesive contact of locally smooth surfaces. If x is the lateral distance from the edge of a contact, then for small x, the separation between surfaces always (31) rises as . We use the standard prefactor for a cylinder with contact radius and equate d_att to the lateral distance where the separation equals (Fig. 1G and SI Text, section S-I). Combined with our expression for P, this gives the constant ratio between attractive and repulsive areas

Inserting this result in Eq. 5, gives the prediction

As shown in Fig. 4, our simple analytic expressions provide a quantitatively accurate description of and for a wide range of surface geometries. Deviations are only larger than the numerical uncertainty when the attractive area has grown too large to be approximated as a thin rim around the repulsive region (i.e., when ), which is well into the sticky regime. The continuum expression for d_att also fails in this limit .

Fig. 4.

Values of and from simulations with the wide range of parameters indicated below are plotted against the predictions from the model, Eqs. 6 and 7. For weak adhesion, deviations from the predictions (solid lines) are comparable to statistical errors that are of the order of the largest symbol size. The geometrical assumptions underlying Eqs. 6 and 7 break down for strong adhesion where A_att becomes comparable to or larger than the contact area A_rep. Adhesion is observed if and only if . The shaded region shows the prediction for adhesion using the value . Results are shown for Hurst exponents (triangles), 0.5 (squares), and 0.8 (circles) and adhesive strengths 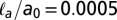(black), 0.005 (blue), and 0.05 (red). Closed and open symbols are for root-mean-square slopes and 0.3, respectively. The symbol size increases as the lower wavelength cutoff increases from 4 to 64 in powers of 2.

Eq. 7 provides a simple and quantitative explanation for the changes in Fig. 2. As the work of adhesion (and therefore ) increases, there is a proportional increase in . At first, adhesion merely produces a small change in the ratio of repulsive contact area to external load. The sign of the ratio changes when becomes bigger than and the surface becomes sticky.

We have also examined how adhesion changes the variation in the mean surface separation u with load. The normal contact stiffness defined as is typically found to rise linearly with external load for nonadhesive surfaces (35, 36). In the regime where surfaces are not sticky, we find that the relation between surface separation and N_rep is nearly unchanged, just as the relation between N_rep and A_rep is nearly the same (Fig. 3 Upper Inset). Because adhesion reduces the external load N by a factor of , the normal stiffness is reduced by the same factor. This is a small correction unless the surfaces are close to becoming sticky.

The length d_rep is always of order and has a simple relation to statistical properties of the undeformed surface. As above and in SI Text, section S-I, we approximate the contacting part of asperities by a cylinder with radius R, where R is calculated from the rms curvature of the rough surface at small scales ,

If the contact has diameter d_rep and slope at the contact edge, then . Following the same reasoning, the length in the numerator of Eqs. 6 and 7 is proportional to the height change from the contact edge to center:

Fig. 3 Lower Inset shows that A_rep and P are proportional and that the proportionality constant is always within a factor of 2 of .

Discussion

Surfaces are sticky when the total adhesive force, which is attractive pressure times attractive area, exceeds the total repulsive force . This corresponds to , and our numerical results show stickiness if and only if this condition is met. It can be recast as a condition on the ratios of pressures and areas, , or using our analytic expressions:

where the first factor on the left reflects the pressure ratio and the second comes from the area ratio.

A simpler necessary condition for adhesion can be obtained from Eq. 10. As noted above and in SI Text, section S-I, the effective range of the potential is typically less than but of the order of the atomic bond distance a₀. Any height change is possible in continuum theory, but there is a natural lower bound of order a₀ in atomic systems. For example, roughness on crystalline surfaces occurs in the form of terraces with height . Using Eq. 9 and inserting the estimates in Eq. 7, one finds a necessary but not sufficient criterion for adhesion: .

Note that the prediction for the onset of adhesion in Eq. 10 is qualitatively different from previous models for rough surface adhesion (9, 16, 27, 34), which do not include two of the key lengths in Eqs. 5–10. The characteristic width of contacting regions d_rep reflects their fractal nature and has not been identified before. Continuum theories have considered the limiting cases of equal to zero (9, 27, 34) or infinity (16) and concluded had little effect (16), whereas we find more adhesion at small because the adhesive pressure is increased. Finally, our relations only include quantities that are determined by roughness at short wavelengths (10, 37)—d_rep and the rms surface slope and curvature . In contrast, the rms height variation is the key surface property in past GW theories. Our numerical results for different , , and H in Fig. 4 collapse onto a universal curve even though the value of h_rms varies more than an order of magnitude for the same predicted value of . SI Text, section S-III presents plots that show qualitative discrepancies between these data and traditional GW theories.

Persson’s theory starts at large length scales and gradually introduces finer and finer structure (26–30). The value of is not explicitly included, but a scale-dependent work of adhesion is introduced that may capture some of the effects of the interaction range. The effect of adhesion has only been determined for a limited range of parameters, and we hope that our predictions will be compared with future results from this model. Persson has also presented a theory of capillary adhesion (38) that includes a calculation of the distribution of surface separations and may be able to predict A_att.

Direct comparisons to past experiments are difficult. Past studies reported h_rms because that was believed to be the control parameter. Values of are not generally reported. They can in principle be obtained from the surface height profile , but this can be challenging in practice. Because is sensitive to roughness at small length scales, must be measured with high spatial resolution (10, 37).

We can reach general conclusions about the experimental implications of Eq. 10 using typical values of . We first consider the extreme case where w is the work of adhesion for joining crystals of the same material. Then, for atomistic solids, the same interactions determine both and w. The value of is of the order of the fractional change in bond length needed to change the elastic energy by the binding energy, and . For example, diamond has and , yielding with a₀ the carbon bond length. The simple Lennard−Jones potential has . For these typical values of , adhesion should occur for of order 0.1 and below. The stickiest cases considered in Fig. 4 (closed red symbols) are indeed for the case , , and small d_rep. Increasing to 0.3 suppresses adhesion.

Exposing surfaces to the environment typically reduces the adhesive forces to weaker van der Waals interactions with . The value of and the root-mean-square slope needed to eliminate adhesion are reduced by two to three orders of magnitude. Only exceptionally smooth surfaces like atomically flat mica (1) and the silicon surfaces used in wafer bonding (39) have slopes low enough to stick . For most surfaces, Eq. 7 predicts and hence . This provides an explanation for the success of models for friction that ignore van der Waals adhesion (15, 31, 40).

Most of the sticky surfaces we are familiar with break the connection between w and to increase . Tape, rubber, and elastomers adhere via van der Waals interactions over the entire surface, but have small elastic moduli associated with the entropy required to stretch polymer segments between chemical crosslinks. Eq. 10 implies that surfaces with , , , and will be sticky if , which is common for soft rubbers and elastomers, whereas paper is much stiffer (> 1GPa). Tapes are normally designed to have moduli below 0.1 MPa, which is known as the Dahlquist criterion (41). Taking and , one finds adhesion for . Adhesives of this type can stick even to structured surfaces with macroscopic grooves. Once an adhesive bond is formed, the viscoelastic properties of the adhesive can be used to greatly increase the force needed to break the adhesive bond (8).

Animals use two different mechanisms to increase that have evolved independently in a number of species (42). Some use smooth pads with a large surface that maximizes w and a sparse fibrous internal structure that minimizes (43). Geckos (2, 3) and recently manufactured mimics (6) break the solid up into a hierarchical series of separate rods with pads at the ends. This allows adjacent pads to contact the surface at different heights without a large elastic energy, leading to a small effective even though the components are stiff.

In summary, we have presented numerical simulations of adhesive contact between rough surfaces for a wide range of adhesion strength, surface geometries, and material properties. In all cases, the area in intimate repulsive contact is proportional to the external load at low-contact areas. The ratio of area to external load increases with adhesion and changes sign when surfaces begin to stick. This transition only occurs in the limits of smooth surfaces, high work of adhesion, and low stiffness. The results are qualitatively inconsistent with traditional GW theories but in quantitative agreement with a simple parameter-free theory based on observed changes in contact geometry. This theory makes specific predictions for experimental systems and may aid in the design of adhesives, and in engineering surface roughness to enhance or eliminate adhesion. It also provides a simple explanation for our everyday experience with macroscopic adhesion. For most materials, the internal cohesive interactions that determine elastic stiffness are stronger than adhesive interactions, and surfaces will only stick when they are extremely smooth. Tape, geckos, and other adhesives stick because the effect of internal bonds is diminished to make them anomalously compliant.

Methods

Self-affine rough surfaces with the desired Hurst exponent H, , , and are generated using a Fourier-filtering algorithm described previously (44). Fourier components for each wavevector have a random phase and a normally distributed amplitude that depends on the magnitude q. The amplitude is zero for , proportional to for , and rolls over to a constant for . Periodic boundary conditions with period L are applied in the plane of the surface to prevent edge effects. The elastic response is determined using a Fourier-transform technique (45, 46) with a linearized surface Green’s function corresponding to Poisson ratio . Results are shown for period with rigid boundary conditions applied at depth L below the surface. Systematic studies were performed with L and from 512a₀ to 8192a₀ to ensure that finite-size effects are small.

Atoms on the elastic substrate interact with the rigid rough surface through a potential that only depends on the height difference z. We use a 9-3 Lennard−Jones potential that represents the integral over a half space of the usual 12-6 Lennard−Jones potential between atoms. The potential is truncated smoothly using a quartic function from the potential minimum at to the cutoff at . The potential and its first two derivatives are continuous and vanish at the cutoff. In our calculations, we fix the stiffness k of the potential at a value that is consistent with the stiffness of interactions within the substrate: . Consistent results were obtained with other potentials, including an untruncated 12-6 Lennard−Jones potential.

As is common for atomic-scale calculations (47−49), the contact area A_rep is defined as the area covered by atoms that feel a repulsive force . Similarly, the attractive area A_att is the area covered by atoms that feel an attractive force . We only show results for , so that there is a statistical number of contacting asperities (20). Numerical values of κ, , and are computed at 1% true contact area from the ratios of the relevant forces and areas.