Predicting the influence of long-range molecular interactions on macroscopic-scale diffusion by homogenization of the Smoluchowski equation

Abstract

The macroscopic diffusion constant for a charged diffuser is in part dependent on (1) the volume excluded by solute “obstacles” and (2) long-range interactions between those obstacles and the diffuser. Increasing excluded volume reduces transport of the diffuser, while long-range interactions can either increase or decrease diffusivity, depending on the nature of the potential. We previously demonstrated [P. M. Kekenes-Huskey , Biophys. J. 105, 2130 (2013)] using homogenization theory that the configuration of molecular-scale obstacles can both hinder diffusion and induce diffusional anisotropy for small ions. As the density of molecular obstacles increases, van der Waals (vdW) and electrostatic interactions between obstacle and a diffuser become significant and can strongly influence the latter's diffusivity, which was neglected in our original model. Here, we extend this methodology to include a fixed (time-independent) potential of mean force, through homogenization of the Smoluchowski equation. We consider the diffusion of ions in crowded, hydrophilic environments at physiological ionic strengths and find that electrostatic and vdW interactions can enhance or depress effective diffusion rates for attractive or repulsive forces, respectively. Additionally, we show that the observed diffusion rate may be reduced independent of non-specific electrostatic and vdW interactions by treating obstacles that exhibit specific binding interactions as “buffers” that absorb free diffusers. Finally, we demonstrate that effective diffusion rates are sensitive to distribution of surface charge on a globular protein, Troponin C, suggesting that the use of molecular structures with atomistic-scale resolution can account for electrostatic influences on substrate transport. This approach offers new insight into the influence of molecular-scale, long-range interactions on transport of charged species, particularly for diffusion-influenced signaling events occurring in crowded cellular environments.

INTRODUCTION

The diffusion of small molecules in the cell cytosol is well-known to deviate from rates observed in dilute solutions, due to diffusional barriers that may include crowders, such as proteins, DNA, or large macromolecules, or boundaries arising from organelles or the cell membrane¹ (reviewed in Ref. 2). A crowded environment manifests small accessible volume fractions compared to bulk solutions, as well as long-range electrostatic and van der Waals (vdW) interactions between diffusers and obstacles, that together conspire to determine effective diffusion rates.^{1, 3, 4} For such regimes, macroscopic models of hindered diffusion that reflect microscopic-scale phenomena are particularly insightful for understanding biological signaling. Particle-based methods such as Brownian dynamics (BD) and molecular dynamics simulations have traditionally been used to explore such interactions in crowded cellular environments (reviewed in Ref. 5), but typically at a computational expense that is orders of magnitude greater than continuum approaches, which limits their application to small systems.

Homogenization theory, on the other hand, is a continuum approach for modeling diffusion in obstructed domains, and has been applied successfully to biological systems including cardiac ventricular myocytes^{6, 7} and brain tissue.⁸ Homogenization is a mathematical method for “spreading out” the influence of micro-scale obstacles on macro-scale transport, namely, by yielding a modified diffusion constant. Generally, the diffusion constant is dependent on the accessible volume fraction⁹ between obstacles, as well as the strength of diffuser/obstacle interactions.^{10, 11} To our knowledge, however, atomistically detailed descriptions of important diffuser/obstacle interactions, namely, long-range electrostatic and van der Waals forces, have not been considered in these methods, which limits their applicability for modeling diffusion in condensed molecular environments like the cell cytosol.

Nevertheless, progress has been made in including electrostatic forces in homogenized diffusion models, which suggest the potential for including other long-range interactions. Schmuck et al., for instance, homogenized the Poisson-Nernst-Planck (PNP) equation to describe the diffusion of charged species when the diffusion and electric potential are strongly coupled.^{12, 13, 14} There, the coupled diffusion and electric potential equations were solved for each time step, which provided the time-evolution of the concentration and electric driving force. When the charged diffuser concentration is small relative to the solvent ionic strength, the electro-potential may be treated as time-invariant, permitting simpler models of electro-diffusion. To this end, Bourbatache et al.¹⁵ homogenized an electro-diffusion equation for the weakly coupled case and demonstrated its ability to capture hindered diffusion of chloride ions in suspensions of negatively charged colloids. However, in order to account for non-electrostatic interactions such as van der Waals interactions, further generalization of these approaches is necessary.

For this purpose, we consider the Smoluchowski equation as a well-established model for the time-evolution of a diffuser probability density subject to a concentration gradient and an arbitrary potential of mean force (PMF). The Smoluchowski equation has already been shown to be a powerful tool for modeling diffusion-controlled processes in atomistically detailed environments, such as the binding of small molecules to protein receptors given electrostatic interactions^{16, 17, 18, 19} or recessed binding sites.²⁰ Hence, by representing diffuser/obstacle interactions through an arbitrary PMF in the Smoluchowski equation, we can estimate the influence of such interactions on effective rates of transport in crowded molecular systems. In this article, we propose and implement a general homogenized Smoluchowski model, thus permitting the up-scaling of arbitrary, microscopically defined PMFs to transport phenomena in atomistic-resolution, crowded systems.

We first derive a homogenized Smoluchowski equation (HSE) assuming that the diffusion constant and the potential of mean force act on particles at the molecular (or “micro”-) scale in a manner decoupled from the macro-scale. This derivation leads to a numerical estimate of the effective diffusion constant at the macro-scale. We next validate the HSE model against “hard cylinders,” for which analytical bounds exist, as well as against published homogenized electro-diffusion models.^{10, 15} We then examine the interplay of vdW and electrostatic forces between a lattice of immobilized spherical proteins and diffuser by parameterizing the HSE with a Derjaguin and Landau, Verwey and Overbeek potential (DLVO). We finally apply this methodology to an atomistic representation of a globular protein (Troponin C) and its electrostatic potential. We find a close interplay between molecular structure, the volume fraction excluded by molecules in solution, as well as specific and long-range non-specific interactions that ultimately determine the effective diffusion rate. Our approach offers new insight into the role of molecular-scale interactions on macroscopic diffusion in physiologically relevant systems.

METHODS

Theory

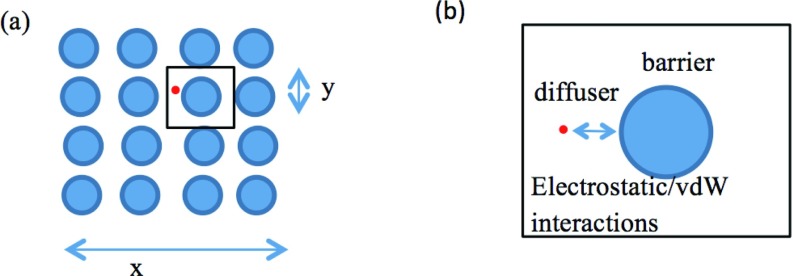
Given a diffusional domain Ω, portrayed in Figure 1, and an arbitrary potential of mean force acting on the diffuser (red dot), $\psi :\Omega \to \mathbb{R}$, the Smoluchowski problem seeks to find a concentration function $c:\Omega \times [0,t_{\text{max}}]\to \mathbb{R}$ such that

$$\frac{\partial c}{\partial t}=\nabla ·D_o{e}^{-\beta \psi }\nabla \left(e^{\beta \psi }c\right)-f\text{on}\Omega ,$$ (1)

where D_o is a known diffusion tensor for unobstructed diffusion, possibly dependent on x ∈ Ω, β ≔ 1/k_BT with k_B the Boltzmann constant and T the temperature. The forcing term f represents the net effect of any ionic sinks or sources in Ω. We assume that Ω has two length scales of interest, x and y ≔ x/ε, which refer to the macro- and micro-scales, respectively. Here, ε is small compared to the dimensions of Ω and it is assumed that Ω is periodic at the y scale; we denote by Ω_u a periodic unit cell at the y-scale with Ω_ε ⊂ Ω_u the non-occluded subregion. We assume that D_o and ψ are estimated at the y-scale by theoretical models^{3, 21} or by physical experiments;²² the y-scale unobstructed diffusion tensor is denoted $D_o^{\epsilon }\left(\mathbf{y}\right)$. This yields the steady-state problem: find $\tilde{c}:{\Omega }_{\epsilon }\to \mathbb{R}$ such that

$$\nabla ·{\tilde{D}}_o^{\epsilon }\nabla \tilde{c}=f\text{on}{\Omega }_{\epsilon },$$ (2)

where ${\tilde{D}}_o^{\epsilon }\left(\mathbf{y}\right):=D_o^{\epsilon }\left(\mathbf{y}\right)e^{-\beta \psi \left(\mathbf{y}\right)}$ and $\tilde{c}\left(\mathbf{y}\right):=e^{\beta \psi \left(\mathbf{y}\right)}c\left(\mathbf{y}\right)$. A detailed derivation is presented in the supplementary material.⁵¹ Since 2 is a diffusion-style problem, we apply the standard homogenization approach:⁶ expand $\tilde{c}$ in terms of powers of ε (i.e., $\tilde{c}={\sum }_i{\tilde{c}}_i{\epsilon }^i$) and write ∇ as a scaled gradient operator (i.e., ∇ = ∂_x + ε⁻¹∂_y). This allows the separation of 2 into two steady-state problems at the y-scale on Ω_u (one at order ε⁻² and one at order ε⁻¹) as well as a time-dependent problem at order ε⁰. The derivation, summarized in Ref. 6 for a standard diffusion equation, ultimately yields coefficients ${\tilde{d}}_{ij}$ of the effective (obstructed) diffusion tensor $\tilde{D}$. The effective diffusion tensor may be used in place of D_o in 2 at the x-scale, or a time-dependent equivalent of 1, such as $\frac{\partial }{\partial t}\tilde{c}{e}^{-\beta \psi }=\nabla ·{\tilde{D}}_o\nabla \left(\tilde{c}\right)$. In this study, our focus is on estimating the effective diffusion constant, which is computed from the integral at the y-scale via

$${\tilde{d}}_{ij}=\frac{1}{|{\Omega }_u|}{\int }_{{\Omega }_{\epsilon }}{\left[{\tilde{D}}_o^{\epsilon }\left(\mathbf{y}\right)\right]}_{ij}\left({\delta }_{jk}+\frac{\partial {\tilde{\chi }}_k}{\partial y_j}\right)dy,$$ (3)

where |Ω_u| is the volume of the unit cell and ${\tilde{\chi }}_k$ are correctors, periodic on Ω_ε, that are the solution to the problem: find $\tilde{\chi }:{\Omega }_{\epsilon }\to {\mathbb{R}}^3$ such that

$$\begin{array}{cc}\hfill \frac{\partial }{\partial y_i}{\left[{\tilde{D}}_o^{\epsilon }\left(\mathbf{y}\right)\right]}_{ij}\left({\delta }_{jk}+\frac{\partial {\tilde{\chi }}_k}{\partial y_j}\right)=0,& \text{on}{\Omega }_{\epsilon },\hfill \\ \hfill {\left[{\tilde{D}}_o^{\epsilon }\left(\mathbf{y}\right)\right]}_{ij}\left({\delta }_{jk}+\frac{\partial {\tilde{\chi }}_k}{\partial y_j}\right)·{\widehat{n}}_i=0,& \text{on}{\Gamma }_{\epsilon }:=\partial {\Omega }_{\epsilon }.\hfill \end{array}$$ (4)

Define $\chi :=e^{-\beta \psi \left(y\right)}\tilde{\chi }$. For non-interacting cases, the potential ψ is zero, and thus $\chi =\tilde{\chi }$, which yields the conventional homogenized diffusion model for obstructed diffusion. The effective diffusion tensor coefficients ${\tilde{d}}_{ij}$ at the x-scale are estimated by first numerically approximating the solution functions χ_k defined by 4 and then evaluating 3. Further details of the potentials used for ψ appear in the supplementary material.⁵¹

Figure 1.

(a) Schematic of crowded domain, Ω, represented by a lattice of diffusional barriers. (b) A unit cell, Ω^ε, for the homogenized Smoluchowski equation.

Numerical solution of the homogenization equation

We generated meshes for cylindrical and spherical obstacles, as well as the globular protein Troponin as described in the supplementary material.⁵¹ Using these meshes, we numerically solve the homogenized diffusion partial differential equation (PDE) for ${\tilde{\chi }}_k$ in 4 and compute the effective diffusivity coefficients ${\tilde{d}}_{ij}$ from 3 using the finite element solver FEniCS²³ as described in Ref. 24. Numerical solution via the finite element method permits the use of meshes with intricate and irregular geometrical features typical of biological molecules. In our previous work,²⁴ we validated our implementation for the standard diffusion equation against benchmarks including Hashin-Shtrikman²⁵ bounds for media with cylindrical inclusions. The homogenized Smoluchowski PDE used here was formulated as described previously, except that we replace a constant $D_o^{\epsilon }\left(\mathbf{y}\right)$ with ${\tilde{D}}_o^{\epsilon }\left(\mathbf{y}\right)$ as described above, where the latter term is dependent on the potential of mean force (ψ). For the PMF we used potentials computed from either the nonlinear Poisson-Boltzmann equation or the Derjaguin and Landau, Verwey and Overbeek model modeling electrostatic interactions alone or both van der Waals and electrostatics, respectively. Details of these PMFs are provided in the supplementary material,⁵¹ while relevant parameters are explained in the text. All other parameters related to the solution of the homogenized PDE pertain to the solver configuration, which are left at their default values in FEniCS. We assume surfaces at the mesh outer boundary belong to the unit cell (Γ∖Γ_ε); all other boundaries are impermeable and thus belong to Γ_ε. We solve the weak form of 4 using a piecewise linear Galerkin finite-element method with the default direct linear solver. The solution is then applied to 3 to yield the diagonal components ${\tilde{d}}_{ii}$ of $\tilde{D}$. We report the effective diffusion constant by its normalized value (unitless), $D:=\tilde{D}/D_o.$ The protocol was validated for the inert diffuser in Ref. 24 and for charged cylinders in the supplementary material.⁵¹ The code will be released at https://bitbucket.org/huskeypm/smolhomog.

RESULTS AND DISCUSSION

Validation of model using a cylindrical periodic system

We first explain the validation of our model via established theories and then discuss the new insights our model provides to biological modeling. Our initial validation confirms that the HSE reproduces the effective diffusion constant predicted by Hashin-Shtrikman (HS) theory for a regular lattice of cylinders.^{9, 25} The HS theory provides upper and lower bounds for the effective diffusivity perpendicular to the parallel cylinders, based on the accessible volume fraction, ϕ, where 0 ⩽ ϕ ⩽ 1. In our previous study,²⁴ we predicted effective diffusion constants perpendicular to a lattice of cylindrical myofilaments using a conventional homogenized diffusion equation without an applied potential. We found that our predictions were in quantitative agreement with the upper HS bound, D = 2ϕ/(3 − ϕ), and in qualitative agreement with experimental measures of anisotropic small molecule diffusion within myofibrils.²⁶ Therefore, we use this upper HS bound to validate our HSE model, where instead we replace the explicit cylinder boundaries (to which the Neumann condition on Γ_ε in 4 would normally be enforced) with boundaries implicitly represented by a potential of mean force. This PMF is defined by a hard-sphere potential for r ⩽ R and ψ = 0 for r > R, where R [m] is the variable cylinder radius, which in essence excludes particles from within the cylinder boundaries, analogous to an explicit cylindrical obstacle.

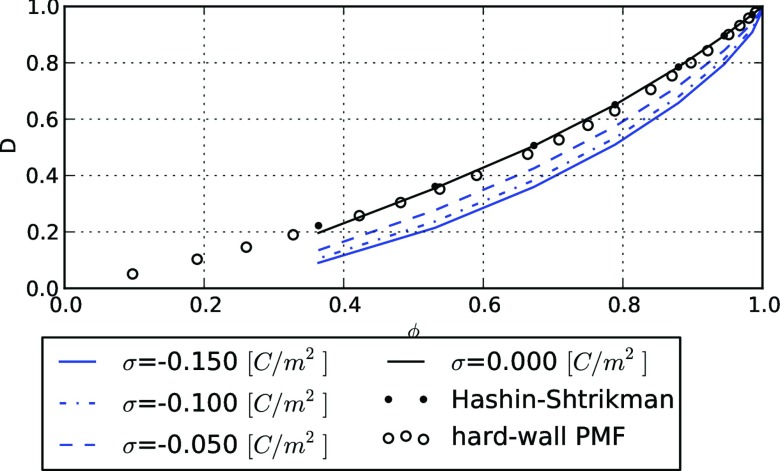
By showing that predictions from this latter approach adhere to well-established analytical bounds for a lattice of cylinders, we provide evidence that the HSE captures the appropriate influence of potentials of mean force on the effective diffusion constant, D. In Figure 2, we indeed find that D (open circles) decreases with decreasing accessible volume fraction, ϕ, in quantitative agreement with the HS bound (dots). To understand how the effective diffusivity varies with respect to the scale of the potential, we report in Figure S4 of the supplementary material,⁵¹ for a fixed cylinder radius the effective diffusion coefficients, given potentials ranging from repulsive (ψ = 10 [kcal mol⁻¹]) to attractive (ψ = −6 [kcal mol⁻¹]). We note that V > 2 [kcal mol⁻¹] is sufficient to recapture the HS limit for the given volume fraction and as ψ → 0, the unhindered (D = 1) diffusion constant is recovered. These results confirm that diffusion obstacles may be represented by potentials of mean force using the HSE formalism and that the diffusivity scales inversely with the amplitude of the repulsive PMF. Interestingly, we also observe diffusion rates greater than 1 (the normalized bulk diffusion rate) for attractive potentials, which will later be discussed in the context of electrostatic interactions.

Figure 2.

Predicted normalized effective diffusion constants (D) as a function of accessible volume fraction (ϕ), where D = 1.0 signifies equivalence with an arbitrary bulk diffusion constant. For a box-shaped, repulsive potential of mean force (PMF) representing a cylindrical obstacle (open circles), the quantitative agreement with the analytical Hashin-Shtrikman (HS) upper bound (dots) indicates that the homogenized Smoluchowski equation (HSE) with a hard-wall PMF sufficiently describes the influence of obstacles. Diffusion constants for a negatively charged diffuser (z = −1) with neutral (σ = 0, black) and electro-negative explicit cylinders (σ < 0, blue) shows that the HSE using an electrostatic potential quantitatively agrees with results from Ref. 27 which showed that repulsive interactions slow diffusion.

We next validate our HSE approach using an electro-diffusion model established by Bourbatache et al.²⁷ In Figure 2, we evaluate D for a diffusing anion (z = −1) given a range of electronegative surface charge densities, σ [C m⁻²], distributed uniformly on an explicit cylinder with radii of up to 50 Å. We estimate the resulting electrostatic potential of mean force by numerical solution of the nonlinear Poisson-Boltzmann equation (see the supplementary material⁵¹), which serves as input for the ψ term in the HSE model. We observe that the diffusion coefficients are reduced as the electro-repulsion increases with more negative σ values and smaller accessible volume fractions. For instance, with a surface charge density of 0.05 [C m⁻²], D = 0.6 at ϕ = 0.8 and D = 0.15 at ϕ = 0.4, in quantitative agreement with Figure 9 of Bourbatache et al.²⁷ The slowing effect of repulsive interactions was previously attributed to an increased effective radius of the obstacles due to exclusion by the repulsive force, which reduces the accessible volume fraction.²⁸ These findings not only validate our model, but also suggest the utility of the HSE framework in modeling small-molecule diffusion within lattices of charged cylinders, such as the negatively charged thick (myosin) and thin (actin) filaments comprising muscle cell myofibrils²⁹ that we previously examined in the absence of electrostatics.

HSE model with electrostatic and van der Waals potential

The HSE formulation permits arbitrary potentials of mean force between a diffuser and immobile obstacles that are periodic on a micro-scale domain, which could be invaluable for modeling small-molecule transport in colloidal solutions or densely packed globular proteins in the cell cytoplasm. We explore diffusion in an analogous environment in this section, where we represent a crowded cytosol as a lattice of spherical proteins, which impact small molecule diffusion through electrostatic and van der Waals interactions. To capture the dominant vdW and electrostatic interactions common to these environments, we use the DLVO model³⁰ given by

$$\psi \left(r_{do}\right)=\frac{1}{2}{R}_{o}Z{e}^{-\kappa r_{do}}-A{R}_o/12r_{do},$$ (5)

where r_do [m] is the diffuser/obstacle separation, R_o [m] is the diffuser radius, κ [m] is the inverse Debye length, A [J] is the Hamaker constant, and Z [J m⁻¹] is the interaction constant specific to sphere-sphere or sphere-surface interactions (see Figure 14.10 in Ref. 30). The first and second terms describe screened electrostatic and attractive vdW interactions, respectively, between the diffuser and the obstacle. We validate our implementation of this DLVO model in Fig. S3 of the supplementary material.⁵¹

While a faithful representation of the biological cell should include unit cells with a distribution of protein types, sizes, shapes, and surface potentials,³¹ as a starting point we assume a uniformly spaced protein lattice consisting of a small spherical protein with 12.5 [Å] radius of gyration and net charge of z = −3. The spherical protein was centered in a unit cell whose edge-lengths were varied to achieve volume fractions typical of a crowded cellular environment (0.19–0.27 excluded³¹). Assuming a physiological ionic strength of 150 mM for a monovalent ion pair, the protein-spacing between unit cells is comparable to the 7.8 [Å] Debye length within which electrostatic interactions are significant.

Similar to the charged cylinders, in Figure 3 we demonstrate for a lattice of spherical protein that D generally decreases for decreasing volume fractions and that repulsive interactions (red) further reduce diffusivity. First, assuming negligible vdW interactions (A = 0), we observe that attractive charge interactions (blue, solid) yield increased effective diffusion rates relative to the electrically neutral (ψ = 0) case (black, solid) and the repulsive charge interactions case (red, solid). We next consider attractive vdW interactions in the DLVO model. Since the Hamaker constant for protein-protein interactions is typically 1 [kT] or greater,³² we assume a smaller value of A = 0.2 [kT] to approximate the vdW interaction between a protein and small diffuser. We find that attractive vdW interactions consistently increase D independent of diffuser charge, and the effects are most significant at small volume fractions where the region of significant obstacle/diffuser attraction represents a greater percentage of the free volume. Furthermore, D was maximized for the positively charged ion at ϕ = 0.9 without vdW interactions, where the accelerating attractive potentials are counterbalanced by the hindrance from a decreasing accessible volume fraction; this maximum shifts to smaller volume fractions (ϕ = 0.8) as the attractive vdW interactions are added. Hence, it is apparent that the electrostatic potential and accessible volume fraction could be tuned to promote or disfavor the diffusion of charged species in a fixed lattice of molecular obstacles.

Figure 3.

Effective diffusion constant, D, for coions (red), counterions (blue), and neutral diffusers (black) for a unit cell with a 12.5 [Å] negatively charged, spherical protein. Attractive counterion/protein interactions have faster diffusion relative to neutral and negatively charged diffusers. Inclusion of attractive van der Waals interactions (+VDW) through the HSE with a DLVO potential increases the effective diffusion constants.

These findings of accelerated diffusion given attractive interactions concur with predictions from a homogenized electro-diffusion equation applied to a layered geometry of charged slabs,¹⁰ between which accelerated and slowed diffusion rates were predicted for counter- and co-ions, respectively. Similarly, Brownian dynamics simulations of diffusion within a lattice of negatively charged, immobile obstacles also indicated attractive particles experienced faster diffusion than repulsive particles.²⁸ These theoretical results are moreover consistent with measurements of the limiting current for cationic and anionic solutions through suspensions for negatively charged, sulfonated silica beads³³ which evidenced accelerated diffusion for attractive electrostatic interactions that diminished with increasing ionic strength. Further quantitative comparison against such experimental data would require atomistic-resolution details of the silica bead lattice and a model for the interaction potential between the lattice and the ionic diffusers that to our knowledge is unavailable.

We suspect that the accelerated diffusion arises due to a macroscopic concentration gradient imposed on the micro domain by the homogenization convention. This gradient gives rise to a steady-state situation in which the diffuser concentration differs on opposite sides of the unit cell. Since more particles are available to diffuse from the higher concentration side toward the attractor in the cell interior, a net flux due to the attractive interaction may be observed. In support of this interpretation, in a previous study³⁴ we considered an analogous configuration, in which diffusion of an anionic reaction intermediate between two positively charged reaction centers was modeled. In that model, one reaction center produced an intermediate while the other absorbed the intermediate, yielding a concentration gradient at steady-state. When the region between the reactive centers was bridged by attractive “crowders,” we found that net rate of transport toward the absorbing center, as measured by the association rate, was faster relative to inert or repulsive crowders. This agrees with our predictions by homogenization theory for attractive obstacles. In the absence of a concentration gradient, e.g., in equilibrium conditions, we expect that the effective diffusion rate is determined by the amplitude of the potential fluctuations, or “roughness,” which universally acts to slow the diffusing particle.³⁵

The notion of cations diffusing faster in the presence of negatively charged obstacles seems counterintuitive, in light of studies such as from Hou et al,³⁶ whereby it was shown by pulsed-field nuclear magnetic resonance (NMR) imaging that specific ionic interactions between a diffusing cation and a negatively charged sulfonated surface slowed diffusion. To explain this apparent discrepancy, we resort to a common model of small-molecular diffusion in the presence of buffers that selectively bind a diffuser.^{37, 38} Assuming that the specific cation/surface interactions are short-ranged (relative to vdW and electrostatic interactions) and reduce the diffuser concentration through a dissociation constant K_D [μM], the effective diffusion constant D_buff can be described by

$$D_{buff}=\frac{D}{1+\left[B\right]/K_D},$$ (6)

where [B] is the concentration of buffer B.^{37, 38} From the equation it is clear that both increasing densities of B on the lattice (increased [B]) and stronger specific binding interactions (decreased K_D) reduce the overall diffusion rate, D_buff, from its unbuffered value, D.

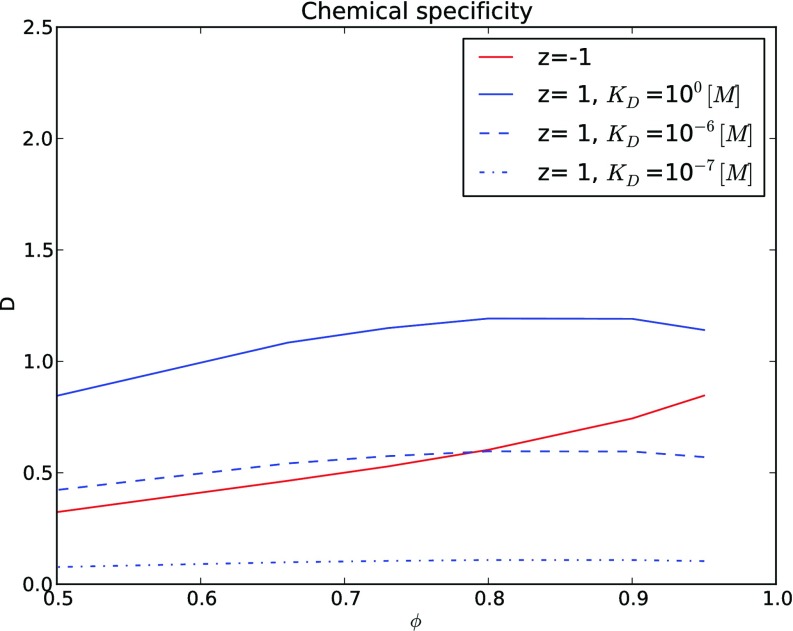
In Figure 4, we compare the effective diffusion constants given very weak (K_D ≫ 1 [μM]) to comparatively strong specific binding interactions (K_D ⩽ 1 [μM]) acting on a cationic diffuser. Assuming that [B] = 1.0 [μM], a modest, but physiologically reasonable concentration, we observe that stronger binding interactions (reduced K_D) depress D for the counter ion. At K_D = [B] the counter ion and co-ion curves intersect near ϕ = 0.8; for volume fractions below this critical value, attractive counter ion diffusion exceeds that of co-ions, whereas the opposite is true above this value. Thus, we believe the disparity between accelerated effective diffusion rates for attractive diffuser/obstacle interactions predicted by us and others¹¹ and experiments demonstrating the opposite, can be partially explained by accounting for the effect of specific-binding interactions on the effective diffusion rate. An additional consideration could include how the distribution of obstacles anneals when subjected to diffusers of different charge polarity, as it has been numerically shown that diffusion rates differ between immobile and annealed obstacle lattices.²⁸ Although it is beyond the scope of this paper, a detailed model that includes estimates of the specific cation/obstacle binding and annealing of the obstacle lattice could provide further insight into the conditions required to favor co-relative to counter-ion diffusion, as well as possible tuning parameters.

Figure 4.

Predicted effective diffusion constants due to specific binding interactions demonstrate that increased binding strength (in terms of the dissociation constant, K_D) can depress counter ion diffusion relative to co-ion.

Simple model of diffusion in a crowded environment using a realistic protein structure

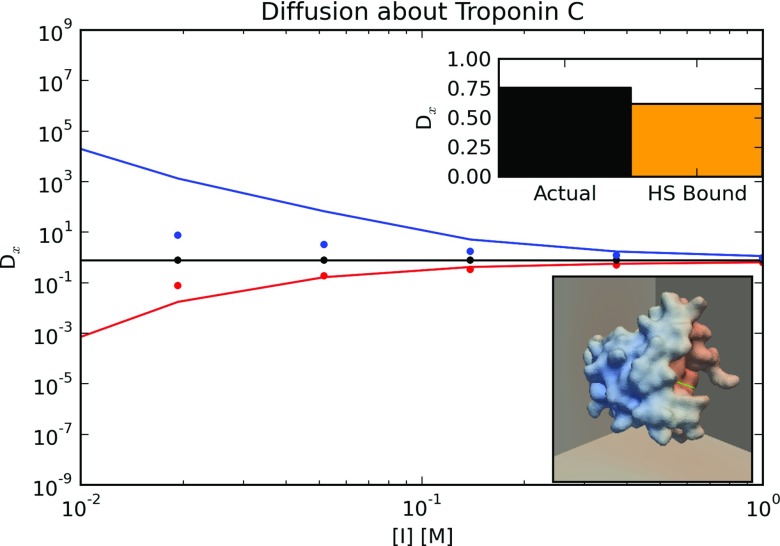
We finally extend the previous protein lattice model by using an atomistic detailed molecular surface, upon which the protein surface charge is nonuniformly distributed. In doing so, we can examine the extent to which molecular-scale details of individual protein obstacles can influence small-molecule diffusion. In lieu of the DLVO model in Sec. 3B, here we use an electrostatic PMF from numerical solution of the Poisson-Boltzmann equation, since we assume that the van der Waals interactions between the diffuser and protein are negligible. We report effective diffusivities using a lattice of obstacles represented by the N-terminal domain of Troponin C (TnC), based on structures available in the Protein Databank (PDB ID: 1SPY³⁹). Although TnC has an overall net negative charge, the surface charge is localized toward the negatively charged amino acids responsible for coordinating metals (namely, Asp 67 to Glu 76). Given its estimated 12.5 [Å] radius of gyration, we create a 40 × 40 × 40 [Å] unit cell to yield a 70% accessible volume fraction comparable to a crowded cellular environment. In the bottom sub-panel of Figure 5, we show the TnC molecular surface, upon which a χ_x solution satisfying 4 is projected. We note that the blue (χ_x < 0) or red (χ_x > 0) shading indicate regions of space where diffusion generally deviates from the bulk. In the top sub-panel, we demonstrate that the effective diffusion constant predicted with the atomistic resolution geometry using the HSE protocol (D = 0.70, black) is in close agreement with the diffusivity predicted using the HS bound for a spherical inclusion (D = 0.6, orange using D = ϕ/(3 − ϕ)), given a neutral diffuser and a volume fraction we determined directly from the protein geometry in our unit cell. The agreement between these two models indicates that under circumstances where interactions between diffuser and obstacle are insignificant, the diffusivity for globular proteins can be analytically computed based on a reasonable estimate of the protein's volume. In a previous study, we found similar agreement with the HS model for diffusion in cylinder lattices given atomistic resolution details of myofibril proteins.²⁴

Figure 5.

Predicted diffusion constants for positively charged (blue) and negatively charged (red) particles diffusing around the charged globular protein Troponin C (TnC) at a range of ionic strengths. Dots and lines represent uniformly distributed and localized charges, respectively. Top inset: Prediction at physiological ionic strength (150 mM) for TnC (black) and based on Hashin-Shtrikman bound (orange) Bottom inset: Projection of χ satisfying 4 for TnC. The blue and red tones indicate the extent of diffusional hinderance imposed by TnC.

In the main panel, we show the diffusivities for a divalent cation (blue), anion (red), and a neutral diffuser versus ionic strength for two choices of charge density: (1) a uniform charge density of σ = −0.01 [Cm⁻²] (dots) and (2) localization of the charge density toward the binding domain (solid). Our results indicate that the non-uniform charge distribution leads to more extreme values of the diffusivity relative to the uniform charge distribution, with larger or smaller diffusivities for the cation and anions, respectively. These findings illustrate that both structural details of the inclusion and the local charge distribution are important determinants of effective diffusion rates. Hence, detailed descriptions of diffuser transport in crowded biological environments may require models that include a representative range of protein sizes, densities, and charge distributions in high detail.

Limitations

We review several assumptions in our model that could be addressed to better generalize the HSE framework. The HSE assumes that the diffusing species evolves according to a concentration gradient and static potential of mean force in the over-damped limit. The static potential assumes that the distribution of the protein charges and solvated co-ions (spectator ions) are fixed relative to the diffusion timescale of the diffuser. Additionally, the HSE assumes that diffusing ions are non-interacting and do not significantly impact the electrostatic field, which is typically appropriate when spectator ions are in equilibrium and the diffuser is dilute. When the co-evolution of ions and the associated electrostatic field is significant, more elaborate models such as the PNP equation may be used, for which recent homogenization prescriptions may be well-suited.¹²

We have also assumed hydrodynamic interactions (HI) are negligible in our simulations given the small sizes assumed for the diffusing particles.⁴⁰ In the event that larger particles are considered, for which HI may be significant,^{41, 42} one may resort to the Rotne-Pragner HI model,⁴³ which yields a position-dependent diffusion tensor for which the diagonal and off-diagonal terms represent self- and inter-particle diffusivities. In principle, this tensor could be used to parameterize the spatially dependent D^ε(y) term of the HSE, under the assumption that the obstacles are fixed relative to the diffuser. Other spatial considerations include the finite size of ions and anomalous diffusion, which may be addressed through homogenization of fractional diffusion models⁴⁴ and finite-ion size models.⁴⁵

CONCLUSIONS

Our simulations support the common belief that long-range interactions and specific interactions between obstacles and charged species serve important roles in diffusion-influenced events in biological environments. The homogenization of the Smoluchowski diffusion equation elegantly captures these regimes and thus provides a powerful, multi-scale framework for understanding the molecular origins of macroscopic diffusion. Furthermore, the generality of the Smoluchowski equation for potentials of mean force arising from a variety of molecular interactions suggests that its homogenization may bridge a variety of diffusion-coupled phenomena across spatial scales, especially where densely packed proteins and macromolecular structures are concerned. Such examples could include metabolic fluxes within the sarcomere^{46, 47} and “compartmentalized” cyclic adenosine monophosphate (cAMP) signaling via localized A-kinase anchor proteins (AKAP) complexes.⁴⁸ We, furthermore, see the prospect of using the HSE to describe molecular phenomena well-represented by low-dimensional diffusional processes subject to a potential of mean force, such as the sliding of proteins along DNA.^{49, 50}