Bias atlases for segmentation-based PET attenuation correction using PET-CT and MR

Abstract

This study was to obtain voxel-wise PET accuracy and precision using tissue-segmentation for attenuation correction. We applied multiple thresholds to the CTs of 23 patients to classify tissues. For six of the 23 patients, MR images were also acquired. The MR fat/in-phase ratio images were used for fat segmentation. Segmented tissue classes were used to create attenuation maps, which were used for attenuation correction in PET reconstruction. PET bias images were then computed using the PET reconstructed with the original CT as the reference. We registered the CTs for all the patients and transformed the corresponding bias images accordingly. We then obtained the mean and standard deviation bias atlas using all the registered bias images. Our CT-based study shows that four-class segmentation (air, lungs, fat, other tissues), which is available on most PET-MR scanners, yields 15.1%, 4.1%, 6.6%, and 12.9% RMSE bias in lungs, fat, non-fat soft-tissues, and bones, respectively. An accurate fat identification is achievable using fat/in-phase MR images. Furthermore, we have found that three-class segmentation (air, lungs, other tissues) yields less than 5% standard deviation of bias within the heart, liver, and kidneys. This implies that three-class segmentation can be sufficient to achieve small variation of bias for imaging these three organs. Finally, we have found that inter- and intra-patient lung density variations contribute almost equally to the overall standard deviation of bias within the lungs.

I. Introduction

Hybrid PET-MR combines the capabilities of PET to measure the four-dimensional concentration histories of tracer amounts of biochemically active compounds with the anatomic information and the visualization of soft tissues provided by MR [1]. For PET, the distribution of the attenuation coefficients for 511-keV annihilation photons must be measured accurately in order to compute a faithful reconstruction of the tracer concentration maps. In stand-alone PET scanning, the attenuation coefficients are obtained by a separate transmission measurement using an external source of positron emitters. In PET-CT scanning, the attenuation coefficients are measured with X-ray transmission and remapped to estimate the attenuation coefficients for 511-keV photons. For PET-MR, the PET attenuation map typically needs to be derived from the MR images. In most cases, MR signals are related to hydrogen density and spin relaxation, whereas the attenuation experienced by photons in a PET scan is related to electron density. Therefore, attenuation coefficients are not directly related to the measured MR signal. Mapping from an MR image volume to a PET attenuation map is one of the major challenges for PET-MR.

There have been several reports on MR-based PET Attenuation Correction (AC). One approach is to use atlas registration [2]-[6]. In order to obtain the attenuation map for an acquired MR image volume, a reference CT image volume can, in principle, be registered to the MR image volume using deformable inter-modality registration. Alternatively, a reference MR image volume, previously registered to a reference CT image volume, can be first registered to the MR image volume using deformable intra-modality registration followed by the same transformation of the reference CT image volume. Atlas registration solves the attenuation problem if a perfect deformable registration between different subjects can be achieved. However, this is rarely the case in whole-body applications due to substantial anatomical differences between subjects and the limitations of the deformable registration method itself (e.g., local minima due to non-convexity of the similarity measure). Another approach, which may have the potential for clinical use, is to segment an MR image volume into different tissue classes and then assign the corresponding attenuation coefficients to them. This approach has been applied to both brain [7]-[12] and whole-body imaging [4],[13]-[20]. In addition to the standard methods described above, Salomon et al [21] developed a maximum-likelihood method to estimate both the attenuation and emission maps simultaneously. Larsson et al [22] and Johansson et al [23] developed a Gaussian mixture regression model to derive the attenuation map from MR images.

Several publications reported MR-based PET AC for whole-body imaging using tissue segmentation. Martinez-Möller et al [13] developed a 4-class MR-based segmentation method (air, lungs, fat, and other tissues) and reported that the bias of Standardized Uptake Value (SUV) due to the segmentation was less than 10% for all the lesions except one in the pelvis using their 35 patient PET-CT samples. Hu et al [14] reported SUV bias of less than 10% using an MR-based 3-class segmentation method (air, lungs, and other tissues) for all the lesions in their patient samples except the ones in pelvis. They also studied lesion detection and found there were no differences in the clinical interpretations of the lesions due to the segmentation. Schulz et al [16] showed that the SUV difference between CT- and MR-based 3-class segmentation methods is less than 5% for the bone lesions found in their 15 whole-body PET-CT/MR patient scans. Hofmann et al [6] also found that SUV bias is less than 10% using both segmentation and atlas-based/pattern recognition methods from 11 patient samples. Eiber et al [17] also showed that no significant difference could be found for SUVs for 81 positive lesions in low-dose CT compared to Dixon-based MR (CT images were actually used for segmentation to avoid registration errors between CT and MR images). Keereman et al [18] also performed Monte Carlo simulation to study MR-based AC using five tissue segmentation (cortical bone, spongeous bone, soft-tissue, lung, and air). Based on PET-CT patient data, Samarin et al [19] found a substantial underestimation of tracer uptake in bone lesions if substitution of bone by soft-tissue values is made in the AC maps. Drzezga et al [20] demonstrated that no significant lesion detectability difference was found between PET-CT and PET-MR using both PET-CT and PET-MR patient data. Marshall et al [24] used the MR signals to derive the attenuation coefficients within the lungs, where density varies considerably within or between beagles. Kim et al [25] studied SUV bias of lesions in the spine and the liver using PET-CT data. They showed that the SUVs of spine lesions were considerably underestimated without bone segmentation. Most of these conclusions were based on bias studies on SUV values for lesions already identified in their patient studies.

In this report, we studied the voxel-wise activity concentration bias across the entire body because many PET applications will require absolute quantitation. Our main goal is to study both the accuracy and precision of voxel-wise bias for segmentation-based PET AC methods for different tissue classes and organs.

II. Methods

Tissue classification was first done on the basis of the CT intensities in Hounsfield Unit (CT-based study) and thus represents the best tissue classification that can be done for the purpose of PET AC. For each segmented tissue class, we assigned a CT intensity value, which was calculated averaging all the CT intensities within the tissue class over 23 patients. A bias image volume was formed as the voxel-wise difference in the activity concentration reconstructed with standard CT AC and segmented CT AC. We registered the CTs for all the patients and transformed the corresponding bias image volumes accordingly. We then obtained the mean and standard deviation bias atlas using all the registered bias image volumes. We also performed a pilot study using MR images to segment fat using MR images (MR-based study).

A. PET-CT and MR patient data

We used 23 PET-CT whole-body scans of patients with lymphoma (11 males, 12 females). The ages of the patients ranged from 23 to 83. The body mass indices (BMI) of the patients ranged from 22 to 32. The CT [120 peak kilovoltage (kVp) was used for all the patients] for PET AC and FluDeoxyGlucose (FDG) PET data were acquired on a Siemens Biograph-64 PET-CT scanner at Massachusetts General Hospital (MGH). The injection dose of FDG for the patients ranges from 370 to 814 MBq. A 20-25 minute PET scan was performed about 45-60 minutes after the injection. Six of the 23 patients also had MR scans acquired on a Siemens 3-Tesla Tim Trio scanner at MGH using the Volumetric Interpolated Breath-hold Examination (VIBE) sequence based on Dixon method. VIBE is a modified fast 3D gradient-echo sequence that has been applied to T1-weighted images in clinical whole-body MRI [26]-[28]. This sequence provides isotropic resolution in 3D (2.6×2.6×2.6 mm³) while preserving wide anatomic coverage in a short acquisition time (short repetition time, TR=3.6 ms), hence reducing motion artifacts. The MR image volume was oriented in the coronal plane with frequency encoding in foot-head direction and phase encoding in left-right direction. The acquisition parameters were field of view of 50×36 cm, 120 slices, and 2.6 mm slice thickness. Standard spine and surface coils were used in the acquisition. The Dixon method [29] acquires two separate images: a conventional gradient- or spin-echo image with water and fat signals in-phase and the other with readout gradient slightly shifted so that the water and fat signals are 180° out-of-phase (opposed-phase). The Echo delay Time (TE) is 2.46 and 1.23 ms for in-phase and opposed-phase, respectively. The sum of these two images produces a water image; the difference between these two images produces a fat image. All PET-CT and MR scans were acquired with arms up. All the patient scans were approved by MGH Institutional Review Board (IRB).

B. CT-based study

In order to assess the performance of the segmentation methods for MR-based PET AC, we performed direct segmentation on CT images to classify tissues.

We define the following tissue classes: air, lungs, fat, non-fat soft tissues, and bones. Based on these tissue classes, we define the 3C, 4C, and 5C segmentation methods listed in Table I. Figure 1 (A) shows the histogram of CT intensities within patient body for all the 23 patient scans. We applied four thresholds, T1 (-950), T2 (-350), T3 (-20), and T4 (140), on CT intensities (t) to segment tissues into air (t<T1), lungs (T1≤t<T2), fat (T2≤t<T3), non-fat soft tissues (T3≤t<T4), and bones (T4≤t). T3, which separates fat and non-fat soft tissues, is the CT intensity that has approximately equal chance to be fat or non-fat soft tissues. Visually, T2≤t<T3 produced almost the same fat mask as what was generated using the MR-based segmentation (See Sec. II.C), for each of the six patients who did both the CT and the MR scans. We converted the CT intensity to the attenuation coefficient at 511 keV using the dual-linear method described by Bai et al [30] assuming the mean CT energy is 70 keV. Figure 1 (B) shows the histogram of the attenuation coefficients at 511 keV. The mean attenuation coefficients at 511 keV, which were calculated using the above four thresholds, are 0.0276, 0.0868, 0.0976, and 0.1201 cm^-1 for lung, fat, non-fat soft tissue, and bone, respectively. For all the tissue types except lung, mean attenuation coefficients are only 1-3% different from the values published in three of the previous studies [13][17][25]. For lung, however, the attenuation coefficient ranged from 0.018 to 0.0349 cm^-1 in these studies [16][17][25]. This is not unexpected due to the fact that lung density varies significantly from one patient to another [16][31]. Additionally, we have performed a CT-based study to assess the bias reduction by further segmenting bones into low-density (T4≤t<500) and high-density bones (500≤t).

Table I.

Segmentation methods.

Segmentation method	Tissue class
3C	air, lungs, other tissues
4C	air, lungs, fat, other tissues
5C	air, lungs, fat, non-fat soft tissues, bones

Fig. 1.

Histograms of CT intensities and attenuation coefficients at 511 keV for all the 23 patient CT scans. (A) Histogram of CT intensities. (B) Histogram of attenuation coefficients at 511 kev.

C. MR-based study

We used the MR images acquired by the Dixon method to identify fat. Figure 2(A) shows the histogram of all the MR voxel values in all the six MR fat image volumes. The histogram does not have a clear fat peak because of the non-uniformity of MR images and voxel intensity variations among patients. However, if we plot the histogram of all the voxel values in fat/in-phase ratio image volumes for all the six patients as shown in Figure 2(B), we can clearly see the fat peak. We applied a single universal threshold of 0.8 to fat/in-phase ratio image volume to identify fat.

Fig. 2.

Histograms of voxel values in the MR fat images and the MR fat/in-phase ratio images for all the 6 patient MR scans. (A) Histogram of voxel intensity values in the MR fat images. (B) Histogram of voxel values in the MR fat/in-phase ratio images.

For hybrid PET-MR, the MR and PET are well registered. However, the MR and PET/CT scans of the same patient in this study were acquired on different scanners at different times. We registered the in-phase MR to CT using B-spline deformable registration with mutual information data fidelity [32] and topology-preserving priors [33]. The registration algorithm estimates a spatial mapping between point coordinates of two image volumes – a target image volume (f_tar, CT volume) and a source image volume (f_src, MR volume) – through the estimation of a non-rigid B-spline warping operator T̂ such that:

$$\widehat{T}={argmin}_T\left[{\mathrm{\psi }}_{\mathit{\text{MI}}}({\mathbf{f}}_{\mathit{\text{tar}}},T{\mathbf{f}}_{\mathit{\text{src}}})+\eta R(T)\right]$$ (1)

where ψ_MI is the mutual information similarity measure, η is a regularization parameter empirically set to η =10000, and R(T) is a regularizer. A bi-level multi-resolution strategy was used to reduce the risk of local minima. Some registration errors, however, are still detectable for patient body contour and lungs. These registration errors, which can be avoided for hybrid PET-MR studies, can contribute to the bias. Given the fact that the patient body contour and lungs should be in principle identified very accurately by MR (even ¹⁸F-FDG PET images without AC can be used for such purpose), the body and the lung masks should be almost the same for CT-based and MR-based study if no registration errors exist. We therefore used the patient body and lung masks identified in the CT-based study for the MR-based study to remove the effect of registration errors for the body contour and the lungs. For each of the six patients involved in the MR-based study, the fat mask, which was identified by applying a threshold of 0.8 to the fat/in-phase ratio image volume, was used to build pseudo CT for PET reconstruction.

D. Pseudo-CTs, reconstruction, and PET activity concentration accuracy

The CT intensity, which was assigned to each segmented tissue class, was calculated by averaging all the CT intensities within the tissue class identified by the segmentation, over all the 23 patients. Table II shows both the mean and the standard deviation of CT intensities for each tissue class and their combinations. Due to the fact that the histogram spectrum of CT intensities for each individual patient is similar for the 23 patients, the mean and standard deviation values listed in Table II will not change much if different patient samples are used (assuming the same kVp is used on the scanner). For each patient, a pseudo-CT was constructed using the assigned CT intensities for each segmentation method. For both the CT- and the MR-based studies, the patient bed in the original CT was first extracted and then added to each pseudo-CT before the reconstruction. All images were reconstructed by Siemens e7 tools with the clinical OSEM protocol at MGH with eight subsets and two iterations. All the images were reconstructed using PSF corrected OSEM with 256×256 matrix and 2.7×2.7×2.7 mm³ voxel size. The reconstructed images were post-filtered using a 5-mm (full width at half maximum) 3D Gaussian filter. As shown in Figure 3, for each patient, we used the PET image volume reconstructed using the original CT as the gold standard and calculated the activity concentration bias of voxel i using:

Table II.

Mean and standard deviation of ct intensities for each tissue class and combinations of tissue classes calculated using all the 23 patient ct Scans. The values in the parentheses are the linear attenuation coefficients for 511 kev photons in unit of cm^-1.

tissue class	mean	standard deviation
lungs	-712 (0.0276)	134
fat	-94 (0.0868)	60
non-fat soft tissues	34 (0.0976)	50
bones	459 (0.1201)	327
non-fat soft-tissues + bones	86 (0.1004)	124
fat + non-fat soft tissues + bones	-3 (0.0955)	98

Fig. 3.

Flow chart for the CT-based study. The notations ref and i represent the reference and ith patients, respectively.

$$b_i=\frac{x_i-x_i^{\mathbf{\text{gs}}}}{x_i^{\mathbf{\text{gs}}}},$$ (2)

where x_i is the value for voxel i for the reconstructed image volume, and $x_i^{\mathbf{\text{gs}}}$ is the value for voxel i for the gold standard image volume reconstructed using the original CT. For each tissue class T, we also calculated the mean (m^T), standard deviation (σ^T), and RMSE bias using:

$$m^T=\frac{\sum _{p=1}^N\sum _{i\in T^p}{b}_i^p}{\sum _{p=1}^N{n}_T^p},{\sigma }^T=\sqrt{\frac{\sum _{p=1}^N\sum _{i\in T^p}{(b_i^p-m^T)}^2}{\sum _{p=1}^N{n}_T^p},}{\mathbf{\text{RMSE}}}^T=\sqrt{{(m^T)}^2+{({\sigma }^T)}^2,}$$ (3)

where $b_i^p$ is the bias calculated using Eq. 2 for voxel i in patient p, and $n_T^p$ is the total number of voxels for tissue class T in patient p.

Both the inter- and intra-patient lung density variations can contribute to the overall standard deviation of bias in the lungs. In order to separate these two contributions, we calculated the mean ( $m_p^{\mathit{\text{Lung}}}$) and standard deviation of bias ( ${\sigma }_p^{\mathit{\text{Lung}}}$) for each patient separately. The standard deviation of $m_p^{\mathit{\text{Lung}}}$ for all the patients was used to estimate the interpatient contribution. The averaged ${\sigma }_p^{\mathit{\text{Lung}}}$ over all the patients was used to estimate the intra-patient contribution.

E. PET activity concentration bias atlas

For the CT-based study, we considered the CT-based AC as the gold standard and computed the bias in PET activity concentration obtained when correcting with one of our strategies as compared to the CT-based AC of the PET activity. As shown in Figure 3, we chose one patient as reference with normal anatomy and BMI, and registered the original CT volumes from the remaining 22 patients to the reference patient CT image volume using B-spline deformable registration with the topology-preserving prior [32][33]. This intra-modality registration algorithm differs from the one presented in section II.C by its different similarity measure, which is the sum of squared intensities differences. For each of the 22 patients, the transformation obtained from the CT registration was used to transform the corresponding CT-based bias image volume (see Figure 3).

For voxel i in the atlas, we computed the mean (m_i), standard deviation (σ_i), and RMSE bias using:

$$m_i=\frac{\sum _{p=1}^N{B}_i^p}{N},{\sigma }_i=\sqrt{\frac{\sum _{p=1}^N{(B_i^p-m_i)}^2}{N-1}},{\mathbf{\text{RMSE}}}_i=\sqrt{m_i^2+{\sigma }_i^2,}$$ (4)

where $B_i^p$ is the bias in voxel i for patient p after registration transformation, and N is the total number of patients. We obtained whole-body mean, standard deviation, and RMSE bias atlases using Eq. 4. We want to emphasize that the calculation of bias volume for each patient, which was performed independently for the patient, is not related to the image registration described above.

The intra-modality deformable registration worked surprisingly well except for small misalignments along the boundaries between different tissue classes among the 23 patients. To further improve the accuracy of mean and standard deviation bias atlases, we considered a voxel in a given patient as “mis-registered” if the absolute difference between the CT intensity in the voxel and the corresponding CT intensity for the reference patient was larger than 100. For a given voxel in the atlas, if more than 7 patients were identified as mis-registered for the voxel, we computed the atlas bias and standard deviation for the voxel using 3D interpolation based on the neighboring voxel values. The interpolation was applied to about 6% of the total voxels within the patient body. This procedure removed the mis-registration artifacts in the standard deviation bias atlas.

III. Results

Figures 4 and 5 show the histograms of voxel-wise bias, which was computed using Eq. 2, for each CT-based segmentation method for all the 23 patients. For each patient, lungs, fat, non-fat soft tissues, and bones were segmented using the methods described in Sec. II.B. For lungs, the bias distribution is almost same for 3C, 4C, and 5C. The probability of having an unacceptable high bias within lungs is significant. We also found the inter- and intra-patient lung density variations contribute almost equally (∼10%) to the overall standard deviation of bias in the lungs (∼14%). For fat, non-fat soft tissues, and bones, higher the segmentation level is, narrower bias distribution is. Less than 10% absolute bias in all the fat regions across entire patient body is achievable with 4C and 5C. Less than 20% and 10% absolute bias in all the non-fat soft tissue regions is achievable with 4C and 5C, respectively. Less than 20% absolute bias in almost all the bone regions is achievable with 5C. Table III shows the mean, standard deviation, and RMSE of voxel-wise bias, which were calculated using Eq. 3, for each tissue class and segmentation method. Table IV shows the mean and standard deviation of voxel-wise bias for heart, liver and kidneys.

Fig. 4.

Histograms of voxel-wise bias for different tissue classes for the CT-based study, which includes all the 23 patients.

Fig. 5.

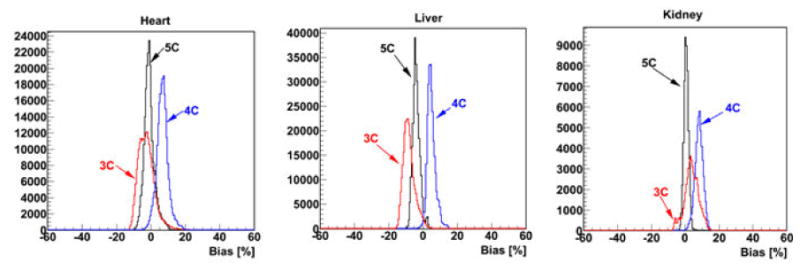
Histograms of voxel-wise bias for the heart, liver, and kidneys for the CT-based study, which includes all the 23 patients.

Table III.

Mean, standard deviation, and rmse of voxel-wise bias for each tissue class for the ct-based study [mean±standard deviation (RMSE)].

method	lungs	fat	non-fat soft tissues	bones
3C	5.8 ± 14.6% (15.7%)	14.2 ± 9.3% (16.9%)	-0.8 ± 8.0% (8.0%)	-15.4 ± 10.5% (18.6%)
4C	4.4 ± 14.4% (15.1%)	2.5 ± 3.2% (4.1%)	4.0 ± 5.3% (6.6%)	-9.0 ± 9.2% (12.9%)
5C	4.5 ± 14.2% (14.9%)	1.2 ± 2.7% (3.0%)	0.2 ± 3.0% (3.0%)	-0.1 ± 7.9% (7.9%)

Table IV.

Mean, standard deviation, and rmse of voxel-wise bias for heart, liver, and kidney for the ct-based study [mean±standard deviation].

method	heart	liver	kidney
3C	-1.8 ± 4.9%	-7.4 ± 3.4%	4.6 ± 4.1%
4C	7.4 ± 3.3%	5.6 ± 2.5%	8.9 ± 2.3%
5C	-0.2 ± 3.1%	-3.1 ± 2.2%	1.4 ± 1.3%

For the reference patient, Figure 6(A) shows a coronal CT slice. For each CT-based segmentation method, the original CT, the pseudo-CTs, and activity concentration bias images are shown. Figure 6(B) shows the corresponding bias slice for the patient. Figures 7(A) shows MR in-phase and fat images, which were registered to the CT images. Figure 7(B) shows the corresponding bias images for the same reference patient. The bias profiles along a line [shown in Figures 6(B) and 7(B)], which is across fat, the liver, the spine, and the lung, are shown in Figure 8. MR-based 4C yields similar results compared to the CT-based 4C.

Fig. 6.

One coronal slice for the CT-based study. (A) The CTs for the reference patient. (B) The bias images for the reference patient.

Fig. 7.

One coronal slice for the MR-based study. (A) The in-phase and fat MR images for the reference patient. (B) The bias images for the reference patient. (C) The mean bias calculated using all the 6 patient data sets.

Fig. 8.

Bias profiles. The profile lines are shown in Figures 6 (B) and 7 (B).

The mean, standard deviation, and RMSE bias atlases for the CT-based studies are shown in Figures 9 and 10 for two different coronary slices. Given only six patients in the MR-based study, we only show the mean bias atlas in Figure 7(C).

Fig. 9.

One coronal atlas slice in the back of the body for the CT-based study. (A) The mean SUV bias atlas calculated using all the 23 patient data sets. (B) The standard deviation atlas of SUV bias. (C) The RMSE SUV bias atlas.

Fig. 10.

One coronal atlas slice in the front of the body for the CT-based study. (A) The mean SUV bias atlas calculated using all the 23 patient data sets. (B) The standard deviation atlas of SUV bias. (C) The RMSE atlas of SUV bias.

Figures 11, 12, and 13 show the standard deviation bias atlas for 3C in three different views and profiles across the heart, liver, and kidneys, respectively. The standard deviation bias within both the heart and the liver is less than 5% although the standard deviation bias in other places, such as fat, lungs, and bones, is much higher. This demonstrates that 3C can be sufficient to achieve small variation of bias for imaging these three organs.

Fig. 11.

The standard deviation atlas of SUV bias and profiles in three different views through the heart for CT-based 3C.

Fig. 12.

The standard deviation atlas of SUV bias and profiles in three different views through the liver for CT-based 3C.

Fig. 13.

The standard deviation atlas of SUV bias and profiles in three different views through the kidneys for CT-based 3C. The black arrows point to the kidneys.

Additionally, we found that the voxel-wise RMSE bias in bones is reduced to 4.5% as compared to 7.9% for 5C if we further segmented bones into low-density and high-density bones as described in Sec. II.B.

IV. Discussions

Lungs have high probability of high bias partly because the attenuation coefficients for lungs have a wide range as shown in Figure 1. Assigning a single attenuation coefficient to the entire lungs is therefore inaccurate. Inter-patient variations of the lung density result in both positive and negative mean bias within the lungs (See Figures 6, 9, and 10). Also, intra-patient variations of the lung density lead to high standard deviation bias (See Figures 9 and 10). The inter- and intra-patient lung density variations contribute almost equally to the overall standard deviation of bias in the lungs. One solution to reduce the high bias is to segment lungs into more than one tissue class. However, further segmentation of lungs is technically challenging using conventional MR. This is because MR signals from lungs are low due to the low proton density in the lung and the fast signal decay caused by susceptibility artifacts at air-tissue interfaces. However, MRI is emerging as a valuable lung imaging modality in clinical setting thanks to recent technical advances. Dedicated fast lung sequences use reasonable high spatial resolution and short echo time to receive as much lung signal as possible. Marshall et al [24] have demonstrated that a linear relationship can be established between MR and CT signals in the lungs. This makes it possible to build a non-uniform and patient-specific attenuation map for the lungs. It is likely that tumors in lungs have similar density as soft-tissues. If lung tumors, especially large ones, can be segmented out as soft-tissue class rather than lung class, the reconstructed activity in the tumors becomes more accurate because the attenuation coefficient assigned to the tumor is closer to the true underlying value.

Fat identification is crucial to achieve low bias in fat regions. With the Dixon method, the fat should also be identified reasonably well. Our CT-based fat identification requires T2≤t<T3. Our MR-based fat identification requires fat/in-phase ratio ≥ 0.8. From the six patient data sets, these two fat identification methods yield very close fat regions visually. These two methods also yield similar bias results in Figure 8.

The effect of bone identification can be seen by comparing 4C and 5C in both Figure 4 and Table III. Less bias is achieved using 5C as compared to 4C in not only the bone regions but in other regions as well. For example, both Figure 4 and Table III show that 5C has lower bias in some non-fat soft tissues than 4C.

In order to segment bones more accurately, a dedicated bone MR sequence, which is not included in this research, is needed. Previously, Ultra-Short Echo (UTE) time sequence has been successfully applied in brain MR-based AC [7]-[9]. The UTE uses radial sampling of k-space and has echo times in the order of 100 µs and below, which makes it possible to detect bones that have transverse relaxation times T₂ in the sub-millisecond range. However, some technical challenges may still exist even if UTE can be successfully applied in whole body. For example, the bone may not be identified accurately given the noise, non-uniformity, and imaging artifacts. Also, additional MR imaging time used by the UTE sequence is another concern unless it can be fully integrated into another MR sequence [9].

Even for 5C, in which bones are identified, absolute bias in bones can still be high (see Table III and Figure 4). One possible solution to further reduce the bias in bones is to segment the bones into more than one tissue class. As we stated in Sec. III, further segmenting bones into low- and high-density bones reduces the RMSE bias in bone regions. However, it can be challenging to segment bones into more than one tissue class using an MR bone sequence. The correlation between MR bone signal and bone density needs to be investigated.

We also want to point out that the RMSE bias values given in Tables III and IV can be further reduced if we modify the SUV values for the identified tissue types to compensate the mean bias. For example, we could reduce all the SUV values within the lungs and fat by 4.4% and 2.5%, respectively, for 4C.

For the identification of the outer contour of the patient body and the segmentation of the lungs and fat, single threshold and region-growing filtering were successfully used in this research. Although such methods were successful for the six MR patient scans in this study, it would be prudent to study these methods using large patient samples. More sophisticated methods, such as the algorithm to smooth the MR images and lung segmentation algorithm described in [16], have been demonstrated to make the segmentation less sensitive to inter-subject differences and image noise. We believe that the outer contour of the patient body and the lungs should be in principle identified reasonably well using conventional MR images. We have also shown that fat segmentation can be achieved using MR fat/in-phase ratio images. Therefore, MR images acquired by the Dixon method can be successfully used to perform both 3C and 4C.

The mean, standard deviation, and RMSE bias atlases require good registration among all the patients. After intra-modality registration algorithm and 3D interpolation (See Sec. II.E) were applied, the bias, the standard deviation, and the RMSE image volume are free of mis-registration artifacts at least visually.

In order to segment tissues into more classes using MRI, it generally requires more MR imaging time. For example, in order to identify fat, a scan using a dedicated MR fat sequence is needed. However, such a scan may become unnecessary if the bias within the region of interest without fat segmentation is small enough. Additionally, more tissue class segmentation generally requires more user interaction in order to verify the segmentation visually. It is therefore desirable to know the bias within the region for different levels of segmentation, i.e., the number of tissue classes to be segmented, so that the minimum segmentation level can be determined. A patient-independent whole-body bias atlas [See Figures 9(B) and 10(B)], which gives a complete view of the standard deviation of bias across the body for each level of segmentation, can be used for such purpose. For example, Figures 11, 12, and 13 clearly shows that CT-based 3C yields less than 5% standard deviation of bias within the heart, liver, and kidneys, respectively. As described previously, it is important to realize that we can modify the SUV values in the heart, liver, or kidneys to compensate the mean bias. The standard deviation of bias is the key that determines whether a segmentation method can produce acceptable results. Therefore, dedicated fat or bone identification is not needed for cardiac or liver imaging using PET-MR. On the other hand, fat and bone identification becomes important when imaging the lower part of the torso, such as pelvis, as Figures 9 and 10 show that CT-based 3C can yield well above 10% bias within the region.

Finally, in the current study, we calculated the average CT intensity value across all the voxels within an identified tissue class for all the patients (see Table II). We then assign the average CT intensity to the corresponding tissue type to build a pseudo-CT for a given patient. To further reduce bias standard deviation of reconstructed activity concentration, we can, in principle, divide patient studies into multiple groups based on patient's BMIs, bed positions, patient's gender, etc. However, this method, which is beyond of the scope of this study, requires hundreds if not thousands of patient studies.

V. Conclusions

Our CT-based results, which represent the limiting performance that could be achieved using MR-based tissue segmentation, show that the segmentation methods as well as location of region of interest determine the bias to be expected. Our CT-based study shows that 4C, which can be achieved using Dixon method on a standard whole-body PET-MR scanner, yields about 15.1%, 4.1%, 6.6%, and 12.9% RMSE bias in lungs, fat, non-fat soft-tissues, and bones, respectively. If bones can be identified by MR to perform 5C, RMSE bias in lungs, fat, non-fat soft-tissues, and bones becomes 14.9%, 3.0%, 3.0%, and 7.9%, respectively. Based on the Dixon method, we have developed a fat identification method using fat/in-phase ratio images. We have shown that a patient-independent bias atlas provides a complete view of the bias across the body and can be used to determine the minimum segmentation level that is required for imaging a particular region of interest. Moreover, we have shown that 3C yields less than 5% standard deviation of bias within the heart, liver, and kidney. This implies that 3C can be sufficient to achieve small variation of bias for imaging these three organs. Finally, we have found that inter- and intra-patient lung density variations contribute almost equally to the overall standard deviation of bias within the lungs.