Machine Learning in Medical Imaging

Statistical methods of automated decision making and modeling have been invented (and reinvented) in numerous fields for more than a century. Important problems in this arena include pattern classification, regression, control, system identification, and prediction. In recent years, these ideas have come to be recognized as examples of a unified concept known as machine learning, which is concerned with 1) the development of algorithms that quantify relationships within existing data and 2) the use of these identified patterns to make predictions based on new data. Optical character recognition, in which printed characters are identified automatically based on previous examples, is a classic engineering example of machine learning. But this article will discuss very different ways of using machine learning that may be less familiar, and we will demonstrate through examples the role of these concepts in medical imaging.

Machine learning has seen an explosion of interest in modern computing settings such as business intelligence, detection of e-mail spam, and fraud and credit scoring. The medical imaging field has been slower to adopt modern machine-learning techniques to the degree seen in other fields. However, as computer power has grown, so has interest in employing advanced algorithms to facilitate our use of medical images and to enhance the information we can gain from them.

Although the term machine learning is relatively recent, the ideas of machine learning have been applied to medical imaging for decades, perhaps most notably in the areas of computer-aided diagnosis (CAD) and functional brain mapping. We will not attempt in this brief article to survey the rich literature of this field. Instead our goals will be 1) to acquaint the reader with some modern techniques that are now staples of the machine-learning field and 2) to illustrate how these techniques can be employed in various ways in medical imaging using the following examples from our own research:

• ■CAD
• ■content-based image retrieval (CBIR)
• ■automated assessment of image quality
• ■brain mapping.

INTRODUCTION TO MACHINE LEARNING

In this brief tutorial, we will attempt to introduce a few basic techniques that are widely applicable and then show how these can be used in various medical imaging settings using examples from our past work in this field. For further information, interested readers should consult well-known introductions to machine learning, such as the excellent treatments in [1] and [2].

SUPERVISED LEARNING

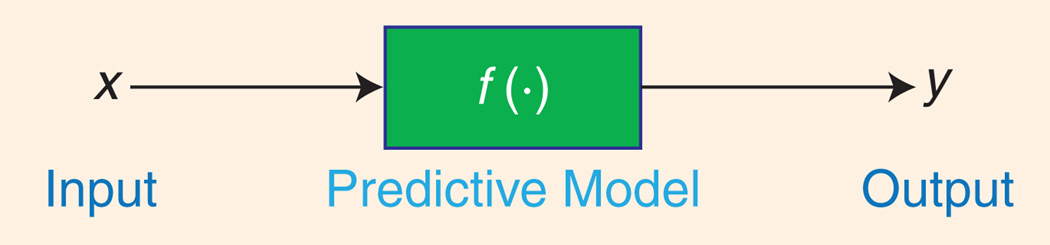
In machine learning, one often seeks to predict an output variable y based on a vector x of input variables. To accomplish this, it is assumed that the input and output approximately obey a functional relationship y=f (x), called the predictive model, as shown in Figure 1. In supervised learning, the predictive model is discovered with the benefit of training data consisting of examples for which both x and y are known. We will denote these available pairs of examples as (x_i, y_i ), i = 1, …, N, and we will assume that x is composed of n variables (called features), so that x_i∈ ℝⁿ. In general, the output of the predictive model can be a vector (e.g., in multiclass classifiers), but for simplicity we will confine our attention to the case of scalar outputs.

FIG 1.

In supervised learning the predictive model represents the assumed relationship between input variables in x and output variabley.

Historically, a somewhat artificial distinction has sometimes been made between two learning problems: classification and regression. Classification refers to decision among a typically small and discrete set of choices (such as identifying a tumor as malignant or benign), whereas regression refers to estimation of a possibly continuous-valued output variable (such as a diagnostic assessment of disease severity y) . If the choices in a classification problem are indicated by discrete numerical values (e.g., y = +1 for the class malignant and y = −1 for benign), then it is easy to see that classification and regression are represented equivalently by the model in Figure 1.

THE SUPPORT VECTOR MACHINE CLASSIFIER: A MAXIMUM-MARGIN APPROACH

Let us consider the simple pattern classification problem depicted in Figure 2, in which the goal is to segregate vectors x =(x₁,x₂) into two classes by using a decision boundary T. Let us employ a linear model f(x)=w^Tx +b, so that T is a line in this two-dimensional example. Traditionally, the model’s parameters (w and b in this case) have been determined using classical criteria such as least squares or maximum likelihood. Figure 2 illustrates how such an approach (in this case, a Fisher discriminant) can easily fail, particularly when the method’s distributional assumptions are violated. In Figure 2(a), data point D adversely influences the Fisher discriminant boundary, causing misclassification of point B even though point D lies very far from Class 1, and perhaps should not be granted this degree of influence.

FIG 2.

Fisher linear discriminant (LD) and the SVM. In this example, (a) the Fisher LD fails to separate two classes because training example D adversely influences decision boundary T. (b) The SVM defines the decision boundary using only points A, B, and C, called support vectors, and is not influenced at all by point D.

The support vector machine (SVM) [2], discovered by Vapnik, resolves this shortcoming by defining the discriminant boundary only in terms of those training examples that lie dangerously close to the class to which they do not belong. This idea is understood most easily in a situation such as the one shown in Figure 2, in which the two classes are strictly separable by a linear decision boundary, as explored by Wernick in [3]. In this case, a separating line that maximizes the margin between the two classes can always be found as follows:

1. Draw the convex hull of each class of data points (imagine stretching a rubber band around each group of points; call these regions S₁ and S₂).

2. Find the points C and E at which regions S₁ and S₂ have their closest approach.

3. Draw the perpendicular bisector of the line segment connecting points C and E to obtain the decision boundary T.

Step 2 is accomplished by solving a quadratic programming (constrained optimization) problem using standard approaches [3]. In linear classifiers, vector w is called the discriminant vector.

In the terminology of the SVM, points A, B, and C in Figure 2 are called support vectors, a term derived from an analogy to mechanics. If points A, B, and C in Figure 2 were physical supports, they would be sufficient to provide mechanical stability to slab S sandwiched between them.

It is evident that the support vectors are the only examples from the training data that explicitly define the model. Specifically, for a particular test example x, one can write the model in terms of the support vectors as follows:

$$f(\mathbf{x})={\sum }_{i\in I_s}{\alpha }_i{y}_i{\mathbf{x}}_i^T\mathbf{x}+b,$$ (1)

in which the summation includes only the training examples x_i that are support vectors, and α_i are coefficients determined as Lagrange multipliers in the optimization procedure.

The benefits of the SVM approach are that the classifier concentrates automatically on examples that are difficult to classify (points A, B, and C); and the calculation in (1) scales with the number of support vectors rather than the dimension of the space (which in some problems is very large). In addition, SVM can be shown to balance training error and model complexity, thereby avoiding overfitting, a pitfall in which the model is too finely tuned to the training examples and fails to perform well on new data. This approach is called structural risk minimization [4].

The formulation described thus far does not allow for the possibility that the two classes cannot be entirely separated by a linear boundary. However, this situation is readily addressed by introducing slack variables into the quadratic optimization problem, thus allowing a minimal number of the training data to be misclassified. In addition, SVM can be easily adapted to accomplish regression instead of classification by using a so-called ε-insensitive cost function [2].

NONLINEAR MODELS: THE KERNEL TRICK

An important breakthrough in machine learning has been the recognition of the so-called kernel trick [2], which provides a simple and broadly applicable means to obtain a nonlinear model from any linear model based on inner products. Even classical techniques, such as the Fisher discriminant or principal component analysis, can be turned easily into flexible nonlinear techniques via the kernel trick.

To understand the kernel trick, consider the following hypothetical series of steps as applied to turn the linear SVM into a nonlinear technique. Suppose we were to first apply a nonlinear transformation Ф to each input vector x_i from the training set and then train a linear classifier to distinguish these classes of transformed vectors Ф(x_i). Separability will be enhanced if the dimension of the transform space is higher than that of the original space, and indeed the transformation’s dimension need not be finite.

At first glance, transforming each input vector into a space of high dimension might appear impractical. However, the kernel trick recognizes that the desired result can be obtained without actually performing the transformation. This can be seen by applying the transformation Ф and then applying the SVM model in (1). After transformation, (1) becomes

$$f(\mathbf{x})={\sum }_{i\in I_s}{\alpha }_i{y}_i\mathrm{\Phi }{({\mathbf{x}}_i)}^T\mathrm{\Phi }(\mathbf{x})+b.$$ (2)

Note that the transformation Φ appears in (2) only in the form of an inner product K(x_i,x) Δ͇ ɸ (x_i)^T ɸ (x), so that (2) can be rewritten as

$$f(\mathbf{x})={\sum }_{i\in I_s}{\alpha }_i{y}_{i}K({\mathbf{x}}_i,\mathbf{x})+b.$$ (3)

Therefore, we can see that it is never actually necessary to compute Φ (or even to define it explicitly). Instead it is sufficient simply to define the kernel function K(·,·) , and it can be shown that any symmetric positive semidefinite function will suffice. Commonly used kernel functions in machine learning include radial basis functions (Gaussians) and polynomials. Intuitively, the effect of the kernel is to measure the “similarity” between a test vector x and each of the support vectors x_i; these similarities are then used in to obtain the output result. Vectors belonging to one of the classes are presumably most “similar” to the support vectors belonging to that class, hence these similarity values convey the needed information. The key point to remember is that these similarity comparisons are made only in relation to the support vectors, which are difficult examples that lie near the discriminant boundary. We will see visual examples of these support vectors later in the setting of mammography.

RELEVANCE VECTOR MACHINES: BAYESIAN LEARNING AND SPARSITY CONSTRAINTS

An important successor of SVM is the so-called relevance vector machine (RVM), developed by Tipping [5]. We have found RVM to perform extremely well in several medical imaging applications, usually with much lower computational cost than alternative methods including SVM. The RVM emphasizes sparsity (i.e., reduced model complexity), and thus is closely related to ideas of compressed sensing [6]. Like SVM, RVM uses a subset of the training data called relevance vectors, but usually there are far fewer relevance vectors than support vectors.

Like SVM, RVM starts with a kernel model

$$f(\mathbf{x})=\sum _{i=1}^N{w}_{i}K(\mathbf{x},{\mathbf{x}}_i),$$ (4)

however, whereas SVM is based on the maximum-margin principle, RVM instead takes a Bayesian approach. RVM assumes a Gaussian prior on the kernel weights w_i, which are assumed to have zero mean and variance $a_i^{-1}$. RVM further assumes a gamma hyperprior on $a_i^{-1}$. The net effect of these modeling choices is that the overall prior on the kernel weights w_i is a multivariate t-distribution. Because this distribution is tightly concentrated about the axes of the w_i space, the prior encourages most values of w_i to be nearly zero. Thus, in the end, the summation in involves only a few nonzero terms, and the associated training examples are called relevance vectors. By this mechanism, overfitting is generally avoided, and computation times for RVM are relatively low. Surprisingly, in spite of its advantages, RVM has been used relatively infrequently in medical imaging, particularly in comparison with the better-known SVM approach.

While RVM and SVM both base their decisions entirely on a subset of the training data (the relevance vectors in RVM; the support vectors in SVM), these subsets are usually quite different. Support vectors are always examples lying near the decision boundary, while relevance vectors are usually spread throughout the distribution. We will see this difference later in the context of mammography.

Unfortunately, RVM does not have a simple geometrical interpretation as SVM does, therefore we will not show a graphical example in this article; instead we refer the reader to [5], which contains several nice illustrations.

MACHINE LEARNING HAS SEEN AN EXPLOSION OF INTEREST IN MODERN COMPUTING SETTINGS SUCH AS BUSINESS INTELLIGENCE, DETECTION OF E-MAIL SPAM AND FRAUD, AND CREDIT SCORING.

STATISTICAL RESAMPLING FOR ROBUSTNESS AND EVALUATION

Statistical resampling [7] refers to a family of techniques that are used to evaluate performance and improve robustness of machine learning models and to estimate statistical significance levels. Although resampling receives less attention than predictive models, it is at least as important.

Machine learning differs from classical decision and estimation theory principally in its emphasis on problems where one’s only knowledge of the data’s underlying distributions comes from the data themselves. In this setting, statistical significance testing cannot be approached in the traditional way because the null distribution is unknown. Fortunately, an empirical estimate of the null distribution can be readily obtained by permutation resampling.

To understand permutation resampling, consider a situation in which there are two sets of data, ω₁ and ω₂, and we wish to test some hypothesis, such as that their means are identical. Since we do not know in truth whether ω₁ and ω₂ obey the same distribution (or even the form of their distributions), we cannot directly assess significance. However, we can create an empirical null distribution by permuting the labels on the data, i.e., deliberately creating two data sets in which the data from ω₁ and ω₂ are mixed. Note that it is often important that just the labels and not the data themselves be permuted (e.g., in time series problems). By permuting the data in every possible way (or at least in some reasonably large number of random ways), we can obtain example data in which we know that the two groups obey identical distributions, thus characterizing the null hypothesis.

Another central role played by resampling is in solving the following problem of model validation: If we train our model on all our available data, then there are no data left for testing the model or optimizing its parameters. The predominant resampling methods used in this regard, which both require independent, identically distributed (i.i.d.) resampling objects, are cross validation and bootstrap methods. In k-fold cross validation, the data set is divided randomly into k groups; (k – 1) of these groups are used to train the model, and one is reserved for testing. This process is performed k times (once for each held out group), then the results are combined, often by averaging. In the basic bootstrap, the data are instead trained on a set of N data examples obtained by sampling randomly with replacement from the entire data set of N. By chance, some examples will not be selected into the training set, and these are reserved for testing. As in cross validation, the process is repeated and the results combined by averaging.

The basic bootstrap is known to reduce the variance of estimated prediction accuracy at the expense of downward bias (i.e., the basic bootstrap provides pessimistic performance estimates). This is remedied by the .632 bootstrap, which utilizes a bias correction term, and the more modern .632+ bootstrap [8], which additionally attempts to account for bias due to overfitting. In problems where an empirical null distribution is obtained using permutations, the empirical distribution of the alternative hypothesis can often be obtained using the bootstrap.

Statistical resampling is widely used not only to test predictive models, but also to improve their performance. Examples of this are bootstrap aggregation (bagging) techniques and the nonparametric, prediction, activation, influence, reproducibility, resampling (NPAIRS) framework in neuroimaging [9], which is explained later in this article.

CAD FOR MAMMOGRAPHY

CAD has been an active research area for decades, so we will not attempt to provide a comprehensive survey of the literature. Interested readers should consult basic reviews of CAD for mammography, such as [10] and [11].

Perhaps CAD’s greatest success is in breast imaging. Studies have shown that having two radiologists read the same mammogram can lead to significantly higher sensitivity in cancer screening, but at the expense of increased workload and cost. CAD software can serve as a surrogate “second reader,” with the aim of improving radiologists’ diagnostic accuracy at lower cost.

CAD encompasses computer-aided detection (CADe), in which the computer alerts the radiologist to potential lesions; and computer-aided diagnosis (CADx), in which the computer predicts the likelihood that a lesion is malignant.

CAD schemes typically consist of the following key steps: 1) apply automated image analysis to extract a vector of quantitative features to characterize the relevant image content and 2) apply a pattern classifier to determine the category to which the extracted feature vector may belong.

Automatically extracted image features can include image contrast, and features based on geometry, morphology, and texture. In addition, there may be other forms of available information about the patient. Machine-learning methods that have been employed range from linear discriminant (LD) analysis, fuzzy logic techniques, neural networks, and committee machines, to the more recent kernel-based methods (e.g., SVM and RVM) explained earlier in this article.

In the following, we describe two examples of machine learning for CAD in digital mammography drawn from our own research: detection (CADe) and classification (CADx) of clustered microcalicifications.

CADe: MICROCALCIFICATION DETECTION

Microcalcifications (MCs) are tiny deposits of calcium that appear as bright spots in mammograms (see Figure 3). Clustered MCs can be an important indicator of breast cancer, appearing in 30–50% of cases. Individual MCs are sometimes difficult to detect due to their variation in shape, orientation, brightness and size (typically, 0.05–1 mm), and because of the confounding texture of surrounding breast tissue. Microcalcification detection has been an intensive target of investigation (e.g., [12]). Modern machine-learning approaches have proven very effective in this application, as we explain next.

FIG 3.

(a) Example mammogram containing microcalcifications. (b) Output y of SVM detector. (c) Detected MC positions obtained by thresholding y.

SVM Detector

In [13], we trained an SVM to decide at each location within a mammogram whether an MC was present (“MC present” class) or absent (“MC absent” class) based on a small region of interest (ROI) surrounding that point. The SVM was trained using “MC present” ROIs identified by expert radiologists (see Figure 4).

FIG 4.

(a) Comparison of support vectors from SVM and (b) relevance vectors from RVM for detection of MCs. SVM automatically chooses the support vectors to be examples lying near the decision boundary (hence the “MC absent” and “MC present” support vectors look very similar), while the relevance vectors chosen by RVM tend to be more prototypical of the two classes (hence the two groups of relevance vectors look very different).

The MCs typically occupy only a small fraction of a mammogram, so there are more ROIs with “MC absent” than with “MC present.” To take advantage of this, we developed a successive enhancement learning (SEL) procedure that improves the predictive power of the SVM classifier. In SEL, SVM training is adjusted iteratively by selecting the most representative “MC absent” examples from all the available training images while keeping the total number of training examples small.

Based on a set of test mammograms, we demonstrated the SEL-SVM method to achieve the best performance among several leading methods in the literature as measured by the free-response receiver operating characteristic (FROC) curve, a plot of detection probability versus the average number of false positives (FPs) per image (Figure 5). Figure 3 shows a portion of an example image and the corresponding SVM output.

FIG 5.

Detection performance of various methods of detecting MCs in mammograms. The best performance was obtained by a successive learning SVM classifier, which achieves around 94% detection rate (TP fraction) at a cost of one FP cluster per image, where a classical technique (DoG) achieves a detection rate of only about 68%.

RVM Detector

Computation time can be a critical issue in mammography, where the image can contain as many as 3,000 × 5,000 pixels that must be evaluated. While the SVM achieves outstanding detection performance, it can be very time consuming because the number of support vectors can be large. To address this issue, in [14] we developed an approach based on the RVM (explained earlier), which yields a very sparse decision function, leading to significant computational savings, while yielding similar detection performance to the SVM.

To further accelerate the algorithm, we explored a two-stage classification approach in which we used a computationally inexpensive linear RVM classifier as an initial triage step to quickly eliminate non-MC pixels, then a nonlinear RVM classifier to detect MCs among the remaining pixels. Our results demonstrated that the RVM approach achieved nearly identical detection accuracy to the SVM at 35 times less computational cost.

SVM Versus RVM

As explained earlier, SVM and RVM are both kernel methods, and both base the decision on only a subset of the training data—the support vectors in SVM and relevance vectors in RVM—that characterize the respective classes. However, SVM and RVM tend to select very different vectors to represent the classes. SVM chooses support vectors that lie very close to the decision boundary, while RVM tends to choose relevance vectors that are more prototypical of the two classes. Examples of support vectors and relevance vectors are shown in Figure 4. Note that the “MC present” and “MC absent” support vectors are very difficult to distinguish, as they all lie near the decision boundary, while the “MC present” and “MC absent” relevance vectors are clear examples of lesion and background regions, respectively.

ALTHOUGH RESAMPLING RECEIVES LESS ATTENTION THAN PREDICTIVE MODELS, IT IS AT LEAST AS IMPORTANT.

CADx: DIAGNOSIS OF CLUSTERED MICROCALCIFICATIONS

A great deal of research has been directed toward computerized CADx methods designed to assist radiologists in the difficult decision of differentiating benign from malignant MCs. In [15], a CADx scheme was demonstrated to classify clustered MCs even more accurately than radiologists. This method used a feedforward neural network (FFNN), which was trained using metrics extracted automatically from the clustered MC images.

Motivated by recent developments in machine learning, we sought in [16] to determine whether state-of-the-art machine-learning methods [SVM, kernel Fisher discriminant (KFD), RVM, and committee machines (including ensemble averaging and Adaboost, a well-known boosting method)] would further improve classification of MC clusters as malignant or benign, as compared with prior methods such as FFNN. We used the features defined in [15] that are based on both the shape and size of individual MCs as well as their overall distribution as a cluster, that are known to correlate qualitatively to features used by radiologists.

The evaluation study demonstrated that the kernel methods (SVM, KFD, and RVM) are similar in performance to one another (in terms of the area under the receiver-operating characteristic (ROC) curve), but all demonstrated statistically significant improvement over FFNN or AdaBoost.

CBIR FOR CADx

Though promising, CADx has met with resistance to adoption in clinical practice, in part because radiologists are trained to interpret visual data and rarely deal with quantitative mammo-graphic information, such as the likelihood of malignancy. Thus, when presented with a numerical value, but without additional supporting evidence, it may be difficult for a radiologist optimally to incorporate this number into the diagnostic decision. As such, traditional CADx classifiers are often criticized for being a “black box” approach.

To avoid this pitfall, an alternative approach we have advocated is to employ CBIR [17], [18], in which an image search engine is used to inform the radiologist’s diagnosis in difficult cases by presenting relevant information from past cases. The retrieved example lesions allow the radiologist to explicitly compare known cases to the unknown case. A key advantage of this approach is that it provides case-based evidence to support case-based reasoning by the radiologist, rather than acting as a supplemental decision maker.

For a retrieval system to be useful as a diagnostic aid, the retrieved images must be truly relevant to the query image as perceived by the radiologist, who otherwise may simply dismiss them. In 2000 [17], we proposed a supervised learning approach for modeling the radiologists’ notion of image similarity for use in CBIR. Our rationale is that mathematical distance metrics designed for general-purpose image retrieval may not adequately characterize clinical notions of image relevance, which are complex assessments made by expert observers.

In our approach, the perceptual similarity between two lesion images is modeled by a nonlinear regression model applied to the image features. The model is determined by using supervised learning from examples collected either in human observer studies or from online user feedback (acquired during use of the system). Specifically, we first characterize a lesion by vector u containing its key relevant features. Next, feature vector u is compared to the corresponding feature vector v of a database entry by way of predictive model f (u, v) to produce a similarity coefficient (SC). The images with the highest SC values are retrieved from the database and displayed for the user. In our studies, we have modeled f (u, v) using a nonlinear regression SVM and a general regression neural network (GRNN). Our learning metric has proven to be much more effective than alternative measures [17], [18].

To illustrate perceptual similarity, Figure 6 is a plot created using a multidimensional scaling (MDS) algorithm showing 30 microcalcification clusters. MDS is a family of techniques that aim to map high-dimensional data into a lower-dimensional representation in such as a way as to preserve relative distances (i.e., if two points are close to one another in the high-dimensional space, then MDS attempts to place them near one another in the low-dimensional space).

FIG 6.

Statistical tool for visualizing relationships among abnormalities seen in various mammograms, in which distances reflect the relative similarities of abnormalities, as judged by human experts. MC clusters are represented in this two-dimensional diagram by using multidimensional scaling, a statistical technique that seeks to represent high-dimensional data in a lower-dimensional plot that can be readily visualized, while aiming to maintain the relative distances (similarities) among the data points. Each group of red plus signs (+) depicts the actual MC cluster associated with a given point in the scatter plot. This shows that the vertical axis of the plot is roughly associated with the density of each cluster, while the horizontal axis is related to its shape.

FOR A RETRIEVAL SYSTEM TO BE USEFUL AS A DIAGNOSTIC AID, THE RETRIEVED IMAGES MUST BE TRULY RELEVANT TO THE QUERY IMAGE AS PERCEIVED BY THE RADIOLOGIST, WHO OTHERWISE MAY SIMPLY DISMISS THEM.

In Figure 6, each microcalcification cluster is represented by a marker (square or circle) in the scatter plot. MDS attempts to place the points so that visually similar microcalcification clusters (as judged by human observers) are placed close to one another in the scatter plot. Examples of the microcalcfication clusters corresponding to these data points are shown as collections of plus (+) signs. Visual inspection of these examples suggests that the vertical axis of the plot is associated roughly with density of the microcalcifications, while the horizontal axis reflects the shape of the cluster. Note that there is a reasonable, but not perfect, separation between malignant and benign lesion classes in this space.

Recently, we proposed to use CBIR to boost the performance of a traditional CADx classifier [18]. Specifically, database images similar to the image being evaluated by the radiologist are used to improve the SVM classifier, thus improving its accuracy in analyzing the present case. We are currently investigating the impact of CBIR on the diagnostic performance of radiologists.

AUTOMATED ASSESSMENT OF IMAGE QUALITY BY PREDICTION OF DIAGNOSTIC PERFORMANCE

Diagnostic imaging can be thought of as a pipeline consisting of an imaging device, an image processor (e.g., image reconstruction algorithm and display), and a human observer (e.g., a radiologist). Principled methods are needed to assess the impact of design choices in the image acquisition and processing stages on the final interpretation stage.

It has been common traditionally to evaluate imaging devices and image reconstruction software using only basic fidelity metrics, such as signal-to-noise ratio (SNR), meansquare error, and bias and variance. However, such metrics have limitations when comparing images affected by statistically different types of blur, noise, and artifacts [19]. This was recognized in the 1970s in the context of radiographic imaging by Lusted [20], who pointed out that the image can reproduce the shape and texture of tissues faithfully from a physical standpoint, while failing to contain useful diagnostic information. In a highly influential article in Science [20], Lusted postulated that, to measure the worth of a diagnostic imaging test, one must assess the observer’s performance when using the imaging test. In other words, if an image is to be used for lesion detection, then image quality should ideally be judged by the ability of an observer to detect lesions. Such an approach has become known as task-based assessment of image quality.

Lusted further argued that the ROC curve from classical detection theory is an ideal means to characterize diagnostic performance, and thus image quality. This approach has led to the wide use of ROC analysis in medical imaging, as implemented, for example, in the ROCKIT software distributed by Metz et al. [21].

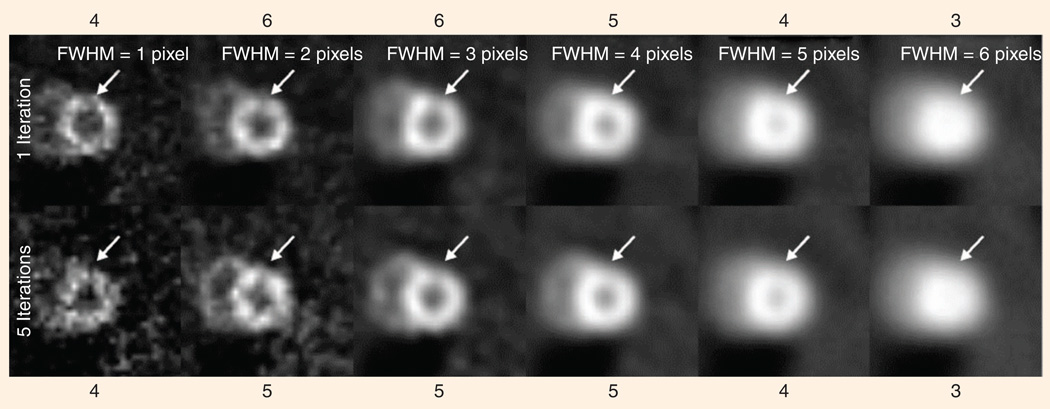
Figure 7 shows an example of how the human observer’s performance is affected by the type of images that are presented. In this case, the observer is shown a perfusion image of the myocardium (heart wall), obtained using single-photon emission computed tomography (SPECT). The observer is asked to judge whether there is a dark region indicating deficient perfusion, based on images reconstructed in different ways from the very same data set. Figure 7 shows 12 different reconstructions obtained by using either one or five iterations of the ordered-subset expectation-maximization algorithm (OS-EM), and with Gaussian filters having varying full width at half-maximum (FWHM).

FIG 7.

A human observer’s judgment as to the presence of an abnormality (in this case a cardiac perfusion defect) depends on the parameters of the reconstruction algorithm used to create the image (here, the parameters are number of iterations and width (FWHM) of the post-reconstruction smoothing kernel). All of the images above have a defect at the location indicated by the arrow, but persons asked to judge whether there is a defect varied in their opinions from a value of three, meaning “defect is possibly not present,” to a value of six, meaning “defect is definitely present.” Our algorithm’s ability to predict this behavior permits us to optimize a given algorithm for this specific diagnostic task.

Along the top and bottom of Figure 7 are values of an observer’s stated confidence in the presence of a lesion at a location indicated by arrows (on a scale of one to six, with six indicating high confidence). Note that the observer’s confidence that a lesion is present increases, then decreases, as the images are made smoother. Selection of the optimal smoothing level is an example of a goal in which a quantitative image-quality metric is needed

MACHINE-LEARNING MODEL OF HUMAN OBSERVERS

In diagnostic imaging, the gold standard for measuring image quality is a statistical study that measures observers’ (e.g., radiologists’) diagnostic performance when using a given set of images. Unfortunately, the expense and complexity of such studies precludes their routine use. Therefore, numerical observers—algorithms that emulate human observer performance—are now widely used as surrogates for human observers.

One particular numerical observer, known as the channelized Hotelling observer (CHO) [22], has come to be widely used, particularly in nuclear medicine imaging. The CHO is a Fisher LD applied to input features obtained by applying band-pass (channel) filters to the image. These channels are inspired by the notion of receptive fields in the human visual system. Because of its principled approach to image quality evaluation, the CHO has justifiably had a major and positive impact on the field and has enjoyed tremendous popularity.

However, the CHO does not perfectly capture human-observer performance; therefore, we have proposed a new approach in which the problem of task-based image-quality assessment is viewed as a supervised-learning or system-identification problem [23]. That is, the goal is to identify the unknown human observer mapping, f (x) , between the image features in x and an observer score y that reflects the human observer’s confidence in the presence of an abnormality in the image. This relationship is learned from example data obtained from human observers; the model is then used to make predictions in new situations where no human-observer data are available.

In our work, we have thus far retained the channels used in the CHO, contained in vector x, but we feed these as inputs to a SVM f (x) , which we train to predict observer score y based on training examples (x_i, y_i ), i = 1, …, N. The resulting algorithm is called a channelized SVM (CSVM).

RESULTS

In [23], we compared the CSVM to the CHO for assessment of image quality in cardiac SPECT imaging. In this experiment, two medical physicists evaluated the defect visibility in 100 noisy images and scored their confidence of a lesion being present on a six-point scale, following a training session involving an additional 60 images. The human observers performed this task for six different choices of the smoothing filter and two different choices of the number of iterations in the OS-EM reconstruction algorithm (see Figure 7).

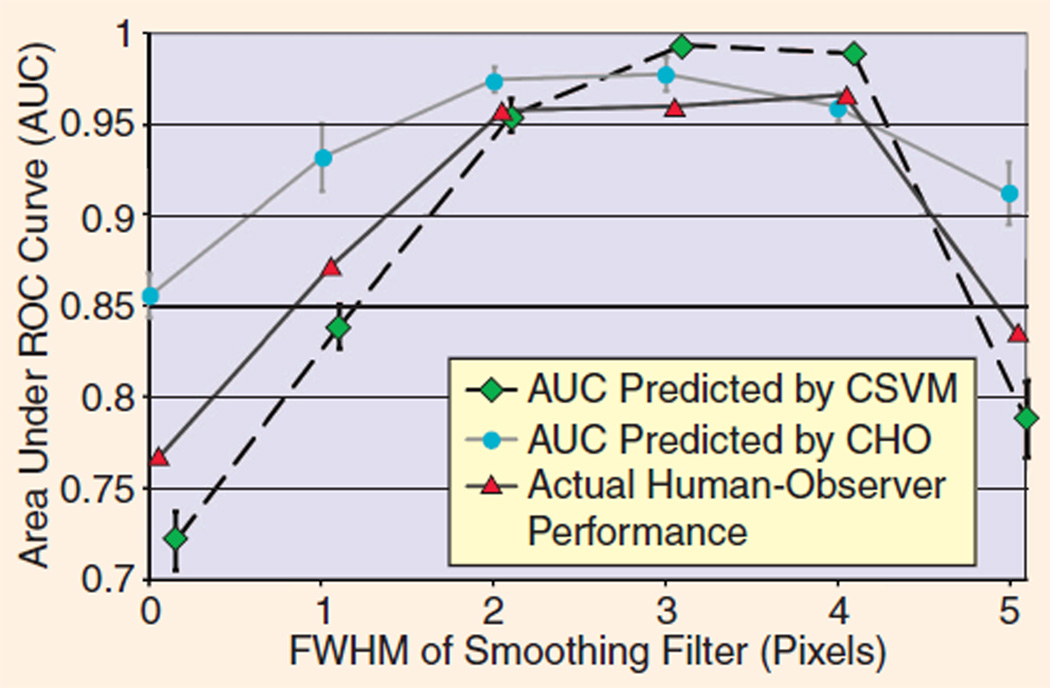
To demonstrate the generalization power of this approach, we trained both the CHO and CSVM on a broad range of images, then tested both on a different, but equally broad, range of images. Specifically, we trained both numerical observers using images for every value of the filter FWHM and five iterations of OS-EM and then tested the observers using all the images for every value of the filter FWHM with one iteration of OS-EM. The parameters of the CHO and CSVM were fully optimized to minimize generalization error measured using five-fold cross validation based on the training images only. Therefore, no test images were used in any way in the choices of the model parameters for either numerical observer. The numerical observers’ predictions of human observers’ area under the ROC curve (AUC) are compared in Figure 8 to human observers’ actual performance. In this situation, the CHO performed relatively poorly, failing to match either the shape or amplitude of the human-observer AUC curves, while the CSVM was able to produce reasonably accurate predictions of AUC in both cases. Each error bar represents the standard deviation calculated using five-fold cross validation on the testing data.

FIG 8.

Predictions of human-observer performance (AUC) by machine learning approach (CSVM) compared with conventional numerical observer (CHO). The CHO does not recognize the degree to which diagnostic performance declines at low and high levels of smoothing, an effect seen in scores along the top and bottom of Figure 7

This experiment demonstrates the potential benefit of using machine learning to make predictions rather than fixed models. Owing to the generality of its approach, machine learning can be used to make predictions of human-observer performance in many clinical tasks other than lesion detection, while CHO is specifically designed for lesion detection and is therefore less amenable to generalization.

MAPPING OF BRAIN FUNCTION

Brain mapping is concerned with the creation of spatial representations (maps) of the brain, shedding light on the roles of various brain regions in normal and disease processes. Brain mapping is an area of application that differs significantly from those we have discussed thus far in the following two principal respects: 1) in many situations, brain mapping is concerned less with the prediction outputs y than with the model f (x) itself, from which brain maps are obtained; and 2) owing to the relatively small number of data examples available in brain mapping, nonlinear models are not always preferred over simpler linear methods.

Brain mapping has been a rapidly growing field of imaging for at least 25 years. It is impossible to give a balanced survey of this field and its use of machine learning in the space available, so we will give only a brief overview.

In the 1980s, brain mapping was dominated by positron emission tomography (PET) and SPECT. The first machine-learning approaches to the analysis of functional brain images applied artificial neural networks (ANNs) to PET images of glucose metabolism [24]. However, following the discovery of the blood oxygenation level dependent (BOLD) signal in 1990 that allows regional neuronal activity to be measured indirectly, there has been explosive growth in the use of functional magnetic resonance imaging (fMRI) and related techniques [25].

The prevailing experimental and analysis paradigm in brain mapping is still based on simple, univariate general linear models (GLM) with inferential statistical tests [26], and in some instances their predictive, machine-learning equivalent, Gaussian Naïve Bayes [27]. There has been a recent surge of papers and interest in using related multivariate classification approaches, dubbed “mind reading” by some in the field. For recent reviews including a historical perspective see [28], and for an overview of the often overlooked power of simple multivariate approaches, e.g., principal component analysis and LD, applied to PET scans of disease groups, see [29], which reflects the results of more than 20 years of work on measuring covariance structures that reflect brain networks. This network theme has gained considerable momentum in the more recent fMRI brain mapping literature with a focus on measuring the so-called “default mode” brain network using pair-wise, voxel correlations [30], or seed-voxel/behavioral partial least squares (PLS) [31], independent component analysis (ICA) [32], [33], and most recently nonlinear dynamics [34] and graph theory coupled with structural scans of white-matter networks [35].

Much of our own work has focused on the question of how to evaluate and optimize performance, and how to select the best signal detector from the broad repertoire of machine learning tools available. We have particularly focused on the impact of smaller sample sizes where analytic asymptotic theory for multivariate machine learning models, if it exists, does not provide much, if any, guidance. Analysis of brain images is a highly ill-posed problem, in which there are typically tens or hundreds of thousands of voxels, but only tens or hundreds of brain scans. Therefore, this small sample limit is the most likely to be important for medical use in brain mapping.

DISCRIMINANT IMAGES AS BRAIN MAPS

To illustrate the use of machine learning in brain mapping, let us consider one type of study in which we wish to produce an image showing the regional effects of a new drug on brain function (two of the authors of this article, Wernick and Strother, conduct such analyses commercially for the pharmaceutical industry). To accomplish this, one can scan a group of N research subjects twice, once after the subject is given the new drug and once after administration of placebo. One can then analyze these 2 N images to obtain an image that describes the drug’s effect. It is hoped that this finding will describe not only this particular group of subjects but will also generalize to some broader population.

The basic idea underlying many machine-learning approaches to this problem is to treat each image as a vector in a high-dimensional space, with each component representing the value of one voxel in a scan. In this example, our data can be viewed as consisting of two classes of images: drug and placebo. To reduce dimensionality to a manageable level, and to mitigate noise, it is common to transform the data using singular value decomposition (SVD). Next, a classifier is trained to discriminate drug images from placebo images based on the dimensionality-reduced data.

In traditional pattern classification applications, the purpose of training the classifier is to make decisions about new data. Indeed, there are a growing number of examples of this in neuroimaging, for example in lie detection, or in diagnosis of disease in an individual patient. However, in many studies, the goal is simply to understand what intrinsically is different about the brain in, say, a drug and a placebo condition. In such instances, the desired information is encoded in the predictive model f (x) itself. When a linear model is used, then the desired brain map is encoded in the components of discriminant vector w, which (after projecting back from SVD space to image space) describes the salience of voxels in the brain for discrimination of drug and placebo conditions.

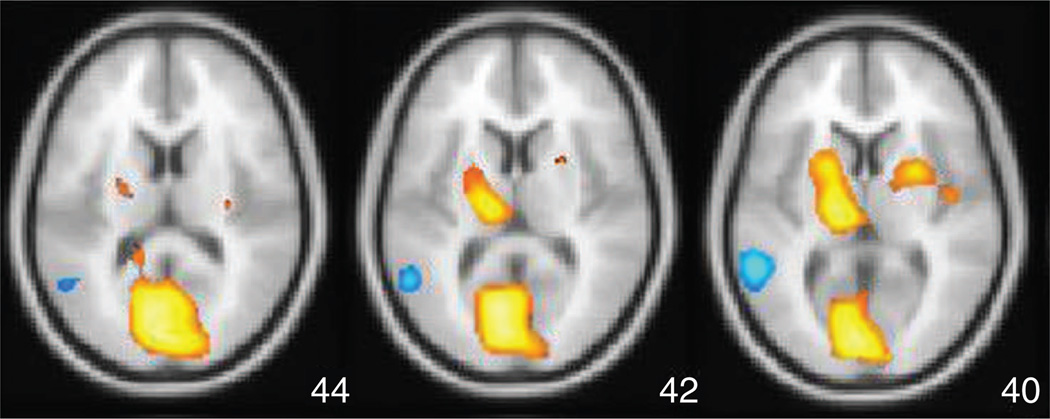
Figure 9 shows an example of such an image (which we will refer to as a spatial activation pattern) after it is thresholded and overlaid on a template structural image used to bring multiple subjects’ brains into an approximate common space. The value of each colored voxel in this image expresses the degree to which that voxel contributes to the discrimination of drug versus placebo, and this image thereby depicts the spatial distribution of effect.

FIG 9.

Spatial activation pattern in the brain, showing effect of the anxiolytic/antidespressant drug buspirone (Buspar) obtained using Fisher LD and NPAIRS split-half resampling applied to FDG-PET images for 12 subjects (data courtesy of Abiant, Inc.; analysis by Predictek, Inc.). The results show striatal activation (upper orange regions), likely due to the drug’s behavior as a dopamine D2 receptor antagonist.

Note that, in this basic introduction, we have refrained from describing a significant series of preprocessing steps that must be applied before the machine learning algorithms can be used. These are discussed at length in [36].

COMPARING MODELS, SAMPLE SIZE, AND SNR

Evaluations of data-analysis techniques have clearly illustrated that optimal tool selection depends critically on the signal and noise structure of the data at hand, and the sample size [37], [38]. For example, Figure 10 (adapted from [38]) illustrates that a simple linear model can outperform a flexible nonlinear model (in this case an ANN) until there are enough data examples to support estimation of the greater number of parameters inherent in the nonlinear model. Nevertheless, these issues are frequently ignored in the current brain mapping literature when discussing or comparing different analysis techniques.

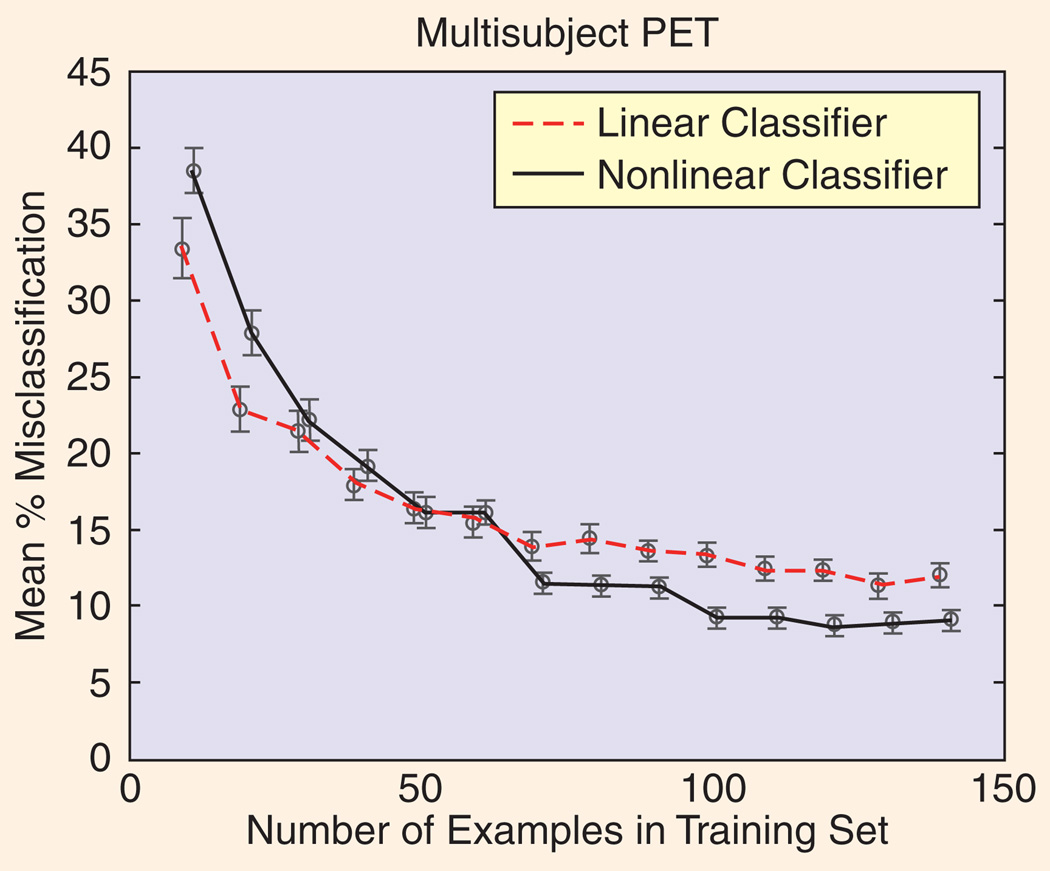
FIG 10.

These crossed learning curves (plots of classifier performance versus training set size) show that a nonlinear classifier (a neural network in this example) can be beaten by a simpler multivariate linear classifier (here, a Fisher discriminant) when the number of training examples is small. This is not unexpected, as small data sets cannot generally support complex models, however this result emphasizes the importance of resisting the temptation for researchers to use high-complexity models in every circumstance.

We have addressed the question of choosing optimal analysis procedures using simulations in [39] based on the simple phantom shown in Figure 11, assuming an experimental design similar to the drug-placebo study described earlier. We varied numerous parameters of the simulation, including number of examples per condition (from 20 to 100), and the amplitude of the activation “blobs” in the phantom (either 3% or 5% above baseline). We added spatially colored, temporally white, Gaussian noise with a standard deviation of 5% of the mean baseline value. We created three spatially distributed “networks” of blobs, and varied the correlation coefficient ρ (rho) between them (ρ = 0.0, 0.5, or 0.9) and the ratio V of their amplitude variance to the noise variance. This ratio can be thought of in analogy to dynamic range in audio, as the blob variance is a source of signal in this application, which is of particular relevance for the field’s recent focus on network detection in brain mapping. In [39], we showed that SVD by itself or followed by a LD that adapts the subspace on which it is estimated is much more sensitive to network interactions than thresholding of pair-wise correlation coefficients [40].

FIG 11.

Simulated phantom used for testing signal detection.

We have repeated and extended the earlier work of Lukic et al. using the same phantom (results shown in Figure 12). Simulations included 3% Gaussian amplitudes, with 30 baseline and 30 activation scans. The models tested include 1) single-voxel t-tests using both local (GLM-S) and spatially pooled (GLM-P) variance estimates, and classification techniques including a 2) two-class Fisher LD, 3) normalized LD (NLD), and 4) quadratic discriminant (QD). All multivariate techniques were estimated on an SVD subspace with dimension determined using optimization of Bayes’ evidence [41], as estimated in the software package MELODIC [42]. For LD and QD, the SVD basis components had length equal to their eigenvalues, and for NLD they were normalized to unit length.

FIG 12.

In (a)–(c), performance in detection of brain activation for five models, as a function of signal-to-noise variance ratio (V) and correlations (rho) among network of activated brain regions, are shown. The QD and NLD perform best, improving with strength of network (increasing V and rho), while the performance of univariate methods lags behind, and actually deteriorates as the signal strength increases.

Using the area under the ROC curve for false positives between [0.0, 0.1], signal detection was measured across the 16 voxels at the peaks of the Gaussian blobs. Even when the t-test with local variance estimates (GLM-S) was the “correct” model (i.e., V = 0.1) better detection performance was obtained using a t-test with a pooled variance estimate or adaptive, multivariate covariance-based detectors. In addition, GLM-S showed a significant drop in performance as the equal variance assumption was violated with increasing V. Variance estimation by spatially pooling (GLM-P) significantly improved signal detection and largely removed this source of model violation.

The multivariate equivalent of the GLM-S model violation is shown by the LD results where the assumption of equal within-class covariances (i.e., a common network structure for baseline and activation scans) is violated with increasing V ; only the activation scans have an off-diagonal, within-class covariance structure that increases with V . However, LD still outperforms GLM-S for all but the strongest violations of the equal covariance assumption for large rho and V [Figure 12(c)]. In the NLD method, the standard machine-learning trick of normalizing input feature variances (i.e., unit SVD basis vectors) significantly improves signal detection performance to always better than GLM-P, and largely removes the LD drop with increasing V. Finally, using the correct multivariate model that assumes different within-class covariances, a QD, further significantly improves performance to close to perfect (partial ROC area approaches 0.1). QD, as used here, represents an alternative to SVM as a solution to the problem of unequal class distributions shown in Figure 2.

The relative performance of LDs and SVM remains controversial in brain mapping with some papers claiming SVM is superior [43] and others that they are approximately equal [44], but that they respond to different input SNR structures differently as suggested by the analysis of Figure 2. Moreover, our most recent simulation results show that signal detection performance is a very strong function of the SVD basis set size and performance may be improved even further than shown in Figure 11 by using a resampled estimate of the optimal SVD subspace based on the reproducibility metric outlined below.

Our final simulation results relate to a comparison of Bayesian kernel methods with a generalized likelihood ratio test for estimating local activation in functional neuroimages. In [45], we compared spatial signal detection using the superposition of spatial Gaussian kernels with their parameters estimated from the data using a maximum a posteriori (MAP) technique based on a reversible-jump Markov-chain Monte Carlo (RJMCMC) algorithm and a RVM. RVM and RJMCMC were better signal detectors than all of the other techniques tried in [39] and achieved values of 0.80 and 0.82 for the partial area under the ROC curve. These performance values cannot be directly compared to Figure 11 as the simulation parameters were quite different. However, the RJMCMC took tens of hours to compute, even in our simple phantom, while the RVM was computed in only minutes. The relative utility of SVM, RVM, and other kernel techniques in brain mapping (e.g., kernel PCA, [28]; kernel canonical correlation analysis [46]) remains to be established

DATA-DRIVEN PERFORMANCE METRICS

In brain mapping, as in general machine-learning applications, it is very important to optimize and evaluate predictive models and to select their most salient features. These tasks must be guided by a quantitative metric of performance. Prediction accuracy often plays this role, for example to guide a greedy search procedure to select the most salient subset of voxels [26]. Some tradeoffs of such purely prediction-driven analysis approaches are discussed in [4] and [27].

Although prediction accuracy alone can be an effective metric for general machine-learning problems, neuroimaging also demands that the spatial pattern (encoded by the predictive model) be reproducibile between different groups of subjects or different scans of the same subject. Together with prediction accuracy, reproducibility turns out to be an important metric that is a very effective data-driven substitute for ROC analysis.

Strother et al. [9] proposed a novel split-half resampling framework dubbed NPAIRS, which simultaneously assesses prediction accuracy and reproducibility. The tradeoff between achievable prediction accuracy and reproducibility of the model is related to the classic tradeoff of bias and variance in estimation theory. In this application, prediction accuracy is generally gained at the expense of decreased reproducibility of the spatial patterns, and vice versa. By plotting prediction accuracy versus reproducibility as a function of some parameter (such as number of SVD basis vectors), we are able to assess the gamut of this tradeoff, in close analogy to the ROC curve, the precision-recall curve from the information retrieval field, or the bias-variance curve from statistics. We call this type of plot produced by the NPAIRS analysis a ( p, r) curve.

To compute a (p, r) curve using NPAIRS, the independent observations of the data set are split into two independent halves (e.g., across subjects): training and test sets. Prediction accuracy is obtained by applying the spatial patterns estimated in one split-half set (i.e., training) to estimate scan class labels in the other split-half set (i.e., test). The roles of the two split-half sets are then reversed so that the each set has been used once as a training set (to produce a spatial activation pattern) and once as a test set. From these results, two prediction accuracy estimates (p) are computed and averaged to obtain the overall prediction accuracy. Next, the reproducibility of the two independent spatial activation patterns is computed as the correlation (r) between all pairs of spatially aligned voxels in the two patterns. This correlation value r is directly related to the available SNR in each extracted pair of split-half patterns. If one forms a scatter plot consisting of the voxel values in one spatial pattern versus corresponding values in the other, one obtains a distribution in which the principal, or signal, axis has associated eigenvalue (1 + r) , and the uncorrelated minor, or noise, axis has eigenvalue (1 − r) . Therefore, one can define a global data set SNR metric gSNR as

$$\text{gSNR}=\sqrt{((1+r)-(1-r))/(1-r)}=\sqrt{2r/(1-r).}$$

In NPAIRS, many split-half resamplings are performed and the average, or median, of the resulting p and r distributions are recorded. This resampling approach has the benefits of smooth robust metrics obtained with the 0.632+ bootstrap [8]. Finally, a robust consensus technique is used to combine the many split-half spatial patterns into a single pattern described on a Z-score (standard normal) scale, providing a robust Z-scoring mechanism for any prediction model that produces voxel-based parameter estimates.

In [29], NPAIRS was applied to PET, and it has been also been applied to fMRI [47]–[49]. While NPAIRS may be applied to any analysis model, we have particularly focused on LDs, and more recently QDs, both built on an SVD basis. This allows us to 1) regularize the model by choosing soft (e.g., ridge) or hard thresholds on an SVD or other basis set [50], 2) maintain the link to covariance decomposition that has proven so useful in PET for elucidating network structures, and 3) produce whole-brain activation maps that enhance the likelihood of discovering new features of brain function and disease.

Figure 13 shows an example of how NPAIRS can be used to study the influence of the key parameters of an image analysis procedure, and thus permit one to make an optimal selection of these parameters. In this example, two parameters of an fMRI image analysis procedure are examined, the number of SVD basis vectors (defining model complexity) and the number of half cosines used for detrending [36]. (We will not elaborate here on details of the SVD and detrending techniques; we show this example only to illustrate how NPAIRS can in general be used to select optimal model parameters.)

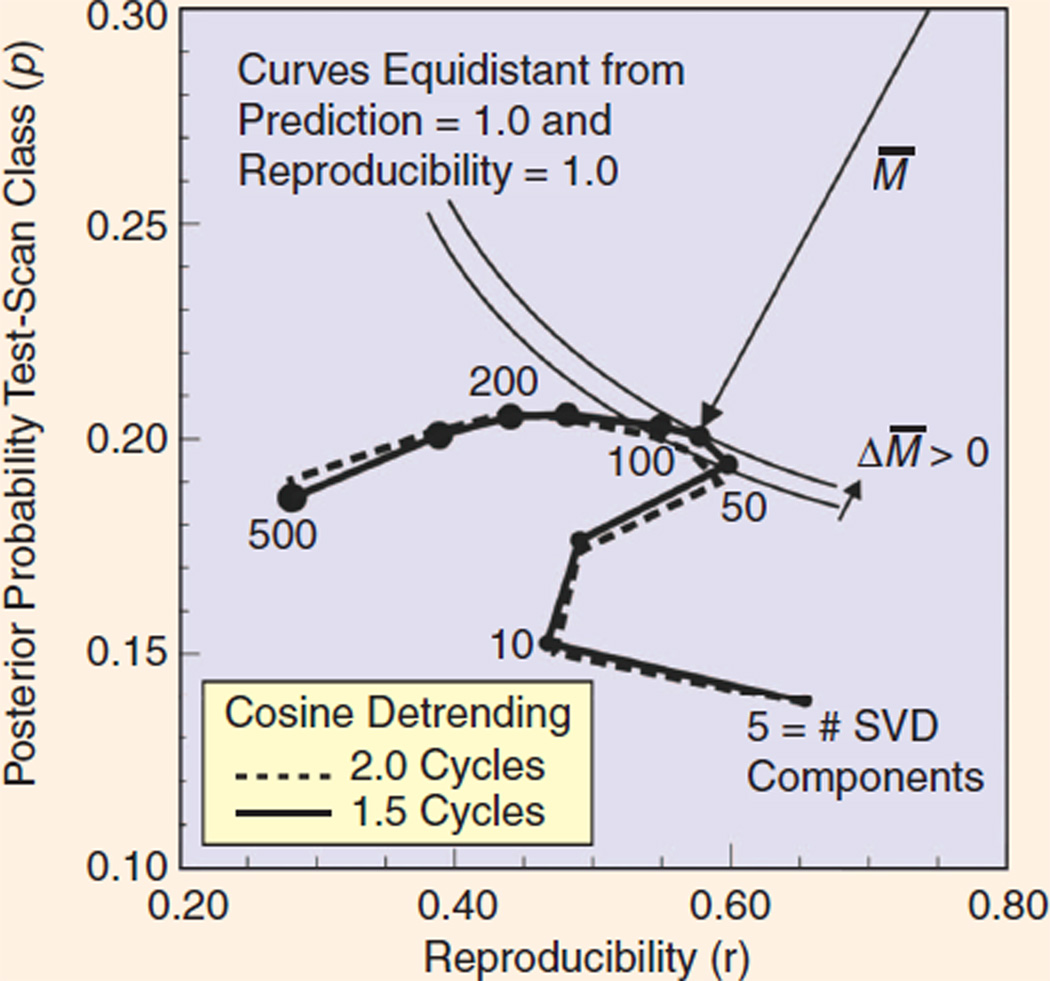
FIG 13.

In the NPAIRS framework, a prediction-reproducibility (p,r) curve shows the tradeoff between prediction accuracy (vertical axis) and reproducibility of the resulting brain map (horizontal axis). Optimal performance is achieved when the curve comes closest to the ideal point (1,1), achieving the smallest distance M̅. This provides a basis for optimizing image analysis procedures, in this example specifying the best parameters in a particular fMRI data analysis problem (number of SVD components and number of cycles in a particular cosine detrending step).

In a ( p, r ) plot, ideal performance is achieved by reaching the upper right corner of the space, where prediction accuracy (described as posterior probability in Figure 13) reaches 1.0 and reproducibility also achieves 1.0. Thus, one approach to defining the optimal choice of parameters is to determine the point at which the ( p, r) curve attains the least Euclidean distance (M̅) to the point (1,1). In this example, we see that performance [distance to (1,1)] improves, then worsens, as the number of SVD components increases. The effect of the cosine detrending parameter is weaker, but indicates that one and a half cycles is a somewhat better choice than two cycles. In this graph, the hook-shaped portion between five and ten SVD components represents reproducible artifacts that are commonplace in fMRI.

The NPAIRS analysis framework provides a very useful way to understand and optimize model performance in the challenging problem of brain mapping, and perhaps in other applications in which one is interested not only in making accurate predictions but also in producing reliable information on the factors driving these predictions.

Biographies

Miles N. Wernick (wernick@iit.edu) received the B.A. degree in physics from Northwestern University in 1983 and the Ph.D. degree in optics from the University of Rochester in 1990. In 1990, he was an NIH Postdoctoral Fellow in radiology at the University of Chicago, where he became a research associate assistant professor. In 1994, he joined the Illinois Institute of Technology, where he is currently director of the Medical Imaging Research Center and Motorola Endowed Chair Professor of Engineering in the Departments of Electrical and Computer Engineering and Biomedical Engineering. He is also president of Predictek, Inc. His research interests include medical imaging, machine learning, image processing, and optics. He is guest editor of this special issue of IEEE Signal Processing Magazine, an associate editor of IEEE Transactions on Image Processing and SPIE/IS&T Journal of Electronic Imaging, and a member of the IEEE Bioimaging and Signal Processing Technical Council.

Yongyi Yang (yy@ece.iit.edu) received the B.S.E.E. and M.S.E.E. degrees from Northern Jiaotong University, Beijing, China, in 1985 and 1988, respectively. He received the M.S. degree in applied mathematics and the Ph.D. degree in electrical engineering from the Illinois Institute of Technology (IIT), Chicago, in 1992 and 1994, respectively. He is currently a professor in the Department of Electrical and Computer Engineering at IIT, where he is with the Medical Imaging Research Center and also holds a joint appointment with the Department of Biomedical Engineering. His research interests are in signal and image processing, medical imaging, machine learning, pattern recognition, and biomedical applications. He is an associate editor of IEEE Transactions on Image Processing.

Jovan G. Brankov (brankov@iit.edu) received the diploma of electrical engineering from the University of Belgrade, Yugoslavia, in 1996. He received the M.S.E.E. and Ph.D. degrees in electrical engineering from the IIT in 1999 and 2002, respectively. He is currently an assistant professor in the Department of Electrical and Computer Engineering at IIT, where he is with the Medical Imaging Research Center. His research interests include medical imaging, image sequence processing, pattern recognition, and data mining. His current research topics include four-dimensional and five-dimensional tomographic image reconstruction methods for medical image sequences, multiple-image radiography (a new phase-sensitive imaging method), and image quality assessment based on a human-observer model. He is author/coauthor of over 80 publications and serves as ad hoc associate editor for Medical Physics.

Grigori Yourganov (gyourganov@rotman-baycrest.on.ca) received the B.S. and M.S. degrees in computer science from York University, Toronto, Canada, in 2000 and 2005, respectively. He is currently completing his Ph.D. degree in the Institute for Medical Sciences at Rotman Research Institute (University of Toronto), under the supervision of Dr. Stephen C. Strother and Dr. Randy McIntosh. His research is focused on application of multivariate analytical techniques to fMRI data.

Stephen C. Strother (sstrother@rotman-baycrest.on.ca) received the B.Sc. and M.Sc. degrees in physics and mathematics from Auckland University, New Zealand in 1976 and 1979, respectively, and a Ph.D. degree in electrical engineering from McGill University, Montreal in 1986. Since 1985, he has been a postdoctoral fellow at Memorial Sloan-Kettering Cancer Center, New York. In 1989 he joined the VA Medical Center, Minneapolis, as senior PET physicist, and the University of Minnesota where he became a professor of radiology in 2002. In 2004, he moved to Toronto as a senior scientist at the Rotman Research Institute and professor of medical biophysics at the University of Toronto, where he is also a core member of the multiinstitutional Centre for Stroke Recovery. His current research interests include neuroinformatics with a focus on machine and statistical learning techniques for optimizing PET and fMRI/MRI neuroimaging in research and clinical applications applied to the aging brain. In 2001 he cofounded Predictek, Inc., in Chicago. He is an associate editor for Human Brain Mapping.