Nonuniform sampling and non-Fourier signal processing methods in multidimensional NMR

Abstract

Beginning with the introduction of Fourier Transform NMR by Ernst and Anderson in 1966, time domain measurement of the impulse response (the free induction decay, FID) consisted of sampling the signal at a series of discrete intervals. For compatibility with the discrete Fourier transform (DFT), the intervals are kept uniform, and the Nyquist theorem dictates the largest value of the interval sufficient to avoid aliasing. With the proposal by Jeener of parametric sampling along an indirect time dimension, extension to multidimensional experiments employed the same sampling techniques used in one dimension, similarly subject to the Nyquist condition and suitable for processing via the discrete Fourier transform. The challenges of obtaining high-resolution spectral estimates from short data records using the DFT were already well understood, however. Despite techniques such as linear prediction extrapolation, the achievable resolution in the indirect dimensions is limited by practical constraints on measuring time. The advent of non-Fourier methods of spectrum analysis capable of processing nonuniformly sampled data has led to an explosion in the development of novel sampling strategies that avoid the limits on resolution and measurement time imposed by uniform sampling. The first part of this review discusses the many approaches to data sampling in multidimensional NMR, the second part highlights commonly used methods for signal processing of such data, and the review concludes with a discussion of other approaches to speeding up data acquisition in NMR.

1. Data sampling in NMR spectroscopy

Beginning with the development of Fourier Transform NMR by Richard Ernst and Weston Anderson in 1966, the measurement of NMR spectra has principally involved the measurement of the free induction decay (FID) following the application of broad-band RF pulses to the sample.¹ The FID is measured at regular intervals, and the spectrum obtained by computing the discrete Fourier transform (DFT). The accuracy of the spectrum obtained by this approach depends critically on how the data is sampled. In multidimensional NMR experiments, the constraint of uniform sampling intervals imposed by the DFT incurs substantial burdens. The advent of non-Fourier methods of spectrum analysis that do not require data sampled at uniform intervals has enabled the development of a host of nonuniform sampling strategies that circumvent the problems associated with uniform sampling. Here, we review the fundamentals of sampling, both uniform and nonuniform, in one and multiple dimensions. We then survey nonuniform sampling methods that have been applied to multidimensional NMR, and consider prospects for new developments.

1.1. Fundamentals: Sampling in One Dimension

Implicit in the definition of the complex discrete Fourier transform (DFT)

$$f_n=\frac{1}{\sqrt{N}}\sum _{k=0}^{N-1}{d}_k{e}^{-2\pi \mathit{\text{ikn}}/N}$$ (1)

is the periodicity of the spectrum, which can be seen by setting n to N in eq. (1). Thus the component at frequency n/NΔt is equivalent to (and indistinguishable from) the components at (n/NΔt) +/− (m/Δt), m= 1, 2, … This periodicity makes it possible to consider the DFT spectrum as containing only positive frequencies, with zero frequency at one edge, or containing both positive and negative frequencies with zero frequency near (but not exactly at) the middle. The equivalence of frequencies in the DFT spectrum that differ by a multiple of 1/Δt is a manifestation of the Nyquist sampling theorem, which states that in order to unambiguously determine the frequency of an oscillating signal from a set of uniformly spaced samples, the sampling interval must be at least 1/Δt. (For additional details of the DFT and its application in NMR, see Hoch and Stern²).

In eq. (1) the data samples and DFT spectrum are both complex. Implicit in this formulation is that two orthogonal components of the signal are sampled at the same time, referred to as simultaneous quadrature detection. Most modern NMR spectrometers are capable of simultaneous quadrature detection, but early instruments had a single detector, so only a single component of the signal could be sampled at a time. With so-called single-phase detection, the sign of the frequency is indeterminate. Consequently the carrier frequency must be placed at one edge of the spectral region and the data must be sampled at 1/2Δt to unambiguously determine the frequencies of signals spanning a bandwidth 1/Δt.

The detection of two orthogonal components permits the sign ambiguity to be resolved while sampling at a rate of 1/Δt. This approach, called phase-sensitive or quadrature detection, enables the carrier to be placed at the center of the spectrum. Simultaneous quadrature detection was originally and for decades achieved by mixing a detected sinusoidal signal oscillating at a reference frequency and the same signal phase shifted by 90° degrees. The output of the phase-sensitive detector is two signals, differing in phase by 90°, containing frequency components of the original signal oscillating at the sum and difference of the reference frequency with the original frequencies. The sum frequencies were then typically filtered out using a low-pass filter. While quadrature detection enables the sign of frequencies to be determined unambiguously while sampling at 1/Δt, it requires just as many data samples as single-phase detection since it samples the signal twice at each sampled interval, whereas single-phase detection samples one at each sampled interval. In modern spectrometers, simultaneous quadrature is eschewed in favor of very high-frequency single-phase sampling. The data are down-sampled, filtered, and processed to emulate the results of simultaneous quadrature detection: a complex data record with the reference carrier frequency in the middle of the spectral range and an interval between samples corresponding to the chosen bandwidth (rather than the sampling interval of the very fast analog-to-digital converter). With some instruments the processing algorithms employed are considered proprietary and the raw primary are not saved, precluding the use of more modern signal processing algorithms or accurate correction of potential artifacts.

Oversampling

The Nyquist theorem places a lower bound on the sampling rate, but what about sampling faster? It turns out that sampling faster than the reciprocal of the spectral width, called oversampling, can provide some benefits. One is that the oversampling increases the dynamic range, the ratio between the largest and smallest signals that can be detected.^3,4 Analog-to-digital (A/D) converters employed in most NMR spectrometers represent the converted signal with fixed binary precision, e.g. 14 or 16 bits. A 16-bit A/D converter can represent signed integers between −32768 and +32767. Oversampling by a factor of n effectively increases the dynamic range by √n. Another benefit of oversampling is that it prevents certain sources of noise that are NOT band-limited to the same extent as the systematic (NMR) signals from being aliased into the spectral window.

How long should one sample?

For signals that are stationary, that is their behavior doesn’t change with time, the longer you sample the better the sensitivity and accuracy. For normally-distributed random noise, the signal-to-noise-ratio (SNR) improves with the square root of the number of samples. NMR signals are rarely stationary, however, and the signal envelope typically decays exponentially in time. For decaying signals, there invariably comes a time when collecting additional samples is counter-productive, because the amplitude of the signal has diminished below the amplitude of the noise, and additional sampling only serves to reduce SNR. The time 1.3/R₂, where R₂ is the decay rate of the signal, is the point of diminishing returns, beyond which additional data collection results in reduced sensitivity⁵. It makes sense to sample at least this long in order to optimize the sensitivity per unit time of an experiment. But limiting sampling to 1.3/R₂ results in a compromise. That’s because the ability to distinguish signals that have similar frequencies increases the longer one samples. Intuitively this makes sense because the longer two signals with different frequencies evolve, the less synchronous their oscillations become. Thus resolution, the ability to distinguish closely-spaced frequency components, is largely related to the longest evolution time sampled. In general, however, determination of the optimal maximum evolution time involves tradeoffs that will depend on many factors, including sample characteristics and the nature of the experiment being performed. Some of these factors are considered below.

1.2. Sampling in Multiple Dimensions

While the FT-NMR experiment of Ernst and Anderson was the seminal development behind all of modern NMR spectroscopy, it wasn’t until 1971 that Jean Jeener proposed a strategy for parametric sampling of a virtual or indirect time dimension that formed the basis for modern multidimensional NMR⁶, including applications to magnetic resonance imaging (MRI). In the simplest realization, an indirect time dimension can be defined as the time between two RF pulses applied in an NMR experiment. The FID is recorded subsequent to the second pulse, and because it evolves in real time, its evolution is said to occur in the acquisition dimension. A single experiment can only be conducted using a given value of the time interval between pulses, but the indirect time dimension can be explored by repeating the experiment using different values of the time delay. When the values of the time delay are systematically varied using a fixed sampling interval, the resulting spectrum as a function of the time interval can be computed using the DFT along the columns of the two-dimensional data matrix, with rows corresponding to samples in the acquisition dimension and columns the indirect dimension. Generalization of the Jeener principle to an arbitrary number of dimensions is straightforward, limited only by the imagination of the spectroscopist and the ability of the spin system to maintain coherence over an increasingly lengthy sequence of RF pulses and indirect evolution times.

Quadrature detection in multiple dimensions

Left ambiguous in the discussion above of multidimensional NMR experiments is the problem of frequency sign discrimination in the indirect dimensions. Because the indirect dimensions are sampled parametrically, i.e. each indirect evolution time is sampled via a separate experiment, the possibility of simultaneous quadrature detection is not available. Quadrature detection in the indirect dimension of a two-dimensional experiment nonetheless can be accomplished by using two experiments for each indirect evolution time to determine two orthogonal responses. This approach was first described by States, Haberkorn, and Ruben, and is frequently referred to as the States method⁷. Alternatively, oversampling could be used by sampling at twice the Nyquist frequency while rotating the detector phase through 0°, 90°, 180°, and 270°, an approach called time-proportional phase incrementation (TPPI)⁸. A hybrid approach is referred to as States-TPPI.⁹ Processing of States-TPPI sampling is performed using a complex DFT, just as for States sampling, while TPPI employs a real DFT.

Sampling-limited regime

An implication of the Jeener strategy for multidimensional experiments is that the length of time required to conduct a multidimensional experiment is directly proportional to the total number of indirect time samples (times two for each indirect dimension if States or States-TPPI sampling is used). In experiments that permit the spin system to return close to equilibrium by waiting on the order of T₁ before performing another experiment, sampling along the acquisition dimension effectively incurs no time cost. Sampling to the Rovnyak limit¹⁰ (1.3/R₂, or 1.3×T₂*) in the indirect dimensions, however, places a substantial burden on data collection, even for experiments on proteins with relatively short relaxation times. Thus a three dimensional experiment for a 20 kDa protein at 14 Tesla (600 MHz for ¹H) exploring ¹³C and ¹⁵N frequencies in the indirect dimensions would require 2.6 days in order to sample to 1.3×T₂* in both indirect dimensions. A comparable four-dimensional experiment with two ¹³C (aliphatic and carbonyl) and one ¹⁵N indirect dimensions would require 137 days. As a practical matter, multidimensional NMR experiments rarely exceed a week, as superconducting magnets typically require cryogen refill on a weekly basis. Thus, multidimensional experiments rarely achieve the full potential resolution afforded by superconducting magnets. The problem becomes more acute at very high magnetic fields. The time required for data collection in a multidimensional experiment to achieve fixed maximum evolution times in the indirect dimensions increases in proportion to the magnetic field raised to the power of the number of indirect dimensions. The same four-dimensional protein NMR experiment mentioned above but performed at 21.4 T (900 MHz for ¹H), sampled to 1.3×T₂*, would require about 320 days.

By reducing the sampling requirements, nonuniform sampling (NUS) approaches have made it possible to conduct high-resolution 4D experiments that would be impractical using uniform sampling. In its most general form, NUS refers to any sampling scheme that does not employ a uniform sampling interval. The sampling can occur at completely arbitrary times, however the classes of NUS that have been mainly used in multidimensional NMR typically correspond either to a subset of the uniformly-spaced samples or to uniform sampling along radial vectors in time. These approaches are called on-grid and off-grid NUS, respectively, and are described in greater detail below. The most important characteristic of any NUS approach is that it enables sampling to long evolution times without requiring the number of samples overall that would be required by uniform sampling.

While there are methods of spectrum analysis capable of super-resolution, that is, methods that can achieve resolution greater than 1/t_max, the most common ones, (e.g. linear prediction (LP) extrapolation) have substantial drawbacks. LP extrapolation and related parametric methods that assume exponential decay of the signal can exhibit subtle frequency bias when the signal decay deviates from the ideal¹¹. This bias can have detrimental consequences for applications that require the determination of small frequency differences, such as determination of residual dipolar couplings (RDCs).

Sensitivity-limited regime

While the majority of extant applications of NUS in multidimensional NMR have focused on achieving high resolution with lower sampling requirements than those posed by uniform sampling, it is possible to utilize NUS to increase sensitivity per unit measuring time. This notion has not been without controversy, because the nonlinearities inherent in most of the methods of spectrum analysis employed with NUS complicate the validation of gains in SNR as true gains in sensitivity.¹² A number of investigators have turned their attention to this problem, notably Wagner¹³ and colleagues and Rovnyak and colleagues.^14,15 Theoretical and empirical investigations of the attainable sensitivity improvements with NUS indicate that gains on the order of two-fold over uniform sampling for an equivalent time are achievable for exponentially decaying signals.^5,14 This improvement at no time cost contrasts with the four-fold increase in signal averaging that would be required to achieve the same improvement in SNR.

1.3. “DFT” of NUS data and point-spread functions

From the definition of the DFT, it is clear that the Fourier sum can be modified by evaluating the summand at arbitrary frequencies, rather than at uniformly spaced frequencies. Kozminksi and colleagues have proposed this approach for computing frequency spectra of NUS data¹⁶, however strictly speaking it no longer is properly called a Fourier transformation of the NUS data. Consider the special case where the summand in eq. 1 is evaluated for a subset of the normal regularly-spaced time intervals. An important characteristic of the DFT is the orthogonality of the basis functions (the complex exponentials),

$$\sum _{n=0}^{N-1}{e}^{-2\pi i(k-k\prime )n/N}=0,k\ne k\prime$$ (2)

When the summation is carried out over a subset of the time intervals, that is, some of the values of n indicated by the sum in eq. 2 are left out, the complex exponentials are no longer orthogonal. A consequence is that frequency components in the signal interfere with one another when the sampling is nonuniform (see also section 2.5.1).

Consider now NUS data sampled at the same subset of uniformly spaced times, but supplemented by the value zero for those times from the uniformly-spaced set that are not sampled. Clearly the DFT can be applied to this zero-augmented data, but it is not the same as “applying the DFT to NUS data”. It is a subtle distinction, but an important one. What is frequently referred to as the DFT spectrum of NUS data is not the spectrum of the NUS data, but the spectrum of the zero-augmented data. The differences between the DFT of the zero-augmented data and the spectrum of the signal are mainly the result of the choice of sampled times, and hence are called sampling artifacts. While the DFT of zero-augmented data is not the spectrum we seek, it can sometimes be a useful approximation if the sampled times are chosen carefully to diminish the sampling artifacts.

The application of the DFT to NUS data has parallels in the problem of numerical quadrature on an irregular mesh, or evaluating an integral on a set of irregularly-spaced points¹⁷. The accuracy of the integral estimated from discrete samples is typically improved by judicious choice of the sample points, or pivots, and by weighting the value of the function being integrated at each of the pivots. For pivots (sampling schedules) that can be described analytically, the weights correspond to the Jacobian for the transformation between coordinate systems (as for the polar FT, discussed below). For sampling schemes that cannot be described analytically, for example those given with a random distribution, the Voronoi area (in two dimensions; the Voronoi volume in three dimensions, etc.) can be used to estimate the appropriate weights¹⁸. The Voronoi area is the area occupied by the set of points around each pivot that are closer to that pivot than to any other pivot in the NUS set.

Under certain conditions the relationship between the DFT of the zero-augmented NUS data and the true spectrum has a particularly simple form. If the sampling is restricted to the uniformly-spaced Nyquist grid (also referred to as the Cartesian sampling grid) and there exists a real-valued sampling function with the property that when it multiplies a uniformly sampled data vector, element-wise (i.e. the Hadamard product of the data and sampling vectors), resulting in the zero-augmented NUS data vector, then the DFT of the zero-augmented NUS data is the convolution of the DFT spectrum of the uniformly sampled data with the DFT of the sampling vector. The sampling vector, or sampling function, has the value 1 for times that are sampled and zero for times that are not sampled. The DFT of the sampling function is variously called the point-spread function (PSF), the impulse response, or the sampling spectrum.

The PSF provides insight into the locations and magnitudes of sampling artifacts that result from NUS, and it can have an arbitrary number of dimensions, corresponding to the number of dimensions in which NUS is applied. The PSF typically consists of a main central component at zero frequency, with smaller non-zero frequency components. Because the PSF enters into the DFT of the zero-augmented spectrum through convolution, each non-zero frequency component of the PSF will give rise to a sampling artifact for each component in the signal spectrum, with positions relative to the signal components that are the same as the relationship of the satellite peaks in the PSF. The amplitudes of the sampling artifacts will be proportional to the amplitude of the signal component and the relative height of the satellite peaks in the PSF. Thus the largest sampling artifacts will arise from the largest-amplitude components of the signal spectrum. The effective dynamic range (ratio between the magnitude of the largest and smallest signal component that can be unambiguously identified) of the DFT spectrum of the zero-augmented data can be directly estimated from the PSF for a sampling scheme as the ratio between the amplitude of the largest non-zero frequency component to the amplitude of the zero-frequency component, called the peak-to-sidelobe ratio (PSR).¹⁹ Note, however, that this does not account for interference between artifacts produced by signals at different frequencies.

The simple relationship between the DFT spectrum of zero-augmented NUS data and the DFT spectrum of the corresponding uniformly-sampled data holds as long as all the quadrature components are sampled for a given set of indirect evolution times. If they are not all sampled, the sampling function is complex, and the relationship between the DFT of the NUS data, the DFT of the sampling function, and the true spectrum is no longer a simple convolution, but a set of convolutions¹⁹.

1.4. Nonuniform sampling: A brief history

The Accordion

It was recognized soon after the development of multidimensional NMR that one way to reduce sampling requirements in multidimensional NMR is to avoid collecting the entire Nyquist grid in the indirect time dimensions. The principal challenge to this idea was that methods for computing the multidimensional spectrum from nonuniformly sampled data were not widely available. In 1981 Bodenhausen and Ernst introduced a means of avoiding the sampling constraints associated with uniform parametric sampling of two indirect dimensions of three-dimensional experiments, while also avoiding the need to compute a multidimensional spectrum from an incomplete data matrix, by coupling the two indirect evolution times²⁰. By incrementing the evolution times in concert, sampling occurs along a radial vector in t₁–t₂, with a slope given by the ratio of the increments applied along each dimension. This effectively creates an aggregate evolution time t = t₁ + α*t₂ that is sampled uniformly, and thus the DFT can be applied to determine the frequency spectrum. According to the projection - cross-section theorem²¹, this spectrum is the projection of the full t₁–t₂ spectrum onto a vector with angle α in the f₁–f₂ plane. Bodenhausen and Ernst referred to this as an “accordion” experiment. Although they did not propose reconstruction of the full f₁–f₂ spectrum from multiple projections, they did discuss the use of multiple projections for characterizing the corresponding f₁–f₂ spectrum, and thus the accordion experiment is the precursor to more recent radial sampling methods that are discussed below. Because the coupling of evolution times effectively combines dimensions, the accordion experiment is an example of a reduced dimensionality (RD) experiment (discussed below).

Random sampling

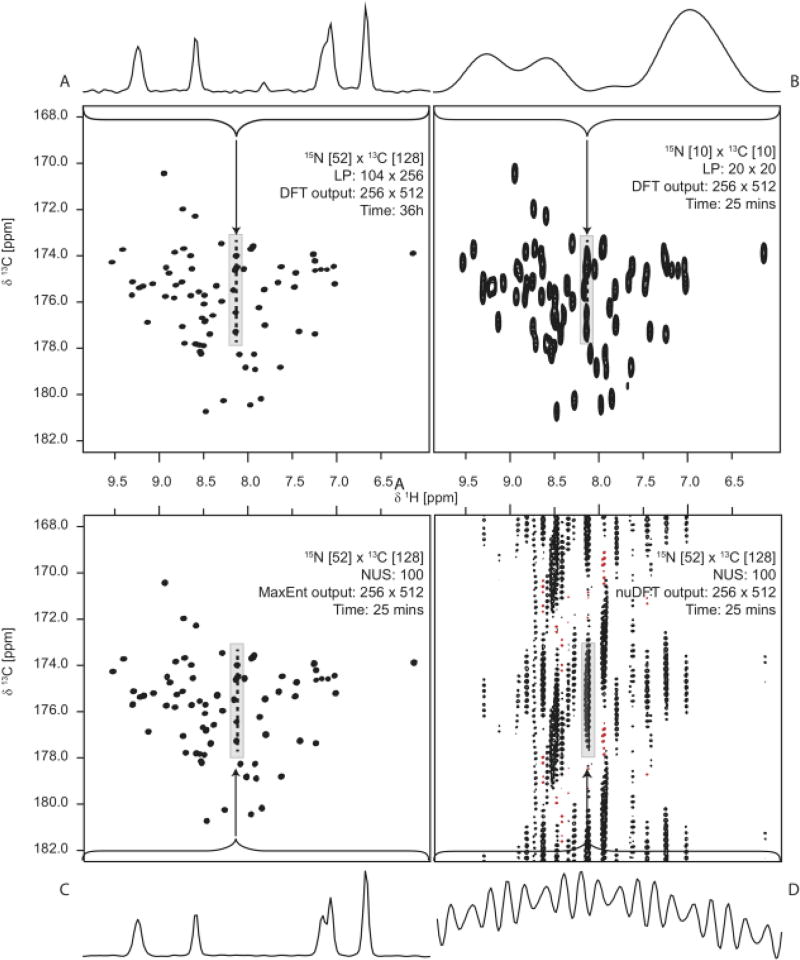
The 3D accordion experiment has much lower sampling requirements because it avoids sampling the Cartesian grid of (t₁, t₂) values that must be sampled in order to utilize the DFT to compute the spectrum along both t₁ and t₂. A more general approach is to eschew regular sampling altogether. A consequence of this approach is that one cannot utilize the DFT to compute the spectrum, so some alternative method capable of utilizing nonuniformly sampled data must be employed. In seminal work, Laue and collaborators introduced the use of maximum entropy (MaxEnt) reconstruction to compute the frequency spectrum from nonuniformly sampled data corresponding to a subset of samples from the Cartesian grid.²² While the combination of non-uniform sampling and MaxEnt reconstruction provided high-resolution spectra with dramatic reductions in experiment time, the approach was not widely adopted, no doubt because neither MaxEnt reconstruction nor nonuniform sampling (NUS) was highly intuitive. Nevertheless, a small cadre of investigators continued to explore novel NUS schemes in conjunction with MaxEnt reconstruction throughout the 1990’s.

The NUS explosion

Since the turn of the 21^st century, there has been a great deal of effort to develop novel NUS strategies for multidimensional NMR. The growing interest in NUS is largely attributable to the development by Freeman and Kupče of a method employing back-projection reconstruction (BPR) to obtain three-dimensional spectra from a series of two-dimensional projections, in analogy with computer-aided tomography (CAT).²³ Although connections between BPR and the approach of Laue et al.²² or RD and other radial sampling methods (e.g. G-Transform FT²⁴) were not initially recognized, the connections were later demonstrated by using MaxEnt to reconstruct 3D spectra from a series of radially-sampled experiments²⁵. The realization that all these fast methods of data collection and spectrum reconstruction belong to a larger class of NUS approaches ignited the search for optimal sampling strategies. Two persistent themes have been the importance of irregularity or randomness in the choice of sampling times to minimize sampling artifacts, and the importance of sampling more frequently when the signal is strong to bolster sensitivity. Approaches involving various analytic sampling schemes (triangular, concentric rings, spirals), as well as pseudo-random distributions (Poisson gap) have been described. These will be considered after first discussing some characteristics of NUS that all these approaches share.

1.5. General aspects of nonuniform sampling

On-grid vs. off-grid sampling

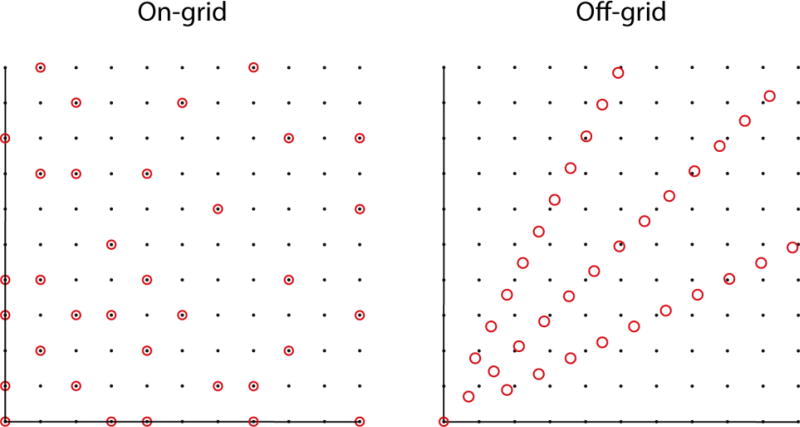
NUS schemes are sometimes characterized as on-grid or off-grid. Schemes that sample a subset of the evolution times normally sampled using uniform sampling at the Nyquist rate (or faster) are called on-grid. In schemes such as radial, spiral or concentric ring, the samples do not fall on the same Cartesian grid (see also Fig 6). As pointed out by Bretthorst,^26,27 however, one can define a Cartesian grid with spacing determined by the precision with which evolution times are specified. Alternatively, “off grid” sampling schemes can be approximated by “aliasing” (this time in the computer graphics sense) the evolution times onto a Nyquist grid, without greatly impacting the sampling artifacts.²⁵

Figure 6.

Sampling grid showing on- and off-grid sampling of the same number of points (circles). The off-grid samples are according to radial sampling and the on-grid samples are distributed randomly. The distances between the radial points are sufficient to reconstruct the same spectral window as the underlying grid (black dots) without aliasing.

Bandwidth and aliasing

Bretthorst was the first to carefully consider the implications of NUS for bandwidth and aliasing^27,28. Among the major points Bretthorst raises is that sampling artifacts accompanying NUS can be viewed as aliases. Consider the special case of sampling every other point of the Nyquist grid. This would effectively reduce the spectral window and result in perfect aliases such that a given signal would appear at its true frequency and again at a frequency shifted by the effective bandwidth (both with the same amplitude). If the sample points are now distributed in a progressively more random distribution, the intensity of the aliased peak is reduced whilst lower amplitude artifacts appear at different frequencies, making it possible to distinguish which of the two initial signals is the true signal and which is the aliasing artifact.

Since sampling artifacts are aliases, then they can be diminished by increasing the effective bandwidth. One way to do this is to decrease the greatest common divisor (GCD) of the sampled times.²⁹ The GCD need not correspond to the spacing of the underlying grid. Introducing irregularity is one way to decrease the GCD to the size of the grid, and this helps to explain the usefulness of randomness for reducing artifacts from nonuniform sampling schemes.

Another way to increase the effective bandwidth is to sample from an oversampled grid. We discussed earlier that oversampling can benefit uniform sampling approaches by increasing the dynamic range. When employed with NUS, oversampling has the effect of shifting sampling artifacts out of the original spectral window³⁰.

1.6. An abundance of sampling schemes

While the efficacy of a particular sampling scheme depends on a host of factors, including the nature of the signal being sampled, the PSF provides a useful first-order tool for comparing sampling schedules a priori. Fig. 1 illustrates examples of several common two-dimensional NUS schemes, together with PSFs computed for varying levels of sampling coverage (30%, 10%, and 5%) of the underlying uniform grid. Some of the schemes are off-grid schemes, but they are approximated here by mapping onto a uniform grid. The PSF gives an indication of the distribution and magnitude of sampling artifacts for a given sampling scheme; schemes with PSFs that have very low values other than the central component give rise to weaker artifacts. Of course the PSF alone does not tell the whole story, because it does not address relative sensitivity. For example, while the random schedule has a PSF with very weak side-lobes, and gives rise to fewer artifacts than a radial sampling scheme for the same level of coverage, it has lower sensitivity for exponentially decaying sinusoids than a radial scheme (which concentrates more samples at short evolution times where the signal is strongest). Thus more than one metric is needed to assess the relative performance of different sampling schemes.

Figure 1.

Radial, Poisson gap, random, and exponentially biased sampling (envelope-matched sampling, EMS) schemes (left column) for 30% sampling coverage of the underlying Nyquist grid, and corresponding point spread functions (PSFs) for 30%, 10%, and 5% sampling coverage (left to right). The intensity scale for the PSFs is shown on the right. The central (zero frequency) component for random sampling is so sharp as to be barely visible. Adapted from Mobli et al.³¹.

Random and biased random sampling

Exponentially-biased random sampling was the first general NUS approach applied to multidimensional NMR.²² By analogy with matched filter apodization (which was first applied in NMR by Ernst, and maximizes the SNR of the uniformly-sampled DFT spectrum), Laue and colleagues reasoned that tailoring NUS so that the signal is sampled more frequently at short times, where the signal is strong, and less frequently when the signal is weak, would similarly improve SNR. They applied an exponential bias to match the decay rate of the signal envelope; we refer to this as envelope-matched sampling (EMS). Generalizations of the approach to sine-modulated signals, where the signal is small at the beginning, and constant-time experiments, where the signal envelope does not decay, were described by Schmieder et al.^32,33 In principal EMS can be adapted to finer and finer details of the signal, for example if frequencies are know a priori (see beat-matched sampling below).

Triangular

Somewhat analogous to the rationale behind exponentially-biased sampling, Delsuc and colleagues employed triangular sampling in two time dimensions to capture the strongest part of a two-dimensional signal³⁴. The approach is easily generalized to arbitrary dimension.

Radial

Radial sampling results when the incrementation of evolution times is coupled, and is the approach employed by GFT²⁴, RD³⁵, and BPR²³ methods. When a multidimensional spectrum is computed from a set of radial samples (e.g. BPR, radial FT³⁶, MaxEnt), the radial sampling vectors are chosen to span orientations from 0° to 90° at regular intervals (0°, 45° and 90° for 3 projections etc.). When the multidimensional spectrum is not reconstructed, but instead the individual one-dimensional spectra (corresponding to projected cross sections through the multidimensional spectrum) are analyzed separately, the sampling angles are sometimes determined using a knowledge-based approach (HIFI, APSY^37,38). Prior knowledge about chemical shift distributions in proteins is employed to sequentially select radial vectors to minimize the likelihood of overlap in the projected cross-section.

Concentric rings

Coggins and Zhou introduced the concept of concentric ring sampling (CRS), and showed that radial sampling is a special case of CRS³⁶. They showed that the DFT could be adapted to CRS (and radial sampling) by changing to polar coordinates from Cartesian coordinates (essentially by introducing the Jacobian for the coordinate transformation as the weighting factor). Optimized CRS that linearly increases the number of samples in a ring as the radius increases and incorporates randomness was shown to provide resolution comparable to uniform sampling for the same measurement time, but with fewer sampling artifacts than radial sampling. Coggins and Zhou also showed that the discrete polar FT is equivalent to weighted back-projection reconstruction.³⁹

Beat-matched sampling

The concept of matching the sampling density to the signal envelope, in order to sample most frequently when the signal is strong and less frequently when it is weak, can be extended to match finer details of the signal. For example, a signal containing two strong frequency components will exhibit beats in the time domain signal separated by the reciprocal of the frequency difference between the components. As the signal becomes more complex, with more frequency components, more beats will occur, corresponding to frequency differences between the various components. If one knows a priori the expected frequencies of the signal components, one can predict the locations of the beats (and nulls), and tailor the sampling accordingly. The procedure is entirely analogous to EMS, except that the sampling density is matched to the fine detail of predicted time-domain data, not just the signal envelope. We refer to this approach as beat-matched sampling (BMS). Possible applications where the frequencies are known include relaxation experiments, and multidimensional experiments in which scout scans or complementary experiments provide knowledge of the frequencies. In practice, BMS sampling schedules appear similar to EMS (e.g. exponentially biased) schedules, however they tend to be less robust, as small difference in noise level or small frequency shifts can have pronounced effects on the locations of beats or nulls in the signal⁴⁰.

Poisson gap sampling

It has been suggested that the distribution of the gaps in a sampling schedule is also important,^41,42 which has led to the development of schedules optimized to be random yet with a non-Gaussian distributions. In Poisson gap sampling this is achieved by adapting an idea employed in computer graphics, where objects are distributed randomly whilst avoiding long gaps between objects. Similar distributions can be generated using other approaches, for example quasi-random (e.g. Sobolev) sequences⁴³. A particularly useful property of Poisson gap sampling schedules is that they show less variation when randomly selecting schedules from the Poisson distribution than other sampling schemes. A potential weakness of Poisson gap sampling, however, is that the minimum distance between samples must not be too small, otherwise aliasing can become significant.

Burst sampling

In burst or burst-mode sampling, short high-rate bursts are separated by stretches with no sampling. It effectively minimizes the number of large gaps, while ensuring that samples are spaced at the minimal spacing when sub-sampling from a grid. Burst sampling has found application in commercial spectrum analyzers and communications gear. In contrast to Poisson gap sampling, burst sampling ensures that most samples are separated by the grid spacing to suppress aliasing²⁹.

Nonuniform averaging

The concept of biasing the sampling distribution to mirror the expected signal envelope (e.g. EMS or BMS) can be applied to uniform sampling by varying the amount of signal averaging performed for each sample. This can be useful in contexts where a significant number of transients must be averaged to obtain sufficient sensitivity. An early application of this idea to NMR employed uniform sampling with nonuniform averaging, and computed the multidimensional DFT spectrum after first normalizing each FID by dividing by the number of transients summed at each indirect evolution time⁴⁴. Although the results of this approach are qualitatively reasonable provided that the SNR is not too low, a flaw in the approach is that noise will not be properly weighted. A solution is to employ a method where appropriate statistical weights can be applied to each FID, e.g. MaxEnt or maximum likelihood reconstruction⁴⁵. More generally, the idea of nonuniform averaging can also be applied to NUS.

Random phase detection

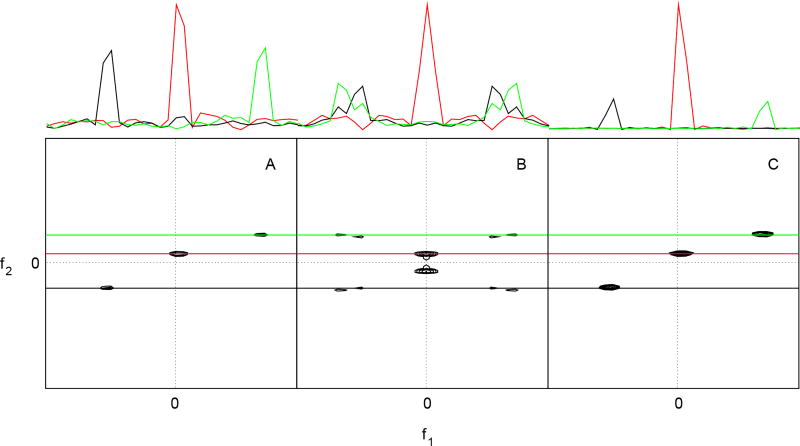
We’ve seen how NUS artifacts are a manifestation of aliasing, and how randomization can mitigate the extent of aliasing. There is another context in which aliasing appears in NMR, and that is determining the signs of frequency components (i.e. the direction of rotation of the magnetization). As discussed earlier the approach widely used in NMR to resolve this ambiguity is to simultaneously detect two orthogonal phases (simultaneous quadrature detection). Single-phase detection using uniform sampling with random quadrature phase (random phase detection, RPD) is able to resolve the frequency sign ambiguity without oversampling, as shown in Fig. 2⁴⁶. This results in a factor of two reduction in the number of samples required, compared to quadrature or TPPI detection methods, for each indirect dimension of a multidimensional experiment. For experiments not employing quadrature or TPPI detection, it provides a factor of two increase in resolution for each dimension.

Figure 2.

Two-dimensional cross-sections from a four-dimensional N,C-NOESY spectrum, obtained from (A) uniformly sampled hypercomplex (States-Haberkorn-Ruben) data, (B) real values only in the indirect dimensions, and (C) using random phase detection. One-dimensional cross-sections at the frequencies depicted by colored lines crossing the contour plots are depicted at the top. Reprinted with permission from Maciejewski et al. (2011).⁴⁶

Optimal sampling?

Any sampling scheme, whether uniform or nonuniform, can be characterized by its effective bandwidth, dynamic range, resolution, sensitivity, and number of samples. Some of these metrics are closely related, and it is not possible to optimize all of them simultaneously. For example, minimizing the total number of samples (and thus the experiment time) invariably increases the magnitudes of sampling artifacts. Furthermore, a sampling scheme that is optimal for one signal will not necessarily be optimal for a signal containing frequency components with different characteristics. Thus the design of efficient sampling schemes involves tradeoffs. Simply put, no single NUS scheme will be best suited for all experiments. However, if a particular metric for quantifying the quality of a sampling scheme is defined it is possible to optimize a given sampling scheme by random search methods.^47,48 Peak-to-sidelobe (PSR) ratio (the ratio of the intensity of the zero-frequency to the intensity of the largest non-zero frequency component) of the PSF is one useful metric.⁴⁹ While a high PSR correlates with low amplitude sampling artifacts it does not reflect the overall distribution of artifacts.¹⁴ Thus the challenge remains to define such a metric for spectral quality that would be universally applicable.

The use of nonuniform sampling in all its guises is transforming the practice of multidimensional NMR, most importantly by lifting the sampling-limited barrier to obtaining the potential resolution in indirect dimensions afforded by ultra high-field magnets. Nonuniform sampling is also beginning to have tremendous impact in magnetic resonance imaging, where even small reductions in the time required to collect an image can have tremendous clinical impact. For all of the successes using NUS, our understanding of how to design optimal sampling schemes remains incomplete. A major limitation is that we lack a comprehensive theory able to predict the performance of a given NUS scheme a priori. This in turn is related to the absence of a consensus on performance metrics, i.e., measures of spectral quality. Ask any three NMR spectroscopists to quantify the quality of a spectrum and you are likely to get three different answers. Further advances in NUS will be enabled by the development of robust, shared metrics. An additional hurdle has been the absence of a common set of test or reference data, which is necessary for critical comparison of competing approaches. Once shared metrics and reference data are established, we anticipate rapid additional improvements in the design and application of NUS to multidimensional NMR spectroscopy.

2. Signal processing methods in NMR spectroscopy

In the first part we discussed how different sampling strategies can lead to vastly different spectral representations. But what about the influence of the methods used to process the NUS data? Ever since the introduction of FT-NMR in the mid 1960s NMR spectroscopists have been investigating methods of accurately and efficiently transforming the measured time series data into a frequency spectrum.¹ Early efforts were aimed at overcoming some of the shortcomings inherent in the DFT and achieving efficient computation and robust application to noisy signals.⁵⁰ The introduction of two-dimensional (2D) NMR in the 1970s introduced a separate problem, as these experiments were very time-consuming.⁵¹ Research was therefore focused on reducing the number of time samples required in 2D experiments, resulting in approaches that could speed up data acquisition by a factor of 2–4 (see Hoch et al.⁵² and references therein). The poor SNR achievable at the time proved a severe limitation to further progress. In the 1990s, however, several key advances resulted in a dramatic boost in the sensitivity of multidimensional NMR experiments at the same time that isotopic labelling of proteins resulted in the design of 3D and 4D experiments with unprecedented sensitivity.^53,54 These 3D and 4D experiments had some very important properties: (1) They were often very sparse, meaning that spectra consisting of tens or hundreds of thousands of data values only contained a few hundred up to a few thousand signals; (2) The available sensitivity was in many cases much higher than that required to produce an accurate spectral representation. These two conditions resulted in a situation where data acquisition was limited by the required resolution rather than sensitivity, a reversal of earlier conditions. Thus, since the turn of the millennium there has been an explosion of methods attempting to use the improved SNR to produce accurate multidimensional spectra of NMR signals.^25,55,56 Considering that the number of signal and post-processing techniques employed in multidimensional NMR has nearly doubled in less than 10 years (see Figure 3), and that each has its own associated terminology, it is no wonder that this area of NMR is bewildering even to the most experienced NMR spectroscopists. Fortunately, most of these new methods rely on a common set of basic principles. Understanding these principles helps to illuminate the relationships between the various methods, and makes signal processing in NMR more “coherent”.

Figure 3.

A timeline showing the introduction of various NMR methods aimed at speeding up NMR data acquisition (below the horizontal line). Entries above the timeline refer to fundamental advances in NMR spectroscopy that indirectly impacted or enabled these methods.

NUS and non-Fourier methods of spectrum analysis are inextricably linked. Here we will discuss the most successful methods for speeding up the acquisition of multidimensional NMR data. The focus will be on introducing the key concepts that link the various methods to one another and discussing their relative strengths and weaknesses. Although a direct comparison of all these methods applied to a common set of data would be the most informative approach, such a critical comparison remains technically beyond reach, primarily because (as in critical comparison of sampling schemes) no common set of test data yet exists that includes data sampled using all of the different sampling regimens employed by the different approaches. Similarly, there is not yet a broad consensus on metrics for characterizing the quality of multidimensional NMR spectra. For this reason, very few studies that compare available fast acquisition methods have been conducted.²⁵ Thus, practical benchmarks or guidelines for the practicing spectroscopist are currently in short supply. Through this review we aim to partially compensate for this lack of guiding principles, by providing the spectroscopist with the information needed to make informed decisions regarding the potential utility of the many methods available, and also to provide sufficient insight to allow a critical assessment of the use of these methods for solving problems encountered in applications of NMR spectroscopy.

2.1. Limitations of the DFT

Data acquired using pulsed experiments results in a time-varying response, the FID, that can be approximated as sum of sinusoids, with each sinusoid representing an excited resonance. The interpretation of an FID directly in the time domain is clearly impractical when it contains more than one sinusoid. The chorus of spins represented can be resolved into its components by converting the time-domain response into a spectral representation, indicating the amount of energy contained in the signal as a function of frequency. The use of FT for this conversion is so intimately associated with the development of modern pulsed NMR that the technique as a whole is often labelled FT-NMR.¹ Although the application of the continuous FT to time domain data theoretically produces an accurate frequency domain spectrum, its application is impractical. Instead, the continuous NMR signal is sampled at discrete time intervals at a fixed rate. The discrete Fourier transform (DFT) can be applied to this data to obtain a frequency spectrum. The DFT is, however, only an approximation of the continuous FT, and the accuracy of the result depends on how well the approximation is satisfied. The two main differences between the FT and the DFT, and hence the sources of errors when applying the DFT, are the discrete sampling and the finite data length.⁵² Sampling less frequently than mandated by the Nyquist criterion leads to the appearance of signals in the spectrum at incorrect frequencies, referred to as aliasing or folding (see also section 1.1).²⁹ Short data records (i.e. too few samples) leads to poor digital resolution of the frequency domain spectrum and can result in baseline distortions. The digital frequency resolution can be increased through “zero filling”, which involves adding zeroes to the end of the time domain data. This operation invariably results in a discontinuity of the time domain data, which in turn results in the appearance of additional unwanted signals in the spectrum, commonly referred to as truncation artifacts or sinc wiggles. To resolve this problem one must either collect longer datasets, or multiply the FID with a “window” or “apodization” function that smoothly reduces the amplitude of the signal near the end of the data record. While this improves digital resolution and reduces truncation artifacts, it also results in line broadening.

This act of balancing sensitivity and resolution provides much of the motivation behind signal processing of NMR data. Ultimately the aim is to resolve signals with similar frequencies without introducing artifacts that could mask weaker signals. In 1D NMR experiments one can often collect a very long data record to improve resolution, but this is not true for multidimensional (nD) NMR experiments, because of the parametric manner in which the additional indirect dimensions are sampled. As can be appreciated from the above, adding a time point in the indirect dimension of a two-dimensional experiment requires the acquisition of an additional one-dimensional dataset. By extension, adding another time point to the second indirect dimension of a three-dimensional experiment requires the acquisition of another two-dimensional experiment (each 2D plane is a time point along the third dimension). Thus, overcoming the inability of the DFT to provide high-resolution spectra from short data records becomes more burdensome with each added dimension.

2.2. Accelerating multidimensional NMR experiments

Multidimensional NMR experiments are essential for resolving individual nuclear resonances for complex biomolecules, and are so ubiquitous that any advance in speeding up the traditionally slow process of acquiring multidimensional NMR data would impact the whole field. It is therefore not surprising that the problem has been attacked by a multitude of novel experimental and computational methods. The need for speed in NMR has become even more urgent recently with the advent of genetic and biochemical tools that enable high-throughput production of biomolecules for structural analysis. In particular, the global effort toward structural genomics has led to new technological developments in the past decade.⁵⁷

The approaches taken to speed up multidimensional NMR experiments can be broadly categorised in two main groups: (i) methods that employ signal processing methods capable of high resolution using short or incomplete data records and (ii) methods that employ alternatives to time evolution along indirect time dimensions to elicit multidimensional correlations. Those in group (i) typically utilize novel post-acquisition processing methods and these will be covered in Sections 2.3–2.5, whereas those in group (ii) involve more dramatic changes to the pulse sequence and/or the hardware and these will be covered in Section 3. Group (i) is where the majority of recent work has been done to overcome the time-barrier imposed by the DFT (Figure 4). The signal processing methods in group (i) can be further categorized according to the sampling regimens that they are compatible with. Typically, the least restrictive processing methods are capable of producing spectra from any type of data record, and include methods such as MaxEnt reconstruction (red in Figure 4). Methods that restrict the sampling method can be further split into those that are applicable to traditional uniformly-sampled data, including extrapolation methods such as linear prediction (black in Figure 4), and those that are not. The final category of processing methods utilise non-uniform sampling but with a deterministic or coherent distribution of samples in the time domain (green in Figure 4). Such data can either be directly used to produce a multidimensional spectrum, or each component (e.g. radial projection) can be analysed using post-processing methods to generate information about the position of the signals in the multidimensional spectrum (the latter are underlined in Figure 4). Typically methods in the first two groups sample on a grid defined by the Nyquist condition, whilst the deterministic sampling methods sample outside this grid (see also Figure 6). In addition, signal processing methods can be characterized as parametric (italic in Figure 4) or nonparametric, depending on whether or not they model the signal and estimate the spectrum by refining parameters of the model.

Figure 4.

Relationships among different methods used for speeding up NMR data acquisition. Processing methods are categorised based on the type of data they are applicable to. The dotted line indicates that the methods appropriate for non-deterministic sampling are also applicable to the other types of sampling, whereas the converse is not true. Parametric methods are italicised and post-processing methods are underlined.

The division according to sampling strategy shown in Figure 4 reveals that methods for speeding up data acquisition applicable to uniform Nyquist sampling are frequently (but not always) parametric (italic). Conversely those applicable to NUS data are commonly non-parametric. Furthermore it can be seen that most methods applicable to radially sampled data are post-processing methods (underlined).

2.3. Uniform (Nyquist) Sampling

The methods in this section are generally only applicable to conventional uniform or Nyquist sampling. These methods can all be considered as extrapolating the time domain NMR signal beyond the measured interval. The resulting extended data record can then be zero-filled and Fourier transformed to produce high-resolution spectra, or the spectrum can be reconstructed from the parameters fitted to the model. The assumption common to most of these methods is that the signal d can be described as a sum of exponentially decaying sinusoids:

$$d_k=\sum _{j=1}^L\left(A_j{e}^{i{\varphi }_j}\right)e^{-k\mathrm{\Delta }t/{\tau }_j}{e}^{2\pi \mathit{\text{ik}}\mathrm{\Delta }t{\omega }_j}$$ (3)

where L is the number of sinusoids, A_j, ϕ_j, τ_j and ω_j are the amplitude, phase, decay time, and frequency respectively, of the j^th sinusoid sampled at a time kΔt, with Δt the sampling interval determined by the Nyquist condition. Signals that decay exponentially have Lorentzian lineshapes. Under certain circumstances some of the parameters in eq. 3 may be known a priori, simplifying the problem of fitting eq. 3 to measured data. An example is data acquired in constant-time experiments, where the signal decay is known (i.e. there is no decay). There is no analytical method for fitting the parameters in eq. 3. Most methods rely on matrix approaches to determine best-fit values in a least-squares sense. Although there are many different approaches to fitting the parameters, the common reliance on the model described by eq. 3 means that the different approaches frequently have similar behaviour. A common feature of methods based on eq. 3, which does not explicitly account for noise, is that they become unreliable when the data is very noisy or the noise is not randomly distributed.

2.3.1. LP and related methods

Linear prediction (LP) extrapolation extends the measured data by assuming that the signal can be described at any time as a linear combination of past values:

$$d_k=\sum _{j=1}^m{a}_j{d}_{k-j}$$ (4)

where a sample (d_k) in the time series can be predicted using m past values (d_k−j) given a set of a_j weights. This turns out to be equivalent to modelling the signal as a sum of exponential sinusoids^58,59. Appropriate choice of the number of coefficients m (referred to as the order) and their values, a_j (referred to as LP coefficients), is not a trivial matter, in particular since NMR data in addition to sinusoids include noise and other imperfections that render eq. 4 only approximate. Functions that obey eq. 4 are called autoregressive and include the class of signals described by Eq. 3. Importantly, the coefficients a_j are related to the parameters of eq. 3. Thus, instead of using the LP equations to explicitly extrapolate the FID, it is possible to use the LP coefficients to solve for the parameters of the corresponding model. The zeroes of the characteristic polynomial formed from the LP coefficients yield the frequencies and decay rates.² By using nonlinear fitting against the measured data, the remaining parameters (amplitudes and phases) can be determined. The result is a table of peak data, rather than a spectrum. A number of closely related methods (HSVD⁶⁰, LPSVD⁶¹, LPQRD⁶²) employ this approach, and have been shown to be especially useful for signals with a modest number of resonances. These approaches obviate the need for subsequent analysis employing a peak picker (these and other related methods are discussed in detail elsewhere^52,58).

Using methods such as LPSVD that explicitly compute the parameters of Eq. 3, the spectrum can be computed from the model. In LP extrapolation, only the weights a_j are determined, and the FID is explicitly extrapolated beyond the measured interval using Eq. 4. The spectrum is obtained by conventional FT of the numerically extrapolated FID. This lessens the need to window the data so that it has very small values near the end of the measured interval to avoid truncation artifacts, and thus also avoids the concomitant line broadening.

In practice, the value of m is determined by the user, bounded by ½ the available number of data samples. The “correct” value is never known a priori, and depends not only on the number of expected sinusoids but also on the noise level. Since the coefficients a_j are approximate and the measured signal contains random noise (which can’t be extrapolated), the prediction error will always increase as the length of the predicted interval increases. Consequently, a conservative and common practice is to limit extrapolation to a doubling of the length of the measured data. The value of m is chosen to be significantly less than the number of measured samples yet larger than the number of expected signals⁶³. Values of m smaller than the number of sinusoids leads to bias and inaccurate predictions, whereas values of m that are too large can result in false peaks.

Another use of LP in NMR data processing is backward LP extrapolation, when the initial data points have been corrupted or cannot be measured.⁶⁴ In these cases the corrupt or missing information can lead to severe baseline distortion or phase errors. Finally, if the data has a known phase (e.g. sinusoidal or cosinusoidal), it is possible to apply “mirror image LP” in which the number of “measured” samples is doubled by reflection (with or without sign inversion, depending on the phase) resulting in substantially improved numerical stability of the LP extrapolation⁶⁴.

2.3.2. Maximum Likelihood and Bayesian Analysis

While LP methods explicitly assume an autoregressive model for the signal, they implicitly are consistent with modelling the signal as a sum of decaying sinusoids. Hybrid parametric LP methods generally compute the LP expansion coefficients as a first step, and then use these to compute the model parameters (amplitudes, phases, frequencies, decay rates). Maximum likelihood and Bayesian methods take a more direct approach to computing the model parameters. Also, the need for a priori estimation of the number of signals with LP methods makes them poorly suited for unsupervised processing. The approach taken by the maximum likelihood method (MLM)^26,45,65,66 and Bayesian analysis (BA)^26,67 is to determine the number of sinusoids in the model using statistical methods. Broadly speaking, by assuming that NMR signals follow the form of eq. 3 they attempt to find a set of parameters that define a model that when subtracted from the experimental data leaves only random noise. MLM and BA differ mainly in the criterion used to determine the best model. In MLM the aim is to maximize the likelihood that the signal was generated by a system with the parameters given by the model. In BA, the posterior probability that the model is correct, which includes the likelihood as well as a priori probability, is maximized. Depending on the nature of the assumed prior probability distribution, the results of MLM and BA can be quite similar, if not identical. We refer the reader to the work of Bretthorst²⁶ for detailed derivations of the two approaches. However, a broad overview of MLM helps to illuminate the differences between LP methods and MLM or BA.

In the MLM implementation described by Chylla and Markley⁴⁵, the measured data is zero-filled (and possibly augmented with zeroes to replace missing samples from the Nyquist grid) and subjected to FT. In the frequency domain a peak picker identifies the signal having the maximum amplitude, and the parameters describing this signal (amplitude, phase, frequency, and decay rate) are determined by least-squares. The model described by Eq. 1 is then populated with a single sinusoid with the determined parameters, and the time-domain signal corresponding to the model is subtracted from the measured data. The residual is then subjected to FT, and the peak picker again finds the largest magnitude signal and its parameters are estimated. Another sinusoid with the parameters for this signal is added to the model, and the time-domain signal for the new model is subtracted from the zero-filled/augmented data. This procedure is repeated until the residual is indistinguishable from noise. A number of statistical tests have been employed as stopping criteria (for determining the number of sinusoids in the model), including the Akaike Information Criterion (AIC) and minimum description length (MDL).⁴⁵

2.3.3. Filter Diagonalization Method

Another method used in NMR data processing capable of super-resolution is the filter diagonalization method (FDM), which was first introduced to NMR by Mandelstahm and Taylor.⁶⁸ The FDM method was initially applied to quantum dynamics, where the problem of solving eq. 3 is also of interest. The basic idea behind FDM is to recast eq. 3 into a problem of diagonalizing small matrices. The filtering refers to breaking up the spectrum into small pieces to reduce the computational burden; the algorithm constructs a matrix where the off-diagonal elements represent the interference between resonances. Diagonalizing this matrix allows one to extract the parameters of eq. 3. We refer the reader to the review by Mandelshtam for details.⁶⁹ One of the advantages of FDM is that all the available data in a multidimensional experiment is used to derive the parameters in eq. 3. For example, if a 2D spectrum has N data points in the direct dimension and M points in the indirect dimension, N × M points are used to solve the linear equations of FDM (generating a N × N matrix). As long as N × M is large enough, accurate spectral estimates and parameters can be obtained. In theory a value of M = 2 should be enough to derive an accurate 2D spectrum having k signals, so long as N × M is larger than 3k. Unfortunately, this is only true for data of very high SNR and where the frequencies of signal components are not overlapped. The resolving power of FDM is very sensitive to both noise and overlap and much of the current development of FDM is focused on improving the stability of the method for noisy data and in finding efficient methods for removing spurious peaks. Like other parametric methods, the output of FDM is a list of the parameters describing the spectrum, rather than a spectrum. The spectrum can be generated as in BA by using the output parameter values to construct an FID which is then subjected to DFT. Alternatively, the closely-related regularized resolvent transform (RRT) can be used, which, using the principles of FDM, performs a transform resulting in a frequency domain spectrum.⁶⁹ In situations where the assumptions of the method (shared by FDM and RRT alike) are not realized the resulting parameters or the spectral estimate can include spurious peaks or baseline distortions. This method has not achieved wide penetration, but is finding interesting applications to sampling-limited experiments such as diffusion-ordered spectroscopy (DOSY)⁷⁰, and holds considerable promise.

2.4. Radially Sampled Data

The utility of radial sampling derives from the projection - cross-section theorem⁷¹, which states that Fourier transformation of data collected along a radial time vector with a given angle in the t₁–t₂ plane is equivalent to the projection of the 2D spectrum onto a frequency-domain vector with the same angle. Most spectroscopists are familiar with looking at orthogonal projections of multidimensional experiments (onto a frequency axis) to assess spectral quality, since these projections are equivalent to simply running a 2D experiment without incrementing the missing (orthogonal) dimension.

2.4.1. Reduced Dimensionality

The first RD experiment was the accordion experiment introduced by Bodenhausen and Ernst in 1981.^20,72 In this approach a 3D experiment was reduced to two dimensions by coupling the evolution of the two indirect dimensions. In the original accordion experiment one indirect dimension represented chemical shift evolution while the second indirect dimension encoded a mixing time designed to measure chemical exchange. Although this experiment established the foundation for all future RD experiments, most of which deal exclusively with chemical shift evolution, its utility for measuring relaxation rates and other applications is still being developed.^73,74 Even though it was clear from the initial description of the accordion experiment that the method was applicable to any 3D experiment, it was nearly a decade before it was applied to an experiment where both indirect dimensions represented chemical shifts.^35,75 This application emerged as a consequence of newly-developed methods for isotopic labelling of proteins that enabled multinuclear, multidimensional experiments, with reasonable sensitivity, for sequential resonance assignment and structure determination of proteins. The acquisition of two coupled frequency dimensions, however, introduces some difficulties. The main problem is that the two dimensions are mixed and must somehow be deconvoluted before any useful information can be extracted.

Since the joint evolution linearly combines the two dimensions, the corresponding frequencies are also linearly “mixed”. The number of resonances observed in the lower dimensionality spectrum depends on the number of linked dimensions. Thus, if two dimensions are linked, the RD spectrum will contain two peaks per resonance of the higher dimensionality spectrum, whereas if three dimensions are coupled each of the two peaks will be split by the second frequency resulting in four resonances, and so on. The position of the peaks in the RD spectrum can be used to extract the true resonance frequency. The problem obviously becomes more complicated as the number of resonances is increased. If overlap can be avoided, however, it is possible to drastically reduce experimental time using this approach.

2.4.2. GFT NMR

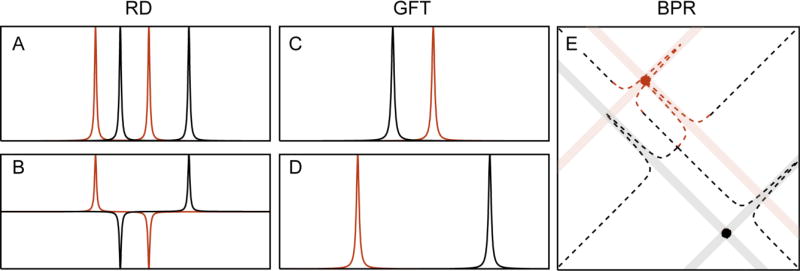
An extension of RD was presented by Kim and Szyperski²⁴ in 2003 in which they used a “G-matrix” to appropriately combine hypercomplex data of arbitrary dimensionality to produce “basic spectra” (see Figure 5. These spectra are much less complicated than the RD projections, and the known relationship between the various patterns can be used to extract true chemical shifts (via nonlinear least-squares fitting). Combination of the hypercomplex planes enables recovery of some sensitivity that is otherwise lost in RD approaches due to peak splitting. A disadvantage is that the data is not combined in a higher dimensional spectrum, so that the sensitivity is related to that of each of the lower dimensional projections rather than the entire dataset. GFT-NMR was developed contemporaneously with advances in sensitivity delivered by higher magnetic fields and cryogenically cooled probes, providing sufficient sensitivity to make GFT experiments feasible

Figure 5.

Schematic depiction of RD, GFT and BPR. (A) The RD method gives rise to chemical shift multiplets, which are separated by the chemical shift of one nucleus (ω₂) and centered at the chemical shift of the other nucleus (ω₁). In GFT processing of RD data, the phases are manipulated (B) so that their combination results in “basic spectra” of reduced complexity (C–D). In projection spectroscopy the delays are scaled by a projection angle. The resulting spectra can be directly projected onto the higher dimensional plane, where an intersection in this higher dimensional spectrum reveals the true chemical shifts (X marks the spot).

2.4.3. Back-Projection Reconstruction

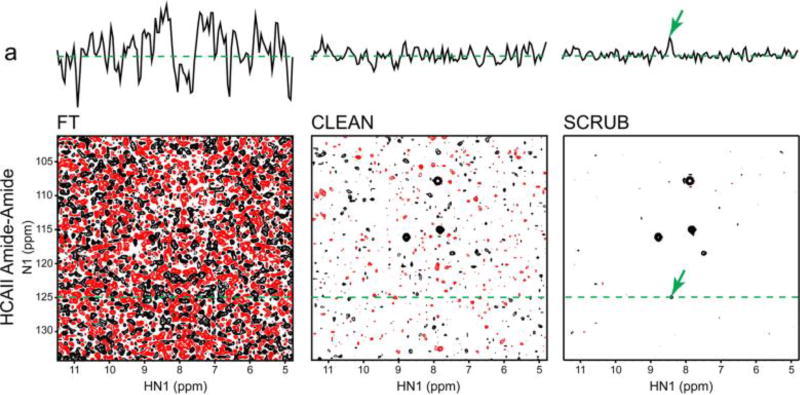
GFT-NMR did much to revitalize interest in RD methods (after a decade of sporadic application), but did not go as far as providing a heuristic link between the coupled dimensions and their higher dimensional (three or higher) equivalents. This was instead done in a series of publications by Kupče and Freeman, who exploited the relationship between a time-domain cross-section and its frequency-domain projection, through the projection - cross-section theorem.⁷⁶ The appeal of this approach was that it reconstructed the higher dimensional spectrum using back-projection reconstruction (BPR), analogous to the methods used in computerized axial tomography (CAT).⁷⁷ It simplified visual interpretation of RD data, making it far more accessible to the broader NMR spectroscopy community. The principle of BPR is rather simple and involves projecting the lower dimensional data onto the higher dimensional plane at the appropriate projection angle (see shaded lines in Figure 5E). By combining multiple projection angles the ridges caused by the peak information from each projection will intersect at the correct frequencies of the higher dimensional object. The accuracy of the reconstruction improves as the number of projections is increased. An important connection is that filtered BPR (fBPR) has been shown to be equivalent to radial FT.⁷⁸ In fBPR a ramp function (an apodization function ranging from 0-1 from the beginning of the FID to the end) is applied to each projection prior to adding it to the higher dimensional spectrum. The fBPR procedure drastically reduces the weight of the high SNR portion of the FID (the beginning where the filter values are low). This helps because the data at short evolution times is greatly oversampled if a very large number of projections are accumulated (this in itself can lead to excessive line-broadening if fBPR is not applied). The method has the advantage that the chemical shifts no longer need to be deconvoluted but can instead be directly extracted from the reconstructed spectrum. The major disadvantage is that as the spectral complexity and dynamic range increase, small features may be masked by strong ridges from projections of other peaks or by accidental intersections that cause false peaks to appear. Several methods have been developed to ameliorate the problems associated with these artifacts. These all attempt to remove the sampling related “ridge” artifacts in the BPR spectrum, and include the simple lowest value algorithm and the CLEAN algorithm.⁷⁹ Each has strengths and weaknesses, but there is currently no consensus on the best approach to post-processing of BPR spectra.

2.4.4. Post-Processing of Projections

RD, GFT and BPR stimulated interest in fast acquisition techniques in multidimensional NMR and established the experimental framework for many other approaches to processing such data. The rising interest was in part due to the impressive results that were demonstrated, but another factor is that the analogy to computer-aided tomography (made explicit by BPR) provided a clear heuristic framework for understanding precisely how NUS works. Another factor was the increased demand for efficient NMR data collection imposed by structural genomics initiatives and by the advent of ultra-high magnetic fields (where the sampling problem is exacerbated by the shorter sampling interval imposed by greater shift dispersion). Thus, soon after the initial findings of Szyperski, Kupče, Freeman and colleagues were reported, a number of new methodologies were proposed for enhancing coupled-evolution approaches.

PRODECOMP

The PRODECOMP (projection decomposition) method was introduced as a method for analysing GFT-type spectra, but instead of using least squares to extract the correct chemical shifts from the chemical shift multiplets, PRODECOMP employs multiway-decomposition (MDD, described in Section 2.5.7) to disentangle the projected spectra into separate resonances⁸⁰.

APSY

APSY (automated projection spectroscopy)³⁸ is a method used to directly analyse projection data, rather than reconstruct the full dimensionality spectrum. APSY uses the information from the projection angle to interpret the peak information in the projected spectrum. Datasets for a number of projection angles are acquired and the projected spectra are analysed to generate a peak list for each projection angle. Since the projection angles are known, the true peak frequency can be determined in the higher dimensionality spectrum. Thus, even though the peak position will change in each projection spectrum the calculated true frequencies can show that the peak represents the same position in the “full” spectrum. The algorithm then calculates how many intersections are present in the spectrum (see also Figure 5 for illustration of an intersection), by comparing the peak position in the various projections after translation to the higher dimensional object. It then ranks the number of intersections (which are multidimensional peak candidates) and removes the peak with the highest rank (most intersections), removing with it all of the contributing peaks from the lower dimensional projections (i.e. from the peak lists). This has two effects, one of which is the desired effect of eliminating artifacts by removing any artifactual peaks that are coincident with the position of a real peak to produce accidental intersections. Conversely, the procedure may also remove support for a real peak if it is truly overlapped in several dimensions. The procedure is repeated, removing a real peak at each iteration, until the number of intersections at the remaining highest ranked peak candidate falls below a user defined threshold. The list of peaks that have been removed is now the true peak list and the remaining peak candidates are discarded. The procedure is repeated a number of times to reduce the likelihood of accidental removal of redundant (overlapped) peaks. The peak positions are then averaged and recorded.

HIFI NMR

HIFI NMR was introduced soon after BPR and addressed the question of the optimal choice of projection angles.³⁷ HIFI NMR uses a statistical approach similar to those described in Section 2.3 to find the projection angle most likely to resolve all the resonances. The best projection angle is determined from likely shift distributions, derived from average chemical shift data contained in the Biological Magnetic Resonance Data Bank⁸¹ (BMRB) and the known amino acid composition of the protein, as well as peak positions. In this sense HIFI is an adaptive method, because the projection angle chosen depends on the results obtained from prior projections. The algorithm (acquiring and analysing data at a specified projection angle) is repeated until no additional information can be extracted.

2.5. Irregular Sampling

In contrast to non-uniform sampling that results from coupling two or more evolution periods, the first application of nonuniform sampling (Figure 1) in multidimensional NMR utilized a random sampling scheme.²² This sampling is not only less regular than the radial sampling employed by RD methods (including BPR and GFT), but it also requires a method for computing the spectrum from time domain data that does not require uniformly-spaced samples. Barna et al.²² employed maximum entropy (MaxEnt) reconstruction to compute spectra from irregularly-spaced data. For a long time the different methods used for spectral analysis obscured both the differences and the similarities between different approaches that are fundamentally all nonuniform sampling methods. More recently it was shown that MaxEnt reconstruction is capable of performing back projection, and more importantly, that when applied to the same data, MaxEnt and BPR yield essentially equivalent results.²⁵ This implied that the differences in the magnitude and nature of artifacts encountered when reconstructing a multidimensional spectrum from data collected using different sampling schemes (e.g. radial or random) are attributable mainly to the sampling scheme, and not the method used to compute the spectrum from the nonuniformly sampled data. The problem of estimating frequency spectra from irregularly-spaced data is one that has been encountered in a host of other fields in science and engineering, and a similarly large number of methods have been developed. In this section we describe the main methods that have been applied to multidimensional NMR.

2.5.1. nuDFT

As discussed in section 1.3 it is in principle possible to reconstruct a spectrum from a set of arbitrarily-distributed time domain samples by estimating the continuous Fourier Transform. Computing the Fourier integral is an exercise in numerical quadrature on an irregular grid.⁸² Provided that the samples fall on a regular grid, however, one can use the DFT to compute the spectrum. One simply inserts zeroes where data has not been sampled and treats this as a normal uniformly sampled dataset. Inserting zeroes at the grid points not sampled is, however, equivalent to leaving the corresponding basis functions out of the Fourier sum. In the absence of these lost basis functions, the remaining basis functions no longer comprise an orthonormal basis set. A consequence is that the sampled basis functions interfere with one another.³⁰

The result of applying the DFT to NUS data can be seen as the convolution of the DFT spectrum for the uniformly sampled data with the DFT of the sampling function (i.e. the point spread function). Sampling functions must be real-valued for the simple convolution relation between the DFT of zero-augmented NUS data and PSF to hold (for nonuniform sampling hypercomplex sampling that does not acquire all components of the hypercomplex datum for a given set of evolution times, the relationship becomes a family of convolutions¹⁹). As seen in the first part of this review, PSFs are valuable for estimating a priori the characteristics of the sampling artifacts associated with a sampling scheme. PSFs typically consist of a major component at zero frequency, with a number of smaller non-zero frequency components. The width of the zero-frequency component conveys the amount of signal broadening, while the non-zero frequency components reflect the magnitudes and relative locations of sampling artifacts. In the DFT of zero-augmented NUS data, every signal component will give rise to artifacts that have the same amplitudes relative to the parent signal as the ratio of the amplitudes of the zero-frequency component and the non-zero components. Deconvolution of these artifacts from the spectrum is the primary motivation behind non-Fourier methods such as MaxEnt and compressed sensing. Thus spectral estimates based on DFT of zero-augmented NUS data can be considered to represent the upper bounds on artifacts associated with NUS (see Figure 7).

Figure 7.

Comparison of spectra obtained with uniform sampling (A and B) and nonuniform sampling (C and D). In C the spectrum was computed using maximum entropy reconstruction, using the same number of samples employed in B. In D the spectrum was computed using nuDFT (FT in which samples not collected are set to zero). Reproduced from Hoch et al.⁴⁹ with permission from the PCCP Owner Societies.

2.5.2. Lagrange Interpolation

A completely different approach to spectral estimation for nonuniformly sampled data is to attempt to approximate what the data would have looked like if it had been sampled uniformly, using the information obtained from a set of nonuniformly sampled data; the DFT can then be applied to the modified dataset. One way to do this is to fit a continuous function to the nonuniformly sampled data, then interpolate using this function to estimate the data values at uniform intervals. Marion and colleagues⁸³ described the use of Lagrange interpolation to perform this re-sampling onto a regular grid. In contrast to LP, where the data is extrapolated beyond the measured interval, only short stretches of data must be reconstructed and the errors therefore do not propagate in the same way they do in LP extrapolation. Another feature of the method is that since the Nyquist grid can be defined post-acquisition one can avoid some of the problems of aliasing when spectral windows are set inappropriately.

2.5.3. Multidimensional FT

More recently, a method called multidimensional FT (MFT)¹⁶ was proposed which involves computation of Fourier-like sums on an arbitrary mesh, possibly including weights. When applied to NUS data corresponding to a subset of uniformly sampled data, the sums can be evaluated using the FFT (with elements not sampled set to zero); otherwise the sums are computed by brute-force summation. Unfortunately the name is something of a misnomer, as it is not truly a Fourier transformation of NUS data. Whether the time domain samples are selected from a uniform grid or are collected off-grid, the orthogonality condition that applies to the Fourier basis on a complete, uniform grid is not satisfied, and so the NUS artifacts that result can be viewed as interference between frequency components. When NUS is restricted to a uniform grid, the artifacts correspond to convolution of the FT of the sampling function (possibly including weights) with the uniformly-sampled FT spectrum. Because no attempt is made to deconvolve the sampling artifacts, this approach works best when the NUS scheme is carefully constructed to minimize the artifacts.

MFT contrasts with regular DFT processing where the FT sums are evaluated one dimension at a time. The method was initially proposed for processing of projection data and shown to be equivalent to the inverse Radon Transform. However, the method is more general than this and its real strength is that it allows for a small spectral window to be reconstructed in cases where a very large spectral window has been acquired. As was discovered for Lagrange interpolation, and explained more generally by Bretthorst⁸⁴, the effect of increasing the spectral window (i.e. reducing the distance between sample points) when sampling non-uniformly is to push sampling-related artifacts to very high frequencies. For multidimensional data the very large spectral windows would eventually produce very large datasets if high digital resolution were to be maintained. MFT would therefore aid in accessing only regions of interest with high resolution. The method relies heavily on the assumption that the sampling related artifacts are reduced to such an extent as to not interfere with the signal components, and can therefore be ignored. On the other hand, sampling at time points other than those stipulated by the Nyquist condition invariably results in oversampling (e.g. see Figure 7 of Mobli & Hoch³⁰). For time equivalent sampling from an exponentially decaying distribution, oversampling in turn leads to line broadening and then one must assume that limited signal overlap is present in the higher dimensional object being reconstructed.

2.5.4. CLEAN

In contrast to the DFT of nonuniformly sampled data, there are a number of methods that attempt to deconvolve the sampling spectrum to arrive at a more accurate spectral estimate. One such method, known as CLEAN, takes a heuristic, iterative approach to deconvolving the PSF from the spectral estimate.^79,82 The algorithm begins by identifying the largest peak in the spectrum and attempts to deconvolve all artifacts associated with that peak. It does this by: (i) fitting the peak to some function (generally a Lorentzian line shape); (ii) creating a mock FID containing only the modelled peak but having the same spectral properties as the original spectrum (e.g. spectral window etc); (iii) discarding the points in the FID that do not exist in the sampling schedule; (iv) applying the Fourier transform; and (v) subtracting the resulting spectrum from the experimental spectrum. Following this procedure the peak and its associated artifacts are identified and removed, and the operation is repeated until a pre-determined threshold is reached (note the similarity to the procedures used in APSY and MLM). The major problem with this approach is that each peak must be accurately identified, modelled and removed from the data individually; errors in this process can propagate reconstruction artifacts. The algorithm requires a user-defined threshold for determining the level at which remaining peaks are not significant. Extensions to the heuristic ideas underlying CLEAN have led to improvements in the ability to suppress NUS artifacts⁸⁵ (Figure 8), but the ad hoc nature of the approach remains an obstacle to deeper understanding of why the method works, what the possible failure modes are, or how to improve on the method. The SCRUB method used in the right-most panel of Fig. 8 differs from the original iterative subtractive CLEAN algorithm by grouping peaks and keeping track of the location of signal peaks from prior iterations, enabling the threshold to achieve lower values closer to the intrinsic noise level.⁸⁵

Figure 8.

Comparison of DFT, CLEAN, and CLEAN with SCRUB post-processing applied to NUS data. Reprinted with permission from Coggins et al. (2012).⁸⁵

2.5.5. Maximum Entropy Reconstruction

Maximum entropy reconstruction (MaxEnt) was first introduced to NMR signal processing in the early 1980s.⁸⁶ MaxEnt reconstruction treats signal processing as an inverse problem. Starting with a trial frequency spectrum, a mock data set is generated via the inverse FT; the resulting time series is then compared to the empirically measured data. The trial spectrum is iteratively improved by applying constraints in both the frequency and time domains. In the frequency domain the constraint is to maximize the entropy, a measure of the absence of information (details of the entropy functional and the iterative algorithm are given in^2,87). In the time domain the mock data is constrained to minimize the difference from the experimental data. The level of agreement between the mock FID and the measured data is generally determined by the user, but to avoid over-fitting it should be comparable to the noise level in the measured data. Following this principle the selection of reconstruction parameters can be made automatically, based on the noise level and trial reconstructions.^88,89

Since the algorithm works in an inverse manner, sampling the FID is uncoupled from the mock FID, and computation of the level of agreement can be restricted to sample times in common between the experimental and mock FIDs. Thus MaxEnt readily supports essentially arbitrary nonuniform sampling, provided that the samples fall on the Nyquist grid corresponding to the mock FID. Another important consequence of the inverse nature of the algorithm is that one can use it to perform deconvolution in a very stable manner. In contrast to linear methods where the FID is divided by a convolution kernel, using MaxEnt one multiplies the mock FID by the kernel prior to comparison with the experimental FID, thus avoiding divide-by-zero instabilities or noise amplification. This approach can be used to deconvolve unwanted J modulation (to achieve virtual decoupling) or signal decay (to achieve line narrowing).^87,90

The reduction in sampling artifacts by MaxEnt (see Figure 7) is in part due to the nonlinearity of the entropy functional. This nonlinearity is not without disadvantages. While the nonlinearity can be minimized by appropriate choice of reconstruction parameters or compensated by calibration^91,92, the nonlinearity means that MaxEnt should only be applied to the last dimension to be sequentially processed in a multidimensional dataset, so as not to compound nonlinearities. Thus, in order to process two indirect dimensions (for example in a 3D experiment) using MaxEnt, the algorithm should be applied to both dimensions simultaneously. In principle MaxEnt can be applied to data with arbitrary dimensionality, but so far the largest number of dimensions that have been simultaneously reconstructed using MaxEnt is three (the three indirect dimensions of a 4D spectrum).⁹³ Though not insignificant, the computational demands of MaxEnt are easily amenable to parallelization, for example using a loosely-coupled cluster. MaxEnt reconstruction in one or two dimensions simultaneously can be readily performed using a laptop computer.

2.5.6. Forward maximum entropy and maximum entropy interpolation

MaxEnt reconstruction is a nonlinear method, and the nature and extent of the nonlinearity depends on the data. This presents challenges for quantitative applications, for example quantifying nuclear Overhauser effects or relaxation rates. One approach is to generate a calibration curve by adding synthetic signals spanning a range of amplitudes to the experimental data. Alternatively, the parameters controlling MaxEnt reconstruction can be adjusted to minimize the nonlinearity. Constraining the inverse DFT in the MaxEnt reconstruction to more tightly match the measured data reduces the nonlinearity. Hyberts and Wagner proposed taking this approach to its logical extreme for NUS data, devising an algorithm called Forward Maximum Entropy (FM) that uses the entropy to regularize the reconstruction so that the inverse DFT exactly matches the measured data for those samples collected.⁹¹ In essence the entropy is used only to determine the values of “missing” data not sampled by the NUS scheme. The results are highly linear, and suitable for quantitative applications. The power of FM is readily apparent from Fig. 9, which compares two-dimensional cross sections from 3D HNCO spectra using 1250 samples in the indirect dimensions sampled uniformly and processed using the DFT (left), and sampled nonuniformly and processed using FM (right).⁹⁴

Figure 9.

Comparison of a spectrum obtained using uniform sampling and conventional DFT processing (left) with a spectrum obtained using the same number of samples in the indirect dimension (the same experiment time) using NUS and FM processing (right). Adapted from Fig. 1 of Hyberts et al. (2014)⁹⁴. Reprinted with permission.

Because no constraint is used to enforce agreement between the inverse DFT of the FM spectrum with the measured data, orthogonality of the gradients for the entropy and the constraint cannot be used as a convergence criterion. Instead convergence is assumed when the step size becomes sufficiently small. As with many fixed-point methods (see IST, below), this can result in false convergence, if the step size becomes too small before the optimum is reached. Polenova and colleagues devised a similar strategy, maximum entropy interpolation (MINT)¹⁵, that employs conventional MaxEnt codes while setting the constraint parameter to a small value, much smaller than the estimated noise. Similar to FM, MINT yields highly linear spectra from NUS data, suitable for quantitative analysis, but takes advantage of highly efficient and robust MaxEnt code, ensuring both uniqueness of the solution and convergence.

2.5.7. Iterative Thresholding, Minimum l₁-norm, and Compressed Sensing

MaxEnt reconstruction uses a regularization functional – the entropy – to produce smooth spectral estimates with minimal artifacts. A number of different approaches to spectrum estimation that on the surface appear quite dissimilar have in common a reliance (either implicit or explicit) on a regularization functional that shares some of the properties of the entropy. The functional these approaches have in common is the l₁-norm, or the sum of the absolute magnitudes of the elements of the spectrum. Regularizing spectral estimates by minimizing the l₁-norm (note the sign difference from the entropy) is a characteristic of a class of fixed-point methods that use iterative thresholding, first applied to image processing problems⁹⁵, in which spectral (image) values below a threshold are set to zero (hard thresholding) or scaled down (soft thresholding). Though the connection to the l₁-norm is not obvious, it was shown that iterative soft thresholding with replacement minimizes the l₁-norm.⁹⁶ More explicit uses of l₁-minimization have become popular due to a remarkable theorem due to Logan⁹⁷ that states that the spectrum of a signal can be perfectly recovered from an incomplete and noisy set of samples - provided that the signal is bandlimited, the noise is below some threshold, and the spectrum to be recovered is sparse (i.e has few nonzero elements) - by minimizing the l₁-norm.

The concept behind iterative thresholding methods, which have a rich history in the field of image processing^95,98, is simple: starting with time domain data (which falls on a Nyquist grid), set the values for points not sampled to zero, then compute the DFT. In the frequency domain, choose a threshold that is below the value of the largest peak in the resulting trial spectrum, and scale down (iterative soft thresholding, or IST) values above the threshold by subtracting the threshold from their values, or set to zero⁹⁹ all spectral values below this threshold (hard thresholding). Then compute the inverse DFT of the thresholded spectral estimate. These methods are called fixed-point methods because in general the same operation is repeatedly applied to the data until the changes become small, lowering the value of the threshold with each iteration. While iterative thresholding methods mainly have been developed ad hoc, formal results are possible for soft (but not hard) thresholding: the fixed point of soft thresholding minimizes the l₁-norm of the spectrum¹⁰⁰. IST is thus closely related to the compressed sensing approach (which explicitly seeks to minimize the l₁- norm) recently applied in magnetic resonance imaging and subsequently to NMR.^47,101,102 A problem frequently encountered with fixed-point methods is that the step size with each iteration can become vanishingly small before the result has minimal l1-norm.⁹⁶ The choice of thresholding schedule can impact the convergence rate, for good or ill. Although utilitarian rules-of-thumb have been offered⁹⁴, there appears to be little evidence to support the existence of an optimal or universal thresholding schedule.

A more fundamental question posed by compressed sensing and IST is whether the l₁-norm functional is well-suited for regularizing NMR spectra. The assumptions attending Logan’s Theorem are that the signal is band-limited, sparse, and contains bounded noise. Lorentzian lineshapes, however, are not band-limited: their tails extend to infinite frequency (or wrap around in the case of the DFT). Furthermore, in contrast to MRI, where signals are typically confined to a single voxel in the image, NMR signals usually span multiple frequency values. Thus NMR spectra may not fully satisfy the requirements for robust recovery from sparse data. Anecdotal evidence that calls the suitability of the l₁-norm into question is shown in Fig. 11.⁹⁶ The top panel (A) show a one-dimensional spectrum computed using l₁-norm minimization, the bottom panel (B) shows the spectrum computed from the same data using MaxEnt reconstruction. Both are constrained to match the input time-domain data, with the same level of agreement. The peaks highlighted by the red oval correspond to a single synthetic exponentially-decaying sinusoid added to the experimental data. MaxEnt reconstruction correctly returns a single peak, while the l₁-norm spectrum yields artifactual splitting of the single Lorenztian. It has been suggested that this is a result of IST-based methods not being suitable for extrapolation of the signal, i.e. where the time-domain data corresponding to the reconstructed spectrum contains data beyond the last experimentally-sampled data point.¹⁰³ This further restricts the design of sampling schedules where low sampling density at long evolution times may result in such instabilities.¹⁰³ Other features of IST (l₁-norm) spectra that remain unexplained include non-Gaussian noise distributions, which are for example readily apparent in Fig. 11.⁹⁴ Similar non-Gaussian noise distributions can arise with MaxEnt reconstruction when the parameter def is too small.² Fundamentally the differences between IST and MaxEnt spectra are a manifestation of nonlinearities inherent in these non-Fourier methods, which can depend not only on the methods themselves but also the nature of the signals to which they are applied. While this remains an active area of research, it is bears emphasizing that error analysis is important when utilizing non-Fourier methods of spectrum analysis.

Figure 11.

IST spectral reconstruction from NUS data illustrating the non-Gaussian (spiky) noise distribution. Reprinted with permission from Fig. 3D in Stern et al.⁹⁶.

2.5.8. Spectroscopy by Integration of Frequency and Time information

A predecessor to IST was a class of iterative hard thresholding algorithms devised for image processing by Papoulis⁹⁸, Jansson^104,105, van Cittert⁹⁵, and others. The basic idea is to iteratively update an image (or spectral estimate) by suppressing information in “black” regions of the image (or blank regions of the spectrum) while replacing values in the conjugate Fourier domain with empirical data. Herzfeld and colleagues applied this idea to spectrum analysis by iteratively thresholding parts of the spectrum that are believed to be “blank”.¹⁰⁶ While the results can be dramatic, the use of hard limits to the thresholded region makes it difficult to derive formal results that would elucidate the nature of the solution. As with other fixed-point methods, detecting premature convergence can be problematic. Because Lorentzian peaks are not bounded, “leakage” into the thresholded regions is a potential source of artifacts or bias.

2.5.9. MDD

Multi-dimensional decomposition (MDD) was introduced to NMR as three-way decomposition and has also been referred to as multi-way decomposition.⁵⁶ MDD is related to methods such as factorial analysis, principal component analysis (PCA) and singular value decomposition (SVD). The aim is to find a set of one-dimensional vectors that best describe the experimental data (Eq. 5). The assumption is that the multidimensional signal (in either the time or frequency domain) can be described as a sum of the vector outer products of independent one-dimensional “shapes”, e.g. for three dimensions:

$$S_{i,j,k}=\sum _{m=1}^R{A}^{m}F{1}_i^m\otimes F{2}_j^m\otimes F{3}_k^m+e_{i,j,k}$$ (5)

Here S is the measured signal at coordinates (i, j, k), e is the noise component at those coordinates, and A is a diagonal matrix containing the intensity of each signal component. F1–F3 are the normalized one-dimensional vectors describing each component (often referred to as shapes) along each of three dimensions, but the method can be extended to any dimensionality greater than 2. The vectors may be either in the time or frequency domain or a mixture (i.e. the decomposition can be applied to a mixed time-frequency data, e.g. an interferogram). From the above it should therefore be possible to describe the data using R• (i+j+k−2) values (the sum of the lengths of the three one-dimensional vectors, less 2 because one value belongs to all thee vectors) and, so long as the size of the measured dataset is much larger than this value, the data is over-determined and can therefore be solved using a least squares approach. In practice the number of expected signals, R, is a user-defined parameter, which in essence sets the noise threshold. Furthermore, a parameter λ is defined that penalizes large amplitude components, ensuring that large amplitude components that cancel out are not kept. The results are not very sensitive to the value of R, so long as it is set to a value slightly larger than the expected number of peaks. Regularization via λ is important in cases where the data suffers from low SNR or in strongly overlapped regions¹⁰⁷. A feature of this method is that even if some values of S are unknown, but sufficient information is available, the vectors F1–F3 can still be calculated. These components will be complete and can be used to reconstruct a complete dataset. The method can therefore be applied to NUS data. There is, however, an inherent limitation on the amount of data that can be omitted before the least squares problem becomes intractable. To improve on this limitation, the algorithm has recently been extended to assume that the time domain signal has autoregressive properties, i.e. to assume Lorentzian lineshapes.¹⁰⁸ Removing a variable reduces the number of unknowns, allowing for larger portions of the data to be omitted, but as always this is only true if the assumption is correct (see also Section 2.3). This new implementation of the method is referred to as recursive MDD (rMDD).¹⁰⁹

2.5.10. Covariance NMR

Covariance NMR was introduced as alternative to spectral analysis (e.g. FT) for identifying coherences in the indirect dimension of 2D NMR experiments.¹¹⁰ It has subsequently been expanded as a general approach for correlating any experiments that have certain symmetry properties.¹¹⁰ The method in its simplest form uses the fact that processing of 2D spectra involves FT of one dimension, which produces a set of 1D datasets all in the frequency dimension along the first dimension but representing different time points along the second dimension. The modulation of each signal is dependent on its correlated partners. Instead of applying the FT along the second dimension, one can simply ask which frequencies are modulated in a correlated way. A correlation is then calculated for each pair of frequencies; this has the important property that, since the result is a matrix containing correlation information between every frequency pair, the indirect frequency dimension has the same digital resolution as the direct dimension, regardless of how many time increments were actually acquired along the indirect dimension. If the operation is, for example, performed on a singled 1D spectrum the result is a 2D spectrum with correlations between all frequencies that contain a signal. The number of samples acquired in the indirect dimensions does therefore not affect the apparent resolution of the spectrum, instead as additional samples are collected in the indirect dimension the intensity of the “false” correlations will be reduced in relation to those at “true” correlations. One of the interesting properties of this treatment of NMR data is that the data does not need to be uniformly sampled, and NUS data can be used. Indeed, the data may be modulated by any variable that affects correlations. Recent extensions to the original method enable application to heteronuclear correlations (and thus unsymmetrical spectra) through indirect covariance.¹¹¹ This extension, however, requires the correlation of two (or more) two-dimensional spectra that have one dimension in common, e.g. a ¹H-¹³C HSQC and a ¹H-¹H TOCSY. In this example one would be able to extract correlations describing all protons in each carbon spin system. This requires additional filtering and spectral manipulation as it is prone to false positives and requires the input spectra to match well (i.e. it assumes negligible chemical shift differences due to pulse sequence-dependent sample heating, etc.).¹¹¹

3. Non-JEENER Experimental Methods For Speeding up Data Acquisition

All the experimental methods for performing multidimensional experiments discussed thus far elicit coherences by parametric sampling of the indirect dimensions – repeating a one-dimensional experiment while varying delays (the parameters) corresponding to the indirect dimensions – still adhering to the Jeener paradigm employed by conventional uniform-sampling multidimensional FT methods, but using NUS for the parametric sampling of the indirect dimensions. These methods can all be applied to existing NMR pulse sequences with little or no change to the pulse program. However, alternative approaches to speeding up multidimensional NMR have also emerged that do not exploit NUS. Some fundamentally change the way coherences in dimensions beyond the acquisition are elicited. Most of these methods involve significant changes to pulse sequences or even to the spectrometer hardware. Some of the methods can be combined with the NUS methods described above to enable further increases in speed.

3.1. Hadamard spectroscopy

The idea of Hadamard spectroscopy¹¹² is to use a set of frequency-selective pulses to excite only those parts of the frequency domain that contain signals of interest. In some sense this resembles the continuous-wave method used in early NMR spectrometers. In practice multiple discrete frequencies are irradiated in the same experiment and the frequencies are encoded by a Hadamard matrix in which the phase of the pulses is varied (not unlike the G-matrix). In this manner each individual frequency is given a different phase. This spectrum will be highly distorted due to the variable pulse phases. However, if the procedure is repeated n times so that the phases of all individual frequencies are varied in such a way that each can uniquely be identified, the resulting n spectra can be combined to produce a conventional spectrum. The matrix is decoded using the Hadamard matrix (which contains the relevant information regarding the phase of each component in each experiment) to reveal individual frequency components.

3.2. Single scan NMR

Conventional multidimensional NMR experiments subject the entire sample to the same manipulations by RF or magnetic field gradient pulses. In single scan experiments, pulsed field gradients are used to physically divide the sample into spatially-distinct subsets that are subjected to different evolution times.¹¹³ Provided that there are sufficient spins in each subset of the sample to elicit a detectable response, this permits parametric sampling of one or more indirect dimensions in space, rather than time. In this way a complete 2D dataset can be acquired in a single scan. As spectrometers continue to improve in sensitivity, we anticipate that these methods will find increasing application.

3.3. SOFAST

Band-Selective Optimized Flip-Angle Short-Transient (SOFAST)¹¹⁴ experiments (later also referred to as BEST experiments¹¹⁵) speed data acquisition by reducing the relaxation delay required in most NMR experiments. The relaxation delay is used to restore the spin system to equilibrium prior to repeating the experiment (whether for collecting multiple transients, or during parametric sampling of an indirect dimension). The relaxation delay is often a second or longer, and is thus the most time-consuming step in most multidimensional experiments. SOFAST exploits two concepts in reducing the relaxation delay. The first is the fact that the less the spins are perturbed the less time it will take for them to be restored to their equilibrium state. For a given relaxation delay, there is an optimal tip angle that will elicit the largest time-averaged signal-to-noise ratio; this angle is referred to as the Ernst angle.⁵⁰ Second, if a source of non-perturbed ¹H spins is present during the observation of (other) ¹H spins, in large molecules (outside the extreme narrowing region) these will serve to efficiently relax the spins under observation due to cross-relaxation (NOE effect). This effect is more pronounced for larger proteins due to spin diffusion. For proteins the aliphatic protons can be used as the source of unperturbed spins by applying shaped pulses in the low-field NH region. Combining these two principles, the SOFAST technique is able to reduce the relaxation delay by an order of magnitude, allowing more parametric sampling of the data in a given time. SOFAST and BEST approaches are compatible with NUS.^{29, 116}

3.4. Conclusions & outlook

The confluence of improvements in magnets, probes, and computational power has contributed to an explosion of novel approaches for reducing the time required to obtain multidimensional NMR spectra through non-uniform sampling.

NUS provides a means by which the precious (and expensive) instrument time dedicated to acquiring multidimensional NMR spectra can be tailored for the sample conditions and the required information. In the sampling limited regime where high-sensitivity is available (high-sample concentration, cryogenic probe etc.) the spectroscopist can through NUS dramatically reduce the experiment time compared to achieving the same resolution using traditional sampling. Evidence from the literature shows that NUS can in extreme cases be used to acquire 4D spectra by sampling less than 1% of a time-domain, which would require months of acquisition time using traditional sampling⁹³. In the sensitivity-limited regime where low SNR poses difficulties in uncovering important correlations (e.g. due to poor solubility of samples at high-concentrations) NUS can be used to improve the SNR per unit time compared to traditional sampling, instead of reducing experiment time.

Regardless of the sampling regime, the gains that can be achieved employing NUS are closely tied to the ability of the method of spectrum analysis employed to suppress sampling artifacts. It is therefore not surprising to find that researchers have intensely investigated a multitude of novel methods for processing NUS data. Each new method (over 10 in the past decade) introduces new terminology, concepts, and acronyms, which unfortunately has contributed to poor penetration of some of the new methods. The situation is exacerbated by the relative dearth of quantitative comparisons of competing methods, so it is the joint responsibility of spectroscopists and method developers to ensure that these methods are critically compared through application to real-world problems. Thus far, most of these methods have been applied mainly to highly sensitive experiments on protein samples with relatively high concentrations of 1–3 mM. Most proteins cannot be concentrated to anywhere near such levels, and the known favourable properties of ubiquitin hardly make this a challenging benchmark sample.

If trends of the past decade hold, then the development of still more methods can be anticipated. To assess the utility of any new method for NMR data acquisition and processing two fundamental questions must be addressed: when does the method break down (i.e. due spectral crowding or low signal-to-noise ratio) and how does the method break down (i.e. what is the nature of any artifacts, and how accurate is the method in terms of false positives, false negatives, and amplitude and frequency?). While there have been some notable attempts to address these questions for the methods described here, there is still much to learn. The qualitative comparisons offered here serve as a prelude to more quantitative critical comparisons that remain sorely needed.

Figure 10.

Spectra computed from uniformly sampled data using IST (A) and MaxEnt (B). A single exponentially decaying sinusoid was added to the experimental time-domain data, with a frequency indicated by the red oval.