Virus-host arms race at the joint origin of multicellularity and programmed cell death

Abstract

Unicellular eukaryotes and most prokaryotes possess distinct mechanisms of programmed cell death (PCD). How an “altruistic” trait, such as PCD, could evolve in unicellular organisms? To address this question, we developed a mathematical model of the virus-host co-evolution that involves interaction between immunity, PCD and cellular aggregation. Analysis of the parameter space of this model shows that under high virus load and imperfect immunity, joint evolution of cell aggregation and PCD is the optimal evolutionary strategy. Given the abundance of viruses in diverse habitats and the wide spread of PCD in most organisms, these findings imply that multiple instances of the emergence of multicellularity and its essential attribute, PCD, could have been driven, at least in part, by the virus-host arms race.

Abbreviations

AI

abortive infection

PCD

programmed cell death

TA

toxin-antitoxin

Introduction

Viruses are the most abundant biological entities on earth: all cellular organisms exist under a constant viral onslaught.^1-4 Emergence of virus-like parasites has been shown to be inevitable even in simplest replicator systems.^5,6 Thus, the entire history of life involves the perennial host-parasite arms race during which the hosts have evolved a vast repertoire of defense systems.^4,7,8 In addition to active defense, i.e. immunity, most if not all cellular organisms possess mechanisms of programmed cell death (PCD)^9-12 to which cells turn when immunity fails. Traditionally, PCD is considered an essential attribute of multicellular eukaryotes, in particular animals.^11,12 In multicellular organisms, PCD appears to be “altruistic” with respect to individual cells, because cell death is beneficial for the organism as a whole, either as a mechanisms of resistance to infection or tumorigenesis or as a developmental mechanism. However, both unicellular eukaryotes and most prokaryotes possess their own, distinct forms of PCD. In bacteria and archaea, PCD is executed by toxin-antitoxin (TA) and abortive infection (AI) systems that are induced in response to genotoxic stress and cause dormancy or cell death.^10,13,14 The TA and AI modules abound in archaeal and bacterial genomes and often are encoded within the same loci with immunity systems, suggestive of coupling between the 2 types of defense.^15,16

The emergence of an “altruistic” trait, such as PCD, in unicellular organisms is a thorny theoretical question. So far the leading explanation appears to be the production of “public goods” whereby dying cells become a source of nutrients for their neighbors. The utility of public goods, especially under stress conditions, could drive evolution of cellular cooperation and its extreme form, PCD.^17-20 Without questioning the plausibility of the public goods concept, we were interested to investigate whether PCD could evolve in unicellular organisms as an anti-pathogen defense strategy. To this end, we developed a mathematical model of virus-host co-evolution in which interaction between immunity, PCD and cellular aggregation was incorporated. Investigation of this model shows that under high virus load and imperfect immunity, co-evolution of cell aggregation (a primitive form of multicellularity) and PCD is the optimal evolutionary strategy.

Results

Under the model, the population of host cells is idealized as a set of clusters of variable sizes which behave independently of each other, and whose growth rates depend on their sizes. A cluster is characterized by the number of cells and pathogens (viruses) that it contains. With respect to the infection dynamics, clusters are considered well-mixed systems. Accordingly, upon arrival of a pathogen to a cluster, all cells become susceptible to infection. The dynamics of a cluster of size k (i.e., a cluster composed of k cells and any number of pathogens) is driven by the following processes:

1. Host replication at a rate ${\displaystyle {\text{r}}_{\text{k}}}$ (where k denotes the size of the cluster) which may result in cluster growth (with probability 1-p_m) or in the formation of a new cluster of size one (with probability p_m). Migration probability p_m determines the propensity of the cells to form singletons instead of multicellular assemblies. The extreme case p_m = 1 corresponds to a purely unicellular population.

2. Host death at a rate ${\displaystyle {\text{d}}_{\text{k}}}$, which results in reduction of the cluster size to k-1. Host death in clusters of unity size leads to the extinction of the cluster.

3. Pathogen arrival at a rate ${\displaystyle {\text{a}}_{\text{k}}}$ which increases by one unit the amount of pathogens in the cluster.

4. Infection at a rate b multiplied by the number of pathogens in the cluster. Infection results in one of 3 outcomes: (a) Cell dies and no pathogen is produced (PCD or suicide), with probability (1-p_i/2) p_s. (b) Cell survives and no pathogen is produced (efficient immunity), with probability (1-p_s/2) p_i. (c) Cell dies and M pathogens are produced (efficient infection), with probability (1-p_s)(1-p_i). Parameters p_s and p_i determine, respectively, the propensity to commit suicide and the immune efficacy of the hosts.

5. Degradation of pathogens at a rate w (per pathogen).

The dependences of growth, death and pathogen arrival rates on the cluster size are based on the following rationales. In the absence of pathogens, isolated cells grow faster than those in clusters because the latter are subject to local depletion of nutrients and other inhibitory interactions.²¹ Thus, the expression ${\displaystyle {\text{r}}_{\text{k}}={\text{rk}}^{\text{γ}}}$ with ${\displaystyle \text{γ}1}$ is used to model the per cluster growth rate. Death rate is assumed to be constant for all cells, independent of the cluster size. Therefore, per cluster death rate is proportional to the cluster size${\displaystyle {\text{d}}_{\text{k}}=\text{dk}}$. Finally, the decreasing surface-volume relation for larger clusters translates into a pathogen arrival rate that grows with the cluster size as ${\displaystyle {\text{a}}_{\text{k}}={\text{ak}}^{\text{α}}}$. Under the assumption that clusters have a globular shape, we take α = 2/3. The same expression, with arbitrary values of ${\displaystyle \text{α}1}$, would account for situations where cell clustering generates any type of barrier against the arrival of pathogens. Fitness costs associated with possessing PCD and immunity are included in the model. These costs are proportional to p_s and p_i, with proportionality constants c_s and c_i, respectively, and are modeled as additional death rates.

The model is implemented as a Markov process, with the states of the system corresponding to the possible cluster configuration, i.e. the number of cells and pathogens in the cluster. For computational efficiency, the maximum cluster size is limited to 30 hosts and 299 pathogens resulting in a total of 9000 possible states. Transition rates between any 2 states are calculated according to the processes described above and stored in a transition matrix Q. Solving the model equals numerically obtaining the largest eigenvalue of Q and its associated eigenvector. The largest eigenvalue corresponds to the mean fitness of the population in the stationary state. In addition, the associated eigenvector provides the stationary composition of the population.

Unless otherwise specified, the parameters of the model were assigned the following values: growth and death rates, r = 1.01 and d = 0.01, so that the net growth rate of singletons defines the unit of time; equal infection and pathogen degradation rates, b = w = 20; offspring size M = 2 (this small value captures the fact that in a 3-dimensional cluster only a limited number of neighboring cells are accessible to the offspring); equal fitness costs for suicide and immunity, c_s = c_i = 0.05; growth scale exponent ${\displaystyle \text{γ}}$ = 0.9. With these particular parameter values, the limitation on the maximum number of pathogens per cluster has little or no effect  because in practice they never get close to the limit. Limiting the cluster size becomes relevant for very small values of the migration probability, which tend to give rise to large clusters. To minimize biases associated to cluster size limitation, we empirically set p_m =0.05 as the minimum possible value of the migration probability.

We first used the model to test whether PCD is an evolvable defense mechanism in multicellular clusters compared to single cells. To this end, the migration probability was assigned a small value (p_m = 0.05) so that hosts self-organize in clusters with characteristic sizes of 5-6 hosts per cluster or a high value (p_m = 1.00) such that no aggregation occurs. For different values of the pathogen arrival rate, the average fitness of hosts was calculated as a function of the suicide probability. For the multicellular population, at sufficiently high pathogen arrival rates, the higher suicide propensities lead to higher fitness (Fig. 1A). In contrast, a population composed of single cells achieves maximum fitness when the suicide probability is equal to zero (Fig. 1B). This outcome is due to the fact that PCD is a costly defense mechanism which only becomes beneficial when PCD-endowed cells are clustered such that suicide of an infected cell prevents the spread of the virus to the rest of the cells in the cluster. Thus, PCD evolves only in structured, i.e., effectively multicellular populations.

Figure 1.

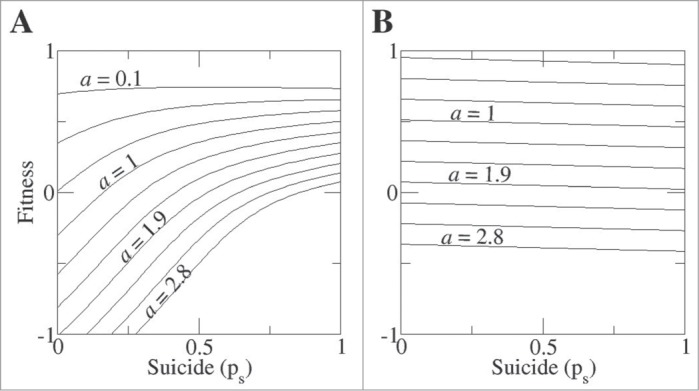
Programmed cell death provides multicellular clusters, but not singletons, with a fitness advantage. The fitness of hosts that form multicellular clusters (A, p_m = 0.05, characteristic cluster size of 5-6 hosts) and singletons (B, p_m = 1) is calculated as a function of the suicide probability. Different curves correspond to increasing values of the pathogen arrival rate a, with top-to-bottom increments of 0.3 between consecutive curves.

To thoroughly explore the continuum of migration and suicide strategies, the combined migration-suicide fitness landscape has to be analyzed. Analysis of these landscapes (Fig. 2) identified 2 fitness peaks that correspond to 2 extreme strategies for the hosts: (i) unicellular with no suicide (p_m = 1, p_s = 0) and (ii) multicellular with high probability of suicide (p_m = 0.05, p_s = 1). The relative heights of the 2 fitness peaks depend on the pathogen arrival rate. Low pathogen arrival rates make the unicellular state the most favorable one (Fig. 2A). Conversely, when pathogens are abundant, the highest fitness corresponds to hosts that form multicellular clusters with high suicide propensity (Fig. 2C). Intermediate pathogen arrival rates result in 2 fitness peaks, one corresponding to the unicellular state without suicide propensity and the other to the multicellular state with the highest suicide probability (Fig. 2B). Notably, the 2 fitness peaks are separated by a valley indicating that the transition to the multicellular state has to be coupled with the acquisition of PCD (Fig. 2B). Thus, neither multicellularity nor PCD alone, but only their combination, is favored by the exposure to pathogens. As the pathogen arrival rate crosses a critical value (in this particular case, a = 1.05), the host population experiences an abrupt transition from the unicellular to the multicellular state (Fig. 3). Further increase in the pathogen arrival rate results in negative fitness values which imply extinction of the host (Fig. 3).

Figure 2.

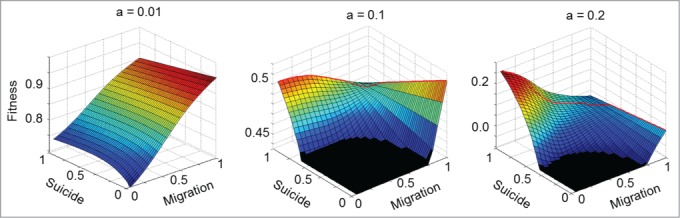
Fitness landscapes associated to the probabilities of host suicide and migration. As the pathogen arrival rate increases, the higher fitness peak transitions from the unicellular state with no suicide (p_m = 1, p_s = 0) to the multicellular state with the highest suicide probability (p_m = 0.05, p_s = 1). The red line shows the evolutionary trajectory with the minimum fitness loss connecting the 2 fitness peaks. Black areas indicate a cutoff in the plot.

Figure 3.

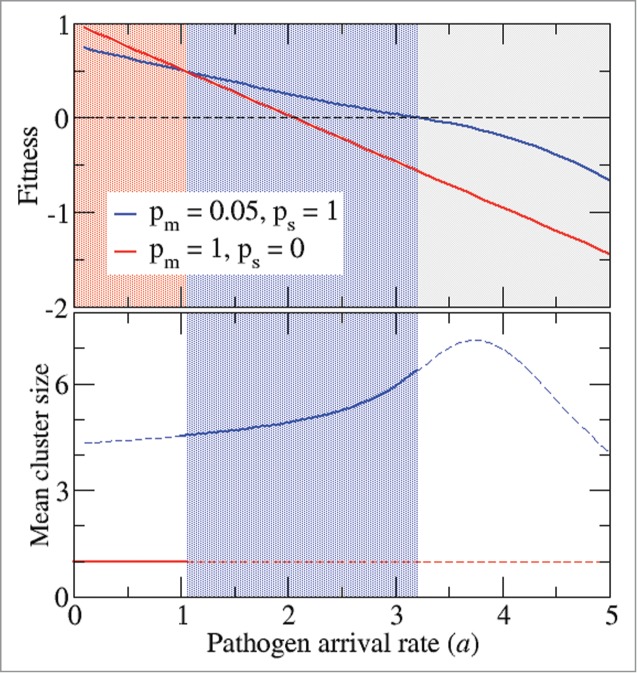
Exposure to pathogens determines the evolutionary outcome. Top: In blue (red), mean fitness of a population of hosts that self-organize in multicellular (unicellular) clusters with (without) programmed cell death. Bottom: Mean cluster size for the same populations. The continuous line indicates the expected cluster size if both classes of hosts compete. When the pathogen arrival rate is greater than 3.2, both classes of hosts become extinct.

These results are qualitatively robust to changes in the growth scale exponent ${\displaystyle \text{γ}}$. Quantitatively, the ranges of pathogen arrival rates that lead to multicellularity vary depending on the value of ${\displaystyle \text{γ}}$ (Fig. 4). Values of ${\displaystyle \text{γ}}$ closer to unity (small growth disadvantage for large clusters) reduce the pathogen pressure that is required for multicellularity to evolve. Concomitantly, larger values of increase the maximum pathogen pressure that the host population can tolerate.

Figure 4.

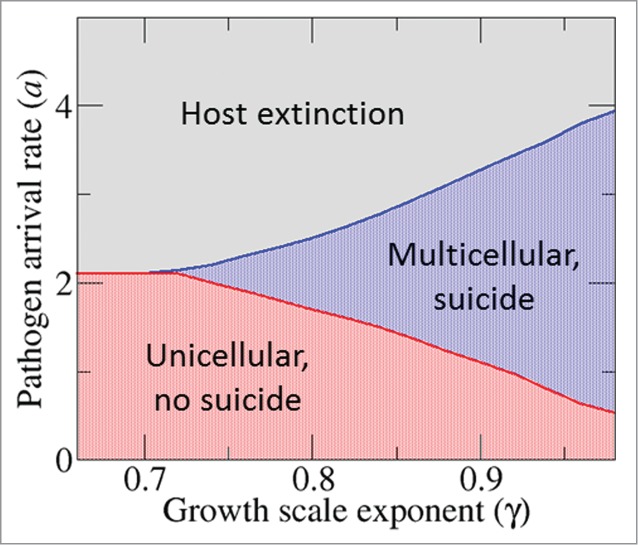
Outcome of the competition between the 2 extreme classes of hosts (p_m = 0.05, p_s = 1; and p_m = 1, p_s = 0) as a function of the pathogen pressure, a, and the growth scale exponent, ${\displaystyle \text{γ}}$. Values of ${\displaystyle \text{γ}}$ close to one expand the range of pathogen arrival rates that lead to the multicellular state.

In contrast to PCD, immunity is beneficial to both clusters and singletons. A comparison between suicide and immunity as defense mechanisms is presented in Figure 5. The fitness of 2 populations with extreme values of the migration probability (giving rise to multicellular clusters and singletons, respectively) was calculated depending on the suicide and immunity propensities. Although immunity greatly increases the fitness of hosts in multicellular clusters, it never allows them to outcompete unicellular forms. Conversely, certain minimum suicide propensity is required to make the multicellular strategy advantageous. Individual-level immunity substantially affects the evolution of multicellularity (Fig. 6A). A comparison of the fitness of multicellular forms with variable suicide and immunity propensities to the fitness of unicellular forms with no suicide and the same level of immunity shows that multicellularity and PCD evolve only when the efficacy of immunity does not exceed a threshold value (Fig. 6). The same result was observed regardless of the pathogen arrival rate (Fig. 6B).

Figure 5.

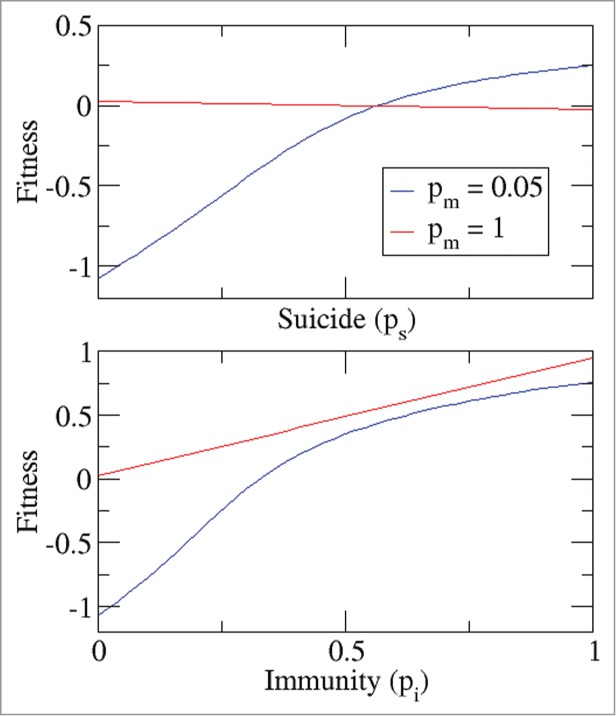
Suicide and immunity are not equivalent. In blue (red), mean fitness of a population of hosts that self-organize in multicellular (unicellular) clusters, as a function of the immune probability p_i (top) and the suicide probability p_s (bottom). Pathogen arrival rate a = 2.

Figure 6.

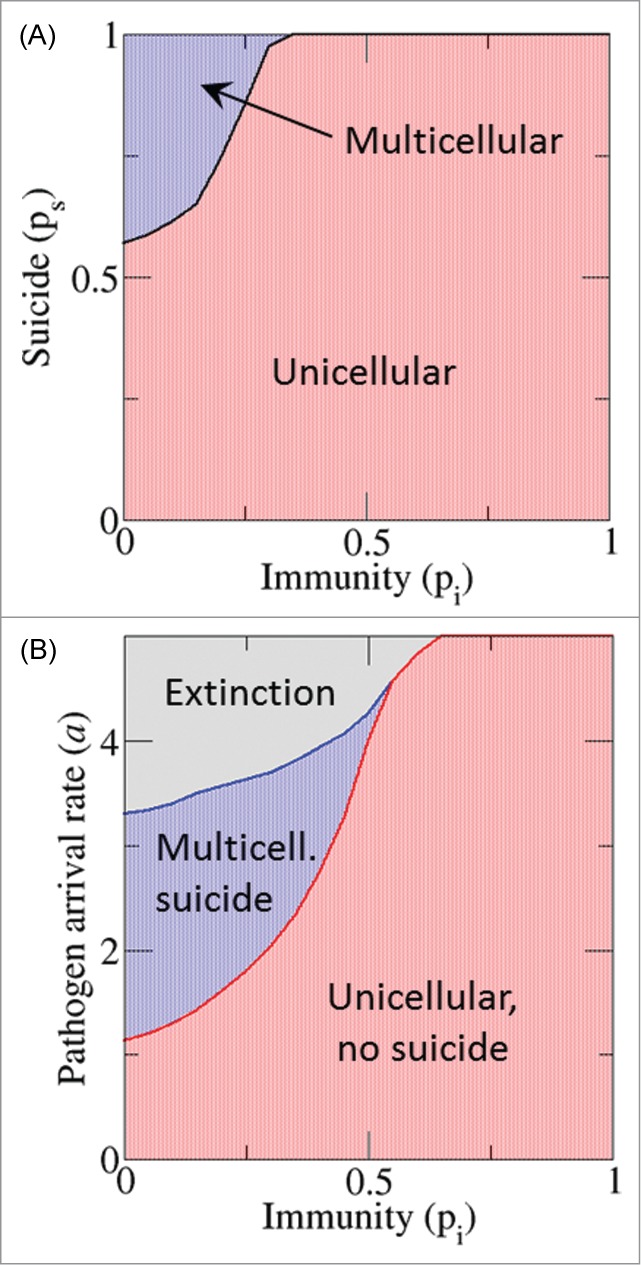
Effect of immunity on the evolution of multicellularity. (A) The fitness of hosts with p_m = 0.05 (multicellular organization) and variable suicide and immune probabilities (p_i on the x-axis, p_s on the y-axis) is compared to those of hosts with p_m = 1 (singletons), same immune probability and no suicide. The border between red and blue regions indicates the minimum suicide probability required for multicellularity to evolve. Pathogen arrival rate a = 2. (B) Evolutionary outcomes for different values of the pathogen arrival rate and the immune probability, with the suicide probability of multicellular hosts fixed to p_s = 1. The border between the blue and gray regions shows the pathogen arrival rate that leads to the extinction of the host at different immune probabilities.

Discussion

Within the framework of the present model, in the absence of pathogens, faster reproduction of single cells favors the unicellular state. In contrast, in the presence of pathogens, clusters of cells can benefit from PCD as a defense mechanism additional to immunity and hence outcompete single cells. A key conclusion from the analysis of the model is that multicellularity and PCD are coupled: one could not evolve without the other. Joint evolution of multicellularity and PCD appears to be beneficial in microbial populations that are regularly exposed to pathogens as a way to overcome the limited the efficacy of immunity mechanisms. Given the extremely high abundance of viruses in diverse habitats^1-3 and the apparent coevolution of viruses and cells throughout the history of life,⁴ the model predicts this to be the case for most cellular life forms. Indeed, numerous bacteria and archaea have been shown to self-organize into various forms of multicellular aggregates, in particular through quorum sensing^17,22,23 or diffusion sensing.²⁴ Independent evolution of such multicellular forms in diverse prokaryotes could have been driven by the necessity of antivirus defense that involves PCD as an essential component.

Clearly, antivirus defense is not the only advantage of multicellularity. In particular, production of “public goods”, i.e. the utility of dying cells as a source of nutrients, especially under starvation, would also favor intercellular cooperation including altruistic PCD.^{17-19,23,25,26} However, given the perennial virus-host race, resistance to infection is likely to have been an important if not the primary driving force of the evolution of PCD-endowed multicellular forms. Notably, it has been shown experimentally that protist predation favors cooperation of Pseudomonas aeruginosa cells via quorum sensing,²⁷ a finding compatible with the result of the present work.

As is the case for any altruistic behavior, evolution of PCD encounters the problem of cheaters, i.e. cells that shed the suicide machinery but benefit from other cells committing suicide.^23,25,26,28 The solution to the cheating problem is kin selection (inclusive fitness)^29,30 whereby microbial cells that form a multicellular aggregate are close relatives.²³ Kin selection is likely to have been essential in the virus-driven evolution of multicellularity predicted by the present model.

The predicted evolutionary coupling of PCD with multicellularity seems to be a chicken-or-egg paradox. The solution might lie in the fact that prokaryotic PCD systems, the TA and AI modules, possess properties of selfish genetic elements that are addictive to cells that harbor them.^10,14 Conceivably, these systems evolved as addiction modules of plasmids and subsequently were recruited by microbes as ready-made PCD devices. The key contribution of selfish genetic elements is emerging as a universal theme in the evolution of defense systems including restriction and modification³¹ and CRISPR-mediated adaptive immunity^32,33 in prokaryotes as well as the immune system of vertebrates.³⁴

Materials and Methods

The model deals with a population of hosts (cells) that self-organize in clusters of different sizes and contain a variable number of pathogens (viruses). All possible cluster compositions in the range from one to 30 hosts and zero to 299 pathogens were considered. The composition of the population was represented by a vector x, where x_(k,l) corresponds to the fraction of clusters which contain k hosts and l pathogens. Based on the rules of the model, transition rates were computed for each possible pair of cluster compositions. Transition rates were stored in a transition matrix Q, with the index q_{(k,l), (m,n)} corresponding to the directed transition from a cluster with k hosts and l pathogens to a cluster with m hosts and n pathogens. The diagonal terms of Q were made equal to one minus the sum of transition rates to other states, including those leading to the implicit "empty" state (i.e., host death in clusters of size one). The population dynamics of this system is governed by the differential equation ${\displaystyle \stackrel{.}{x}=Qx-\varphi x}$, where ${\displaystyle \varphi ={{\displaystyle \sum }}_{\left(\text{k},\text{l}\right),(\text{m},\text{n})}{\text{q}}_{\left(\text{k},\text{l}\right),(\text{m},\text{n})}{\text{x}}_{\left(\text{k},\text{l}\right)}}$ ensures that ${\displaystyle {{\displaystyle \sum }}_{(\text{k},\text{l})}{\text{x}}_{(\text{k},\text{l})}=1}$ Because Q is non-negative and irreducible, it follows from the Perron-Frobenius theorem that the system has at least one stationary state. Such a stationary state is described by the principal eigenvalue and eigenvector of Q, the former corresponding to the average fitness of the population and the latter to its composition. The eigenvalue and eigenvector were numerically computed by using the function "eigs()", as implemented in Octave, version 3.8.1 (http://www.gnu.org/software/octave/).

Funding Statement

The authors’ research is supported by intramural funds of the US Department of Health and Human Services (to the National Library of Medicine).

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.

Acknowledgments

We thank Koonin group members for useful discussions.