Abstract
Biochemical reaction networks consisting of coupled enzymes connect substrate signaling events with biological function. Substrates involved in these reactions can be strongly influenced by diffusion “barriers” arising from impenetrable cellular structures and macromolecules, as well as interactions with biomolecules, especially within crowded environments. For diffusion-influenced reactions, the spatial organization of diffusion barriers arising from intracellular structures, non-specific crowders, and specific-binders (buffers) strongly controls the temporal and spatial reaction kinetics. In this study, we use two prototypical biochemical reactions, a Goodwin oscillator, and a reaction with a periodic source/sink term to examine how a diffusion barrier that partitions substrates controls reaction behavior. Namely, we examine how conditions representative of a densely packed cytosol, including reduced accessible volume fraction, non-specific interactions, and buffers, impede diffusion over nanometer length-scales. We find that diffusion barriers can modulate the frequencies and amplitudes of coupled diffusion-influenced reaction networks, as well as give rise to “compartments” of decoupled reactant populations. These effects appear to be intensified in the presence of buffers localized to the diffusion barrier. These findings have strong implications for the role of the cellular environment in tuning the dynamics of signaling pathways.
I. INTRODUCTION
Biochemical pathways often involve coupled enzyme reactions linked through diffusing substrates. Numerous physical and chemical factors within the cell influence the time scale and efficiency of these reactions, including diffusion coefficients, crowding, long-range electrostatic interactions, and enzyme distribution.1–3 Recently, we quantified the impact of crowding and competition on a substrate/enzyme association rate4 as well as the impact of proximity and electrostatic interactions on reaction rates in coupled enzyme systems.5 In the first study, we found that the density of off-target crowders greatly attenuated the substrate association rate, which was not unexpected given the inverse relationship between effective diffusion coefficients and the accessible volume fraction6,7 (see also Figure 1(a) and Fig. 3 of Ref. 8). Moreover, we demonstrated that competitive binding of substrate by these crowders further reduced the effective reaction rate in a non-linear fashion, in a manner analogous to strongly buffered systems, where the effective diffusion coefficient may be significantly attenuated depending on the buffer concentration, equilibrium constant, and diffusivity.9 In the second study,5 we quantified the competition between the proximity of two enzymes participating in a sequential set of reactions, electrostatic interactions between a diffuser and the enzymes or crowders, and the volume excluded by those enzymes (see Figure 1(b)). We found that the evolution of product could be accelerated by favorable electrostatic interactions between a substrate and the enzyme at which it is consumed, or by lining a channel between enzymes with charges complementary to the intermediate, similar to electrostatic channeling observed between active sites in bifunctional enzymes.10–14 The interplay between enzyme proximity and interactions, between substrates and crowders, or the enzymes themselves raises an interesting question: to what extent does the crowded cell cytosol and co-localization of sequential enzymes influence diffusion-influenced reaction kinetics, and furthermore, could these perturbations tune the kinetics of biochemical reaction pathways?
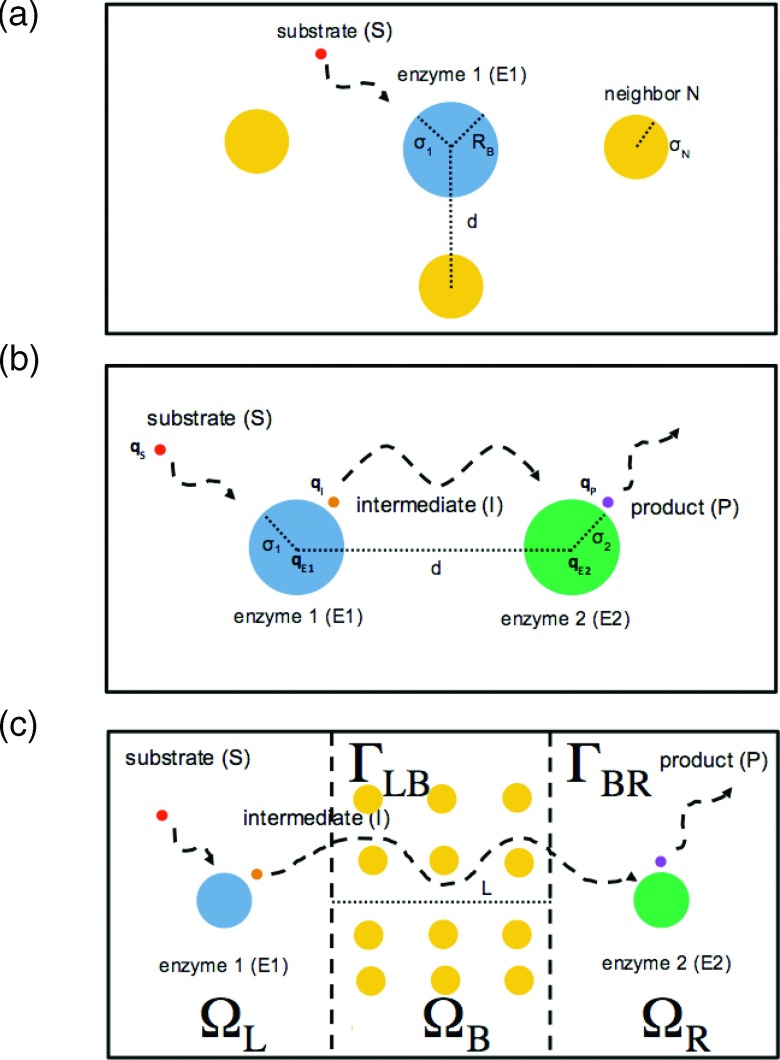
FIG. 1.
(a) Reaction with crowded enzyme, (b) sequential reactions, and (c) reaction-diffusion compartments. Reactions are generally restricted to compartments L and R. Diffusion through compartment B may be fast (unrestricted) or slow (hindered).
We approached this problem by partitioning enzymes into well-mixed compartments (ΩL, ΩR) separated by a variable-length diffusion barrier (ΩB), whose composition (accessible volume fraction, interaction potentials, and buffering capacity) modulates substrate diffusion rates, which can ultimately result in decoupled, or “compartmented,” reaction behavior (see Figure 1(c)). The basic idea of our model is that the biochemical reactions in two separate compartments are coupled and regulated by signaling molecules transported between enzyme populations. In general, well-mixed compartmented reactions are frequently described by ordinary differential equations (ODEs) that account for reaction kinetics in two or more sub-volumes that communicate through a diffusion barrier.15 A popular model for compartmented calcium signaling in the heart,16 for instance, assumes that the diffusional flux between two substrate pools, or compartments, J, scales as J ∝ Δc/Δx, where Δc and Δx correspond to the concentration difference and distance between compartments, respectively. Such formulations assume that concentration gradients between compartments are linear, yet challenging this assumption are recent simulations17,18 demonstrating that concentration gradients can be strongly non-linear between regions traditionally designated as compartments. At a minimum, one dimensional partial differential equation (PDE) models of the barrier compartment are sufficient to describe the spatial variation of the concentration gradient radiating from the compartment boundaries, provided that care is taken to conserve its volume as its length between the well-mixed compartments is varied. While this could be accomplished for reduced-dimension systems by appropriately scaling the governing differential equations by the barrier’s volume fraction, we proposed a three-dimensional model to facilitate its extension to intracellular structural data, which has previously been shown to introduce significant spatial heterogeneity and diffusional anisotropy.19,20
Specifically, we modeled signal transfer through the diffusion barrier, by defining ΩL and ΩR as well-mixed compartments (no spatial concentration dependence), whereas the spatial evolution of the substrate concentrations was explicitly modeled in the middle compartment (ΩB). We assumed that the three compartments were sequentially linked (see Figure 1(c)), for which the enzymes were restricted to the first (ΩL) and third compartments (ΩR), within which substrate diffusion was rapid and concentrations were spatially uniform. This formulation allowed us to neglect details of the enzyme shape and size, in contrast to our previous studies,14,21 for which the close enzyme proximity necessitated detailed geometries for each enzyme. In the second compartment linking the first and third enzyme-containing compartments, we used physiologically reasonable diffusion coefficients. It was within the second compartment that we explicitly considered the time-dependent changes in the spatial distribution of substrates via the numerical solution of reaction-diffusion partial differential equations, which would be difficult to solve analytically or via simplified ordinary differential equation models.
With this model system, we analyzed how the diffusional barrier composition influences reaction kinetics by modifying the transport of signal substrates between two intracellular compartments, namely, by defining a diffusion constant as a function of position, D(r), within the barrier region; we varied this constant in accordance with accessible volume fraction due to crowders, substrate-crowder interactions, and buffer concentrations. We applied these position-dependent substrate diffusion constants to two reaction-limited oscillatory systems reminiscent of signal transduction pathways, to investigate their impact on oscillation frequency and amplitude. We emphasize that this oscillatory behavior is a common motif in the regulation of biochemical processes22–24 and the role of diffusion in controlling oscillations has recently been examined.25 Specifically, we considered two systems, a Goodwin oscillator and a reaction with a periodic source/sink term, whose periodicity arises either from an endogenous source (negative feedback within the cell compartment) or exogenous source (oscillatory production by a process external to the cell compartment), respectively.23 By varying substrate diffusivity, we showed that the dynamics of oscillatory systems were highly dependent on enzyme separation and diffusion rates within the barrier. Overall, these simulations reveal a mechanism for tuning biological reactions by enzyme distributions and interactions of reaction substrates with the crowded cellular environment.
II. METHODS
A. System configuration
We considered three compartments that were sequentially linked (see Figure 1(c)): compartment L (ΩL), compartment B (ΩB), and compartment R (ΩR). Compartments ΩL and ΩR were treated by ordinary differential equations (described below), while we explicitly modeled diffusion in ΩB. Fluxes between domains occurred at ΓLB and ΓBR, which were surfaces linking compartments L and B and compartments B and L, respectively. We fixed the volumes of ΩL and ΩR to 1.0 μm 3 and ΩB to 0.001 μm 3 for both reaction schemes. For the periodic reaction, we modulated barrier distance between well-mixed compartments by changing the length of ΩB, while resizing the orthogonal dimensions to preserve the compartment volume. By altering the diffusion coefficients for each substrate in compartment B, we simulated the effect of barriered diffusion between compartments ΩL and ΩR.
B. Biological reaction systems
1. Generalized Goodwin oscillator
We generalized a Goodwin oscillator model of negative feedback inhibition26 (see S1 in Ref. 68) to take into account the compartmentation of enzymes and transport of substrate between the compartments. Our model for the reactions inside the ΩL and ΩR regions is represented by the ordinary differential equations,
| (1) |
| (2) |
| (3) |
| (4) |
where the ki are reaction rates and Km is a binding constant. The first term in the right-hand side (RHS) of Eq. (1) represents the synthesis of AL, while the second RHS term of Eq. (4) represents the degradation of CR; all other reactions represent conversion of one substrate to the next in sequence. In this study, we assume k1 = k2 = k3 = 1.0 ms−1 for simplicity. We further partitioned the first two reactions (generation of substrates A and B) into compartment ΩL and the last two reactions (consumption of substrate B and production of substrate C) to compartment ΩR. Note that in connection to signal transduction, the substrate B (substrate for second reaction) and the substrate C (negative feedback substrate) can be considered as signal molecules between two separate reactions in the compartments ΩL and ΩR. No reactions occurred in ΩB, which we assumed was 10 nm in length. Our model thus deviated from the typical well-mixed assumption of all reactions occurring in the same compartment. The transport of the chemical species, A, B, and C in ΩB is described by diffusion partial differential equations, subject to boundary conditions representing the diffusive flux between compartments (see Section II C).
2. Periodic reaction
We also considered a single substrate/enzyme reaction, in which the substrate is periodically produced and degraded to represent an oscillatory source/sink arising from an external source (ES),
| (5) |
where v0 controls the amplitude of A and α sets the frequency. This reaction was restricted to compartment ΩL, while no reactions occurred in compartments ΩB and ΩR.
C. Numerical solutions
We generated three-dimensional meshes for the diffusion barrier ΩB of length barrierDist using the UnitCube function from the finite element solver FEniCs.27 Similar to a previous study,28 we modeled the coupled reaction diffusion systems by operator-splitting the diffusion and reaction components. For the latter, we solved reactions 1-4 or reaction 5 over dt = 0.03 ms time intervals for 1500 steps using the scipy ODE integrator scipy.integrate.odeint under its default configuration that calls the lsoda algorithm.29 The ODE integrator yields an updated reaction term Rj for each species j that we applied to the following reaction-diffusion PDE system:
| (6) |
| (7) |
where cj(t) is the concentration of species j at time t, Dj is the diffusion constant for species j, and jkB is the diffusional flux between compartment k = L, R and spatial domain ΩB. θkB is the volume fraction defined as θkB = VΩB/VΩk, for which VΩB and VΩk are the volumes of ΩB and Ωk, respectively. The diffusional flux across interface ΓkB (jkB) was determined by
| (8) |
where DkB is the diffusion constant through a thin interface comprising ΓkB with area Akb and depth dkB. The interface depth is chosen such that dkB ≪ barrierDist. All other boundaries were assumed reflective (e.g., ). We then determined the weak form of time-dependent diffusion system Eq. (6) via standard procedure,30 which was solved using a piecewise linear Galerkin finite-element method with the default direct linear solver and solver parameters. Initial conditions for all species in each compartment are summarized in Table 1.68 Concentrations within compartments ΩL and ΩR were provided as outputs from the scipy.integrate.odeint, while those from compartment ΩB were obtained by calling the assemble function. In Figure S7,68 we verify that numerical estimation of the time-dependent concentration within ΩB agrees with analytical estimates of the diffusion equation, subject to the conditions of no reactions and no diffusion between compartments (e.g., Rj = 0 and DkB = 0). Given the computational expense for performing the reaction-diffusion simulations, we did not pursue rigorous sensitivity analysis, although we believe the range of diffusion coefficients, barrier lengths, and kinetic parameters explored in the manuscript provide an adequate demonstration of the model’s behavior. The code will be released at https://bitbucket.org/huskeypm/enzymekineticsacs.
III. RESULTS
A. Goodwin oscillator
We first compare the well-mixed (ODE) formulation of the Goodwin oscillator with our PDE implementation under nearly well-mixed conditions. In this example, we assumed very fast (effectively infinite) diffusion (Di ≫ Dwater = 2.6 μm2/ms (Ref. 67)) of all substrates across ΩB, which separates the well-mixed compartments ΩL and ΩR by 10 nm. The total concentrations of substrates A (red), B (blue), and C (green) for all compartments in the PDE model are reported in Figure S1,68 for which we show that the PDE solutions (dots) closely tracked the ODE solution (lines). For all substrates, we observe stable oscillations about mean values of approximately 1.2 μM, while A presented the largest fluctuations (≈0.6-2.0 μM), B the second largest (≈0.8-1.6 μM), and C the smallest (≈1.0-1.4 μM). The period length was approximately 4 ms and we also note that the maxima for B and C lagged those for A by less than 1.0 and 2.0 ms, respectively. We furthermore demonstrate in Figure S2(a)68 that the substrate concentration profiles within each compartment were oscillatory and nearly identical in amplitude, although we note some variation for B, with largest and smallest profiles evident in ΩL and ΩR, respectively. In Figure S2(b),68 we present spatiotemporal plots of substrate concentrations within ΩB, where the x-axis is the distance (nm) along the barrier and the y-axis is time (ms), to illustrate substrate diffusion between compartments. We note that the time-dependent substrate distributions were nearly uniform as a function of position owing to rapid diffusion; in other words, the concentration profiles for a given substrate were nearly synchronized at boundaries ΓLB and ΓBR.
We next reduced the substrate diffusion coefficients to a non-infinite but nonetheless rapid rate (Dwater = 2.6 μm2/ms) to simulate the spatial separation of enzyme reactions 1 and 2 from those of reactions 3 and 4. By using a diffusion constant comparable to bulk water, we are effectively assuming rapid, barrierless diffusion between compartments. In Figure 2(a), we show that the period was nearly identical to the very fast diffusion case, although most significantly there was a greater degree of dispersion, or spreading out, of the concentration profiles between compartments for substrate B. This dispersion was particularly evident in the spatiotemporal plot for substrate B (Figure 2(b), middle), where a clear concentration gradient emerged during the upswing of B’s concentration profile, with [B] = 1.7 μM at ΓLB relative to 1.6 μM at ΓBR. The gradient arises because B was generated in ΩL and consumed in ΩR, which is similar to behavior expected for a standard steady-state diffusion equation subject to a positive Dirichlet condition (or source) on ΓLB and an absorbing condition (or sink) on ΓBR.
FIG. 2.
Goodwin oscillator with spatially decoupled enzymes. (a) Concentrations of A (red), B (blue), and C (green, the inhibitory substrate) for compartments ΩL (+), barrier ΩB (.), and ΩR (×) in the presence of a 10 nm diffusion gap and diffusion coefficient equal to bulk water (Di = 2.6 μm2/ms). (b) Substrate concentrations for A (left panel), B (middle panel), and C (right panel) as a function of time and position within the diffusion barrier (ΩB).
In the cell cytosol, diffusion coefficients for small molecules, like adenosine triphosphate (ATP), are often depressed relative to bulk solution, which is in part be attributed to densely packed cytosolic proteins that restrict the volume accessible to diffusion. We therefore reconsidered the kinetics of the Goodwin oscillator using a reference diffusion constant typical for small molecules (e.g., DATP = 0.175 μm2/ms for fluorescent alexa-ATP in bulk solution31), which we further reduced to reflect cytosolic crowding to yield an effective constant, . To emulate the effect of densely packed protein crowders, we used a well-known lower bound from Hashin and Shtrikman,6 hereafter named HS bound, which provides the effective “hindered” diffusion constant given a regular lattice of spheres. The HS lower bound is given by
| (9) |
where Dbulk is the original (unhindered) diffusion constant, DHS is the effective diffusion constant, and ϕ is the accessible volume fraction. Hence, decreasing accessible volume fraction (ϕ) leads to smaller effective diffusion constants. Given that estimates of the occupied volume fraction in the bacterial cytoplasm approach 0.27,32 the corresponding effective diffusion via the HS limit is 0.6 times its bulk value (D = 0.11 μm2/ms), assuming a 70% accessible volume fraction (ϕ = 0.7). This substantial reduction of bulk diffusion rate essentially renders ΩB as a diffusion barrier between the well-mixed ΩL and ΩR compartments.
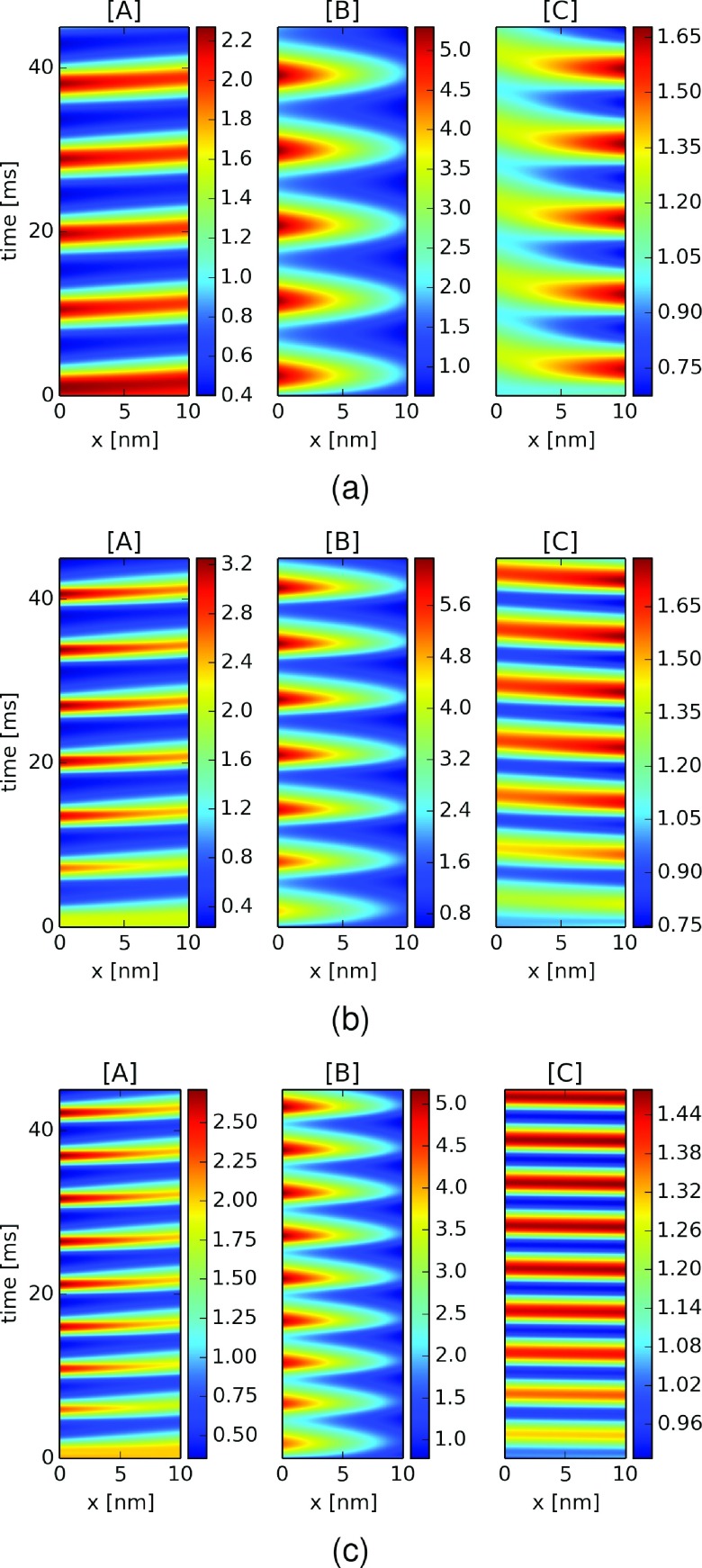
Substituting the rapid diffusion constants of the well-mixed system for the hindered constants (D = 0.11 μm2/ms) altered the Goodwin oscillator reaction kinetics, as shown in Figure 3(b). The reduced diffusion rates extended the period by approximately 20% to 5 ms, intensified the amplitude fluctuations of B in particular by three-fold (≈0.8-5.6 μM), and led to larger spatial concentration gradients along the barrier (≈0.5 μM/nm). We note that the peak intensities increased moderately over the simulation interval, as the systems con verged toward steady oscillations. Moreover, we note that the concentration extrema for substrates A and C in particular exhibited lags of 1-2 ms at opposing boundaries (e.g., lags were observed for A at ΓBR relative to ΓLB and vice versa for C). The 1-2 ms lag over the 10 nm diffusion barrier equates to a wave velocity of 5-10 nm/ms.
FIG. 3.
Goodwin oscillator dynamics with hindered diffusion of substrates and selective inhibitor diffusivity. Substrate concentrations for A (left panel) B (middle panel) and C (right panel) as a function of time and position within a 10 nm diffusion barrier (ΩB) using hindered diffusion coefficients DA = DB = 0.11 μm2/ms and selective inhibitor diffusivities (a) DC = 0.02 (b) DC = 0.11 and (c) DC = 5.3 μm2/ms.
The HS formulation introduced in Equation (9) assumes that the diffuser and crowders are non-interacting. However, it is well-known that long-range interactions between macromolecular crowders, like proteins, and diffusing substrates can modulate diffusion-influenced phenomena, such as substrate/protein association kinetics.33,34 For the case of electrostatic interactions, we could expect that a charged particle would have faster or slower effective diffusion rates when subject to a complementary or like-charged field, relative to an inert particle of the same size. We thus tested whether selective modulation of a substrate’s diffusivity would impact the oscillator kinetics, by arbitrarily varying DC of substrate C, the negative feedback inhibitor, while DA and DB remain constant. To account for this modulation, we refer to a previous study,8 in which we used homogenization theory to predict the effective diffusion coefficients for a charged substrate (z = − 1, 0, or 1) in a densely packed lattice of charged spherical proteins (13 Å in diameter, z = − 3). These data indicated that electrostatic interactions between the charged diffuser and an immobile obstacle (such as a protein) accelerated or attenuated the diffusion constant for attractive and repulsive interactions, respectively. Similar findings were reported by Putzel et al.35
In this spirit, we assumed that the inhibitor diffusion coefficient was reduced 5-fold to DC = 0.02 μm2/ms (Figure 3(a)) and increased to DC = 5.3 μm2/ms (Figure 3(c)) to emulate the modulatory effects of repulsive and attractive interactions. The corresponding spatiotemporal plots suggest that as the diffusion coefficient was reduced, the period length increased to almost 7 ms, as well as the lag between extrema at the ΓLB and ΓBR boundaries. We furthermore observed greater temporal broadening of the oscillations, to the extent that for DC = 0.02 μm2/ms, there was little variation in C at ΓLB, the boundary with ΩL, where C would inhibit the first reaction (Reaction (1)). In other words, smaller C fluctuations associated with the reduced diffusion coefficient maintained nearly a constant level of inhibition of Reaction (1), compared with results from faster diffusion coefficients. This was especially apparent when comparing the concentrations of A and C in ΩL; namely, although one might initially expect that slower C diffusion from ΩR would relieve inhibition of Reaction (1) and thereby lead to higher A in ΩL, the slower clearance rate of C from ΩL owing to slower diffusion actually prolonged its inhibition of the reaction and thereby attenuated the amplitude of A (see green and red “+”s in Figures S3(a) and S3(b)68). When DC was increased, however, we observed a reduction in period length and narrowing of the temporal broadening. Within ΩL, we report attenuated A concentrations in ΩL, which arose from accelerated inhibition owing to the nearly spatially uniform distribution of rapidly diffusing C across compartments (see Figures S3(b) and S3(c)68).
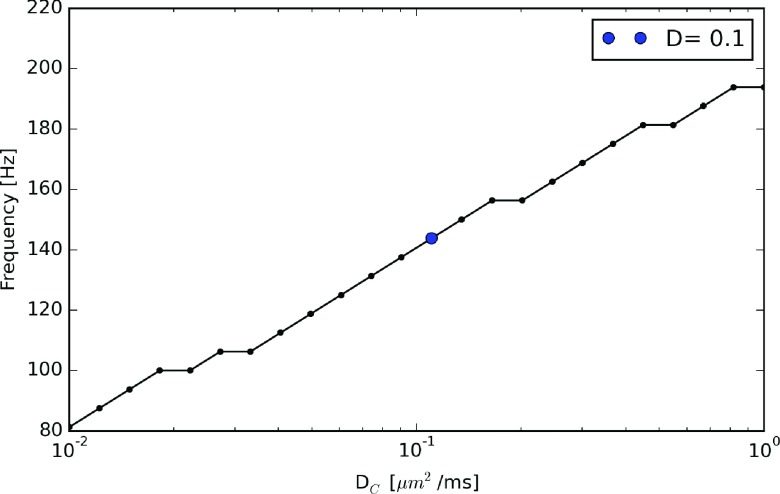
It was apparent from these data that the baseline frequency (≈140 Hz), which we defined as the frequency obtained when DA = DB = DC, could be modulated purely by varying the inhibitor’s diffusion coefficient. We thus investigated the capacity of the diffusion barrier for modulating the baseline frequency by considering a wide range of DC values. We found that the frequencies reported in Figure 4 decreased to 80 Hz as DC approached 0.01 μm2/ms. Further reduction of DC (not shown) yielded over-damped oscillations that eventually converged to stable (non-oscillatory) substrate concentrations. In contrast, for DC approaching large values, the baseline frequency increased by almost 40% to just under 200 Hz, at which the frequency leveled off. This upper bound reflects the reaction-limited oscillations obtained in the well-mixed (rapid diffusion) regime.
FIG. 4.
Modulation of Goodwin frequency by inhibitor-selective diffusion barrier. Inhibitor (C) oscillation frequencies with respect to DC. D = 0.11 μm2/ms is marked as the reference case as shown in Figure 3(b).
B. Oscillatory system with a periodic external source
In Sec. III A, we demonstrated that in addition to modulating oscillator frequencies, the diffusion barrier gave rise to concentration gradients that evidenced a disparity in the concentration profiles within each linked compartment. We examined this behavior with a simpler system, a reaction with an input periodic source/sink as an example of an exogenously-driven oscillatory system. In the figures below, we report the concentrations of A and B in each of the three compartments. For this system, we used a larger barrier length (100 nm, with some variations) to make the difference in diffusion transport times more apparent. For a diffusion coefficient equivalent to water (Dwater = 2.6 μm2/ms), we demonstrate in Figure 5(a) that the average concentration of [A] in each compartment is nearly identical in amplitude and there is negligible lag in the phases; we further observed that the spatial distribution of A within the diffusion barrier was nearly uniform (Figure 5(b)).
FIG. 5.
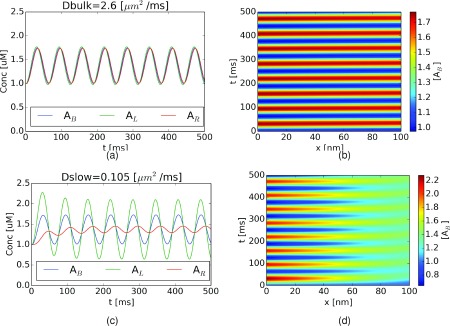
External source system dynamics and the influence of hindered substrate diffusion. Total A concentration in each compartment for external source oscillatory system (originating in ΩL) given (a) fast (DA = 2.6 μm2/ms) and (c) slow (DA = 0.11 μm2/ms) diffusion coefficients. Corresponding spatiotemporal plots for fast and slow diffusion coefficients are given in (b) and (d), respectively.
Upon reducing the diffusion coefficient to reflect hindered diffusion (DA = 0.10 μm2/ms), we observed in Figure 5(c) that the fluctuations of [A] in ΩR were suppressed, or “compartmented,” relative to those in ΩL. The physical interpretation of unequal compartment concentrations is the following: as the diffusion coefficient across ΩL was reduced, a smaller total amount of A diffused from ΩL across the barrier and into ΩR; hence, the concentration in ΩL reached greater extrema than the barrierless case (e.g., rapid diffusion), while in ΩR, smaller amplitude fluctuations were observed. Moreover, we note that the phase was shifted by roughly 10 ms, owing to the delay associated with diffusing across ΩB. The physical basis for this compartmentation effect becomes clear in the spatiotemporal plots of A within the diffusion barrier (Figure 5(d)), where we observed a more diffuse, attenuated, and delayed signal along ΓBR relative to ΓLB. In general, there are two time scales in this model system; the source/sink conversion frequency for [A] and the substrate’s diffusion time through the middle compartment. If diffusion is very rapid, the overall kinetic behavior is determined by the frequency of the reaction involving [A] (Figure 5(a)); otherwise, the effects of diffusion become apparent as shifts in the oscillation phases and variation of oscillation magnitudes with respect to position (Figure 5(c)).
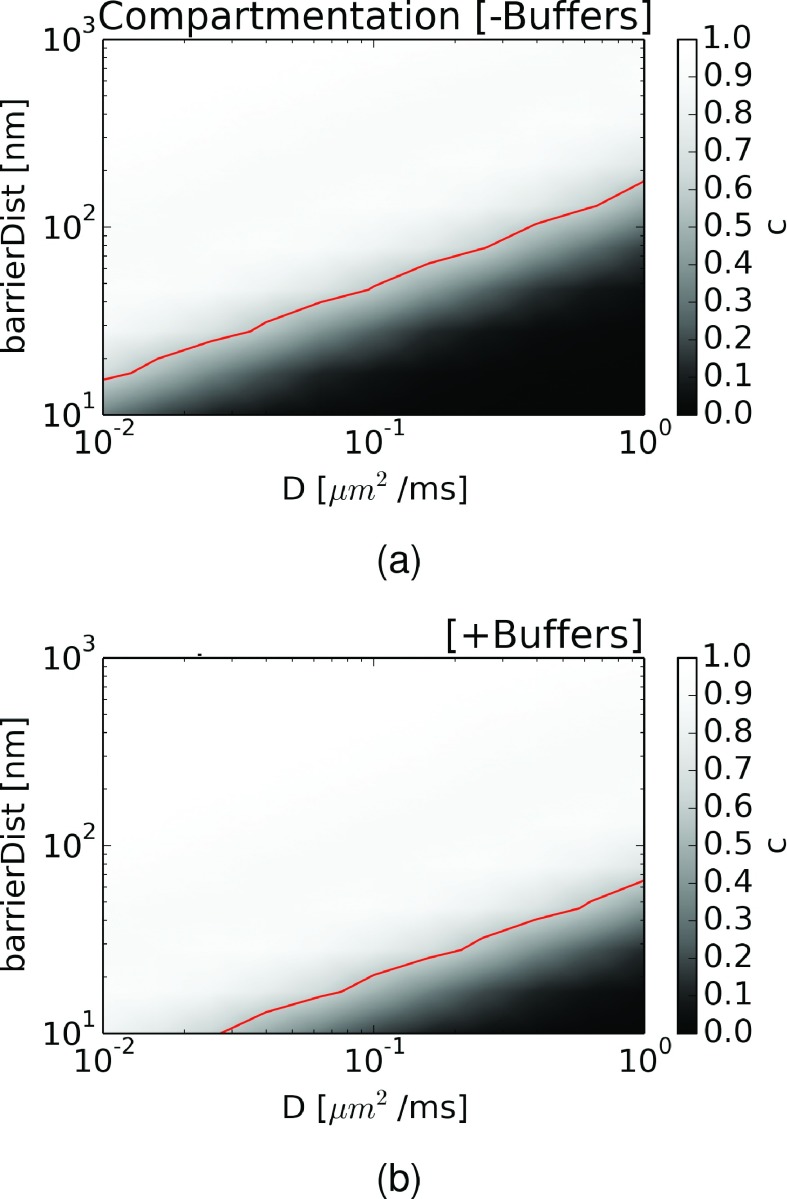
We next quantified the degree of compartmentation as a function of barrier distance and diffusion coefficient. For this, we defined a compartmentation metric, c ≡ 1 − σAR/σAL, where σAi denotes the standard deviation of A in compartment i. Based on this metric, c → 1 for a compartmented system since σAL ≫ σAR, while c → 0 for a well-mixed system, given that σAL = σAR. In Figure 6(a), we plot c with respect to barrier distance and diffusion coefficients. For diffusion coefficients approaching Dbulk (1 μm2/ms), we observed that the system was well-mixed for small barrier distances (10-100 nm), while the system became more compartmented as the barrier distance approached 1000 nm. At intermediate diffusion coefficients (0.1 μm2/ms), compartmentation occurred at smaller barrier distances, while for very slow diffusion coefficients, compartmentation emerged at distances in the tens of nanometers. For ease of comparison between regions of strong versus weak compartmentation, we have plotted a red line where c ≥ 0.5, above which we designate a system as “compartmented.”
FIG. 6.
Compartmented behavior of external source oscillatory system and its dependence on crowders and buffers. Dependence of compartmented behavior (c ≡ 1 − σA3/σA1, where σAi denotes the standard deviation of A in compartment i) as a function of barrier distance and diffusion coefficient. Values of c ≥ 0.5 are arbitrarily designated as “compartmented” systems (indicated by red line). (a) Crowders only and (b) crowders and buffering conditions: [B] = 5 μM, KD = 1 μM.
In addition to crowding, it is well-known that mobile (freely diffusing) and immobile binders, or buffers, specific to a given diffuser can impact apparent diffusion coefficients.9 Thus, we sought to understand how the presence of buffers within the diffusion barrier, using physiologically reasonable buffer concentrations and binding constants, could enhance compartmentation. We thus modified the diffusion coefficients used in ΩB by
| (10) |
where DB is the apparent diffusion constant due to buffering, D is the unbuffered, hindered diffusion coefficient, B is the concentration of buffer, and KD is the dissociation constant.9 We show in Figure S468 that varying buffer concentrations can substantially reduce the effective diffusion rate, hence diffusion could be slowed even in uncrowded (bulk solution) conditions for which the accessible volume fraction approaches 1. For the sake of illustration, we assumed buffer parameters appropriate for intracellular calcium diffusion in the presence of the buffer troponin C ([B] = 5, KD = 1 μM16), which reduced the unbuffered coefficient by a factor of 6. Based on these parameters, we observed that the dividing line between strong and weak compartmentation was pressed downward, indicating that compartmentalization emerged at higher (unbuffered) diffusion coefficients and shorter compartment distances as shown in Figure S6(b).68
IV. DISCUSSION
A. Spatially decoupled diffusion-influenced reaction networks
Coupled, diffusion-influenced reaction pathways are commonplace in biology, including ligand binding to cell receptors,36 and protein/protein association.37 Many of these exhibit oscillatory behavior, such as oscillations and waves of intracellular free calcium observed in a variety of cell types38 or periodic fluctuations arising from transcriptional regulation, whereby feedback mechanisms regulate gene expression via controlling transcription rates.22 Common to each of these pathways is the role of diffusion in transporting intermediate substrates between enzymatic steps. Since the time scale of diffusive transport depends on both the distance between enzymes and the substrates’ diffusion coefficients, we sought to understand whether the dynamics and synchrony of oscillatory reaction pathways could be indirectly controlled by non-uniform distributions of enzymes and environmentally influenced substrate diffusion coefficients, in addition to conventional direct control via modulating enzymatic reaction kinetics.
Specifically, we investigated the interplay between enzyme localization and diffusion for coupled, oscillatory biochemical reactions using a system of partial differential equation models, where we considered the transport of substrates through diffusion. Given the relative importance of feedback in generating sustained oscillations in a variety of biological signaling pathways, we numerically solved a PDE representing the Goodwin model of negative feedback inhibition. Although more advanced models of oscillatory feedback in biological systems are well-established,39 the Goodwin model’s simplicity and reliance on a small number of parameters facilities its use in the partial differential equation modeling described here. Moreover, by using a PDE formation of this reaction system, we could control the coupling between populations of enzymes in the Goodwin system by varying substrate diffusion rates and distances.
It is routinely observed that enzymes are frequently restricted to distinct regions of the cell, in order to orchestrate a variety of physiological functions.40 Hence, we sought to compare the dynamics of the Goodwin oscillator under “well-mixed” conditions relative to a system with spatially decoupled enzymes. Specifically, we separated the first two steps of the Goodwin system from the final feedback inhibition step by a distance of 10 nm and compared the oscillation frequencies for over a range of diffusion constants. This spatial partitioning potentially introduces a time lag in driving the feedback inhibition step, which we anticipated would lead to localized regions where substrate concentration amplitudes would deviate from those inherent to well-mixed conditions. We furthermore postulated that poorly mixed conditions stemming from the spatial decoupling of the Goodwin enzyme reactions would reduce the frequency of stable oscillations.
We thus first solved the Goodwin system using a very fast diffusion constant for each substrate, in order to eliminate latency arising from substrate transport between enzymes through the diffusion region ΩB. We found that our predictions of substrate concentrations with respect to time were nearly equivalent to those modeled by an ODE representation, of which the latter assumes substates and enzymes are well-mixed. For both differential equation models, the Goodwin system was reaction-limited and hence the oscillation frequencies were determined directly by the enzyme kinetics. We then reduced the diffusion coefficients to that of bulk water (Dwater = 2.6 μm2/ms) in order to model how the decoupled system would behave in a bulk solution. Upon reducing the coefficient, we observed progressively longer phase shifts for species B and C relative to the oscillations of substrate A. These phase shifts reflected the additional latency for substrate B generated in ΩL to diffuse to ΩR, as well as the transport of the feedback inhibitor, C, from ΩR to ΩL. Moreover, we saw that the substrate fluctuations amplitudes modestly increased relative to the well-mixed system, which reflected reduced rates of substrate influx and efflux between compartments. These results indicate that even modest separation of enzymes can influence the dynamics of coupled reactions that rely on diffusive transport.
To qualitatively validate our observations, we refer to delay-differential equations (DDEs), which are useful for describing negative feedback inhibition in biological systems involving time delays.41 DDEs of the form
| (11) |
are similar to our implementation of the Goodwin model, where Y is a function of time, t, d is a constant time delay, while Km, k, and r are kinetic parameters. The primary difference, however, is that our PDE model explicitly models the attenuation of a signal through diffusion into a volumetric region, whereas the DDE model assumes no attenuation, only an implicit time delay. To compare against our implementation of the Goodwin model, we plotted a DDE trajectory using a fitted lag-time of d = 1.46 ms, which demonstrates oscillations similar to our well-mixed validation example in Figure S5(a).68 For the well-mixed system, the transit time across the diffusion barrier was negligible, thus any lag in the system arose solely from the reaction kinetics. When the reactions were spatially decoupled, additional latency was introduced into the system, which extended the period length. In Figure S5(b),68 we demonstrate that the period length increases with increasing lag-times, which is consistent with our results using the Goodwin model.
While ODE- (eigenvalue decomposition26) and DDE-based42 techniques are commonly used for analyzing the stability of oscillatory systems, there are several features of our spatially decoupled system that complicate this analysis. The primary challenge is how to adapt the intrinsic oscillations determined by the enzyme reaction rates to reflect the influences of diffusion, as well as the topology and boundary conditions of the domain that encompasses the enzymes. First, diffusion rates in the regime surrounding an enzyme necessarily influence the observed enzyme kinetics, as has been well-described in simple analytic forms for association rates to spherical or planar reaction centers.36,43,44 To our knowledge, however, closed-form, analytical solutions are intractable for more complex geometries, such as the barrier considered in this study. Second, the propensity for non-linear substrate transport dynamics between enzymes4,5,14,18 challenges the application of standard stability analysis or ordinary differential equation approaches that assume well-mixed conditions. As an example, it was apparent for substrate B that a concentration gradient within the diffusion barrier emerged, with larger concentration extrema attained along ΓLB relative to ΓBR. This arose because of the boundary conditions specific to each substrate, as on one hand, the consumption of substrate B in ΩR behaved as an absorbing boundary condition at ΓBR, whereas C was effectively reflected at ΓLB, since it was not consumed in ΩL. Additionally, we demonstrated that substrate concentration profiles within the diffusion barrier could be highly dispersive in time and attenuated in amplitude as the diffusion coefficient was reduced. In this regard, our PDE approach readily accounted for the spatial extent of the diffusion barrier and boundary conditions specific to the enzyme populations.
B. Computational evidence for frequency modulation of oscillatory system through hindered diffusion
There is strong evidence that intracellular structures, like organelles, and cytosolic crowding influence the spatio-temporal distribution of substrates and their transport rates.45 For instance, intracellular semipermeable bilayers, like those comprising the mitochondrial matrix or the endoplasmic reticulum, constitute obvious barriers to diffusion. On the other hand, cytosolic crowding by obstacles such as proteins can perturb small molecule transport through a combination of effects, including a restricted accessible volume relative to a bulk solution,46 intermolecular interactions between substrates and crowders,9 as well as hydrodynamic effects.47,48 These myriad factors tend to hinder diffusion by reducing the effective diffusion coefficient relative to bulk solution and potentially introducing anisotropy.31,49 We investigated the hypothesis that hindered diffusion could modulate the dynamics of well-coupled biological reactions by examining how the Goodwin oscillator behavior differed from well-mixed conditions upon using diffusion coefficients that account for crowder density and crowder-substrate interactions. Specifically, we treated the gap between the two well-mixed ΩL and ΩR compartments as a “diffusion barrier,” wherein diffusion constants were substantially reduced relative to bulk rates.
We first represented the influence of inert crowders on small molecule diffusion (e.g., ATP), which reduces the accessible volume fraction, by using the Hashin-Shtrikman bound for diffusion in a matrix of spheres. Assuming an 70% accessible volume fraction for cellular environments, the HS bound for a comparable lattice would suggest a 50% reduction in the diffusion coefficient relative to the bulk (see blue line in Figure S468). Upon using diffusion constants that reflected hindered, small-molecule diffusion, we noted that the gradients of signals along the diffusion barrier were significantly more pronounced relative to the rapid diffusion cases, owing to larger concentration extrema where substrates were generated or consumed. To understand the basis of increased amplitude fluctuations, we reduced diffusion coefficients for the feedback inhibitor C from ΩR, where C was generated, to ΩL, where C inhibits the generation of A; this delayed the inhibition of A’s production, and thereby allowed greater accumulation of A. Conversely, transport of C from ΩL to ΩR, where it was degraded, was delayed, which prolonged its inhibition of A production although A’s consumption by the second reaction remained fixed. Hence, more extreme minima for A were observed.
We also note that the reduction of the diffusion coefficients to reflect crowding reduced the frequency of stable oscillations in the system. This delay stems directly from the lag time introduced for substrates to diffuse across the barrier. This was evident as larger slopes (time versus distance) of the concentration maxima in the spatiotemporal plots relative to the fast diffusion case. For instance, in Figure 3, the maxima for A along ΓBR lagged their maxima along ΓLB by approximately 2 ms, which corresponded to a wave velocity of 10 nm/2 ms = 5 nm/ms. In contrast, the lag for the fast diffusion case was less than 0.1 ms in Figure 2, which corresponded to a velocity of 100 nm/ms. To investigate this effect further, we modulated the diffusivity of substrate C, the negative feedback inhibitor, relative to the other substrates, which were held fixed at D = 0.11 μm2/ms. We found that increasing DC led to faster oscillation frequencies and attenuation of the magnitude of concentration gradients within the barrier, with a minor increase in the wave velocity for C. Conversely, decreasing DC reduced the oscillation frequency, enhanced concentration gradients, yet in addition, we noted considerable dampening of the fluctuations for C at ΓLB (1.2-1.4 μM) relative to those at ΓBR (0.6-1.85 μM). In fact, the average concentration of C at ΓLB (approximately 1.3 μM) was elevated relative to all other case, including that for the rapid diffusion case (approximately 1.15 μM), which implies that C overall maintained a greater suppression of A. Further reduction of DC is expected to eventually quench C fluctuations, thus leading to annihilation of the system oscillations.
Studies by us8 and others35,50,51 indicate that the diffusivity of charged molecules can be modulated by the strength and sign of their long-range interactions with obstacles. Thus, our findings that the oscillator frequency could be controlled exclusively by tuning the diffusion coefficient for C is significant, as it suggests that a cell could exploit differences in electrostatic potentials to selectively slow or accelerate a charged signaling molecule, relative to other substrates with differing (or non-existent) surface charges. Interesting still is that changes in pH, for instance, could significantly alter the electrostatic environment imposed on a charged particle, which could modulate the time course of coupled biological reactions. This also raises the possibility that the cell may compensate for changes in the diffusion environment (e.g., electrostatic potentials or diffusion distances) by modulating enzyme reaction rates. For instance, to counteract the decreased frequency owing to diffusive lag, a lower affinity Km (e.g., by reducing kon) may be used, as demonstrated for the well-mixed ODE system in Figure S6.68
C. Computational evidence for amplitude modulation in “compartmented” system
An interesting finding from our simulations of the Goodwin oscillator is that the diffusion barrier has the capacity to dampen fluctuations between compartments (as reported by the concentrations at the barrier domain boundaries). In this fashion, the barrier behaved as a buffer that effectively narrows the range of concentrations visited in ΩR, which is a phenomenon commonly referred to as “compartmentation.”40 In the creatine kinase (CK)/phosphocreatine shuttle system, for instance, the mitochondrial outer matrix acts as a diffusional barrier to nucleotides and anions, thus giving rise to nucleotide pools with distinct oscillation amplitudes;52 to better understand this behavior, we also presented data from a simplified system without inter-dependent reactions to examine transmission of substrate from a periodic source between regions separated by a diffusion barrier.
Our model of compartmentation suggests that under typical diffusion distances (10-100 nm) and diffusion rates (≈0.1-1.0 μm2/ms), there is limited capacity to evoke strong compartmented behavior, as defined by our metric. As could be expected from analytic solutions to the diffusion equation, such as
| (12) |
for diffusion from a point source, concentration profiles have greater dependence on diffusion distances than diffusion rates. Hence, changes in enzyme co-localization will have a more pronounced impact on compartmentation than proportional variations in the diffusion constant arising from crowding. The progression of heart failure, as an example, is often accompanied by intracellular remodeling that decouples key calcium channels like the L-type calcium channel (LCC) and the Ryanodine receptor (RyR);53 as a result, the ability of the cell to generate an efficacious, synchronous response is compromised, which ultimately deprecates the integrity of contractile force generation.54 It is certainly possible, however, that strong intermolecular interactions and in particular electrostatic interactions with crowders may further suppress apparent intracellular diffusion rates.8,55 In this regard, decreased pH resulting from ischemia reperfusion56 or alterations in intracellular ionic strength are both expected to influence the strength of electrostatic factors governing diffusion.
As an extreme example of strong diffuser/crowder interactions, the presence of high-affinity buffers that selectively bind substrates can drastically reduce apparent diffusion rates.9 Our study indicated that buffers with micromolar concentrations and dissociation rates typical of common buffering proteins, like Troponin C,57 can promote compartmented behavior over smaller distances than unbuffered substrates. Thus, in scenarios where compartmented behavior in absence of obvious diffusion barriers is suggested,58 such as in the blunted response of sarcolemmal ATPases and ATP-dependent channels to metabolic fluctuations,40 it is plausible that localized buffers can impose implicit barriers with effectiveness comparable to explicit, impermeable intracellular structures. In a similar fashion, it is reasonable to expect that pathological cardiac remodeling responsible for decoupling LCC and RyR53 could impair buffering properties of closely localized calcium binders like calmodulin (CaM),59 and CaMKII60 which could further impair compartmented calcium signaling vital to effective cellular function.61 Finally, while this study restricts buffering within a diffusion barrier, it is likely that the presence of buffers within a well-equilibrated compartment, such as that adjacent to the cell membrane,62 would further influence reaction kinetics, either by ensuring an elevated local concentration of substrate or altering apparent dissociation kinetics.
D. Conclusions
Our study reveals how (1) compartmentalized reaction behavior can develop within crowded, intracellular-scale spatial regimes and (2) reaction dynamics, namely, amplitudes and oscillation frequencies, are not only defined by the intrinsic reaction rates but also are shaped by substrate concentration gradients that develop between enzyme populations. We demonstrate that the reaction kinetics of substrate pools can vary significantly between compartments separated by diffusion barriers typical of those suggested by our lattice model in Ref. 8. These findings provide insight into the ability of the cellular environment to tune biochemical reaction kinetics, namely, by altering factors such as packing, specific binding (buffering), and charge. This raises the possibility that the kinetics of biochemical reactions may be in part controlled by the cellular environment through its interaction with diffusing substrates, in complement to more direct modulation of enzyme expression or activity. As such, our findings are directly applicable to biomolecular signaling pathways that exploit enzyme localization and compartmentation, including sodium handling,63 A-kinase anchoring protein-coupled cyclic AMP signaling,64 as well as metabolically linked ion channels, like the ATP-dependent potassium channel.40
While ordinary and time-delay differential equation models provide means to qualitatively demonstrate these phenomena, explicit consideration of the barrier’s spatial attributes via partial differential equations permits quantitative assessments using measurable physiological quantities, such as protein localization and crowder composition. Our PDE model of substrate transport provides additional insight into the space- and time-dependent substrate transport dynamics within the diffusion barrier, as well as facilitating the integration of experimentally derived structural data for reaction compartments, informed from high-resolution intracellular data65 or simulations of crowded cytosolic environments.32 This knowledge could provide important constraints for modeling heterogeneously distributed, diffusion-controlled biochemical reactions occurring with the cell cytosol, especially in the presence of crowders and buffers. We further propose that our predictions could be tested in a controlled reaction system by introducing neutral crowders, such as dextrans commonly used in crowding studies,2 functionalized/charged crowders,66 or rapid, uniformly distributed buffers, in a manner that preserves intrinsic enzyme function.
Acknowledgments
P.K.H. thanks the American Heart Association (No. 13POST14510036) and the National Institutes of Health (NIH Award No. 1F32HL114365-01A1) for postdoctoral funding. J.A.M. is supported in part by NIH, NBCR, the Center for Theoretical Biophysics (through the National Science Foundation Award No. PHY-0216576), and the Howard Hughes Medical Institute.
REFERENCES
- 1.Zhou H.-X., Rivas G., and Minton A. P., Annu. Rev. Biophys. 37, 375 (2008). 10.1146/annurev.biophys.37.032807.125817 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Elcock A. H., Curr. Opin. Struct. Biol. 20, 196 (2010). 10.1016/j.sbi.2010.01.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dix J. A. and Verkman A. S., Annu. Rev. Biophys. 37, 247 (2008). 10.1146/annurev.biophys.37.032807.125824 [DOI] [PubMed] [Google Scholar]
- 4.Eun C., Kekenes-Huskey P. M., and McCammon J. A., J. Chem. Phys. 139, 044117 (2013). 10.1063/1.4816522 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Eun C., Kekenes-Huskey P. M., Metzger V. T., and McCammon J. A., J. Chem. Phys. 140, 105101 (2014). 10.1063/1.4867286 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hashin Z. and Shtrikman S., Phys. Rev. 130, 129 (1963). 10.1103/PhysRev.130.129 [DOI] [Google Scholar]
- 7.Auriault J. L., Boutin C., and Geindreau C., Homogenization of Coupled Phenomena in Heterogenous Media (Wiley-ISTE, 2010). [Google Scholar]
- 8.Kekenes-Huskey P., Gillette A. K., and McCammon J., J. Chem. Phys. 140, 174106 (2014). 10.1063/1.4873382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wagner J. and Keizer J., Biophys. J. 67, 447 (1994). 10.1016/s0006-3495(94)80500-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Elcock A. H., Potter M. J., Matthews D. A., Knighton D. R., and McCammon J. A., J. Mol. Biol. 262, 370 (1996). 10.1006/jmbi.1996.0520 [DOI] [PubMed] [Google Scholar]
- 11.Elcock A. H., Huber G. A., and McCammon J. A., Biochemistry 36, 16049 (1997). 10.1021/bi971709u [DOI] [PubMed] [Google Scholar]
- 12.Elcock A. H. and McCammon J. A., Biochemistry 35, 12652 (1996). 10.1021/bi9614747 [DOI] [PubMed] [Google Scholar]
- 13.Cheng Y., Chang C.-e. A., Yu Z., Zhang Y., Sun M., Leyh T. S., Holst M. J., and Andrew McCammon J., Biophys. J. 95, 4659 (2008). 10.1529/biophysj.108.140038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Metzger V. T., Eun C., Kekenes-Huskey P. M., Huber G., and McCammon J. A., Biophys. J. 107, 2394 (2014). 10.1016/j.bpj.2014.09.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Keener J. and Sneyd J., Mathematical Physiology. II: Systems Physiology (Springer Science & Business Media, 2009). [Google Scholar]
- 16.Shannon T., Wang F., Puglisi J., Weber C., and Bers D., Biophys. J. 87, 3351 (2004). 10.1529/biophysj.104.047449 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Torres N. S., Sachse F. B., Izu L. T., Goldhaber J. I., Spitzer K. W., and Bridge J. H., J. Mol. Cell. Cardiol. 68, 1 (2014). 10.1016/j.yjmcc.2013.12.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Higgins E. R., Goel P., Puglisi J. L., Bers D. M., Cannell M., and Sneyd J., J. Theor. Biol. 247, 623 (2007). 10.1016/j.jtbi.2007.03.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hake J., Edwards A. G., Yu Z., Kekenes-Huskey P. M., Michailova A. P., McCammon J. A., Holst M. J., Hoshijima M., and McCulloch A. D., J. Physiol. 590, 4403 (2012). 10.1113/jphysiol.2012.227926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kekenes-Huskey P., Cheng Y., Hake J., Sachse F., Bridge J., Holst M., McCulloch A., McCammon J., and Michailova A., Front. Physiol. 3, 351 (2012). 10.3389/fphys.2012.00351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kekenes-Huskey P., Gillette A., Hake J., and McCammon J., Comput. Sci. Discovery 5, 014015 (2012). 10.1088/1749-4699/5/1/014015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.J. E. Ferrell, Jr., Tsai T. Y.-C., and Yang Q., Cell 144, 874 (2011). 10.1016/j.cell.2011.03.006 [DOI] [PubMed] [Google Scholar]
- 23.Goldbeter A., FEBS Lett. 587, 2778 (2013). 10.1016/j.febslet.2013.07.031 [DOI] [PubMed] [Google Scholar]
- 24.Shen P. and Larter R., Biophys. J. 67, 1414 (1994). 10.1016/S0006-3495(94)80615-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bánsági T. and Taylor A. F., J. Phys. Chem. B 118, 6092 (2014). 10.1021/jp5019795 [DOI] [PubMed] [Google Scholar]
- 26.Tyson J. J., Comput. Cell Biol. 20, 230 (2002). 10.1007/978-0-387-22459-6_9 [DOI] [Google Scholar]
- 27.Logg A., Wells G. N., and Hake J., “DOLFIN: A C++/Python finite element library,” inAutomated Solution of Differential Equations by the Finite Element Method (Springer, 2012). [Google Scholar]
- 28.Kekenes-Huskey P. M., Liao T., Gillette A. K., Hake J. E., Zhang Y., Michailova A. P., McCulloch A. D., and McCammon J. A., Biophys. J. 105, 2130 (2013). 10.1016/j.bpj.2013.09.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Petzold L., SIAM J. Sci. Stat. Comput. 4, 136 (1983). 10.1137/0904010 [DOI] [Google Scholar]
- 30.Holst M., Baker N., and Wang F., J. Comput. Chem. 21, 1319 (2000). [DOI] [Google Scholar]
- 31.Vendelin M. and Birkedal R., AJP: Cell Physiol. 295, C1302 (2008). 10.1152/ajpcell.00313.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.McGuffee S. R. and Elcock A. H., PLoS Comput. Biol. 6, e1000694 (2010). 10.1371/journal.pcbi.1000694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Elcock A., Gabdoulline R., Wade R., and McCammon J., J. Mol. Biol. 291, 149 (1999). 10.1006/jmbi.1999.2919 [DOI] [PubMed] [Google Scholar]
- 34.Wade R. C., Gabdoulline R. R., Ludemann S. K., and Lounnas V., Proc. Natl. Acad. Sci. U. S. A. 95, 5942 (1998). 10.1073/pnas.95.11.5942 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Putzel G. G., Tagliazucchi M., and Szleifer I., Phys. Rev. Lett. 113, 138302 (2014). 10.1103/PhysRevLett.113.138302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Berg H. and Purcell E., Biophys. J. 20, 193 (1977). 10.1016/S0006-3495(77)85544-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhou H. X., Biophys. J. 73, 2441 (1997). 10.1016/S0006-3495(97)78272-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sneyd J., Keizer J., and Sanderson M. J., FASEB J. 9, 1463 (1995). [DOI] [PubMed] [Google Scholar]
- 39.Bliss R. D., Painter P. R., and Marr A. G., J. Theor. Biol. 97, 177 (1982). 10.1016/0022-5193(82)90098-4 [DOI] [PubMed] [Google Scholar]
- 40.Alekseev A. E., Reyes S., Selivanov V. A., Dzeja P. P., and Terzic A., J. Mol. Cell. Cardiol. 52, 401 (2012). 10.1016/j.yjmcc.2011.06.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bodnar M., Foryś U., and Poleszczuk J., J. Math. Anal. Appl. 376, 74 (2011). 10.1016/j.jmaa.2010.10.038 [DOI] [Google Scholar]
- 42.Wagner J. and Stolovitzky G., Proc. IEEE 96, 1398 (2008). 10.1109/JPROC.2008.925427 [DOI] [Google Scholar]
- 43.Samson R. and Deutch J., J. Chem. Phys. 67, 847 (1977). 10.1063/1.434853 [DOI] [Google Scholar]
- 44.Bamford C., Tipper C., and Compton R., Diffusion-Limited Reactions, Comprehensive Chemical Kinetics Vol. 25 (Elsevier, 1985). [Google Scholar]
- 45.Verkman A. S., Trends Biochem. Sci. 27, 27 (2002). 10.1016/S0968-0004(01)02003-5 [DOI] [PubMed] [Google Scholar]
- 46.Mathias R. T., Biophys. J. 42, 55 (1983). 10.1016/S0006-3495(83)84368-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Nitsche J. M. and Balgi G., Ind. Eng. Chem. Res. 33, 2242 (1994). 10.1021/ie00033a030 [DOI] [Google Scholar]
- 48.Phillips R. J., Deen W. M., and Brady J. F., AIChE J. 35, 1761 (1989). 10.1002/aic.690351102 [DOI] [Google Scholar]
- 49.Shorten P. R. and Sneyd J., Biophys. J. 96, 4764 (2009). 10.1016/j.bpj.2009.02.060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Moyne C. and Murad M. A., Transp. Porous Media 63, 13 (2006). 10.1007/s11242-005-1291-7 [DOI] [Google Scholar]
- 51.Bourbatache K., Millet O., and Aït-Mokhtar A., Int. J. Heat Mass Transfer 55, 5979 (2012). 10.1016/j.ijheatmasstransfer.2012.06.008 [DOI] [Google Scholar]
- 52.Wallimann T., Wyss M., Brdiczka D., Nicolay K., and Eppenberger H. M., Biochem. J. 281, 21 (1992). 10.1042/bj2810021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Louch W. E., Sejersted O. M., and Swift F., J. Biomed. Biotechnol. 2010, 1. 10.1155/2010/503906 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Louch W. E., Hake J., Mørk H. K., Hougen K., Skrbic B., Ursu D., Tønnessen T., Sjaastad I., and Sejersted O. M., J. Mol. Cell. Cardiol. 58, 41 (2013). 10.1016/j.yjmcc.2013.01.014 [DOI] [PubMed] [Google Scholar]
- 55.Schmuck M., J. Appl. Math. Mech./Z. Angew. Math. Mech. 92, 304 (2012). 10.1002/zamm.201100003 [DOI] [Google Scholar]
- 56.Bond J. M., Chacon E., Herman B., and Lemasters J. J., Am. J. Physiol. 265, C129 (1993). [DOI] [PubMed] [Google Scholar]
- 57.Bers D., in Excitation-Contraction Coupling and Cardiac Contractile Force, 1st ed., edited by Bers D. (Kluwer Academic Publishers, 2001), Vol. 1. [Google Scholar]
- 58.Illaste A., Laasmaa M., Peterson P., and Vendelin M., Biophys. J. 102, 739 (2012). 10.1016/j.bpj.2012.01.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Yang Y., Guo T., Oda T., Chakraborty A., Chen L., Uchinoumi H., Knowlton A. A., Fruen B. R., Cornea R. L., Meissner G., and Bers D. M., Circ. Res. 114, 295 (2014). 10.1161/CIRCRESAHA.114.302857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Bers D. M., Physiology 21, 380 (2006). 10.1152/physiol.00019.2006 [DOI] [PubMed] [Google Scholar]
- 61.Bers D. M., Despa S., and Bossuyt J., Ann. N. Y. Acad. Sci. 1080, 165 (2006). 10.1196/annals.1380.015 [DOI] [PubMed] [Google Scholar]
- 62.Aronsen J. M., Swift F., and Sejersted O. M., J. Mol. Cell. Cardiol. 61, 11 (2013). 10.1016/j.yjmcc.2013.06.003 [DOI] [PubMed] [Google Scholar]
- 63.Bers D. M. and Despa S., IUBMB Life 61, 215 (2009). 10.1002/iub.163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Carnegie G. K., Means C. K., and Scott J. D., IUBMB Life 61, 394 (2009). 10.1002/iub.168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Hake J., Kekenes-Huskey P. M., and McCulloch A. D., Curr. Opin. Struct. Biol. 25, 92 (2014). 10.1016/j.sbi.2014.01.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Smith J. J. and Zharov I., Langmuir 24, 2650 (2008). 10.1021/la7013072 [DOI] [PubMed] [Google Scholar]
- 67.Holz M., Heil S. R., and Sacco A., Phys. Chem. Chem. Phys. 2, 4740 (2000). 10.1039/b005319h [DOI] [Google Scholar]
- 68.See supplementary material at http://dx.doi.org/10.1063/1.4929528 E-JCPSA6-143-024533 for further details of model validation, parameterization or results.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- See supplementary material at http://dx.doi.org/10.1063/1.4929528 E-JCPSA6-143-024533 for further details of model validation, parameterization or results.