There Is a “U” in Clutter: Evidence for Robust Sparse Codes Underlying Clutter Tolerance in Human Vision

Abstract

The ability to recognize objects in clutter is crucial for human vision, yet the underlying neural computations remain poorly understood. Previous single-unit electrophysiology recordings in inferotemporal cortex in monkeys and fMRI studies of object-selective cortex in humans have shown that the responses to pairs of objects can sometimes be well described as a weighted average of the responses to the constituent objects. Yet, from a computational standpoint, it is not clear how the challenge of object recognition in clutter can be solved if downstream areas must disentangle the identity of an unknown number of individual objects from the confounded average neuronal responses. An alternative idea is that recognition is based on a subpopulation of neurons that are robust to clutter, i.e., that do not show response averaging, but rather robust object-selective responses in the presence of clutter. Here we show that simulations using the HMAX model of object recognition in cortex can fit the aforementioned single-unit and fMRI data, showing that the averaging-like responses can be understood as the result of responses of object-selective neurons to suboptimal stimuli. Moreover, the model shows how object recognition can be achieved by a sparse readout of neurons whose selectivity is robust to clutter. Finally, the model provides a novel prediction about human object recognition performance, namely, that target recognition ability should show a U-shaped dependency on the similarity of simultaneously presented clutter objects. This prediction is confirmed experimentally, supporting a simple, unifying model of how the brain performs object recognition in clutter.

SIGNIFICANCE STATEMENT The neural mechanisms underlying object recognition in cluttered scenes (i.e., containing more than one object) remain poorly understood. Studies have suggested that neural responses to multiple objects correspond to an average of the responses to the constituent objects. Yet, it is unclear how the identities of an unknown number of objects could be disentangled from a confounded average response. Here, we use a popular computational biological vision model to show that averaging-like responses can result from responses of clutter-tolerant neurons to suboptimal stimuli. The model also provides a novel prediction, that human detection ability should show a U-shaped dependency on target–clutter similarity, which is confirmed experimentally, supporting a simple, unifying account of how the brain performs object recognition in clutter.

Introduction

Much of what is known about how the brain performs visual object recognition comes from studies using single objects presented in isolation, but real-world vision is cluttered, with scenes usually containing multiple objects. Therefore, the ability to recognize objects in clutter is crucial for human vision, yet its underlying neural bases are poorly understood. Numerous studies have shown that the addition of a nonpreferred stimulus generally leads to a decrease in the response to a preferred stimulus when compared to the response to the preferred stimulus alone (Sato, 1989; Miller et al., 1993; Rolls and Tovee, 1995; Missal et al., 1999). More specifically, Zoccolan et al. (2005) showed that single-cell responses in monkey inferotemporal cortex (IT) to pairs of objects were well described by the average of the responses to the constituent objects presented in isolation. A follow-up study showed that monkey IT cells' responses to pairs of objects ranged from averaging-like to completely clutter invariant, meaning the response to the preferred stimulus was not affected by the addition of a nonpreferred stimulus (Zoccolan et al., 2007). However, a number of previous fMRI studies continued to report evidence of averaging responses to object pairs in object-selective cortex at the voxel level (MacEvoy and Epstein, 2009, 2011; Baeck et al., 2013). These findings have been taken as support for an “averaging” model, in which neurons respond to simultaneously presented objects by averaging their responses to the constituent objects. This averaging model poses a difficult problem, however, in that it requires the visual system to achieve recognition by somehow disentangling the identity of individual objects from the confounded neuronal responses. Indeed, previous theoretical work has shown that linear mixing, especially averaging, results in poor representations of object identity information for multiple objects that are to be read out by downstream areas (Orhan and Ma, 2015).

An appealingly straightforward alternative is that recognition is based on a subpopulation of neurons that are robust to clutter. This theory is supported by intracranial recordings in human visual cortex (Agam et al., 2010) and fMRI recordings from object-specific cortex (Reddy and Kanwisher, 2007; Reddy et al., 2009), in which the response to a preferred object was largely unaffected by the addition of a nonpreferred object. Is there a mechanistic explanation that can account for the seemingly disparate findings for how the brain responds to clutter?

In the present study we use HMAX, a popular model of object recognition in cortex (Fig. 1), to provide a unifying account of how responses to suboptimal stimuli can lead to averaging-like responses at both the voxel/population level and the single cell level despite nonlinear pooling steps in the visual processing hierarchy. We then, for the first time, explore the relationship between shape similarity in pairs of objects, expected level of interference in the neuronal or BOLD response, and the implications of this interference on object detection behavior. Interestingly, simulations using the HMAX model provide a novel behavioral prediction of a U-shaped relationship between target–distractor similarity and object recognition performance in clutter, with maximal interference at intermediate levels of similarity. This interference pattern arises from the MAX-pooling step at the feature level. Highly similar distractors activate the relevant S2 feature detectors at a similar enough level to the target object to cause little interference, and highly dissimilar distractors activate those relevant S2 feature detectors only weakly so that they are ignored at the MAX-pooling step, but there is an intermediate level of distractor dissimilarity where some of the relevant S2 feature detectors are activated at a higher level by the distractor which is passed on to the C2 level by the MAX-pooling function, causing a different enough activation pattern over the afferents to the object-tuned units to cause interference. We finally show that this U-shaped pattern for clutter interference is indeed found in human behavior.

Figure 1.

The HMAX model of object recognition in cortex. Feature specificity and invariance to translation and scale are gradually built up by a hierarchy of “S” (performing a “template match” operation, solid red lines) and “C” layers (performing a MAX-pooling operation, dashed blue lines), respectively, leading to VTUs that show shape-tuning and invariance properties in quantitative agreement with physiological data from monkey IT. These units can then provide input to task-specific circuits located in higher areas, e.g., prefrontal cortex. This diagram depicts only a few sample units at each level for illustration (for details, see Materials and Methods).

Materials and Methods

HMAX model.

The HMAX model (Fig. 1) was described in detail previously (Riesenhuber and Poggio, 1999a; Jiang et al., 2006; Serre et al., 2007b). Briefly, input images are densely sampled by arrays of two-dimensional Gabor filters, the so-called S1 units, each responding preferentially to a bar of a certain orientation, spatial frequency, and spatial location, thus roughly resembling properties of simple cells in striate cortex. In the next step, C1 cells, which roughly resemble complex cells (Serre and Riesenhuber, 2004), pool over sets of S1 cells of the same preferred orientation (using a maximum, MAX-pooling function), with similar preferred spatial frequencies and receptive field locations, to increase receptive field size and broaden spatial frequency tuning. Thus, a C1 unit responds best to a bar of the same orientation as the S1 units that feed into it, but over a range of positions and scales. To increase feature complexity, neighboring C1 units of similar spatial frequency tuning are then grouped to provide input to an S2 unit, roughly corresponding to neurons tuned to more complex features, as found in V2 or V4. Intermediate S2 features can either be hard wired (Riesenhuber and Poggio, 1999a) or learned directly from image sets by choosing S2 units to be tuned to randomly selected patches of the C1 activations that result from presentations of images from a training set (Serre et al., 2007a,b). This latter procedure results in S2 feature dictionaries better matched to the complexity of natural images (Serre et al., 2007b). For the simulations involving generic objects (the fMRI voxel-level and single-unit simulations), S2-level features were the general-purpose 2000 “natural image” features used previously (Serre et al., 2007b), constructed by extracting C1 patches from a large database of natural images collected from the Web. To obtain a more face-specific set of features for the simulations of human face recognition performance in clutter, S2 features were learned by extracting patches from the C1-level representation of 180 face prototypes [the method used to create “class-specific patches” in the study by Serre et al. (2007b)] that were not used as testing stimuli, resulting in 1000 S2 face-specific features. To achieve size invariance over all filter sizes and position invariance over the modeled visual field while preserving feature selectivity, all S2 units selective for a particular feature are again pooled by a MAX operation to yield C2 units. Consequently, a C2 unit will respond at the same level as the most active S2 unit with the same preferred feature, but regardless of its scale or position. C2 units are comparable to V4 neurons in the primate visual system (Cadieu et al., 2007). Finally, the recognition of complex objects in the model is mediated by view-tuned units (VTUs), modeling neurons tuned to views of complex objects such as faces, as found in monkey inferotemporal cortex (Riesenhuber and Poggio, 2002). The VTUs receive input from C2 units. A VTU's response to a given object is calculated as a Gaussian response function of the Euclidean distance between the preferred object's activation over the d most activated C2 units for that object and the current activation for those same d units at the C2 level (Riesenhuber and Poggio, 1999b). The selectivity of the VTUs is determined by the Gaussian tuning-width parameter, σ, and the number of C2 afferents, d, with more C2 afferents leading to higher selectivity.

A key prediction of the model is that object recognition is based on sparse codes at multiple levels of the visual processing hierarchy (Riesenhuber and Poggio, 1999b; Jiang et al., 2006). Viewing a particular object causes a specific activation pattern over the intermediate feature detectors, activating some strongly and others only weakly, depending on the features contained in the object. A sparse subset of the most activated feature detectors for a familiar object forms the afferents that determine the activation of the VTUs for that object. Then, in turn, a sparse readout of the most activated VTUs for a given object underlies the recognition of that object.

fMRI voxel-level simulation.

To model the fMRI data from MacEvoy and Epstein (2009), a VTU population tuned to the same 60 objects (15 exemplar images from four general object categories: cars, shoes, brushes, and chairs) as those used in that study was defined, and the same stimulus presentation conditions were simulated. Paired object images contained one object on top and one on bottom, and both possible object configurations were used to calculate VTU activations for each pair. The object images were 128 × 128 pixels in size on a gray background, and were all padded with a border of 39 extra background pixels to avoid edge effects. This made the image inputs into the model 412 × 206 pixels, with a minimum separation of 78 background pixels for all image pairs. Model VTU responses were calculated for the single objects in both the top position with the bottom position empty and vice versa. For each object pair and the constituent individual objects, the activation of a simulated object-selective cluster from the lateral occipital complex (LOC; a visual cortical brain region thought to play a key role in human object recognition; Grill-Spector et al., 2001) was calculated by averaging across the responses of the 58 VTUs in the population. Since it is unlikely that object-selective neurons in the LOC happen to be optimally tuned to the particular object prototypes used in the MacEvoy and Epstein (2009) fMRI experiment, the VTUs tuned to the two objects used for a particular object pair were excluded, thus modeling the processing of novel instances of prototypes from familiar object categories as in the MacEvoy and Epstein (2009). Results were similar, however, even if those VTUs were included (see Results, below). For each object pair, a pair “average” response was calculated by averaging the simulated voxel responses to the two possible object configurations (the average of object A on top and object B on bottom, and object B on top and object A on bottom). A corresponding sum of the responses to the constituent objects of the pair was calculated by adding the averages of the presentations of the two possible locations for each single-object presentation (the average of object A on top with the bottom empty and the top empty with object A on the bottom plus the average of object B on top with bottom empty and the top empty with object B on the bottom). Similar to our previous study (Jiang et al., 2006), the selectivity of the VTU population was varied across different simulation runs by varying the number of afferents, d (i.e., using the d strongest C2 activations for each object), and the tuning width of the VTU's Gaussian response function, σ.

Single-unit simulation.

Zoccolan et al. (2007) defined an index of “clutter tolerance” (CT) as CT = <(R_{ref and flank} − R_flank)/(R_ref − R_flank)>, with R_{ref and flank} denoting the mean neuronal response to a given reference/flanker object pair presented simultaneously, R_ref and R_flank the mean responses to the constituent objects of the pair presented in isolation, and < and > indicating the average over all flanking conditions. Using the same 60 object-tuned VTUs from the fMRI voxel simulation, each VTU's response was determined for the 59 stimuli different from its preferred object (to simulate the experimental situation in which a neuron's preferred object was likewise not known). Following the procedure used in Zoccolan et al. (2007), the one object of the 59 test stimuli that activated each VTU most strongly was taken as its “reference” object, and any of the other test stimuli that activated the VTU less than half as strongly as the reference were taken as “flankers.” The model VTU responses to the reference/flanker pairs were computed, and the results were used to calculate CT values for each unit, as well as the mean CT values for each parameter set.

Model predictions for human behavior.

A model containing 180 VTUs tuned to a set of prototype faces that would not be used as the faces tested in the behavior prediction simulation was created to predict human face recognition performance in clutter (Jiang et al., 2006). Unlike the fMRI and single-unit simulations already described that used generic objects and S2/C2 features extracted from a database of natural images, the S2/C2 features used in the face detection simulations were extracted from the face prototype images to obtain a face-specific set of intermediate features, following evidence from fMRI studies for face feature-tuned neurons in the occipital face area (Gauthier et al., 2000; Liu et al., 2010). A key advantage of working with the object class of faces is that there are ample behavioral data to constrain model parameters: instead of a brute-force test of a large range of parameter sets, we used the procedure described by Jiang et al. (2006) to find a small number of parameter sets that could account for human face discrimination behavior on a task testing upright versus inverted face discrimination (Riesenhuber et al., 2004). This fitting process produced sets of parameters that determined the selectivity of the model face units by setting the number of afferents d as well as the tuning width parameter σ for each VTU. This fitting process also determined the level of sparseness of the readout from the VTU representation by fitting the number of VTUs, n, on which the simulated behavioral decision is made. This fitting process resulted in 149 unique parameter sets to test in the clutter behavior prediction simulation.

The VTU activation for a target face presented in isolation, as well as the activations for the target face paired with a distractor face of varying dissimilarity, was computed for each of the fitted parameter sets (see Fig. 5). Distractor faces of 0, 20, 40, 60, 80, or 100% dissimilarity were created using a photorealistic face-morphing software (Blanz and Vetter, 1999). The predicted level of interference for each distractor condition was then calculated as the Euclidean distance between the activation vector of the n most active VTUs when the target face was presented in isolation and the activation vector for those same n units when the target face was presented with the distractors of varying dissimilarity. This process was repeated for each parameter set for 10 separate face “morph lines,” with the face prototype at one end of the morph line as the target, and the value reported for each distractor condition is the average across the morph lines (see Fig. 5).

Figure 5.

Predicting the interfering effect of clutter at the behavioral level. A, An example a “morph line” between a pair of face prototypes (shown at the far left and right, respectively), created using a photorealistic morphing system (Blanz and Vetter, 1999). The relative contribution of each face prototype changes smoothly along the line. For example, the third face from the left (the second morph) is a mixture of 60% of the face on the far left and 40% of the face on the far right. B, Example of the target-plus-distractor clutter test stimuli used in the model simulations. Each test stimulus contained a target prototype face in the upper left-hand corner (in this case, prototype face A from the morph line in A) and a distractor face of varying similarity to the target in the bottom right-hand corner (in this case, the distractor is 20% face A and 80% face B, or a morph distance of 80%). C, An example (for one parameter set) of the predicted amount of interference as a function of clutter–target dissimilarity, showing a significant decrease in predicted interference once the distractor face became dissimilar enough. *p < 0.05; ^∼p < 0.1 (paired t test). The neural representation of a target face was defined as a sparse activation pattern over the set of face units with preferred face stimuli most similar to the target face (see Materials and Methods, Model predictions for human behavior). Interference was calculated as the Euclidean distances between these face units' responses to the target in isolation versus the response pattern caused by the target-plus-distractor images. Data shown are averages over 10 morph lines (same morphs as used by Jiang et al., 2006). Error bars indicate SEM. Distractor faces for a particular target face were chosen to lie at different distances along the morph line (0, 20,, 100%, with 0% corresponding to two copies of the target face and 100% corresponding to the target face along with another prototype face), resulting in six different conditions. For this parameter set, maximal interference is found for distractors at 60% distance to the target face. D, Group data for all the parameter sets tested with the HMAX model. The histogram depicts the counts of the locations of the peaks in the clutter interference curves (like the one shown in C) for each parameter set.

A second set of simulations using a divisive normalization rule were performed, following suggestions that divisive normalization could account for the neuronal responses in clutter (Reynolds et al., 1999; Zoccolan et al., 2005; Li et al., 2009; MacEvoy and Epstein, 2009). For these simulations, VTU activations for the target and distractor objects were calculated individually and then combined using a divisive normalization rule as described by Li et al. (2009); namely, R = (R_T + R_D)/||R_T + R_D||, where R is the VTU activation vector for the pair, R_T is the activation vector for the target alone, and R_D is the activation vector for the distractor alone. It should be noted that this is an idealized case, and it is not clear how the visual hierarchy could process two stimuli in such a way that their activations do not interfere at all before the level of IT. In this model, activation patterns are compared using a correlation distance measure (Li et al., 2009) instead of the Euclidean distance as in the HMAX simulations. The correlation distance measure is computed as 1 − r, where r is the correlation between the response of n most activated units for the target and the response of those same units for the target/distractor pairs. The parameters for the tightness of tuning of the VTUs (number of afferents, d, and the tuning width parameter, σ) and the sparseness of the readout (n most active VTUs to base behavior on) were determined in a similar manner as above and in the study by Jiang et al. (2006), except the Euclidean distance measure was replaced by a distance measure based on the 1 − r correlation distance. This resulted in 77 parameter sets that could account for the previous behavioral data. Additional simulations were attempted using the correlation distance readout over the entire face-tuned VTU population, but no parameter sets were found that could account for human face discrimination performance in that model.

Participants.

A total of 13 subjects (five female; mean ± SD age, 23.9 ± 4.8 years) took part in the psychophysical experiment. All participants reported normal or corrected-to-normal vision. Georgetown University's Institutional Review Board approved experimental procedures, and each participant gave written informed consent before the experiment.

Behavior experiment stimuli.

Face stimuli were ∼3° of visual angle in size and were created with the same automatic computer graphics morphing system (Blanz and Vetter, 1999; Jiang et al., 2006) used in the behavior prediction simulations. For the behavioral experiment, the morphing software was used to generate 25 “morph lines” through interpolation between 25 disjoint sets of two prototype faces, as in the study by Jiang et al. (2006). We then chose face images separated by a specified distance along a particular morph line continuum as target/distractor pairs, with 100% corresponding to the distance between two prototype faces, and 120% difference created by extrapolation to increase diversity in face space (Blanz and Vetter, 1999; see Fig. 6A). Stimuli were selected so that each face was presented the same number of times to avoid adaptation effects. Experiments were written in MATLAB using the Psychophysics toolbox and Eyelink toolbox extensions (Brainard, 1997; Cornelissen et al., 2002).

Figure 6.

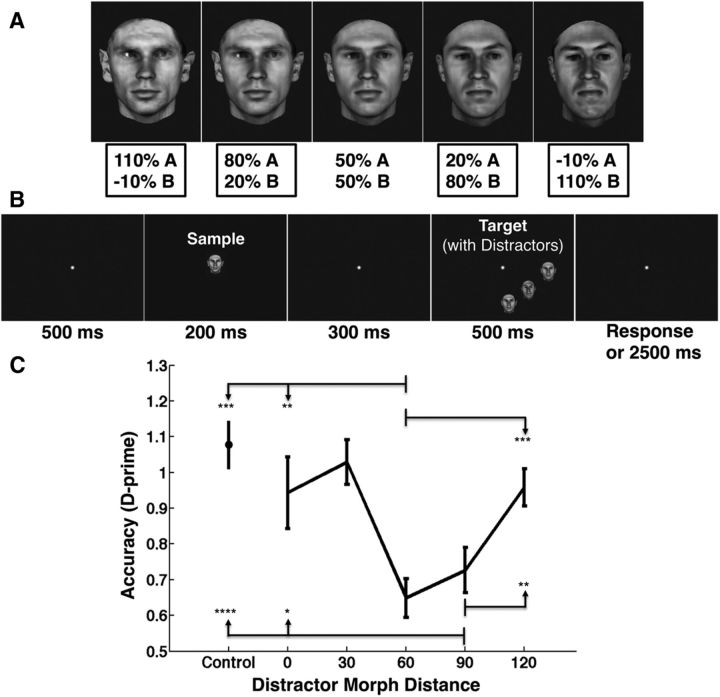
Testing behavioral performance for target detection in clutter. A, Face stimuli were created for the behavior experiment by morphing between and beyond two prototype face stimuli in 30% steps (Blanz and Vetter, 1999). The four stimuli with the box around the labels were possible sample/target stimuli, and the 50% A/50% B face stimulus was used only as a distractor. For details, see Materials and Methods. B, Experimental paradigm. Subjects (N = 12) were asked to detect whether a briefly presented “sample” face was the same as or different from a “target” face that was presented in isolation (control condition, not pictured) or surrounded by distractor faces of varying similarity to the target face. For details, see Materials and Methods. The trial shown here is a “different” trial, with a distractor morph distance of 60% (the “sample” is the 80% A/20% B face in A, the “target” is the −10% A/110% B face in A, and the “distractors” are the 50% A/50% B face in A). C, Behavioral performance for each target face/distractor face similarity condition tested. As predicted, there is an initial drop in performance as distractor dissimilarity increases, followed by a subsequent rebound in performance as the distractor faces become more dissimilar (comparisons are between the conditions at the tail of each arrow and the arrowhead, with significance demarcated at the arrowhead; *p < 0.05, **p < 0.005, ***p < 0.0005, ****p < 0.00005). Accuracy is measured here using d′, though similar results were found by analyzing the percentage of correct responses. Error bars show SEM.

Behavioral experiment procedure.

Subjects performed a “same/different” task in which a sample face was presented at fixation for 200 ms, followed by a 300 ms blank, followed by presentation of a target face 9° of visual angle away from fixation toward one of the four corners of the screen for 500 ms. The sample face was selected from one of four possible morph line positions (110% prototype A/−10% prototype B, 80% prototype A/20% prototype B, 20% prototype A/80% prototype B, or −10% prototype A/110% prototype B; see Fig. 6A). On control trials, the target face was presented in isolation, and on distractor trials, the target face was presented in the middle of two flanking distractor faces at equal eccentricity from the fovea as the target face, each arranged with a center-to-center distance of 3.5° from the target face. On the “different” trials, the target face was 90% different from the sample face, and if a distractor was present, it was morphed the defined distance back toward the sample face. The similarity of the distractor faces to the target face was varied in steps of 30% morph distance along the morph line, resulting in five different distractor conditions, from 0 to 120% dissimilarity. Subjects were instructed to press the “1” key if the target face was the same as the preceding sample face and the “2” key if it was different, and were given up to 2500 ms to respond (see Fig. 6B). Each session included 1000 distractor trials (500 target same as sample/500 target different from sample) and 200 control trials (100 target same/100 target different). One hundred trials were presented for each distractor condition and target same/different combination (four possible morph line positions for the sample face across 25 independent morph lines), and the trial type order was randomized for each subject. Subjects were instructed to maintain fixation on a cross in the center of the screen throughout each trial. Gaze position was tracked using an Eyelink 1000 eye tracker (SR Research), and trials were aborted and excluded from analysis if subjects' gaze left a 3° window centered around the center of the fixation cross. One subject was removed for failing to maintain fixation on at least 80% of the trials. The remaining 12 subjects maintained fixation on 94.56 ± 2.73% (mean ± SD) of the trials.

Behavior experiment analysis.

Performance is reported here in terms of d′, which is a standard measure of target selectivity derived from signal detection theory; it accounts for response bias by taking the Z-transform of the hit rate for a target (the rate at which a subject correctly responds “same” when the target is the same as the sample) and subtracting the Z-transform of the false alarm rate (the rate at which a subject responds “same” when the target is actually different from the sample). An analysis of the average percentage of correct responses on all trials showed similar results.

Results

The HMAX model can account for previous average-like responses in fMRI despite its nonlinear MAX-pooling steps

Some previous fMRI findings show that the responses to visual stimuli from the preferred object classes in some high-level visual brain areas [faces in the fusiform face area (FFA) and houses in the parahippocampal place area] are not affected by the presence of stimuli from another nonpreferred object class (Reddy and Kanwisher, 2007; Reddy et al., 2009). These findings are in good agreement with the hypothesis that object recognition in clutter is driven by sparse object selective responses that are robust in the presence of clutter. However, some previous human fMRI studies (MacEvoy and Epstein, 2009; MacEvoy and Epstein, 2011; Baeck et al., 2013) argued for an account of object recognition in clutter based on neurons showing response averaging as opposed to neurons whose responses are minimally affected by the presence of clutter. Specifically, one elegantly straightforward human fMRI study measured the activation in the LOC in response to the presentation of single objects versus pairs of objects (MacEvoy and Epstein, 2009). Stimuli were 15 exemplars from four object classes (cars, brushes, chairs, and shoes), and objects were presented in isolation or in pairs, with the two objects in each pair belonging to different categories. The authors performed linear regressions of the fMRI responses to stimulus pairs versus the sum of responses to their constituent objects and reported that in the most object-selective clusters of LOC voxels, regression slopes fell near 0.5, with r² values reaching up to 0.4. This was taken as support for some type of averaging mechanism.

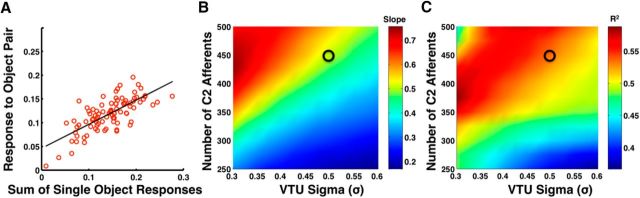
To investigate whether these fMRI results could be accounted for with the HMAX model, we simulated an object-selective cluster of 60 neurons as a group of 60 view-tuned model IT units selective for each of the same 60 objects used by MacEvoy and Epstein (2009). It should be noted that our model of voxel-level activity is simply the average simulated spiking activity over a population of object-tuned units. Although the relationship between the BOLD response and the underlying neural activity is a complicated one (Logothetis et al., 2001; Sirotin and Das, 2009), our simplified model is in line with previous reports that average neuronal response is a surprisingly good predictor of BOLD responses (Mukamel et al., 2005; Issa et al., 2013). To model the LOC responses for each object pair (90 total pairs, 15 from each of the six possible object type pairings)and each pair's constituent objects, we took the average response over all VTUs (excluding the two VTUs selective for the objects in a particular pair to model the case where the stimuli presented were novel instances of objects from familiar object classes and thus unlikely be the optimal stimuli for LOC neurons) to that object pair and its constituent objects presented in isolation, respectively. These simulations were performed over a range of VTU selectivities (see Materials and Methods). Interestingly, the simulations revealed broad regions in the tested parameter space with slopes similar to those found by MacEvoy and Epstein (2009). To illustrate, Figure 2A shows an example for a particular parameter set yielding a slope of 0.51 and an r² value of 0.53, whereas B and C show slopes and r² values, respectively, for a range of VTU parameter values demonstrating a large region of parameter space that results in slopes near 0.5 with high r² values. A second set of simulations in which the two VTUs selective for the constituent objects in the pair were not removed, modeling the case where the voxel contained neurons optimally tuned to the stimulus, gave results that were not qualitatively different, with a similar region of parameter space with slopes near 0.5 with high r² values (results not shown).

Figure 2.

Accounting for human fMRI data. A, One example plot showing the linear relationship between the average model VTU population response to object pairs and the sum of the average population responses to the individual objects from that pair (see Results). Fitting with linear regression gives a line with a slope of 0.51 and an r² value of 0.53. B, The slopes of the best-fit lines for a range of different VTU selectivity parameter sets. In the simulation data shown, the number of C2 afferents to each VTU was varied from 250 to 500 in increments of 25 and VTU σ was varied from 0.3 to 0.6 in increments of 0.025 to simulate different levels of neuronal selectivity, with selectivity increasing for larger numbers of C2 afferents and smaller values of σ (see Materials and Methods). C, The r² values corresponding to the slopes shown in B. The black circles in B and C indicate the location of the parameter set used for the simulations in A (corresponding to 450 C2 afferents and a VTU σ of 0.5), and a large subset of the tested parameter space shows similar slopes and r² values.

Although this agreement of model and fMRI data might at first seem surprising, given the nonlinearities at several stages in the model, it can be understood as arising from a population of object-tuned neurons that, on average, respond similarly to the single- and two-object displays producing a slope of ∼0.5 when comparing the two-object response to the sum of the single-object responses, as was observed in the experiment. There are on the order of 100,000 neurons in a single voxel, and, given the large number of possible objects neurons can be selective to, the majority of these neurons are likely tuned to objects different from either of the single objects that make up a given pair. For the simulated units in the HMAX model, where a VTU's response is determined by how closely the current C2 feature activation pattern matches the preferred C2 activation pattern, the combination of the two nonpreferred objects in a pair will almost always produces another suboptimal C2 activation pattern, leading to a similar average VTU response across the simulated population for the object pair and each of its constituent single objects. The model therefore shows that the averaging-like responses found at the voxel level in fMRI studies might result from the fact that the average activation level in the population inside the voxel is quite similar for the object pair and each of its constituent single objects because all three are suboptimal stimuli for all or nearly all neurons in the population, rather than resulting from an averaging mechanism at the single cell level. To get a better idea of the interactions of simultaneously presented objects at the neuronal level, one must therefore turn to single-unit data.

Actual IT neurons and simulated HMAX VTUs show a similar range of clutter tolerances

A previous single-unit electrophysiology study compared responses of monkey IT neurons to object pairs to the responses to the constituent objects, and initially reported that the responses to the object pairs were often well modeled as the average of the responses to the constituent objects presented in isolation (Zoccolan et al., 2005). The same group then expanded upon these findings in a follow-up study (Zoccolan et al., 2007). In that study, clutter tolerance was quantified using a clutter tolerance index, which was defined to have a value of 0.5 for neurons perform an averaging operation, and 1.0 for neurons showing complete clutter invariance, i.e., being unaffected by clutter (see Materials and Methods). Across the population of neurons recorded from, CT values showed a broad distribution from near 0.5 to values of 1 or more (Zoccolan et al., 2007; reproduced in Fig. 3A). Interestingly, the individual model IT units of Figure 2A that fit the fMRI data of MacEvoy and Epstein (2009) also exhibited a broad distribution of CT values (Fig. 3B) whose range and average were similar to those found in the IT recordings, showing that the same parameter set that fit the fMRI data also produced model neurons with clutter tolerances similar to those found in the single-unit electrophysiology experiment. In both the previously recorded data and the simulated data, there are a number of single-unit responses that demonstrate responses that are very robust to clutter, i.e., with CT values close to 1. According to the model, these units are the ones selective for objects similar to their preferred presented stimuli, and it is these units that are hypothesized to drive the recognition behavior of these stimuli. In the following sections, this hypothesis will be tested by examining in the model and experimentally how the recognition of target objects is affected by simultaneously presented distractors whose similarity to the target object is varied parametrically, which allows us a finer investigation of the effect of clutter than in previous studies in which target–distractor similarity was not always controlled. We first present simulations using the HMAX model to predict human object recognition performance in these conditions, followed by a psychophysics experiment to test the model predictions.

Figure 3.

Accounting for monkey electrophysiology data. A, Distribution of CT values of single-unit IT recordings from Zoccolan et al.'s (2007) Figure 8. The black arrow indicates the mean CT values for the entire population (mean CT, 0.74). B, Results from our simulations. Results shown used the same parameter set as in Figure 2A, which provided a good fit for the fMRI data. The black arrow indicates the mean CT value from the simulated population of 60 VTUs (mean CT of model VTUs, 0.71). Notice that the CT values from the model VTUs cover a range of CT values that is quite similar to the electrophysiological single-unit recordings in A, with similar means. In both panels, the dashed lines indicate the CT values corresponding to an averaging rule (CT, 0.5) and complete clutter invariance (CCI; CT, 1.0).

The HMAX model predicts a U-shaped performance curve for object recognition behavior in clutter as a function of distractor similarity

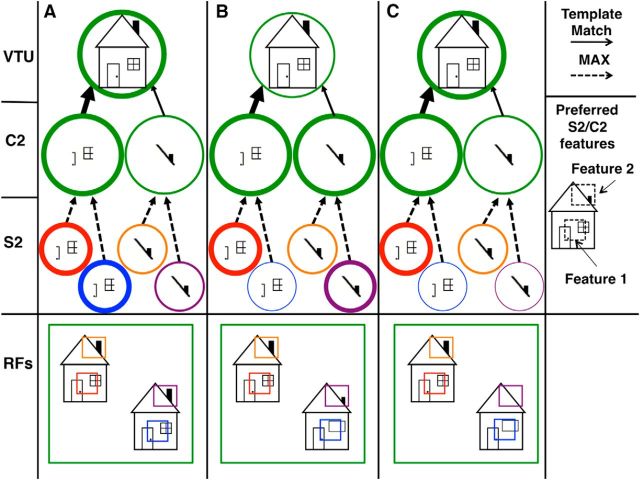
As stated previously, in the HMAX model, visual object recognition is mediated by a sparse readout of VTUs, modeling neurons tuned to views of complex objects (Riesenhuber and Poggio, 1999a), and the response of these VTUs is determined by the activation patterns of their afferents, C2-level feature detectors. Crucially, a view-tuned unit that is to exhibit robust selectivity to its preferred object even in the simultaneous presence of a nonpreferred object should receive input only from feature-tuned (C2) units strongly activated by the preferred object in isolation (Riesenhuber and Poggio, 1999b). That way, if an instance of the preferred object appears together with nonpreferred objects within the same C2 unit's receptive field, the MAX-pooling operation of the C2 unit will tend to ignore the presence of the nonpreferred objects, because its S2 afferents whose receptive fields contain the nonpreferred objects will tend to be activated to a lower degree than the S2 cell whose receptive field contains the preferred object, thus avoiding interference and preserving selectivity (Fig. 4C).

Figure 4.

The predicted U-shaped effect of clutter on neuronal responses of object-tuned units in the visual processing hierarchy. This diagram demonstrates the effects of clutter objects of varying levels of dissimilarity on a VTUs response to its preferred object. A–C, Highly similar or identical (A) or highly dissimilar (C) clutter objects produce little to no interference, but at an intermediate level of clutter similarity (B), clutter interference is maximal. This is an extremely simplified example containing only two feature-tuned C2 units, whereas actual simulations use on the order of hundreds of intermediate features (Fig. 2). The image shown inside each unit is that unit's preferred stimulus: the VTU prefers a particular house stimulus with a medium-sized chimney and paned window to the right of the door, whereas the C2 afferents respond to different house-specific features (one tuned to a door/paned window feature and one tuned to a small chimney feature). The unit activation level is represented by outline thickness, with thicker outlines representing higher activation. The dotted arrows represent a MAX-pooling function, and the solid lines represent a template-matching function (see Fig. 1), with the thickness of the arrow corresponding to the preferred activation level of the afferent (when the thickness of the arrow matches the thickness of the unit at the tail of the arrow, the response of the downstream unit will be highest). The bottom row of each panel depicts the visual stimulus and parts of the stimulus covered by the receptive field (RF) of each unit, with each units' outline color corresponding to the color of its outlined RF in the bottom row. The VTU's preferred object is always shown in the upper left of the visual input image, together with a simultaneously presented clutter object (the house in the lower right). A, When two copies of the preferred object are presented in the VTU's RF, the S2-level feature-tuned units tuned to the same feature (but receiving separate input from the two copies of the house) activate identically. Taking the maximum of the two at the C2 level will therefore lead to the same C2 response as when the preferred object is presented by itself, thus causing no interference at the VTU level (strong response, thick outline). B, When the preferred object is presented together with a similar clutter object, there are two possible scenarios: (1) the clutter object could activate a particular S2 feature-tuned unit less strongly than the target (as in the left, door/paned window feature); in this case the corresponding C2 unit due to its MAX integration will show the same activation as in the no-clutter case, i.e., there will be no interference; (2) the clutter object could activate the S2 feature tuned unit more strongly (as in the right, small chimney feature), leading to a higher C2 unit activation as a result of the MAX-pooling operation, thus causing interference (shown by the thinner circle at the VTU level) because the afferent activation pattern to the VTU unit is now suboptimal. Note the mismatch between actual C2 activation and the VTU's preferred activation here, demonstrated by the thickness of the circle depicting the activation for the C2 small chimney feature and the preferred activation for the house VTU indicated by the thickness of the arrow between the C2 small chimney feature and the house VTU: although the particular chimney causes a strong activation of the small chimney feature (thick circle outline), this is suboptimal for the particular house VTU whose preferred house stimulus activates the chimney feature more weakly due to its medium-sized chimney (indicated by the thinner arrow from the chimney feature to house VTU). C, A clutter object that is very dissimilar to the preferred object activates the relevant features only weakly, making it unlikely that activation from the clutter object will interfere at the C2 MAX-pooling level. This leads to the behavioral prediction that recognition ability should show a U-shaped curve as a function of target–distractor similarity.

Thus, whether the visual system can rapidly recognize a particular object in the presence of another object crucially depends on the similarity between the objects as well as the selectivity of the visual system's intermediate features, as illustrated in Figure 4. In the first panel (Fig. 4A), two copies of a VTU's preferred object are presented within the VTU/C2 receptive field. The resulting two identical S2 activation patterns at the two respective object locations lead to the same C2 activation pattern as in the single target case, due to the MAX pooling at the C2 level. Thus, in this idealized case, there is no interference caused at the VTU level by the simultaneous presence of the two identical objects. In the second panel (Fig. 4B), an object that is similar but not identical to the VTU's preferred object is presented together with the preferred object. In this case, one of the S2/C2-level features that is included in the afferents to the VTU is activated more strongly by the nonpreferred object. This leads to a change in activation of the C2 afferent for that feature relative to the no-clutter case, creating a nonoptimal afferent activation pattern for the VTU and resulting in decreased VTU activation due to clutter interference. Finally, Figure 4C depicts a scenario with a nonpreferred object that is even more dissimilar to the VTU's preferred object, with lower S2 activation levels for both of the pertinent features compared to the S2 activations for those features caused by the preferred object, because the nonpreferred object now contains features that are different from the ones relevant for the VTU's activation to the preferred object. MAX-pooling at the C2 level ignores this lower S2 activation, resulting in reduced clutter interference compared to the case with the more similar distractor. Since behavior is read out from the VTU level, this leads to the salient prediction for target detection in clutter that, with a sufficiently selective intermediate feature representation, the interfering effect of clutter of varying similarity to a particular target should follow an inverted U shape, with little interference for distractors that are both highly similar and highly dissimilar to the target, and highest interference for distractors of intermediate similarity. Correspondingly, behavioral performance for target detection in clutter should show the inverse profile (because performance is expected to be high if interference is low), resulting in the prediction of a U-shaped curve for target detection performance as a function of distractor dissimilarity.

To test this hypothesis quantitatively, we ran simulations using the HMAX model (for model details, see Materials and Methods), applying it to the example of detecting a face target in clutter. Faces are an attractive object class to focus on. Because of their importance for human cognition, they are a popular stimulus class to use in studies of object recognition in the presence of interfering objects (Louie et al., 2007; Farzin et al., 2009; Sun and Balas, 2014), and we showed previously (Jiang et al., 2006) that the HMAX model can quantitatively account for human face discrimination ability (of upright and inverted faces presented in isolation) as well as the selectivity of “face neurons” in the human FFA (Kanwisher et al., 1997). Here we first created a VTU population of 180 “face units,” modeling face neurons in the FFA, each tuned to a different face prototype, as in the study by Jiang et al. (2006). To account for the typically high human discrimination abilities for upright faces and reduced discrimination ability for inverted faces (Yin, 1969), the model previously predicted that face discrimination is based on a population of face neurons tightly tuned to different upright faces, which, as a result of their tight tuning, show little response to inverted faces (Jiang et al., 2006). This high selectivity of face neurons implied that viewing a particular face would cause a sparse activation pattern (Riesenhuber and Poggio, 1999b; Olshausen and Field, 2004), in which, for a given face, only a subset of face neurons, whose preferred face stimuli were similar to the currently viewed face, would respond strongly. The model predicted that face discrimination is based on these sparse activation patterns, specifically the activation of the face units most strongly activated by a particular face, i.e., those face neurons selective to faces most similar to the currently viewed face. Indeed, previous fMRI studies have shown that behavior appears to be driven by only subsets of stimulus-related activations (Grill-Spector et al., 2004; Jiang et al., 2006; Williams et al., 2007), in particular, those activations with optimal selectivity for the task. The discriminability of two faces is then directly related to the dissimilarity of their respective face unit population activation patterns. Previous behavioral and fMRI experiments have provided strong support for this model (Jiang et al., 2006; Gilaie-Dotan and Malach 2007).

For the present simulations that investigate the effects of clutter, model parameters were fit as described previously (Jiang et al., 2006) to obtain face unit selectivity compatible with the previously acquired face discrimination behavioral data on upright and inverted faces (Riesenhuber et al., 2004). We then probed the responses of model face units to displays containing either a target face by itself (here a prototype from one end of a morph line) or two face images, a target face and a distractor face, whose similarity was parametrically varied by steps of 20% between two face prototypes using a photorealistic face-morphing program (Blanz and Vetter, 1999; Fig. 5A,B). Simulation results revealed that the degree of interference (here calculated as the Euclidean distance between the activation vector for the n most activated face VTUs for the target in isolation and the activation for those same n units in response to the target–distractor pairs; see Materials and Methods) caused by clutter depended on target–distractor similarity in 148 of 149 of the fitted parameter sets that were tested (p < 0.05, one-way repeated measures ANOVA). As predicted, a vast majority of the parameter sets tested (128 of 149) showed an inverted U-shaped effect of distractor similarity on target interference. Figure 5C shows interference for an example parameter set, and Figure 5D depicts a histogram of the peak locations of all tested parameter sets. Note the remarkable degree of agreement in predictions of maximum interference for distractors 60–80% different from the target face.

It was suggested previously that divisive normalization may account for the averaging-like behavior in single-unit and fMRI responses in clutter (Reynolds et al., 1999; Zoccolan et al., 2005; Li et al., 2009; MacEvoy and Epstein, 2009). In the divisive normalization account, the activity of individual neurons in a population is normalized by the overall activity of the population or the overall level of input to that population. It was also suggested that the absolute firing rate of the neurons that represent an object are not what matters for object recognition in clutter, but rather the preservation of the rank order of the firing rates of those neurons (Li et al., 2009), motivating the use of a correlation-based interference measure as opposed to the Euclidean distance measure used previously. To test whether divisive normalization mechanisms would likewise predict a U-shaped interference effect, a second set of simulations using a divisive normalization model were performed in addition to the HMAX simulations, and the effects of clutter were measured with an interference measure based on correlation distance (see Materials and Methods). Unlike the HMAX clutter simulations, which consistently showed a significant effect of distractor condition on interference level, with peak interference at intermediate levels of distractor dissimilarity (M6 or M8; Fig. 5D), the effect of distractor condition on clutter interference in the divisive normalization clutter simulations with the correlation distance were not significant (one-way repeated measures ANOVA, p > 0.05) for any of the 77 candidate parameter sets, meaning that the divisive normalization model predicted no effect of distractor similarity on object recognition performance in clutter.

Behavior shows a U-shaped effect of distractor interference

To behaviorally test the modeling predictions, we performed a psychophysical experiment (for details, see Materials and Methods). Briefly, subjects were asked to perform a target detection task in clutter, in which a sample face was presented foveally on each trial followed by a display containing a target face in the periphery flanked tangentially by distractor faces (Fig. 6B), or in a control condition, with no distractor faces. On a given trial, the target face was either the same as the sample face or a different face that was 90% dissimilar from the sample. The subject's task was to decide whether the target face was the same as the sample face or not. To investigate the effect of distractor similarity on target discrimination, the similarity between the target face and the simultaneously presented distractor faces was varied parametrically across trials in steps of 30% up to a morph distance of 120%. Peripheral presentation of the target stimuli was used because the larger receptive fields in the periphery (Dumoulin and Wandell, 2008) made it more likely that the target and distractor faces fell within one cell's receptive field and interfered with one another. Note that in the HMAX model, receptive field size does not vary with eccentricity. Yet, since the target and distractor stimuli in the behavioral experiment were presented at the same eccentricity, this simplification in the model does not affect the predicted effect of target–distractor similarity on clutter interference. The basic paradigm is similar to paradigms in the crowding literature that investigate interference on discrimination performance (e.g., for letters, digits, or bars/gratings) caused by related objects presented in spatial proximity (Bouma, 1970; Andriessen and Bouma, 1976; He et al., 1996; Intriligator and Cavanagh, 2001; Parkes et al., 2001; Pelli et al., 2004; Balas et al., 2009; Levi and Carney, 2009; Dakin et al., 2010; Greenwood et al., 2010). Whereas most of these studies have focused on the effect of varying spatial arrangements between crowding stimuli (Pelli and Tillman, 2008), we focus here on the effect of varying shape similarity between stimuli to test the model predictions regarding how the human visual system performs object detection in clutter, in particular, the U-shaped interference effect.

A one-way repeated-measures ANOVA with d′ as the dependent variable and the five distractor conditions as the within-subject factor revealed a significant effect of distractor condition on behavioral performance (p = 1.35e-05), in agreement with the HMAX simulation predictions, but not the predictions from the divisive normalization model. Motivated by the model predictions, we expanded the morph lines to 120% different to maximize the opportunity to see the predicted rebound. Given that distractor faces of intermediate levels of dissimilarity caused the most interference in the model predictions, particularly in the 60–80% range, we used planned post hoc one-tailed paired t tests to test the hypothesis that performance on the 60 and 90% conditions was lower than on the control, 0 and 120%, conditions (Figure 6C). The moderately dissimilar distractor faces (60 and 90% dissimilarity) did, in fact, lead to a decrease in subjects' ability to discriminate the target compared to the control condition (p = 0.0001 for control vs 60%; p = 1.59e-05 for control vs 90%), as well as the conditions in which the distractors were identical to the target face (p = 0.0048 for 0 vs 60%; p = 0.0283 for 0 vs 90%). Moreover, there was a significant rebound in detection performance for distractor faces that were increasingly dissimilar to the target face (p = 0.0002 for the 60 vs 120%; p = 0.0011 for 90 vs 120%, one-tailed paired t-tests). This rebound confirms the U-shaped prediction derived from the HMAX model simulations (Fig. 5C,D). It is worth noting here that the distractor faces were the same as the sample face on the 90% dissimilar condition for the “different” trials, and this could have led to decreases in performance if the subjects mistook the distractor faces for the target face. However, this cannot account for the overall U shape seen in behavioral performance because the 60 and 120% distractor dissimilarity conditions on the “different” trial both contained distractors that were equally similar to the sample face (30% morph distance from the sample), and yet the 60% condition shows low performance and the 120% condition shows high performance. This rebound was also not due to a speed/accuracy trade-off, because reaction time was not modulated significantly by distractor dissimilarity (p = 0.2423, one-way repeated measures ANOVA across the five distractor conditions).

Discussion

The feedforward account of rapid object recognition in clutter

Numerous studies have shown that humans are able to rapidly and accurately detect objects in cluttered natural scenes containing multiple, possibly overlapping, objects on complex backgrounds even when only presented for fractions of a second (Potter, 1975; Intraub, 1981; Thorpe et al., 1996; Keysers et al., 2001). We examined a simpler form of clutter, consisting of two or three nonoverlapping objects on a uniform background, to investigate the core issue of feature interference that arises when the visual system simultaneously processes multiple objects. Although these stimuli do not permit the investigation of object segmentation issues associated with clutter-induced object occlusion, they allowed us to directly model previous results using similar displays (Zoccolan et al., 2007; MacEvoy and Epstein, 2009) and to parametrically probe the effect of target–distractor similarity on behavioral performance. It was proposed that rapid object detection in cluttered scenes is based on a single pass of information through the brain's ventral visual stream (Riesenhuber and Poggio, 1999a; VanRullen and Thorpe, 2002; Hung et al., 2005; Serre et al., 2007a; Agam et al., 2010). How can the neural representation of multiple simultaneously presented objects enable such “feedforward” recognition in clutter? One popular hypothesis is that recognition in clutter is mediated by neurons in high-level visual cortex that respond to displays containing multiple stimuli with a response that is the average of the responses to the objects presented individually (Zoccolan et al., 2005; MacEvoy and Epstein, 2009, 2011; Baeck et al., 2013). However, basing recognition on neurons responding to multiple objects via an averaging mechanism requires that the visual system achieve recognition by somehow disentangling the identity of individual objects from the confounded population responses. It has been proposed by MacEvoy and Epstein (2009, p. 946) that the visual system scales “population responses by the number of stimuli present.” But this proposal creates a chicken-and-egg problem: to determine neuronal responses to cluttered displays, the visual system would have to recognize the objects in a scene first to determine how many there are, and then scale the responses accordingly. Indeed, recent computational work has shown that linear mixing of the neural response to multiple stimuli is a poor way of encoding object identity information to be read out by downstream areas, with averaging performing particularly poorly (Orhan and Ma, 2015). Divisive normalization (Heeger, 1992; Heeger et al., 1996; Carandini et al., 1997; Recanzone et al., 1997; Simoncelli et al., 1998; Britten and Heuer, 1999; Reynolds et al., 1999; Schwartz and Simoncelli, 2001; Heuer and Britten, 2002), a mechanism whereby the activity of a neuron within a population is normalized by the overall activity of that population or the level of input to the population, was proposed as a possible explanation of the averaging phenomenon that would not require explicitly recognizing the number of objects in a scene to carry out the normalization step (Zoccolan et al., 2005; MacEvoy and Epstein, 2009). These models predict that at the individual neuron level, there is interference because the magnitude of the firing rate is decreased, but at the population level, the rank order of responses is maintained and that is what is important for behavior (Li et al., 2009). The preservation of rank order along with a correlation-based readout over the relevant neurons leads to the prediction of no clutter interference, as was seen in the lack of a relationship between distractor similarity and clutter interference in the divisive normalization simulations above, which does not agree with the finding from our psychophysics results that distractors of intermediate dissimilarity cause maximal clutter interference. Alternatively, simulations have shown that the visual system could learn to identify objects in clutter after being trained on thousands of clutter examples to extract individual object identity from IT neuron population activity (Li et al., 2009). However, given the virtually infinite variability of real-world visual scenes, it is unclear how such a solution scales to variable numbers of objects present and how much training would be required to recognize novel objects in new contexts.

In contrast to these theories, the HMAX model offers the hypothesis that individual neurons can maintain their selectivity in clutter as long as their afferents are selective enough that they respond more strongly to the neuron's preferred object than to the clutter. Then downstream areas devoted to performing categorization and identification tasks, like the ones shown by human fMRI and monkey electrophysiology to reside in prefrontal cortex (Kim and Shadlen, 1999; Freedman et al., 2003; Heekeren et al., 2004, 2006; Jiang et al., 2006, 2007), only read out the most active neurons. This simple readout for behavior confers an advantage to this model over the other models where the addition of more stimuli drives down the activity of the behaviorally relevant neurons, making it unclear how downstream neurons “know” to use those neurons for behavior. Reddy and Kanwisher (2007) found that classification accuracy for face and house stimuli based on fMRI voxel activation was robust to the addition of clutter when based on the most active voxels, supporting this method of readout. This model leads to the novel hypothesis that target detection performance should show a U shape as a function of target–distractor similarity, predicting a rebound in performance as distractors become dissimilar enough to activate disjoint feature sets. This effect, not predicted by the other models, was shown in the behavioral experiment.

Neuronal selectivity and object recognition in clutter

The relationship between neuronal selectivity in IT and clutter tolerance was explored by Zoccolan et al. (2007) using electrophysiology and modeling using the same HMAX model used here, revealing an inverse relationship: the more selective a neuron, the less clutter tolerant it was (and indeed, we find the same result in our simulations of single-unit clutter tolerance; results not shown). As was shown by Zoccolan et al. (2007), this relationship can easily be understood in terms of the model parameters that determine the selectivity of a VTU, with the number of C2 afferents d playing a particularly important role. For a given feature set, increasing the number of feature-level afferents to a particular VTU that have to match a specific preferred activation level leads to a more selective VTU, but it also leads to the inclusion of features that are activated more weakly by the preferred object, leading to increased susceptibility to clutter interference. However, both selectivity and clutter tolerance are required for successful object recognition in clutter. This can be achieved by increasing the specificity of the feature-level representation to better match the objects of interest (as in the case of our simulations involving face stimuli), enabling VTUs to respond selectively with fewer afferents. This leads to the interesting prediction that behavioral requirements to perform object detection in clutter (rather than on blank backgrounds) might lead to increased selectivity of feature-level representations, e.g., in intermediate visual areas.

Implications of the model

In addition to predicting the U-shaped curve for the target detection performance, the HMAX model also offers a parsimonious explanation for existing single-unit (Zoccolan et al., 2007) and fMRI data (MacEvoy and Epstein, 2009) for responses to multiple objects in the visual scene. The model shows that object-selective neurons can show behavior that appears average-like in response to suboptimal stimuli, especially when averaging over large neuronal populations. These results present an important caveat for fMRI and single-unit recording studies of clutter, where it is generally not known whether the particular neurons recorded from are actually involved in the recognition of the objects used in the experiment. In fact, sparse coding models predict that a particular object is represented by the activity of small numbers of neurons (Olshausen and Field, 2004), and it has been postulated that sparse coding underlies the visual system's ability to detect objects in the presence of clutter (Riesenhuber and Poggio, 1999b; Reddy and Kanwisher, 2006) by minimizing interference of neuronal activation patterns in ventral visual cortex caused by different objects. Indeed, fMRI and single-neuron studies have shown that only a subset of neurons responsive to a particular object appear to drive recognition behavior (Afraz et al., 2006; Reddy and Kanwisher, 2007; Williams et al., 2007). Therefore, an absence of robustness to clutter in some neurons' or voxels' responses might have little bearing on the behavioral ability to perform detection in clutter, because the neurons recorded from simply might not be involved in the perceptual decision. Conversely, the HMAX model's prediction that the neurons driving behavior are robust to clutter is supported by previous reports of robust neuronal object selectivity, as found previously in human temporal cortex (Agam et al., 2010) and suggested by fMRI (Reddy and Kanwisher, 2007). In summary, the sparse robust coding model not only accounts for behavioral object detection abilities, but also provides a unified explanation for human fMRI and monkey electrophysiology data, providing an appealingly simple and integrative account for how the brain performs object detection in the real world.