Novel Human Intervertebral Disc Strain Template to Quantify Regional Three-Dimensional Strains in a Population and Compare to Internal Strains Predicted by a Finite Element Model

Abstract

Tissue strain is an important indicator of mechanical function, but is difficult to noninvasively measure in the intervertebral disc. The objective of this study was to generate a disc strain template, a 3D average of disc strain, of a group of human L4–L5 discs loaded in axial compression. To do so, magnetic resonance images of uncompressed discs were used to create an average disc shape. Next, the strain tensors were calculated pixel-wise by using a previously developed registration algorithm. Individual disc strain tensor components were then transformed to the template space and averaged to create the disc strain template. The strain template reduced individual variability while highlighting group trends. For example, higher axial and circumferential strains were present in the lateral and posterolateral regions of the disc, which may lead to annular tears. This quantification of group-level trends in local 3D strain is a significant step forward in the study of disc biomechanics. These trends were compared to a finite element model that had been previously validated against the disc-level mechanical response. Depending on the strain component, 81–99% of the regions within the finite element model had calculated strains within one standard deviation of the template strain results. The template creation technique provides a new measurement technique useful for a wide range of studies, including more complex loading conditions, the effect of disc pathologies and degeneration, damage mechanisms, and design and evaluation of treatments.

The intervertebral disc supports significant loads while simultaneously permitting spinal mobility. However, injury and degeneration alter disc structure and composition, which in turn affects disc mechanical function and the motion of the surrounding spinal column. Tissue strain is an important indicator of mechanical function in load-bearing joints such as the intervertebral disc. Internal disc strains can be used to study healthy disc function and degeneration, to identify injurious loading conditions, and to design and evaluate therapeutic interventions.

The disc's structure, a pressurized gelatinous nucleus pulposus surrounded by the layered fiber-reinforced annulus fibrosus, hampers direct measurement of internal disc strain. Early experiments measuring internal disc strain relied on invasive methods such as bisecting the disc or tracking inserted markers.^1–3 However, because invasive methods cause structural modifications that inherently alter strain, these measurements may not accurately reflect actual tissue strains. To overcome these difficulties, recent studies have used magnetic resonance imaging (MRI) to noninvasively measure internal deformation under static load.^4–7 These studies have measured internal strain in a two-dimensional plane of interest, typically a midsagittal or midaxial plane. This method, while noninvasive, may be limited due to out-of-plane motion during loading. Moreover, to date these studies have not captured strain in the damage-prone regions of the disc, such as the posterolateral annulus fibrosus.⁸ To address these challenges, we recently used ultra-high field MRI and image registration to measure three-dimensional internal strain of human intervertebral discs undergoing static axial compression.⁹ MR images were acquired with 0.3 mm isotropic resolution and the resulting strain maps provided unparalleled definition of the internal mechanical response of the disc.

The large amounts of data provided and the variability between individual discs in the 3D data set has made discerning group-relevant trends difficult.⁹ This is a significant drawback, because group-level trends can be used to identify regions that are generally susceptible to high local strains, and are thus more susceptible to tissue damage. Although group trends are important, peak strains present in individual discs may also be indications of local tissue damage, similar to the way in which contact stress peaks in individual hip joints are likely the cause of pain.¹⁰ By establishing group trends, abnormal peaks in individual disc strain can be more readily identified by comparing and contrasting an individual disc strain map to a group average. This challenge of separating group trends from individual variation is addressed within the field of neuroimaging by using data from several individuals to create templates, which are essentially averages of the imaging data.^11–16 These templates may be single-modality, which are derived from a single imaging source, or they may be multi-modality, by utilizing information from multiple sources.^17,18 Because templates minimize individual variation in order to highlight key population traits, they are ideally suited for analyzing the recently acquired 3D disc images and strain maps.

Finite element models (FEMs) of disc strain are regularly used to examine the entire disc stress–strain profile.^19–22 Finite element models can perform parametric studies much more quickly and cost-effectively than experimental studies can, but these models also inherently include assumptions that potentially affect the results. Because of this, finite element models are validated against a set of in vitro experimental studies before being used for in silico experiments. To date, finite element models of intervertebral discs are validated against disc-level mechanical parameters. The strain template provides the opportunity for the internal strain calculations of a disc-finite element model to be validated, which is a much higher standard of fidelity than a disc-level response. We recently created a biphasic disc FEM using the average geometry of the L4–L5 disc and region specific tissue properties obtained from a wide range of experiments.^23,24 This FEM was validated by comparing its calculated disc-level mechanical response of human grade III L4–L5 discs to experimental compressive slow loading ramp, creep, and stress-relaxation tests. Because this model has undergone rigorous validation of the disc's nonlinear compression response, it is well suited for examination of the disc's internal strain profile and for comparison to a template of MRI calculated internal strains.

The objective of this study was to use previously acquired 3D MRI strain data⁹ to create an internal disc strain template based on a sample set of discs undergoing physiologically relevant compressive loading. We hypothesized that strains would be highest in the posterolateral and posterior regions of the disc. For greater insight into the strain template technique, template results were compared to a recently created finite element model.²⁴ Creating a 3D internal strain template marks significant progress toward quantifying internal disc strains, which in turn can be used to study normal and degenerate disc function and to design and evaluate therapeutic interventions.

METHODS

Template Creation Overview

The disc strain template was created using a process similar to dual-modality templates.^17,25 First, multiple MR images of the disc were acquired and strain maps for each disc were calculated using an image registration methodology as previously described (Fig. 1A).⁹ Next, a disc anatomical template was created using the MR images (Fig. 1B). During that process, the transformations between the individual discs and the anatomical template were calculated. Those transformations were used to transform the individual strain maps to the template space (Fig. 1C). Finally, the transformed sample strains were averaged to create the disc strain template. Note that during this process, image registration is performed and strain maps are calculated for the entire disc. Regions in which the image registration has not been validated,⁹ such as the nucleus pulposus, are later manually excluded prior to data analysis. The template creation process is described in more detail below.

Figure 1.

Disc strain template creation process. First, MR images of individual discs are acquired and subject strain maps are calculated (A). Next, the MR images are used to create a disc anatomical template (B). The transformations from the subject discs to the template are saved (T₁, T₂, …, T_n). Those transformations are used to transform the subject disc strains to the template space, which are then averaged to create the disc strain template (C). Although images shown are two-dimensional, the process was completed using three-dimensional data.

Data Acquisition

Internal three-dimensional strain maps were created for seven grade III human L4–L5 discs using methods that have recently been reported in detail (Fig. 1A).⁹ Briefly, bone-disc-bone samples were prepared by removing the posterior elements and then potting the samples in PMMA. Samples were potted under fluoroscopic guidance to ensure that the disc's mid-axial plane was parallel to the PMMA blocks. This was done so that the load applied during testing would result in axial compression. For testing, a sample was placed in a loading rig and 50 N of axial compression was applied using a servohydraulic tester (Instron 8874, Norwood, MA) to prevent overhydration. The loading rig was then used to fix the displacement and to transfer the sample to a 7T whole-body MR scanner (Magnetom, Siemens Medical Solutions, Malvern, PA). Three-dimensional images with 0.3 mm isotropic resolution were acquired with a sequence designed to enhance lamellar contrast (Turbo Spin Echo, TR/TE=3,000/34 ms, Echo Train Length=7). After imaging, the sample was loaded to −3.6±1.5% axial strain for 3 h, after which the resulting displacement was fixed and the sample was reimaged using the same parameters. The sample was then loaded and imaged at −7.1±2.9% and −10.3±3.5% strain. Only experimental data acquired in the preload (50 N) and −10.3±3.5% steps were used to create the disc template in this study and were called the reference and loaded images, respectively. Peak stress as a result of the −10.3±3.5% applied strain was 0.35±0.22MPa, which is comparable to the stresses experienced in a wide range of daily activities such as sitting, walking, and climbing stairs.²⁶

Strain within the annulus fibrosus was calculated by using Advanced Normalization Tools (ANTs) to register the reference and loaded images.^27–29 Due to the lack of contrast within the nucleus pulposus region and because of decreasing signal-to-noise ratio with distance from the RF coil, strain was only calculated in the two-thirds of the annulus fibrosus facing the coil. In the original experiment, samples were imaged with either the left or right lateral side facing the coil. To create the template, images acquired with the right lateral side of the disc facing the coil were flipped. This was done for three of the seven discs used so that the regions of high signal intensity were matched between all seven data sets.

Disc Anatomical Template

From each reference image, the disc was manually segmented from the bone and image background using ITK-Snap.³⁰ The disc-only images were then used to create a disc anatomical template using an optimization algorithm in ANTs (Fig. 1B). The algorithm is included in the Supplemental Material and described briefly here. The algorithm began by creating an initial template shape, which was all of the individual samples overlaid in a single image. Each of the seven subject discs was then registered to the initialized template shape using diffeomorphic transformations (transformations were smooth, differentiable, and invertible). Transform magnitudes for each of the seven registrations were calculated using the cross-correlation similarity metric. An adjusted template shape designed to decrease the transformation magnitudes was created, after which the subject discs were registered to the adjusted template shape. This process continued until the change in transform magnitudes between iterations converged. The resulting template shape was called the disc anatomical template.

Transform quality between samples to the anatomical template was assessed using a segmentation image (Fig. 2A). A segmentation image of each sample was created by manually selecting five annular regions using ITK-Snap. Next, the segmentation image was placed over the disc anatomical template to visualize the difference between the sample and the template (Fig. 2B). The segmentation image was then transformed to the template space using the transform calculated between the sample image and the template (Fig. 2C). The transformed segmentation image was qualitatively assessed to determine if the annular regions of the sample corresponded to the appropriate template regions. Target overlap was calculated to quantitatively evaluate the transforms in each annular region. Target overlap is the amount of overlapping voxels between the transformed subject labels and the template labels divided by the total number of template voxels.

Figure 2.

(A) A segmentation image (colored) overlays one of the individual disc images (grayscale) used to create the template. (B) The same segmentation from (A) overlays the template, demonstrating that the individual disc is notably larger than the template. (C) The individual disc segmentation is transformed to the template. The transformed mask matches the outer contour of the template and original features of the original mask are preserved, including the diagonal lines between the annular regions, indicating a reasonable transformation between the individual disc and the template.

Disc Strain Template

The disc strain template was created by first expressing the sample strain tensors in an anatomical coordinate system consisting of three orthogonal basis vectors: axial vectors perpendicular to the midaxial slice, circumferential vectors parallel with the outer disc contour, and radial vectors perpendicular to the outer disc contour (Fig. 3).⁹ Strain components of each sample were then transformed to template space using the transformations between each sample and the disc anatomical template. Because the strain tensors were expressed in terms of local coordinates, vector orientation relative to disc anatomy was preserved during transformation. The transformed strain components were averaged to create the disc strain template.

Figure 3.

Circumferential and radial basis vectors for a local disc coordinate system. Defining the strain in local coordinate system facilitates transformation of strain tensors from the subjects to the template and interpreting results in the context of disc coordinate system.

The template's effectiveness in reducing the variability of individual strain maps while preserving general trends was evaluated using the first invariant of the Lagrangian strain tensor. The first invariant is a scalar that is independent of coordinate system and represents the dilatational strain (volumetric change) at that point. Invariant maps were created for each sample and for the template. Then, the invariant template was qualitatively examined to determine if the specimen-specific peaks evident in the sample maps had been reduced while preserving general trends.

Regional Strain Analysis

Disc strain was analyzed as a function of anatomic location. The annulus fibrosus was partitioned into five regions of interest: Anterior, anterolateral, lateral, posterolateral, and posterior (Fig. 4A). There were between 6,100 and 13,000 voxels within each of the regions, depending on the region's annular thickness. To evaluate the difference between the inner and outer annulus, the five regions were divided in half. To avoid bone-disc edge effects, data was analyzed in the mid-third of the disc height (Fig. 4B and C).

Figure 4.

Midaxial (A), midcoronal (B), and midsaggital (C) slices of the disc anatomical template. The annulus approximately the mid-third of axial region of the disc was divided into five regions (anterior, anterolateral, lateral, posterolateral, and posterior). The lower lateral side of the template was more poorly defined than the upper lateral side (A), because the original images had lower signal-to-noise and contrast-to-noise ratios in the lower lateral side as it was further away from the RF coil. As a result, this side was not included in the strain analysis.

Each voxel of the strain template represents data for seven individual discs spatially normalized to the same anatomical location. For plotting purposes, the mean strain was calculated at each voxel. Boxplots and overlay images were then created using the voxel means within the region of interest. For statistical analysis, the mean strain in each annular region of interest was calculated for each of the transformed sample discs. The differences in region means of the seven samples were then evaluated using a repeated measure ANOVA with a Holm–Sidak Multiple Comparison Test. Significance for all tests was set at p<0.05.

Comparison to Finite Element Model

Both the finite element model and the anatomical template are average shapes of human L4–L5 discs. However, the finite element model used principal component analysis of an independent set of L4–L5 disc images to define the model geometry.¹¹ As geometry affects FEM results,²⁰ the shapes of the disc anatomical template and the finite element model were compared before comparing the FEM strain results with the strain template.

The internal strain results of a recently validated biphasic FEM²⁴ of the intervertebral disc were compared to the strain template. After simulating the same loading conditions as the samples used to create the strain template (−10.3% strain applied perpendicular to the disc's mid-axial plane), the finite element model strain results were sampled to match the strain template voxel distribution. The finite element model was then registered to the template, so that each voxel of the strain template corresponded to a voxel representing FEM results. At each voxel, the mean and standard deviation of the transformed sample disc strains was compared with the FEM strain results. Because there was no standard deviation associated with the finite element calculations, no statistical tests were performed. Instead, the difference between the FEM calculation and template mean strain was compared in terms of the template standard deviation. In studies using disc-level parameters, calculated FEM results that fall within one standard deviation of the experimental results are considered sufficient to validate the FEM.^24,31,32

RESULTS

Disc Anatomical Template

The final disc anatomical template held the expected shape of an intervertebral disc (Fig. 4). Total computational time to create the anatomical template was 10 h using 7 Intel Xeon nodes. The most striking difference between the original images and the template is the darker and less defined edges of the lower lateral side of the disc (Fig. 4A and B). However, this lack of edge definition was expected given the lower contrast on the lower lateral side of the disc in the original images and this third of the disc was not used for any analysis. Also, the template lacked lamellar contrast. Again, this was expected because the template is an average of multiple discs. Target overlap was lowest in the posterolateral region (84.0±10.6%) and highest in the anterior region (94.8±3.6%) (Table 1). The resulting values are comparable to the target overlap of the whole disc (94.4±0.9%) and better than the target overlap for individual lamella (65.2±12.4%) that were reported previously for disc registrations using ANTs.⁹

Table 1.

Target Overlap for the Five Annular Regions

Region	Target Overlap (%)
Anterior	94.8±3.6
Anterolateral	87.6±13.0
Lateral	87.3±7.5
Posterolateral	84.0±10.6
Posterior	90.1±3.5

Importantly, labels transformed from the samples to the template matched the expected areas well (Fig. 2). The disc shown in Figure 2A had the largest cross-sectional area of the sample set, and hence the transformation between the sample and the template was larger than that of most of the other samples. Irrespective of the difference between each sample and the template, the general features of the sample labels are appropriately transformed to the template (Fig. 2C). Specifically, after transformation the outer contour of the discs match, the relative thicknesses of the annulus are similar, the inner boundary of the annulus remains smooth, the boundaries between the five annular regions remain diagonal lines, and the five annular regions match the appropriate location in the template. These features are evidence that locations in the individual discs correspond to the appropriate template location. This successful spatial normalization allows for the creation of the disc strain template.

Disc Strain Template

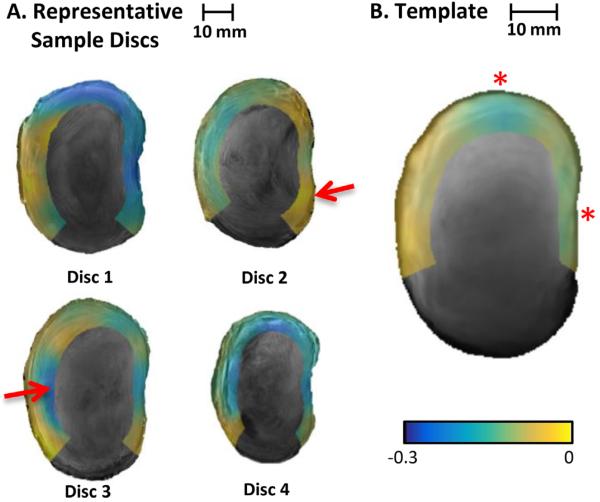
The first invariant of the strain tensor for the individual samples ranged between −0.3 and 0 (Fig. 5). Negative values indicate decreased volume, which is consistent with axial compression loading. There was considerable variation in the magnitude of invariants between samples and the location of the peak invariants (Fig. 5A). The strain template notably reduced individual peaks evident in the invariant distributions of the individual discs while preserving the general trends such as greater volumetric change in the posterior and lateral regions of the discs compared to the anterior regions (Fig. 5B).

Figure 5.

Midaxial disc slices showing the first invariant of the Lagrangian strain tensor of four of the seven individual discs (A) and the template (B). The negative values indicate decreased volume, which is consistent with the applied compression load. The template does not have the invariant peaks evident in many of the samples (e.g., the peaks located at arrows in Discs 2 and 3). The template preserved general trends, such as higher invariants in the lateral and posterior regions (e.g., the regions of blue-green shading in the template marked with *).

Regional Strain Analysis

Axial strain varied from −6.8% to −22.0% (Fig. 6A). The magnitude of axial strain was lower in the anterior region (−9.9%) than in the lateral region (−16.6%). The mean axial strain in the lateral, posterolateral, and posterior regions were similar, with values of −14.3% to −16.6% (p > 0.2). The range of circumferential strain (1.4–5.3%, Fig. 6B) was much smaller than the range of axial strain. There was an area of high circumferential strain in the lateral and the border between the lateral and posterolateral regions of the annulus, although this difference from the other regions of interest was not statistically significant (p > 0.2). In contrast to the axial strain, the circumferential strain component was similar in the anterior and posterior regions (p > 0.9). The radial strain components had twice the range (−3.5% to 4.4%, Fig. 6C) of the circumferential strain. Mean radial strain in the lateral region (−0.5%) was lower than radial strain in the anterior (2.5%), anterolateral (1.4%), posterolateral (2.5%), and posterior (2.8%) regions (p < 0.05). Similar to the circumferential strain, radial strain magnitude is similar in the anterior and posterior regions (p > 0.7).

Figure 6.

Boxplots of the voxel strain distributions in the five annular regions for the axial (A), circumferential (B), and radial (C) strain components. The data represents the average strain values for all of the voxels within the regions as defined in Figure 4. Midaxial slices of the strain template are also shown. Solid lines are significant differences between means of the seven subject discs transformed to the template space (p<0.05), and dotted lines are trends (p<0.1).

Between the inner and outer annulus regions, the difference in mean axial, circumferential, and radial strain components was not significant (Fig. 7). However, there was a statistical trend between the inner and outer sections of the radial strain in the lateral region, with a mean strain of −1.4% in the outer annulus and 1.1% in the inner annulus (p < 0.1).

Figure 7.

Comparison of voxel distributions axial (A), circumferential (B), and radial (C) strain components between the inner and outer annulus of the strain template. In most regions, there was minimal difference and no statistical difference between the inner and outer annulus. # indicates trend of difference between means of the seven subject discs transformed to the template (p<0.1).

Comparison to Finite Element Model

The geometry of the FEM and the disc anatomical template were very similar, differing by only a few millimeters in disc height, anteroposterior width, and lateral width (Fig. 8). The contours of the midaxial slices were also very similar. However, the midcoronal and midsagittal profiles differed in that the disc anatomical template had peaks along the outer rim of the inferior and superior edges that were not present in the FEM geometry. The difference between profiles is probably due to the different MR imaging sequences used to acquire the FEM and template data sets. The FEM data set was acquired using a 3D fast low-angle shot (FLASH) sequence,¹¹ while the template data set was acquired using a 3D turbo spin echo sequence. In the FLASH sequence, the outer rim of the disc was not visible, and hence was lacking in the FEM shape.

Figure 8.

Comparison of the disc template created in this study (red) and the finite element model geometry, which were created using different samples and methods¹⁰ (blue). The template and shape model are similar in both shape and size. The shapes differed in that the disc anatomical template had peaks along the outer rim of the inferior and superior edges that were not evident in the FEM geometry (see arrows in midcoronal and midsagittal views).

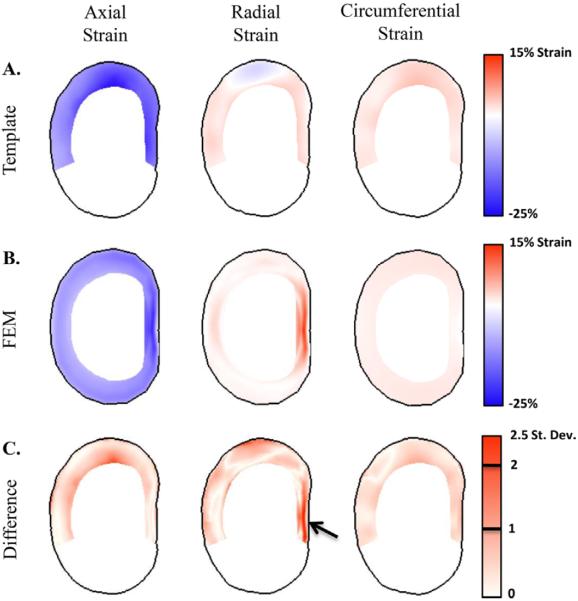
The FEM internal strains were similar in magnitude to the disc strain template (Fig. 9A and B). The finite element results were within one standard deviation of the template values for 85.5%, 99.5%, and 81.4% of all voxels for the axial, circumferential, and radial strain components, respectively (Fig. 9C). The areas of largest difference were in the anterolateral and lateral regions for the axial strain component and the lateral and posterior regions of the radial strain component. These differences are also evident in the average of template mean strains and the finite element results (Fig. 10). The template mean axial strain was lower than the calculated values of the FEM in the anterolateral and lateral regions of the disc (4.2% and 6.0% strain, respectively) (Fig. 10A). The mean radial strains in the template were also 2.0% strain lower than the FEM in the lateral region and 3.8% strain lower in the posterior region (Fig. 10C). Of the 15 comparisons between the template and the FEM (three strain components and five regions), the difference in medians between the two was less than 2.5% strain for all but three of the comparisons.

Figure 9.

Midaxial slices of the strain template (A) and finite element model (B). The difference of the FEM from the template mean is also shown in terms of the standard deviation at each voxel (C). The strains predicted by the FEM are within one standard deviation for the majority of the annulus in all three strain components. The greatest difference between the FEM and template is in the peak radial strains in the posterior region (arrow).

Figure 10.

Comparison of mean template strains and finite element model strains in the mid-third of the disc. The boxplots represent range of strain values found in the voxels within each annular region. Median strains between the template and finite element model are within 0.2–2.5% strain for all compared regions except for the axial component in the anterolateral and lateral regions and the radial component in the posterior region, which have a difference in median strain of 3.8–6.0% strain (*).

DISCUSSION

This work successfully completed the objective of creating an internal disc strain template for human grade III L4–L5 discs undergoing a compressive load. The individual strain maps contained 3D strain data that was measured noninvasively. As expected, the combination of 3D maps from individual discs into a single template reduced individual variability to allow for the study of group-level trends in local 3D strain such as high compression strain in the posterolateral and posterior regions (Fig. 5). Moreover, these trends were compared to the internal strains predicted by a validated finite element model with strong similarities in greater than 80% of the annulus fibrosus volume analyzed. Completing this objective is a substantial improvement in studying internal disc mechanics and provides a new methodology useful for multiple experimental studies, such as studying the effect of disc degeneration and treatments on internal disc strain. Beyond experimental measures, the results generated with this methodology may also further add validity to FEM studies, which until now have relied on gross deformation measures for validation.

The strain distributions of the template can be interpreted within the context of disc anatomy. Axial strains were much greater in magnitude (−7% to −22%) than circumferential and radial strains (−3.5% to 5.5%), which is consistent with the compression load causing an internal pressure that subsequently pushes the annulus outward. The amount of bulging as measured by mean radial strain is consistent with 2D MR strain measurements (1.8% vs. 2.1% strain).³³ Axial strain was greater in the posterior, posterolateral, and lateral regions of the disc than the anterior region (Fig. 6A). This may be due to lower disc height in the posterior of the disc compared to the anterior as seen in the midsagittal section (Fig. 8). The contributions of other anatomic and tissue mechanical property variations remain unknown, as do the strain variations outside the middle third of the disc. Also, circumferential strain was highest in the lateral and posterolateral regions of the disc (Fig. 6B). In conjunction with the thinner annulus in the posterior and posterolateral regions, this may explain why there is a higher occurrence of radial tears in the posterolateral region.⁸ Also, in the region with the highest circumferential strain (lateral), the radial strain was compressive, which is a consistent with a normal Poisson's effect. It is interesting to note that in most disc regions, the strains of the inner and outer annulus were not different (Fig. 7). The notable exception is the lateral region, in which the inner annulus had greater strain magnitudes. This difference between inner and outer annulus could be due to several factors, including the higher curvature of the disc in that region, the lower disc height over the inner annulus than outer annulus, and potentially different mechanical properties between the inner and outer annulus tissue.^23,34 However, the continuum of structure and composition from outer to inner annulus makes it difficult to distinctly separate these regions.

The wide range of observed axial strain magnitudes (−6.8% to −22.0%) highlights the inhomogeneity created by the disc's structure and composition. The circumferential and radial strain components also had wide ranges of 1.4% to 5.3% and −3.5% to 4.4%, respectively. Thus, even in a very simple loading condition that is representative of daily activities such as sitting and walking,^9,26 there are specific regions of the disc's structure that experience high strains that may eventually lead to tissue damage. The wide range is also important to consider in the context of the disc's cellular environment. Strain is attenuated between the tissue and cellular levels of fibrous tissue, including the intervertebral disc.^35–37 However, the magnitude of measured strain in this work indicate that even with attenuation, the cells that inhabit the disc likely experience a varied mechanical environment with the potential to influence cellular mechanobiology.

The majority of the strain template results were consistent with those of the FEM. For example, in both methods the highest circumferential strain was in the lateral region with a corresponding minimum of radial strain (Fig. 10B and C). Overall, the FEM results were within one standard deviation for 81–99% of the voxels examined depending on the strain component (Fig. 9C). This high level of agreement for a disc undergoing axial compression gives confidence that both the template internal strain measurements and the finite element model are reasonable. This comparison between experimentally measured strain and the finite element model is made possible by the template technique, which provides a way for averaging 3D strain data from multiple samples.

While the strain template was compared to the finite element model to ensure that the template results were reasonable compared to a widely accepted method of evaluating internal strains, the experimentally derived template can also serve as an internal validation of the finite element model. Finite element models are valuable tools in evaluating a disc's mechanical function because they have the ability to rapidly evaluate more complex loading conditions and to perform experiments altering properties that are not feasible to adjust in physical experiments. Unfortunately, disc FEMs are often constructed with significant assumptions concerning internal structure and mechanical properties, such as disc geometry, tissue constitutive models, viscoelasticity, collagen fiber angle, and material properties of the tissue structures. Furthermore, they are routinely validated using only simple, and often single, global parameters such as the amount of height loss during compression. As a result, the validity of disc FEM results is of concern. This concern may be reduced with internal validation using strain templates, and the comparison completed in this study provides strong support for the internal outputs for the FEM examined in this work.²⁴

The finite element model examined in this study had already gone through extensive validation of geometry, material model selection, and of the nonlinear response to compressive loads.²⁴ Despite the extensive validation of the finite element model, the comparison to the strain template uncovered two regions where the FEM did not match the measured results: the axial strains in the anterolateral region and the radial strains in the posterior region (Figs. 9C and 10). The peak radial strains in the posterior region are possibly due to the rectangular, rather than cube, shape elements in the region that may cause small discontinuities in fiber distribution within the model. The difference between the FEM and template axial strain may be due to the difference in the superior and inferior vertebral edges between the template and FEM (Fig. 8). Note that these differences did not cause discrepancies in the extensive testing and validation of the nonlinear disc-level mechanical response of this finite element model,²⁴ indicating that care should be taken in using internal outputs of finite element models that have been validated only using disc-level parameters. However, despite the need for some further refinements to the model, the mean predictions of the current FEM and template were similar in most respects.

While the purpose of creating the template was to eliminate individual variation in order to highlight group trends, the template can also be used to examine individual variations. Studying individual variations can be done by comparing and contrasting the strain distributions of an individual disc with the template strain map. This is important, because peak strains present in individual discs may be indications of local tissue damage, similar to the way in which contact stress peaks in individual hip joints are likely the cause of pain.¹⁰ By using a template to establish normal strain patterns, individual deviations can be more readily identified and interpreted.

In conclusion, the disc strain template provides an unprecedented view of the internal intervertebral disc strain. The combination of multiple 3D maps into a single template allows for the study of general strain trends within the disc. While the results presented in this paper were obtained using grade III L4–L5 discs undergoing axial compression, the technique can be extended to evaluate other degeneration grades, disc levels, and loading modalities. The comparison between the template strains and finite element model indicate that the template strains are reasonable and demonstrates a need for validating the internal strains calculated by finite element models. Studying tissue strain by using templates is a technique that is readily applicable for use in other joints and tissues. Moreover, the technique provides a new methodology useful for a wide range of studies, including more complex loading conditions, the effects of disc pathologies and degeneration, damage mechanisms, and design and evaluation of treatments.