Simultaneous multi-plane imaging of neural circuits

Summary

Recording the activity of large populations of neurons is an important step towards understanding the emergent function of neural circuits. Here we present a simple holographic method to simultaneously perform two-photon calcium imaging of neuronal populations across multiple areas and layers of mouse cortex in vivo. We use prior knowledge of neuronal locations, activity sparsity and a constrained nonnegative matrix factorization algorithm to extract signals from neurons imaged simultaneously and located in different focal planes or fields of view. Our laser multiplexing approach is simple and fast and could be used as a general method to image the activity of neural circuits in three dimensions across multiple areas in the brain.

Introduction

The coherent activity of individual neurons, firing in precise spatiotemporal patterns, is likely to underlie the function of the nervous system, so methods to record the activity of large neuronal populations appear necessary to identity these emergent patterns in animals and humans (Alivisatos et al., 2012). Calcium imaging can be used to capture the activity of neuronal populations (Yuste and Katz, 1991), and one can use it, for example, to image the firing of nearly the entire brain of the larval zebrafish, with single-cell resolution (Ahrens et al., 2013). But the larval zebrafish is transparent, and in scattering tissue, where nonlinear microscopy is necessary (Denk et al., 1990; Williams et al., 2001; Zipfel et al., 2003; Helmchen and Denk, 2005), progress toward imaging large numbers of neurons in three dimensions has been slower. In fact, in nearly all existing two-photon microscopes, a single laser beam is serially scanned in a continuous trajectory across the sample, in a raster pattern or with a specified trajectory that intersects targets of interest along the path. To image several focal planes one needs to change the focus and then reimage. This serial scanning leads necessarily to a low imaging speed, which becomes slower with increases in the number of neurons or focal planes to be imaged. Since the inception of two-photon microscopy, there have been many efforts to increase the speed and depth of imaging. One approach is to use inertia-free scanning using acousto-optic deflectors (AODs) (Reddy et al., 2008; Otsu et al., 2008; Grewe et al., 2010; Kirkby et al., 2010; Katona et al., 2012). Another approach is to parallelize the light and use many laser beams instead of a single one. Parallelized multifocal scanning has been developed (Bewersdorf et al., 1998; Carriles et al., 2008; Watson et al., 2009), as well as scanless approaches utilizing spatial light modulators (SLMs) which build holograms that target specific regions of interest (Nikolenko et al., 2008; Ducros et al., 2013; Quirin et al., 2014). As a further innovation of SLM-based imaging, we describe a novel “hybrid” multiplexed approach, combining traditional galvanometers and a spatial light modulator (SLM) to provide a powerful, flexible, and cost-effective platform for 3D two-photon imaging. We demonstrate its performance by simultaneously imaging multiple areas and layers of the mouse cortex, in vivo.

In particular, one key challenge in non-linear microscopies is expanding the spatial extent of imaging while still maintaining high temporal resolution and high sensitivity. This is because of the inverse relationship between the total volume scanned per second, and the signal collected per voxel, in that time. Our SLM hybrid-multiplexed scanning approach helps overcome this limitation by creating multiple beamlets that scan the sample simultaneously, and leverages advanced computational methods (Pnevmatikakis et al., 2016), companion paper in this issue of Neuron to extract the underlying signals reliably.

Results

The basic configuration of our SLM microscope consists of a two-photon microscope, with traditional galvanometers, along with an added SLM module. Fig. 1A shows a schematic of the SLM-based multiplexed two-photon microscope. The layout is based on that described in detail in (Nikolenko et al., 2008; Quirin et al., 2014) and similar to that in (Dal Maschio et al., 2010). The SLM module was created by diverting the input path of the microscope, prior to the galvanometer mirrors, with retractable kinematic mirrors, onto a compact optical breadboard with the SLM and associated components. The essential features of the SLM module are folding mirrors for redirection, a pre-SLM afocal telescope to resize the incoming beam to match the active area of the SLM, the SLM itself, and a post-SLM afocal telescope to resize the beam again to match the open aperture of the galvanometers and to fill the back focal plane of the objective appropriately. The SLM is optically conjugated to the galvanometers, and to the back aperture of the microscope objective (see Experimental Procedures for details). We coupled this module, with negligible mechanical changes, to a home-built two-photon microscope, as well as a lightly modified Prairie/Bruker system. The SLM is used as a programmable optical multiplexer that allows for high-speed independent control of each generated beamlet. The SLM performs this beam splitting by imprinting a phase profile across the incoming wavefront, resulting in a farfield diffraction pattern that yields the desired illumination pattern. These multiple beamlets are directed to different regions or depths on the sample simultaneously. When the galvanometers are scanned, each individual beamlet sweeps across its targeted area on the sample, and the total fluorescence is collected by a single photomultiplier tube. The resultant “image” is a superposition of all of the individual images that would have been produced by scanning each separate beamlet individually (see Fig. 1B, C).

Figure 1. SLM Two-photon Microscope and Multiplane Structural Imaging.

(A) SLM two-photon microscope. The laser beam from the Ti:Sapphire laser is expanded to illuminate the SLM. The spatially-modulated reflected beam from the SLM passes through a telescope, followed by an XY galvanometric mirror, and directed into a two-photon microscope. This setup is essentially composed of a conventional two-photon microscope, and an SLM beam shaping component (red dashed box).

(B) Illustration of axial dual plane imaging, where two planes at different depths can be simultaneously imaged.

(C) Illustration of lateral dual plane imaging, where two fields of view at the same depth can be simultaneously imaged.

(D) Two-photon structural imaging of a shrimp at different depths through the sample, obtained by mechanically moving the objective with a micrometer. Each imaging depth is pseudo-colored. The last image is constructed by overlaying all other images together. Scale bar, 100 µm.

(E) Software based SLM focusing of the same shrimp as (D). The SLM is used to modify the wavefront of the light to control the focal depth, while the position of the objective is fixed. The nominal focus of the objective is fixed at the 100 µm plane. This set of images looks similar to that in (D). Scale bar, 100 µm.

(F) Arithmetic sum of all the images at the seven planes shown in (D).

(G) Arithmetic sum of all the images at the seven planes shown in (E).

(H) Seven-axial-plane imaging of the same shrimp as (D)–(G), using the SLM to create 7 beamlets that simultaneously target all seven planes.

(I) Same as (H), but using the SLM to increase the illumination intensity only for the 50 µm plane. Features on that plane are highlighted compared to panel (H). Scale bar, 100 µm.

To demonstrate the multi-plane imaging system, we first performed structural imaging of a brine shrimp, Artemia naupili, collecting its intrinsic autofluorescence. First, we acquired a traditional serial “z-stack”, with seven planes, by moving the objective 50 µm axially between each plane (Fig. 1D). Next, we acquired a serial z-stack with seven planes separated by 50 µm each, but with the objective fixed, and the axial displacements generated by imparting a lens phase function on the SLM (Fig. 1E). In Fig.1F and 1G, we show the arithmetic sums of the individual sections in D and E, respectively. Finally, we used the SLM to generate all seven axially displaced beamlets simultaneously, and scanned them across the sample (Fig. 1H). We note that we can control the power delivered to each beamlet independently, which differentiates this method from traditional extended depth of field approaches, where near uniform intensity is imposed across the entire depth of field. Fig. 1I shows the image where the power at the 50 µm plane is selectively increased to enhance the signal at that depth. This flexibility is important for inhomogeneously stained samples, and is especially critical for multi-depth in vivo imaging in scattering tissue. Additionally, we can effectively control the complexity of the final image - we deterministically control the number of sections we illuminate.

To demonstrate functional imaging on our system, we perform in vivo two-photon imaging of layer 2/3 (L2/3) in the primary visual cortex (V1) in an awake head-fixed mouse, at a depth of 280 µm, at 10 Hz, (Fig. 2A) that expresses the genetically encoded calcium indicator, GCaMP6f (Chen et al., 2013) (details in Experimental Procedures). We configure the SLM as illustrated in Fig. 1C. We split the beam laterally, creating two beams with an on-sample separation of ~300 µm, centered on the original field-of-view (FOV) (Fig. 2A). A small beam block is placed in the excitation path to eliminate the zero order beam, leaving only the two SLM steered beams for imaging (details in Experimental Procedures). Figs. 2B–D, top, show images of the intensity standard deviation (std. dev.) of the time series image stack that results from scanning each of these displaced beams individually, and their arithmetic sum, respectively; while Fig. 2E, top, shows the std. dev. image acquired when both beams are simultaneously scanned across the sample. The lower images in Fig. 2B–E show the spatial components of detected sources from the images, with the colors coded to reflect the originated FOV. The areas contained in the red rectangle in Fig.2B and 2C highlights the area that is scanned by both beams, and hence their spatial components are present twice in the dual plane image.

Figure 2. Lateral Dual Plane in-vivo Functional Imaging of Mouse V1.

(A) Schematic of the in-vivo experiment, imaging V1 in the mouse. In this experiment, two fields of view (FOV), laterally displaced by 300 µm, are simultaneously imaged.

(B) /(C) Top panel, temporal standard deviation image of the sequential single plane recording (10 fps) of FOV 1 (B), and FOV 2 (C), of mouse V1 at a depth of 280 µm from the pial surface. Bottom panel, spatial component contours overlaid on the top panel. The boxes in dashed line show the overlapped region, shared in both FOVs. Scale bar, 50 µm.

(D) Arithmetic sum of (B) and (C).

(E) Top panel, temporal standard deviation image of the simultaneous dual plane recording (10 fps) of the two FOVs. Bottom panel, overlaid spatial component contours from the two FOVs.

(F) Representative extracted ΔF/F traces, using the CNMF algorithm, of the selected spatial components from the two field of views (red, FOV 1; green, FOV 2), from the sequential single plane recording.

(G) Extracted ΔF/F traces, using the CNMF algorithm, of the same spatial components shown in (F), from the simultaneous dual plane recording. The areas highlighted in blue in the dual plane ΔF/F traces are two spatial components taken from the overlapped area of the two FOVs. Their spatial contours are shown with the black box in the bottom panel in (E).

(H) Zoomed view of the ΔF/F traces in the shaded area in (G), showing the extremely high correlation between the independently extracted dynamics from the twinned spatial components.

Fig.2F and 2G show some representative fluorescence time series extracted from the detected spatial components (40 out of 235 shown), from the sequential single plane imaging and simultaneous dual plane imaging respectively. The same spatial components are displayed in both 2F and 2G, with the same ordering, to facilitate direct comparison of the single and dual plane traces. For Fig. 2F, the red and green traces from the two FOVs were collected sequentially, whereas in Fig. 2G, they were collected simultaneously. Because of the spatial sparsity of active neurons (see Fig. 2E, bottom), many of the spatial components are separable even in the overlaid dual region image, and fluorescence time series data can be easily extracted using conventional techniques. However, some spatial components show clear overlap, and more sophisticated methods, such as independent component analysis (ICA) (Mukamel et al., 2009), or non-negative matrix factorization methods (NMF) (Maruyama et al., 2014), perform better at extracting the activity. The traces shown were extracted using a novel constrained NMF method (CNMF), which is discussed in greater detail later in this paper (Fig. 4), and is described fully in the companion paper by Pnevmatikakis et al.. The collected multi-region image is simply the arithmetic sum of the two single region images, and thus we can use the detected spatial components from the single region image as prior for source localization. We leverage this to get very good initial estimates on the number of independent sources, and their spatial locations in the dual region image. We examine the “uniqueness” of signal recovery by looking at the spatial components that appear twice in the dual plane image and hence should display identical dynamics. Two examples are highlighted in blue on Fig. 2G, and expanded in Fig. 2H – each respective color shows the source copy generated from each beamlet, and show the extremely high correlation between the extracted traces (R>0.985).

Compared to the original FOV, the dual region image includes signals from a significantly larger total area, with no loss in temporal resolution. The maximal useful lateral displacement of each beamlet from the center of the FOV depends on the whole optical system, and is discussed in details in Supplemental Information. Besides increasing the effective imaged FOV, we can instead choose to also increase the effective frame rate, while keeping the same FOV (see Supplemental Information).

While the lateral imaging method increase performance, the full power of multiplexed SLM imaging lies in its ability to address axially displaced planes, with independent control of beamlet power and position. We can introduce a defocus aberration to the wavefront, which shifts the beam focus away from the nominal focal plane. In practice, we also include higher order axially dependent phase terms to correct higher-order aberrations (see Supplemental Information), and impose lateral displacements between the beamlets if desired. The SLM could also be used for further wavefront engineering such as adaptive optics to correct any beam distortion from the system or the sample, but it was not necessary in these experiments. Our current system can address axial planes separated by ~ 500 µm while maintaining the total collected two-photon fluorescence at >50% to that generated at the objective’s natural focal plane (see Supplemental Fig. S1 B). This gives considerable range for scanning without moving the objective, which eliminates vibrations and acoustic noise, and simplifies coupling with targetable photostimulation (Packer et al., 2015).

Using the SLM, we can address multiple axial planes simultaneously (schematic shown in Fig. 3A). Fig.3B and 3C show two examples of conventional “single-plane” two-photon images (intensity std. dev. of the time series image stack) in mouse V1, the first 170 µm below the pial surface, in L2/3, and the second 500 µm below the surface, in L5. These images were acquired with SLM focusing – the objective’s focal plane was fixed at a depth of 380 µm, and the axial displacements were generated by imposing the appropriate lens phase on the SLM (see Experimental Procedures for details.). At each depth, we recorded functional signals at 10 Hz, with Fig. 3F showing some representative extracted fluorescence traces from L2/3, and L5, in red and green, respectively (154 and 191 total spatial components detected across the upper and lower planes, respectively). The SLM was then used to simultaneously split the incoming beam into two axially displaced beams, directed to these two cortical depths, and scanned over the sample at 10 Hz (Fig. 3E). The power delivered to the two layers is adjusted such that the collected fluorescence from each plane was approximately equal (see Supplemental Information for details). Scanning these beamlets over the sample, we collect the dual plane image. This is shown together with the spatial components in Fig. 3E, which corresponds very well to the arithmetic sum of the individual plane images as shown in Fig. 3D. In Fig. 3G, we show 20 representative traces (out of 345 spatial source components), showing spontaneous activity across L2/3 and L5. The ordering of traces is identical with that of Fig. 3F, which facilitates comparison. The lightly shaded regions in Fig. 3F, G, are enlarged and shown in Fig. 3H, I. The signals show very clear events, with high apparent SNR. Further zooms of small events are shown in Fig. 3J, which reveals expanded views of the small peaks labeled i-iv on Figs. 3H, I.

Figure 3. Axial Dual Plane in-vivo Functional Imaging of Mouse V1 at Layer 2/3 and 5.

(A) Schematic of the in-vivo experiment, imaging V1 in the mouse. In this experiment, two different planes, axially separated by 330 µm, are simultaneously imaged.

(B) / (C) Top panel, temporal standard deviation images of the sequential single plane recording (10 fps) of mouse V1 at depth of 170 µm (layer 2/3) and depth of 500 µm (layer 5) from the pial surface. The images are false-colored. Bottom panel, spatial component contours overlaid on the top panel. Scale bar, 50 µm.

(D) Arithmetic sum of (B) and (C).

(E) Top panel, temporal standard deviation image of the simultaneous dual plane (10 fps) recording of the two planes shown in (B) and (C). Bottom panel, overlaid spatial component contours from the two planes.

(F) Representative extracted ΔF/F traces, using the CNMF algorithm, of 20 spatial components out of 345 from the two planes (red, layer 2/3; green, layer 5), from the sequential single plane recording.

(G) Extracted ΔF/F traces, using the CNMF algorithm, of the same spatial components shown in (F), from the simultaneous dual plane recording.

(H) / (I) Zoomed in view of the extracted ΔF/F traces in the shaded area in (F) and (G) respectively.

(J) Further enlargement of the small events in the ΔF/F traces shown in the blue shaded areas in (H) and (I).

In the dual plane image, it is clear that there is significant overlap between a number of sources. As mentioned earlier, CNMF (Pnevmatikakis et al., 2016) is used to demix the signal. We use a statistical model to relate the detected fluorescence from a source (neuron) to the underlying activity (spiking) (Vogelstein et al., 2009; Vogelstein et al., 2010). We extend this to cases where the detected signal (fluorescence plus noise) in each single pixel can come from multiple underlying sources, which produces a spatiotemporal mixing of signals in that pixel. The goal is, given a set of pixels of time varying intensity, infer the low-rank matrix of underlying signal sources that generated the measured signals. We take advantage of the non-negativity of the underlying neuronal activity to allow computationally efficient constrained non-negative matrix factorization methods to perform the source separation.

Operationally, to extract signals from the multiplane image, we initialize the algorithm with the expected number of sources (the rank), along with the nominal expected spatial location of the sources as prior knowledge, as identified by running the algorithm on the previously acquired single plane image sequences. For the single plane images, the complexity and number of overlapping sources are significantly less than the multi-plane images, and the algorithm works very well for identifying sources without additional guidance (see Supplemental Information). Supplemental Fig. S2 shows a single plane imaging example, from which various spatial components, including doughnut shape cell body and perisomatic dendritic processes, can be automatically extracted using CNMF, together with various calcium dynamics in the extracted temporal signals. The effectiveness of this method applied to multi-plane imaging is highlighted in Fig. 4, where we compare it against our “best” human effort at selecting only the non or minimally overlapping pixels from each source, and against ICA, which previously has proved successful in extracting individual sources from mixed signals in calcium imaging movies (Mukamel et al., 2009).

Figure 4. Source Separation.

Source separation of the fluorescent signal from spatially overlapped spatial components (SCs) in the dual plane images shown in Fig 3. (A) and (B) show two different examples with increasing complexity. In each example, the contours of the overlapped spatial components are plotted in red (from layer 2/3) and green (from layer 5) with their source ID. A pixel maximum projection of the recorded movie are shown to illustrate the spatial overlap of these SCs. Raw image frames from the recorded movie show the neuronal activity of these individual spatial components. For the temporal traces, the first trace (in gray) shows that extracted from all the pixels of the overlapped SCs. The following traces show the demixed signal of the individual SCs. Three different methods are used to extract the signal from individual SCs: non-overlapped pixel (NOL), with the extracted signal shown in orange, independent component analysis (ICA) in green, and constrained non-negative matrix factorization (CNMF) in red. The corresponding SC contours result from these methods are shown next to their ΔF/F traces, and the color code of the pixel weighting is shown immediately below (B). Using the SC contour from CNMF, but with uniform pixel weighting and without temporal demixing, the extracted ΔF/F trace is plotted in cyan, superimposed onto the traces extracted from CNMF. In (B), ICA fails to find the spatial component 2. The traces are plotted independently scaled for display convenience. The scaling applied is as follows: the scale bar of ΔF/F is 1.27 for SC 1 and 1.46 for SC 2 in (A); 1.24 for SC 1, 0.48 for SC 2, 0.36 for SC 3, 0.24 for SC 4, 0.78 for SC 5, 0.85 for SC 6, and 0.79 for SC 7 in (B).

In Fig. 4A–B, we show progressively more complex spatial patches of the dual plane image series. The overall structure of Fig. 4A and B is identical. In each panel, the uppermost row of images shows first the boundary of the spatial component contour, then the maximum intensity projection of the time series, along with the subsequent images showing representative time points where the component sources are independently active. The spatial components in red and in green come from L2/3, and L5, respectively. The leftmost column of images shows the weighted mask, labeled with the spatial component selection scheme (binary mask from maximum intensity projection, human selected non-overlapped region (NOL), ICA, or CNMF) that produces the activity traces presented immediately to the right of these boxes. On top of the full CNMF extracted traces in red, we also show, in cyan, the signal extracted considering only the CNMF spatial component, but with uniform pixel-weighting, and no spatio-temporal demixing. This comparison shows the power and effectiveness of the source separation.

We first discuss the spatial component selection scheme using NOL. In simple cases, like in Fig. 4A, we see only a subset of the events in the combined binary mask. In more complex cases (Fig. 4B, and Supplemental Fig. S4 B–D), where multiple distinct sources can overlap with the chosen source, the non-overlapped portion may only contain a few pixels, yielding poor SNR, or those pixels may not be fully free from contamination, yielding mixed signals. Nevertheless, in regions where the non-overlapped portion is identifiable, we can use this as a reference to evaluate the other two algorithms.

We then examine the ICA extracted sources. ICA identifies the sources automatically without human intervention, and with high speed. For cases where the number of sources in space is low and there are “clean” non-overlapping pixels with high SNR (Fig. 4A), the extracted components are spatially consistent with the known source location (cf. top row of images). In many cases, they include a region of low magnitude negative weights, which on inspection, appear to spatially overlap with adjacent detected sources, presumably because this decreases the apparent mixing of signals between the components. More consequential is that for the complex overlapping signals in our experiment, ICA routinely fails to identify human and CNMF identified spatial source components, and appears to have less clean separation of mixed signals (cf. activity traces in Fig 4A, and the complete failure of ICA to identify spatial component 2 in Fig. 4B). See also Supplemental Fig. S3 for the comparison on a large population.

We further compare CNMF traces against the human selected non-overlapping traces for a larger population in Fig. 5 (and additionally in Supplemental Fig. S4, and S5). Fig. 5A shows the cross correlation between 250 CNMF sources and the NOL source related to it. The correlation is high, as would be expected if the CNMF traces accurately detect the underlying source. The majority of the signals show a correlation coefficient of > 0.94, and the mean correlation coefficient is 0.91. The distribution of coefficients is strongly asymmetric, and it contains some notable outliers. Examining the underlying traces of these outliers (Fig. 5C, and Supplemental Fig. S4 B–E), we can identify the origin of the poor correlation between the NOL traces and the CNMF traces. In these cases, the NOL spatial component consists of only a few pixels, and is extremely noisy; they also contain contamination from neighboring sources. The related spatial component from CNMF contains more pixels, has less noise, and shows clean demixed signal. They have generally higher SNR, especially for those NOL spatial components with low SNR (Fig. 5B–E; see Experimental Procedure for definition of SNR).

Figure 5. Comparison between CNMF and NOL.

(A) Correlation coefficient between the ΔF/F extracted from CNMF and NOL for a total of 250 spatial components (SCs) in the dual plane imaging shown in Fig. 3. The blue dashed line indicates the median (0.947) of the correlation coefficients. The SC IDs are sorted by the SNR of the signals extracted by NOL.

(B) Signal to noise ratio (SNR) comparison between the ΔF/F extracted from CNMF (with residue) and the ΔF/F extracted from NOL for the 250 SCs. The overall SNR of CNMF (with residue) is 13% higher than that from NOL.

(C) An example where three sources that are spatially overlapped in the dual plane imaging is studied. The contours of the overlapped SCs are plotted in red (from layer 2/3) and green (from layer 5) with their spatial component ID. The CNMF and NOL extracted ΔF/F signals are plotted in red and orange respectively. The signal that CNMF extracted, with residual noise is plotted in blue. Using the SC contour in the CNMF but with uniform pixel weighting and without temporal demixing, the extracted ΔF/F trace is plotted in gray, and labelled as “Raw”. The corresponding correlation and SNR values for these two SC are labelled in (A) and (B). The traces are plotted independently scaled for display convenience. The scaling applied is as follows: the scale bar of ΔF/F is 0.29 for SC 1, 0.14 for SC 2, and 0.51 for SC 3.

(D) / (E) Histogram of the ΔF/F noise for (D) SC 1 and (E) SC 2. The orange color shows that for the NOL extracted signal, whereas blue shows that for CNMF with residue. The histograms are fitted with a Gaussian function, shown as a solid-line curve.

The fraction of cells with low correlation between the NOL and CNMF components are exactly the sources that simple signal extraction techniques cannot cleanly separate – they are the imaged sources that require CNMF. Without CNMF, extracted signals would falsely show high correlation between sources that are imaged into the same region in the dual plane image. In the dual plane image collected in Fig. 3 and analyzed here, we find that ~26% of the cells have correlations below 0.9. The SNR comparison in Fig. 5B is between the NOL signal and that from CNMF with residue (i.e. noise, see Experimental Procedure), to not simply boost the CNMF SNR from full deconvolution. Globally, the SNR of CNMF is 13% higher than that from NOL. The pooled data (~1800 spatial components from 10 dual-plane imaging sessions across 5 mice) presented in Supplemental Fig. S5 show similar results.

The power of our simultaneous multi-plane imaging and source separation approach can be seen in Fig. 6, where we are able to record spontaneous and evoked activity across multiple layers, which is critical for understanding microcircuit dynamics in the brain. We examined visually evoked activity in L2/3 and L5, simultaneously, while we projected drifting gratings to probe the orientation and directional sensitivity of the neuronal responses (OS and DS, see Experimental Procedures). This paradigm was chosen because drifting gratings produce robust responses in V1 (Niell and Stryker, 2008). They are used frequently in the community (Huberman and Niell, 2011; Rochefort et al., 2011), and can be used to examine the performance of our imaging method in a functional context. Fig. 6A shows some representative extracted traces from cells with different OS, along with an indicator showing the timings of presentation of stimuli (traces shown were acquired under the dual-plane paradigm). During the entire recording period, this mouse had particularly strong spontaneous activity in nearly all of the cells in the FOV. Nonetheless, many cells showed strong and consistent orientation tuning across the trials (76 out of 260 cells). For these cells, we compared the computed single-plane DS and OS to those computed from the same neurons, but from the dual-plane image series. If the dual-plane images had increased noise, or more seriously, if overlapping sources could not be cleanly separated, we would expect decreased, or even altered OS. This is neither the case on the population level, nor on the single cell level, as seen in Fig. 6B and C. In Fig. 6D we show the std. dev. dual-plane image, and the extracted spatial component contours. The two small boxes on the contour image indicate two pairs of cells with significant spatial overlap in the dual-plane image. We examine the DS of these cells in more detail in Fig. 6E, and it is clear that we can fully separate the functional activity of even strongly overlapping cells, without cross contamination.

Figure 6. Orientation and Direction Selectivity Analysis with Simultaneous Dual Plane Imaging.

(A) Normalized ΔF/F traces for selected spatial components (SCs) with strong response to drifting grating visual stimulation, recorded with simultaneous dual plane imaging. The red and green color traces are from SCs at depths of 200 µm and 450 µm from the pial surface of mouse V1. The color bar in the bottom of each trace indicates the visual stimulation orientation of the drifting grating, with the legend shown on top of (B), i.e. red: 0°/180°, yellow: 45°/225°, green: 90°/270°, purple: 135°/315°.

(B) Left panel, response of the SCs to the drifting grating in visual stimulation. The SCs are on the 200 µm plane. The SCs are separated into four groups, corresponding to a preferred orientation angle of 0°/180°, 45°/225°, 90°/270°, and 135°/315°. The black curves are the average response of the group. Right panel, comparison of the SCs’ preferred orientation angle to the drifting gratings, between signals extracted from the single plane recording (blue dots) and the dual plane recording (orange dots).

(C) Same as (B), for spatial components located at 450 µm depth from pial surface.

(D) Left, overlaid temporal standard deviation image (with false color) of the sequential single plane recording from the 200 µm plane (red) and from the 450 µm plane (green). Right, extracted SC contours from the two planes. Scale bar, 50 µm.

(E) Examples of the evoked responses of the SCs with spatial lateral overlaps from the two planes. The blue color shows that extracted from single plane recording, and the orange shows that extracted from dual plane recording. The arrow inside each SC indicates its preferred direction. The locations of these SCs are indicated in the small black boxes in the SC contours in (D).

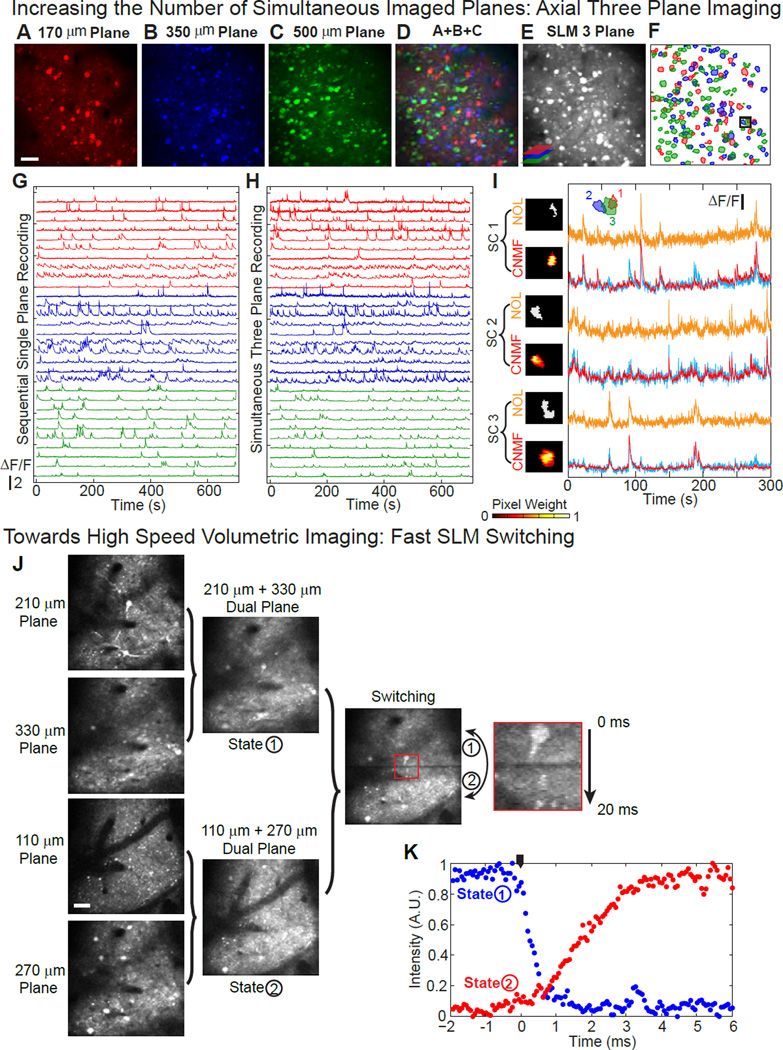
The data shown in Figs. 3–5 and 6 were taken with two planes, with inter-plane spacing of 330 µm and 250 µm, respectively, which is far from the limit of the method. In Fig. 7A–I, we show experimental results from simultaneous three-plane imaging of mouse V1. The intermediate plane is set to be the same as the nominal focal plane (the undiffracted beam’s location). Fig. 7A–C show the images of the intensity std. dev. of the time series image stack from single-plane imaging at three different depths. The SLM simultaneous three-plane imaging is shown in Fig. 7E, well corresponding to the arithmetic sum of Fig. 7A–C shown in Fig. 7D. The spatial contour of the extracted source components are shown in Fig. 7F, along with the representative fluorescence traces shown in Fig. 7G and H for sequential single plane and simultaneous three plane imaging respectively. In Fig. 7I, we show an example where three overlapped sources from the three planes can be cleanly separated using CNMF. We can further extend the extremal range between planes to over 500 µm, shown in Supplemental Fig. S6 A–G.

Figure 7. Axial Three Plane in-vivo Functional Imaging of Mouse V1, and Fast SLM Switching between Different Holograms.

(A) – (C) Temporal standard deviation image of the sequential single plane recording (10 fps) of mouse V1 at depths of 170 µm, 350 µm and 500 µm from the pial surface. The images are false-colored. Scale bar, 50 µm.

(D) Arithmetic sum of (A) – (C).

(E) Temporal standard deviation image of the simultaneous three-plane recording (10 fps) of the same planes shown in (A) – (C).

(F) Overlaid spatial component (SC) contours from the three planes.

(G) Representative extracted ΔF/F traces of the selected SCs from the three planes (red, 170 µm plane, 10 SCs out of 58; blue, 350 µm plane, 10 SCs out of 65; green, 500 µm depth, 10 SCs out of 95), from the sequential single plane recording.

(H) Extracted ΔF/F traces of the same SCs shown in (G), from the simultaneous three-plane recording.

(I) An example of source separation of the fluorescent signal from spatially overlapped components in the three plane imaging. The locations of these SCs are shown in the small black box in (F). The contours of the overlapped SCs are plotted in color with their SC ID. For each SC, the signal is extracted using NOL shown in orange, and CNMF in red. The corresponding SC contours result from these methods are shown next to their ΔF/F traces. A raw trace, generated from the CNMF SC, but with uniform pixel weighting, and without temporal demixing, is plotted in cyan, superimposed onto the traces extracted with CNMF. Fluorescent traces are independently scaled for display convenience. The scale bar of ΔF/F is 0.268, 0.376, and 0.351 for SC 1–3 respectively.

(J) SLM switching between two sets of dual plane imaging on mouse V1. State 1 is the dual plane for depth of 210 µm and 330 µm from pial surface, and state 2 is the dual plane for depth of 110 µm and 270 µm from pial surface. Imaging frame rate is 10 fps. The SLM switching happens at the middle and at the end of each frame. The zoom-in-view of the switching region shows that the switching time between the two state is less than 3 ms. Scale bar, 50 µm.

(K) SLM switching time between two different states, measured from the change in fluorescent signal emitted from spatially localized planes of Rhodamine 6G. The switching time between different states is less than 3 ms. The black indicator marks when the switching starts.

The multiplane imaging can be further extended with a time-multiplexed scheme. The SLM used in our experiments can switch between different holograms at high speed (> 300 Hz). In Fig. 7J, we show that we can fully transition between two sets of simultaneous dual-plane images in < 3 ms, a switching time confirmed “offline”, using a simple structured Rhodamine 6G target, in Fig. 7K. This spatial-multiplane imaging and time-multiplexed scheme paves the path towards high speed volumetric imaging (schematic shown in Supplemental Fig. S6 H).

Discussion

In this work, we extend two-photon holographic microscopy (Nikolenko et al., 2008; Anselmi et al., 2011) to demonstrate successful simultaneous 3D multi-plane in vivo imaging with a hybrid SLM multiplexed-scanning approach that leverages spatiotemporal sparseness of activity and prior structural information to efficiently extract single cell neuronal activity. We can extend the effective area that can be sampled, target multiple axial planes over an extended range, > 500 µm, or do both, at depth within the cortex. This enables the detailed examination of intra- and inter-laminar functional activity. The method can be easily implemented on any microscope with the addition of a relatively simple SLM module to the excitation path, and without any additional hardware modifications in the detection path. The regional targeting is performed remotely, through holography, without any motion of the objective, which makes the technique a strong complement to 3D two-photon activation (Packer et al., 2012; Rickgauer et al., 2014; Packer et al., 2015). This approach is an initial demonstration of an essential paradigm for future high speed in vivo volumetric imaging in scattering tissue, combining structured multiplexed excitation along with computational reconstruction that is aided by additional prior knowledge - in this case, the simplified single plane source locations.

Comparisons to alternative methods

There are many imaging modalities today that are capable of collecting functional data within a 3D volume. The simplest systems that provide volumetric imaging combine a piezo mounted objective with resonant galvanometers, which have high optical performance throughout their focusing range. A critical component for determining the imaging rate is the speed of the piezo - how fast the objective can be translated axially. For deep imaging in scattering tissue, the fluorescence collection efficiency scales as $\frac{N{A}^2}{M^2}$, with M being the objective magnification (Beaurepaire and Mertz, 2002). The combination of high NA with low magnification invariable means that the objectives are large, and heavy. This large effective mass lowers the resonant frequency of the combined piezo/objective system, and necessitates significant forces to move axially quickly, as well as lengthens the settle times (~15 ms); this also lowers the duty cycles as imaging cannot take place during objective settling. The distance that the piezo can travel is also limited, with the current state-of-the-art systems offering 400 µm of total travel. Compared to piezo-based systems, our SLM-based approach has significantly greater axial range, and couples no vibrations into the sample. Additionally, we can change between different planes through the full range very rapidly, in <3 ms and allows for axial switching within a frame (Fig. 7J–K).

Remote focusing has also been used for faster volumetric imaging, either with the use of a secondary objective and movable mirror (Botcherby et al., 2012), with electrotunable lenses (ETL) (Grewe et al., 2011), and very recently, with ultrasound lenses (Kong et al., 2015). While these have higher performance than piezo mounted objectives, none of these have yet been demonstrated to allow for in vivo functional imaging at the axial span that we show here. For applications where a perfect PSF is paramount, remote focusing with a mirror may offer better optical performance, but requires careful alignment and engineering. Ultrasound lenses give very high speed axial scanning, but must be continuously scanned, a severe limitation of the technology. The standalone ETL, when properly inserted into the microscope, represents perhaps the most cost effective solution for fast focusing. While the electrotunable lens provides a lower cost solution, it is not as fast as the SLM and it cannot provide any adaptive optics capabilities, nor flexible beam reconfiguration, such as lateral shift or multiplexed excitation. Ultrasound lenses also lack convenient beam multiplexing or complex optical corrections. SLMs, on the other hand, allow for all of these.

While fast sequential imaging strategies such as acousto-optic deflector (AOD) systems offer good performance, with the state-of-the-art 3-D AOD systems currently providing high performance imaging over relatively large volumes of tissue (Reddy et al., 2008; Kirkby et al., 2010; Katona et al., 2012), these systems are very complex and expensive, with a cost that is at least a few times that of conventional two-photon microscopes, severely limiting their practical use. They are also very sensitive to wavelength, requiring extensive realignment with changes in wavelength. An additional complication of any point targeting strategy, like AOD systems, is that sample motions are significantly more difficult to treat (Cotton et al., 2013).

A bigger limitation of all of these serially scanned systems is that all are near the fundamental limits on their speed, as finite dwell times are required on each pixel to maintain SNR. As fluorophore saturation ultimately limits the maximum emission rate regardless of excitation intensity, increases in intensity simply cause photodamage, bleaching, and reduced spatial resolution. Wide-field fluorescence imaging can overcome the speed limit with the developments of high speed cameras. Despite their high performance, wide-field imaging schemes such as light-sheet microscopy (Ahrens et al., 2013), light field microscopy (Prevedel et al., 2014), or swept confocally-aligned planar excitation (SCAPE) (Bouchard et al., 2015), suffer from light scattering in deep tissues and are thus better suited for relatively superficial imaging or imaging in weakly scattering samples.

Multiplexed two-photon based approaches become a clear way to increase overall system performance by taking advantage of the benefits of nonlinear imaging, while maintaining sufficient dwell times for high sensitivity. Spatially multiplexed strategies have been used before (Bewersdorf et al., 1998; Fricke and Nielsen, 2005; Bahlmann et al., 2007; Kim et al., 2007; Matsumoto et al., 2014), but with very limited success for imaging neuronal activity in scattering samples. The fluorescence produced deep in the samples scatters extensively while travelling through the sample, which limits the ability to “assign” each fluorescence photon to its source (Andresen et al., 2001; Kim et al., 2007; Cha et al., 2014). A more successful approach has been to temporally multiplex each separate excitation beam (Egner and Hell, 2000; Fittinghoff et al., 2000; Andresen et al., 2001; Cheng et al., 2011), and use customized electronics for temporal demixing. For multilayer imaging, our current system exceeds the demonstrated FOV and axial range of published implementations using temporally multiplexed beams, and provides a cleaner signal demixing, with significantly greater flexibility and speed in choosing targeted depths. However, we do not consider other spatially separated multibeam or temporally multiplexed strategies as competitors, but rather as complementary methods that could be leveraged to further increase the overall system performance.

Current limitations and Technical Outlook

Phase only SLMs for beam steering

The performance of our current system is strongly dependent on the SLM, a 512×512 pixel phase-only device that performs beam-splitting by imparting phase modulation on the incoming laser pulse, and uses diffraction to redirect the beams to their targeted sites. Multiple factors are needed to be considered when designing an SLM based imaging system. Firstly, the efficiency of the SLM diffraction is notably affected by the fill factor and the effective number of phase levels per “feature”. The effective power throughput from the SLM module ranges from ~82% to 40% for the patterns used in this paper. This is significantly better than <20% overall efficiency of a full 3-D AOD system. The efficiency of this method can be improved by better SLMs; that is devices that have higher fill factors, increased pixel number, and increased phase modulation – all of which are the subject of active development. Secondly, any diffractive device is inherently chromatic – the deflection depends on the wavelength of the light. This chromatic dispersion can be reduced with the incorporation of a custom dispersion compensation optical element. For axial displacements on our system, the effect of chromatic dispersion on performance is markedly less. More details are presented in Supplemental Information.

Regarding the maximal number of planes addressable, and limitations to the axial spacing, practically, we find acceptable results when the separation between planes is at least 5 times the axial PSF for shifts without lateral displacements. Shorter separations appear to give decreased sectioning. In our experiments, the maximal number of planes (3) demonstrated for functional imaging was limited by the total power deliverable on sample, as we specifically aimed to target deeper layers where scattering losses are significant. By targeting more superficial layers, more planes were addressable. Adaptive optics could also extend the gains to deeper layers. Fundamentally, the maximal usable number of planes is limited by the biology and functional indicators – relatively sparse signals with little background would promote the use of more planes, while dense, complex sources may require limiting the number of planes to low numbers to achieve effective demixing. In the dual plane experiments shown in Fig. 3–5, the strongly overlapped sources represent ~30% of all detected sources (as can be seen in the correlation between NOL and CNMF in Fig. 5A), so we believe there is significant room to push the total number of planes with the current setup.

Volumetric imaging

The overall speed of multiplane imaging can be increased with additional simple methods. With the current system’s high apparent sensitivity, we anticipate that we could reduce the nominal dwell time per pixel, and still collect enough photons for effective detection. By transitioning our microscope from conventional galvanometers to resonant galvanometers, we could speed up the imaging by at least a factor of three. Combined with the fast switching time of our device (< 3 ms, see Fig. 7J–K, and Thalhammer, et al. (Thalhammer et al., 2013)), we anticipate being able to image large volumes of neural tissue at high speed. Our strategy is to rapidly interleave multiplane images in successive scans to generate a complete picture of neural activity with schematics shown in Supplemental Fig. S6 H.

Outlook

SLM-based multi-region imaging is one implementation of the general strategy of computationally enhanced projective imaging, which will make possible the ability to interrogate neurons over a very large area, with high temporal resolution and SNR. Projective imaging is extremely powerful, especially when combined with prior information about the system to be studied. Basic knowledge of the underlying physical structure of the neural circuit and sparsity of its activity are used to define constraints for the recovery of the underlying signal, and allow for higher fidelity reconstruction and increased imaging speed in complex samples. With our multiplexed SLM approach we determine the number of areas simultaneously illuminated and have direct control over the effective number of sources, in contrast to alternate extended two-photon approaches, such as Bessel beam scanning (Botcherby et al., 2006; Theriault et al., 2014), where the sample alone controls the complexity of the signal.

There are many questions that can be addressed by high speed volumetric imaging. First, the simple increase in total neurons monitored in the local circuit greatly increases the chances for capturing the richness and variability of the dynamics in cortical processing (Alivisatos et al., 2013a; Alivisatos et al., 2013b; Insel et al., 2013). For instance, what is the organization of functionally or behaviorally relevant ensembles in cortical columns? How do upstream interneurons affect downstream activity and synchrony, and output (Helmstaedter et al., 2008; Helmstaedter et al., 2009; Meyer et al., 2011)? Without the ability to probe interlaminar activity simultaneously, answering these questions definitively will be very difficult, if not impossible. Though we have focused on somatic imaging in this paper, this technique works equally well for imaging dendrites, or dendrites and soma together (data not shown, see companion paper (Pnevmatikakis et al., 2016), for dendritic source separation with CNMF). The extended axial range of our method would allow exploring L5 soma and their apical tufts simultaneously, and may give direct insight into the role of dendritic spikes and computation in neuronal output (London and Hausser, 2005; Shai et al., 2015). Thus, SLM-based multiplane imaging appears to be a powerful method for addressing these, and other questions that require high speed volumetric imaging with clear cellular resolution. The system is flexible, easily configurable, and compatible with most existing two photon microscopes, and could thus provide a novel powerful platform with which to study neural circuits function and computation.

Experimental Procedures

Animals and Surgery

All experimental procedures were carried out in accordance with animal protocols approved by Columbia University Institutional Animal Care and Use Committee. All Experiments were performed with C57BL/6 wild-type mice at the age of postnatal day (P) 60–120. Virus AAV1synGCaMP6f (Chen et al., 2013) was injected to both layer 2/3 and layer 5 of the left V1 of the mouse cortex, 4–5 weeks prior to craniotomy. The virus (6.91e13 GC/ml) was front-loaded into the injection pipette and injected at a rate of 80 nl/min. The injection sites were at 2.5 mm lateral and 0.3 mm anterior from the lambda, putative monocular region at the left hemisphere. Injections (500 nL per site) were made at two different depths from the cortical surface, at 200 µm-250 µm and 400 µm-500 µm respectively.

After 4–5 weeks of expression, mice were anesthetized with isoflurane (1–2% v/v in air). Before surgery, dexamethasone sodium phosphate (2 mg per kg of body weight; to prevent cerebral edema) and bupivacaine (5 mg/ml) were administered subcutaneously, and enrofloxacin (4.47 mg per kg) and carprofen (5 mg per kg) were administered intraperitoneally. A 2 mm diameter circular craniotomy was made over the injection cite with a dental drill and the dura mater was removed. 1.5% agarose was placed over the craniotomy and a 3-mm circular glass coverslip (Warner instruments) was placed and sealed using a cyanoacrylate adhesive. A titanium head plate was attached to the skull using dental cement. The imaging experiments were performed 1–14 days after the chronic window implantation. During imaging, the head-fixed mouse is awake and can walk on a circular treadmill.

The shrimp used in the structural imaging were artemia nauplii (Brine Shrimp Direct).

Two-photon SLM laser scanning microscope

The setup of the two-photon SLM laser scanning microscope is illustrated in Fig. 1. The laser source is a pulsed Ti:Sapphire laser (Coherent Mira HP) tuned to 940 nm with a maximum output power of ~1.4 W (~140 fs pulse width, 80 MHz repetition rate). The laser power is controlled with a Pockels cell (ConOptics EO350-160-BK). A λ/2 waveplate (Thorlabs AHWP05M-980) is used to rotate the laser polarization so that it is parallel with the active axis of the spatial light modulator (Meadowlark Optics, HSP512-1064, 7.68 × 7.68 mm² active area, 512 × 512 pixels). The laser beam is expanded by a 1:1.5 telescope (f1=50 mm, f2=75 mm, Thorlabs plano-convex lenses, “B” coated) to fill the active area of the SLM. The light incident angle to the SLM is ~ 3.5°. The reflected beam is scaled by a 4:1 telescope (f3=400 mm, f4=100 mm, Thorlabs achromatic doublets lenses, “B” coated), and imaged onto a set of close-coupled galvanometer mirrors (Cambridge 6215HM40B). In the dual lateral plane imaging, a beam block made of a small metallic mask on a thin pellicle is placed at the intermediate plane of this 4:1 telescope to remove the zero order beam. The galvanometer mirrors are located conjugate to the microscope objective pupil of a modified Olympus BX-51 microscope through an Olympus pupil transfer lens (f5=50 mm) and tube lens (fTL=180 mm). An Olympus 25× NA 1.05 XLPlan N objective is used for the imaging. The fluorescent signal from the sample is detected with a photo-multiplier tube (PMT, Hamamatsu H7422P-40) and a low noise amplifier (Stanford Research Systems SR570). ScanImage 3.8 (Pologruto et al., 2003), is used to control the galvanometer mirrors, and digitize and store the signal from the PMT amplifier. The line scanning is bidirectional with a single line scan rate of 2 kHz. For a 256 × 200 pixel image, the frame rate is 10 fps.

A detailed characterization of the performance of SLM beam steering, and its dependence on other optics in the microscope, such as the objective, are presented in Supplemental Information.

Hologram generation

Custom software using MATLAB (The MathWorks, Natick, MA) was developed to generate and project the phase hologram pattern on the SLM through a PCIe interface (Meadowlark Optics). At the operating wavelength of 940 nm, the SLM outputs ~ 80 effective phase levels over a 2π phase range, with relatively uniform phase-level spacing (see Supplemental Fig. S1 A).

To create a 3D beamlet pattern on the sample (a total of N beamlets, each with coordinates[x_i, y_i, z_i], i=1,2…N), the phase hologram on the SLM, ϕ(u, v), can be expressed as:

$$\mathrm{\varphi }(\mathrm{u},\mathrm{v})=\text{phase}\{{\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{A}}_{\mathrm{i}}{\mathrm{e}}^{2\mathrm{\pi }\mathrm{j}\{{\mathrm{x}}_{\mathrm{i}}\mathrm{u}+{\mathrm{y}}_{\mathrm{i}}\mathrm{u}+[{\mathrm{Z}}_2^0(\mathrm{u},\mathrm{v}){\mathrm{C}}_2^0({\mathrm{z}}_{\mathrm{i}})+{\mathrm{Z}}_4^0(\mathrm{u},\mathrm{v}){\mathrm{C}}_4^0({\mathrm{z}}_{\mathrm{i}})+{\mathrm{Z}}_6^0(\mathrm{u},\mathrm{v}){\mathrm{C}}_6^0({\mathrm{z}}_{\mathrm{i}})]\}}\}$$ (1)

A_i is the electrical field weighting factor for the individual beamlet. ${\mathrm{Z}}_{\mathrm{m}}^0(\mathrm{u},\mathrm{v})$ and ${\mathrm{C}}_{\mathrm{m}}^0({\mathrm{z}}_{\mathrm{i}})$ are the Zernike polynomials and Zernike coefficients, respectively, which fulfills the defocusing functionality and compensates some of the higher order spherical aberrations due to defocusing. The expressions of ${\mathrm{Z}}_{\mathrm{m}}^0(\mathrm{u},\mathrm{v})$ and ${\mathrm{C}}_{\mathrm{m}}^0({\mathrm{z}}_{\mathrm{i}})$ are shown in Supplemental Table S1 (Anselmi et al., 2011). A 2D coordinate calibration between the SLM phase hologram and the PMT image is carried out on a pollen grain slide, and an affine transformation can be extracted to map the coordinates. For the axial defocusing, the defocusing length set in the SLM phase hologram is matched with the actual defocusing length by adjusting the apparent “effective N.A.” in the Zernike coefficients, after calibration following the procedure described in (Quirin et al., 2013). This is done mainly for convenience, and it changes very little over the full axial range of the SLM (range 0.43–0.48). In multiplane imaging, the field weighting factors A_i in Eq. 1 alter the power ratio of different imaging planes. We adjust the parameter empirically to achieve similar fluorescent signals from different imaging planes, but can also calculate the expected power ratio from first principles, considering the depths of each plane, nominal scattering length of light in the tissue, the SLM steering efficiency (see Supplemental Information), and perform numerical beam propagation of the electric field (Schmidt, 2010).

Visual Stimulation

Visual stimuli were generated using MATLAB and the Psychophysics Toolbox (Brainard, 1997) and displayed on a monitor (Dell P1914Sf, 19-inch, 60-Hz refresh rate) positioned 28 cm from the right eye, at ~45° to the long axis of the animal. Each visual stimuli session consisted of 8 different trials, each trial with a 3 s drifting square grating (100% contrast, 0.035 cycles per degree, two cycles per second), followed by 5 s of mean luminescence gray screen. Eight drifting directions (separated by 45 degrees) were presented in random order in the 8 trials in each session. 17 sessions were recorded continuously (1088 s).

Image Analysis and Source Separation Algorithm

The raw images are motion corrected using a pyramid approach (Thevenaz et al., 1998), and analyzed using a novel constrained non-negative matrix factorization algorithm detailed in the companion paper (Pnevmatikakis et al., 2016), coded in MATLAB. The core of the CNMF algorithm is that the spatiotemporal fluorescence signals Y from the whole recording can be expressed as a product of two matrices: a spatial matrix A that encodes the location of each spatial component and a temporal matrix C that characterizes the fluorescent signal of each spatial component, as well as the background B and noise (residue) E, expressed as Y=AC+B+E. This can be solved using a constrained minimization method. The method imposes sparsity penalties on the matrix A to promote localized spatial footprints, and enforces the dynamics of the calcium indicator in the temporal components of C, which results in increased SNR. The individual single plane recordings are first analyzed per Pnevmatikakis (Pnevmatikakis et al., 2016), and the resulting spatial matrix A for the spatial components and the background, as well as the temporal calcium transient characteristics of each spatial component, are used as initial estimates for the sources in the analysis of the multiplane recording. The matrix A, which characterizes the individual pixel weights for each spatial component, is no longer re-optimized. We then apply the identical procedure as in the single plane analysis to solve the convex optimization problem for the multiplane data. Once C, and B are estimated, the fluorescence signal, as well as the background baseline of each spatial component can be extracted from these matrices, and ΔF/F can be calculated.

To detect the events from the extracted fluorescent signal, the ΔF/F is first normalized and then temporally deconvolved with the parametrized fluorescent decay (from fitting the auto-regressive model). Independently, a temporal first derivative is also applied to the ΔF/F signal. The deconvolved signal and the derivative are then thresholded with 2% and at least 2 std. dev. from mean derivative signal respectively. At each time point, if both of them are larger than the threshold, an activity event is recorded, in binary format.

Evaluation of CNMF, NOL and ICA

To evaluate the signals extracted from CNMF, we compared them against signals extracted from pixels of each spatial component that do not have contribution from other sources. Temporal signals from these pixels are averaged with a uniform weighting, followed by subtraction of the background baseline obtained from CNMF. We term this non-overlapped (NOL) signal. This is similar to conventional fluorescence extraction methods, except that the background baselines subtraction is automated.

The signals extracted from CNMF are compared with the NOL signals in two aspects: similarity (or correlation) and signal-to-noise ratio (SNR). In the calculation of SNR, the “signal” is estimated by the maximum of the ΔF/F trace, and the “noise” is estimated as described below. A histogram of the difference between the ΔF/F values of adjacent time points is first calculated. Considering temporal regions where there are few transients, this histogram should have a maximum around 0, and the local distribution around 0 should characterizes the noise. The shape of this histogram can then be fitted with a Gaussian function, and the standard deviation coefficient of this Gaussian function is considered as the “noise” in the SNR calculation.

ICA was also used to analyze the data, with software written in Matlab (Mukamel et al., 2009). The motion-corrected image stack is first normalized, followed by principal component analysis (PCA) for dimensionality reduction and noise removal. ICA is then applied to extract the spatiotemporal information of each independent sources. Supplemental Fig. S3 provides a comparison between the performance of ICA and CNMF on a large population.

Analysis of the Cell Orientation Selectivity of the Drifting Grating Visual Stimulation

To analyze the orientation and direction selectivity of the spatial components in response to the drifting grating visual stimulation, the total number of neuronal events are counted during the visual stimulation period in each session, for all 8 different grating angles. These event numbers are then mapped into a vector space (Mazurek et al., 2014). The direction and magnitude of their vector sum represents the orientation selectivity and the orientation index. With N_{visualsession} visual stimulation sessions, N_{visualsession} vectors are obtained. Hotelling’s T²-test is used to calculate whether these vectors are significantly different from 0 (i.e. whether the spatial component has a strong orientation selectivity). Only spatial components with their vectors significant different from 0 (<0.25 probability that null 0 is true) are selected, and their orientation selectivity is calculated by averaging the N_{visualsession} vectors and extracting the angle (N_{visualsession}=17 for the experiments shown in Fig. 6).