Computation of breast ptosis from 3D surface scans of the female torso

Abstract

Stereophotography is now finding a niche in clinical breast surgery, and several methods for quantitatively measuring breast morphology from 3D surface images have been developed. Breast ptosis (sagging of the breast), which refers to the extent by which the nipple is lower than the inframammary fold (the contour along which the inferior part of the breast attaches to the chest wall), is an important morphological parameter that is frequently used for assessing the outcome of breast surgery. This study presents a novel algorithm that utilizes three-dimensional (3D) features such as surface curvature and orientation for the assessment of breast ptosis from 3D scans of the female torso. The performance of the computational approach proposed was compared against the consensus of manual ptosis ratings by nine plastic surgeons, and that of current 2D photogrammetric methods. Compared to the 2D methods, the average accuracy for 3D features was ~13% higher, with an increase in precision, recall, and F-score of 37%, 29%, and 33%, respectively. The computational approach proposed provides an improved and unbiased objective method for rating ptosis when compared to qualitative visualization by observers, and distance based 2D photogrammetry approaches.

1. Introduction

Breast ptosis is a measurement used clinically for characterizing breast morphology that estimates the amount of drooping of the breast [1–3]. Ptosis refers to the extent by which the nipple is lower than the inframammary fold (IMF), i.e., the fold or crease that forms where the inferior part of the breast attaches to the chest wall [4–6]. Current approaches for assessing breast ptosis include (1) subjective visual assessment by human observers, (2) direct physical measurements (anthropometry) of the breasts and torso, (3) manual or automated computer-aided measurements on clinical photographs (photogrammetry), and (4) computer-aided measurements on three-dimensional (3D) images (stereophotogrammetry).

Subjective assessment of breast aesthetics is highly influenced by the observer’s experience and may be biased by his/her visual perception of breast aesthetics. This assessment is typically based on vaguely defined rating scales that are inherently subjective and qualitative. Several studies have reported low intraobserver and interobserver agreement and reliability for subjective assessment, primarily due to the lack of consistency in the manual perception and interpretation of aesthetic outcomes [7–9].

Anthropometry is any measurement performed directly on the patient’s body using a measuring tape. Measurement of fundamental parameters, such as distances along the contoured surface of the breast, may be imprecise because of the inherent mobility of the subcutaneous glandular tissues. Despite being a useful approach for quantifying breast aesthetics in clinical practice, anthropometry has several practical limitations. For example, anthropometry not only requires direct physical contact with the patient but also is impractical when evaluating a large group of patients in clinical studies. Moreover, retrospective measurements are not feasible.

Photogrammetry is an alternative method that allows indirect anthropometry on two-dimensional (2D) clinical photographs. In photogrammetry, observers mark measurements on digital images displayed on a computer monitor or on conventional printed photographic images. Compared to anthropometry, photogrammetry is relatively more feasible and easy to implement since standard clinical practice involves the collection of 2D photographs to document outcomes. Among the drawbacks of photogrammetry is that this method cannot capture the 3D nature of the human torso. To get a complete view of the torso, multiple photographs must be taken with the patient positioned at different viewing angles. Furthermore, a few anatomic landmarks that are critical for obtaining reproducible assessment of aesthetic outcomes by photogrammetry may not be visible in 2D photographs. Some studies have reported substantial intraobserver and interobserver variation for assessment from photographs, attributed to the lack of consistent guidelines for standard photography [10,11].

Stereophotogrammetry, which involves measurements performed on 3D scans, is finding a niche in surgical planning, patient education, and evaluation of surgical outcomes. 3D stereophotogrammetry of the torso is being evaluated as an alternative method to assess breast aesthetics. 3D digital photography systems have the capacity to generate precise images at high speeds without requiring direct physical contact with a patient. A single 3D image yields more information on breast appearance than multiple conventional 2D photographs. In contrast to 2D photography, 3D scans enable objective determination of properties, such as surface area, volume, and surface curvature, and can be interactively viewed from several different angles [12–14]. Thus 3D imaging has tremendous potential for analysis of breast appearance and many advantages over 2D photography.

Assessment of ptosis involves identification of fiducial points (such as the nipple and the IMF) on patients. However, the IMF is often difficult to identify by photogrammetry or stereophotography because it is not only difficult to distinguish [15] but also occluded in patients with large breasts. We hypothesized that a method that minimizes the use of fiducial points would provide a more accurate quantitative assessment of breast ptosis than current methods and that 3D stereophotogrammetry offers such accuracy. We developed a 3D stereophotogrammetric approach for measuring ptosis that excludes identification of the IMF, thereby mitigating the variability associated with its accurate identification. The approach we developed is presented here.

We utilized two different 3D measures, surface curvature and surface orientation, to generate histogram templates of breast shape and employed a histogram matching model for classification. The performance of this 3D classification was evaluated by a leave-one-out cross-validation approach and via comparison with results from existing anthropometric and 2D photogrammetric methods in a set of images from 150 women.

1.1. Subjective assessment of breast ptosis

Plastic surgeons use a visual classification system to categorize the degree of breast ptosis by estimating the extent to which the nipple is lower than the IMF. In women with large breasts, however, the IMF typically is partially occluded from view, and ptosis is assessed by a combination of landmarks, such as the IMF, the lowest visible contour, and the lowest visible point (LVP) on the breast. The lowest visible contour is the inferiormost contour of the breast that is visible with the woman in a frontal standing position or lateral position (as seen in Fig. 1), and is typically much lower than the IMF in breast ptosis. The LVP is the inferiormost point along the lowest visible contour of the breast. In women with no breast ptosis, the lowest visible contour is the same as the IMF.

Fig. 1.

Visual classification of breast ptosis in lateral (top) and frontal (bottom) views. The red cross indicates the nipple, pink indicates the level at which the IMF is visualized, and the cyan indicates the lowest visible point. Grade 0 (no ptosis) is defined as a breast that has the nipple and parenchyma (glandular tissue and fat which compose the breast) sitting above the IMF. In grade 1 (minor ptosis), the nipple lies at the level of the IMF and above the lowest contour of the breast. In grade 2 (moderate ptosis), the nipple lies below the level of the IMF but remains above the lowest contour of the breast, and in grade 3 (major ptosis), the nipple lies well below the IMF and close to or at the lower contour of the breast. Note that the IMF is occluded in the frontal view for moderate and major ptosis. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Several visual classification systems have been proposed for rating ptosis, such as those described by Regnault (1976) [16], Lewis (1983) [17], Brink (1990) [18] and (1993) [19], LaTrenta and Hoffman (1994) [20], and Kirwan (2002) [21]. Typically, clinical assessment of ptosis is based on a modified version of the Regnault grading system and includes the ratings shown in Fig. 1. Grade 0 (no ptosis) is defined as a breast that has the nipple and parenchyma (glandular tissue and fat which compose the breast) sitting above the IMF. In grade 1 (minor ptosis), the nipple lies at the level of the IMF and above the lowest contour of the breast. In grade 2 (moderate ptosis), the nipple lies below the level of the IMF but remains above the lowest contour of the breast, and in grade 3 (major ptosis), the nipple lies well below the IMF and close to or at the lower contour of the breast.

Classification of breast ptosis can be used to help determine the type of surgery needed, such as breast augmentation or reduction or mastopexy. Ptosis assessments are also used by physicians when discussing with the patient the pros and cons of different surgical procedures [22].

1.2. Anthropometric assessment of breast ptosis

Several methods have been proposed for objective assessment of ptosis by measuring the distance of the nipple from the IMF, either directly on the subject or on clinical photographs. For example, LaTrenta and Hoffman [20] in 1994 developed a quantitative measurement for ptosis classification based on the vertical distance from the nipple to the IMF. They quantified the classification using distance in centimeter metrics as follows: (1) grade 1 or minor ptosis: nipple position lies within 1 cm of the level of the IMF; (2) grade 2 or moderate ptosis: nipple position lies 1–3 cm below the IMF; and (3) grade 3 or major ptosis: nipple position lies more than 3 cm below the level of the IMF and below the lower contour of the breast and skin envelope. Similarly, Kirwan [21] proposed a quantitative measurement comprising six stages of breast ptosis covering a 5-cm distance in 1-cm increments, as follows: (A) nipple position 2 cm above the IMF; (B) nipple position 1 cm above the IMF; (C) nipple position even with IMF; (D) nipple position 1 cm below the IMF; (E) nipple position 2 cm below the IMF; and (F) nipple position more than 2 cm below the IMF. In this study, we compared the performance of the 3D stereophotogrammetric assessment of ptosis with that of the LaTrenta and Hoffman scheme.

1.3. 2D Photogrammetric assessment of breast ptosis

Kim et al. [23] proposed an objective, quantitative measurement of breast ptosis based on the ratio of distances between fiducial points, such as nipple, sternal notch, lateral terminus, and LVP, manually identified in digitized/digital images of oblique and lateral preoperative photographs. They employed a simple linear regression approach to transform two distance ratios (measure 1: distance from sternal notch to the point of lateral terminus of inframammary fold divided by the distance from the sternal notch to the nipple, and measure 2: distance between the nipple to the lowest visible point divided the distance from the point of the lateral terminus of inframammary fold to the lowest visible point) to subjective scales, based on a clinical group of 10 patients. The distribution of the measurements in neither group illustrated strong linear relationships with the 4-point ptosis scale (R² values of 0.4808 and 0.5793 for measure 1 and 2, respectively).

Lee et al. [24] developed an algorithm for measuring breast ptosis automatically from lateral photographs. They measured distances between three fiducial points: the nipple, the LVP, and the lateral terminus of the IMF. The efficacy of determining ptosis depended on the accuracy of automated localizations of the fiducial points. In this study, we compared the performance of the 3D stereophotogrammetric assessment of ptosis against that of the distance-based assessment of ptosis proposed by [23].

2. Methods

2.1. Imaging system

The 3D images used in this study were captured by using two stereophotogrammetric systems, the DSP800 and 3dMDTorso systems manufactured by 3dMD (Atlanta, GA). The later 3dMDTorso version has greater accuracy, enabling capture of 3D data clouds of 75,000 points, whereas the older DSP800 system allows capture of data clouds consisting of 15,000 points. Each reconstructed surface image consists of a 3D point cloud, i.e., x, y, and z coordinates, and the corresponding 2D color map. Only the frontal portion of the torso is imaged, resulting in a surface mesh that excludes the back region.

2.2. Study sample

Women undergoing breast reconstruction surgery at The University of Texas MD Anderson Cancer Center and commissioned volunteers were recruited under protocols approved by the Institutional Review Board. A data set consisting of surface images from 150 participants, 145 patients and 5 volunteers, was analyzed. All participants enrolled in the study received $20 per study visit. An inclusion criterion for image selection was the presence of one or both breast mounds with nipples. The 88% of the study sample for which race was documented comprised 78% white, 8.6% African American, 0.7% Asian, and 0.7% American Indian/Alaskan; race was not documented for 12%. In the 49% for which ethnicity was documented, 41% were Not Hispanic/Latino and 8% were Hispanic/Latino; ethnicity was not available for 51%. Based on body mass index (BMI), 0.7% were underweight (BMI ≤ 18), 31.3% were normal weight (BMI=18.5–24.9), 31.3% were overweight (BMI=25–29.9), and 33.3% were obese (BMI ≥ 30); for the remaining 3.4%, BMI was not available. The age range was 24–73 years and the average age was 50 years. From the total 150 torso images, a data set of 203 cropped images consisting of either the right or left breast were used for the computation of ptosis. The 203 breasts comprised 78 breasts with ptosis grade 0, 73 breasts with ptosis grade 1, 43 breasts with ptosis grade 2, and 9 breasts with ptosis grade 3.

2.3. Algorithm for ptosis prediction

Until now, no algorithm for direct assessment of ptosis using 3D measures has been reported. A flowchart of the algorithm we used for assessing ptosis in 3D images is illustrated in Fig. 2. The first step is defining and selecting the region of interest (ROI) enclosing the breast mound; then each ROI is sectioned into four quadrants. The 3D measures surface curvature and surface orientation are computed for the ROI, and template histograms are generated to determine ptosis grade. For assessing ptosis in a test sample, a histogram matching algorithm was used; its performance was evaluated by the leave-one-out cross-validation approach and validated by direct comparison with the manually assessed ground truth (consensus of nine surgeon ratings) and with existing anthropometric and 2D photogrammetric approaches.

Fig. 2.

Flowchart for ptosis assessment from 3D surface images.

2.4. ROI selection and quadrant sub-division

The torso data are manually cropped to select each right or left breast as the ROI. As shown in Fig. 3, the ROI is defined to enclose the breast mound, extending in height from the mid-clavicle down to the just below the LVP, and extending in width from the medial point to the lateral point. Furthermore, each breast is divided into four quadrants with the nipple at the origin. The four quadrants are named a, b, c, and d clockwise as follows: the upper left quadrant (from the viewer’s perspective) a, the upper right quadrant b, the lower right quadrant c, and the lower left quadrant d (see Fig. 3D).

Fig. 3.

Selection of the region of interest (ROI). (A) Image with both breasts. (B) Cropped ROI for the right breast. (C) Cropped ROI for the left breast. (D) ROI for the left breast with four quadrants labeled a, b, c, and d.

2.5. Surface curvature analysis

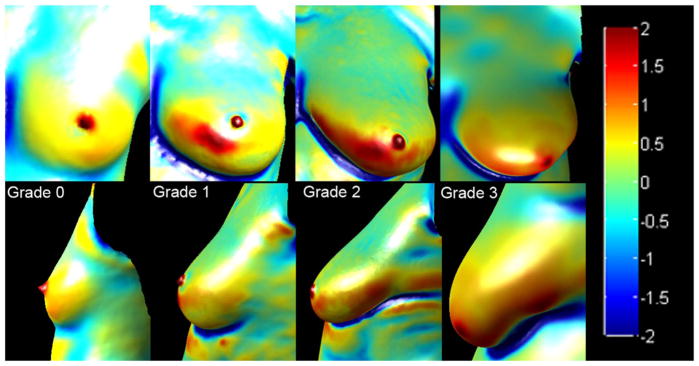
Curvature analysis can be used to highlight the shape of the underlying 3D surface. Surface curvature is determined for each ROI by computing the Gaussian curvature using a toolbox developed by Gabriel Peyre [25] based on the algorithms proposed by Cohen-Steiner et al. [26]. For this study, we employed a pseudo-color visualization method for viewing the Gaussian curvature of the 3D mesh. Fig. 4 shows the color-mapped Gaussian curvature for a left breast of each grade. The curvature values are mapped so that nearly planar or cylindrical regions with values close to 0 are green, while positive values ranging from yellow to red represent convexity, and negative values ranging from cyan to dark blue represent concavity.

Fig. 4.

Representative Gaussian curvature maps of breasts from all four ptosis grades. The top panel shows the front view of the breast, while the bottom panel shows the lateral view. The curvature values are mapped so that nearly planar or cylindrical regions with values close to 0 are green, while positive values ranging from yellow to red represent convexity, and negative values ranging from cyan to dark blue represent concavity. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

As seen in Fig. 4, a breast without ptosis is relatively symmetrical across the superior and inferior parts, whereas increasing ptosis results in a non-symmetric breast shape with asymmetry in curvature across the superior and inferior poles of the breast. To evaluate the feasibility of using Gaussian curvature as a feature for ptosis classification, we generated histograms to visualize the distribution of curvature values in each of the four quadrants. Curvature values for each quadrant were distributed into 40 bins, and the total number of points in each bin was normalized with respect to the total number of points in the ROI. Histograms for the four quadrants were generated and concatenated in alphabetical order (a–d), such that quadrants a, b, c, and d were represented by bins 1–40, 41–80, 81–120, and 121–160, respectively.

2.6. Surface orientation analysis

The 3D torso surface image is composed from an underlying triangular mesh, as shown in Fig. 5. The surface normal vector is computed for each triangle within the surface mesh as the cross product of two edges from each triangle. If a⃗ and b⃗ are two vectors denoting two sides of one triangle, the surface normal of this triangle is a⃗ × b⃗, where n⃗ is the vector of surface normal, including three components, n_x, n_y, and n_z, in the X, Y, and Z directions, respectively. The surface normal vector is normalized to unit length, i.e. |n⃗|=1. The X component of the surface normal, n_x, represents the expanse of the breast along X direction, whereas the Z component of the surface normal, n_z, represents the degree of projection of the breast from the chest wall. Because n_x and n_z do not include information pertinent to breast ptosis, n_y was estimated to be the most informative component among the three for the analysis of ptosis, and thus n_x and n_z were eliminated from further analysis. n_y represents the orientation of the breast along the Y-axis and hence indicates the amount of drooping of the breast. Points on the superior part of the breast largely exhibit positive values for n_y (corresponding to an upward orientation), while points on the inferior part are typically negative (downward orientation). To portray the orientation of the breast, concatenating the histograms from each quadrant in alphabetical order generated a histogram of the distribution of n_y. Each quadrant covers 10 bins, such that quadrants a, b, c, and d cover bins 1–10, 11–20, 21–30, and 31–40, respectively. The Y component of the surface normal has a range of [−1, 1], so each bin represents a range of 0.2. Within each quadrant, lower bins represent negative surface normal values, while higher bins represent positive surface normal values.

Fig. 5.

Calculation of surface normal from the triangular surface mesh. (A) A portion of the surface mesh of a breast. (B) A single triangle from the surface mesh showing the surface normal vector n and vectors a and b, representing the two sides of the triangle. (C) The computed surface normals (shown as blue arrows) are superimposed on the curvature mapped image. The direction of the arrows denotes the orientation of the surface. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.7. Histogram template generation

For each of the two 3D features, curvature and orientation, histogram templates were generated for each of the four ptosis grades. For surface curvature, the histogram templates were generated by taking the average of the curvature histograms for all breasts within that grade. Fig. 6 shows the Gaussian curvature and orientation histogram templates for grades 0, 1, 2, and 3.

Fig. 6.

Representative histogram templates for the four ptosis grades generated from concatenated histograms of quadrants a, b, c and d for (A) surface curvature and (B) orientation. (For improved visualization of the color line graphs of the different ptosis grades in this figure, the reader is referred to the web version of this article.)

The changes across the four ptosis grades for the curvature histogram templates are subtle. The superior pole (quadrants a and b) of the breast exhibits a larger area whose curvature values indicate a flatter shape, whereas the inferior pole (quadrants c and d) depicts relatively fewer flat areas but a larger number of points of convexity, reflecting ptosis. In addition to the difference in the number of points acquired in each quadrant, the histogram templates depict a transitional change in quadrants c and d across all four grades.

For the orientation analysis, similarly, a histogram template for each ptosis grade was generated by taking the average of all the orientation histograms for all breasts within each grade. As seen in Fig. 6, besides the difference in the number of points acquired in each quadrant, the histogram templates depict a transitional change in quadrants c and d across the four grades. For grade 0, quadrants c and d had peaks in bin 25 and bin 35, respectively, which represent the range [−0.2, 0]. Points around the nipple areas, which are pointing straight ahead in the outward direction, rather than downward, populate these bins. As ptosis increases, points acquired in the range [−0.2, 0] decrease because the nipple moves downward and the number of down-pointing points in the nipple-areola area increases, while the number of points exhibiting a lower (negative) orientation becomes larger. For ptosis grade 3, most of the points in quadrants c and d point downward.

2.8. Histogram matching-based predictive model

Ptosis grade was classified via histogram matching. The similarity of the histogram template and the histogram for a breast image that was to be assessed for ptosis (test case) was computed by measuring the Bhattacharyya distance [27]. If H and R represent two normalized histograms such that Σ_i H_i=1 and Σ_i R_i=1 for each H_i and R_i histogram value for bin i in the two histograms, the Bhattacharyya distance can be computed by using the formula:

$$d(H,R)=\sqrt{1-\frac{1}{\sqrt{\overline{H}\overline{R}{N}^2}}}{\sum }_i{H}_i.R_i,$$

where $\overline{H}=\frac{1}{N}{\sum }_i{H}_i$ and N is the total number of bins in the histogram. The computed Bhattacharyya distance lies with the range [0,1], where values close to 0 indicate a better match (i.e., similar histograms) and values close to 1 indicate a poor match (i.e., dissimilar histograms). The rule of prediction is that by computing the Bhattacharyya distance between the test case histogram and the four template histograms for each ptosis grade, the grade with the smallest distance is the predicted ptosis grade.

2.9. Cross-validation approach for evaluation

Cross-validation is a technique typically used to estimate the performance of a predictive model. For each round of cross-validation, the data set is partitioned into two complementary subsets, a training set and a test set. The training set is used to perform the analysis, while the test set is used to validate the analysis. Usually multiple rounds of cross-validation are performed on different partitions of the data set and the validation result is averaged over rounds. In leave-one-out cross-validation, as its name suggests, the data set is partitioned into two subsets: one sample in the test set and the remaining samples in the training set. This analysis is repeated so that all samples are used once as a test sample. We performed leave-one-out cross-validation on the data set of 203 breasts. The data set of 203 breasts included 78 breasts of grade 0, 73 breast of grade 1, 43 breasts of grade 2, and 9 breasts of grade 3. The sample population used in our study reflects the demographics of the patient population at the Department of Plastic Surgery at The University of Texas MD Anderson Cancer Center, Houston, TX, and the proportion of the four ptosis grade samples in the data are reflective of this patient population. An increase in ptosis may result from pregnancy and breast feeding, not wearing a bra, smoking, and loss of elastic tissue due to aging. Therefore ptosis grades of 3 are limited to individuals of advanced age, large breast size, and heavy smokers and found in a relatively small proportion of the population. Accordingly, in our study population we see a smaller occurrence of individuals with a breast ptosis grade of 3. In order to avoid sampling bias in training and prediction, we performed proportionate sampling across the four ptosis grades. In order to match the lower sample size for grade 3, the sample population was randomly sub-sampled to size 36 (9 breasts in each ptosis grade category), with one test case and 35 samples in the training set. This cross-validation analysis was repeated 10 times. In each run, template histograms were generated for each grade by taking an average of all the individual histograms for each breast image in the training data set. The consensus rating by the nine plastic surgeons for each of the 203 breasts was selected as the ground truth. The most experienced surgeon’s rating was used as the tiebreaker in the absence of a consensus.

2.10. Performance assessment

In general, the result of classification can be characterized into four categories: true positive (TP), false positive (FP), true negative (TN), and false negative (FN) when compared with the ground truth. Sensitivity was determined as the proportion of actual positives that were correctly identified (TP/(TP+FN)), and specificity was determined as the proportion of negatives that were correctly identified (TN/(TN+FP)). In addition, precision (positive prediction value [PPV]) was computed as the proportion of true positives against all positive results (TP/(TP+FP)), and accuracy was determined as the proportion of all results that were true ((TP+TN)/(TP+TN+FP+FN)).

3. Results

3.1. Subjective (manual) rating of ptosis

Individual ratings of breast ptosis by nine plastic surgeons with experience in breast reconstruction surgery were subjected to intraclass correlation coefficient (ICC) analysis to evaluate interobserver variability. A two-way random effect model was used to evaluate the ICC values for each surgeon against all the others, as shown in Table 1. Overall, the comparison of ptosis ratings across the surgeons indicates 69% good agreement (0.4≤ICC<0.75), and 31% excellent agreement (ICC≥0.75). The average ICC value from 36 comparisons (i.e. pairwise comparisons across all 9 surgeons) was 0.69±0.07, indicating good agreement for the subjective rating process.

Table 1.

ICC values estimating interobserver variability across nine surgeons.

Surgeon	2	3	4	5	6	7	8	9
1	0.77	0.79	0.69	0.63	0.68	0.76	0.79	0.75
2		0.77	0.54	0.57	0.67	0.72	0.75	0.70
3			0.71	0.62	0.71	0.75	0.80	0.75
4				0.55	0.59	0.61	0.73	0.60
5					0.56	0.59	0.64	0.68
6						0.71	0.68	0.68
7							0.74	0.69
8								0.75

We also evaluated each surgeon’s rating performance against the ground truth (consensus across the nine surgeons). Table 2 shows the results of our statistical analysis of individual surgeon performance, which indicates that subjective rating of ptosis provides good performance, with an average value for accuracy at 82±8% and for precision at 67±16%.

Table 2.

Evaluation of the performance of subjective rating of ptosis by surgeons.

Surgeon	Sensitivity	Specificity	Accuracy	Precision
1	0.81	0.93	0.89	0.71
2	0.52	0.81	0.70	0.43
3	0.77	0.96	0.95	0.92
4	0.49	0.85	0.81	0.72
5	0.49	0.85	0.80	0.53
6	0.71	0.87	0.81	0.60
7	0.56	0.82	0.72	0.49
8	0.59	0.90	0.87	0.79
9	0.69	0.90	0.86	0.80

3.2. 2D photogrammetric rating of ptosis

To assess the performance of the 3D measures against previously described 2D approaches for rating ptosis, we performed the LaTrenta and Hoffman quantitative classification [20] and the Kim distance ratio measurements [23] on the same data set (203 breasts). For the LaTrenta and Hoffman classification, vertical distances were evaluated on 3D images using our customized software [15]. An observer manually recorded the nipple and IMF location and computed the vertical distance between nipple and IMF. Grade was determined by LaTrenta and Hoffman’s quantitative classification scheme described in Methods. Next, the two measurements described by Kim et al. [23] were evaluated for the same 203 breasts. We computed two distance ratios: measure 1: (s−i)/(s−n); measure 2: (n−v)/(i−v), where s−i represents the vertical distance between the sternal notch and the lateral terminus, s−n the vertical distance between sternal notch and nipple, n−v the vertical distance between nipple and the LVP, and I−v the vertical distance between lateral terminus and LVP. The ratios are expected to have values in the range of [0,1], with 1 representing no ptosis. Linear regressions between the two distance ratios and the ground truth were determined for quantifying ptosis, as described by Kim et al. [23]. On the basis of the linear regressions of the two measurements, we evaluated the test set by mapping the distance ratios into a scale of [0,3] for the four ptosis grades. The nearest integer was determined as the predicted grade. Table 3 shows the performance of the 2D measurements, including the Kim distance ratio measurements and the LaTrenta and Hoffman classification, for each ptosis grade and overall. As seen in Table 3, the 2D approaches provided accuracies in the range of 43–97% for the different categories of ptosis, with overall lower accuracy for grades 0 and 1 (<65%) and higher accuracy for grades 2 (67–81%) and 3 (>90%).

Table 3.

Evaluation of 2D photogrammetric methods for ptosis^a.

	Sensitivity	Specificity	Accuracy	Precision (PPV)	Recall	F-score
Grade 0
Kim1	0.00	1.00	0.62	UND	0.00	0.00
Kim2	0.00	1.00	0.62	UND	0.00	0.00
LH	0.69	0.62	0.65	0.53	0.69	0.60
Grade 1
Kim1	0.97	0.12	0.43	0.38	0.97	0.55
Kim2	0.95	0.15	0.44	0.39	0.95	0.55
LH	0.05	0.85	0.57	0.17	0.05	0.08
Grade 2
Kim1	0.23	0.96	0.81	0.81	0.23	0.34
Kim2	0.30	0.95	0.81	0.62	0.30	0.41
LH	0.47	0.73	0.67	0.32	0.47	0.38
Grade 3
Kim1	0.22	1.00	0.97	1.00	0.22	0.36
Kim2	0.22	0.99	0.96	0.67	0.22	0.33
LH	0.44	0.94	0.92	0.25	0.44	0.32
Overall
Kim1	0.36	0.77	0.70	UND	0.36	0.31
Kim2	0.37	0.77	0.71	UND	0.37	0.32
LH	0.41	0.79	0.70	0.32	0.41	0.35

UND: Undefined.

^aKim1 and Kim2 represent the Kim’s distance ratio measures 1 and 2, respectively [23]. LH represents the LaTrenta and Hoffman classification [20].

For grade 0, precision for measures 1 and 2 from Kim et. al., could not be computed because, the algorithm failed to accurately classify the breasts with false positive and true positive values at 0, and a false negative value of 78. Overall performance was inconsistent across the different grades, with poor performance for grade 1 (43–57% accuracy) and excellent performance for grade 3 (92–97% accuracy).

3.3. 3D rating of ptosis using gaussian curvature and orientation features

We evaluated the performance of the 3D measurements, including Gaussian curvature and orientation individually as well as in combination, in determining ptosis grade. To evaluate these 3D features in combination, the individual histogram templates for curvature and orientation for each ptosis grade were concatenated to create a combined histogram template. Table 4 shows the performance of each using the leave-one-out cross-validation with proportional sampling approach for validation described earlier. Table 4 presents results for each ptosis grade and for the overall average for the 3D features, including surface, orientation, and the combination of surface and orientation.

Table 4.

LOOCV evaluation of 3D features for rating ptosis.

	Sensitivity	Specificity	Accuracy	Precision	Recall	F-score
Grade 0
G	0.38±0.20	0.94±0.04	0.80±0.03	0.69±0.09	0.38±0.20	0.46±0.17
O	0.73±0.08	0.90±0.04	0.86±0.03	0.71±0.08	0.73±0.08	0.72±0.06
G+O	0.60±0.17	0.93±0.04	0.85±0.03	0.75±0.10	0.60±0.17	0.65±0.10
Grade 1
G	0.70±0.15	0.80±0.10	0.77±0.06	0.56±0.10	0.70±0.15	0.60±0.07
O	0.56±0.17	0.86±0.06	0.78±0.07	0.57±0.17	0.56±0.17	0.56±0.16
G+O	0.66±0.18	0.86±0.11	0.81±0.06	0.65±0.14	0.66±0.18	0.62±0.10
Grade 2
G	0.60±0.26	0.89±0.07	0.82±0.05	0.69±0.15	0.60±0.26	0.60±0.16
O	0.68±0.14	0.87±0.07	0.82±0.05	0.64±0.09	0.68±0.14	0.65±0.09
G+O	0.69±0.10	0.89±0.06	0.84±0.04	0.69±0.13	0.69±0.10	0.68±0.07
Grade 3
G	0.93±0.06	0.90±0.06	0.91±0.04	0.78±0.12	0.93±0.06	0.84±0.06
O	0.66±0.10	0.91±0.05	0.85±0.03	0.74±0.12	0.66±0.10	0.68±0.06
G+O	0.80±0.07	0.91±0.06	0.88±0.06	0.76±0.13	0.80±0.07	0.77±0.09
Overall
G	0.65±0.27	0.88±0.09	0.83±0.07	0.68±0.14	0.65±0.27	0.63±0.18
O	0.66±0.14	0.89±0.06	0.83±0.06	0.67±0.13	0.66±0.14	0.65±0.11
G+O	0.69±0.15	0.9±0.07	0.84±0.05	0.71±0.13	0.69±0.15	0.68±0.11

G, Gaussian; O, orientation.

Overall, the 3D measures showed higher sensitivity, specificity, accuracy, and precision than the 2D measures. 3D features provided accuracies in the range of 77–91% for the different categories of ptosis and an average accuracy of 83±7%, with relatively consistent performance across the three features tested (Table 4). Overall the performance was relatively robust across the different grades, with the lowest accuracy for grade 1 (77–81%) and highest accuracy for grade 3 (85–91%).

3.4. Comparison of 2D and 3D features for ptosis classification

In exploring the utility of 3D surface measures, such as curvature and orientation, for rating the ptosis grade from 3D surface images, we also tested the performance of subjective ratings made by nine experienced plastic surgeons and previously published 2D quantitative measures of ptosis computed from relative distances between fiducial points. In assessing performance, it is essential to consider not just accuracy but measures such as precision, recall, and F-score computations for overall performance; these measures for the 2D and 3D approaches are presented in Fig. 7. Precision (PPV) is representative of a classifier’s exactness: a low precision, for example, indicates a large number of false positives. Recall, also known as the sensitivity or the true positive rate, is a measure of a classifier’s completeness: a low recall, for example, indicates many false negatives. The F-score conveys the balance between the precision and the recall.

Fig. 7.

Comparison of 2D and 3D features for rating breast ptosis. Kim1 and Kim 2, measures of Kim et al.; LH, LaTrenta and Hoffman classification; G, Gaussian; O, orientation.

Overall, the 3D measures had higher accuracy than the 2D measures, and the combined use of Gaussian curvature and orientation provided the highest accuracy (84±5%). This is better than the average accuracy for the nine surgeons, which was 82±8%. Compared to the 2D measures, the precision, recall, and F-score of the 3D features classification models were higher by 37% (LH only, since precision for Kim1 and Kim2 could not be computed), 29%, and 33%, respectively. Most importantly, when compared to the 2D features, 3D features showed robust performance across the four different grades of ptosis, as shown in Fig. 8.

Fig. 8.

Comparison of classification accuracy of 3D and 2D features for ptosis grades. Kim1 and Kim 2, measures of Kim et al.; LH, LaTrenta and Hoffman classification; G, Gaussian; O, orientation.

Each of the three 3D features showed the best accuracy for grade 3 (85–91%), whereas the performances for the remaining three ptosis grades were in the range of 80–85% (grade 0), 77–81% (grade 1) and 82–84% (grade 2). Although, the 2D features had highest accuracy for ptosis grade 3 (92–97%), their accuracy was poor for other ptosis grades at 62–65% (grades 0), 43–57% (grade 1), and 67–81% (grade 2).

4. Discussion

The recent growth in the use of 3D imaging in aesthetic and reconstructive breast surgery has resulted in the development of quantitative objective measures for assessing breast morphometry for surgical planning and outcome assessment. Breast morphology is described in terms of physical characteristics such as shape, position and appearance, symmetry, and ptosis. Several methods have been described for the development of quantitative measures for breast shape, symmetry, projection, ptosis, and volume. Symmetry, projection, and ptosis measures are typically based on distances between fiducial points, or the ratios of such distances. While distance-based symmetry quantitation has been applied for both 2D photogrammetry and 3D stereophotogrammetry, so far methods for ptosis quantitation have been described only for 2D photogrammetry. Objective measurements of breast ptosis based on ratios of distances between fiducial points manually or automatically identified in lateral and oblique views of clinical photographs are amenable to stereophotogrammetry but have several limitations, and this was the rationale for this study exploring the utility of 3D features for assessing ptosis.

An inherent limitation of distance-based objective measures for ptosis is their dependence on fiducial point identification and detection, which in turn is a subjective process subject to interobserver and intraobserver variability. Moreover, a number of the fiducial points are difficult to locate and require a fairly sophisticated understanding of surgical terminology and human anatomy. These limitations affect both anthropometric and computational image–based manual identification of fiducial points. Moreover, distance-based ptosis measures utilize multiple fiducial points (nipple, LVP, IMF) and views (anterior-posterior and oblique or lateral), which further compounds the magnitude of dependence on fiducial point identification. Another limitation of the distance-based measures is the difficulty in interpreting the ptosis grade directly from distance ratios; typically a mathematical model such as linear regression is essential for relating the objective measurements to ptosis ratings.

Our objective in this study was to evaluate distance-independent 3D features for ptosis assessment, thereby mitigating these limitations of distance-based measures. We are the first to present a method for using surface curvature and orientation in conjunction with anthropometric characteristics of breast anatomy to automatically assess ptosis grade from manually cropped ROIs of the breast. Although the approach described here is not fully automated, it is amenable to complete automation in future studies. Our group has developed fully automated algorithms for fiducial point detection, including the nipple [15] and the lower breast contour [28], which will permit full automation of the algorithm. Furthermore, the only fiducial point utilized is the nipple, which has the lowest intraobserver and interobserver variability in identification and annotation of all the pertinent fiducial points [15] and, most importantly, its location is not directly utilized for assessing ptosis. Rather, the rationale behind the approach proposed is to utilize attributes of breast shape, related to curvature (convexity versus concavity) and orientation (vertical droop), and anthropometric features of breast anatomy to assess ptosis. In the proposed approach, the nipple is used to sub-divide the ROI into 4 subquadrants, and its surface curvature and orientation characteristics do not contribute to ptosis determination. In terms of size, published anthropometric measurements define the average size of the female nipple to be 20 mm [29]. Clinically nipples are at the pinnacle of the breast mounds can be classified as everted, flat, or inverted based on their shape. Everted nipples are most common and appear as raised tissue in the center of the areola, whereas inverted nipples appear to be indented in the areola and flat nipples appear to have no shape or contour. Most importantly, although the nipple position is used as a landmark in manually rating ptosis, the size or shape of the nipple does not influence ptosis rating, i.e. ptosis is indicative of breast sagging and the shape of the breast changes across the ptosis grades. Indeed, our goal in this study was to evaluate the utility of 3D features that reflect changes in breast shape for computing ptosis. In terms of the 3D features used in this study, nipples exhibit maximal Gaussian curvature and the orientation can vary with points on the tip of the nipple pointing outwards (i.e. perpendicular to the medial axis), whereas points along the edges sloping downward from the tip to areola exhibiting a wider range of orientation. Maximal curvature points from the nipple approximately fall within bins 40, 80, 120 and 160 in the curvature histograms, and orientation values are distributed across the histogram range. Most importantly, points from the nipple region represent low (i.e. non-dominant peaks) in the curvature and orientation histograms, since the size of the nipple is relatively small (~1%) compared to the region of interest analyzed (see Supplementary Table 1 and Supplementary Fig. 1). Thus, the proposed algorithm is independent of nipple shape and size. Supplementary Table 1 presents an analysis showing the results of classification with and without nipples, both for accurate and misclassified samples. The performance of the classification is unchanged with and without nipples included in the analysis. From an implementation perspective, it is pragmatic to leave the nipples in the images, since this eliminates the extra effort and any user bias associated with cropping the nipples out of the images. Furthermore, our data suggests that the majority of curvature and orientation differences across the various ptosis grades are dominant in the lower half of the breast mound (i.e., quadrants c and d as seen in Fig. 6). We found the classification results were equivalent for both, (1) analyzing the data using concatenated histograms for regions a, b, c, and d, and (2) analyzing the data using concatenated histograms for regions c, and d only (data not shown). From an implementation perspective, it is pragmatic to analyze the entire ROI as proposed.

In investigating the potential of the 3D features surface curvature and orientation for assessing breast ptosis, we compared their performance with that of consensus rating from nine experienced plastic surgeons. While the results of the subjective assessment of ptosis revealed high rates of good or excellent agreement overall, these results also confirm that some amount of subjectivity is inherent in the manual rating process. Moreover, the average accuracy of manual rating was found to be 82%±8% and precision across the nine surgeons ranged from 43% to 92% (average 67±16%), corroborating that manual ratings are subject to user bias and inter-user variability. When manually rating for ptosis, surgeons have to perceive the position of the nipple relative to the inframammary fold (IMF) and the lowest visible point (LVP) by looking at the patient in the front-facing and the lateral views when standing. Thus the surgeons line of view can influence his/her perception of the nipple position relative to the IMF or LVP and is most often responsible for the variance observed in ratings across different surgeons, and was noted in this study too. The nine surgeons participating in this study included senior surgeons and surgical trainees with experience in the range of 1–25 years. Thus it is highly likely that the large variance (16%) observed for these surgeons was not influenced by their experience, but rather approach (the line-of-view utilized during visualization)..

The performance of the proposed 3D features was robust and relatively consistent in assessing the four different ptosis grades. The overall accuracy was 83±7% for curvature and 83±6% for orientation. The combination of the two features had the best performance, with an accuracy of 84±5%, which was 2% higher than the accuracy of the surgeons’ rating (82±8%). Similarly, the overall accuracies for the 2D methods, Kim’s ratio measure 1, Kim’s ratio measure 2, and the LaTrenta and Hoffman scheme, were 70%, 71%, and 70%, respectively. The performance of Kim’s ratio measure 2, the best of the three, was 11% lower than that of the surgeons’ rating. Most importantly, the 2D features showed extreme variability in performance across the four different grades of ptosis.

Overall, compared to the 2D measures, the proposed 3D measures showed higher accuracy, precision, recall, and F-score values, indicating that use of 3D features is robust. While the best performing 3D approach, the combination of curvature and orientation, had the highest overall values for all of these measures, the 2D measures had varying values for precision, recall, and F-score, and no single approach showed the highest values for all measures as seen with the 3D classifiers. Across all the 3D and 2D features tested, the accuracy was highest for predicting grade 3 ptosis and lowest for predicting grade 1 ptosis. Grade 3 ptosis exhibits the greatest breast drooping and consequently the most pronounced changes in breast shape, which may contribute to the greater accuracies in its prediction. The greater ambiguity related to the prediction of grade 1 ptosis is probably related to the relatively subtle differences in drooping and breast shape between grade 0 and grade 1 and between grade 1 and grade 2. Collectively, our results demonstrate that the proposed 3D features can be used successfully for objective categorization of breast ptosis.

In summary, development of an objective and quantitative method for measuring ptosis from 3D images is an important yet challenging task. Prior work focused mainly on assessment by subjective ratings, anthropometry, or 2D photogrammetry. In this study, we proposed a new approach for measuring breast ptosis using 3D torso scans. We explored unique 3D morphological features from stereophotogrammetry that surpass the need for pre-defining fiducial points, such as the IMF. We investigated Gaussian curvature and surface orientation as predictive features and built a 3D ptosis classification model. The results demonstrate that our new 3D image approach yielded better performance than 2D photogrammetry.

Appendix A. Supporting information

Supplementary data associated with this article can be found in the online version at http://dx.doi.org/10.1016/j.compbiomed.2016.09.002.