Development of a source-exposure matrix for occupational exposure assessment of electromagnetic fields in the INTEROCC study

Abstract

Introduction

To estimate occupational exposures to electromagnetic fields (EMF) for the INTEROCC study, a database of source-based measurements extracted from published and unpublished literature resources had been previously constructed. The aim of the current work was to summarize these measurements into a source-exposure matrix (SEM), accounting for their quality and relevance.

Methods

A novel methodology for combining available measurements was developed, based on order statistics and log-normal distribution characteristics. Arithmetic and geometric means, and estimates of variability and maximum exposure were calculated by EMF source, frequency band and dosimetry type. Mean estimates were weighted by our confidence on the pooled measurements.

Results

The SEM contains confidence-weighted mean and maximum estimates for 312 EMF exposure sources (from 0 Hz to 300 GHz). Operator position geometric mean electric field levels for RF sources ranged between 0.8 V/m (plasma etcher) and 320 V/m (RF sealer), while magnetic fields ranged from 0.02 A/m (speed radar) to 0.6 A/m (microwave heating). For ELF sources, electric fields ranged between 0.2 V/m (electric forklift) and 11,700 V/m (HVTL-hotsticks), while magnetic fields ranged between 0.14 μT (visual display terminals) and 17 μT (TIG welding).

Conclusion

The methodology developed allowed the construction of the first EMF-SEM and may be used to summarize similar exposure data for other physical or chemical agents.

INTRODUCTION

Population-based case-control studies require the use of retrospective exposure assessment tools based on quality historical exposure data. However, the collection and analysis of these data is difficult, since measurements for some environmental and occupational agents, such as electromagnetic fields (EMF), are not systematically collected and, when available, are almost exclusively reported as aggregated and summarized results. Past efforts analysed and combined available exposure data in the literature for different agents^1–8. They involved estimation of specific parameters from scarce measurements, using a limited number of equations based on the assumption of data log-normality. Monte-Carlo simulations^1,2,7 were also used to recreate exposures when measurement data were sparse.

Measurements collected from the literature have been used in the construction of job-exposure matrices (JEMs), either alone or in combination with expert judgments. For EMF, JEMs have been created only for extremely low frequency (ELF) magnetic fields^9–12 and electric shocks^13,14. However, a worker’s job title is insufficient to explain between-subject variability since exposure levels are influenced by other characteristics, such as industry, worker’s tasks, specific equipment used or physical configuration of the workplace^15,16. Using the JEM’s mean exposure for all subjects in an occupation introduces Berkson error into the risk estimate (i.e. error relative to risks from each subject’s exposure), reducing the study’s power to detect true hazards¹⁷ and potentially biasing risk estimates¹⁸. Some authors¹⁶ suggested the use of source-based measurements and questionnaires to improve EMF exposure assessment, allowing for a more individualized exposure estimation.

The INTEROCC EMF measurement database

As part of the INTEROCC/INTERPHONE study of brain cancer, detailed information was collected for each job held by the study participants through a questionnaire on work organization (e.g. manual/automated), tasks (e.g. welding) and sources of exposure (e.g. type of equipment), divided in twelve occupational sections to take industrial activity into account. The aim was to combine the interview data and EMF exposure measurements from the literature for each source and/or task to estimate individual cumulative exposures to electric fields (E) and magnetic fields (B for lower frequencies and H for higher frequencies²¹) in four frequency bands: 0 Hz for static magnetic fields (SMF), 3–3,000 Hz for extremely low frequencies (ELF), 3 kHz – 10 MHz for intermediate frequencies (IF) and 10 MHz – 300 GHz for radio frequencies (RF).

Measurements for all the EMF sources identified through the study questionnaire (i.e. over 3 000 records) were compiled into an occupational exposure measurement database (OEMD). The measurements collected were abstracted from published and unpublished resources (i.e. 95 articles and technical reports), which were assessed based on their quality and relevance for our study. The OEMD was augmented with estimates of exposure range for 39 RF sources without available measurements in the literature, obtained from expert judgments. In total, exposures were compiled for 312 EMF sources commonly found in workplaces, covering the entire EMF frequency range. In this database, an EMF source refers to a specific piece of equipment and/or task which can lead to EMF exposure. Details of the construction and content of the OEMD were recently published¹⁹ and public access to this database is available at www.crealradiation.com/index.php/en/databases.

EMF data are usually reported using a variety of summary statistics, from arithmetic and geometric means (AM & GM), minimum (Min) and maximum (Max), only maximum, or values below or above the EMF meter’s limits of detection, i.e. outside its dynamic range (ODR). Several dosimetry types can be used when sampling EMF (i.e. personal, operator position or spot). Personal measurements are obtained with dosimeters by collecting exposures over an hour, a shift, or longer. Spot measurements are made at different distances from the source over shorter periods of time. Spot measurements performed at the usual worker’s position are called operator position measurements²⁰. The analysis and combination of these data entail several difficulties, as highlighted in similar efforts^3,4,7. Since measurements are collected for different purposes and following different sampling strategies, quality and relevance for epidemiological studies also needs to be considered.

The aim of this article is to describe the methodology developed to combine the OEMD data into a source-exposure matrix (SEM), that contain representative exposure estimates and their within-source variability for all EMF sources identified in the study.

METHODS

The methodology developed has two main stages: 1) calculation of semi-empiric estimates of missing summary statistics in OEMD studies; and 2) pooling of reported and/or estimated summary statistics. Pooled statistics were weighted by semi-quantitative ratings from expert confidence evaluations of whether a study’s measurement data are accurate and representative of long-term brain exposure.

Semi-empiric methods for estimating missing summary statistics

Each OEMD record for a given EMF source may contain values for combinations of Min, Max, AM, GM, N (sample size) and the minimum or maximum ODR limit for a specific frequency band and dosimetry type. To construct the SEM, we estimated AM, GM, SD and GSD for all EMF sources using these varied metrics. Our approach assumed that EMF exposure, like other environmental and occupational agents^21–23, is log-normally distributed. The summary statistics from log-normal data obey several mathematical relationships (see Appendix), including this equation for the standard normal quantile z of the maximum data point:

$$z_{\mathit{Max}}=\frac{ln\mathit{Max}-ln\mathit{GM}}{ln\mathit{GSD}}$$ (1)

and the analogous equation for z_Min. Our second assumption was that z_Max and z_Min are symmetric about zero:

$$z_{\mathit{Max}}=-z_{\mathit{Min}}$$ (2)

Equation 1 and other relationships²⁴ between the summary statistics AM, SD, GM, GSD, of a log-normal distribution, and parameters z_Max, Min and Max, were used to derive estimation formulas for missing statisticsfrom the available values in the OEMD (Table 1). For OEMD records with values for N (22% of the total), we further assumed that z_Min and z_Max were equal to their expected normal order statistics^25,26, which we call E_N[z_Min] and E_N[z_Max], since the expectation values of the extreme normal quantiles also have the symmetric quantile property²².

Table 1.

Formulas for estimating AM, GM, SD and GSD from the OEMD data. In addition to the log-normality and symmetric quantile (eq. 2) assumptions, the derivation of some formulas require one of more of these additional assumptions: A) Expected normal order statistic approximation: z_Max = E_N[z_Max]; B) semi-empiric value for z_Max; C) Semi-empiric value for GSD.

Method #	OEMD data	Estimated statistic	Formula	Assumptions
1	aN, Min, Max & AM	$\widehat{AM}=$	AM	—
		$\widehat{\mathit{GSD}}=$	${(\sqrt{\mathit{Max}/\mathit{Min}})}^{1/E_n\left[z_{\mathit{Max}}\right]}$	A or Ba
		$\widehat{GM}=$	$\text{AM}/\sqrt{{\widehat{\mathit{GSD}}}^{ln\widehat{\mathit{GSD}}}}$	—
		$\widehat{SD}=$	$\frac{AM}{\widehat{GM}}\sqrt{A{M}^2-{\widehat{GM}}^2}$	—
2	N, Min & Max	$\widehat{GM}=$	$\sqrt{\mathit{Min}\ast \mathit{Max}}$	—
		$\widehat{\mathit{GSD}}=$	${\left(\sqrt{\mathit{Max}/\mathit{Min}}\right)}^{1/\overline{z_{\mathit{Max}}}}$	B
		$\widehat{AM}=$	$\widehat{GM}\sqrt{{\widehat{\mathit{GSD}}}^{\widehat{\mathit{GSD}}}}$	—
		$\widehat{SD}=$	$\frac{\widehat{AM}}{\widehat{GM}}\sqrt{{\widehat{AM}}^2-{\widehat{GM}}^2}$	—
3	aN & bMax	$\widehat{GM}=$	$\mathit{Max}/{\overline{\mathit{GSD}}}^{E_N\left[z_{\mathit{Max}}\right]}$	A
		$\widehat{AM}=$	$\mathit{Max}\sqrt{Q^{-2E_N\left[z_{\mathit{Max}}\right]}}$, where Q =	A or Ba, C
		c $\widehat{\mathit{GSD}}=$	$\overline{\mathit{GSD}}$	C
		$\widehat{SD}=$	$\frac{\widehat{AM}}{\widehat{GM}}\sqrt{{\widehat{AM}}^2-{\widehat{GM}}^2}$	—
4	AM	$\widehat{AM}=$	AM	—
		$\widehat{GM}=$	$AM/\sqrt{Q}$	C
		$\widehat{\mathit{GSD}}=$	$\overline{\mathit{GSD}}$	C
		$\widehat{SD}=$	$\frac{AM}{\widehat{GM}}\sqrt{A{M}^2-{\widehat{GM}}^2}$	—
5	GM	$\widehat{GM}=$	GM	—
		$\widehat{AM}=$	$GM\sqrt{Q}$	C
		$\widehat{\mathit{GSD}}=$	$\overline{\mathit{GSD}}$	C
		$\widehat{SD}=$	$\frac{\widehat{AM}}{GM}\sqrt{{\widehat{AM}}^2-G{M}^2}$	—

^aWhere N is not available, E_N [z_Max] is replaced with $\overline{z_{\mathit{Max}}}$ which equals the median E_N[z_Max] from all available N values (except for method #2, see main text).

^bFormulas when Min is the only input data are omitted because this case does not occur in the OEMD.

^cThe semi-empiric parameter $\overline{\mathit{GSD}}$ is calculated from OEMD records with data for methods #1 & #2.

^dIn addition to the log-normality assumption and the symmetric quantile approximation (eq. 2).

Notation: Hats denote estimates; bars denote semi-empiric parameters; other symbols are input values.

With values for E_N[z_Max] obtained from a numerical algorithm²⁵, these log-normal relationships could be solved exactly to obtain all summary statistics for OEMD records with 3 or more parameter values (estimation methods 1 and 2 in Table 1). When less information was available, solutions for the desired summary statistics were made possible by replacing the unknown GSD with its central tendency, $\overline{\mathit{GSD}}$, calculated from an OEMD sub-set with enough data for exact calculations using these two methods. This semi-empiric parameter plus the above approximations resulted in the formulas for estimation methods 3 – 5 in Table 1. For OEMD records without N, we replaced E_N[z_Max] with a semi-empiric parameter, $\overline{z_{\mathit{Max}}}$, which equals the central tendency of E_N[z_Max] from all OEMD records with values for N. With this substitution plus the symmetric quantile relationship (eq.2), formulas similar to those in Table 1 were derived (see Appendix). OEMD records with N=1 were considered to equal their AM and GM, while SD and GSD are undetermined.

When ODR measurements were reported, providing their corresponding limits of detection, they were entered into OEMD as ODRMin or ODRMax, with the corresponding Max or Min. For these entries, we estimated the desired statistics with models for the extreme exposures outside the dynamic range:

$$\mathit{Min}=\mathit{ODRMin}\ast k_{\mathit{under}}$$ (3a)

$$\mathit{Max}=\mathit{ODRMax}\ast k_{\mathit{over}}$$ (3b)

The correction factors k_under and k_over were estimated semi-empiricly from a sub-set of ODR measurements that also reported the AM, so that:

$$k_{\mathit{under}}=\frac{A{M}^2}{\mathit{Max}\ast \mathit{ODRMin}\ast \sqrt{Q}}$$ (4a)

$$k_{\mathit{over}}=\frac{A{M}^2}{\mathit{Min}\ast \mathit{ODRMax}\ast \sqrt{Q}}$$ (4b)

where the parameter $Q={\overline{\mathit{GSD}}}^{ln\overline{\mathit{GSD}}}$ uses the central tendency $\overline{\mathit{GSD}}$, previously described. The central tendencies $\overline{k_{\mathit{over}}}$ and $\overline{k_{\mathit{under}}}$ were then used to obtain the desired statistics with the formulas in Table 2 (derived in the Appendix).

Table 2.

Formulas for calculating AM, GM, SD, and GSD from OEMD data, including values outside the dynamic range (ODR). In addition to the log-normality and symmetric quantile assumptions, the derivation of some formulas required one or more of these additional approximations: Assumptions A–C from Table 1, D) Semi-empiric value for k_over; and E) Semi-empiric value for k_under.

Method #	OEMD data	Estimated statistic	Formula	Assumptions
6	bN, Min, ODRMax & AM	a $\widehat{k_{\mathit{over}}}=$	$\frac{A{M}^2}{\mathit{Min}\ast \mathit{ODRMax}\ast \sqrt{Q}}$	C & D
		$\widehat{AM}=$	AM	—
		$\widehat{\mathit{GSD}}=$	${\left(\mathit{ODRMax}\ast \overline{k_{\mathit{over}}}/\mathit{Min}\right)}^{1/2E_N\left[z_{\mathit{Max}}\right]}$	A or Bb, & D
		$\widehat{GM}=$	$\sqrt{\mathit{Min}\ast \overline{k_{\mathit{over}}}\ast \mathit{ODRMax}}$	D
		$\widehat{SD}$	$\frac{AM}{\widehat{GM}}\sqrt{A{M}^2-{\widehat{GM}}^2}$	—
7	bN, ODRMin, Max & AM	a $\widehat{k_{\mathit{under}}}=$	$\frac{A{M}^2}{\mathit{ODRMax}\ast \mathit{Max}\ast \sqrt{Q}}$	C & E
		$\widehat{AM}=$	AM	—
		$\widehat{\mathit{GSD}}=$	${\left(\mathit{Max}/\mathit{ODRMin}\ast \overline{k_{\mathit{under}}}\right)}^{1/2E_N\left[z_{\mathit{Max}}\right]}$	A or Bb, & E
		$\widehat{GM}=$	$\sqrt{\mathit{ODRMin}\ast \overline{k_{\mathit{under}}}\ast \mathit{Max}}$	E
		$\widehat{SD}=$	$\frac{AM}{\widehat{GM}}\sqrt{A{M}^2-{\widehat{GM}}^2}$	—
8	bN, Min & ODRMax	$\widehat{GM}=$	$\sqrt{\mathit{Min}\ast \overline{k_{\mathit{over}}}\ast \mathit{ODRMax}}$	D
		$\widehat{\mathit{GSD}}=$	${\left(\mathit{ODRMin}\ast \overline{k_{\mathit{over}}}/\mathit{Min}\right)}^{1/2E_N\left[z_{\mathit{Max}}\right]}$	A or Bb, & D
		$\widehat{AM}=$	$\widehat{GM}\sqrt{{\widehat{\mathit{GSD}}}^{\widehat{\mathit{GSD}}}}$	—
		$\widehat{SD}=$	$\frac{\widehat{AM}}{\widehat{GM}}\sqrt{{\widehat{AM}}^2-{\widehat{GM}}^2}$	—
9	bN, ODRMin & Max	$\widehat{GM}=$	$\sqrt{\mathit{Max}\ast \overline{k_{\mathit{over}}}\ast \mathit{ODRMin}}$	E
		$\widehat{\mathit{GSD}}=$	${\left(\mathit{Max}/\mathit{ODRMin}\ast \overline{k_{\mathit{under}}}\right)}^{1/2E_N\left[z_{\mathit{Max}}\right]}$	A or Bb, & E
		$\widehat{AM}=$	$\widehat{GM}\sqrt{{\widehat{\mathit{GSD}}}^{\widehat{\mathit{GSD}}}}$	—
		$\widehat{SD}=$	$\frac{\widehat{AM}}{\widehat{GM}}\sqrt{{\widehat{AM}}^2-{\widehat{GM}}^2}$	—

^aOEMD records with the data in methods #6 and #7 are used to calculate the semi-empiric parameters $\overline{k_{\mathit{over}}}$ and $\overline{k_{\mathit{under}}}$.

^bWhere N is not available, E_N [z_Max] is replaced with $\overline{z_{\mathit{Max}}}$ which equals the median of E_N[z_Max] from all available N values in OEMD.

Notation: Same as Table 1.

The distributional characteristics of the data sets used to compute the semi-empiric parameters $\overline{\mathit{GSD}},\overline{z_{\mathit{Max}}},\overline{k_{\mathit{under}}}$, and $\overline{k_{\mathit{over}}}$ were examined to decide the best measure of their central tendency. Overall, data used for estimation of these semi-empiric statistics was not normally distributed; hence the AM was never selected. When we confirmed that the data followed a log-normal distribution, the GM was used as the best measure of the central tendency. However, when the shape of the distribution was not clearly right-skewed, we chose the median value as it is considered the most appropriate metric for general skewed distributions²⁷. Finally, we estimated mid-point values for k_over and k_under using (eq. 4a) and (eq. 4b). The median value was selected as the best estimate of the central tendency for these correction factors since their distributions are truncated by the assumptions that k_over>1 and k_under<1.

Confidence-weighting of pooled estimates

The lack of information on sample size and/or variance for many OEMD measurements ruled out inverse variance and other traditional measurement quality weighting procedures.²⁸ Therefore, a methodology was developed to weight our pooled measurements based on their quality and relevance for epidemiological studies, in particular for INTEROCC. The weighting approach was based on the use of expert confidence ratings as weights. These ratings had been initially used to include/exclude measurements from the OEMD. INTEROCC experts, with experience in occupational EMF measurements, used a semi-quantitative approach to derive an average rating for each set of measurements extracted from a study. Using a confidence evaluation form published with the OEMD paper¹⁹, each EMF expert first assigned a rating between 0 and 3 (0–1: low confidence; ≥1–2: moderate confidence; ≥2–3: high confidence) to eight specific factors of interest: sampling strategy, sample size, type of statistic reported, duty factor, dosimetry type, anatomical location, nature of exposure scenario, and overall quality and reliability. Each set of measurements was rated by at least two experts and an average rating was assigned. We now used these ratings to adjust the pooled estimates to our confidence in the quality and relevance of the measurements.

Data pooling and calculation of confidence-weighted statistics

Finally, the EMF exposure statistics (AM_i & GM_i), for each OEMD record i, were pooled to obtain mean exposure statistics by EMF source, frequency band and dosimetry type, using the expert ratings as confidence weights (C_i). Thus, confidence-weighted means (_cwAM and _cwGM) and standard deviations (_cwSD and _cwGSD) were calculated for each electric or magnetic field with these formulas derived in the Appendix:

$${}_{cw}AM=\sum _{i=1}^N{C}_i{N}_i{AM}_i/\sum _i{C}_i{N}_i$$ (5)

$$ln{}_{cw}GM=\sum _{i=1}^N{C}_i{N}_{i}ln{GM}_i/\sum _i{C}_i{N}_i$$ (6)

$${}_{cw}S{D}^2=\frac{{\displaystyle \sum _i}{C}_i\left[\left(N_i-1\right)S{D}_i^2+N_i\left({AM}_i^2-{}_{cw}A{M}^2\right)\right]}{{\displaystyle \sum _i}{C}_i{N}_i-\left({\displaystyle \sum _i}{C}_i^2{N}_i/{\displaystyle \sum _i}{C}_i{N}_i\right)}$$ (7)

$${ln}^2{}_{cw}GSD=\frac{{\displaystyle \sum _i}{C}_i\left[\left(N_i-1\right){\text{ln}}^2{\mathit{GSD}}_i+N_i\left({\text{ln}}^2{GM}_i-{\text{ln}}^2{}_{cw}GM\right)\right]}{{\displaystyle \sum _i}{C}_i{N}_i-\left({\displaystyle \sum _i}{C}_i^2{N}_i/{\displaystyle \sum _i}{C}_i{N}_i\right)}$$ (8)

where N_i is the number of individual measurements i used to calculate the pooled summary statistics for each record i in the OEMD. When N_i was not available, the median N = 10 from the OEMD records was used. Equations 7 and 8 were derived from the general formula for the unbiased weighted sample variance with non-random (a.k.a., reliability) weights²⁹ and when C_i = 1, are simply the classic formulas for the unweighted SD and GSD.

Since measurement data pooling was performed by dosimetry type, pooled exposure estimates obtained from spot measurements comprise several distances while those obtained from personal or operator position involve several anatomical locations (e.g. head, chest). Due to the different availability of measurements, some sources in the SEM may have estimates for just one dosimetry type while others may have estimates for two or more. Maximum values, by source, frequency and dosimetry, were also included in the SEM, as well as information on the exact number of measurements pooled for each estimate.

To compare the values between pooled estimates for different dosimetries, we analyzed the overall difference between estimates for the same source by comparing different possible combinations (i.e. operator position versus spot; personal versus operator position and personal versus spot). For this analysis, we used the intraclass correlation coefficient (ICC) which, similarly to a one-way ANOVA, allows comparing continuous values between groups³⁰.

Quality control

To check the quality of the estimation process and ensure the assumptions in our semi-empiric methods were appropriate for OEMD data, we performed tests based on fundamental statistical characteristics of log-normal distributions (such as Min<GM<AM<Max) as well as more specific checks based on EMF physical properties¹⁹. Manual calculations were also performed, comparing the results with those from the programmed algorithms. Identified errors were corrected, thus ensuring that both statistical characteristics and physical laws were not breached in the final dataset.

Analysis of variance (ANOVA)

To test the ability of the SEM to assign different exposures to subjects in an epidemiological study, we performed a one-way ANOVA with EMF source as the independent variable and the (reported or estimated) AM_i from OEMD as the response variable. Because of the large number of sources in the matrix and the diversity of frequencies and EMF magnitudes, as an example, we compared the values for mean electric fields for RF sources with three or more measurements at the operator position. Since ANOVA requires normal residuals and equal variances, data were log-transformed for this analysis. Furthermore, after confirming heterocedasticity (unequal variances between groups) using Levene’s test and assuming log-normality, we also used the non-parametric Welch’s test with untransformed data.

Validation

To test the validity of our methods to estimate parameters from limited summary statistics, Monte Carlo simulations were performed using the formulas in Table 1 on 10 000 random samples from a log-normal distribution with parameters similar to those found with EMF measurements (i.e. GM=20 and GSD=2.5). To make a realistic simulation, the sample size N for each simulation was drawn randomly from the values in the OEMD and the semi-empiric parameters were derived from the simulated data, using the methods described above for obtaining $\overline{z_{\mathit{Max}}}$ and $\overline{\mathit{GSD}}$. For each simulation, the relative errors in the summary statistic estimates for all methods were calculated relative to the sample statistics (GM, AM, GSD, SD) calculated from the N random draws:

$$\text{Relative}\text{error}\left(\text{RE}\right)=100\%\frac{\text{Statistic}\text{estimate}-\text{Sample}\text{statistic}}{\text{Sample}\text{statistic}}$$ (9)

The mean of the RE over all simulations is, therefore, a measure of the bias, and its standard deviation equals the relative standard deviation (RSD), a measure of the precision. The overall uncertainty, which is considered an approximation to the accuracy^31,32, can be estimated from these two values:

$$\text{Overall}\text{uncertainty}\equiv \mid \text{bias}\mid +2\ast \mathit{RSD}\approx \text{Accuracy}$$ (10)

Additionally, a split data set validation was performed for an RF source (dielectric heater), for which mean pooled estimates were obtained from 84 E-field measurements. The confidence-weighted arithmetic mean was computed using both a test subset (i.e. random 50% samples) and the entire data set, repeating these computations 1 000 times. To shed some light regarding possible changes over time for both exposure levels and measurements quality, we analyzed the available data for operator position measurements and confidence ratings – averaged by year – for two RF sources (aircraft radar, n=71, years=1974–1997; dielectric heater, n=84, years=1986–2004). Finally, to test our hypothesis that the measurements used in the SEM follow a log-normal distribution, we used the Shapiro-Wilk test on log-transformed data from EMF sources with three or more records. All statistical analyses and graphics were performed using R, version 3.2.3³³.

RESULTS

Semi-empiric parameters $\overline{\mathit{GSD}},\overline{z_{\mathit{Max}}},\overline{k_{\mathit{under}}}$, and $\overline{k_{\mathit{over}}}$

Univariate statistics obtained for the parameters, E_N[z_Max], GSD, k_over and k_under, are presented in Table 3. With E_N[z_Max], its distribution over all N_i in OEMD was a priori unknown, so we chose its median as the central tendency ( $\overline{z_{\mathit{Max}}}=1.54$). GSD values tend to be log-normally distributed, so we chose its GM as the semi-empiric parameter ( $\overline{\mathit{GSD}}=2.31$). Following the logic with GSD’s central tendency that the models are linear in the parameters logarithms, the GM was selected as the central tendency measure for the corrections factors ( $\overline{k_{\mathit{over}}}=1.47$) and ( $\overline{k_{\mathit{under}}}=0.48$).

Table 3.

Descriptive statistics for the estimated parameters calculated from sub-sets of the OEMD data. The statistics selected as a central tendency for use as semi-empiric parameters in Tables 1 and 2 are marked in bold.

Statistics	EN[zMax]	GSD	akover	bkunder	cN
# records	372	100	7	22	372
Min	0.56	1.1	0.09	0.01	2
Max	3.26	6.4	18.44	44.54	1075
AM	1.45	2.59	5.69	5.81	19
Median	1.54	2.09	0.26	0.58	10
GM	1.33	2.31	1.47	0.48	9
SD	0.56	1.3	8.00	13.70	59
CV%	39%	67%	141%	236%	3%

^ak_over values less than 1 were not included in the calculations.

^bk_under values greater than 1 were not included in the calculations.

^cN=1 records were not considered in this table nor in the simulations.

Exposure estimates in the SEM

The SEM contains AM, GM and maximum exposure estimates for 312 occupational sources of EMF exposure by frequency band, and estimates of their associated variability (SD and GSD). The maximum values for each source are the maxima of both the Max and AM values from the input OEMD records. Exposure estimates are provided for various types of dosimetry (i.e. personal, spot, operator position) as well as for literature reviews and expert judgments. In total, there are 401 combinations of EMF source, frequency band and dosimetry type. Table 4 summarizes the records used to obtain the different mean estimates. In total, over 3 000 measurements were compiled to create the SEM.

Table 4.

Description of estimation methods and measurements used in the SEM

Estimation method # (data available)	Number of OEMD measurements
	E-field	H-field	B-field	PD	Total	%
1 (AM, Min & Max)	13	2	156	4	175	8
2 (Min & Max)	226	133	115	40	514	23
3 (Max)	269	163	134	30	596	27
4 (AM)	71	34	317	17	439	20
5 (GM)	12	18	19	0	49	2
6 (AM, a ODRMax & Min)	0	0	1	0	1	0.1
8b (Min & ODRMax)	4	1	0	2	7	0.3
9 (Max & ODRMin)	0	0	1	0	1	0.1
10c (single measurement)	218	35	95	88	436	20
# measurements per estimate	Number of SEM estimates
1 measurement	98	152	142	--	392	49
2 measurements	23	51	31	--	105	13
3–5 measurements	31	76	59	--	166	21
6–10 measurements	23	35	31	--	89	11
> 10 measurements	14	21	11	--	46	6

^aODR: Outside Dynamic Range.

^bEstimation method 7 (AM, ODRMin & Max) was not used since the OEMD did not have any cases with these values.

^cOEMD records with N=1 (i.e. single measurements) were considered as AM = GM, hence method 10 is not considered for Tables 1 & 2.

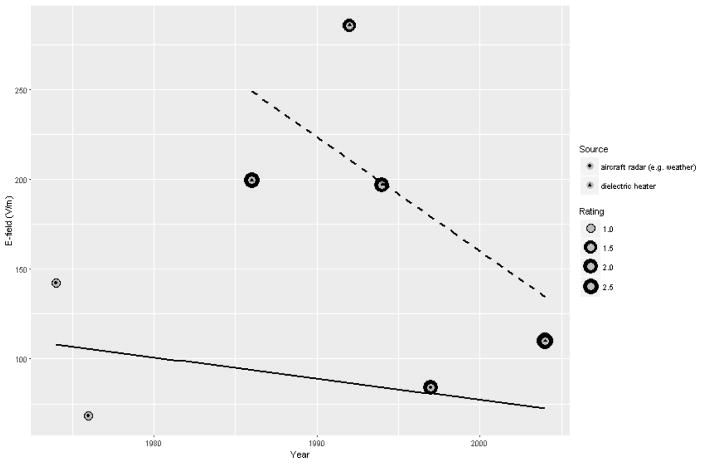
This table also outlines the different estimation methods used. While methods 2–5 were more frequently used, methods 1, 6, 8 and 9 were used less often. More than 400 single measurements were used in the calculations; hence method 10 was also common. More than 50% of the estimates were obtained from 2 or more measurements, while the remainder used only one. As an example of the SEM results, Figure 1 shows the EMF sources with the minimum and maximum confidence-weighted geometric means (operator position) in the RF, IF and ELF frequency bands. Figure 2 shows the evolution of exposure levels and measurement quality for two RF sources over time. A considerable decrease of exposure levels and a slight increase of data quality are appreciable.

Figure 1.

Quartile plots (25^th and 75^th percentiles) for EMF sources in the SEM with the highest and lowest _cwGM for E-, H-, and B-fields for operator position by frequency band. Estimates without whiskers (i.e. “transmission lines”, “electric forklift truck” and “sewing machine”) were obtained from only one measurement. To indicate within-source variability, the graphs include estimates for the first and third quartiles = e^{[ln(cwGM)±0.675ln(cwGSD)]}, where 0.675 is the z-value for the 75th percentile.

Figure 2.

Operator position E-field measurements for two RF sources (i.e. aircraft radar and dielectric heater) collected from documents covering the time span 1986–2004. Data points and corresponding confidence ratings (i.e. the size of the point) were obtained by averaging the available data by year. The lines represent modeled linear regressions based on the averaged data.

The confidence evaluation process

A total of 268 quantitative ratings were used as weights, since the same rating was assigned to two or more measurements if they shared the same characteristics. Of these, 135 (~50%) are above 2 (high confidence), 120 (~45%) are between 1 and 2 (moderate confidence) while only 13 ratings (~5%) are below 1 (low confidence). To illustrate the impact of the weighting process in the SEM calculations, Figure 3 shows the distribution of the E-field measurements used to calculate the mean (spot) estimate for the RF source “continuous shortwave diathermy”. These plots show weighted and unweighted regression lines over distance, highlighting the impact of the ratings on the weighted line (dashed). Measurements rated as low confidence are downplayed while moderate and high confidence values have a stronger influence on the final estimate.

Figure 3.

E-field measurements versus distance for OEMD data used to estimate the confidence-weighted mean exposure for the source “continuous shortwave diathermy” in the SEM. The bubbles represent data points with size proportional to the assigned rating level. The lines represent modeled exponential regression lines (dashed line, weighted) with y-axis in the linear (left graph) and logarithmic (right graph) scales. No ratings were assigned to these measurements below 1 or above 2. Thus, the “Rating” legend only includes a scale of sizes between these levels.

ANOVA

In the ANOVA analysis to assess the ability of the SEM estimates to assign exposure variation for epidemiological analysis, the RF source explained almost 60% of the variability of the E-field and these differences were significant (p<0.0001). The Welch’s test (p<0.0001) also confirmed this heterocedasticity.

Validation

The simulations based on the estimation formulas in Table 1 yielded overall uncertainties (i.e. accuracy) for GM and AM estimates between 47–143% (Table 5). For variability statistics, GSD estimates were obtained with accuracies between 33–78% while SD estimates yielded extreme overall uncertainties. An additional simulation using different N values showed a clear pattern of better performance with larger sample sizes (data not shown). Furthermore, these simulations showed that some estimation methods have less overall uncertainty when $\overline{z_{\mathit{Max}}}$ is used instead of E_N[z_Max] (see Table A-III in the Appendix). Hence, our SEM calculations used the z_Max parameter which gave the best accuracy in the simulations of each statistic/method combination in Table 5. The split data set validation yielded a median relative error of −18%.

Table 5.

Uncertainties of the methods in Table 1 for estimating unknown summary statistics. The uncertainty measures are calculated with Monte Carlo methods with 10 000 simulations of a random sample from a log-normal distribution with GM = 20, GSD = 2.5, and sample size ^aN randomly drawn from those in OEMD.

Estimated statistic	Measures of the relative error (RE)	Estimation methoda (statistics with values from simulated sampleb)
		1 (AM, Min & Max)	2 (Min & Max)	3 (Max)	4 (AM)	5 (GM)
$\widehat{GM}$	Mean RE (bias)	−12%	3%	14%	−5%
	SD of RE (precision)	17%	25%	64%	21%
	Accuracy	47%	53%	143%	47%
$\widehat{AM}$	Bias		21%	16%		9%
	Precision		52%	36%		20%
	Accuracy		125%	88%		50%
c $\widehat{\mathit{GSD}}$	Bias	6%	6%	9%	9%	9%
	Precision	13%	13%	35%	35%	35%
	Accuracy	33%	33%	78%	78%	78%
$\widehat{SD}$	Bias	37%	85%	72%	113%	170%
	Precision	74%	254%	411%	1 101%	1 651%
	Accuracy	185%	593%	894%	2 316%	3 472%

^aEstimation methods #1, 3, 4 & 5 use E_N[z_Max] while method #2 uses $\overline{z_{\mathit{Max}}}$ (i.e. median of E_N[z_Max]).

^bThe median of the N values in OEMD = 10.

^cMethods #3–5 for $\widehat{\mathit{GSD}}$ have the same results since they all use $\overline{\mathit{GSD}}$.

The Shapiro-Wilk test confirmed the log-normal hypothesis (p-value > 0.05) in around 85% of the analysed sources. The ICC analysis showed moderate to substantial agreement for the compared dosimetries (i.e. ICC=0.80 for spot versus operator position, n=18; ICC=0.69 for personal versus operator position, n=9; ICC=0.53 for spot versus personal dosimetries, n=20).

DISCUSSION

This work allowed the construction of a SEM containing estimated exposure statistics for the most common occupational sources of EMF exposure, identified through the INTEROCC study questionnaire. This database represents a new approach for occupational exposure assessment, based on EMF sources independent of occupation. The SEM will be available on-line as a free-access tool at http://www.crealradiation.com/index.php/es/databases. Although the current version does not include all possible EMF sources, it can be updated with new or newly identified measurements and sources.

One advantage of the source-based approach is that personal determinants of exposure obtained from questionnaires should reduce Berkson errors, increasing the validity and reliability of both exposure and risk estimates¹⁵. However, the SEM mean exposures will still leave residual Berkson errors due to the combination of measurements from different studies and locations (i.e. distances or anatomical positions). Another advantage is the SEM’s ability to evaluate occupational exposures to RF and IF fields. Since no JEM yet exists for these higher frequencies, only a source-based approach can provide quantitative estimates of exposure for INTEROCC and other studies. The results of the ANOVA and the non-parametric test confirmed the existence of significant between-source variability, which allows the assignment of different exposures to study subjects, necessary for identifying exposure-response relationships in risk analysis. Previous efforts to reduce exposure misclassification included the development of task-exposure matrices for other agents^34–37. However, earlier advocates of a source-based approach for EMF exposure assessment^38–41 recommended the use of combined estimates from a JEM together with information such as duration and location related to specific sources of exposure. To our knowledge, this is the first time that a full source-based approach, independent of the occupation, has been attempted.

The mean exposure (i.e. AM or GM) was selected as the primary exposure metric in the SEM because it best represents measurements taken in diverse settings. There has been considerable discussion whether the AM or GM from JEMs best reduces Berkson errors in an epidemiological analysis^42–45, and these same considerations apply to the SEM. Although the GM is the best estimate of the central tendency for log-normally distributed data, the AM has been considered the best summary measure for linear and convex dose-response relationships, while the GM would be a better metric when the proposed mechanism is log-linear (i.e. the response is proportional to the logarithm of the exposure/dose)^45–49. The availability of both AM and GM in the SEM allows selection of the more appropriate metric for the study hypothesis. The provision of within-source variability statistics (i.e. _cwSD and _cwGSD) also allows correction of risk estimates for bias attributable to Berkson error as well as for uncertainty propagation analysis^18,50–52. Moreover, although bias estimates were provided for only half the methods, use of this information as weights for the pooled statistics should be explored in the future.

Several methods were developed for estimating parameters based on scarce measurement data. Methods 1 and 2 require enough available variables but allow estimating AM, GM, GSD, and SD based on exact relationships between the true statistics of a log-normal distribution²⁴. Method 2, in particular, was based on an estimation formula, $\widehat{GM}=\sqrt{\mathit{Min}\ast \mathit{Max}}$, which has recently been popularized by physicists for “guesstimation”^53,54 and variants have been used in exposure assessment efforts^3,4,7. To extend this estimation technique to the other combinations of statistics, we introduced several semi-empiric methods to derive equations where the literature provided insufficient data for exact solutions. Although these semi-empiric estimates fill many gaps in the available data, they add to exposure assessment uncertainty, as shown by the simulations in Table 5. Moreover, the method we used to reliably estimate parameters from only maximum values, as proved by the relatively low bias obtained in the simulations, provides a novel approach which, to our knowledge, was lacking in the present literature. For data combinations not considered in Tables 1 and 2, which may also be found in the literature, we provided the assumptions and premise formulas needed to easily derive appropriate methods.

We provided evidence for the reliability of our methodology through both simulations and a split-dataset validation. While the simulated accuracies are far greater than the 25% accuracy criterion established by NIOSH for occupational exposure measurements (NIOSH, 1994), most methods for GM had overall uncertainties of 53% or less, which we consider sufficient for retrospective epidemiology. Moreover, these accuracies are expected to improve if GSD and/or SD are extracted from the literature, or larger sample sizes are used, as seen in our additional simulations and previous studies⁵⁵. However, the impact of these exposure assessment errors on risk estimates should be investigated. For the methods in Table 2, a comprehensive approach for evaluating uncertainties was not found. Although some of the estimated values violated the assumptions k_over>1 and k_under<1, one of the semi-empiric estimated parameters ( $\overline{k_{\mathit{over}}}=1.47$) compared well with a calculated value (k_over =1.41) based on empirical monitoring data (i.e. measurements of the same location using two different ELF-MF meters at a car factory in the Netherlands). However, further validations are indicated for these correction factors, as well as for the equations in Tables 1 and 2.

The influence of measurement quality on exposure and risk estimates requires a rigorous evaluation, including transparency in the way data are weighted for their actual or relative value^28,56. Some authors^5,6,28 proposed the use of sample size or inverse variance to obtain quality-weighted exposure estimates. However, the frequent lack of this information for measurements in the EMF literature makes such approaches unfeasible. We overcame this difficulty by using expert confidence ratings to adjust our estimates to the quality and relevance of the pooled measurements. The adopted scoring system agrees with a recent proposal for the evaluation of exposure data quality²⁸, which introduced a method to classify measurements into four quality groups (i.e. good, moderate, poor and unacceptable). Although we did not distinguish between poor and unacceptable measurements, those rated as low confidence (0–1) were generally excluded from the pooling. However, some low confidence measurements, for which no better data were available, were included in the SEM. Based on this confidence classification, sensitivity analysis may be conducted (e.g. excluding lower quality data). This method also allows accounting for sampling characteristics, while other weighting approaches, such as inverse variance, only account for statistical uncertainty and do not consider other potentially important factors (e.g. quality of the task description and the sampling devices or focus on high exposures) which can be easily identified in the literature and may determine the quality and relevance of a measurement²⁸. Thus, similarly to meta-analysis in epidemiology⁵⁷, measurements with higher confidence have a larger contribution to the weighted mean. Finally, this approach allowed the raters to use a simple additive method to assign scores, which has been shown to be a good predictor of overall methodological quality^58,59.

One weakness of the SEM was our inclusion of less accurate spot and operator position dosimetries in order to provide exposure data for some of the reported sources. However, the results of the ICC showed that the overall differences between the three dosimetry types are small. Estimates obtained from operator position or spot measurements may, therefore, be reliably used as surrogates when personal exposure is not available. Moreover, confidence-weighted estimates were adjusted to head exposure through the confidence weighting process. Measurements made at head location obtained higher ratings and were upgraded in the pooling. To allow use of the SEM in studies on other locations (e.g. chest, gonads) – where different weighting approaches may be applied – the unweighted estimates were also provided. Since the confidence evaluations for all eight factors are stored in the SEM database, future studies may reduce the weight given to head measurements while retaining the other seven factors affecting measurement quality.

Another weakness is the lack of use of anatomical location and distance information collected in the OEMD for spot and operator position measurements. SEM values refer, therefore, to average levels over different exposure scenarios, which provide the within-source variability inherent within each mean estimate. Pooled estimates represent different situations of exposure depending on the dosimetry type. Estimates for personal and operator position comprise measurements at different anatomical locations (e.g. head, chest, or waist) while spot estimates include exposures at different distances (e.g. 30–100 cm for most ELF sources). However, as shown in Figure 2, the availability of this information may allow future modelling of exposures at specific distances and locations, useful in studies interested in other body parts.

The analysis of the available measurement data for different years showed signs of a slight data quality increase over time, which is reasonable considering the improvements in industrial hygiene⁶⁰. Exposure levels, on the contrary, showed a clear decrease pattern, which is in line with the trends shown by other technologies such as mobile phones⁶¹. However, since level changes are limited to one order of magnitude and OEMD data for the same source seldom span several years, we do not expect that these changes will have a strong effect on the SEM estimates.

The SEM can be used to assess EMF exposures for other occupational and residential epidemiologic studies that have collected individual information on the use of EMF sources. Such studies require questionnaires that elicit individual information about the type of EMF sources used/exposed, as well as about conditions of use (e.g. distance to the source, automation) to adjust the SEM estimates to the specific tasks and work characteristics of the individual. If the time-weighted average or cumulative exposures are desired, the questionnaire also needs to obtain information on the frequency and duration of use/exposure. In INTEROCC, industry was considered through the classification of all EMF sources into twelve occupational sections¹⁹. Therefore, the variability due to industrial differences is embedded within the type of source itself, which together with the aforementioned information on other exposure determinants allows a detailed estimation of a subject’s level of exposure. While the means in the SEM are most useful in chronic disease studies, the EMF maxima can be applied to acute effects, such as electromagnetic interference with pacemakers and other medical devices⁶².

CONCLUSION

The methodology described in this paper allowed the construction of the first SEM for EMF exposure assessment, based on measurements identified in the literature, and supplemented with expert judgment estimates for sources without available measurements. These methods made use of measurement data which more conventional methods would have discarded. Although more analyses of their uncertainty and validity are needed, the SEM methodology may also be useful for other physical and chemical agents for which available measurement data are sparse and traditional methods are insufficient.

The SEM will be used to estimate cumulative RF and ELF exposures of the INTEROCC subjects, through algorithms which combine SEM means with individual data on exposure determinants collected by interviews. This more individualized exposure assessment will potentially increase within-job variability among subjects while reducing uncertainty due to misclassification and Berkson errors. We expect that this approach will strengthen our ability to evaluate potential health effects from EMF exposures.

GLOSSARY

EMF

Electromagnetic fields

E-field

Electric field strength, in volts per meter (V/m)

H-field

Magnetic field strength, in amperes per meter (A/m) [high frequency fields]

B-field

Magnetic flux density, in microTesla (μT) [low frequency fields]

PD

Power Density, in watts per square meter (W/m²)

SMF

Static Magnetic Fields, in microTesla (μT), 0 Hz

ELF

Extremely Low Frequency (3–3000 Hz)

IF

Intermediate Frequency (3 kHz – 10 MHz)

RF

Radiofrequency (10 MHz – 300 GHz)

Min

Minimum

Max

Maximum

N

sample size

AM

Arithmetic mean

GM

Geometric mean

SD

Standard deviation

GSD

Geometric standard deviation

z_Max

Standard normal quantile of a data set’s maximum value

ODR

utside Dynamic Range (The range between an EMF instrument’s overload input and its minimum input with acceptable accuracy)

OEMD

Occupational Exposure Measurement Database

HVTL

High Voltage Transmission Lines

TIG

Tungsten Inert Gas

CVD

Chemical Vapor Deposition

Appendix: Statistical Methods Developed for the INTEROCC Study’s Assessment of EMF Exposures

Summary

We here derive the formulas for calculating the confidence-weighted arithmetic means (AM), geometric means (GM) and their corresponding standard deviations (SD and GSD) from EMF data obtained from the Occupational Exposure Measurement Database (OEMD). In part A of this appendix, we derive the formulas in Tables 1 and 2 for estimating summary statistics which are not in OEMD. Part B contains derivations for the confidence weighted means and standard deviations from OEMD’s summary statistics

A. Semi-empiric methods for estimating summary statistics for the SEM

The problem is to estimate these statistics from sparse information, typically the minimum (Min) and maximum (Max) but also the number of measurements (N), arithmetic or geometric mean, and outside-dynamic-range values (ODRMin or ODRMax). Our solution is to derive the summary statistics from the assumption that the exposure data are distributed log-normally, and any unknown variable (such as the GSD) needed to complete the derivation is replaced with its central tendency calculated from an appropriate data set – a semi-empiric approach.

This approach is an extension of the expert judgment method developed by Bowman, Sivaganesan, Shulman and Cardis [2013], which starts with the log-normal relationships for the standard normal quantiles, z, corresponding to Min and Max:

$$ln\mathit{Min}=ln\mathit{GM}+{\mathrm{z}}_{\text{Min}}ln\mathit{GSD}$$ (A1a)

$$ln\mathit{Max}=ln\mathit{GM}+z_{\mathit{Max}}ln\mathit{GSD}$$ (A1b)

By adding and subtracting these two equations, Bowman et al. [2013] derived formulas for estimating GM and GSD as functions of Min and Max:

$$ln\widehat{GM}=ln\mathit{GME}-\frac{\alpha }{2}(ln\mathit{Max}-ln\mathit{Min})$$ (A2a)

$$ln\widehat{\mathit{GSD}}=\frac{1}{2\zeta }(ln\mathit{Max}-ln\mathit{Min})$$ (A2b)

where the hat designates estimates and the symbols α, ζ, and GME are defined as:

$$\begin{array}{ll}\hfill \alpha & \equiv \frac{z_{\text{Max}}+z_{\text{Min}}}{z_{\text{Max}}-z_{\text{Min}}}\\ \hfill \zeta & \equiv \frac{1}{2}\left(z_{\text{Max}}-z_{\text{Min}}\right)\end{array}$$ (A3)

$$\begin{array}{l}\mathit{GME}=\text{geometric}\text{mean}\text{of}\text{the}\text{extremes}\\ \equiv \sqrt{\mathit{Max}\ast \mathit{Min}}\end{array}$$ (A4)

The parameter α is an asymmetry parameter that measures how far z_Min and z_Max deviate from being symmetric about zero (i.e. z_Min = −z_Max). ζ is the average distance of z_Min and z_Max from the mean of the log-transformed data, and therefore serves as the “effective quantile” in the estimation formula for the GSD (eq. A2b). GME, the geometric mean of the extreme values (Min and Max), has a long history, which we traced back from Enrico Fermi through Voltaire, Sir Isaac Newton and Euclid to the Pythagorean mathematician Archytas in the fifth century BCE [Bowman and Vila, unpublished].

In expert judgment studies, values for Min and Max are elicited from an expert panel, which provides values for two of the four variables on the right hand side of the two equations for GM and GSD (eqs. A2). The two remaining unknown variables, α and ζ, are the semi-empiric parameters, whose central tendencies ᾱ and ζ̄ (means or medians as best fits the calibration data) are calculated from the expert judgment results with a calibration data set whose GM and GSD are known. After determining ᾱ and ζ̄ estimated summary statistics, $\widehat{GM}$ and $\widehat{\text{GSD}}$, can then be calculated for exposures beyond the calibration set with eqs. A1, using only their Min and Max. Next, the AM and SD are derived from the exact relationships between the statistics of a log-normal distribution [Aitchison and Brown, 1957]:

$$ln\mathit{AM}=ln\mathit{GM}+\frac{1}{2}{ln}^2\mathit{GSD}$$ (A5)

$$SD=\frac{AM}{GM}\sqrt{A{M}^2-G{M}^2}$$ (A6)

Formulas for all the statistics in the expert judgment method are in the first row of Table A-I. Note that the formulas in Table A-I are the anti-logs of eqs. A2 and A6, which results in more compact equations with greater computational efficiency.

Summary statistics from OEMD data

A similar approach is used to estimate summary statistics with data from OEMD, although the formalism is made more complicated by the many combinations of Min, Max, AM, GM, N, ODRMin, and/or ODRMax whose values were extracted into OEMD from different publications. In order to structure a semi-empiric derivation of formulas for all the summary statistics, we start with a theorem from algebra that a system of simultaneous polynomial equations has solutions if the number of equations equals the number of unknown variables.

With the formalism outlined above, there are 2 linear equations (eqs. A2a and A2b). (Note that the log-transformed statistics like ln GM and ln Min are treated as the variables in order to make these equations linear) If eq. A4 is substituted into eq. A2a, these two have a total of 6 linear variables (ln GM, ln GSD, ln Max, ln Min, α and ζ). Since values for Max and Min are provided by the expert panel, only four of the variables are unknown, but this is greater than the number of equations, leaving their solution underdetermined. In order to evaluate the formal solutions for the unknowns, ln $\widehat{GM}$ and ln $\widehat{\text{GSD}}$ in eqs. A2, the expert judgment method therefore provided values for the 2 semi-empiric variables α and ζ. This reasoning can be expressed numerically as:

$$2\text{equations}=2\text{unknowns}=6\text{total}\text{variables}-2\text{variables}\text{with}\text{values}-2\text{semi-empiric}\text{variables}$$ (A7)

An algebraic form of eq. A7 can be re-arranged into a general expression for the number of semi-empiric variables needed to solve a system of simultaneous equations:

$$s=t-m-v$$ (A8)

where s = number of semi-empiric variables, t = total number of variables, m = number of equations, and v = number of variables with values.

To illustrate the application of this semi-empiric method to OEMD data, consider a record with values for Min and Max, so there are v=2 variables with values (method #2 in Table A-I). To obtain estimates for GM and GSD, we use eqs. A2a and A2b, creating a system of m=2 simultaneous equations with t = 6 variables. According to eq. A8, values are needed for s = 2 semi-empiric variables in order to solve these two equations for the unknown summary statistics.

The first semi-empiric variable is provided by assuming z_Min = −z_Max, so that α = 0 (eq. A-3). We call this “the symmetric quantile” assumption because the minimum and maximum quantiles are symmetric about zero (the mean quantile), and the corresponding percentiles also have the symmetry P_Min = 1− P_Max, (e.g. the 5^th and 95^th percentiles). The symmetric quantile assumption makes eq. A2a into $ln\widehat{GM}=ln\mathit{GME}$, whose anti-log is the estimation formula in Table A-I.

From the definitions of α and ζ (eqs. A3), this assumption also implies that z_Max= −z_Min = ζ, so eq. A2b becomes $\widehat{\mathit{GSD}}=(ln\mathit{Max}-ln\mathit{Min})/2z_{\mathit{Max}}$. A solution for $\widehat{\mathit{GSD}}$ therefore requires the second semi-empiric parameter $\overline{z_{\mathit{Max}}}$, where the bar represents the central tendency of z_Max calculated exactly from the formula in Table A-I from OEMD records with v=3. With semi-empiric estimates for $\widehat{GM}$ and $\widehat{\mathit{GSD}}$, AM and SD can now be estimated with the relationships A5 and A6 between exact values for the summary statistics of a log-normal distribution, as shown for method #2 in Table A-I.

Note that the formulas for SD in Table A-I only require values for AM and GM, which are either input values or have already been estimated by the other formulas in Table A-I. Since the same situation applies to all other combinations of input data in Tables A-I and A-II, slight variations of eq. A6 are used to estimate SD throughout the SEM calculations.

With 2 or less variables with values in an OEMD record, semi-empiric values are needed in addition to the α = 0 assumption to obtain solutions for the missing summary statistics. As shown in Table A-I, v = 2 values for Max and Min requires a central tendency for $\overline{z_{\text{Max}}}$ in order to estimate the summary statistics, while a record with a value for only Max (v = 1) requires an additional central tendency for $\overline{\mathit{GSD}}$. These central tendencies are calculated from a sub-set of OEMD records with values for enough variables for the simultaneous equations to have exact solutions (i.e. s ≤ 0). Whether the median, AM or GM is the best central tendency for these semi-empiric parameters is addressed in the main paper.

Summary statistics from OEMD data that include N

In addition to the summary statistics examined above, some OEMD records also contained the number of measurements N used to calculate the statistics. To employ the reported N values in our summary statistic estimates, z_Max and z_Min are equated to their expected values for a sample of N quantiles z from the standard normal distribution (Zwillinger and Kokoska 2000). When the N expected values E_N[z] are ranked according to their values, these “expected normal order statistics” [also called “rankits” by Ipsen and Jerne (1944)] are widely used in normal probability plots (Snedecor and Cochran, 1989).

In the SEM calculations, the expected normal order statistics for the extreme quantiles, E_N[z_Max] and E_N[z_Min], are calculated by a numeric algorithm (Royston, 1982) and assumed to equal the actual minimum and maximum quantiles for OEMD records that have values for the sample size N:

$$z_{\text{Min}}=E_N[z_{\text{Min}}]$$ (A9a)

$$z_{\text{Max}}=E_N[z_{\text{Max}}]$$ (A9b)

In addition, the extremes of the expected normal order statistics for a given N are symmetric (Zwillinger and Kokoska 2000):

$$E_N[z_{\text{Min}}]=0E_N[z_{\text{Max}}]$$ (A10)

In other words, they fulfil the symmetric quantile (α = 0) assumption.

Using these results in the summary statistics calculations, there are now n = 6 simultaneous equations (eqs. A1a, A1b, A5, A9a, A9b and A10) with 2 additional variables with values (E_N[z_Min] and E_N[z_Max]), giving a total of t = 9 variables. When OEMD has Min, Max and AM in addition to N, the number of variables with values is now v = 5, so eq. A8 now gives s = −1. This negative result means there are more simultaneous equations than unknown variables, so this over-determined system of equations has more than one solution for both AM and GM in Table A-II. The common-sense resolution to this “embarrassment of riches” is to set AM equal to the reported AM, rather than use the solution: $AM=\mathit{GME}\sqrt{{\mathit{GSD}}^{ln\mathit{GSD}}}$ derived from the 6 simultaneous equations.

Estimation formulas for other data combinations in OEMD that include N are given in Table A-II.

Table A-I.

Formulas for estimating summary statistics from expert judgments for Min and Max and from OEMD data for Min, Max, AM and GM.

Input values	Estimate	Formula
Method #0: v = 2 values, m = 2 equations (eqs. A2a & A2b), s = 2 semi-empiric parameters (α and ζ)
Min & Max	$\widehat{GM}=$	$\mathit{GME}/{\left(\sqrt{\mathit{Max}/\mathit{Min}}\right)}^{\overline{\alpha }}$ where $\mathit{GME}\equiv \sqrt{\mathit{Max}\ast \mathit{Min}}$
	$\widehat{\mathit{GSD}}=$	${\left(\sqrt{\mathit{Max}/\mathit{Min}}\right)}^{1/\overline{\zeta }}$
	$\widehat{AM}=$	$\widehat{GM}\sqrt{{\widehat{\mathit{GSD}}}^{ln\widehat{\mathit{GSD}}}}$
	$\widehat{SD}=$	$\frac{\widehat{AM}}{\widehat{GM}}\sqrt{{\widehat{AM}}^2-{\widehat{GM}}^2}$
Method #1: v = 3 values, m = 3 equations (eqs. A2a, A2b & A5), s = 1 assumption (α= 0)
Min, Max & AM	$\widehat{AM}=$	AM
	$\widehat{z_{\mathit{Max}}}=$	$\raisebox{1ex}{$ln\left(\mathit{Max}/\mathit{Min}\right)$}\!\left/ \!\raisebox{-1ex}{$2\sqrt{ln\left[A{M}^2/\left(\mathit{Min}\ast \mathit{Max}\right)\right]}$}\right.$
	$\widehat{\mathit{GSD}}=$	${\left(\sqrt{\mathit{Max}/\mathit{Min}}\right)}^{1/\widehat{z_{\text{Max}}}}$
	$\widehat{GM}=$	$AM/\sqrt{{\widehat{\mathit{GSD}}}^{ln\widehat{\mathit{GSD}}}}$
	$\widehat{SD}=$	$\frac{AM}{\widehat{GM}}\sqrt{A{M}^2-{\widehat{GM}}^2}$
Method #2: v = 2 values, m = 3 equations, s = 2 = 1 assumption + 1 semi-empiric parameter (zMax)
Min & Max	$\widehat{GM}=$	GME
	$\widehat{\mathit{GSD}}=$	${\left(\sqrt{\mathit{Max}/\mathit{Min}}\right)}^{1/\overline{z_{\text{Max}}}}$
	$\widehat{AM}=$	$\widehat{GM}\sqrt{{\widehat{\mathit{GSD}}}^{ln\widehat{\mathit{GSD}}}}$
	$\widehat{SD}=$	$\frac{\widehat{AM}}{\widehat{GM}}\sqrt{{\widehat{AM}}^2-{\widehat{GM}}^2}$
Method #3: v = 1 value, m = 3 equations, s = 3 = 1 assumption + 2 semi-empiric parameters (zMax & GSD)
Max*	$\widehat{GM}=$	$\mathit{Max}/{\overline{\mathit{GSD}}}^{\overline{z_{\text{Max}}}}$
	$\widehat{AM}=$	$\mathit{Max}\sqrt{Q^{-2\overline{z_{\text{Max}}}}}$, where $Q={\overline{\mathit{GSD}}}^{ln\overline{\mathit{GSD}}}$
	$\widehat{\mathit{GSD}}=$	$\overline{\mathit{GSD}}$
	$\widehat{SD}=$	$\frac{\widehat{AM}}{\widehat{GM}}\sqrt{{\widehat{AM}}^2-{\widehat{GM}}^2}$
Methods #4 and 5: v = 1 value (AM or GM), m = 1 equation (eq. A5), s = 1 semi-empiric parameter (GSD or Q)
AM	$\widehat{AM}=$	AM
	$\widehat{GM}=$	$AM/\sqrt{Q}$
	$\widehat{\mathit{GSD}}=$	$\overline{\mathit{GSD}}$
	$\widehat{SD}=$	$\frac{AM}{\widehat{GM}}\sqrt{A{M}^2-{\widehat{GM}}^2}$
GM	$\widehat{GM}=$	GM
	$\widehat{AM}=$	$GM\sqrt{Q}$
	$\widehat{\mathit{GSD}}=$	$\overline{\mathit{GSD}}$
	$\widehat{SD}=$	$\frac{\widehat{AM}}{GM}\sqrt{{\widehat{AM}}^2-G{M}^2}$

^*Formulas when Min is the only input are not given because this case does not occur in OEMD.

Note: The formulas for the estimated statistics, designated by hats, are re-defined for each method. Therefore, applications of estimated statistics in subsequent formulas have values defined for the same method with the given set of input data. The only statistics whose values are the same in multiple methods are the central tendencies for z_Max and GSD, designated by bars.

Table A-II.

Formulas for estimating summary statistics from OEMD data that include N.

Input values	Estimate	Formula
Method #1′: v = 5 values, m = 6 equations (eqs. A1a, A1b, A5, A8a, A8b & A9), s = −1 (over-determined solutions)
N, Min, Max & AM	$\widehat{AM}=$	AM or $\mathit{GME}\sqrt{{\widehat{\mathit{GSD}}}^{ln\widehat{\mathit{GSD}}}}$
	$\widehat{\mathit{GSD}}=$	${\left(\sqrt{\mathit{Max}/\mathit{Min}}\right)}^{1/E_N\left[z_{\mathit{Maz}}\right]}$
	$\widehat{GM}=$	GME or $AM/\sqrt{{\widehat{\mathit{GSD}}}^{ln\widehat{\mathit{GSD}}}}$
Method #2′: v = 4 values, m = 6 equations, s = 0 (exact solution)
N, Min & Max	$\widehat{GM}=$	GME
	$\widehat{\mathit{GSD}}=$	${\left(\sqrt{\mathit{Max}/\mathit{Min}}\right)}^{1/E_N\left[z_{\mathit{Maz}}\right]}$
	$\widehat{AM}=$	$\widehat{GM}\sqrt{{\widehat{\mathit{GSD}}}^{ln\widehat{\mathit{GSD}}}}$
Method #3′: v = 3 values, m = 6 equations, s = 1 semi-empiric parameters (GSD)
N & Max	$\widehat{GM}=$	$\mathit{Max}/{\overline{\mathit{GSD}}}^{E_N\left[z_{\mathit{Max}}\right]}$
	$\widehat{AM}=$	$\mathit{Max}\sqrt{Q^{-2E_N\left[z_{\text{Max}}\right]}}$, where $Q={\overline{\mathit{GSD}}}^{ln\overline{\mathit{GSD}}}$
	$\widehat{\mathit{GSD}}=$	$\overline{\mathit{GSD}}$

Thus, for OEMD records with N, two alternative methods in Tables A-I and II provide estimates for the unknown summary statistics for OEMD data combinations #1, 2 and 3. Comparing methods in these two tables, their formulas are identical, except for the exponents of $\widehat{\mathit{GSD}}$ in methods 1 and 2 and the exponents of $\widehat{AM}$ and $\widehat{GM}$ in method 3. Those exponents contain $\widehat{z_{\mathit{Max}}}$ or $\overline{z_{\mathit{Max}}}$ in Table A-I, but are replaced with E_N[z_Max] in Table A-II. Those exponents do not appear explicitly in methods 4 and 5.

In deciding which methods to use for the SEM calculations, we first note that methods in Table A-II have the additional assumption that the extreme quantiles for an OEMD record equal their expected values for the reported sample size N (eqs. A9). In order to evaluate the effects of this “expected quantile assumption,” we used the Monte Carlo simulations described in the main paper. Those simulations take 10,000 samples of N measurements from a log-normal distribution with GM = 20 and GSD = 2.5, where N for each simulation is a random selection from all values in OEMD. From these simulated data, we calculated the overall uncertainty in the estimated summary statistics (as described in the Methods of the main paper) with the methods in Tables A-I and A-II. From the simulation results, we chose the methods with the lower overall uncertainty for the arithmetic and geometric means to use in the SEM calculations.

The resulting overall uncertainties for the two alternative exponents are given in Table A-III. The minimum uncertainty for the means are achieved with the exponent E_N[z_Max] for methods #1 and 3, but with z_Max for method #2. These optimal exponents are used in the estimation formulas for both the SEM calculations (Table 1) and the validation calculations (Table 5).

Note that the uncertainty pattern for the standard deviations in Table A-III are somewhat different than for the means. In selecting the optimal methods, we focused on the mean estimates since only the SEM means are needed for obtaining risk estimates, which are INTEROCC’s primary objectives. We included the uncertainties in the standard deviations in Table A-III and Table 5, so that they can be taken into account by any future studies of the variabilities and uncertainties in the risk estimates by simulations with the SEM.

Table A-III.

Simulated uncertainties of the alternative estimation formulas in Tables A-I and A-II with the lower uncertainty for each combination of the estimated statistic and method in bold.

Estimated statistic	Exponent alternatives*	Overall uncertainty of the estimated statistics by method # (with the OEMD statistics used)
		1(AM, Min & Max)	2(Min & Max)	3(Max)
$\widehat{AM}$	zMax	51%	53%	212%
	EN[zMax]	47%	53%	143%
$\widehat{GM}$	zMax		125%	166%
	EN[zMax]		682%	88%
$\widehat{\mathit{GSD}}$	zMax	75%	75%	78%
	EN[zMax]	33%	33%	78%
$\widehat{SD}$	zMax	185%	593%	894%
	EN[zMax]	1793%	262,450%	2098%

^*In the simulations, these alternatives were used as $\widehat{z_{\mathit{Max}}}$ for estimation method #1, and as $\overline{z_{\mathit{Max}}}$ in methods #2 and 3.

Statistics for measurements outside the meter’s dynamic range

The last type of record in OEMD are from studies which report measurements outside the meter’s dynamic range. In these cases, Min or Max are replaced with the dynamic range’s lower limit (ODRMin) or upper limit (ODRMax). In those cases, we model the actual Min or Max with the reported ODR values times empiric parameters k_under < 1 and k_over > 1:

$$\widehat{\mathit{Min}}=\mathit{ODRMin}\ast \widehat{k_{\mathit{under}}}$$ (A11a)

$$\widehat{\mathit{Max}}=\mathit{ODRMax}\ast \widehat{k_{\mathit{over}}}$$ (A11b)

Initially, we were able to calculate an average k_over empirically based on data from two sets of measurements of personal exposures to a magnetic field source using two different ENERTECH EMF meters (http://www.enertech.net), a Standard EMDEX II (ODRMax=300 μT) and a Hi-Field EMDEX II (ODRMax = 12,000 μT). However, no such data were available for EMF measurements below a meter’s limit of detection, so we needed a semi-empiric approach to obtain k_under. We identified two suitable methods by using the same assumptions (a log-normal distribution and α = 0) and similar algebra to the derivations above.

In the first approach, the input data are ODRMin and Max, so eqs. A1 and A11a are adequate to derive k_under with the semi-empiric methods described above. The m=2 simultaneous equations are:

$$ln\mathit{ODRMin}+ln\widehat{k_{\mathit{under}}}=ln\widehat{GM}-\widehat{z_{\mathit{Max}}}ln\widehat{\mathit{GSD}}$$ (A12a)

$$ln\mathit{Max}=ln\widehat{GM}+\widehat{z_{\mathit{Max}}}ln\widehat{\mathit{GSD}}$$ (A12b)

These equations have a total of t = 6 variables of which v = 2 have values, so they can be solved for the summary statistics with s = 2 semi-empiric values for z_Max and GSD.

$$\widehat{k_{\mathit{over}}}=\frac{\mathit{Max}}{\mathit{ODRMin}\ast {\overline{\mathit{GSD}}}^{\overline{z_{\text{Max}}}}}$$ (A13a)

$$\widehat{GM}=\sqrt{\widehat{k_{\mathit{under}}}\ast \mathit{ODRMin}\ast \mathit{Max}}$$ (A13b)

This approach gives specific values for k_under with each OEMD record reporting ODRMin, but the results for k_under were often greater than 1, a violation of the model’s assumptions and therefore implausible.

In the second approach, a sub-set of the ODRMin records were used that also have a value for AM. By adding eq. A5 to the set of simultaneous equations (eq. A12), we derive a different formula for k_under with only one semi-empiric parameter as follows:

Add eqs. A12a and A12b, and re-arrange to give:

$$ln\widehat{GM}=\frac{1}{2}\left(ln\mathit{Max}+ln\widehat{k_{\mathit{under}}}+ln\mathit{ODRMin}\right)$$ (A14)

Now, substitute eq. A14 for ln GM in eq. A5, use the semi-empiric parameter $\overline{\mathit{GSD}}$, solve for ln k_under, and take the anti-log to obtain the desired result:

$$\widehat{k_{\mathit{under}}}=\frac{A{M}^2}{\mathit{Max}\ast \mathit{ODRMin}\ast \sqrt{Q}}$$ (A15)

With this approach, the mean of k_under over the sub-set is less than one, which allows for realistic estimates of the GM for each ODRMin record from the ODR equivalent of the GME (eq. A4):

$$\widehat{GM}=\sqrt{\overline{k_{\mathit{under}}}\ast \mathit{ODRMin}\ast \mathit{Max}}$$ (A16)

The other statistics for these ODRMin records are then calculated with analogs of the m = 2 formulas in Table A-I. The resulting formulas are reported in Table 2 in the main paper.

B. Confidence-Weighted Means and Standard Deviations for the SEM

For each source in OEMD, the exposure statistics AM_i, SD_i, GM_i and GSD_i for all applicable records i are pooled with confidence weights C_i. To derive formulas for the confidence-weighted means and standard deviations from the summary statistics for individual records, we start with general formulas for the weighted arithmetic mean and unbiased weighted sample standard deviation in terms of the primary data x_k and non-random weights w_k (a.k.a “reliability weights” (Harrel et al., 2015) :

$$\begin{array}{c}{}_{w}AM=\sum _k{w}_k{x}_k/\sum _k{w}_k\\ {}_{w}S{D}^2=\frac{{\displaystyle \sum _k}{w}_k{(x_k-\mathit{wAM})}^2}{{\displaystyle \sum _k}{w}_k-\left({\displaystyle \sum _k}{w}_k^2/{\displaystyle \sum _k}{w}_k\right)}\end{array}$$

In our derivation of the confidence weighted statistics, we next group the primary data x_k (which is seldom present in OEMD) by their record i, so that their k indices are renumbered as follows:

$$\begin{array}{cccccc}\hfill i=& 1& 2& \mathrm{....}& i& \mathrm{....}\\ \hfill j=& 1,2\dots N_{\mathit{1}}& 1,2\dots N_{\mathit{2}}& \mathrm{....}& 1,2\dots N_i& \mathrm{....}\end{array}$$

Since the same confidence weight C_i for a given record i is applied to all the primary data x_ij in that record, the confidence weighted statistics are:

$$\begin{array}{l}{}_{cw}AM=\sum _i{C}_i\sum _{j=1}^{N_i}{x}_{ij}/\sum _i\sum _{j=1}^{N_i}{C}_i\\ =\sum _i{C}_i\sum _{j=1}^{N_i}{x}_{ij}/\sum _i{C}_i{N}_i\end{array}$$ (A17a)

$${}_{cw}S{D}^2=\frac{{\displaystyle \sum _i}{C}_i{\displaystyle \sum _{i=1}^{N_i}}{\left(x_{ij}-{}_{cw}AM\right)}^2}{{\displaystyle \sum _i}{C}_i{N}_i-\left({\displaystyle \sum _i}{C}_i^2{N}_i/{\displaystyle \sum _i}{C}_i{N}_i\right)}$$ (A17b)

Now the summary statistics written in terms of the primary data are:

$${AM}_i=\frac{1}{N_i}\sum _j{x}_{ij}$$ (A18a)

$${\text{SD}}_{\mathrm{i}}^2=\frac{{\displaystyle \sum _{\mathrm{j}=1}^{{\mathrm{N}}_{\mathrm{i}}}}{\left({\mathrm{x}}_{\text{ij}}-{\text{AM}}_{\mathrm{j}}\right)}^2}{{\mathrm{N}}_{\mathrm{i}}-1}=\frac{{\displaystyle \sum _{\mathrm{j}}}{\mathrm{x}}_{\text{ij}}^2-{\mathrm{N}}_{\mathrm{i}}{\text{AM}}_{\mathrm{i}}^2}{{\mathrm{N}}_{\mathrm{i}}-1}$$ (A18b)

So they can be re-arranged as:

$$\sum _{\mathrm{j}}{\mathrm{x}}_{\text{ij}}={\mathrm{N}}_{\mathrm{i}}{\text{AM}}_{\mathrm{i}}$$ (A19a)

$$\sum _{\mathrm{j}}{\mathrm{x}}_{\text{ij}}^2=\left({\mathrm{N}}_{\mathrm{i}}-1\right){\text{SD}}_{\mathrm{i}}^2+{\mathrm{N}}_{\mathrm{i}}{\text{AM}}_{\mathrm{i}}^2$$ (A19b)

Now, eq. A19a can be substituted into eq. A17a in order to obtain the desired formula for the confidence weighted AM in terms of its component exposure AMs:

$${}_{cw}AM=\sum _i{C}_i{N}_i{AM}_i/\sum _i{C}_i{N}_i$$ (A20)

To obtain the equivalent results for the confidence weighted SD, expand the numerator of eq. A17b:

$${}_{cw}S{D}^2=\frac{{\displaystyle \sum _{i,j}}{C}_i{x_{ij}}^2-2{}_{cw}AM{\displaystyle \sum _{i,j}}{C}_i{x}_{ij}+{}_{cw}A{M}^2{\displaystyle \sum _i}{C}_i{N}_i}{{\displaystyle \sum _i}{C}_i{N}_i-\left({\displaystyle \sum _i}{C}_i^2{N}_i/{\displaystyle \sum _i}{C}_i{N}_i\right)}$$

to get:

$${}_{cw}S{D}^2=\frac{{\displaystyle \sum _i}{C}_i{\displaystyle \sum _j}{x_{ij}}^2-{}_{cw}A{M}^2{\displaystyle \sum _i}{C}_i{N}_i}{{\displaystyle \sum _i}{C}_i{N}_i-\left({\displaystyle \sum _i}{C}_i^2{N}_i/{\displaystyle \sum _i}{C}_i{N}_i\right)}$$

where eq. A19 was used.

Finally substitute eq. A18b to obtain the desired formula:

$${}_{cw}S{D}^2=\frac{{\displaystyle \sum _i}{C}_i\left[\left(N_i-1\right)S{D}_i^2+N_i\left({AM}_i^2-{}_{cw}A{M}^2\right)\right]}{{\displaystyle \sum _i}{C}_i{N}_i-\left({\displaystyle \sum _i}{C}_i^2{N}_i/{\displaystyle \sum _i}{C}_i{N}_i\right)}$$ (A21)

To obtain the confidence weighted geometric means and standard deviations, start with the log-transforms of eqs. A17 and A18:

$$\begin{array}{l}ln{}_{cw}GM=\sum _{i,j}{C}_i{y}_{ij}/\sum _i{C}_i{N}_i\\ {ln}^2{}_{cw}GSD=\frac{{\displaystyle \sum _i}{C}_i{\displaystyle \sum _{i=1}^{N_i}}{\left(y_{ij}-ln{}_{cw}GM\right)}^2}{{\displaystyle \sum _i}{C}_i{N}_i-\left({\displaystyle \sum _i}{C}_i^2{N}_i/{\displaystyle \sum _i}{C}_i{N}_i\right)}\\ ln{GM}_i=\frac{1}{N_i}\sum _j{y}_{ij}\\ {ln}^2{\text{GSD}}_{\mathrm{i}}=\frac{{\displaystyle \sum _{\mathrm{j}}}{\mathrm{y}}_{\text{ij}}^2-{\mathrm{N}}_{\mathrm{i}}\text{ln}{}^2\mathrm{G}{\mathrm{M}}_{\mathrm{i}}}{{\mathrm{N}}_{\mathrm{i}}-1}\end{array}$$

where y_ij= ln x_ij.

Following the same procedures as above, the desired formulas are quickly obtained:

$$ln{}_{cw}GM=\sum _i{C}_i{N}_{i}ln{GM}_i/\sum _i{C}_i{N}_i$$ (A22)

$${ln}^2{}_{cw}GSD=\frac{{\displaystyle \sum _i}{C}_i\left[\left(N_i-1\right){ln}^2{\mathit{GSD}}_i+N_i\left({ln}^2{GM}_i-{ln}^2{}_{cw}GM\right)\right]}{{\displaystyle \sum _i}{C}_i{N}_i-\left({\displaystyle \sum _i}{C}_i^2{N}_i/{\displaystyle \sum _i}{C}_i{N}_i\right)}$$ (A23)

Q.E.D.

Note that these pooling formulas (eqs. A20 – A23) can work correctly with OEMD records with a single measurement x_i (N_i = 1) if their summary statistics are treated appropriately. From the definitions above of the arithmetic and geometric means, x_i = AM_i = GM_i when N_i = 1. By making these substitutions for N_i = 1 records, eqs. A20 and A22 correctly calculate the confidence weighted means.

The values of the standard deviations for N_i =1 records are arbitrary since their contributions to the pooling formulas (eqs. A21 and A23) are:

$$(N_i-1){{SD}_{\mathrm{i}}}^2=(N_i-1){ln}^2{\mathit{GSD}}_i=0$$

For convenience in our SEM calculations, we set SD_i = 0 and GSD_i = 1 for N_i = 1 records, so they work correctly with the confidence-weighted variance formulas.