Abstract
The nuclear envelope (NE) in lower eukaryotes such as Schizosaccharomyces pombe undergoes large morphology changes during closed mitosis. However, which physical parameters are important in governing the shape evolution of the NE, and how defects in the dividing chromosomes/microtubules are reflected in those parameters, are fundamental questions that remain unresolved. In this study, we show that improper separation of chromosomes in genetically deficient cells leads to membrane tethering or asymmetric division in contrast to the formation of two equal-sized daughter nuclei in wild-type cells. We hypothesize that the poleward force is transmitted to the nuclear membrane through its physical contact with the separated sister chromatids at the two spindle poles. A theoretical model is developed to predict the morphology evolution of the NE where key factors such as the work done by the poleward force and bending and surface energies stored in the membrane have been taken into account. Interestingly, the predicted phase diagram, summarizing the dependence of nuclear shape on the size of the load transmission regions, and the pole-to-pole distance versus surface area relationship all quantitatively agree well with our experimental observations, suggesting that this model captures the essential physics involved in closed mitosis.
Introduction
The nuclear envelope (NE) not only functions to spatially separate the cytoplasm and the nucleus but also plays an important role in accurate chromosome segregation, aging, and cancer development (1, 2). In general, the NE maintains a spherical shape during interphase but then starts to break down when mitosis begins in higher eukaryotic cells (3). In contrast, in many lower eukaryotes, such as the fission yeast Schizosaccharomyces pombe, the NE remains intact during mitosis despite undergoing remarkable morphological transformations, usually from a sphere to a spherical cylinder, and then to a dumbbell before eventually separating into two identical daughter nuclei (a process often referred to as “closed mitosis”) (3, 4). It is widely known that such shape evolution is driven by the poleward force generated by kinesins along with other microtubule-associated proteins that reside at the overlapping region of antiparallel spindle microtubules (MTs) nucleated from the two spindle pole bodies (SPBs) at both ends of a dividing nucleus (5, 6, 7, 8). Throughout interphase, there is only one SPB in the cytoplasm that starts to duplicate in G1/S phase, resulting in two SPBs embedded in the NE during mitosis (9). Besides generating forces, spindle MTs are also responsible for moving sister chromatids toward the opposite poles through capturing the kinetochore, a large proteinaceous complex on chromosomes (10).
Interestingly, defects in SPBs or spindle MTs often lead to abnormal shape transformations of the NE. For example, it has been reported that overexpression of Ned1 (11) (a protein known to influence the stability of chromosome) or Mia1 (12), deletion of Msd1 (13), or malfunction of the Msd1-Wdr8-Pkl1 complex (14) and the knockout of pkl1 (15), all induce improper anchoring of MTs to the SPBs, resulting in panhandle-shaped protrusions of NE driven by elongating microtubule bundles. Similar effect can also be achieved by the abscission of SPBs using laser microsurgery (16, 17). On the other hand, deletion of kinesins or other microtubule-associated proteins (functioning in the overlapping zone of spindle MTs) affected the proper segregation of chromosomes and eventually led to asymmetric nuclear division (7, 18). For instance, it has been shown that kinesin-8 klp5p and klp6p function as a heterodimer to promote proper kinetochore-microtubule attachment during mitosis and ensure faithful chromosome separation (19, 20). Consequently, absence of kinesin-8 klp5p or klp6p causes improper binding between kinetochores and spindle MTs, and ultimately results in chromosome mis-segregation in dividing fission yeast cells.
Several attempts have been made to explain the aforementioned nuclear morphologies based on energy minimization, an approach widely used in examining the shapes of cells or lipid vesicles (21, 22, 23, 24). For instance, a minimum energy model capable of predicting the formation of tethers in dividing nuclei has been developed where spindle MTs were treated as a cylinder with two hemispherical caps (25). Recently, by simplifying the dividing chromosomes as rigid cones that provide confinement to the NE near the two poles, Castagnetti and co-workers showed how a dumbbell shape of the NE could be energetically more favorable during mitosis (26). A common feature in these studies is that the final shape of the nucleus is essentially determined by prior assumptions. For example, the size of the tether predicted in Lim et al. (25) was the same as that of the elongating cylinder (representing the bundle of spindle MTs) assumed at the beginning. Similarly, the diameter of the dumbbell examined in Castagnetti et al. (26) was set by how large the rigid cones are, which again was introduced as a prior assumption. Furthermore, only one specific configuration (i.e., a tether or a dumbbell) was considered in those investigations. As such, the fundamental questions of how distinct shape transformations of the NE take place (i.e., from sphere to spherical cylinder/spindle-shape to dumbbell/tether or from symmetric to asymmetric shapes), as well as the key factors dictating such transitions, are still poorly understood.
Here we report a combined experimental and modeling study to address these important questions. Specifically, morphology evolutions of fission yeast nuclei in the wild-type and kinesin klp5 mutants were monitored using live-cell imaging at high temporal resolution. Interestingly, we found that deletion of klp5 induced improper separation of chromosomes and ultimately led to membrane tethering or asymmetric division, in direct contrast to the formation of two equal-sized spherical daughter nuclei in wild-type cells. On the theoretical side, by taking into account the work done by the poleward force as well as the bending and surface energies stored in the deformed membrane, a model was developed to predict the nuclear shape during mitosis. We showed that the spatial distribution of internally generated pushing forces on the NE, through the contact with the separated sister chromatids at the poles, played a key role in its morphology transformation. When forces localized on both poles, it resulted in membrane tethering while a load distributed over a broader area led to dumbbell-shaped nuclei. Our results provide physical explanations to the complex nuclear shapes observed in various experiments as well as connect their appearance to abnormalities found in dividing chromosomes/nucleoskeleton.
Materials and Methods
Experiments
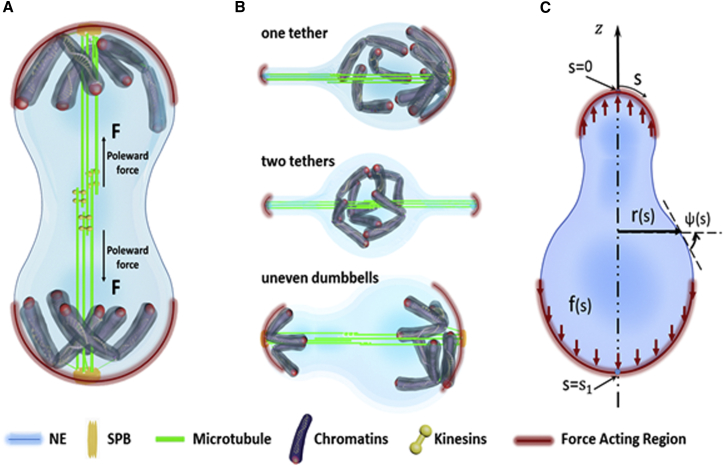
Fission yeast strains were created by random spore digestion or tetrad-dissection, and live-cell imaging was performed with a spinning-disk confocal microscope. Specifically, cut11p, hht1p, and sid4p were used to mark the NE, chromatin, and SPB, respectively (see Supporting Material Section A). As shown in Fig. 1 (top row), during closed mitosis in wild-type cells, spindle MTs push equal-sized sister chromatids toward opposite poles of the NE and then induce its shape transformation from a sphere to a spherical cylinder and ultimately to a dumbbell. On the other hand, abnormal separation of chromosomes can take place in kinesin klp5-deleted mutants (with an incidence rate of ∼50%) despite the fact that their spindle structures appear to be intact (27). In particular, no sister chromatids could be pushed to the cell poles in some cases, leading to a lemonlike (or spindlelike) nucleus and ultimately membrane tethering (Fig. 1, second and third rows). Uneven segregations of chromosomes can also occur that trigger asymmetric nuclear division (Fig. 1, bottom row), i.e., uneven dumbbells. These results suggest that normal nuclear division requires equal distribution of sister chromatids to both spindle poles. In comparison, long tethers will be formed if the NE is directly pushed by growing microtubule bundles over a small region surrounding SPBs.
Figure 1.
Shape evolution of the NE in a wild-type fission yeast cell and klp5-deleted mutants during anaphase. The top row shows time-lapse sequences of a wild-type cell expressing cut11-RFP (in red, representing the nuclear envelope) and hht1-GFP (in green, representing chromatin). Numbers refer to the time in min while red dots correspond to the SPBs (marked by sid4p). The three bottom rows display time-lapse sequences of klp5Δ cells undergoing aberrant DNA segregation during anaphase. Scale bar, 2 μm. To see this figure in color, go online.
Theoretical model
Motivated by the aforementioned experimental observations, we hypothesized that the physical contact between the separated sister chromatids and the nuclear membrane effectively distributes the poleward force F on the NE (Fig. 2). This spatially distributed load, denoted as f in Fig. 2, will then drive the shape transformation of the nucleus by overcoming the elevated bending and surface energies stored in the deformed membrane. Recent evidence has indeed shown that various inner nuclear membrane proteins such as Heh1, Heh2, and Ima1 can bind and anchor chromatids to the NE (28, 29, 30, 31). Thus, it is conceivable that such connection prevents chromosomes from sliding away from the nuclear membrane during their contact and ultimately allows the poleward force to be transmitted to the NE. The total free energy of the nuclear membrane, in this case, can be expressed as:
| (1) |
where A and V are the surface area and volume of the nucleus, while Σ and P correspond to the surface tension and internal pressure, respectively. represents the bending energy which, according to Helfrich (32, 33), takes the form
| (2) |
with being the bending rigidity of the NE, and and corresponding to the two principal curvatures of the deformed NE. Assuming that the membrane maintains an axis-symmetric shape, the location of any point on the NE can then be described by its radial separation (r) from the axis of symmetry and vertical displacement (z) from the apex point (Fig. 2 C). Both r and z are treated as functions of the arc coordinate s, which varies from 0 to when moving from the zenith to the nadir point of the nucleus (Fig. 2 C). From geometry, we have
| (3) |
where represents the angle between the tangential direction of the membrane and the horizontal axis. The two principal curvatures, in this case, can be expressed as and (34), allowing us to calculate the bending energy in an explicit manner. The term in Eq. 1 comes from the work done by the spatially distributed poleward force, a quantity that can be estimated by multiplying f with the corresponding membrane displacement. Given that most spindle microtubules tend to align parallel to the long axis of a dividing nucleus, the poleward force generated will also be along that direction (Fig. 2). As such, we proceed by assuming that the distributed load is acting vertically. Under such circumstance, takes the form
| (4) |
Finally, Eq. 1 can be reduced to
| (5) |
with
| (6) |
The variables α and β are introduced here to enforce the kinematic constraints specified in Eq. 3. At this point, we can minimize W to determine the equilibrium shape of the nucleus. Specifically, setting the variation of W to zero (i.e., ) leads to a set of so-called Euler-Lagrange equations, similar to those in (35), which can then be solved numerically (see the Supporting Material Section B). It must be pointed out that various experiments have demonstrated that while the total surface area of cell nucleus keeps increasing during mitosis, its volume remains unchanged (4). As such, the internal pressure P is also treated here as a Lagrange multiplier (a constant) to ensure that volume conservation is maintained.
Figure 2.
Schematic diagram illustrating the shape transformation of the dividing nucleus driven by the internally generated poleward force. (A) Equal separation of chromosomes in wide-type cells transmits the poleward forces to the NE over a broad region surrounding each pole and results in the formation of a dumbbell-shaped nucleus. (B) Improper separation of chromatids causes the transmission of the poleward force over a small area on the NE, ultimately leading to membrane tethering or the formation of a pear-shaped nucleus (or uneven dumbbell). (C) The axis-symmetric shape of the nucleus can be described by two geometric parameters r and ψ, both as a function of the arc coordinate s. The physical contact between the separated sister chromatids and the NE is assumed to uniformly distribute the poleward force to the membrane (in the vertical direction) within the contact region. To see this figure in color, go online.
Results and Discussion
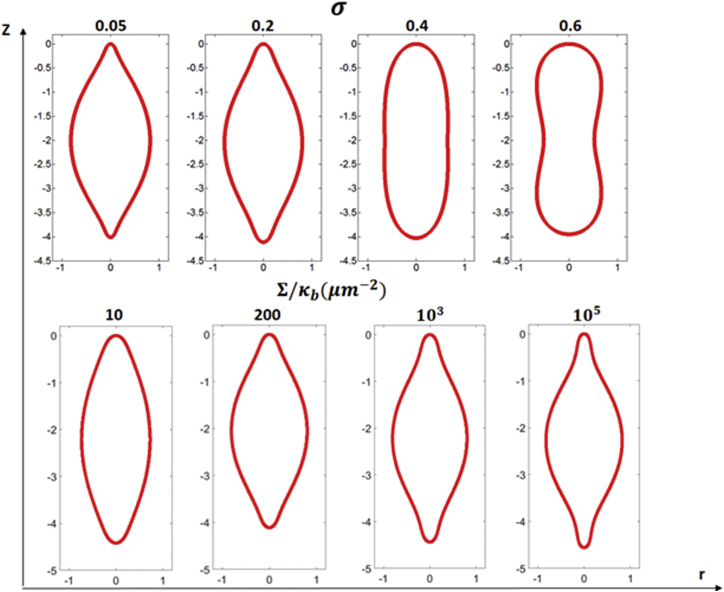
Before presenting numerical results, we first consider the ranges of different parameters in the model. The radius R of fission yeast nuclei (before mitosis starts) is found to be ∼1.5–2 μm (Fig. 1), which sets the length scale of the problem. Experiments on lipid bilayer vesicles suggested that κb is on the order of 20–200 kBT (36, 37, 38, 39, 40, 41, 42), with kBT ≈ 4.1 pN·nm being the thermal energy. The surface tension Σ of fluid membrane vesicles has also been measured to be in the range of 0.01–1 mN/m (43, 44, 45), with a tension >2 mN/m often resulting in membrane rupture. On the other hand, another study showed that the tension in mammalian cell membranes could reach the order of 10 mN/m or higher (46). As such, the value of is estimated to be ∼. Next, to reveal the essential features of the problem in the simplest manner, we proceed by assuming that the poleward force is uniformly distributed over a small region surrounding each pole (that is f is constant within and , but in opposite directions to ensure the total force equals to zero). The size of the load transmission region is given by the parameter σ here. The morphological transformation of the NE during mitosis is then captured by finding the shapes that minimize W, defined in Eq. 5, as the poleward force F increases gradually.
Note that, at any given level of F, the nuclear morphology is fully determined by the values of and σ. For example, choosing as the influence of these two parameters on the minimum energy shape is shown in Fig. 3. Clearly, as σ increases, the nuclear shape changes from spindle to spherical cylinder and then to dumbbell. On the other hand, not surprisingly, reducing the bending rigidity (or, equivalently, increasing the surface tension) of the membrane leads to profiles with larger curvature variations, so that the geometry changes from being entirely convex to having both convex and concave portions.
Figure 3.
Predicted axis-symmetric NE shapes under the fixed poleward force of . The top panel shows the predicted nuclear shapes as σ varies from 0.05 to 0.6 for a given value of . The bottom panel shows the transition of the minimum energy shape when the value of increases from 10 to 105μm−2 while σ is fixed at 0.1. To see this figure in color, go online.
By quantitatively comparing model predictions with experiments, the values of and σ corresponding to the yeast cells used in our study can also be estimated. Specifically, choosing and , the predicted pole-to-pole distance Z ( (see Fig. 2) versus surface area A relationship of the dividing nucleus matches with the data from wild-type S. pombe very well (Fig. 4). In addition, the predicted nuclear shapes are almost identical to those observed in our experiment (see the insets in Fig. 4). It must be pointed out that the value of adopted is within the range reported in the literature as mentioned earlier. Also, the radius of daughter chromatids (labeled in green in Fig. 4) is observed to be ∼0.5R in experiment, in good agreement with the value of σ (0.8R) chosen here. Hence, although we were unable to visualize the load transmission region directly in this study, the basic assumption that the poleward force is distributed to the NE through its physical contact with the separated chromatids should be reasonable.
Figure 4.
The pole-to-pole distance versus the surface area relationship of the dividing nucleus. Square symbols represent data from confocal micrographs of 30 wild-type fission yeasts nuclei where the error bar shows the standard error of the mean. Theoretical prediction is given by the solid curve with and σ = 0.8. Comparison between the predicted and observed nuclear shapes at different dividing stages is included in the insets where, similar to that in Fig. 1, cut11p, hht1p, and sid4p were used as markers for NE (red), chromatin (green), and SPB (red dots), respectively. The prediction corresponding to is also shown by the dashed line. Scale bar, 1 μm. To see this figure in color, go online.
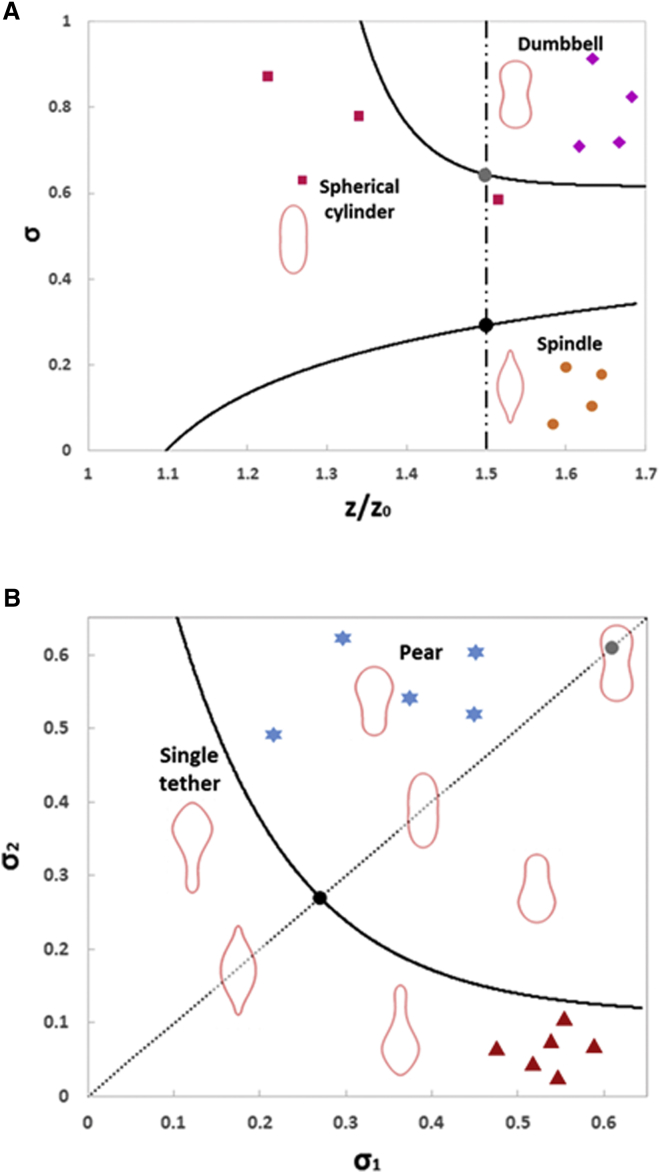
As shown in Fig. 1, improper separation of chromatids results in the transmission of the poleward force over a smaller area on the NE and eventually leads to a spindle-shaped or tethered nucleus. A phase diagram summarizing our results is given in Fig. 5 A. Depending on the values of σ, the NE can undergo sphere → spherical cylinder → dumbbell or sphere → spindle → tether transitions as the dividing process progresses (i.e., as the pole-to-pole distance increases). Measurement data from 12 wide-type and klp5-deleted yeast cells undergoing symmetric division are shown in Fig. 5 A. The phase diagram captures the main trend observed in our experiment. The nucleus in genetically deficient cells can also divide in an asymmetric manner, leading to the formation of a single tether or pear-shaped NE (see Fig. 1 and (7, 18)). This interesting phenomenon can be simulated in this model by assuming that the poleward force is transmitted to the nuclear membrane through two contact regions with different sizes (i.e., over and near two poles). Specifically, at the given pole-to-pole distance of , the predicted nuclear shapes under different combinations of and shown in Fig. 5 B compare favorably with our experimental results. Because the values of and reflect the sizes of dividing chromatids, Fig. 5 B effectively provides a way for us to quantitatively assess the degree of asymmetric separation of chromosomes inside the nucleus from its mitotic shape. In addition, phase diagrams corresponding to different values will also allow us to estimate how these two quantities (i.e., the surface tension and bending rigidity of the nuclear membrane) vary in different mutants.
Figure 5.
(A) Phase diagram summarizing how the size of the load-transmitting region, along with the pole-to-pole distance, affects the axis-symmetric shape of the NE. (B) The phase diagram illustrating how the morphology of nucleus undergoing asymmetric division is governed by the sizes of two load-distributing regions, where the pole-to-pole distance is fixed at . Note that the dotted line here corresponds to symmetric division (that is ) and hence carries the same information as the dashed line in (A). Different nuclear shapes observed in our experiment are also indicated in the phase diagram by markers, with square, diamond, circular, triangle, and star symbols corresponding to spherical cylinder, dumbbell, spindle, single tether, and pear, respectively. To see this figure in color, go online.
It should be pointed out that, up to this point, f was assumed to be uniformly distributed within the contact region between the NE and the separated sister chromatids. We have also conducted calculations by adopting a Gaussian or parabolic distribution of f. Interestingly, as long as the approximate size of the load-transmitting region is fixed, the exact form of f does not affect the final results in any significant manner (see Fig. S3), indicating that the conclusions obtained here are quite robust.
Conclusions
In this article, we report a combined experimental and modeling investigation on the nuclear shape evolution of fission yeast S. pombe during closed mitosis. It was found that improper separation of chromosomes in klp5-deleted mutants led to membrane tethering or asymmetric division of the nucleus, in direct contrast to the formation of two equal-sized spherical daughter nuclei in wild-type cells.
On the theoretical side, by assuming that the poleward force is distributed to the nuclear membrane through its physical contact with the separated chromatids, a minimum energy model was developed to predict the morphology transformation of the NE. We showed that, depending on the size of load-transmitting regions near the two spindle poles, the nucleus could undergo symmetric or asymmetric division where the occurrence of shapes such as spherical cylinder, dumbbell, pear, and tether have all been predicted, in excellent agreement with our experimental observations. We further demonstrated that, as long as the size of such region is fixed, details regarding how the poleward force is distributed to the nuclear membrane have little influence on the shape transformation of the dividing nucleus. In addition to providing a physical understanding of the diverse nuclear shapes observed in, for example, wild-type, klp5-, Msd1-, and pk11-deleted fission yeast cells (13, 15), this model can also quantitatively explain the markedly reduced elongation rate of the dividing nucleus in klp9Δ cells (Supporting Material Section C), where a weaker poleward force is believed to be generated (7, 47).
We must reemphasize that, unlike many previous studies where size of the tether (17, 35, 48) or dumbbells (26) was essentially assumed from the beginning, here the appearance of different shapes is a natural consequence of how chromatids are separated, which then serve to transmit the poleward force to the nuclear membrane in our model. As such, a link between the morphology evolution of the NE and structural abnormalities taking place inside the dividing nucleus has been established, which may provide an alternative way for us to interrogate the roles of key players such as spindle MTs, SPBs, or kinetochores during closed mitosis. In addition, it is also conceivable that this approach can be extended to study phenomena such as actin polymerization-induced deformation of cells (49) or vesicles (50, 51), which are governed by the interplay between forces and membrane elasticity.
Finally, several simplifications made in our model warrant future investigations. For example, the surface tension of NE was assumed a constant in this study. In reality, it is possible that this quantity will change as the dividing process progresses (i.e., as the surface area of the nucleus increases). Furthermore, as shown in Fig. 1 (bottom row), a long membrane tether connecting two daughter nuclei can form in late anaphase. Actually, it is possible to predict the appearance of such a shape in our model if the radius of the tether is assumed (see Figs. S4 and S5). However, given that the main objective of this study is to explain the shape transformation of the NE without introducing prior assumptions, this scenario is not further pursued here. Another reason is that the nuclear volume could start to deviate from its original value slightly when the pole-to-pole distance becomes relatively large (4). As such, proper modifications in the formulation may be needed to describe such phenomena in an accurate manner.
Author Contributions
Y.L. and C.F. designed research; Q.Z. and F.Z. performed research; A.P.L. and J.Q. contributed analytic tools; Q.Z., F.Z., C.F., and Y.L. analyzed data; and Q.Z., A.P.L., J.Q., C.F., and Y.L. wrote the article.
Acknowledgments
This work was supported by grants from the Research Grants Council (Project Nos. HKU 7143/12E, HKU 7147/13E, and HKU 17205114) of the Hong Kong Special Administration Region and National Natural Science Foundation of China (Project No. 11572273), as well as seed funds (Project Nos. 201311159128 and 201411159167) from The University of Hong Kong. C.F. is supported by grants from the National Natural Science Foundation of China (Nos. 31271439 and 31301109) and an award from the Thousand Young Talents Program of China. A.P.L. acknowledges support from National Science Foundation grant No. CMMI-1561794.
Editor: Sean Sun.
Footnotes
Supporting Materials and Methods, six figures, and one table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30931-6.
Contributor Information
Chuanhai Fu, Email: chuanhai@ustc.edu.cn.
Yuan Lin, Email: ylin@hku.hk.
Supporting Citations
Reference (52) appears in the Supporting Material.
Supporting Material
References
- 1.Méndez-López I., Worman H.J. Inner nuclear membrane proteins: impact on human disease. Chromosoma. 2012;121:153–167. doi: 10.1007/s00412-012-0360-2. [DOI] [PubMed] [Google Scholar]
- 2.Scaffidi P., Misteli T. Lamin A-dependent nuclear defects in human aging. Science. 2006;312:1059–1063. doi: 10.1126/science.1127168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Arnone J.T., Walters A.D., Cohen-Fix O. The dynamic nature of the nuclear envelope: lessons from closed mitosis. Nucleus. 2013;4:261–266. doi: 10.4161/nucl.25341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yam C., He Y., Oliferenko S. Divergent strategies for controlling the nuclear membrane satisfy geometric constraints during nuclear division. Curr. Biol. 2011;21:1314–1319. doi: 10.1016/j.cub.2011.06.052. [DOI] [PubMed] [Google Scholar]
- 5.Jaspersen S.L., Winey M. The budding yeast spindle pole body: structure, duplication, and function. Annu. Rev. Cell Dev. Biol. 2004;20:1–28. doi: 10.1146/annurev.cellbio.20.022003.114106. [DOI] [PubMed] [Google Scholar]
- 6.Brust-Mascher I., Scholey J.M. Mitotic motors and chromosome segregation: the mechanism of anaphase B. Biochem. Soc. Trans. 2011;39:1149–1153. doi: 10.1042/BST0391149. [DOI] [PubMed] [Google Scholar]
- 7.Fu C., Ward J.J., Tran P.T. Phospho-regulated interaction between kinesin-6 Klp9p and microtubule bundler Ase1p promotes spindle elongation. Dev. Cell. 2009;17:257–267. doi: 10.1016/j.devcel.2009.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Goshima G., Scholey J.M. Control of mitotic spindle length. Annu. Rev. Cell Dev. Biol. 2010;26:21–57. doi: 10.1146/annurev-cellbio-100109-104006. [DOI] [PubMed] [Google Scholar]
- 9.Ding R., West R.R., McIntosh J.R. The spindle pole body of Schizosaccharomyces pombe enters and leaves the nuclear envelope as the cell cycle proceeds. Mol. Biol. Cell. 1997;8:1461–1479. doi: 10.1091/mbc.8.8.1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kline-Smith S.L., Sandall S., Desai A. Kinetochore-spindle microtubule interactions during mitosis. Curr. Opin. Cell Biol. 2005;17:35–46. doi: 10.1016/j.ceb.2004.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tange Y., Hirata A., Niwa O. An evolutionarily conserved fission yeast protein, Ned1, implicated in normal nuclear morphology and chromosome stability, interacts with Dis3, Pim1/RCC1 and an essential nucleoporin. J. Cell Sci. 2002;115:4375–4385. doi: 10.1242/jcs.00135. [DOI] [PubMed] [Google Scholar]
- 12.Zheng L., Schwartz C., Oliferenko S. The spindle pole bodies facilitate nuclear envelope division during closed mitosis in fission yeast. PLoS Biol. 2007;5:e170. doi: 10.1371/journal.pbio.0050170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Toya M., Sato M., Toda T. γ-tubulin complex-mediated anchoring of spindle microtubules to spindle-pole bodies requires Msd1 in fission yeast. Nat. Cell Biol. 2007;9:646–653. doi: 10.1038/ncb1593. [DOI] [PubMed] [Google Scholar]
- 14.Yukawa M., Ikebe C., Toda T. The Msd1-Wdr8-Pkl1 complex anchors microtubule minus ends to fission yeast spindle pole bodies. J. Cell Biol. 2015;209:549–562. doi: 10.1083/jcb.201412111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Syrovatkina V., Tran P.T. Loss of kinesin-14 results in aneuploidy via kinesin-5-dependent microtubule protrusions leading to chromosome cut. Nat. Commun. 2015;6:7322. doi: 10.1038/ncomms8322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Khodjakov A., La Terra S., Chang F. Laser microsurgery in fission yeast; role of the mitotic spindle midzone in anaphase B. Curr. Biol. 2004;14:1330–1340. doi: 10.1016/j.cub.2004.07.028. [DOI] [PubMed] [Google Scholar]
- 17.Lim G.H.W., Huber G., Sazer S. Vesicle-like biomechanics governs important aspects of nuclear geometry in fission yeast. PLoS One. 2007;2:e948. doi: 10.1371/journal.pone.0000948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Syrovatkina V., Fu C., Tran P.T. Antagonistic spindle motors and MAPs regulate metaphase spindle length and chromosome segregation. Curr. Biol. 2013;23:2423–2429. doi: 10.1016/j.cub.2013.10.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Garcia M.A., Koonrugsa N., Toda T. Spindle-kinetochore attachment requires the combined action of Kin I-like Klp5/6 and Alp14/Dis1-MAPs in fission yeast. EMBO J. 2002;21:6015–6024. doi: 10.1093/emboj/cdf611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tang N.H., Toda T. Alp7/TACC recruits kinesin-8-PP1 to the Ndc80 kinetochore protein for timely mitotic progression and chromosome movement. J. Cell Sci. 2015;128:354–363. doi: 10.1242/jcs.160036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nelson P., Powers T., Seifert U. Dynamical theory of the pearling instability in cylindrical vesicles. Phys. Rev. Lett. 1995;74:3384–3387. doi: 10.1103/PhysRevLett.74.3384. [DOI] [PubMed] [Google Scholar]
- 22.Seifert U., Berndl K., Lipowsky R. Shape transformations of vesicles: Phase diagram for spontaneous-curvature and bilayer-coupling models. Phys. Rev. A. 1991;44:1182–1202. doi: 10.1103/physreva.44.1182. [DOI] [PubMed] [Google Scholar]
- 23.Jiang H., Powers T.R. Curvature-driven lipid sorting in a membrane tubule. Phys. Rev. Lett. 2008;101:018103. doi: 10.1103/PhysRevLett.101.018103. [DOI] [PubMed] [Google Scholar]
- 24.Jiang H., Sun S.X. Morphology, growth, and size limit of bacterial cells. Phys. Rev. Lett. 2010;105:028101. doi: 10.1103/PhysRevLett.105.028101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lim H.G., Huber G., Sazer S. Vesicle-like biomechanics governs important aspects of nuclear geometry in fission yeast. PLoS One. 2007;2:e948. doi: 10.1371/journal.pone.0000948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Castagnetti S., Božič B., Svetina S. Mechanical and molecular basis for the symmetrical division of the fission yeast nuclear envelope. Phys. Chem. Chem. Phys. 2015;17:15629–15636. doi: 10.1039/c5cp01243k. [DOI] [PubMed] [Google Scholar]
- 27.West R.R., Malmstrom T., McIntosh J.R. Kinesins klp5+ and klp6+ are required for normal chromosome movement in mitosis. J. Cell Sci. 2002;115:931–940. doi: 10.1242/jcs.115.5.931. [DOI] [PubMed] [Google Scholar]
- 28.King M.C., Drivas T.G., Blobel G. A network of nuclear envelope membrane proteins linking centromeres to microtubules. Cell. 2008;134:427–438. doi: 10.1016/j.cell.2008.06.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gonzalez Y., Saito A., Sazer S. Fission yeast Lem2 and Man1 perform fundamental functions of the animal cell nuclear lamina. Nucleus. 2012;3:60–76. doi: 10.4161/nucl.18824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yewdell W.T., Colombi P., Lusk C.P. Lumenal interactions in nuclear pore complex assembly and stability. Mol. Biol. Cell. 2011;22:1375–1388. doi: 10.1091/mbc.E10-06-0554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.King M.C., Lusk C.P., Blobel G. Karyopherin-mediated import of integral inner nuclear membrane proteins. Nature. 2006;442:1003–1007. doi: 10.1038/nature05075. [DOI] [PubMed] [Google Scholar]
- 32.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 33.Zhong-can O.-Y., Helfrich W. Bending energy of vesicle membranes: general expressions for the first, second, and third variation of the shape energy and applications to spheres and cylinders. Phys. Rev. A Gen. Phys. 1989;39:5280–5288. doi: 10.1103/physreva.39.5280. [DOI] [PubMed] [Google Scholar]
- 34.Lin Y., Freund L. Forced detachment of a vesicle in adhesive contact with a substrate. Int. J. Solids Struct. 2007;44:1927–1938. [Google Scholar]
- 35.Božič B., Svetina S., Zeks B. Theoretical analysis of the formation of membrane microtubes on axially strained vesicles. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1997;55:5834. [Google Scholar]
- 36.Henriksen J., Rowat A.C., Ipsen J.H. Vesicle fluctuation analysis of the effects of sterols on membrane bending rigidity. Eur. Biophys. J. 2004;33:732–741. doi: 10.1007/s00249-004-0420-5. [DOI] [PubMed] [Google Scholar]
- 37.Bermúdez H., Hammer D.A., Discher D.E. Effect of bilayer thickness on membrane bending rigidity. Langmuir. 2004;20:540–543. doi: 10.1021/la035497f. [DOI] [PubMed] [Google Scholar]
- 38.Phillips R., Ursell T., Sens P. Emerging roles for lipids in shaping membrane-protein function. Nature. 2009;459:379–385. doi: 10.1038/nature08147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rawicz W., Olbrich K.C., Evans E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 2000;79:328–339. doi: 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Vaziri A., Lee H., Mofrad M. Deformation of the cell nucleus under indentation: mechanics and mechanisms. J. Mater. Res. 2006;21:2126–2135. [Google Scholar]
- 41.Dahl K.N., Kahn S.M., Discher D.E. The nuclear envelope lamina network has elasticity and a compressibility limit suggestive of a molecular shock absorber. J. Cell Sci. 2004;117:4779–4786. doi: 10.1242/jcs.01357. [DOI] [PubMed] [Google Scholar]
- 42.Boal D., Boal D.H. Cambridge University Press; Cambridge, UK: 2012. Mechanics of the Cell. [Google Scholar]
- 43.Evans E., Heinrich V., Rawicz W. Dynamic tension spectroscopy and strength of biomembranes. Biophys. J. 2003;85:2342–2350. doi: 10.1016/s0006-3495(03)74658-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Evans E., Metcalfe M. Free energy potential for aggregation of giant, neutral lipid bilayer vesicles by van der Waals attraction. Biophys. J. 1984;46:423–426. doi: 10.1016/S0006-3495(84)84039-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Simson R., Wallraff E., Sackmann E. Membrane bending modulus and adhesion energy of wild-type and mutant cells of Dictyostelium lacking talin or cortexillins. Biophys. J. 1998;74:514–522. doi: 10.1016/S0006-3495(98)77808-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Janmey P.A., Kinnunen P.K. Biophysical properties of lipids and dynamic membranes. Trends Cell Biol. 2006;16:538–546. doi: 10.1016/j.tcb.2006.08.009. [DOI] [PubMed] [Google Scholar]
- 47.Choi S.H., McCollum D. A role for metaphase spindle elongation forces in correction of merotelic kinetochore attachments. Curr. Biol. 2012;22:225–230. doi: 10.1016/j.cub.2011.12.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Powers T.R., Huber G., Goldstein R.E. Fluid-membrane tethers: minimal surfaces and elastic boundary layers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;65:041901. doi: 10.1103/PhysRevE.65.041901. [DOI] [PubMed] [Google Scholar]
- 49.Rudel T., Bokoch G.M. Membrane and morphological changes in apoptotic cells regulated by caspase-mediated activation of PAK2. Science. 1997;276:1571–1574. doi: 10.1126/science.276.5318.1571. [DOI] [PubMed] [Google Scholar]
- 50.Liu A.P., Richmond D.L., Fletcher D.A. Membrane-induced bundling of actin filaments. Nat. Phys. 2008;4:789–793. doi: 10.1038/nphys1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Liu A.P., Fletcher D.A. Actin polymerization serves as a membrane domain switch in model lipid bilayers. Biophys. J. 2006;91:4064–4070. doi: 10.1529/biophysj.106.090852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Derényi I., Jülicher F., Prost J. Formation and interaction of membrane tubes. Phys. Rev. Lett. 2002;88:238101. doi: 10.1103/PhysRevLett.88.238101. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.